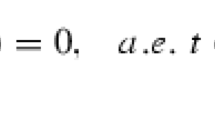Abstract
This paper is concerned with the following nonlinear fractional boundary value problem:
where \(2<\alpha\leq3\), \(0<\beta\leq1\) are real numbers and \(\int _{0}^{1}D_{0+}^{\beta}u(t)\, dA(t)\) denotes a Riemann-Stieltjes integral. By means of monotone iterative technique and some inequalities associated with the Green function, not only the existence of nontrivial solutions or positive solutions is obtained but also iterative schemes for approximating the solutions are established, which start off with simple functions, which are feasible for computational purposes. An example is also included to illustrate the main results.
Similar content being viewed by others
1 Introduction
Differential equations with fractional order are a generalization of ordinary differential equations to non-integer order. This generalization is not merely one of the mathematical curiosities but rather has interesting applications in various fields of sciences and engineering such as control, porous media, electromagnetic, and other branches of science. The need for fractional order differential equations stems in part from the fact that many phenomena cannot be modeled by differential equations with integer derivatives. For details, see [1–4].
In recent years, there has grown a vast literature devoted to the applications of fixed point theorems focused on solutions or positive solutions of boundary value problems (BVPs for short) for fractional differential equations, for example, we mention only [5–16]. Note that Wang et al. [16] studied a fractional BVP with changing sign nonlinearity,
where \(2<\alpha\leq3\). By means of the Guo-Krasnoselskii fixed point theorem, the existence of positive solutions was established. In [6], Xu and Fei investigated multiple positive solutions of the singular BVP
subject to the three-point boundary conditions
where \(1<\alpha\leq2\), \(0<\beta\leq1\). Their tool was Schauder’s fixed point theorem.
Recently, iterative methods have been successfully employed to prove the existence of solutions or positive solutions of nonlinear BVPs. However, only few papers considered the computational methods of solutions for fractional differential equations; see [8, 9, 17–19]. In particular, it should be pointed out that Jiang and Zhong [8] obtained the existence of nontrivial sign-changing solutions to fractional differential equations with integral boundary conditions, the main tool used was monotone iterative method. Sun and Zhao [9] studied the fractional differential equation with integral boundary conditions
The existence result of monotone positive solutions was obtained.
Motivated greatly by the above mentioned excellent works, in this paper we investigate the existence and iteration of nontrivial solutions and positive solutions for the following BVP:
where \(2<\alpha\leq3\), \(0<\beta\leq1\) are real numbers and A is of bounded variation, the nonlinear term \(f(t,u)\) may change sign on some set and \(\int_{0}^{1}D_{0+}^{\beta}u(t)\,dA(t)\) denotes a Riemann-Stieltjes integral with a signed measure. This includes both the multi-point and a Riemann integral in a single framework. For more comments on the Stieltjes integral and its importance, we refer the reader to the papers by Webb and Infante [20–22] and their other related works. To the best of our knowledge, the results are new and BVP (1.3) is studied in this form for the first time. The proofs of our main results are based on the monotone iterative technique, which we present now.
Theorem 1.1
[23]
Let K be a normal cone of a Banach space E and \(u_{0}\preceq v_{0}\). Suppose that
-
(1)
\(T:[u_{0},v_{0}]\rightarrow E\) is completely continuous;
-
(2)
T is monotone increasing on \([u_{0},v_{0}]\);
-
(3)
\(u_{0}\) is a lower solution of T, that is, \(u_{0}\preceq Tu_{0}\);
-
(4)
\(v_{0}\) is an upper solution of T, that is, \(Tv_{0}\preceq v_{0}\).
Then the iterative sequences \(u_{n}=Tu_{n-1}\), \(v_{n}=Tv_{n-1}\), \(n=1,2,3,\ldots \) , satisfy \(u_{0}\preceq u_{1}\preceq\cdots\preceq u_{n}\preceq\cdots\preceq v_{n}\preceq \cdots\preceq v_{1}\preceq v_{0}\), and converge to, respectively, \(u, v\in[u_{0},v_{0}]\), which are fixed points of T.
2 Preliminary lemmas
For convenience of the reader, we present here some necessary definitions.
Definition 2.1
[24]
Let X be the Banach space with norm \(\|\cdot\|\). A nonempty closed set \(K\subset X\) is called a cone if K satisfies the following conditions: (i) if \(x,y\in K\), then \(x+y\in K\); (ii) if \(x\in K\), then \(\mu x\in K\), for any \(\mu\geq0\); (iii) if \(0\neq x\in K\), then \(-x\notin K\). Let \(x_{1}, x_{2} \in X\). We write \(x_{1}\preceq x_{2}\), if \(x_{2}-x_{1}\in K\). The cone K is called normal, if there exists \(\rho>0\) such that
We call the set \([x_{1},x_{2}]=\{x \in X, x_{1}\preceq x\preceq x_{2}\}\) an order interval in X. The operator \(T:[x_{1},x_{2}]\rightarrow X\) is called increasing if \(T\bar{x}\preceq T\tilde{x}\) for any \(\bar{x}, \tilde{x}\in[x_{1},x_{2}]\) with \(\bar{x}\preceq \tilde{x} \).
Definition 2.2
[3]
The Riemann-Liouville fractional integral of order \(\alpha>0\) of a function \(y:(0,\infty)\rightarrow R\) is given by
provided the right side is pointwise defined on \([0,\infty)\).
Definition 2.3
[3]
The Riemann-Liouville fractional derivative of order \(\alpha>0\) of a function \(y:(0,\infty)\rightarrow R\) is given by
where \(n=[\alpha]+1\), \([\alpha]\) denotes the integer part of number α, provided the right side is pointwise defined on \([0,\infty)\).
From the definitions of Riemann-Liouville’s derivative, we can obtain the statements.
Lemma 2.4
[3]
Let \(\alpha>0\), if we assume \(u\in C(0,1)\cap L^{1}(0,1)\), then the fractional differential equation
has \(u(t)=C_{1}t^{\alpha-1}+C_{2}t^{\alpha-2}+\cdots+C_{N}t^{\alpha-N}\), from some \(C_{i}\in R\), \(i=1,2,\ldots,N\), as a unique solution, where N is the smallest integer greater than or equal to α.
Lemma 2.5
[3]
Let \(\alpha>0\), if we assume \(u\in C(0,1)\cap L^{1}(0,1)\), then the fractional differential equation
from some \(C_{i}\in R\), \(i=1,2,\ldots,N\), where N is the smallest integer greater than or equal to α.
Lemma 2.6
Assume that \(y\in C(0,1)\cap L^{1}(0,1)\), α, β are two positive constants with \(\alpha-\beta\geq0\). Then
Proof
Let \(h(t)=\int_{0}^{t}(t-s)^{\alpha-1}y(s)\,ds\). Then by Definition 2.3,
On the other hand, let \(\frac{\tau-s}{t-s}=u\), then
Therefore, we have
□
In the remainder of the paper, we always assume that \(2<\alpha\leq3\) and \(0\leq\beta\leq1\), so we also easily get \(0<\alpha-\beta-1\leq2\).
Lemma 2.7
Let \(y\in C(0,1)\cap L^{1}[0,1]\) and \(\delta:=\int_{0}^{1}t^{\alpha-\beta -1}\,dA(t)<1\), the unique solution of
is \(u(t)=\int_{0}^{1}G(t,s)y(s)\,ds\), in which
where
and
Proof
As deduced from Lemma 2.5, we have
Consequently, the solution of (2.1) is
By \(u(0)=u'(0)=0\), there is \(C_{2}=C_{3}=0\). Moreover, \(D_{0+}^{\beta}u(1)=\int_{0}^{1}D_{0+}^{\beta}u(t)\,dA(t)\) and Lemma 2.6 yield
Therefore, the solution of (2.1) is
□
Lemma 2.8
For any \(t,s\in[0,1]\), \(H(t,s)\) has the following property:
Proof
Case 1: \(0<\alpha-\beta-1\leq1\). If \(s\leq t\), then
and
If \(s\geq t\), then
and
Case 2: \(1<\alpha-\beta-1\leq2\). We have
The proof is similar to Lemma 2.3 in [16], so it is omitted. □
Lemma 2.9
The function \(K(t,s)\) satisfies:
-
(i)
\(\Gamma(\alpha)K(t,s)\leq t^{\alpha-1}(1-s)^{\alpha-\beta-1}\), \(t,s\in[0,1]\);
-
(ii)
\(\Gamma(\alpha)K(t,s)\geq t^{\alpha-1}\beta s(1-s)^{\alpha-\beta -1}\), \(t,s\in[0,1]\).
Proof
Since (i) holds obviously, we only show that (ii) is true. Here we need the fact \(1-(1-s)^{\beta}\geq\beta s\), \(0<\beta\leq1\), \(s\in[0,1]\). In fact,
which implies \(1-(1-s)^{\beta}-\beta s\) is nondecreasing in \([0,s]\), so \(1-(1-s)^{\beta}\geq\beta s\).
If \(s\leq t\), then
If \(t\leq s\), then
□
Lemma 2.10
Let
and
Then the function \(G(t,s)\) has the following property:
Proof
For any \(t,s\in[0,1]\), it follows from Lemmas 2.8 and 2.9 that
On the other hand, for any \(t,s\in[0,1]\), we have
□
Lemma 2.11
The function \(G(t,s)\) is continuous and satisfies
for \(0\leq t_{1}\leq t_{2}\leq1\).
Proof
For \(0\leq t_{1}\leq t_{2}\leq1\), we have
Note that, applying the mean value theorem, we arrive at \(t_{2}^{\alpha -1}-t_{1}^{\alpha-1}<(\alpha-1)(t_{2}-t_{1})\) and \((t_{2}-s)^{\alpha -1}-(t_{1}-s)^{\alpha-1}<(\alpha-1)(t_{2}-t_{1})\), which implies that
for \(0\leq t_{1}\leq t_{2}\leq1\). □
3 Main results
Let \(E=C [ 0,1 ]\) be equipped with the norm \(\Vert u\Vert =\Vert u\Vert _{\infty}\), where \(\Vert u \Vert _{\infty}\) is the usual supremum norm in \(C[0,1]\).
Define the cone K by
Then it is easy to verify that K is a cone in E. For \(u, v\in C[0,1]\), \(u\preceq v\) if and only if \(u(t)\leq v(t)\), \(t\in[0,1]\). Moreover, the cone K is normal on account of \(\Vert u+v\Vert \geq \Vert u\Vert =1\) for any \(u, v\in K\) and \(\Vert u\Vert =\Vert v\Vert =1\).
Define the operator \(T:K\rightarrow K\) as follows:
It is clear that the existence of a solution for BVP (1.3) is equivalent to the existence of a fixed points of T in K.
Theorem 3.1
Assume that there exist two real numbers a, b such that \(a< b\) and the following conditions are satisfied:
- (H1):
-
There exists a nonnegative function \(h\in C(0,1)\cap L^{1}[0,1]\) such that one of the following conditions is satisfied:
-
(i)
\(a\geq0\), \(f:(0,1)\times[0,b]\rightarrow R\) is continuous, \(|f(t,u)|\leq h(t)\), \((t,u)\in(0,1)\times[0,b]\) and increasing with respect to u in \([0,b]\);
-
(ii)
\(b\leq0\), \(f:(0,1)\times[a,0]\rightarrow R\) is continuous, \(|f(t,u)|\leq h(t)\), \((t,u)\in(0,1)\times[a,0]\) and increasing with respect to u in \([a,0]\);
-
(iii)
\(a< 0<b\), \(f:(0,1)\times[a,b]\rightarrow R\) is continuous, \(|f(t,u)|\leq h(t)\), \((t,u)\in(0,1)\times[a,b]\) and increasing with respect to u in \([a,b]\).
-
(i)
- (H2):
-
The following inequalities hold:
$$\begin{aligned}& \int_{0}^{1}\Phi_{1}(s)\max\bigl\{ f \bigl(s,as^{\alpha-1}\bigr),0\bigr\} \, ds+ \int_{0}^{1}\Phi _{2}(s)\min\bigl\{ f \bigl(s,as^{\alpha-1}\bigr),0\bigr\} \, ds\geq a, \\& \int_{0}^{1}\Phi_{2}(s)\max\bigl\{ f \bigl(s,bs^{\alpha-1}\bigr),0\bigr\} \, ds+ \int_{0}^{1}\Phi _{1}(s)\min\bigl\{ f \bigl(s,bs^{\alpha-1}\bigr),0\bigr\} \, ds\leq b. \end{aligned}$$ - (H3):
-
\(f(t,0)\not\equiv0\), for \(0\leq t\leq1\).
Then the problem (1.3) has two nontrivial solutions \(u^{*}, v^{*}\in C^{2}[0,1]\cap C^{3}(0,1)\) (\(u^{*}\), \(v^{*}\) may be coincident) such that \(at^{\alpha-1}\leq u^{*}\leq v^{*}\leq bt^{\alpha-1}\), \(t\in[0,1]\), and \(\lim_{n\rightarrow\infty}u_{n}=u^{*}\), \(\lim_{n\rightarrow\infty}v_{n}=v^{*}\), where the two iterative sequences are generated by
Proof
Consider the order interval \([u_{0},v_{0}]\) in \(C[0,1]\), then \(T:[u_{0},v_{0}]\rightarrow C[0,1]\) is completely continuous. In fact, let \(u\in[u_{0},v_{0}]\), then \(at^{\alpha-1}\leq u\leq bt^{\alpha -1}\), \(0\leq t\leq1\). By the assumption (H1), we have
which shows that \(T([u_{0},v_{0}])\) is uniform bounded in \(C[0,1]\).
On the other hand, for any \(u\in[u_{0},v_{0}]\) and \(0\leq t_{1}\leq t_{2}\leq 1\), by Lemma 2.11,
This shows that the set \(T ([u_{0},v_{0}] )\) is equicontinuous in \(C[0,1]\). Furthermore, for \(u\in[u_{0},v_{0}]\), the operator T is continuous obviously. By the Arzelá-Ascoli theorem, the operator \(T:[u_{0},v_{0}]\rightarrow C[0,1]\) is completely continuous.
Now, we divide our proof into the following steps.
Step 1. We assert that T is monotone increasing on \([u_{0},v_{0}]\). By the assumption (H1), it is easy to know T is an increasing operator.
Step 2. We prove that \(u_{0}\) is a lower solution of T.
In view of the assumption (H2), (H3), and Lemma 2.10, we have
It shows
Step 3. We prove that \(v_{0}\) is an upper solution of T. We have
It yields
Step 4. We claim that the BVP (1.3) has monotone nontrivial solutions.
In fact, if we construct sequences \(\{ u_{n} \} _{n=1}^{\infty}\) and \(\{ v_{n} \} _{n=1}^{\infty}\) as follows:
then it follows from Theorem 1.1 that
and \(\{ u_{n} \} _{n=1}^{\infty}\) and \(\{ v_{n} \} _{n=1}^{\infty}\) converge to, respectively, \(u^{*}\) and \(v^{*}\in [u_{0},v_{0}]\), which are monotone solutions of the BVP (1.3). Moreover, in view of \(f(t,0)\not\equiv0\), we know that the zero function is not a solution of BVP (1.3). Thus \(u^{*}\) and \(v^{*}\) are nontrivial. □
Remark 3.2
We do not require that \(f:(0,1)\times R\rightarrow R\) is continuous and increasing, we only require the local continuity and local monotonicity; \(f(t,u)\) in our case may change sign. If \(a>0\), then the two nontrivial solutions \(u^{*}\), \(v^{*}\) (\(u^{*}\), \(v^{*}\) may be coincident) satisfy \(0< at^{\alpha-1}\leq u^{*}\leq v^{*}\leq bt^{\alpha -1}< b\), \(0\leq t\leq1\), which implies that \(u^{*}\), \(v^{*}\) are positive solutions of BVP (1.3).
Corollary 3.3
Assume that there exist two positive constants a, b such that \(a< b\) and the following conditions are satisfied:
- (C1):
-
\(f:(0,1)\times[0,b]\rightarrow R^{+}\) is continuous and there exists a nonnegative function \(h\in C(0,1)\cap L^{1}[0,1]\) such that \(|f(t,u)|\leq h(t)\), \((t,u)\in (0,1)\times[0,b]\) and increasing with u in \([0,b]\);
- (C2):
-
\(\int_{0}^{1}\Phi_{1}(s) f(s,as^{\alpha-1})\,ds\geq a\) and \(\int _{0}^{1}\Phi_{2}(s) f(s,bs^{\alpha-1})\,ds\leq b\);
- (C3):
-
\(f(t,0)\not\equiv0\), for \(0\leq t\leq1\).
Then the problem (1.1) has two positive solutions \(u^{*}, v^{*}\in C^{2}[0,1]\cap C^{3}(0,1)\) such that \(0< at^{\alpha-1}\leq u^{*}\leq v^{*}\leq bt^{\alpha-1}\), \(t\in[0,1]\) and \(\lim_{n\rightarrow \infty}u_{n}=u^{*}\), \(\lim_{n\rightarrow\infty}v_{n}=v^{*}\) (\(u^{*}\), \(v^{*}\) may be coincident), where the two iterative sequences are generated by
4 Example
In this section, we give an example to illustrate our main results.
Consider the BVP
where \(\alpha=\frac{5}{2}\), \(\beta=\frac{1}{2}\), \(A(t)=t\),
A simple calculation shows that
and
Let \(a=0\), \(b=2\), so \(f(t,u)\) is continuous and nondecreasing with respect to u. Thus, the condition (H1) holds and \(f(t,0)=4t^{5}-\frac{1}{100}\), \(f(t,2t^{\frac{5}{2}})=8t^{\frac {5}{2}}-\frac{1}{100}\). By direct calculation, we have
and
which show that the condition (H2) holds. So, it follows from Theorem 3.1 that BVP (4.1) has two nontrivial solutions \(u^{*}\) and \(v^{*}\) (\(u^{*}\), \(v^{*}\) may be coincident), such that \(0\leq u^{*}\leq v^{*}\leq2t^{\frac{3}{2}}\leq2\), \(0\leq t\leq1\), and which start off with the zero function or \(2t^{\frac{3}{2}}\), which are very feasible for computational purposes.
References
Kilbas, AA, Srivastava, HM, Trujillo, JJ: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier, Amsterdam (2006)
Miller, KS, Ross, B: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Podlubny, I: Fractional Differential Equations. Mathematics in Science and Engineering. Academic Press, New York (1999)
Nonnenmacher, TF, Metzler, R: On the Riemann-Liouville fractional calculus and some recent applications. Fractals 3, 557-566 (1995)
Li, CF, Luo, XN, Zhou, Y: Existence of positive solutions of the boundary value problem for nonlinear fractional differential equations. Comput. Math. Appl. 59, 1363-1375 (2010)
Xu, XJ, Fei, XL: The positive properties of Green’s function for three point boundary value problems of nonlinear fractional differential equations and its applications. Commun. Nonlinear Sci. Numer. Simul. 17, 1555-1565 (2012)
Zhai, CB, Xu, L: Properties of positive solutions to a class of four-point boundary value problem of Caputo fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 19, 2820-2827 (2014)
Jiang, M, Zhong, SM: Successively iterative method for fractional differential equations with integral boundary conditions. Appl. Math. Lett. 38, 94-99 (2014)
Sun, YP, Zhao, M: Positive solutions for a class of fractional differential equations with integral boundary conditions. Appl. Math. Lett. 34, 17-21 (2014)
Zhang, X, Han, Y: Existence and uniqueness of positive solutions for higher order nonlocal fractional differential equations. Appl. Math. Lett. 25, 555-560 (2012)
Zhang, X, Liu, L, Wu, Y: The uniqueness of positive solutions for a singular fractional differential system involving derivatives. Commun. Nonlinear Sci. Numer. Simul. 18, 1400-1409 (2013)
Goodrich, CS: Positive solutions to boundary value problems with nonlinear boundary conditions. Nonlinear Anal. 75, 417-432 (2012)
Goodrich, CS: Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions. Comput. Math. Appl. 61, 191-202 (2011)
Goodrich, CS: Existence of a positive solution to systems of differential equations of fractional order. Comput. Math. Appl. 62, 1251-1268 (2011)
Liang, S, Zhang, J: Existence of three positive solutions of m-point boundary value problems for some nonlinear fractional differential equations on an infinite interval. Comput. Math. Appl. 61, 3343-3354 (2011)
Wang, Y, Liu, L, Wu, Y: Positive solutions for a class of fractional boundary value problems with changing sign nonlinearity. Nonlinear Anal. 74, 6434-6441 (2011)
Mohammed, AR, Mohamed, AH: Monotone iterative sequences for nonlinear boundary value problems of fractional order. Nonlinear Anal. 74, 3531-3539 (2011)
Wang, GT: Monotone iterative technique for boundary value problems of a nonlinear fractional differential equation with deviating arguments. J. Comput. Appl. Math. 236, 2425-2430 (2012)
Zhang, X, Liu, L, Wu, Y, Lu, Y: The iterative solutions of nonlinear fractional differential equations. Appl. Math. Comput. 219, 4680-4691 (2013)
Webb, JRL, Infante, G: Positive solutions of nonlocal boundary value problems: a unified approach. J. Lond. Math. Soc. 74, 673-693 (2006)
Webb, JRL, Infante, G: Nonlocal boundary value problems of arbitrary order. J. Lond. Math. Soc. 79, 238-258 (2009)
Webb, JRL: Positive solutions of some higher order nonlocal boundary value problems. Electron. J. Qual. Theory Differ. Equ. 2009, 29 (2009)
Amann, H: Fixed point equations and nonlinear eigenvalue problems in order Banach spaces. SIAM Rev. 18, 620-709 (1976)
Guo, DJ: Nonlinear Functional Analysis (II). Press of Science and Technology of Shandong Province, Jinan (2001)
Acknowledgements
The work is supported by the Scientific Research Foundation of Tangshan College (15003B) and the young teachers training program of Tangshan College. The author would like to thank the anonymous referees very much for helpful comments and suggestions which led to the improvement of presentation and quality of the work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that she has no competing interests.
Author’s contributions
The author read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, HE. Iterative solutions for fractional nonlocal boundary value problems involving integral conditions. Bound Value Probl 2016, 3 (2016). https://doi.org/10.1186/s13661-015-0517-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-015-0517-z