1 Introduction

The helical screw rheometer (HSR) is being used for rheological measurements of fluid food suspensions. The geometry of an HSR is similar to a single screw extruder [1]. Extrusion processes are widely used in multi-grade oils, liquid detergents, paints, polymer solutions and polymer melts [2], the injection molding process for polymeric materials, the production of pharmaceutical products, food extrusion, and processing of plastics [3]. Various food items in daily life, such as cookie dough, sevai, pastas, breakfast cereals, French fries, baby food, ready to eat snacks and dry pet food are most commonly manufactured using the extrusion process.

The study of rheological characteristics of different fluids is essential in the process of processing to obtain the desired quality and shape of the products. Bird et al. [4] presented an asymptotic solution and arbitrary values of the flow behavior index for the power-law fluid in a very thin annulus. A brief discussion is given by Mohr et al. [5] for the same problem considering the Newtonian fluid in a screw extruder. Tamura et al. [1] also investigated the flow of a Newtonian fluid in HSR.

The classical Navier-Stokes equations have been proved inadequate to describe the complete characteristics of the above mentioned complex rheological fluids, which are generally known as non-Newtonian fluids. These complex fluids have led to the development of different new theories to study non-Newtonian fluids. For this purpose different models have been proposed [4, 6]. In this paper we study the flow of a co-rotational Maxwell fluid in HSR. The developed second order nonlinear coupled differential equations are reduced to first order nonlinear differential equations by integrating and then combining into a single first order differential equation with the help of a transformation. The solution is obtained by using a perturbation method (PM) as this method is extensively applied for getting approximate solutions for the problems arising in engineering and science [7]. The paper is organized as follows. Section 2 contains the governing equations of the fluid model. In Section 3 the problem under consideration is formulated. Section 4 contains the solution of the problem under consideration: analytical expressions for the velocity components in the x- and z-directions, the resultant velocity in the direction of the screw axis, volume flow rates, shear and normal stresses, shear at wall, and the forces exerted on fluid and average velocity. In Section 5 the results are discussed with the help of graphs. Section 6 contains our conclusion.

2 Basic equations

The basic equations, governing the motion of an isothermal, homogeneous, incompressible co-rotational Maxwell fluid are

$$\begin{aligned}& \operatorname {div}\mathbf{V} = 0, \end{aligned}$$
(1)
$$\begin{aligned}& \rho\frac{D\mathbf{V}}{Dt} = \rho\mathbf{f}- \operatorname {grad}P +\operatorname {div}\mathbf{S}, \end{aligned}$$
(2)

where ρ is the constant fluid density, V is the velocity vector, and f is the body force per unit mass, P denotes the dynamic pressure, \(\frac{D}{Dt}\) denotes the material time derivative defined as

$$ \frac{D(\ast)}{Dt}=\frac{\partial}{\partial t}(\ast)+(\mathbf{V} \cdot\nabla) (\ast). $$
(3)

S is the extra stress tensor; for a co-rotational Maxwell fluid model it can be defined as [8]

$$ \mathbf{S}+\lambda_{1}\mathbf{S}^{\nabla}+\frac{1}{2} \lambda_{1}(\mathbf{A}_{1}\mathbf{S}+\mathbf{S} \mathbf{A}_{1}) =\eta_{0}\mathbf{A}_{1}, $$
(4)

where \(\eta_{0}\) and \(\lambda_{1}\) are zero shear viscosity and relaxation time, respectively. The upper contravariant convected derivative designated by ∇ over S is defined as

$$ \mathbf{S}^{\nabla}=\frac{D\mathbf{S}}{Dt}- \bigl\{ (\operatorname {grad}\mathbf{V})^{T}\mathbf{S}+\mathbf{S}(\operatorname {grad}\mathbf{V}) \bigr\} , $$
(5)

and

$$ \mathbf{A}_{1}=(\operatorname {grad}\mathbf{V})+(\operatorname {grad}\mathbf{V})^{T} $$
(6)

is the first Rivlin-Ericksen tensor.

3 Problem formulation

Consider the steady flow of an isothermal, incompressible, and homogeneous co- rotational Maxwell fluid in HSR. The geometry of HSR is simplified in such a way that the curvature of the screw channel is ignored; it is unrolled and laid out on a flat surface. The barrel surface is also flattened. Assume that the screw surface, the lower plate, is stationary and the barrel surface, the upper plate, is moving across the top of the channel with velocity V at an angle ϕ to the direction of the channel; see Figure 1. The phenomenon is the same as the barrel held stationary and the screw rotating. The geometry is approximated by a shallow infinite channel, by assuming the width B of the channel large compared with the depth h; edge effects in the fluid at the land are ignored. The coordinate axes are positioned in such a way that the x-axis is perpendicular to the flight walls and the y-axis is normal to the barrel surface and the z-axis is in the downward channel direction. The liquid wets all the surfaces and moves by the shear stresses produced by the relative movement of the barrel and channel. No leakage of the fluid occurs across the flights. For simplicity, the velocity of the barrel relative to the channel is decomposed into two components (see Figure 1): U along the x-axis and W along the z-axis [5, 9, 10]. Under these assumptions the velocity profile and extra stress tensor can be considered as

$$ \mathbf{V}=\bigl[u(y), 0, w(y)\bigr] \quad \mbox{and} \quad \mathbf{S}=\mathbf{S}(y). $$
(7)
Figure 1
figure 1

The geometry of the ‘unwrapped’ screw channel and barrel surface.

Full size image

On substituting the velocity profile (7) in (4) we obtain the following components of the extra stress tensor S:

$$\begin{aligned}& S_{xx} = \lambda_{1} S_{xy}\frac{du}{dy} , \end{aligned}$$
(8)
$$\begin{aligned}& S_{xy} = S_{yx}=\frac{\eta_{0}\frac{du}{dy}}{1+\lambda_{1}^{2} \{ (\frac{du}{dy})^{2}+(\frac{dw}{dy})^{2} \}}, \end{aligned}$$
(9)
$$\begin{aligned}& S_{xz} = S_{zx}=\frac{1}{2}\lambda_{1} \biggl\{ S_{yz}\frac {du}{dy}+S_{xy}\frac{dw}{dy} \biggr\} , \end{aligned}$$
(10)
$$\begin{aligned}& S_{yy} = -\lambda_{1} \biggl\{ S_{yz} \frac{dw}{dy}+S_{xy}\frac {du}{dy} \biggr\} , \end{aligned}$$
(11)
$$\begin{aligned}& S_{yz} = S_{zy}=\frac{\eta_{0}\frac{dw}{dy}}{1+\lambda_{1}^{2} \{ (\frac{du}{dy})^{2}+(\frac{dw}{dy})^{2} \}}, \end{aligned}$$
(12)
$$\begin{aligned}& S_{zz} = \lambda_{1} S_{yz}\frac{dw}{dy}. \end{aligned}$$
(13)

Equation (1) satisfies (7) identically and (2) in the absence of body forces reduces to

$$\begin{aligned}& 0 = -\frac{\partial P}{\partial x}+\frac{\partial S_{xy}}{\partial y} , \end{aligned}$$
(14)
$$\begin{aligned}& 0 = -\frac{\partial P}{\partial y}+\frac{\partial S_{yy}}{\partial y} , \end{aligned}$$
(15)
$$\begin{aligned}& 0 = -\frac{\partial P}{\partial z}+\frac{\partial S_{yz}}{\partial y}. \end{aligned}$$
(16)

On defining the modified pressure as \(\hat{P}=P-S_{yy}\) (14)-(16) become

$$\begin{aligned}& \frac{\partial\hat{P}}{\partial x} = \frac{d}{dy} \biggl[\frac{\eta _{0}\frac{du}{dy}}{1+\lambda_{1}^{2} \{ (\frac{du}{dy} )^{2} + (\frac{dw}{dy} )^{2} \}} \biggr], \end{aligned}$$
(17)
$$\begin{aligned}& \frac{\partial\hat{P}}{\partial y} = 0, \end{aligned}$$
(18)
$$\begin{aligned}& \frac{\partial\hat{P}}{\partial z} = \frac{d}{dy} \biggl[\frac{\eta_{0}\frac{dw}{dy}}{ 1+\lambda_{1}^{2} \{ (\frac{du}{dy} )^{2} + (\frac{dw}{dy} )^{2} \}} \biggr]. \end{aligned}$$
(19)

The associated boundary conditions can be taken as in Figure 1. We have

$$ \begin{aligned} & u = 0, \qquad w = 0, \quad \mbox{at } y=0, \\ & u = U, \qquad w=W, \quad \mbox{at } y=h. \end{aligned} $$
(20)

Eliminating the hat from P and introducing dimensionless parameters,

$$\begin{aligned}& x^{\ast} = \frac{x}{h}, \qquad y^{\ast}=\frac{y}{h},\qquad z^{\ast }=\frac{z}{h},\qquad u^{\ast}=\frac{u}{W},\qquad w^{\ast}=\frac{w}{W}, \\& P^{\ast} = \frac{P}{\mu (\frac{W}{h} )}, \end{aligned}$$

in (17), (19), and (20) results in

$$\begin{aligned}& \frac{\partial P^{\ast}}{\partial x^{\ast}} = \frac{d}{dy^{\ast}} \biggl[\frac{\frac{du^{\ast}}{dy^{\ast}}}{1+(Wi)^{2} \{ (\frac {du^{\ast}}{dy^{\ast}} )^{2} + (\frac{dw^{\ast}}{dy^{\ast}} )^{2} \}} \biggr], \end{aligned}$$
(21)
$$\begin{aligned}& \frac{\partial P^{\ast}}{\partial z^{\ast}} = \frac{d}{dy^{\ast}} \biggl[\frac{\frac{dw^{\ast}}{dy^{\ast}}}{ 1+(Wi)^{2} \{ (\frac{du^{\ast}}{dy^{\ast}} )^{2} + (\frac{dw^{\ast}}{dy^{\ast}} )^{2} \}} \biggr], \end{aligned}$$
(22)

and

$$ \begin{aligned} & u^{\ast} = 0,\qquad w^{\ast} = 0, \quad \mbox{at } y^{\ast}=0, \\ & u^{\ast} = \frac{U}{W}, \qquad w^{\ast}=1, \quad \mbox{at } y^{\ast}=1. \end{aligned} $$
(23)

Here \(Wi=\frac{\lambda_{1} W}{h}\) denotes the Weissenberg number. Dropping ‘*’ from (21)-(23) onward and then integrating the ‘*’ free form of (21) and (22) with respect to y, we get

$$\begin{aligned}& \frac{du}{dy} = (P_{,x} y + C_{1}) \biggl[1+(Wi)^{2} \biggl\{ \biggl(\frac {du}{dy} \biggr)^{2}+ \biggl(\frac{dw}{dy} \biggr)^{2} \biggr\} \biggr], \end{aligned}$$
(24)
$$\begin{aligned}& \frac{dw}{dy} = (P_{,z} y + C_{2}) \biggl[1+(Wi)^{2} \biggl\{ \biggl(\frac{du}{dy} \biggr)^{2}+ \biggl(\frac {dw}{dy} \biggr)^{2} \biggr\} \biggr], \end{aligned}$$
(25)

where \(P_{,x}=\frac{\partial P}{\partial x}\), \(P_{, z}=\frac{\partial P}{\partial z}\); \(C_{1}\) and \(C_{2}\) are arbitrary constants of integration, which can be determined using the associated boundary conditions.

On defining

$$ F=u+\iota w,\qquad G=P_{,x} + \iota P_{,z},\qquad K=C_{1}+ \iota C_{2} \quad \mbox{and} \quad V_{0}=\frac{U}{W}+\iota1, $$
(26)

in (24) and (25) yielding

$$ \frac{d F}{d y} = (G y + K) + (Wi)^{2}(G y + K)\frac{d F}{d y} \frac{d \bar{F}}{d y}, $$
(27)

the boundary conditions (23) become

$$ \begin{aligned} &F = 0 \quad \mbox{at } y=0, \\ &F = V_{0} \quad \mbox{at } y=1, \end{aligned} $$
(28)

where F̄ is the complex conjugate of F.

Equation (27) is a second order nonlinear, inhomogeneous ordinary differential equation, and its exact solution seems to be difficult. In the following section we use PM to obtain the approximate solution. To obtain the expressions for the velocity components in the x- and z-directions (27) together with the boundary conditions (28) is solved up to the second order approximation by using the symbolic computation software Wolfram Mathematica 7.

4 Solution of the problem

Assume \(\xi= (Wi)^{2}\) to be a small parameter (perturbation parameter) in (27) and expand \(F(y)\) and K in a series of the form

$$\begin{aligned}& F(y) = F_{0}(y)+\xi F_{1}(y)+\xi^{2}F_{2}(y)+ \cdots, \end{aligned}$$
(29)
$$\begin{aligned}& K = K_{0}+\xi K_{1}+\xi^{2}K_{2}+ \cdots, \end{aligned}$$
(30)

where \(K_{0}, K_{1}, K_{2},\ldots\) , are arbitrary constants to be determined using boundary conditions.

Substituting the series (29) and (30) into (27)-(28) and equating the coefficients of like powers of ξ, we get the following problems of different orders.

4.1 Zeroth order problem

We have

$$ \xi^{0}: \frac{d F_{0}}{dy} = (G y + K_{0}), $$
(31)

where \(K_{0}\) is an arbitrary constant. The boundary conditions associated to (31) are

$$ \begin{aligned} &F_{0} = 0 \quad \mbox{at } y=0, \\ &F_{0} = V_{0} \quad \mbox{at } y=1, \end{aligned} $$
(32)

having the solution

$$ F_{0} = V_{0} y+\frac{1}{2}G \bigl(y^{2} - y \bigr), $$
(33)

and separating real and imaginary parts we get

$$\begin{aligned}& u_{0} = \frac{U}{W} y+\frac{1}{2}P_{, x} \bigl(y^{2} - y \bigr), \end{aligned}$$
(34)
$$\begin{aligned}& w_{0} = y+\frac{1}{2}P_{, z} \bigl(y^{2} - y \bigr), \end{aligned}$$
(35)

thus (34) and (35) are the solution of the Newtonian case.

4.2 First order problem

We have

$$ \xi^{1}: \frac{d F_{1}}{dy} = K_{1} + (G y + K_{0})\frac{d F_{0}}{dy}\frac{d \bar{F_{0}}}{dy}, $$
(36)

with the boundary conditions

$$ \begin{aligned} &F_{1} = 0 \quad \mbox{at } y=0, \\ &F_{1} = 0 \quad \mbox{at } y=1, \end{aligned} $$
(37)

where \(K_{1}\) is a constant to be determined, giving a solution of the form

$$ F_{1} = (L_{0} + \iota T_{0}) \bigl(y^{2} - y \bigr)+(L_{1} + \iota T_{1}) \bigl(y^{3} - y \bigr)+(L_{2} + \iota T_{2}) \bigl(y^{4} - y \bigr), $$
(38)

which has real and imaginary parts as follows:

$$\begin{aligned}& u_{1} = L_{0} \bigl(y^{2} - y \bigr)+L_{1} \bigl(y^{3} - y \bigr)+L_{2} \bigl(y^{4} - y \bigr), \end{aligned}$$
(39)
$$\begin{aligned}& w_{1} = T_{0} \bigl(y^{2} - y \bigr)+T_{1} \bigl(y^{3} - y \bigr)+T_{2} \bigl(y^{4} - y \bigr), \end{aligned}$$
(40)

where \(L _{i}\), \(T_{j}\), \(i=0, \ldots,2\), \(j=0,\ldots,2\), are constant coefficients given in the Appendix.

4.3 Second order problem

We have

$$ \xi^{2}: \frac{d F_{2}}{dy} = K_{2} + (G y + K_{0}) \biggl\{ \frac{d F_{0}}{dy}\frac{d \bar{F_{1}}}{dy}+\frac{d\bar{F_{0}}}{dy} \frac{d F_{1}}{dy} \biggr\} + K_{1}\frac{d F_{0}}{dy} \frac{d \bar{F_{0}}}{dy}, $$
(41)

using the boundary conditions

$$ \begin{aligned} &F_{2} = 0 \quad \mbox{at } y=0, \\ &F_{2} = 0\quad \mbox{at } y=h, \end{aligned} $$
(42)

where \(K_{2}\) is a constant. Solving (41) under the boundary conditions (42) results in

$$\begin{aligned} F_{2} =& (L_{3} + \iota T_{3}) \bigl(y^{2} - y \bigr)+(L_{4} + \iota T_{4}) \bigl(y^{3} - y \bigr)+(L_{5} + \iota T_{5}) \bigl(y^{4} - y \bigr) \\ &{}+ (L_{6} + \iota T_{6}) \bigl(y^{5} - y \bigr)+(L_{7} + \iota T_{7}) \bigl(y^{6} - y \bigr). \end{aligned}$$
(43)

Separation of real and imaginary parts gives

$$\begin{aligned}& \begin{aligned}[b] u_{2} ={}& L_{3} \bigl(y^{2} - y \bigr)+L_{4} \bigl(y^{3} - y \bigr)+L_{5} \bigl(y^{4} - y \bigr) \\ &{}+ L_{6} \bigl(y^{5} - y \bigr)+L_{7} \bigl(y^{6} - y \bigr), \end{aligned} \end{aligned}$$
(44)
$$\begin{aligned}& \begin{aligned}[b] w_{2} ={}& T_{3} \bigl(y^{2} - y \bigr)+T_{4} \bigl(y^{3} - y \bigr)+T_{5} \bigl(y^{4} - y \bigr) \\ &{}+ T_{6} \bigl(y^{5} - y \bigr)+ T_{7} \bigl(y^{6} - y \bigr), \end{aligned} \end{aligned}$$
(45)

where \(L _{i}\), \(T_{j}\), \(i=3, \ldots,7\), \(j=3,\ldots,7\), are constant coefficients given in the Appendix.

4.4 Velocity profiles

4.4.1 Velocity profile in x-direction

Combining (34), (39), and (44) gives the approximate solution for the velocity profile in the x-direction as

$$\begin{aligned} u =&\frac{U}{W} y + \biggl(\frac{1}{2}P_{,x}+\xi L_{0}+\xi^{2}L_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl(\xi L_{1} + \xi^{2} L_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl(\xi L_{2} + \xi^{2} L_{5} \bigr) \bigl(y^{4} - y \bigr)+\xi^{2} L_{6} \bigl(y^{5} - y \bigr)+\xi^{2} L_{7} \bigl(y^{6} - y \bigr), \end{aligned}$$
(46)

and (46) gives

$$\begin{aligned} u =&\frac{U}{W} y + \biggl(\frac{1}{2}P_{,x}+(Wi)^{2} L_{0}+(Wi)^{4}L_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl((Wi)^{2} L_{1} + (Wi)^{4} L_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl((Wi)^{2} L_{2} + (Wi)^{4} L_{5} \bigr) \bigl(y^{4} - y \bigr)+(Wi)^{4} L_{6} \bigl(y^{5} - y \bigr)+(Wi)^{4} L_{7} \bigl(y^{6} - y \bigr). \end{aligned}$$
(47)

4.4.2 Velocity profile in z-direction

Combining (35), (40), and (45) we obtain the solution for the velocity profile in the z-direction as

$$\begin{aligned} w =& y + \biggl(\frac{1}{2}P_{,z}+\xi T_{0}+ \xi^{2} T_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl(\xi T_{1} + \xi^{2} T_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl(\xi T_{2} + \xi^{2} T_{5} \bigr) \bigl(y^{4} - y \bigr)+ \xi^{2} T_{6} \bigl(y^{5} - y \bigr)+\xi^{2} T_{7} \bigl(y^{6} - y \bigr), \end{aligned}$$
(48)

and (48) gives

$$\begin{aligned} w =& y + \biggl(\frac{1}{2}P_{,z}+(Wi)^{2} T_{0}+(Wi)^{4} T_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl((Wi)^{2} T_{1} + (Wi)^{4} T_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl((Wi)^{2} T_{2} + (Wi)^{4} T_{5} \bigr) \bigl(y^{4} - y \bigr)+ (Wi)^{4} T_{6} \bigl(y^{5} - y \bigr) \\ &{}+ (Wi)^{4} T_{7} \bigl(y^{6} - y \bigr). \end{aligned}$$
(49)

4.4.3 Velocity in the direction of the axis of screw

The velocity along the axis of the screw at any depth in the channel can be calculated using (47) and (49) as

$$\begin{aligned}& s = w \sin\phi+u\cos\phi, \end{aligned}$$
(50)
$$\begin{aligned}& \begin{aligned}[b] s ={}& \biggl\{ \biggl(\frac{1}{2}P_{,z}+(Wi)^{2} T_{0}+(Wi)^{4} T_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl((Wi)^{2} T_{1} + (Wi)^{4} T_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl((Wi)^{2} T_{2} + (Wi)^{4} T_{5} \bigr) \bigl(y^{4} - y \bigr)+(Wi)^{4} T_{6} \bigl(y^{5} - y \bigr) \\ &{}+ (Wi)^{4} T_{7} \bigl(y^{6} - y \bigr) \biggr\} \sin\phi \\ &{}+ \biggl\{ \biggl(\frac{1}{2}P_{,x}+(Wi)^{2} L_{0}+(Wi)^{4}L_{3} \biggr) \bigl(y^{2} - y \bigr)+ \bigl((Wi)^{2} L_{1} + (Wi)^{4} L_{4} \bigr) \bigl(y^{3} - y \bigr) \\ &{}+ \bigl((Wi)^{2} L_{2} + (Wi)^{4} L_{5} \bigr) \bigl(y^{4} - y \bigr)+(Wi)^{4} L_{6} \bigl(y^{5} - y \bigr) \\ &{}+ (Wi)^{4} L_{7} \bigl(y^{6} - y \bigr) \biggr\} \cos\phi, \end{aligned} \end{aligned}$$
(51)

(51) has no drag term, which shows that the net velocity at any point in the channel depends on the pressure gradients \(P_{,x}\) and \(P_{,z}\).

4.5 Stresses

Substituting the derivatives of the velocity components (47) and (49) in (9), (10), and (12) we obtain the shear stresses as

$$\begin{aligned}& \begin{aligned}[b] S^{*}_{xy} ={}& S^{*}_{yx} = \frac{1}{1+Wi^{2}\Pi_{1}} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \bigl(-1+3 y^{2} \bigr)\\ &{}+ \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} L_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} L_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} , \end{aligned} \end{aligned}$$
(52)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{yz} ={}& S^{*}_{zy} = \frac{1}{1+Wi^{2}\Pi_{1}} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) \bigl(-1+3 y^{2} \bigr)\\ &{}+ \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} T_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} T_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} , \end{aligned} \end{aligned}$$
(53)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{xz} ={}& S^{*}_{zx} = \frac{Wi}{2} \biggl[S_{yz}^{*} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+ \frac{P_{,x}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \bigl(-1+3 y^{2} \bigr)\\ &{}+ \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} L_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} L_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} + S_{xy}^{*} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) \bigl(-1+3 y^{2} \bigr)+ \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \bigl(-1+4 y^{3} \bigr) \\ &{}+ Wi ^{2} T_{6} \bigl(-1+5 y^{4} \bigr)+Wi ^{2} T_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} \biggr], \end{aligned} \end{aligned}$$
(54)

where

$$\begin{aligned} \Pi_{1} =& \biggl[ \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) (-1+2 y)+ \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \bigl(-1+3 y^{2} \bigr) \\ &{}+ \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} L_{6} \bigl(-1+5 y^{4} \bigr)+ Wi ^{2} L_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} ^{2} \\ &{}+ \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) (-1+2 y)+ \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) \bigl(-1+3 y^{2} \bigr) \\ &{}+ \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} T_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} T_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} ^{2} \biggr]. \end{aligned}$$
(55)

Then the shears exerted by the fluid on the wall at \(y=1\) are

$$\begin{aligned}& \begin{aligned}[b] S^{*}_{w_{xy}} ={}& S^{*}_{w_{xy}} = \frac{1}{1+Wi^{2}\Pi_{2}} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) \\ &{}+ 2 \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr)+ 3 \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr)+ 4 Wi ^{2} L_{6} \\ &{}+ 5 Wi ^{2} L_{7} \biggr\} , \end{aligned} \end{aligned}$$
(56)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{w_{yz}} ={}& S^{*}_{w_{zy}} = \frac{1}{1+Wi^{2}\Pi_{2}} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) \\ &{}+ 2 \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr)+ 3 \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr)+ 4 Wi ^{2} T_{6} \\ &{}+ 5 Wi ^{2} T_{7} \biggr\} , \end{aligned} \end{aligned}$$
(57)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{w_{xz}} ={}& S^{*}_{w_{zx}} = \frac{Wi}{2} \biggl[S_{yz}^{*} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) \\ &{}+ 2 \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr)+ 3 \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) + 4Wi ^{2} L_{6} \\ &{}+ 5 Wi ^{2} L_{7} \biggr\} + S_{xy}^{*} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+ \frac{P_{,z}}{2} \biggr) \\ &{}+ 2 \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) + 3 \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \\ &{}+ 4 Wi ^{2} T_{6}+ 5 Wi ^{2} T_{7} \biggr\} \biggr], \end{aligned} \end{aligned}$$
(58)

where

$$\begin{aligned} \Pi_{2} =& \biggl[ \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) + 2 \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \\ &{}+ 3 \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr)+ 4Wi ^{2} L_{6} + 5Wi ^{2} L_{7} \biggr\} ^{2} + \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) \\ &{}+ 2 \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) + 3 \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr)+ 4 Wi ^{2} T_{6} + 5 Wi ^{2} T_{7} \biggr\} ^{2} \biggr]. \end{aligned}$$
(59)

Similarly, we can calculate the normal stresses (8), (11), and (13) as

$$\begin{aligned}& \begin{aligned}[b] S^{*}_{xx} ={}& Wi \biggl[S_{xy}^{*} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \bigl(-1+3 y^{2} \bigr)\\ &{}+ \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} L_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} L_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} \biggr], \end{aligned} \end{aligned}$$
(60)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{yy} ={}& -Wi \biggl[S_{xy}^{*} \biggl\{ \frac{U}{W}+ \biggl(Wi L_{0}+Wi ^{2} L_{3}+\frac{P_{,x}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi L_{1}+Wi ^{2} L_{4} \bigr) \bigl(-1+3 y^{2} \bigr)\\ &{}+ \bigl(Wi L_{2}+Wi ^{2} L_{5} \bigr) \bigl(-1+4 y^{3} \bigr)+ Wi ^{2} L_{6} \bigl(-1+5 y^{4} \bigr) \\ &{}+ Wi ^{2} L_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} + S_{yz}^{*} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+\frac{P_{,z}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) \bigl(-1+3 y^{2} \bigr)+ \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \bigl(-1+4 y^{3} \bigr) \\ &{}+ Wi ^{2} T_{6} \bigl(-1+5 y^{4} \bigr)+Wi ^{2} T_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} \biggr], \end{aligned} \end{aligned}$$
(61)
$$\begin{aligned}& \begin{aligned}[b] S^{*}_{zz} ={}& Wi \biggl[S_{yz}^{*} \biggl\{ 1+ \biggl(Wi T_{0}+Wi ^{2} T_{3}+ \frac{P_{,z}}{2} \biggr) (-1+2 y) \\ &{}+ \bigl(Wi T_{1}+Wi ^{2} T_{4} \bigr) \bigl(-1+3 y^{2} \bigr)+ \bigl(Wi T_{2}+Wi ^{2} T_{5} \bigr) \bigl(-1+4 y^{3} \bigr) \\ &{}+ Wi ^{2} T_{6} \bigl(-1+5 y^{4} \bigr)+Wi ^{2} T_{7} \bigl(-1+6 y^{5} \bigr) \biggr\} \biggr]. \end{aligned} \end{aligned}$$
(62)

Here \(S_{ij}^{\ast} = \frac{S_{ij}}{\frac{\mu W}{h}}\), \(i, j=x,y,z\), \(i\neq j\), are the non-dimensional stresses.

The shear forces per unit width required to move the barrel in the x- and z-directions are

$$ \frac{F_{x}}{B}=-\int_{0}^{L_{x}}S_{w_{xy}} \,dx, $$
(63)

or

$$\begin{aligned}& F_{x}^{\ast}=-S_{w_{xy}}^{\ast} \delta_{1}, \end{aligned}$$
(64)
$$\begin{aligned}& \frac{F_{z}}{B}=-\int_{0}^{L_{z}}S_{w_{yz}} \,dz, \end{aligned}$$
(65)

or

$$ F_{z}^{\ast}=-S_{w_{yz}}^{\ast} \delta_{2}, $$
(66)

where \(F_{i}^{\ast}=\frac{F_{i}}{\mu W B}\), \(i=x, y\) are dimensionless shear forces, \(\delta_{1}=\frac{L_{x}}{h}\) and \(\delta_{2}=\frac{L_{z}}{h}\) are the dimensionless lengths of the channel in the x- and z-directions, respectively, and \(L_{x}\) and \(L_{z}\) are the dimensional lengths of the channel in the x- and z-directions, respectively. Therefore

$$ F^{\ast} = F_{z}^{\ast} \sin\phi+F_{x}^{\ast} \cos\phi $$
(67)

is the net shear force per unit width in the direction of the axis of the screw.

4.6 Volume flow rate

The volume flow rate in the x-direction per unit width is

$$ Q_{x}^{*}=\int_{0}^{1} u \,dy, $$
(68)

where \(Q_{x}^{*}=\frac{Q_{x}}{W h B}\), and (68) gives

$$\begin{aligned} Q_{x}^{*} =&\frac{U}{2 W}-\frac{1}{6} \biggl( \frac{1}{2}P_{,x} + (Wi)^{2} L_{0}+(Wi)^{4}L_{3} \biggr) - \frac{1}{4} \bigl((Wi)^{2} L_{1} + (Wi)^{4} L_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} L_{2} + (Wi)^{4} L_{5} \bigr) - \frac{1}{3}(Wi)^{4} L_{6} -\frac{5}{14}(Wi)^{4} L_{7}. \end{aligned}$$
(69)

The volume flow rate in the z-direction per unit width is

$$ Q_{z}^{*} =\int_{0}^{1} w \,dy, $$
(70)

where \(Q_{z}^{*}=\frac{Q_{z}}{W h B}\), and (70) gives

$$\begin{aligned} Q_{z}^{*} =& \frac{1}{2}- \frac{1}{6} \biggl(\frac{1}{2}P_{,z}+(Wi)^{2} T_{0}+(Wi)^{4} T_{3} \biggr)-\frac{1}{4} \bigl((Wi)^{2} T_{1} + (Wi)^{4} T_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} T_{2} + (Wi)^{4} T_{5} \bigr) - \frac{1}{3}(Wi)^{4}T_{6} -\frac{5}{14}(Wi)^{4} T_{7}. \end{aligned}$$
(71)

The resultant volume flow rate forward in the screw channel, which is the product of the velocity and cross-sectional area integrated from the root of the screw to the barrel surface, is calculated from (51),

$$ Q^{*} =\frac{n}{\sin\phi}\int_{0}^{1} s\, dy, $$
(72)

where \(Q^{*}=\frac{Q}{W h B}\) and n is the number of parallel flights in a multiflight screw.

Equation (72) gives

$$\begin{aligned} Q^{*} =& \frac{n}{\sin\phi} \biggl[ \biggl\{ \frac{1}{2}- \frac{1}{6} \biggl(\frac{1}{2}P_{,z}+(Wi)^{2} T_{0}+(Wi)^{4} T_{3} \biggr) - \frac{1}{4} \bigl((Wi)^{2} T_{1} + (Wi)^{4} T_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} T_{2} + (Wi)^{4} T_{5} \bigr)- \frac{1}{3}(Wi)^{4} T_{6} -\frac{5}{14}(Wi)^{4} T_{7} \biggr\} \sin\phi \\ &{}+ \biggl\{ \frac{U}{2 W}-\frac{1}{6} \biggl( \frac{1}{2}P_{,x} +(Wi)^{2} L_{0}+(Wi)^{4}L_{3} \biggr) - \frac{1}{4} \bigl((Wi)^{2} L_{1} + (Wi)^{4} L_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} L_{2} + (Wi)^{4} L_{5} \bigr)-\frac{1}{3}(Wi)^{4} L_{6}-\frac{5}{14}(Wi)^{4} L_{7} \biggr\} \cos\phi \biggr]. \end{aligned}$$
(73)

Equation (73) can be written as

$$ Q^{*}=\frac{n}{\sin\phi} \bigl\{ Q^{*}_{z}\sin \phi+Q^{*}_{x}\cos\phi \bigr\} . $$
(74)

4.7 Average velocity

The average velocity in the direction of the axis of the screw is

$$ \bar{s^{\ast}} = n\int_{0}^{1} s \,dy, $$
(75)

where \(\bar{s^{\ast}}=\frac{\bar{s}}{W}\) is the non-dimensional average velocity. Using (51) gives

$$\begin{aligned} \bar{s^{\ast}} =& n \biggl[ \biggl\{ \frac{1}{2}- \frac{1}{6} \biggl(\frac{1}{2}P_{,z}+(Wi)^{2} T_{0}+(Wi)^{4} T_{3} \biggr) - \frac{1}{4} \bigl((Wi)^{2} T_{1} + (Wi)^{4} T_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} T_{2} + (Wi)^{4} T_{5} \bigr)- \frac{1}{3}(Wi)^{4} T_{6} -\frac{5}{14}(Wi)^{4} T_{7} \biggr\} \sin\phi \\ &{}+ \biggl\{ \frac{U}{2 W}-\frac{1}{6} \biggl( \frac{1}{2}P_{,x} +(Wi)^{2} L_{0}+(Wi)^{4}L_{3} \biggr) - \frac{1}{4} \bigl((Wi)^{2} L_{1} + (Wi)^{4} L_{4} \bigr) \\ &{}- \frac{3}{10} \bigl((Wi)^{2} L_{2} + (Wi)^{4} L_{5} \bigr)-\frac{1}{3}(Wi)^{4} L_{6}-\frac{5}{14}(Wi)^{4} L_{7} \biggr\} \cos\phi \biggr]. \end{aligned}$$
(76)

5 Results and discussion

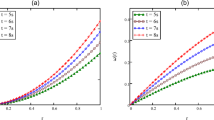
In the present work we have considered the steady flow of an incompressible, isothermal, and homogeneous co-rotational Maxwell fluid in HSR. The geometry is given in Figure 1. Second order nonlinear coupled differential equations are transformed to a single differential equation. Using perturbation methods analytical expressions are obtained for the velocities u and w in the x- and z-directions, respectively, and also in the direction of the axis of the screw, s. Expressions for the shear stresses in the flow field and at barrel surface, forces exerted on fluid, volume flow rates, and the average velocity are also derived. We discussed the behavior of co-rotational Maxwell fluid in HSR in terms of the non-Newtonian parameter \(Wi^{2}\), the flight angle ϕ, and the pressure gradients \(P_{,x}\) and \(P_{,z}\) on the velocities given by (47), (49), and (51). From Figures 2-4 it is seen that the velocity profiles are strongly dependent on the non-Newtonian parameter \(Wi^{2}\). Figure 2 is sketched for u, the back flow is seen toward the barrel surface after some points in the channel height, which suggests that the fluid circulates inside the confined channel, thus the velocity in the x-direction helps in the process of mixing during processing. In Figure 3 we observe that with the increase in the value of \(Wi^{2}\) the velocity w increases and helps to move the fluid in the forward direction in the channel. The resultant velocity s is shown in Figure 4, which resembles Poiseuille flow in the channel. Due to s the fluid moves toward the die. It is worthwhile to note that the shear thinning occurs with the increase in the value of \(Wi^{2}\), which increases the extrusion process. The velocity profiles for the Newtonian case are retrieved for \(\tilde{\beta}=0\) [6].

Figure 2
figure 2

Velocity profile \(\pmb{u(y)}\) for different values of \(\pmb{Wi^{2}}\) , keeping \(\pmb{P_{, x}=-1.5}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 3
figure 3

Velocity profile \(\pmb{w(y)}\) for different values of \(\pmb{Wi^{2}}\) , keeping \(\pmb{P_{, x}=-1.5}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 4
figure 4

Velocity profile \(\pmb{s(y)}\) for different values of \(\pmb{Wi^{2}}\) , keeping \(\pmb{P_{, x}=-1.5}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image

Moreover, Figures 5, 7, and 9 are sketched for the velocity profiles u, w, and s for different values of \(P_{, x}\). Figures 5 and 9 show that the rise in pressure gradient increases the speed of the flow. However, Figure 7 depicts that \(P_{,x}\) resists the flow in the z-direction. Figures 6, 8, and 10 are plotted for the velocity profiles u, w, and s for different values of \(P_{, z}\). Figures 8 and 10 show that the increase in the value of \(P_{, z}\) increases the speed of the flow. However, Figure 6 shows that \(P_{,z}\) resists the flow in the x-direction and is responsible for the forward flow.

Figure 5
figure 5

Velocity profile \(\pmb{u(y)}\) for different values of \(\pmb{P_{, x}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 6
figure 6

Velocity profile \(\pmb{u(y)}\) for different values of \(\pmb{P_{, z}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, x}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 7
figure 7

Velocity profile \(\pmb{w(y)}\) for different values of \(\pmb{P_{, x}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 8
figure 8

Velocity profile \(\pmb{w(y)}\) for different values of \(\pmb{P_{, z}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, x}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 9
figure 9

Velocity profile \(\pmb{s(y)}\) for different values of \(\pmb{P_{, x}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, z}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image
Figure 10
figure 10

Velocity profile \(\pmb{s(y)}\) for different values of \(\pmb{P_{, z}}\) , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, x}=-1.5}\) , and \(\pmb{\phi=45^{\circ}}\) .

Full size image

Figure 11 is plotted for different values of ϕ. It is observed that the resultant velocity attains its maximum value at \(\phi=45^{\circ}\), which conforms the results given in [11]. From the resultant velocity (51) we conclude that the \(\phi=0^{\circ}\) velocity has only a component in the x-direction and \(\phi=90^{\circ}\) gives the velocity in the z-direction only.

Figure 11
figure 11

Velocity profile \(\pmb{s(y)}\) for different values of ϕ , keeping \(\pmb{Wi^{2}=0.25}\) , \(\pmb{P_{, x}=-1.5}\) , and \(\pmb{P_{, z}=-1.5}\) .

Full size image

6 Conclusion

The steady flow of an isothermal, homogeneous, and incompressible co-rotational Maxwell fluid is investigated in HSR. The geometry of the problem under consideration gives second order nonlinear coupled differential equations, which are reduced to a single differential equation by using a transformation. A perturbation method is used to obtain analytical expressions for the flow profiles, volume flow rate, shear and normal stresses, shear at wall, forces exerted on the fluid, and the average velocity. The calculations of these values are of great importance during the production process and very useful to obtain the desired quality and shape of the products. It is noticed that the zeroth component solution matches with the solution of the linearly viscous fluid in HSR and we also found that the net velocity of the fluid is due to the pressure gradient as the expression for the net velocity is free from the drag term. A graphical representation shows that the velocity profiles are strongly dependent on the non-Newtonian parameter and pressure gradients in the x- and z-direction. Thus the extrusion process strongly depends on the parameters involved.