Inertial iterative method for solving generalized equilibrium, variational inequality, and fixed point problems of multivalued mappings in Banach space

Abstract

We devise an iterative algorithm incorporating inertial techniques to approximate the shared solution of a generalized equilibrium problem, a fixed point problem for a finite family of relatively nonexpansive multivalued mappings, and a variational inequality problem. Our discussion encompasses the strong convergence of the proposed algorithm and highlights specific outcomes derived from our theorem. Additionally, we provide a computational analysis to underscore the significance of our findings and draw comparisons. The results presented in this paper serve to extend and unify numerous previously established outcomes in this particular research domain.

1 Introduction

Consider a real Banach space E with dual $E^{*}$, and let D be a nonempty closed convex subset of E. The normalized duality mapping $\mathbb{J}:E \to 2^{E^{*}}$ is defined by $\mathbb{J}(\mathfrak{w})=\{\mathfrak{w}_{0}\in E^{*}: \langle \mathfrak{w}_{0},\mathfrak{w}\rangle =\|\mathfrak{w}\|^{2}=\| \mathfrak{w}_{0}\|^{2}\}$ for all $\mathfrak{w}\in E$. The fixed point of a multivalued mapping $\mathbb{S}:D\to 2^{D}$, where $2^{D}$ denotes the power set of D, is a point $\mathfrak{w} \in D$ such that $\mathfrak{w} \in \mathbb{S}\mathfrak{w}$.

Consider bifunctions ε and $\mathbb{G}$ defined on $D\times D\to \mathbb{R}$. The generalized equilibrium problem (GEP) seeks a solution $\mathfrak{w}_{0}\in D$ satisfying the inequality

$$ \mathbb{G}(\mathfrak{w}_{0},\mathfrak{v})+\varepsilon (\mathfrak{w}_{0}, \mathfrak{v})-\varepsilon (\mathfrak{w}_{0},\mathfrak{w}_{0})\geq 0,~~ \forall \mathfrak{v}\in D. $$

(1.1)

The solution to this problem is denoted as ${\mathrm{Sol(GEP)}}$. When ε is identically zero, GEP(1.1) reduces to the equilibrium problem (EP)

$$ \mathbb{G}(\mathfrak{w}_{0},\mathfrak{v})\geq 0,~~\forall \mathfrak{v}\in D. $$

(1.2)

The EP (1.2) has been studied by Blum and Oettli [5], and its solution is denoted as Sol(EP).

If we set $\mathbb{G}(\mathfrak{w}_{0},\mathfrak{v})=\langle \mathfrak{h} \mathfrak{w}_{0}, \mathfrak{v}-\mathfrak{w}_{0}\rangle$, where $\mathfrak{h}:D\to D$ is a nonlinear mapping, then GEP(1.1) transforms into the variational inequality problem (VIP)

$$ \langle \mathfrak{h}\mathfrak{w}_{0}, \mathfrak{v}-\mathfrak{w}_{0} \rangle \geq 0,~\forall \mathfrak{v}\in D, $$

(1.3)

introduced by Hartmann and Stampacchia [12]. The solution of (1.3) is denoted as Sol(VIP). The generalized equilibrium problem plays a pivotal role in various scientific and engineering domains, providing a natural and unified framework for problems in nonlinear analysis, optimization, economics, finance, game theory, physics, and engineering; see [1, 27, 29].

In 1973, Markin [19] introduced the fixed point problem (FPP) for multivalued nonexpansive mappings, which has found extensive applications in various fields such as convex optimization and control theory, as illustrated in [11, 16, 20, 26]. In 2011, Homaeipour et al. [13] presented an iterative algorithm involving relatively nonexpansive multivalued mapping $\mathbb{S}$:

$$ \left \{ \textstyle\begin{array}{l} \mathfrak{w}_{0}\in D, \\ \mathfrak{w}_{n+1}=\Pi _{D}J^{-1}(\beta _{n}J\mathfrak{w}_{n}+(1- \beta _{n})J\mathfrak{v}_{n}),~~~\mathfrak{v}_{n}\in \mathbb{S} \mathfrak{w}_{n}. \end{array}\displaystyle \right \} $$

Under certain conditions on the control sequence, Homaeipour et al. observed the convergence of the sequence $\{\mathfrak{w}_{n}\}$. More recently, Zegeye et al. [32] investigated an iterative method to approximate the common solution of the equilibrium problem (EP) and the fixed point problem (FPP) for relatively nonexpansive multivalued mappings, providing a convergence analysis under appropriate parameters. Very recently, Taiwo et al. [28] introduced the following Halpern-S-iteration method:

$$ \left \{ \textstyle\begin{array}{l} \mathfrak{w},\mathfrak{w}_{1},\in D, \\ \mathfrak{u}_{n}\in D~~{\mathrm{such~that}}~\mathbb{G}(\mathfrak{u}_{n}, \mathfrak{q})+\frac{1}{r_{n}}\langle \mathfrak{q}-\mathfrak{u}_{n}, J \mathfrak{u}_{n}-J\mathfrak{w}_{n}\rangle \geq 0~~{\mathrm{for~all}}~ \mathfrak{q}\in D, \\ \mathfrak{z}_{n}=\Pi _{D}J^{-1}((1-\beta _{n})J\mathfrak{w}_{n}+ \beta _{n}J\mathfrak{v}_{n}),~~~\mathfrak{v}_{n}\in \mathbb{S} \mathfrak{w}_{n}, \\ \mathfrak{w}_{n+1}=J^{-1}(\beta _{n}J\mathfrak{w}+\gamma _{n}J \mathfrak{v}_{n}+\eta _{n}J\mathfrak{t}_{n}),~~~\mathfrak{t}_{n}\in \mathbb{S}\mathfrak{z}_{n}. \end{array}\displaystyle \right \} $$

They aimed to approximate the common solution of the EP and FPP for relatively nonexpansive multivalued mappings within uniformly convex and uniformly smooth Banach spaces. Moreover, they established strong convergence under appropriate conditions on the parameters.

An effective strategy for accelerating the convergence rate of iterative algorithms is to integrate an inertial term into the iterative scheme. This term $\gamma _{n}(\mathfrak{s}{n}-\mathfrak{s}{n-1})$ serves as a powerful tool to enhance algorithm performance, showcasing favorable convergence characteristics. The concept of the inertial extrapolation method was initially introduced by Polyak [23] and inspired by an implicit discretization of a second-order-in-time dissipative dynamical system known as the “Heavy Ball with Friction.”

In 2008, Mainge [17] introduced the following inertial Krasnosel’skiı̌–Mann algorithm by integrating the Krasnosel’skiı̌–Mann algorithm with inertial extrapolation:

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} \mathfrak{z}_{n} &= \mathfrak{s}_{n}+\theta _{n}(\mathfrak{s}_{n}- \mathfrak{s}_{n-1}), \\ \mathfrak{s}_{n+1}&=(1-\varsigma _{n})\mathfrak{z}_{n}+\varsigma _{n} \mathbb{S}\mathfrak{z}_{n}, \end{array}\displaystyle \right \}\quad n\geq 1. $$

He demonstrated that the sequence $\{\mathfrak{s}_{n}\}$ generated by the algorithm converges weakly to a fixed point of $\mathbb{S}$ under certain conditions on parameters. This has sparked growing interest among authors working in this area, as evidenced in works such as [2, 4, 6–9, 14].

Question: Could we apply the inertial technique involving projection method for solving GEP, VIP, and FPP for relatively nonexpansive multivalued mapping in the setting of a 2-uniformly convex and uniformly smooth Banach space?

Explanations: Certainly! The inertial technique, when integrated with projection methods, is applicable to address the GEP, VIP, and FPP associated with relatively nonexpansive multivalued mappings in the context of a 2-uniformly convex and uniformly smooth Banach space. The inherent 2-uniform convexity and uniform smoothness properties of the Banach space create favorable conditions for the utilization of these techniques, leading to improved convergence behavior of iterative algorithms.

The inertial technique, characterized by its incorporation of an extrapolation term, is renowned for its capacity to expedite convergence in iterative approaches. When coupled with projection methods, it proves especially advantageous in solving complex problems involving multivalued mappings, equilibrium problems, variational inequalities, and fixed point problems.

Inspired by the contributions of Taiwo et al. [28], Zegeye et al. [32], Mainge [17], and Farid et al. [9], we present a novel iterative algorithm employing the inertial technique. This algorithm aims to determine the common solution of the generalized equilibrium problem (GEP), variational inequality problem (VIP), and fixed point problem (FPP) for relatively nonexpansive multivalued mappings. We delve into the strong convergence properties of our proposed method, highlighting specific aspects of our theorem. Additionally, we provide a computational analysis to underscore the significance of our findings and draw comparisons. The results presented in this paper serve to extend and unify numerous previously established outcomes in this particular research domain.

Our paper is organized as follows: In Sect. 2, we offer basic concepts, essential lemmas, and underlying assumptions. Section 3 encompasses our main results, numerical analysis, and graphical presentations. In Sect. 4, we delve into the interpretation of our results.

2 Preliminaries

Here we present a brief overview of some essential concepts that will be utilized in the subsequent discussion. The modulus of smoothness on the set D is represented by the mapping $\varrho _{D}:[0,\infty )\to [0,\infty )$, defined as follows:

$$ \varrho _{D}(\vartheta )=\sup \{1- \frac{\|\mathfrak{w}_{1}+\mathfrak{w}_{2}\|+\|\mathfrak{w}_{1}-\mathfrak{w}_{2}\|}{2}: \|\mathfrak{w}_{1}\|=1, \|\mathfrak{w}_{2}\|=\vartheta \}. $$

If $\varrho _{D}(\vartheta ) > 0$ for all $\vartheta > 0$, then D is termed smooth, and it is uniformly smooth if and only if $\lim _{s\to 0^{+}}\frac{\varrho _{D}(s)}{s}=0$. The strict convexity of D is characterized by the condition $\frac{|\mathfrak{w}_{1}+\mathfrak{w}_{2}|}{2} < 1$ for all $\mathfrak{w}_{1},\mathfrak{w}_{2}\in \mathbb{U}$ with $\mathfrak{w}_{1}\neq \mathfrak{w}_{2}$, where $\mathbb{U}=\{\mathfrak{w}\in D: \|\mathfrak{w}\|=1\}$.

The modulus of convexity on D is the map $\delta _{D}:(0,2]\to [0,1]$ defined as follows:

$$ \delta _{D}(\varepsilon )=\inf \{1- \frac{\|\mathfrak{w}_{1}+\mathfrak{w}_{2}\|}{2}:\|\mathfrak{w}_{1}\|= \|\mathfrak{w}_{2}\|=1,~\|\mathfrak{w}_{1}-\mathfrak{w}_{2}\|= \varepsilon \}. $$

A space E is uniformly convex if and only if $\delta _{D}(\varepsilon )>0$ for all $\varepsilon \in (0,2]$. In the context of a space E, it is said to be p-uniformly convex if there exists a constant $c_{p}>0$ such that $\delta _{D}(\varepsilon )\geq c_{p}$ for all $\varepsilon \in (0,2]$, as outlined in [30]. For more detailed information, we refer to the cited source.

The Lyapunov function $\phi : E\times E\to \mathbb{R}$ is defined by

$$ \phi (\mathfrak{w}_{1},\mathfrak{w}_{2})=\|\mathfrak{w}_{1}\|^{2}-2 \langle \mathfrak{w}_{1},J\mathfrak{w}_{2}\rangle + \|\mathfrak{w}_{2} \|^{2},~\forall \mathfrak{w}_{1},\mathfrak{w}_{2}\in D. $$

(2.1)

It is worth noting that the characterization of the metric projection on a subset of a Hilbert space as nonexpansive is specific to Hilbert spaces and is not readily applicable to more general Banach spaces. In addressing this limitation, Alber [3] introduced an operator in a Banach space known as the generalized projection, as further discussed in [24].

For $\mathfrak{w}_{1},\mathfrak{w}_{2},\mathfrak{w}_{3}\in D$ and $\lambda \in (0,1)$, the function ϕ as defined by Alber [3] satisfies the following well-known properties:

• (L1) $(\|\mathfrak{w}_{1}-\mathfrak{w}_{2}\|)^{2}\leq \phi (\mathfrak{w}_{1}, \mathfrak{w}_{2})\leq (\|\mathfrak{w}_{1}+\mathfrak{w}_{2}\|)^{2}$;

• (L2) $\phi (\mathfrak{w}_{1},J^{-1}(\lambda J\mathfrak{w}_{2}+(1-\lambda ) J \mathfrak{w}_{3})\leq \lambda \phi (\mathfrak{w}_{1},\mathfrak{w}_{2})+(1- \lambda )\phi (\mathfrak{w}_{1},\mathfrak{w}_{3})$;

• (L3) $\phi (\mathfrak{w}_{1},\mathfrak{w}_{2})=\phi (\mathfrak{w}_{1}, \mathfrak{w}_{3})+\phi (\mathfrak{w}_{3},\mathfrak{w}_{2})+2\langle \mathfrak{w}_{3}-\mathfrak{w}_{1}, J\mathfrak{w}_{2}-J\mathfrak{w}_{3} \rangle$;

• (L4) $\phi (\mathfrak{w}_{1},\mathfrak{w}_{2})\leq 2 \langle \mathfrak{w}_{2}- \mathfrak{w}_{1}, J\mathfrak{w}_{2}-J\mathfrak{w}_{1} \rangle$.

Continuing, we introduce the functional $\Phi :E\times E^{*}\to \mathbb{R}$ defined as

$$ \Phi (\mathfrak{w},\mathfrak{w}^{*})=\|\mathfrak{w}\|^{2}-\langle \mathfrak{w}, \mathfrak{w}^{*}\rangle +\|\mathfrak{w}^{*}\|^{2},~~ \forall \mathfrak{w}\in E,\mathfrak{w}^{*}\in E^{*}. $$

(2.2)

It is worth noting that $\Phi (\mathfrak{w},\mathfrak{w}^{*})=\phi (\mathfrak{w}, J^{-1} \mathfrak{w}^{*})$, and Φ exhibits convexity in its second argument. Additionally,

$$ \Phi (\mathfrak{w},\mathfrak{w}^{*})+2\langle J^{-1}\mathfrak{w}^{*}- \mathfrak{w}, \mathfrak{v}^{*}\rangle \leq \Phi (\mathfrak{w}, \mathfrak{w}^{*}+\mathfrak{v}^{*}); $$

(2.3)

this convexity property holds for all $\mathfrak{w}\in E$ and $\mathfrak{w}^{*}, \mathfrak{v}^{*}\in E^{*}$, as demonstrated in [3].

An element $\mathfrak{w}_{0}\in D$ is referred to as an asymptotic fixed point of $\mathbb{S}:D \to D$ if there exists a sequence $\{\mathfrak{w}_{n}\}\subset D$ with $\mathfrak{w}_{n}\rightharpoonup \mathfrak{w}_{0}$ such that $\lim _{n\to \infty}\|\mathbb{S}\mathfrak{w}_{n}-\mathfrak{w}_{n}\|=0$. We denote the set of asymptotic fixed points as $\widehat{{{\mathrm{F}}}}(\mathbb{S})$. A map $\mathbb{S}$ is considered relatively nonexpansive if $\widehat{{{\mathrm{F}}}}(\mathbb{S})={\mathrm{F}}(\mathbb{S})\neq \emptyset ~ \text{and}~\phi (\mathfrak{w}_{0},\mathbb{S}\mathfrak{w})\leq \phi ( \mathfrak{w}_{0},\mathfrak{w})$, $\forall \mathfrak{w}\in D$, $\mathfrak{w}_{0}\in F(\mathbb{S})$.

Consider $N(D)\neq \emptyset$ as a family of subsets of D, and $CB(D)\neq \emptyset$ as a family of closed bounded subsets of D. The Hausdorff metric, denoted as $\mathbb{H}(D_{1}, D_{2})$, between $D_{1}$ and $D_{2}$ in $CB(D)$ is defined as

$$ \mathbb{H}(D_{1}, D_{2})=\max \{\sup _{\mathfrak{w}\in D_{1}} d( \mathfrak{w},D_{2} ), \sup _{\mathfrak{v}\in D_{2}} d(\mathfrak{v},D_{1} ) \}, $$

where $d(\mathfrak{w},D_{2} )=\inf \{ \|\mathfrak{w} - \mathfrak{w}_{0}\|: \mathfrak{w}_{0} \in D_{1}\}$.

A map $\mathbb{S}:D \to N(D)$ is nonexpansive if $\mathbb{H}(\mathbb{S}w_{1},\mathbb{S}w_{2})\leq \|w_{1}-w_{2}\|$. An element $w_{0}\in D$ is considered an asymptotic fixed point if there exists a sequence $\{w_{n}\}\subset D$ such that $w_{n}\rightharpoonup w_{0}$ and $\lim _{n\to \infty}d(\mathbb{S}w_{n},w_{n})=0$.

A map $\mathbb{S}$ is said to be relatively nonexpansive if $\widehat{{{\mathrm{F}}}}(\mathbb{S})={\mathrm{F}}(\mathbb{S})\neq \emptyset$ and $\phi (w_{0},s)\leq \phi (w_{0},v)$ for all $v\in D$, $s\in \mathbb{S}v$, and $w_{0}\in F(\mathbb{S})$. It is worth noting that Homaeipour et al. [13] provided a counterexample for a relatively nonexpansive multivalued mapping that is not nonexpansive.

Definition 2.1

A map $\mathfrak{h}:E\to E^{*}$ is called

• (i) monotone if $\langle \mathfrak{w}_{1}-\mathfrak{w}_{2}, \mathfrak{h}\mathfrak{w}_{1}- \mathfrak{h}\mathfrak{w}_{2} \rangle \geq 0,~~~\forall \mathfrak{w}_{1}$, $\mathfrak{w}_{2}\in E$;

• (ii) σ-inverse strongly monotone (in short, ism) if there is $\sigma > 0$ such that

  $$ \langle \mathfrak{w}_{1}-\mathfrak{w}_{2}, \mathfrak{h}\mathfrak{w}_{1}- \mathfrak{h}\mathfrak{w}_{2} \rangle \geq \sigma \|\mathfrak{h} \mathfrak{w}_{1}-\mathfrak{h}\mathfrak{w}_{2}\|^{2},~~\forall \mathfrak{w}_{1},\mathfrak{w}_{2}\in {E}; $$

• (iii) Lipschitz continuous if there is $L > 0$ such that $\|\mathfrak{h}\mathfrak{w}_{1}-\mathfrak{h}\mathfrak{w}_{2} \|\leq L \|\mathfrak{w}_{1}-\mathfrak{w}_{2}\|$.

Lemma 2.1

[15] Consider a smooth uniformly convex Banach space E and two sequences $\{\mathfrak{u}_{n}\}$ and $\{\mathfrak{v}_{n}\}$ in E such that either $\{\mathfrak{u}_{n}\}$ or $\{\mathfrak{v}_{n}\}$ is bounded. If $\lim _{n\to \infty}\phi (\mathfrak{u}_{n},\mathfrak{v}_{n})=0$, then $\lim _{n\to \infty}\|\mathfrak{u}_{n}-\mathfrak{v}_{n}\|=0$.

Remark 2.1

It is evident that the converse of Lemma 2.1 holds whenever both sequences $\{\mathfrak{u}_{n}\}$ and $\{\mathfrak{v}_{n}\}$ are bounded, as discussed in [15].

Lemma 2.2

[21] Let D be a nonempty closed convex subset of a real Banach space E, and let $\mathfrak{h}$ be a monotone hemicontinuous mapping from D into $E^{*}$. Then the solution set of the VIP (1.3), denoted as ${\mathrm{VIP}}(D, \mathfrak{h})={\mathrm{Sol(VIP\textit{(1.3)})}}$, is closed and convex.

Lemma 2.3

[13] Consider a strictly convex and smooth Banach space E and a nonempty closed convex subset D of E. Let $\mathbb{S}:D\to CB(D)$ be a relatively nonexpansive multivalued mapping. Then the fixed point set ${\mathrm{F}}(\mathbb{S})$ is closed and convex.

Lemma 2.4

[3] In a reflexive strictly convex smooth Banach space E, with D being a nonempty closed convex subset of E, the following inequality holds for all $\mathfrak{w}\in D$ and $\mathfrak{v}\in E$:

$$ \phi (\mathfrak{w},\Pi _{D}\mathfrak{v})+\phi (\Pi _{D}\mathfrak{v}, \mathfrak{v})\leq \phi (\mathfrak{w},\mathfrak{v}). $$

Lemma 2.5

[3] In a reflexive strictly convex Banach space E, considering a nonempty closed convex subset D of a smooth Banach space E, and given $\mathfrak{w}\in E$ and $\mathfrak{z}\in D$, we have the following equivalence:

$$ \mathfrak{z}=\Pi _{D}\mathfrak{w} \Longleftrightarrow \langle \mathfrak{z}-\mathfrak{v},J\mathfrak{w}-Jw\rangle \geq 0,~~~\forall \mathfrak{v}\in D. $$

Lemma 2.6

[31] For a closed ball $E_{R}(0)$ of a uniformly convex Banach space E, there exists a continuous strictly increasing convex function $g:[0,\infty )\to [0,\infty )$ with $g(0)=0$ such that

$$ \|\lambda _{1}\mathfrak{w}_{1}+\lambda _{2}\mathfrak{w}_{2}+\cdots + \lambda _{N}\mathfrak{w}_{N}\|^{2}\leq \sum \limits _{i=1}^{N} \lambda _{i}\|\mathfrak{w}_{i}\|^{2}-\lambda _{i}\lambda _{j}g(\| \mathfrak{w}_{i}-\mathfrak{w}_{j})\|), $$

where $\lambda _{i}\in (0,1)$ with $\sum \limits _{i=1}^{N} \lambda _{i}=1$, and $\mathfrak{w}{i}\in E_{R}(0)=\{\mathfrak{w}\in E:\|\mathfrak{w}\| \leq R\}$.

Lemma 2.7

[18] Let $\{c_{n}\}$ be a sequence of real numbers that is nondecreasing at infinity. Then there exists a subsequence $\{c_{n_{i}}\}$ of $\{c_{n}\}$ such that $c_{n_{i}}< c_{n_{i+1}}$ for all $i\in \mathbb{N}$. Additionally, for a nondecreasing sequence $\{m_{k}\}\subset \mathbb{N}$ with $m_{k}\to \infty$ and $m_{k}=\max \{j\leq k:c_{j}\leq c_{j+1}\}$, it satisfies the inequalities

$$ c_{m_{k}}\leq c_{m_{k+1}}, ~~~c_{k}\leq c_{m_{k+1}}. $$

Lemma 2.8

[22] Let $\{c_{n}\}$ be a sequence of nonnegative real numbers satisfying

$$ c_{n+1}\leq (1-\gamma _{n})c_{n}+\gamma _{n}\xi _{n},~~n\geq m, ~~{ \mathrm{for~some}}~m\in N, $$

where $\gamma _{n}\in (0,1)$ and $\xi _{n}\in R$ with $\lim \limits _{n\to \infty}\gamma _{n}=0$, $\sum \limits _{n=1}^{ \infty}\gamma _{n}=\infty$, and $\limsup \limits _{n\to \infty}\xi _{n}\leq 0$. Then $\lim \limits _{n\to \infty}c_{n}=0$.

Lemma 2.9

[25] Let E be a p-uniformly convex Banach space. Then the relation between the metric and Bregman distance is

$$ \pi _{p}\|\mathfrak{w}-\mathfrak{v}\|^{p}\leq D_{p}(\mathfrak{w}, \mathfrak{v})\leq \langle \mathfrak{w}-\mathfrak{v}, J_{E}^{p}( \mathfrak{w})-J_{E}^{q}(\mathfrak{v}) \rangle $$

for all $\mathfrak{w},\mathfrak{v}\in E$, where $\pi _{p}$ is a fixed positive number. Moreover, using Young’s inequality, for all $p,q>1$ such that $\frac{1}{p}+\frac{1}{q}=1$, we have

$$\begin{aligned} \langle J_{E}^{p}(\mathfrak{w}),\mathfrak{v}\rangle \leq \|J_{E}^{p}( \mathfrak{w})\|\|\mathfrak{v}\| \leq &\frac{1}{q}\|J_{E}^{p}( \mathfrak{w})\|^{q}+\frac{1}{p}\|\mathfrak{v}\|^{p} \\ =&\frac{1}{q}(\|\mathfrak{w}\|^{p-1})^{q}+\frac{1}{p}\|\mathfrak{v} \|^{p} \\ =&\frac{1}{q}\|\mathfrak{w}\|^{p}+\frac{1}{p}\|\mathfrak{v}\|^{p}. \end{aligned}$$

Lemma 2.10

[30] In a 2-uniformly convex Banach space E,

$$ \|\mathfrak{w}-\mathfrak{v}\|\leq \frac{2}{c}\|J\mathfrak{w}-J \mathfrak{v}\| $$

for all $\mathfrak{w},\mathfrak{v}\in E$, where $0< c\leq 1$; c is referred to as the 2-uniformly convex constant of E.

Assumption 2.1

[9] Let $\mathbb{G},\varepsilon :D\times D\to \mathbb{R}$ be bifunctions satisfying the following properties:

• (i) $\mathbb{G}(\mathfrak{w},\mathfrak{w})=0$, $\forall \mathfrak{w}\in D$;

• (ii) $\mathbb{G}$ is monotone, i.e., $\mathbb{G}(\mathfrak{w},\mathfrak{v})+\mathbb{G}(\mathfrak{v}, \mathfrak{w})\leq 0,~~\forall \mathfrak{w}$, $\mathfrak{v}\in D$;

• (iii) for all $\mathfrak{w},\mathfrak{v},\mathfrak{z}\in D$, $\lim \limits _{\alpha \to 0^{+}}\mathbb{G}(\alpha \mathfrak{z}+(1- \alpha )\mathfrak{w},\mathfrak{v})\leq \mathbb{G}(\mathfrak{w}, \mathfrak{v})$;

• (iv) for each $\mathfrak{w}\in D$, $\mathfrak{v}\to \mathbb{G}(\mathfrak{w},\mathfrak{v})$ is convex and lower semicontinuous.

• (v) ε is skew-symmetric, i.e.,

  $$ \varepsilon (\mathfrak{w},\mathfrak{w})-\varepsilon (\mathfrak{w}, \mathfrak{v})-\varepsilon (\mathfrak{v},\mathfrak{w})+\varepsilon ( \mathfrak{v},\mathfrak{v})\geq 0,\quad \forall \, \mathfrak{w}, \mathfrak{v}\in D; $$

• (vi) ε is convex in the second argument;

• (vii) ε is continuous.

For a given $r > 0$, the mapping $\Psi _{r}: E \to D$ is defined as follows:

$$ \begin{aligned} &\Psi _{r}{\mathfrak{w}}=\Big\{ \mathfrak{z}\in D :\mathbb{G}( \mathfrak{v},\mathfrak{z})+\frac{1}{r}\langle \mathfrak{v}- \mathfrak{z},J\mathfrak{z}-J\mathfrak{w}\rangle +\varepsilon ( \mathfrak{z},\mathfrak{v})-\varepsilon (\mathfrak{z},\mathfrak{z}) \geq 0,\;\forall \mathfrak{v}\in D\Big\} ,\\ & \forall \;\; \mathfrak{w}\in E. \end{aligned} $$

(2.4)

Lemma 2.11

[10] Let D be a nonempty closed convex subset of a smooth strictly convex reflexive Banach space E. Let $\mathbb{G},\varepsilon :D\times D\to \mathbb{R}$ satisfy Assumption 2.1. Then the mapping $\Psi _{r}$ defined in (2.4) satisfies the following:

• (i) $\Psi _{r}$ is single-valued;

• (ii) $\langle \Psi _{r}{\mathfrak{w}}-\Psi _{r}{\mathfrak{v}},J\Psi _{r}{ \mathfrak{w}}-J\Psi _{r}\mathfrak{v}\rangle \leq \langle \Psi _{r}{ \mathfrak{w}}-\Psi _{r}{\mathfrak{v}},J{\mathfrak{w}}-J\mathfrak{v} \rangle , \quad \forall \;\; \mathfrak{w}$, $\mathfrak{v}\in E$;

• (iii) ${\mathrm{F}}(\Psi _{r})={\mathrm{Sol(GEP\textit{(1.1)})}}$ is closed and convex;

• (iv) $\phi (q,\Psi _{r}{\mathfrak{w}})+\phi (\Psi _{r}{\mathfrak{w}}, \mathfrak{w})\leq \phi (q,\mathfrak{w})$, $\quad \forall \;\; q\in { \mathrm{F}}(\Psi _{r})$, $\mathfrak{w}\in E$.

3 Main outcome

Let $\mathbb{G},\varepsilon : D\times D\to \mathbb{R}$ be bifunctions, and let $\mathfrak{h}: E\to E^{*}$ be a nonlinear mapping. Let $\mathcal{S}_{i}: D\to CB(D)$, $i=1, 2, 3,\ldots,\mathbb{N}$, represent a finite family of multivalued mappings. We now present our algorithm.

Algorithm 3.1

Theorem 3.1

Let E be a 2-uniformly convex and uniformly smooth real Banach space with dual space $E^{*}$, and let D be a nonempty closed convex subset of E. Consider bifunctions $\mathbb{G},\varepsilon :D\times D\to \mathbb{R}$ that satisfy Assumption 2.1, and let $\mathfrak{h}:E\to E^{*}$ be a σ-ism mapping, where $\sigma \in (0,1)$. Additionally, let $\mathcal{S}_{i}:D\to CB(D)$, $i=1, 2, 3,\ldots,\mathbb{N}$, constitute a finite family of relatively nonexpansive multivalued mappings. Suppose $\Theta :=\cap _{i=1}^{\mathbb{N}}{\mathrm{F}}(\mathcal{S}_{i})\cap{\mathrm{Sol(GEP(\textit{1.1}))}}\cap {\mathrm{Sol(VIP(\textit{1.3}))}} \neq \emptyset$. Then the sequence $\{\mathfrak{s}_{n}\}$ generated by Algorithm 3.1converges strongly to $x^{*}\in \Theta$, where $x^{*}=\Pi _{\Theta}\mathfrak{s}_{0}$.

Proof

We state that the sequence $\{\mathfrak{s}_{n}\}$ is bounded. Consider any $q\in \Theta$. Using properties of ϕ, we estimate

$$\begin{aligned} \phi (q,\mathfrak{u}_{n}) =&\phi (q,\Pi _{D}J^{-1}(\varsigma _{n}J \mathfrak{z}_{n}+(1-\varsigma _{n})J\mathfrak{t}_{n})) \\ \leq &\phi (q,J^{-1}(\varsigma _{n}J\mathfrak{z}_{n}+(1-\varsigma _{n})J \mathfrak{t}_{n})) \\ =&\|q\|^{2}-2\langle q, \varsigma _{n}J\mathfrak{z}_{n}+(1- \varsigma _{n})J\mathfrak{t}_{n} \rangle + \|\varsigma _{n}J \mathfrak{z}_{n}+(1-\varsigma _{n})J\mathfrak{t}_{n}\|^{2} \\ \leq & \|q\|^{2}-2\varsigma _{n}\langle q, J\mathfrak{z}_{n}\rangle -2(1- \varsigma _{n})\langle q, J\mathfrak{t}_{n} \rangle +\varsigma _{n} \|\mathfrak{z}_{n}\|^{2}+(1-\varsigma _{n})\|\mathfrak{t}_{n}\|^{2} \\ \leq & \varsigma _{n} \phi (q,\mathfrak{z}_{n})+(1-\varsigma _{n}) \phi (q,\mathfrak{t}_{n}). \end{aligned}$$

(3.1)

Using Lemmas 2.4, 2.5, and 2.10, we compute

$$\begin{aligned} \phi (q,\mathfrak{t}_{n}) =&\phi (q,\Pi _{D}J^{-1}(J\mathfrak{z}_{n}- \eta _{n}\mathfrak{h}\mathfrak{z}_{n}) \\ \leq &\phi (q,J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h} \mathfrak{z}_{n}) \\ =&\Phi (q,J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n}) \\ \leq & \Phi (q,J\mathfrak{z}_{n})-2\eta _{n}\langle (J\mathfrak{z}_{n}- \eta _{n}\mathfrak{h}\mathfrak{z}_{n})-q, A\mathfrak{z}_{n} \rangle \\ =&\phi (q,\mathfrak{z}_{n})- 2\eta _{n}\langle \mathfrak{z}_{n}-q, \mathfrak{h}\mathfrak{z}_{n} \rangle - 2\eta _{n}\langle J^{-1}(J \mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})-\mathfrak{z}_{n}, A\mathfrak{z}_{n} \rangle \\ =&\phi (q,\mathfrak{z}_{n})- 2\eta _{n}\langle \mathfrak{z}_{n}-q, \mathfrak{h}\mathfrak{z}_{n}-\mathfrak{h}q \rangle - 2\eta _{n} \langle J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})- \mathfrak{z}_{n}, \mathfrak{h}\mathfrak{z}_{n} \rangle \\ \leq & \phi (q,\mathfrak{z}_{n})- 2\eta _{n}\sigma \|\mathfrak{h} \mathfrak{z}_{n}\|^{2}+2\eta _{n}\|J^{-1}(J\mathfrak{z}_{n}-\eta _{n} \mathfrak{h}\mathfrak{z}_{n})-J^{-1}J\mathfrak{z}_{n}\|\|\mathfrak{h} \mathfrak{z}_{n}\| \\ \leq & \phi (q,\mathfrak{z}_{n})- 2\eta _{n}\sigma \|\mathfrak{h} \mathfrak{z}_{n}\|^{2}+4\frac{\eta _{n}^{2}}{c^{2}}\|\mathfrak{h} \mathfrak{z}_{n}\|^{2} \\ =& \phi (q,\mathfrak{z}_{n})- 2\eta _{n}(\sigma - \frac{2\eta _{n}}{c^{2}}) \|\mathfrak{h}\mathfrak{z}_{n}\|^{2}. \end{aligned}$$

(3.2)

Since $\eta _{n}<\frac{c^{2}\sigma}{2}$,

$$ \phi (q,\mathfrak{t}_{n}) \leq \phi (q,\mathfrak{z}_{n}). $$

(3.3)

By (3.1) and (3.3) we get

$$ \phi (q,\mathfrak{u}_{n}) \leq \varsigma _{n} \phi (q,\mathfrak{z}_{n})+(1- \varsigma _{n})\phi (q,\mathfrak{z}_{n})=\phi (q,\mathfrak{z}_{n}). $$

(3.4)

Since $\mathfrak{z}_{n}=J^{-1}(J\mathfrak{s}_{n}+\gamma _{n}(J\mathfrak{s}_{n}-J \mathfrak{s}_{n-1}))$, by using Lemma 2.9 we estimate

$$\begin{aligned} \langle \mathfrak{z}_{n}-q, J\mathfrak{z}_{n}-J\mathfrak{s}_{n} \rangle \leq &\|\mathfrak{z}_{n}-q\| \| J\mathfrak{z}_{n}-J \mathfrak{s}_{n}\| \\ =&\gamma _{n}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1}\| \| \mathfrak{z}_{n}-\mathfrak{s}_{n}\| \\ \leq &\gamma _{n}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1}\| [ \frac{1}{2}\|\mathfrak{z}_{n}-\mathfrak{s}_{n}\|^{2}+\frac{1}{2}] \\ \leq &\frac{\gamma _{n}}{2}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1} \|[2(\|\mathfrak{s}_{n}-\mathfrak{z}_{n}\|^{2}+\|\mathfrak{s}_{n}-q\|^{2})]+ \frac{\gamma _{n}}{2}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1}\| \\ \leq &\frac{\gamma _{n}}{2}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1} \|(\phi (\mathfrak{s}_{n},\mathfrak{z}_{n})+\phi (\mathfrak{s}_{n},q))+ \frac{\gamma _{n}}{2}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1}\| \\ \leq & \frac{\lambda _{n}}{2}(\phi (\mathfrak{s}_{n},\mathfrak{z}_{n})+ \phi (\mathfrak{s}_{n},q))+\frac{\lambda _{n}}{2},~~{\mathrm{where}}~ \lambda _{n}= \gamma _{n}\| J\mathfrak{s}_{n}-J\mathfrak{s}_{n-1}\|. \end{aligned}$$

(3.5)

Using property (L3) of ϕ, we get

$$ \phi (q,\mathfrak{z}_{n}) = \phi (q,\mathfrak{s}_{n})-\phi ( \mathfrak{z}_{n},\mathfrak{s}_{n})+\langle q-\mathfrak{z}_{n}, J \mathfrak{z}_{n}-J\mathfrak{s}_{n} \rangle . $$

(3.6)

Combining (3.5) and (3.6), we get

$$\begin{aligned} \phi (q,\mathfrak{z}_{n}) \leq & (1+\frac{\lambda _{n}}{2})\phi (q, \mathfrak{s}_{n})-(1-\frac{\lambda _{n}}{2})\phi (\mathfrak{s}_{n}, \mathfrak{z}_{n})+ \frac{\lambda _{n}}{2} \\ \leq &(1+\varsigma _{n})\phi (q,\mathfrak{s}_{n})-(1-\varsigma _{n}) \phi (\mathfrak{s}_{n},\mathfrak{z}_{n})+ \varsigma _{n},~~{\mathrm{take~ \frac{\lambda _{n}}{2}< \varsigma _{n}}} \\ \leq &(1+\varsigma _{n})\phi (q,\mathfrak{s}_{n})+ \varsigma _{n}. \end{aligned}$$

(3.7)

Next, using (3.7), we compute

$$\begin{aligned} \phi (q,\mathfrak{s}_{n+1}) =&\phi (q,J^{-1}(\delta _{n,0}J \mathfrak{v}_{n}+\sum \limits _{i=1}^{N}\delta _{n,i} J\mathfrak{w}_{n,i}) \\ \leq &\delta _{n,0} \phi (q,\mathfrak{v}_{n})+\sum \limits _{i=1}^{N} \delta _{n,i}\phi (q,\mathfrak{w}_{n,i}) \\ \leq &\delta _{n,0} \phi (q,T_{r_{n}}\mathfrak{u}_{n})+\sum \limits _{i=1}^{N} \delta _{n,i}\phi (q,\mathfrak{w}_{n,i}) \\ \leq &\delta _{n,0} \phi (q,\mathfrak{u}_{n})+(1-\delta _{n,0})\phi (q, \mathfrak{u}_{n}) \\ \leq &\phi (q,\mathfrak{u}_{n})\leq \phi (q,\mathfrak{z}_{n}) \\ \leq &(1+\varsigma _{n})\phi (q,\mathfrak{s}_{n})+ \varsigma _{n}. \end{aligned}$$

(3.8)

Using induction, we get

$$ \phi (q,\mathfrak{s}_{n})\leq \max \{\phi (q,\mathfrak{s}_{N})\}, ~~~ \forall n\geq \mathbb{N}. $$

This concludes that $\{\mathfrak{s}_{n}\}$ is bounded, and consequently, $\{\mathfrak{z}_{n}\}$, $\{\mathfrak{t}_{n}\}$, $\{\mathfrak{u}_{n}\}$, and $\{\mathfrak{v}_{n}\}$ are also bounded.

Next, we show that $q\in \Theta$ and $\mathfrak{s}_{n}\to q$. Setting $\rho _{n}=J^{-1}(\varsigma _{n}J\mathfrak{z}_{n}+(1-\varsigma _{n})J \mathfrak{t}_{n})$. Let $q\in \Theta$. Then by (2.3) we compute

$$\begin{aligned} \phi (q,\mathfrak{u}_{n}) \leq &\phi (q,\rho _{n})=\Phi (q,J\rho _{n}) \\ \leq &\Phi (q,J\rho _{n}-\varsigma _{n}(J\mathfrak{z}_{n}-Jq))-2 \langle \rho _{n}-q, -\varsigma _{n}(J\mathfrak{z}_{n}-Jq) \rangle \\ =&\phi (q,J^{-1}(\varsigma _{n}Jq+(1-\varsigma _{n})J\mathfrak{t}_{n}))+2 \varsigma _{n}\langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle \\ \leq &(1-\varsigma _{n})\phi (q,\mathfrak{t}_{n})+2\varsigma _{n} \langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle \\ \leq &(1-\varsigma _{n})\phi (q,\mathfrak{z}_{n})+2\varsigma _{n} \langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle . \end{aligned}$$

(3.9)

Using the concept of $\mathcal{S}_{i}$ and Lemmas 2.6, 2.11, and (3.9), we compute

$$\begin{aligned} \phi (q,\mathfrak{s}_{n+1}) =&\phi (q,J^{-1}(\delta _{n,0}J \mathfrak{v}_{n}+\sum \limits _{i=1}^{\mathbb{N}}\delta _{n,i} J \mathfrak{w}_{n,i})) \\ \leq &\delta _{n,0}\phi (q,\mathfrak{v}_{n})+\sum \limits _{i=1}^{ \mathbb{N}}\delta _{n,i}\phi (q,\mathfrak{w}_{n,i})-\delta _{n,0} \delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i}\|) \\ =&\delta _{n,0}\phi (q,\Psi _{r_{n}}\mathfrak{u}_{n})+\sum \limits _{i=1}^{ \mathbb{N}}\delta _{n,i}\phi (q,\mathfrak{w}_{n,i})-\delta _{n,0} \delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i}\|) \\ \leq &\delta _{n,0}(\phi (q,\mathfrak{u}_{n})-\phi (\mathfrak{u}_{n}, \mathfrak{v}_{n}))+(1-\delta _{n,0})\phi (q,\mathfrak{u}_{n})-\delta _{n,0} \delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i}\|) \\ \leq &(1-\varsigma _{n})\phi (q,\mathfrak{z}_{n})+2\varsigma _{n} \langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle -\delta _{n,0}\phi ( \mathfrak{u}_{n},\mathfrak{v}_{n}) \\ &-\delta _{n,0}\delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i} \|) \\ \leq &(1-\varsigma _{n}^{2})\phi (q,\mathfrak{s}_{n})-(1-\varsigma _{n})^{2} \phi (\mathfrak{s}_{n},\mathfrak{z}_{n})+ \varsigma _{n}(1-\varsigma _{n}) +2\varsigma _{n}\langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle \\ &-\delta _{n,0}\phi (\mathfrak{u}_{n},\mathfrak{v}_{n})-\delta _{n,0} \delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i}\|), \end{aligned}$$

(3.10)

which implies that

$$ \phi (q,\mathfrak{s}_{n+1})\leq (1-\varsigma _{n}^{2})\phi (q, \mathfrak{s}_{n})+2\varsigma _{n}\langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle + \varsigma _{n}(1-\varsigma _{n}). $$

(3.11)

We are evaluating two scenarios outlined below.

Case 1. Assume that for some $m_{0}\in \mathbb{N}$, $\phi (q,\mathfrak{s}_{n})$ is nonincreasing for all $n\geq m_{0}$, and since $\phi (q,\mathfrak{s}_{n})$ is bounded, it must be convergent. Therefore by utilizing (3.10) it follows that $\phi (\mathfrak{s}_{n},\mathfrak{z}_{n})\to 0$ and $\phi (\mathfrak{u}_{n},\mathfrak{v}_{n})\to 0$ as $n\to \infty$. Additionally, according to (2.1), we obtain

$$ \lim \limits _{n\to \infty}\|\mathfrak{s}_{n}-\mathfrak{z}_{n}\|=0~~{ \mathrm{and}}~~\lim \limits _{n\to \infty}\|\mathfrak{u}_{n}-\mathfrak{v}_{n} \|=0. $$

(3.12)

Also, by (3.10), $\delta _{n,0}\delta _{n,i}g(\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i} \|)\to 0$ as $n\to \infty$, which yields that $\|J\mathfrak{v}_{n}-J\mathfrak{w}_{n,i}\|\to 0$, and thus by the uniform continuity of $J^{-1}$ we have

$$ \lim \limits _{n\to \infty}\|\mathfrak{v}_{n}-\mathfrak{w}_{n,i}\|=0~~{ \mathrm{for ~ all}}~i=1,2,\ldots, \mathbb{N}. $$

(3.13)

Using (3.1) and (3.2), we get

$$\begin{aligned} \phi (q,\mathfrak{u}_{n}) \leq & \varsigma _{n} \phi (q,\mathfrak{z}_{n})+(1- \varsigma _{n})\phi (q,\mathfrak{t}_{n}) \\ \leq & \phi (q,\mathfrak{z}_{n})-2\eta _{n}(\sigma - \frac{2\eta _{n}}{c^{2}}) \|\mathfrak{h}\mathfrak{z}_{n}\|^{2}, \end{aligned}$$

which yields that

$$ 2\eta _{n}(\sigma -\frac{2\eta _{n}}{c^{2}}) \|\mathfrak{h} \mathfrak{z}_{n}\|^{2} \leq \phi (q,\mathfrak{z}_{n})-\phi (q, \mathfrak{u}_{n}). $$

(3.14)

Since $\liminf \limits _{n\to \infty}(1-\varsigma _{n})>0$, $\eta _{n}( \sigma -\frac{2\eta _{n}}{c^{2}})>0$, we have

$$ \lim \limits _{n\to \infty}\|\mathfrak{h}\mathfrak{z}_{n}\|=0. $$

(3.15)

Using (2.3) and Lemma 2.10, we get

$$\begin{aligned} \phi (\mathfrak{z}_{n},\mathfrak{t}_{n}) =&\phi (\mathfrak{z}_{n}, \Pi _{D}J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})) \\ \leq &\phi (\mathfrak{z}_{n},J^{-1}(J\mathfrak{z}_{n}-\eta _{n} \mathfrak{h}\mathfrak{z}_{n})) \\ \leq & \Phi (\mathfrak{z}_{n},(J\mathfrak{z}_{n}-\eta _{n} \mathfrak{h}\mathfrak{z}_{n})) \\ \leq & \Phi (\mathfrak{z}_{n},(J\mathfrak{z}_{n}-\eta _{n} \mathfrak{h}\mathfrak{z}_{n})+\eta _{n}\mathfrak{h}\mathfrak{z}_{n})-2 \langle J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})- \mathfrak{z}_{n},\eta _{n}\mathfrak{h}\mathfrak{z}_{n} \rangle \\ =& \phi (\mathfrak{z}_{n},\mathfrak{z}_{n})+2\langle J^{-1}(J \mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})-\mathfrak{z}_{n},- \eta _{n}\mathfrak{h}\mathfrak{z}_{n} \rangle \\ =& 2\eta _{n}\langle J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h} \mathfrak{z}_{n})-\mathfrak{z}_{n},-\mathfrak{h}\mathfrak{z}_{n} \rangle \\ \leq &\|J^{-1}(J\mathfrak{z}_{n}-\eta _{n}\mathfrak{h}\mathfrak{z}_{n})-J^{-1}J \mathfrak{z}_{n}\| \\ \leq &\frac{4}{c^{2}}\eta _{n}^{2}\|\mathfrak{h}\mathfrak{z}_{n}\|^{2}, \end{aligned}$$

(3.16)

and by (3.15)

$$ \lim \limits _{n\to \infty}\phi (\mathfrak{z}_{n},\mathfrak{t}_{n})= 0. $$

(3.17)

By Lemma 2.1

$$ \mathfrak{z}_{n}-\mathfrak{t}_{n}\to 0~~{\mathrm{as}}~n\to \infty . $$

(3.18)

Applying Lemmas 2.4 and 2.5, we compute

$$\begin{aligned} \phi (\mathfrak{z}_{n},\mathfrak{u}_{n}) =&\phi (\mathfrak{z}_{n}, \Pi _{D}\rho _{n})\leq \phi (\mathfrak{z}_{n},\rho _{n}) \\ =&\phi (\mathfrak{z}_{n},J^{-1}(\varsigma _{n}J\mathfrak{z}_{n}+(1- \varsigma _{n})J\mathfrak{t}_{n})) \\ \leq & \varsigma _{n}\phi (\mathfrak{z}_{n},\mathfrak{z}_{n})+(1- \varsigma _{n})\phi (\mathfrak{z}_{n},\mathfrak{t}_{n})\to 0~~{\mathrm{as}}~n \to \infty , \end{aligned}$$

(3.19)

which implies that

$$ \mathfrak{z}_{n}-\mathfrak{u}_{n}\to 0,~~~ \mathfrak{z}_{n}-\rho _{n} \to 0~~{\mathrm{as}}~n\to \infty . $$

(3.20)

Thus ${\mathrm{for ~ each}}~i=1,2,\ldots, \mathbb{N}$, we have

$$ d(\mathfrak{u}_{n}-\mathcal{S}_{i}\mathfrak{u}_{n})\leq \| \mathfrak{u}_{n}-\mathfrak{w}_{n,i}\|\leq \|\mathfrak{u}_{n}- \mathfrak{v}_{n}\|+\|\mathfrak{v}_{n}-\mathfrak{w}_{n,i}\|\to 0~~{ \mathrm{as}}~n\to \infty . $$

(3.21)

Let $\{\rho _{n_{i}}\}$ be a subsequence of $\{\rho _{n}\}$ such that $\rho _{n_{i}}\rightharpoonup \rho$ and $\sup \limits _{n\to \infty}\langle \rho _{n}-q,J\mathfrak{z}_{n}-Jq \rangle =\lim \limits _{i\to \infty}\langle \rho _{n_{i}}-q,J \mathfrak{z}_{n_{i}}-Jq \rangle$. Thus by (3.18), (3.20), and the concept of J we get

$$ \mathfrak{u}_{n_{i}}, \mathfrak{v}_{n_{i}}\rightharpoonup \rho ,~J \mathfrak{u}_{n}-J\mathfrak{v}_{n}\to 0 ~~{\mathrm{as}}~n\to \infty . $$

(3.22)

Next, we show that $q \in {\mathrm{Sol(VIP\text{(1.3)})}}$. Applying the concept of σ-ism mapping of $\mathfrak{h}$, by (3.15) and (3.12) we obtain $\lim \limits _{n\to \infty}\mathfrak{s}_{n}= q$ and $q\in \mathfrak{h}^{-1}(0)$. Hence $q \in {\mathrm{Sol(VIP\text{(1.3)})}}$.

Further, we need to show that $q\in {\mathrm{Sol(GEP\text{(1.1)})}}$. Since $\mathfrak{v}_{n}=\Psi _{r_{n}}\mathfrak{u}_{n}$, ${\mathrm{for ~ each}}~i=1,2,\ldots, \mathbb{N}$, we get

$$ \mathbb{G}(\mathfrak{v}_{n_{i}},y)+\varepsilon (y,\mathfrak{v}_{n_{i}})- \varepsilon (\mathfrak{v}_{n_{i}},\mathfrak{v}_{n_{i}})+ \frac{1}{r_{n_{i}}}\langle y-\mathfrak{v}_{n_{i}}, J\mathfrak{v}_{n_{i}}-J \mathfrak{u}_{n_{i}} \rangle \geq 0,~~\forall y\in D. $$

Let $y_{s}=(1-s)q+sy$, $\forall s\in (0,1]$. Since $y\in D$ and $q\in D$, we get $y_{s}\in D$, and hence

$$ \mathbb{G}(\mathfrak{v}_{n_{i}},y_{s})+\varepsilon (y_{s}, \mathfrak{v}_{n_{i}})-\varepsilon (\mathfrak{v}_{n_{i}},\mathfrak{v}_{n_{i}})+ \frac{1}{r_{n_{i}}}\langle y_{s}-\mathfrak{v}_{n_{i}}, J\mathfrak{v}_{n_{i}}-J \mathfrak{u}_{n_{i}}\rangle \geq 0. $$

Using the concept of ε and G, we have

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} \mathbb{G}(q,y_{s})+\varepsilon (y_{s},q)-\varepsilon (q,q) &\geq & 0 \\ \varepsilon (y_{s},q)-\varepsilon (q,q)&\geq &\mathbb{G}(y_{s},q). \end{array} $$

For $s > 0$, we have

$$ \textstyle\begin{array}{l@{\quad}l@{\quad}l} 0&=&h(y_{s}, y_{s}) \\ &\leq & s \mathbb{G}(y_{s}, y)+(1-s)h(y_{s}, q) \\ &\leq & s \mathbb{G}(y_{s}, y)+(1-s)[\varepsilon (y_{s},q)- \varepsilon (q,q)] \\ &\leq & s \mathbb{G}(y_{s}, y)+(1-s)s[\varepsilon (y,q)-\varepsilon (q,q)] \\ &\leq & s [\mathbb{G}(y_{s}, y)+(1-s)(\varepsilon (y,q)-\varepsilon (q,q))], \end{array} $$

which yields

$$ \mathbb{G}(q,y)+\varepsilon (y,q)-\varepsilon (q,q)\geq 0. $$

Thus $q\in {\mathrm{Sol(GEP\text{(1.1)})}}$. Further, we prove that $q\in \cap _{i=1}^{\mathbb{N}}{\mathrm{F}}(\mathcal{S}_{i})$. Using (3.20), (3.22), and the concept of $\mathcal{S}$, we get $q\in {\mathrm{F}}(\mathcal{S}_{i})$ and $q\in \cap _{i=1}^{\mathbb{N}}{\mathrm{F}}(\mathcal{S}_{i})$. Hence $q\in \Theta$. By Lemma 2.5 we get $\sup \limits _{n\to \infty}\langle \rho _{n}-x^{*}, J\mathfrak{z}_{n}-Jx^{*} \rangle = \lim \limits _{i\to \infty} \langle \rho _{n_{i}}-x^{*}, J \mathfrak{z}_{n_{i}}-Jx^{*} \rangle \leq 0$. By Lemma 2.8 and (3.11), $\phi (\mathfrak{s}_{n},x^{*})\to 0$. Further, using Lemma 2.1, we obtain that $\{\mathfrak{s}_{n}\}$ converges strongly to $x^{*}=\Pi _{\Theta}\mathfrak{s}_{0}$.

Case 2. Let $\{\phi (q,\mathfrak{s}_{n})\}$ be not decreasing. Then there exists a subsequence $\{\mathfrak{s}_{n_{i}}\}$ of $\{\mathfrak{s}_{n}\}$ such that $\phi (q,\mathfrak{s}_{n_{i}})<\phi (q,\mathfrak{s}_{n_{i+1}})$ ${\mathrm{for ~ each}}~i=1,2,\ldots, \mathbb{N}$. By Lemma 2.7 there exists a nondecreasing sequence $\{m_{j}\}\subset \mathbb{N}$ such that $m_{j}\to \infty$ and $\phi (q,\mathfrak{s}_{m_{j}})\leq \phi (q,\mathfrak{s}_{m_{j+1}})$ and $\phi (q,\mathfrak{s}_{j})\leq \phi (q,\mathfrak{s}_{m_{j+1}})$ for $j\in \mathbb{N}$. Using (3.10), we get

$$\begin{aligned} (1-\varsigma _{m_{j}})^{2}\phi (\mathfrak{s}_{m_{j}},\mathfrak{z}_{m_{j}})+ \delta _{m_{j},0}\phi (\mathfrak{u}_{m_{j}},\mathfrak{v}_{m_{j}}) +& \delta _{m_{j},0}\delta _{m_{j},i}g(\|J\mathfrak{v}_{m_{j}}-J \mathfrak{w}_{m_{j},i}\|) \\ \leq &(1-\varsigma _{m_{j}}^{2})\phi (x^{*},\mathfrak{s}_{m_{j}})- \phi (x^{*},\mathfrak{s}_{m_{j}+1})\\ &+ \varsigma _{m_{j}}(1-\varsigma _{m_{j}}) \\ &+2\varsigma _{m_{j}}\langle \rho _{m_{j}}-x^{*},J\mathfrak{z}_{m_{j}}-Jx^{*} \rangle . \end{aligned}$$

Using arguments similar to those in case 1, we have that for each $i=1,2,\ldots, \mathbb{N}$, $\mathfrak{s}_{m_{j}}-\mathfrak{z}_{m_{j}}\to 0$, $\mathfrak{v}_{m_{j}}-\mathfrak{w}_{m_{j},i}\to 0$, and $\mathfrak{v}_{m_{j}}-\mathfrak{w}_{m_{j},i}\to 0$ as $j\to \infty$.

Thus

$$ \limsup \limits _{j\to \infty} \langle \rho _{m_{j}}-x^{*},J \mathfrak{z}_{m_{j}}-Jx^{*} \rangle \leq 0. $$

(3.23)

Using (3.11), we obtain

$$ \phi (x^{*},\mathfrak{s}_{m_{j+1}})\leq (1-\varsigma _{n}^{2})\phi (x^{*}, \mathfrak{s}_{m_{j}})+2\varsigma _{m_{j}}\langle \rho _{m_{j}}-x^{*},J \mathfrak{z}_{m_{j}}-Jx^{*} \rangle + \varsigma _{m_{j}}(1-\varsigma _{m_{j}}). $$

(3.24)

Since $\phi (x^{*},\mathfrak{s}_{m_{j}})\leq \phi (x^{*},\mathfrak{s}_{m_{j+1}})$ for each $j\in \mathbb{N}$, from (3.23) and (3.24) we have $\phi (x^{*},\mathfrak{s}_{m_{j}})\to 0$ and $\phi (x^{*},\mathfrak{s}_{m_{j+1}})\to 0$ as $j\to \infty$. Also, $\phi (x^{*},\mathfrak{s}_{j})\leq \phi (x^{*},\mathfrak{s}_{m_{j+1}})$ for each $j\in \mathbb{N}$, and therefore $\mathfrak{s}_{j}\to x^{*}$ as $j\to \infty$. Thus, based on the above two cases, we observe that the sequence $\{\mathfrak{s}_{n}\}$ converges strongly to $x^{*}=\Pi _{\Theta}\mathfrak{s}_{0}$. □

In a similar vein, we proceed to enumerate some corollaries derived from the implications of Theorem 3.1. This enumeration not only serves as a concise summary of the theoretical outcomes but also lays the groundwork for further exploration and application of the proposed iterative scheme in diverse mathematical and computational contexts.

If we specialize Theorem 3.1 by considering the case where $N=1$, a pertinent corollary unfolds. This corollary encapsulates a more specific scenario.

Corollary 3.1

Let E be a 2-uniformly convex and uniformly smooth real Banach space with dual space $E^{*}$, and let D be a nonempty closed convex subset of E. Consider bifunctions $\mathbb{G},\varepsilon :D\times D\to \mathbb{R}$ that satisfy Assumption 2.1, and let $\mathfrak{h}:E\to E^{*}$ be a σ-ism mapping, where $\sigma \in (0,1)$. Additionally, let $\mathcal{S}:D\to CB(D)$ be a relatively nonexpansive multivalued mapping. Suppose $\Theta :={\mathrm{F}}(\mathcal{S})\cap{\mathrm{Sol(GEP\textit{(1.1)})}}\cap { \mathrm{Sol(VIP\textit{(1.3)})}} \neq \emptyset$. Then the sequence $\{\mathfrak{s}_{n}\}$ generated by Algorithm 3.1converges strongly to $x^{*}\in \Theta$, where $x^{*}=\Pi _{\Theta}\mathfrak{s}_{0}$.

Continuing in the same vein, we explore further implications and consequences arising from the conditions established in Theorem 3.1 when $\mathbb{G}$ and ε are specifically assumed to be zero.

Corollary 3.2

Let E bedenote a 2-uniformly convex and uniformly smooth real Banach space, with dual space $E^{*}$, and let D be a nonempty, closed, and convex subset of E. Consider bifunctions $\mathbb{G},\varepsilon :D\times D\to \mathbb{R}$ that satisfy Assumption 2.1, and let $\mathfrak{h}:E\to E^{*}$ be a σ-ism mapping, where $\sigma \in (0,1)$. Additionally, let $\mathcal{S}:D\to CB(D)$ be a relatively nonexpansive multivalued mapping. Suppose $\Theta :=\cap \_{i=1}^{\mathbb{N}}{\mathrm{F}}(\mathcal{S}_{i})\cap {\mathrm{Sol(VIP( \textit{1.3}))}} \neq \emptyset$. Then, the sequence $\{\mathfrak{s}_{n}\}$ generated by Algorithm 3.1converges strongly to $x^{*}\in \Theta$, where $x^{*}=\Pi _{\Theta}\mathfrak{s}_{0}$.

Remark 3.1

If E is a Hilbert space H, then $E^{*}=H$, $J=I$, the identity mapping, $\phi (u,v)=\|u-v\|^{2},~\forall u$, $v\in E$, $c=1$, 2-uniformly convex constant of E, $\Pi _{D}=P_{D}$, the metric projection onto D, and a relatively nonexpansive mapping is nonexpansive. These simplifications result from the specific properties and structures of Hilbert spaces, making certain operations and concepts more straightforward.

3.1 Numerical example

Example 3.1

Consider $E=\mathbb{R}$ and $D=[0,5]$. We define the bimappings $\mathbb{G}$ and ε by $\mathbb{G}(p,s)=p(s-p)$ and $\varepsilon (p,s)=ps$ for $p,s \in \mathbb{R}$. It is obvious that $\mathbb{G}$ and ε satisfy Assumption 2.1. Let $\mathfrak{h}(p)=3p$ and $\mathcal{S}(p)=[0,\frac{p}{8}]$. Here $\mathfrak{h}$ is $\frac{1}{3}$-ism. Also, ${\mathrm{F}}(\mathcal{S})=0$, and for all $s\in \mathcal{S}p$, $\phi (0,s)=|0-s|^{2}\leq |0-p|^{2}=\phi (0,p)$. Let $q\in \hat{{\mathrm{F}}}(\mathcal{S})$. Then there exists $\{p_{n}\}$ such that $p_{n}\rightharpoonup q$ and $d(p_{n},\mathcal{S}p_{n})=\frac{7}{8}|p_{n}|\to 0$ as $n\to \infty$. This yields that $p_{n}\to 0$, and thus $q=0$. Therefore $\hat{{\mathrm{F}}}(\mathcal{S})={\mathrm{F}}(\mathcal{S})=\{0\}$, that is, $\mathcal{S}$ is a relatively nonexpansive multivalued mapping. Notice that $r_{n}=\{\frac{1}{10}\}$, $\eta _{n}=\{\frac{1}{6}\}$, $\varsigma _{n}=\{\frac{1}{10n}\}$, and $\delta _{n,0}=\{\frac{1}{2n+1}\}$ with $\sum \limits _{j=0}^{\mathbb{N}}\delta _{n,j}=1$. Choose $\gamma _{n}=\left \{ \begin{array}{l} \min \{\frac{1}{5(n+1)\|\mathfrak{s}_{n}-\mathfrak{s}_{n-1}\|},~ 0.25 \}~~~{\mathrm{if}}~\mathfrak{s}_{n}\neq \mathfrak{s}_{n-1}, \\ 0.25 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~{\mathrm{else.}} \end{array} \right \}$

Then the sequences originated by Algorithm 3.1 converges to $q=\{0\}\in \Theta$.

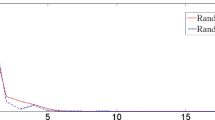
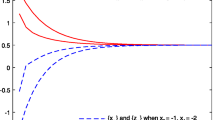
We use Matlab R2015(a) for the computation and comparison of our result with [13, 17]. For the computation and graphical representation of the proposed and Mainge algorithms, we use same initial points $(s_{0},s_{1})$, whereas for Homaeipur et al., we use $s_{1}$. The stopping criterion for our computation is $\|\mathfrak{s}_{n+1}-\mathfrak{s}_{n}\|<10^{-10}$. The computation and comparison graphs are shown in Table 1 and Figs. 1–4, respectively.

Figure 1

Plotting for $(s_{0},s_{1})=(0,0.22)$ and $(s_{0},s_{1})=(1,1.5)$

Figure 2

Plotting for $(s_{0},s_{1})=(0,0.22)$ and $(s_{0},s_{1})=(1,1.5)$

Figure 3

Plotting for $(s_{0},s_{1})=(0.93,1.5)$ and $(s_{0},s_{1})=(1.13,2.4)$

Figure 4

Plotting for $(s_{0},s_{1})=(0.93,1.5)$ and $(s_{0},s_{1})=(1.13,2.4)$

Table 1 Comparison of Algorithms

4 Conclusions

In conclusion, our investigation has yielded several key findings. The proposed algorithm, presented in this work, demonstrates strong convergence to a solution in 2-uniformly convex and uniformly smooth real Banach space setting with relatively nonexpansive multivalued mapping. The theoretical results are supported by numerical experiments, where we employed Matlab R2015(a) for computation and compared our findings with existing algorithms, particularly those proposed by Homaeipour et al. and Mainge. The use of consistent initial points and a specified stopping criterion allowed for a fair comparison across different algorithms. The results presented in Table 1 and Figs. 1–4 showcase the effectiveness of our approach in terms of convergence behavior. These findings contribute to the ongoing research in optimization algorithms and provide valuable insights into the applicability of the proposed method in various contexts.