Abstract
The present research is aimed to analyze the existence of strict fixed points (SFPs) and fixed points of multivalued generalized contractions on the platform of controlled metric spaces (CMSs). Wardowski-type multivalued nonlinear operators have been introduced employing auxiliary functions, modifying a new contractive requirement form. Well-posedness of obtained fixed point results is also established. Moreover, data dependence result for fixed points is provided. Some supporting examples are also available for better perception. Many existing results in the literature are particular cases of the results established.
Similar content being viewed by others
1 Introduction
The fixed point theory has significant applications in numerous branches of pure and applied mathematics, as it offers many considerable tools to find fixed points. The theory has remarkable implications since it provides a criterion for the existence of solutions for many differential and integral equations. The famous Banach contraction principle (BCP) [4] was established on metric spaces by Stephan Banach in 1922. Two directions for constructing new fixed point results use a more generalized space or modifying the contraction inequality. BCP is extended and modified in many directions in numerous ways. For example, the authors of [2, 9] considered Kannan-type contractions to prove certain fixed point results, and in [3, 17] the underlined space is changed.
It is worth mentioning that many authors used F-contractions to extend many existing results. In 2015, an F-contraction was extended in terms of nonlinear F-contractions by Klim and Wardowski [11]. The authors extended the notion of F-contractive mappings to the case of nonlinear F-contractions and proved a fixed point theorem via the dynamic processes. Following this, Wardowski [19] introduced nonlinear F-contractions by omitting one of the conditions on the F-mappings. In another paper by Wardowski [20], we can find some theorems concerning the existence of fixed points of nonlinear F-contractions and the sum of mappings of this type with a compact operator.
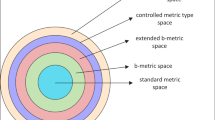
In 1989, the concept of a b-metric space (BMS) was given by Bakhtin [3]. It was further incorporated by Czerwick [8] to develop certain fixed point results endowed by this space. Kamran et al. [17] paved a new pathway using a function \(p:\xi \times \xi \longrightarrow [1,\infty )\) and weakened the triangle inequality of a b-metric space. In this perspective, Mlaiki et al. [12] made another advancement by generalizing the notion of an extended b-metric space and declaring it a controlled metric-type space.
A data dependence problem is to estimate the distance between the sets of fixed points of two mappings. This idea is only meaningful if we are sure that there are nonempty fixed point sets of these two operators. The data dependence problem mostly deals with set-valued mappings since multivalued mappings often have larger fixed point sets than single-valued mappings. In 2021, Iqbal et al. [10] discussed data dependence, the existence of fixed points, strict fixed points, and the well-posedness of some multivalued generalized contractions in the setting of complete metric spaces using auxiliary functions. In the present paper, we extend the results of Iqbal et al. [10] by utilizing the controlled metric platform.
2 Preliminaries
This section is devoted to refreshing some of the crucial concepts. Let \((\xi , d)\) be a metric space (MS), and let \(P(\xi )\) contain all subsets of ξ. We denote by \(\mathit{CL}(\xi ) \), \(\mathit{CB}(\xi )\), and \(\mathit{K}(\xi )\) the sets of nonempty closed subsets of ξ, nonempty closed bounded subsets of ξ, and nonempty compact subsets of ξ, respectively.
Let \(\Omega \colon \xi \longrightarrow P(\xi )\) be a multivalued mapping (MVP). An element \(\mathsf{\varrho} \in \xi \) such that \(\mathsf{\varrho} \in \Omega \mathsf{\varrho} \) is called a fixed point of Ω. The set of all fixed points of Ω is denoted by FixΩ. An element \(\bar{\mathsf{\varrho}} \in \xi \) such that \(\lbrace \bar{\mathsf{\varrho}} \rbrace = \Omega \mathsf{\varrho} \) is called a strict fixed point of Ω. The set of strict fixed points is denoted \(\mathsf{S}\operatorname{Fix}\Omega \).
Definition 2.1
[12] Consider a nonempty set ξ and a function \(\mathsf{\mathit{\mathfrak{f}}} :\xi \times \xi \longrightarrow [1, \infty ) \). The mapping \(d : \xi \times \xi \longrightarrow [0,\infty ) \) is said to be a CMS if for all \(\mathsf{\varrho}_{\mathfrak{1}}, \mathsf{\varrho}_{\mathfrak{2}},\mathsf{\varrho}_{\mathfrak{3}} \in \xi \),
- \((i)\):
-
\(d(\mathsf{\varrho}_{\mathfrak{1}} , \mathsf{\varrho}_{\mathfrak{2}})= 0 \ \Leftrightarrow \ \mathsf{\varrho}_{\mathfrak{1}} = \mathsf{\varrho}_{\mathfrak{2}} \);
- \((ii)\):
-
\(d(\mathsf{\varrho}_{\mathfrak{1}} ,\mathsf{\varrho}_{\mathfrak{2}} ) = d( \mathsf{\varrho}_{\mathfrak{2}},\mathsf{\varrho}_{\mathfrak{1}} ) \);
- \((iii)\):
-
\(d(\mathsf{\varrho}_{\mathfrak{1}} ,\mathsf{\varrho}_{\mathfrak{2}} ) \leq \mathsf{\mathit{\mathfrak{f}}} (\mathsf{\varrho}_{\mathfrak{1}} , \mathsf{\varrho}_{\mathfrak{3}}) d( \mathsf{\varrho}_{\mathfrak{1}} , \mathsf{\varrho}_{\mathfrak{3}} ) + \mathsf{\mathit{\mathfrak{f}}} ( \mathsf{\varrho}_{\mathfrak{3}},\mathsf{\varrho}_{\mathfrak{2}} ) d( \mathsf{\varrho}_{\mathfrak{3}},\mathsf{\varrho}_{\mathfrak{2}}) \).
The pair \((\xi ,d,\mathsf{\mathit{\mathfrak{f}}})\) is called a CMS.
Berinde and Pacurar [5] defined the Hausdorff distance as follows. Let \(\mathfrak{\mathsf{X}} , \mathfrak{\mathsf{Y}} \in \mathit{CB}(\xi )\). The mapping \(H : \mathit{CB}(\xi ) \times \mathit{CB}(\xi ) \longrightarrow [0, \infty ) \) defined by
is called a Pompei–Hausdorff metric space, where \(D ( \mathsf{\varrho} , \mathfrak{\mathsf{Y}} ) =\inf \lbrace d (\mathsf{\varrho} , \bar{\mathsf{\varrho}}) : \bar{\mathsf{\varrho}} \in \mathfrak{\mathsf{Y}} \rbrace \).
Following definition is due to Wardowski [19]. Let \(F:(0,\infty )\longrightarrow \mathbb{R}\) satisfy the following conditions:
- \((\mathbb{F}\mathsf{1})\):
-
F is strictly increasing;
- \((\mathbb{F}\mathsf{2})\):
-
For all sequences \(\lbrace \Psi _{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \subseteq (0, \infty )\), \(\lim_{\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty}\Psi _{\mathit{\mathsf{\mathfrak{s}}}}=0\) iff \(\lim_{\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty}F({\Psi _{\mathit{\mathsf{\mathfrak{s}}}}})=-\infty \);
- \((\mathbb{F}\mathsf{3})\):
-
There exists \(\mathsf{k} \in (0,1)\) such that \(\lim_{\Psi \longrightarrow 0^{+}}\Psi ^{\mathsf{k}}F( \Psi )=0\).
Let us denote by \(\Delta (\mathbb{F}) \) the set of all functions F that satisfy \((\mathbb{F}\mathsf{1}) \), \((\mathbb{F}\mathsf{2})\), and \((\mathbb{F}\mathsf{3})\), Also, assume that
where
- \((\mathbb{F}\mathsf{4})\):
-
\(F(\inf \mathfrak{\mathsf{X}})=\inf F(\mathfrak{\mathsf{X}})\) for all \(\mathfrak{\mathsf{X}} \subset (0, \infty )\) such that \(\inf \mathfrak{\mathsf{X}} >0\).
Turinici [18] replaced \((\mathbb{F}\mathsf{2})\) by
- \((\mathbb{F}\mathsf{2}')\):
-
\(\lim_{\mathsf{t} \longrightarrow 0^{+}} F(\mathsf{t}) = - \infty \).
Denote by \(\Delta ( \mathsf{0} * )\) the set of functions F that satisfy \((\mathbb{F}\mathsf{1}) \), \((\mathbb{F}\mathsf{2}')\), \((\mathbb{F} \mathsf{3})\), and \((\mathbb{F}\mathsf{4})\), A mapping \(\Omega : \xi \longrightarrow CB(\xi )\) is called a multivalued F-contraction if there exist \(\upsilon >0\) and \(F\in \Delta (\mathbb{F}) \) such that for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}}\in \xi \), \(H(\Omega \mathsf{\varrho}, \Omega \bar{\mathsf{\varrho}})>0\) implies \(\upsilon +F(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})) \leq F(d(\mathsf{\varrho},\bar{\mathsf{\varrho}}))\) [1].
Definition 2.2
[13] A mapping \(\Omega :\xi \longrightarrow \xi \) is called an \((\mathsf{\alpha},F)\)-contraction (or a nonlinear F-contraction) if there exist \(F\in \Delta (\mathbb{F}) \) and a function \(\Xi :(0,\infty )\longrightarrow (0,\infty )\) that fulfill the following conditions:
- \((H_{1})\):
-
\(\lim \inf_{s\longrightarrow \Psi ^{+}}\Xi (s)>0\) for all \(\Psi >0\);
- \((H_{2})\):
-
\(\Xi (d(\mathsf{\varrho},\bar{\mathsf{\varrho}}))+F(d(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}}))\leq F(d( \mathsf{\varrho},\bar{\mathsf{\varrho}}))\) for all ϱ, \(\bar{\mathsf{\varrho}}\in \xi \) such that \(\Omega \mathsf{\varrho}\neq \Omega \bar{\mathsf{\varrho}}\).
Definition 2.3
[10] By Φ we denote the set of functions \(\chi :(0, \infty )\longrightarrow (0,\infty )\) such that
3 Main results
The following definitions are indispensable before proving the main result.
Definition 3.1
By \(\mathcal{P}\) we denote the set of all continuous mappings \(\rho :[0,\infty )^{5}\longrightarrow [0,\infty )\) that satisfy the following conditions:
-
(i)
\(\rho (1,1,1,\zeta +\eta ,0)\in (0,1]\) for \(\zeta ,\eta \geq 1\),
-
(ii)
ρ is subhomogeneous, that is, for all \((\varrho _{1},\mathsf{\varrho}_{2},\mathsf{\varrho}_{3}, \mathsf{\varrho}_{4},\mathsf{\varrho}_{5})\in (0,\infty ]^{5}\) and \(\lambda \geq 0\), we have \(\rho (\lambda \mathsf{\varrho}_{1},\lambda \mathsf{\varrho}_{2}, \lambda \mathsf{\varrho}_{3},\lambda \mathsf{\varrho}_{4},\lambda \mathsf{\varrho}_{5})\leq \lambda \rho (\mathsf{\varrho}_{1}, \mathsf{\varrho}_{2},\mathsf{\varrho}_{3},\mathsf{\varrho}_{4}, \mathsf{\varrho}_{5}) \),
-
(iii)
ρ is a nondecreasing function, i.e., for \(\mathsf{\varrho}_{i},\bar{\mathsf{\varrho}}_{i} \in \mathbb{R}^{+} \mathsf{\varrho}_{i}\) such that \(\leq \bar{\mathsf{\varrho}}_{i}\), \(i=1,2,3,4,5 \), we have \(\rho (\mathsf{\varrho}_{\mathsf{1}},\mathsf{\varrho}_{\mathsf{2}}, \mathsf{\varrho}_{\mathsf{3}},\mathsf{\varrho}_{\mathsf{4}}, \mathsf{\varrho}_{\mathsf{5}})\leq \rho (\bar{\mathsf{\varrho}}_{ \mathsf{1}},\bar{\mathsf{\varrho}}_{\mathsf{2}}, \bar{\mathsf{\varrho}}_{\mathsf{3}},\bar{\mathsf{\varrho}}_{ \mathsf{4}},\bar{\mathsf{\varrho}}_{\mathsf{5}}) \). If \(\mathsf{\varrho}_{i}, \bar{\mathsf{\varrho}}_{i} \in \mathbb{R}^{+} \) are such that \(\mathsf{\varrho}_{i} < \bar{\mathsf{\varrho}}_{i} \) for \(i=1,2,3,4 \), then
$$ \rho (\mathsf{\varrho}_{\mathsf{1}},\mathsf{\varrho}_{\mathsf{2}}, \mathsf{ \varrho}_{\mathsf{3}},\mathsf{\varrho}_{\mathsf{4}},0)< \rho ( \bar{\mathsf{ \varrho}}_{\mathsf{1}},\bar{\mathsf{\varrho}}_{ \mathsf{2}},\bar{\mathsf{ \varrho}}_{\mathsf{3}}, \bar{\mathsf{\varrho}}_{\mathsf{4}},0 ), $$and
$$ \rho (\mathsf{\varrho}_{\mathsf{1}},\mathsf{\varrho}_{\mathsf{2}}, \mathsf{ \varrho}_{\mathsf{3}}, 0 , \mathsf{\varrho}_{\mathsf{4}} )< \rho (\bar{ \mathsf{\varrho}}_{\mathsf{1}},\bar{\mathsf{\varrho}}_{ \mathsf{2}},\bar{ \mathsf{\varrho}}_{\mathsf{3}}, 0 , \bar{\mathsf{\varrho}}_{\mathsf{4}} ). $$
Also, define \(\mathit{\mathbb{P}}= \lbrace \rho \in \mathcal{P}:\rho (1,0,0, \zeta ,\eta )\in (0,1] \rbrace \). Note that \(\mathit{\mathbb{P}} \subseteq \mathcal{P}\).
Example 3.1
-
1.
Define \(\rho _{1}:[0,\infty )^{5}\longrightarrow [0,\infty )\) by \(\rho _{1} (\mathsf{\varrho}_{1},\mathsf{\varrho}_{2}, \mathsf{\varrho}_{3},\mathsf{\varrho}_{4},\mathsf{\varrho}_{5} )=g \min \lbrace \mathsf{\varrho}_{1},\frac{1}{2}(\mathsf{\varrho}_{2}, \mathsf{\varrho}_{3}),\frac{1}{2}(\mathsf{\varrho}_{4}, \mathsf{\varrho}_{5}) \rbrace \), where \(g\in (0,1)\). Then \(\rho _{1}\in \mathcal{P}\), as \(\rho _{1} (1,0,0,\zeta ,\eta )=0\notin (0,1]\). Hence \(\rho _{1}\notin \mathit{\mathbb{P}} \).
-
2.
Define \(\rho _{2}:[0,\infty )^{5}\longrightarrow [0,\infty )\) by \(\rho _{2} (\mathsf{\varrho}_{1},\mathsf{\varrho}_{2}, \mathsf{\varrho}_{3},\mathsf{\varrho}_{4},\mathsf{\varrho}_{5} )= \frac {\mathsf{\varrho}_{1}}{2}+ \frac {\mathsf{\varrho}_{2}+\mathsf{\varrho}_{3}}{4}\). Then \(\rho _{2}\in \mathit{\mathbb{P}} \).
-
3.
Define \(\rho _{3}:[0,\infty )^{5}\longrightarrow [0,\infty )\) by \(\rho _{3} (\mathsf{\varrho}_{1},\mathsf{\varrho}_{2}, \mathsf{\varrho}_{3},\mathsf{\varrho}_{4},\mathsf{\varrho}_{5} )=g \min \lbrace \frac{1}{2}(\mathsf{\varrho}_{1}+\mathsf{\varrho}_{3}), \frac{1}{2}(\mathsf{\varrho}_{4}+\mathsf{\varrho}_{5}) \rbrace \), where \(g\in (0,1)\). Then \(\rho _{3}\in \mathit{\mathbb{P}} \).
Lemma 3.1
If \(\rho \in \mathcal{P}\), \(\gamma ,\delta \in [0,\infty )\), and \(\zeta ,\eta \in \mathbb{R}\) be such that \(\zeta ,\eta \geq 1\) and
Then \(\gamma \leq \delta \).
Proof
Without loss of generality, we can assume that
On the contrary, suppose that \(\delta <\gamma \). Now consider
which is a contradiction to (1). Hence our supposition is wrong, so \(\gamma \leq \delta \). □
Definition 3.2
(χF-contraction) Let \(F_{1}\), \(F_{2}\) be real-valued functions on \((0,\infty )\), and let \(\rho \in \mathcal{P}\) and \(\chi \in \Phi \). The mapping \(\Omega : \xi \longrightarrow CB(\xi )\) is called a χF-contraction if
- \(\mathsf{(Ni)}\):
-
\(F_{1} (\mathfrak{c}) \leq F_{2} (\mathfrak{c})\) for all \(\mathfrak{c} >0 \),
- \(\mathsf{(Nii)}\):
-
\(H(\Omega \mathsf{\varrho}, \Omega \bar{\mathsf{\varrho}})>0\) implies
$$ \chi \bigl(d(\mathsf{\varrho},\bar{\mathsf{\varrho}})\bigr)+F_{2} \bigl(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})\bigr)\leq F_{1} \bigl\lbrace \rho \bigl( d(\mathsf{\varrho},\bar{\mathsf{ \varrho}}),D( \mathsf{\varrho},\Omega \mathsf{\varrho}),D(\bar{\mathsf{\varrho}}, \Omega \bar{\mathsf{\varrho}}),D(\mathsf{\varrho},\Omega \bar{\mathsf{\varrho}}) ,D(\bar{\mathsf{\varrho}},\Omega \mathsf{\varrho}) \bigr) \bigr\rbrace $$for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}} \in \xi \).
Theorem 3.1
Suppose that \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) is a complete CMS. Let \(\Omega :\xi \longrightarrow K(\xi )\) be a χF-contraction. Suppose that \(F_{1}\) is nondecreasing and \(F_{2}\) satisfies conditions \((\mathbb{F}\mathsf{2}')\) and \((\mathbb{F}\mathsf{3})\). For \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \), define the Picard sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}=\Omega ^{ \mathit{\mathsf{\mathfrak{s}}}} \mathsf{\varrho}_{\mathsf{0}}\rbrace \) so that
Also, suppose
Then FixΩ is nonempty.
Proof
Let \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \) and \(\mathsf{\varrho}_{1}\in \Omega \mathsf{\varrho}_{\mathsf{0}}\). If \(\mathsf{\varrho}_{1}\in \Omega \mathsf{\varrho}_{1}\) then \(\mathsf{\varrho}_{1} \in \operatorname{Fix}\Omega \). Suppose \(\mathsf{\varrho}_{1}\notin \Omega \mathsf{\varrho}_{1}\), which implies \(D(\mathsf{\varrho}_{1}, \Omega \mathsf{\varrho}_{1})> 0\), and, consequently, \(H(\Omega \mathsf{\varrho}_{\mathsf{0}},\Omega \mathsf{\varrho}_{1})>0\). As \(\Omega \mathsf{\varrho}_{1}\) is compact, there exists \(\mathsf{\varrho}_{2}\in \Omega \mathsf{\varrho}_{1}\) such that \(d(\mathsf{\varrho}_{1},\mathsf{\varrho}_{2})=D(\mathsf{\varrho}_{1}, \Omega \mathsf{\varrho}_{1})\). Now
As \(F_{1}\) is nondecreasing, we have
By Lemma 3.1
Similarly, we get \(\mathsf{\varrho}_{3}\in \Omega \mathsf{\varrho}_{2}\) such that \(d(\mathsf{\varrho}_{2},\mathsf{\varrho}_{3})=D(\mathsf{\varrho}_{2}, \Omega \mathsf{\varrho}_{2})\) with \(D(\mathsf{\varrho}_{2},\Omega \mathsf{\varrho}_{2})>0\), and we have
By induction we get a sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace _{ \mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}} \subset \xi \) such that \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}\in \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\) satisfies \(d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}+1})=D(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}})\) with \(D(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}})>0\) and
So \(\lbrace d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})\rbrace _{ \mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}}\) is a decreasing sequence of real numbers. Now
Hence, for all \(\mathit{\mathsf{\mathfrak{s}}}\in \mathbb{N} \), we have
As \(\chi \in \Phi \), there exist \(\mathsf{h}>0\) and \(\mathit{\mathsf{\mathfrak{s}}}_{0}\in \mathbb{N}\) such that \(\chi (d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}))> \mathsf{h} \) for all \(\mathit{\mathsf{\mathfrak{s}}} \geq \mathit{\mathsf{\mathfrak{s}}}_{0}\). Now from (4) we have
Taking the limit in (5) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \), we get \(F_{2}(H(\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})) \longrightarrow -\infty \) and then by \((\mathbb{F}\mathsf{2}') \) we have
which further implies that
Now by \((\mathsf{\mathit{F}}\mathfrak{3}) \) there exists \(k\in (0,1)\) such that
Then from (5), for all \(\mathit{\mathsf{\mathfrak{s}}} \geq \mathit{\mathsf{\mathfrak{s}}}_{0}\), we have
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) and using (6) and (7), we get that
By the above equation there exists \(\mathit{\mathsf{\mathfrak{s}}}_{1}\in \mathbb{N}\) such that \(\mathit{\mathsf{\mathfrak{s}}}(H(\Omega \mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}+1}))^{k}\leq 1\) for all \(\mathit{\mathsf{\mathfrak{s}}} \geq \mathit{\mathsf{\mathfrak{s}}}_{1}\). Thus for all \(\mathit{\mathsf{\mathfrak{s}}} \geq \mathit{\mathsf{\mathfrak{s}}}_{1}\), we have \(H(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})\leq \frac {1}{\mathit{\mathsf{\mathfrak{s}}}^{\frac{1}{k}}}\).
Now
To prove that \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \rbrace _{ \mathit{\mathsf{\mathfrak{s}}}\in \mathbb{N}}\) is a Cauchy sequencem consider \(\tau ,\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}\) such that \(\tau >\mathit{\mathsf{\mathfrak{s}}} >\mathit{\mathsf{\mathfrak{s}}}_{1}\). Then
Therefore
Now
where \(U_{i}=\frac {1}{i^{\frac{1}{k}}}\) and \(V_{i}= (\prod_{j=0}^{i} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{j},\mathsf{\varrho}_{ \tau}) )\mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{i}, \mathsf{\varrho}_{i+1})\). Since \(\frac{1}{k}>0\), the series \(\sum_{i=\mathit{\mathsf{\mathfrak{s}}}+1}^{\infty} (\frac {1}{i^{\frac{1}{k}}} )\) converges. Also, \(\lbrace V_{i}\rbrace _{i}\) is increasing and bounded above, so \(\lim_{i\longrightarrow \infty}\lbrace V_{i}\rbrace _{i}\) (which is nonzero) exists. Hence \(\lbrace \lim_{i\longrightarrow \infty}U_{i}V_{i} \rbrace _{\mathit{\mathsf{\mathfrak{s}}}}\) converges.
Consider the partial sums \(S_{q}=\sum_{i=0}^{q} (\prod_{j=0}^{i} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{j},\mathsf{\varrho}_{ \tau}) )\mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{i}, \mathsf{\varrho}_{i+1})\frac {1}{i^{\frac{1}{k}}}\). From (8) we have
By using the ratio test and condition (2) we get that \(\lim_{\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty} \lbrace S_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) exists. By taking in (9) the limit as \({\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty}\) we get \(\lim_{\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty}d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \mathsf{\varrho}_{\tau})=0\). Therefore \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) is a Cauchy sequence, and the completeness of ξ implies that there exists \(\mathsf{\varrho}^{\mathfrak{*}}\in \xi \) such that
Now
Since \(F_{1}\) is a nondecreasing function, we obtain that for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}}\in \xi \),
To prove that \(\mathsf{\varrho}^{\mathfrak{*}}\) is a fixed point of ξ, on the contrary, assume that \(D(\mathsf{\varrho}^{\mathfrak{*}},\Omega \mathsf{\varrho}^{ \mathfrak{*}})>0\). Now due to the compactness of \(\Omega \mathsf{\varrho}^{\mathfrak{*}} \), there exists \(\mathsf{\varrho}\in \Omega \mathsf{\varrho}^{\mathfrak{*}}\) such that
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in the above inequality and using (3), we have
Using Lemma 3.1, we get \(D(\mathsf{\varrho}^{\mathfrak{*}},\Omega \mathsf{\varrho}^{ \mathfrak{*}})\leq 0\), and hence \(D(\mathsf{\varrho}^{\mathfrak{*}},\Omega \mathsf{\varrho}^{ \mathfrak{*}})=0\). As \(\Omega \mathsf{\varrho}^{\mathfrak{*}}\) is closed, we have \(\mathsf{\varrho}^{\mathfrak{*}}\in \Omega \mathsf{\varrho}^{ \mathfrak{*}}\). Hence FixΩ is nonempty. □
Example 3.2
Let \(\xi =\lbrace 0,\frac{1}{2},\frac{1}{3},\frac{1}{4} \rbrace \). Define \(d:\xi \times \xi \longrightarrow \mathbb{R^{+}}\) and \(f:\xi \times \xi \longrightarrow [1,\infty )\) by \(d(\mathsf{\varrho}_{1},\mathsf{\varrho}_{2})=(\mathsf{\varrho}_{1}- \mathsf{\varrho}_{2})^{2}\) and
Then \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) is a complete CMS.
Define \(F_{1},F_{2}:(0,\infty )\longrightarrow \mathbb{R}\) by
and \(F_{2}(u)=\ln (u)+u \) for \(u\in (0,\infty )\). Then \(F_{1}\) is nondecreasing, \(F_{2}\) satisfies \((F2^{\mathsf{'}})\) and \((F3)\), and \(F_{1}(u)\leq F_{2}(u) \) for all \(u>0\). Now define \(\Omega :\xi \longrightarrow K(\xi )\), \(\rho :[0,\infty )^{5}\longrightarrow [0,\infty )\), and \(\chi : (0,\infty )\longrightarrow (0,\infty )\) by
\(\rho (\mathsf{\varrho}_{1},\mathsf{\varrho}_{2}, \mathsf{\varrho}_{3},\mathsf{\varrho}_{4},\mathsf{\varrho}_{5} ) =\frac{\mathsf{\varrho}_{1}}{2}+28 \mathsf{\varrho}_{5}\), and \(\chi (t)=\frac{1}{t}\), \(t\in (0,\infty )\). Then \(\rho \in \mathcal{P}\) and \(\chi \in \Phi \). Since \(H(\Omega \mathsf{\varrho}, \Omega \bar{\mathsf{\varrho}})>0\), it follows that,
Note that \(\lim_{n\longrightarrow \infty} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{n},\mathsf{\varrho}) \leq 1\). Hence the assumptions of Theorem 3.1 are fulfilled, and \(\operatorname{Fix}\Omega =\lbrace 0,\frac{1}{2}\rbrace \).
Theorem 3.2
Let \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) be a complete CMS. Let \(\Omega :\xi \longrightarrow K(\xi )\) be an MVM, and let \(F_{1}\), \(F_{2}\) be functions satisfying χF-contraction. Suppose that \(F_{1}\) is nondecreasing and \(F_{2}\) satisfies condition \((\mathbb{F}\mathsf{2}') \). Also, suppose \(\lim_{ k \longrightarrow \infty} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{\tau _{k}}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}_{k}})\leq 1\). Then FixΩ is nonempty.
Proof
Let \({\varrho}_{0}\in \xi \) and \({\varrho}_{1}\in \Omega {\varrho}_{0}\). As in proof of Theorem 3.1, let \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \subset \xi \) be a sequence such that \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}\in \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\). It satisfies \(d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}+1})=D(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}})\) with \(D(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}})>0\) and
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in (11), we get \(F_{2}(H(\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})) \longrightarrow - \infty \), and by \((\mathbb{F}\mathsf{2}') \)
which further implies
Also, we claim that
If not, then there exists \(\delta >0\) such that for all \(r\geq 0\), there are \(\tau _{k}>\mathit{\mathsf{\mathfrak{s}}}_{k}>r\) such that
Moreover, there exists \(r_{0}\in \mathbb{N}\) such that
There are two sub sequences \(\lbrace \mathsf{\varrho}_{{\mathit{\mathsf{\mathfrak{s}}}}_{k}} \rbrace \) and \(\lbrace \mathsf{\varrho}_{{\tau}_{k}}\rbrace \) of \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) such that
Note that
Also, \(\tau _{k}\) is the minimal index for which (15) is fulfilled.
Note that \(\mathit{\mathsf{\mathfrak{s}}}_{k}+2\leq \tau _{k} \) for all k, because the case \(\mathit{\mathsf{\mathfrak{s}}}_{k}+1\leq \mathit{\mathsf{\mathfrak{s}}}_{k}\) is impossible due to equations (14) and (15). This shows that
By the triangle inequality, using (14) and (15), we have
Taking the limit as \(k\longrightarrow \infty \),
Now using (12) and (16), we get
Consider
As \(F_{1}\) is continuous, taking the limit as \({k\longrightarrow \infty}\) and using (16) and (17), we obtain
Since \(\rho \in \mathbb{P}\), we have \(\rho (1,0,0, \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{{ \mathit{\mathsf{\mathfrak{s}}}}_{k}},\mathsf{\varrho}_{{\tau}_{k}}) , \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{{ \mathit{\mathsf{\mathfrak{s}}}}_{k+1}},\mathsf{\varrho}_{{\tau}_{k+1}}) )\in (0,1]\)
which is a contradiction, and hence (13) holds. Therefore \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) is a Cauchy sequence, and thus there exists \(\mathsf{\varrho}^{\mathfrak{*}}\in \xi \) such that \(\lim_{\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty}\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}= \mathsf{\varrho}^{\mathfrak{*}}\). The rest of the proof follows from Theorem 3.1, and we get \(\mathsf{\varrho}^{\mathfrak{*}}\in \Omega \mathsf{\varrho}^{ \mathfrak{*}}\). □
Theorem 3.3
Let \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) be a complete CMS, and let \(\Omega :\xi \longrightarrow C(\xi )\) be an MVM. Assume that there are \(\chi \in \Phi \), \(F\in \Delta ( \mathsf{0} * ) \), and a real-valued function L on \((0,\infty )\) such that following conditions hold:
- \((G_{1})\):
-
\(F(\varrho )\leq L(\varrho ) \) for all \(\varrho > 0\);
- \((G_{2})\):
-
\(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})> 0\) implies,
$$ \chi \bigl(d(\mathsf{\varrho},\bar{\mathsf{\varrho}})\bigr)+L\bigl(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})\bigr)\leq F \bigl\lbrace \rho \bigl(d(\mathsf{\varrho},\bar{\mathsf{\varrho}}),D( \mathsf{\varrho},\Omega \mathsf{\varrho}),D(\bar{\mathsf{\varrho}}, \Omega \bar{\mathsf{\varrho}}),D( \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}}),D(\bar{\mathsf{\varrho}},\Omega \mathsf{\varrho}) \bigr) \bigr\rbrace $$
for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}}\in \xi \) and \(\rho \in \mathcal{P}\). Let \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \). Define the Picard sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}=\Omega ^{ \mathit{\mathsf{\mathfrak{s}}}}\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}}\rbrace \) such that
Also, suppose that \({\lim_{\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty}\mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho})}\leq 1 \) for all \(\mathsf{\varrho} \in \xi \). Then FixΩ is nonempty.
Proof
Let \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \) and \(\mathsf{\varrho}_{1}\in \Omega \mathsf{\varrho}_{\mathsf{0}}\). If \(\mathsf{\varrho}_{1}\in \Omega \mathsf{\varrho}_{1}\) then \(\mathsf{\varrho}_{1} \in \operatorname{fix}\Omega \). Suppose \(\mathsf{\varrho}_{1}\notin \Omega \mathsf{\varrho}_{1}\). This implies \(D(\mathsf{\varrho}_{1}, \Omega \mathsf{\varrho}_{1})> 0\), and, consequently, \(H(\Omega \mathsf{\varrho}_{\mathsf{0}},\Omega \mathsf{\varrho}_{1})>0 \). Due to \((\mathbb{F}\mathsf{4}) \), we obtain
Then (19) with \((G_{1})\) and \((G_{2})\) imply that
Hence there exists \(\mathsf{\varrho}_{2}\in \Omega \mathsf{\varrho}_{1}\) such that
Since F is a nondecreasing function, so (20) with \((\rho _{3})\) yield that
By Lemma 3.1
Next, arguing as previously, we get \(\mathsf{\varrho}_{3}\in \Omega \mathsf{\varrho}_{2}\) with \(D(\mathsf{\varrho}_{2},\Omega \mathsf{\varrho}_{2})>0\). By Lemma 3.1, using \((G_{1})\) and \((G_{2})\), we have
By induction we have a sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \subset \xi \) such that \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}\in \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\) with \(D(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}})>0\) and
Now (21) implies that \(\lbrace d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})\rbrace _{ \mathit{\mathsf{\mathfrak{s}}}\in \mathbb{N}}\) is a decreasing sequence of positive real numbers. Hence from \((F{4})\)
Since \(\xi \in \phi \), there exist \(h>0\) and \(\mathit{\mathsf{\mathfrak{s}}}_{0}\in \mathbb{N}\) such that \(\chi (d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}))< h\) for all \(\mathit{\mathsf{\mathfrak{s}}}\geq \mathit{\mathsf{\mathfrak{s}}}_{0}\). From (22)
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in (23), we get \(F(d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}-1}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}))\longrightarrow - \infty \), and from \((\mathbb{F}\mathsf{2}') \)
Now by \((\mathbb{F}\mathsf{3})\) there exists \(0 < k < 1\) such that
Thus from (23) for all \(\mathit{\mathsf{\mathfrak{s}}}\geq \mathit{\mathsf{\mathfrak{s}}}_{0}\), we have
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in (26) and using (24) and (25), we get
Note that by (28) there exists \(\mathit{\mathsf{\mathfrak{s}}}_{1}\in \mathbb{N}\) such that \(\mathit{\mathsf{\mathfrak{s}}}(d(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}-1},\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}}))^{k}\leq 1\) for all \(\mathit{\mathsf{\mathfrak{s}}}\geq \mathit{\mathsf{\mathfrak{s}}}_{1}\). We get
Now to prove that \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace _{ \mathit{\mathsf{\mathfrak{s}}}\in \mathbb{N}}\) is a Cauchy sequence, consider \(\tau ,\mathit{\mathsf{\mathfrak{s}}}\in \mathbb{N}\) such that \(\tau >\mathit{\mathsf{\mathfrak{s}}}>\mathit{\mathsf{\mathfrak{s}}}_{1}\). The rest of the proof follows from Theorem 3.1, and by using (18) with ratio test we deduce that \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) is a Cauchy sequence, and thus there exists \(\mathsf{\varrho}^{\mathfrak{*}}\in \xi \) such that
Now
Since F is a nondecreasing function, we get
Let \(\mathsf{\varrho}^{\mathfrak{*}}\) be a fixed point of ξ. On the contrary, we have \(D(\mathsf{\varrho}^{\mathfrak{*}},\Omega \mathsf{\varrho}^{ \mathfrak{*}})>0\). Then by following the proof of Theorem 3.1, \(D(\mathsf{\varrho}^{\mathfrak{*}},\Omega \mathsf{\varrho}^{ \mathfrak{*}})=0\). Since \(\Omega \mathsf{\varrho}^{\mathfrak{*}}\) is closed, \(\mathsf{\varrho}^{\mathfrak{*}}\in \Omega \mathsf{\varrho}^{ \mathfrak{*}}\). Hence FixΩ is nonempty. □
Theorem 3.4
Let \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) be a complete CMS, and let \(\Omega :\xi \longrightarrow C(\xi )\) be a multivalued mapping. Suppose there exist \(\chi \in \phi \), \(\rho \in \mathit{\mathbb{P}}\), and a nondecreasing continuous real-valued function \(F:(0,\infty )\longrightarrow \mathbb{R}\) that satisfy \((\mathbb{F}\mathsf{2}') \). Moreover, L be a real-valued function on \((0,\infty )\) such that the following conditions hold:
- \((G_{1})\):
-
\(F(\varrho )\leq L(\varrho )\) for all \(\varrho > 0\);
- \((G_{2})\):
-
\(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})> 0\) implies
$$ \chi \bigl(d(\mathsf{\varrho},\bar{\mathsf{\varrho}})\bigr)+L\bigl(H(\Omega \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}})\bigr)\leq F \bigl\lbrace \rho \bigl(d(\mathsf{\varrho},\bar{\mathsf{\varrho}}),D( \mathsf{\varrho},\Omega \mathsf{\varrho}),D(\bar{\mathsf{\varrho}}, \Omega \bar{\mathsf{\varrho}}),D( \mathsf{\varrho},\Omega \bar{\mathsf{\varrho}}),D(\bar{\mathsf{\varrho}},\Omega \mathsf{\varrho}) \bigr) \bigr\rbrace $$for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}}\in \xi \).
Also, suppose
Then FixΩ is non-empty.
Proof
Let \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \) be an arbitrary point, and let \(\mathsf{\varrho}_{1}\in \Omega \mathsf{\varrho}_{\mathsf{0}}\). As in proof of Theorem 3.1, we get a sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \subset \xi \) such that \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1}\in \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\) with \(D(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1})>0\),
and
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in (29), we get \(F(d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}-1}, \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}))\longrightarrow - \infty \), and by \((\mathbb{F}\mathsf{2}') \)
Now we claim that
If (30) does not hold, then there exists \(\delta >0\) such that for all \(r\geq 0\), we have \(\tau _{k}>\mathit{\mathsf{\mathfrak{s}}}_{k}>r \),
Also, there exists \(r_{0}\in \mathbb{N}\) such that
There exist two subsequences \(\lbrace \mathsf{\varrho}_{\tau _{k}}\rbrace \) and \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}_{k}} \rbrace \) of \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \). Then following the proof of Theorem 3.2, we get \(\lim_{k\longrightarrow \infty}d(\mathsf{\varrho}_{ \tau _{k}},\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}_{k}})= \delta \) and also
By the monotonicity of F, using \((G_{1})\) and \((G_{2})\), we get
By the continuity of F, taking the limit as \({{k}\longrightarrow \infty}\) and using (31) and (32), we have
Since \(\rho \in \mathbb{P}\), we have \(\rho (1,0,0, \lim_{k\longrightarrow \infty} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{{ \mathit{\mathsf{\mathfrak{s}}}}_{k}},\mathsf{\varrho}_{{\tau}_{k}}), \lim_{k\longrightarrow \infty} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{{ \mathit{\mathsf{\mathfrak{s}}}}_{k+1}},\mathsf{\varrho}_{{\tau}_{k+1}}) )\in (0,1]\). Hence
which is a contradiction to definition of Φ. Therefore (30) is fulfilled and ensures that \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}\rbrace \) is a Cauchy sequence. Hence there exists \(\mathsf{\varrho}^{\mathfrak{*}}\in \xi \) such that
By following the proof of Theorem 3.3 we get \(\mathsf{\varrho}^{\mathfrak{*}}\in \Omega \mathsf{\varrho}^{ \mathfrak{*}}\). □
4 Data dependence
For a metric space \((\xi , d)\) and mappings \(\Omega _{1}, \Omega _{2} : \xi \rightarrow P(\xi )\), the fixed points sets \(\operatorname{Fix}\Omega _{1}\) and \(\operatorname{Fix}\Omega _{2}\) are nonempty. The problem of finding the Pomeiu–Hausdroff distance H between \(\operatorname{Fix}\Omega _{1}\) and \(\operatorname{Fix}\Omega _{2}\) under the condition that for \(s>0\), \(H(\Omega _{1} \mathsf{\varrho},\Omega _{2} \mathsf{\varrho})< s \) for all \(\mathsf{\varrho}\in \xi \), is addressed by many authors. See, for example, [6, 7, 16]. In this section, we give a data dependence result of the established result.
Definition 4.1
Let \((\xi , d)\) be an MS, and let \(\Omega \colon \xi \longrightarrow CL(\xi ) \) be a multivalued operator. Supopse that for all \(\mathsf{\varrho} \in \xi \) and \(\bar{\mathsf{\varrho}} \in \Omega \mathsf{\varrho} \), there exists sequence \(\lbrace \varrho _{\mathit{\mathsf{\mathfrak{s}}}} \rbrace _{\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}}\) such that
-
(i)
\(\mathsf{\varrho}_{0} = \mathsf{\varrho} \) and \(\mathsf{\varrho}_{1} = \bar{\mathsf{\varrho}}\),
-
(ii)
\(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}+1} = \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \) for all \(\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N} \), and
-
(iii)
the sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \rbrace _{\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}}\) is convergent, and the fixed point of Ω is its limit.
Then Ω is said to be a multivalued weakly Picard operator (MWP operator). The sequence of successive approximations is defined as a sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \rbrace _{\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N}}\) that satisfies conditions (ii) and (ii) of Definition 4.1.
The main result of this section is as follows.
Theorem 4.1
Let \(( \xi , d ) \) be a CMS, let \(\Omega _{1} , \Omega _{2} : \xi \longrightarrow K(\xi ) \) be multivalued mappings, and let \(\chi \in \Phi \). Let \(F_{1} \) be a real-valued nondecreasing function on \((0, \infty )\), and let \(F_{2} \) be a real-valued function on \((0, \infty )\) satisfying \((\mathbb{F}\mathsf{2}')\) and \((\mathbb{F}\mathsf{3})\) such that χF-contraction is satisfied for \(\Omega _{\mathsf{i}} \), where \(\mathsf{i} \in \lbrace 1 , 2 \rbrace \), and there exists \(\mathsf{\lambda} > 0 \) such that \(H ( \Omega _{1} (\mathsf{\varrho}) , \Omega _{2} ( \mathsf{\varrho}) ) \leq \mathsf{\lambda} \) for all \(\mathsf{\varrho} \in \xi \). For \(\mathsf{\varrho}_{\mathsf{0}}\in \xi \), define a Picard sequence \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}=\Omega ^{ \mathit{\mathsf{\mathfrak{s}}}} \mathsf{\varrho}_{\mathsf{0}}\rbrace \) such that
Also, suppose that \(\lim_{\mathsf{\mathit{\mathsf{\mathfrak{s}}}} \longrightarrow \infty}\mathsf{\mathit{\mathfrak{f}}}( \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho}) \leq 1\) for all \(\mathsf{\varrho} \in \xi \). Then
- \((a)\):
-
\(\operatorname{Fix} \Omega _{\mathsf{i}} \in \mathit{CL}(\xi )\) for \(\mathsf{i} \in \lbrace 1 , 2 \rbrace \),
- \((b)\):
-
\(\Omega _{1} \), \(\Omega _{2} \) are MWP operators, and
$$ H ( \operatorname{Fix}\Omega _{1} , \operatorname{Fix}\Omega _{2} ) \leq \frac {\mathsf{\lambda}}{1- \max \lbrace \rho _{1} (1,1,1,\zeta +\eta ,0) , \rho _{2} (1,1,1,\zeta +\eta ,0) \rbrace } , $$where \(\zeta , \eta \geq 1 \).
Proof
\((a)\) Using Theorem 3.1, we have that \(\operatorname{Fix} \Omega _{ \mathsf{i}} \) is not empty for \(\mathsf{i} \in \lbrace 1 , 2 \rbrace \). Now we prove that for \(\mathsf{i} \in \lbrace 1 , 2 \rbrace \), the fixed point set of \(\Omega _{\mathsf{i}} \) is closed. Consider a sequence \(\lbrace \mathsf{\mathsf{\varrho}_{\mathsf{\mathit{\mathsf{\mathfrak{s}}}}}} \rbrace \) in \(\operatorname{Fix}\Omega _{\mathsf{i}}\) such that \(\mathsf{\varrho _{\mathit{\mathsf{\mathfrak{s}}}}} \longrightarrow \mathsf{\varrho} \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \). Now
Since \(F_{1}\) is a nondecreasing function, we have thatfor all \(\mathsf{\varrho} , \bar{\mathsf{\varrho}} \in \xi \),
Assume that \(D(\bar{\mathsf{\varrho}},\Omega \bar{\mathsf{\varrho}})>0\). Then there exists \(\mathsf{\varrho}\in \Omega \bar{\mathsf{\varrho}}\) such that
Taking the limit as \(\mathit{\mathsf{\mathfrak{s}}}\longrightarrow \infty \) in the above inequality, we get
Using Lemma 3.1, \(D(\bar{\mathsf{\varrho}},\Omega \bar{\mathsf{\varrho}})\leq 0\), and hence \(D(\bar{\mathsf{\varrho}},\Omega \bar{\mathsf{\varrho}})=0\). As Ωϱ̄ is closed, \(\bar{\mathsf{\varrho}}\in \Omega \bar{\mathsf{\varrho}}\).
\((b)\) Using Theorem 3.1, we get that \(\Omega _{1} \), \(\Omega _{2} \) are MWP operators. So we have to prove that
Suppose \(\mathsf{q} > 1\) and \(\mathsf{\varrho}_{\mathsf{0}} \in \operatorname{Fix} \Omega _{2} \). Then there exists \(\mathsf{\varrho}_{1} \in \Omega _{2} (\mathsf{\varrho}_{\mathsf{0}}) \) such that \(d(\mathsf{\varrho}_{\mathsf{0}} , \mathsf{\varrho}_{1}) = D ( \mathsf{\varrho}_{\mathsf{0}} , \Omega _{2} (\mathsf{\varrho}_{ \mathsf{0}}))\) and \(d(\mathsf{\varrho}_{1} , \mathsf{\varrho}_{2}) \leq \mathsf{q} H ( \Omega _{1} (\mathsf{\varrho}_{\mathsf{0}}) , \Omega _{2} ( \mathsf{\varrho}_{\mathsf{0}}) ) \). Now there exists \(\mathsf{\varrho}_{2} \in \Omega _{2} (\mathsf{\varrho}_{1}) \) such that \(d(\mathsf{\varrho}_{\mathsf{0}} , \mathsf{\varrho}_{1}) = D ( \mathsf{\varrho}_{\mathsf{0}} , \Omega _{2} (\mathsf{\varrho}_{ \mathsf{0}}))\) and \(d(\mathsf{\varrho}_{1} , \mathsf{\varrho}_{2}) \leq \mathsf{q} H ( \Omega _{2} (\mathsf{\varrho}_{\mathsf{0}}) , \Omega _{2} ( \mathsf{\varrho}_{1}) ) \). Also, we get \(d(\mathsf{\varrho}_{1} , \mathsf{\varrho}_{2}) \leq d( \mathsf{\varrho}_{\mathsf{0}} , \mathsf{\varrho}_{1}) \) and
Hence we get a sequence of successive approximations of Ω starting from \(\mathsf{\varrho}_{\mathsf{0}}\) that satisfies
Taking the limit as \({\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty}\), we conclude that \(\lbrace \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \rbrace \) is a Cauchy sequence in \((\xi , d)\) and thus converges to some \(\mathsf{v} \in \xi \). Using the proof of Theorem 3.1, we have \(\mathsf{v} \in \operatorname{Fix}\Omega _{2}\). Taking the limit as \({\mathit{m} \longrightarrow \infty}\), we get
Letting \(\mathit{\mathsf{\mathfrak{s}}}=0\),
Interchange the role of \(\Omega _{1}\) and \(\Omega _{2} \), for each \(\mathsf{v}_{0} \in \operatorname{Fix}\Omega _{1} \), we get
So
By taking the limit as \(\mathsf{q} \longrightarrow 1\) the result is proved. □
5 Strict fixed point and well-posedness
Definition 5.1
Consider an MS \((\xi , d)\), \(\mathbb{B} \in P(\xi ) \), and a multivalued mapping \(\Omega \colon \mathbb{B} \longrightarrow C(\xi ) \). The fixed point problem is said to be well posed for Ω with respect to D if
-
(a)
\(\operatorname{Fix}\Omega = \lbrace \mathsf{\varrho}^{\mathfrak{*}} \rbrace \),
-
(b)
if \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \in \mathbb{B} \), \(\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N} \) and \(D(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} , \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}) \longrightarrow 0 \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \),
then \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \longrightarrow \mathsf{\varrho}^{\mathfrak{*}} \in \operatorname{Fix}\Omega \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \) [14, 15].
Definition 5.2
Consider an MS \((\xi , d)\), \(\mathbb{B} \in P(\xi ) \), and a multivalued mapping \(\Omega \colon \mathbb{B} \longrightarrow C(\xi ) \). The fixed point problem is said to be well posed for Ω with respect to H if
-
(a)
\(\mathsf{S}\operatorname{Fix}\Omega = \lbrace \mathsf{\varrho}^{ \mathfrak{*}} \rbrace \),
-
(b)
if \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \in \mathbb{B} \), \(\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N} \), and \(H(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} , \Omega \mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}}) \longrightarrow 0 \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \),
then \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \longrightarrow \mathsf{\varrho}^{\mathfrak{*}} \in \mathsf{S}\operatorname{Fix}\Omega \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \) [14, 15].
Theorem 5.1
Let \((\xi , d, \mathsf{\mathit{\mathfrak{f}}})\) be a complete CMS, let \(\Omega :\xi \longrightarrow K(\xi )\) be a multivalued mapping, and let \(F_{1}\), \(F_{2}\) be functions satisfying a χF-contraction. Suppose \(F_{1}\) is nondecreasing, \(F_{2}\) satisfies condition \((\mathbb{F}\mathsf{2}')\) with \(\rho (1,0,0,1,1) \in (0, 1) \), and \(\mathsf{S}\operatorname{Fix}\Omega \neq \phi \). Also, suppose \(\lim_{\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty}\mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho})\leq 1\) for all \(\mathsf{\varrho} \in \xi \). Then
- (a):
-
\(\operatorname{Fix}\Omega = \mathsf{S}\operatorname{Fix} \Omega = \lbrace \mathsf{\varrho}^{\mathfrak{*}} \rbrace \);
- (b):
-
The fixed point problem is well posed for the multivalued mapping Ω with respect to H.
Proof
(a) Using Theorem 3.2, we conclude that \(\operatorname{Fix} \Omega \neq \phi \). Now we prove that \(\operatorname{Fix}\Omega = \lbrace \mathsf{\varrho}^{\mathfrak{*}} \rbrace \). Using \(\mathsf{(Ni)}\) and \(\mathsf{(Nii)} \), we have
Since \(F_{1}\) is a nondecreasing function, we obtain that for all \(\mathsf{\varrho},\bar{\mathsf{\varrho}}\in \xi \),
Let \(\mathsf{v} \in \operatorname{Fix}\Omega \) with \(\mathsf{v} \neq \mathsf{\varrho}^{\mathfrak{*}} \). Then \(D(\mathsf{\varrho}^{\mathfrak{*}} , \Omega \mathsf{v} ) > 0 \). Now we have
As \(\rho (1,0,0,1,1) \in (0,1) \), we have
which is a contradiction, and hence \(d(\mathsf{\varrho}^{\mathfrak{*}},\mathsf{v}) = 0 \) and \(\mathsf{\varrho}^{\mathfrak{*}} = \mathsf{v}\).
(b) Let \(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} \in \mathbb{B}\) and \(\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N} \) be such that
Now we claim that
where \(\mathsf{\varrho}^{\mathfrak{*}} \in \operatorname{Fix}\Omega \). If the above equation is not true, then for every \(\mathit{\mathsf{\mathfrak{s}}} \in \mathbb{N} \), there exists \(\boldsymbol{\epsilon} > 0 \) such that
But (36) implies that there exists \(\mathit{\mathsf{\mathfrak{s}}}_{\boldsymbol{\epsilon}} \in \mathbb{N} - \lbrace 0 \rbrace \) such that
for each \(\mathit{\mathsf{\mathfrak{s}}} > \mathit{\mathsf{\mathfrak{s}}}_{ \boldsymbol{\epsilon}} \). Hence for each \(\mathit{\mathsf{\mathfrak{s}}} > \mathit{\mathsf{\mathfrak{s}}}_{ \boldsymbol{\epsilon}} \), we obtain
The compactness of \(\Omega \mathsf{\varrho}^{\mathfrak{*}}\) implies that there exists \(\mathsf{\varrho} \in \Omega \mathsf{\varrho}^{\mathfrak{*}} \) such that
As \(\lim_{\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty} \mathsf{\mathit{\mathfrak{f}}}(\mathsf{\varrho}_{ \mathit{\mathsf{\mathfrak{s}}}},\mathsf{\varrho}) \leq 1 \) and \(\rho (1,0,0,1,1) \in (0,1) \), taking the limit as \(\mathsf{\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty } \), we get \(d(\mathsf{\varrho}_{\mathit{\mathsf{\mathfrak{s}}}} , \mathsf{\varrho}^{\mathfrak{*}} ) \longrightarrow 0 \) as \(\mathit{\mathsf{\mathfrak{s}}} \longrightarrow \infty \), which is a contradiction. Hence the fixed point problem is well posed for the multivalued mapping Ω with respect to D. Also, \(\operatorname{Fix}\Omega = \mathsf{S}\operatorname{Fix}\Omega \), and hence the fixed point problem is well posed with respect to H. □
6 Conclusion
In this research, we have established some fixed and strict fixed point results on controlled metric spaces. We followed the scheme of Iqbal et al. [10] and used the platform of controlled metric setting, and hence results given in [10] are particular cases of those given in the present paper. We have also provided the well-posedness of the theorems. The data dependence problem of fixed points of the considered mappings is also established. Many nontrivial examples are provided for authentication purposes.
Availability of data and materials
The data used to support the findings of this study are available from the corresponding author upon request.
References
Altun, I., Minak, G., Dalo, H.: Multi-valued F-contraction on complete metric space. J. Nonlinear Convex Anal. 16, 659–666 (2015)
Azam, A., Arshad, M.: Kannan fixed point theorems on generalized metric spaces. J. Nonlinear Sci. Appl. 1, 45–48 (2008)
Bakhtin, I.A.: The contraction mapping principle in almost metric spaces. Func. Anal. Gos. Ped. Inst. Unianowsk 30, 26–37 (1989)
Banach, S.: Sur les opérations dans les ensembles abstraits et leurs applications aux équations intégrals. Fundam. Math. 3, 133–181 (1922)
Berinde, V., Pacurar, M.: The role of Pompei–Hausdorff metric in fixed point theory. Creative Math. Inform. 22, 35–42, pp. 35 (2013)
Chifu, C., Petruşel, G.: Existence and data dependence of fixed points and strictly fixed points for contractive-type multivalued operators. Fixed Point Theory Appl. 2007, 034248, 1–8 (2007)
Choudhury, B.S., Metiya, N., Kundu, S.: Coupled fixed point sets with data-dependence and stability. Surv. Math. Appl. 17, 205–223 (2022)
Czerwik, S.: Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1, 5–11 (1993)
Gornicki, J.: Fixed point theorems for Kannan type mappings. J. Fixed Point Theory Appl. 19, 2145–2152 (2017)
Iqbal, I., Hussain, N., Al-Sulami, H.H., Hassan, S.: Fixed point, data dependence, and well-posed problems for multivalued nonlinear contractions. J. Funct. Spaces 2021, Article ID 2200903 (2021)
Klim, D., Wardowski, D.: Fixed points of dynamic processes of set-valued F-contractions and application to functional equations. Fixed Point Theory Appl. 2015(1), 22 (2015)
Mlaiki, N., Aydi, H., Souayah, N., Abdeljawad, T.: Controlled metric type spaces and the related contraction principle. Mathematics 6(10), 194 (2018)
Olgun, M., Minak, G., Altun, I.: A new approach to Mizoguchi–Takahshi type fixed point theorems. J. Nonlinear Convex Anal. 17(3), 579–587 (2016)
Petruşel, A., Rus, I.A.: Well-posedness of the fixed point problem for multivalued operators. In: Applied Analysis and Differential Equations, pp. 295–306 (2007)
Petrusel, A., Rus, I.A., Yao, J.C.: Well-posedness in the generalized sense of the fixed point problems for multivalued operators. Taiwan. J. Math. 11, 903–914 (2007)
Rus, I.A., Petruşel, A., Sintamarian, A.: Data dependence of the fixed point set of some multivalued weakly Picard operators. Nonlinear Anal. 52, 1947–1959 (2003)
Samreen, M., Kamran, T., Ain, Q.U.: A generalization of b-metric space and some fixed point theorems. Mathematics 5, 19 (2017)
Turinici, M.: Wardowski implicit contractions in metric spaces (2012). https://arxiv.org/abs/1211.3164
Wardowski, D.: Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012(1), 94 (2012)
Wardowski, D.: Solving existence problems via F-contractions. Proc. Am. Math. Soc. 146, 1585–1598 (2017)
Funding
Not Applicable
Author information
Authors and Affiliations
Contributions
Conceptualization and methodology, D.S., S.B., A.D., and A.S.; validation and formal analysis, S.B., H.A., S.M., and W.K.; investigation and data curation, D.S., S.B., A.D., A.S., and H.A.; writing—original draft preparation, D.S., and S.B.; funding acquisition, S.M., and W.K. All authors have read and agreed to the published version of the manuscript. All authors read and approved the final manuscript
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sagheer, D., Batul, S., Daim, A. et al. Well-posed fixed point results and data dependence problems in controlled metric spaces. J Inequal Appl 2024, 31 (2024). https://doi.org/10.1186/s13660-023-03062-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-023-03062-5