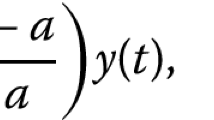Some noncompact types of fixed point results in the generalized Banach spaces with respect to the G–weak topology contexts and applications

Abstract

This research deals with Krasnoselskii’s fixed point theorem where the entries operators do not need to be G-weakly compact and contraction. These results were obtained by using the so-called generalized measure of weak noncompactness and some user-friendly lemmas. Moreover, these gained fixed point results are applied to study the existence of solutions of a coupled system for integral equations in the generalized Banach space $\mathcal{{ C }} ( [0,1], E_{1} )\times \mathcal{{ C }} ( [0,1], E_{2} )$.

1 Introduction

The history of generalized Banach spaces in the sense of Perov began in 1934 due to the Serbian mathematician Duro Kurepa who generalized the notion of metric spaces into vector-valued metric spaces. In 1965, Perov started the fixed point theory in these spaces by publishing his remarkable paper [21]. Numerous works of great importance studied the fixed point theory and its applications in generalized normed spaces; for example, see [6, 12, 17, 19, 22, 24, 25, 29, 31] and the references therein.

In [4], Laksaci et al. introduced the G–weak topology $\tau _{{\mathcal{E}}}^{G}$ on generalized Banach spaces. Furthermore, they gave several properties and characterizations that allow extending some existing results of Schauder and Tychonoff [8], Arino et al. [1], and Krasnoselskii to G–weak topology context.

The measures of (weak) noncompactness are useful techniques in the existence theory for several types of integral and integral-differential equations [15, 20, 26]. In 1997, Banaś [2] presented a fixed point result using the concept of k-set weakly contractive formulated in terms of the measure of weak noncompactness. After that, a number of interesting papers [5, 9, 11, 13, 14, 18, 27] on the solvability of various problems associated with measures of weak noncompactness have appeared.

Motivated by the aforementioned notes, in this manuscript we aim to investigate a number of extensions of the Krasnoselskii-type theorem by relaxing the G-weakly compact and the M-contraction conditions of the involved operators defined in the G–weak topology features. These results are based on the use of the so-called generalized measure of noncompactness tool.

The scheme of this manuscript is ordered as follows. In Sect. 2, we gather some notations and preliminary facts. In Sect. 3, we prove the noncompact type of Schauder–Tychonoff’s, Arino’s, and Krasnoselskii’s fixed point theorems in $\tau _{{\mathcal{E}}}^{G}$ topology. Finally, our results are used to prove the existence of solutions for the following system of functional integral equations:

$$ \textstyle\begin{cases} \zeta _{1} ( \iota ) = ( \int _{ 0 } ^{ \iota }\mathbb{H} _{1}( \varsigma ,\iota )\varXi _{1} ( \iota ,\varsigma , \zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma ) )\,d\varsigma )\cdot u_{1} \\ \hphantom{\zeta _{1} ( \iota ) =}{} + \varPi _{1} (\iota , \int _{0}^{\phi _{ 1 } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{1}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{1}, \\ \zeta _{2} ( \iota ) = ( \int _{ 0 } ^{ \iota }\mathbb{H} _{2}( \varsigma ,\iota ) \varXi _{2} ( \iota ,\varsigma , \zeta _{1} ( \varsigma ), \zeta _{2} (\varsigma ) )\,d\varsigma ) \cdot u_{2} \\ \hphantom{\zeta _{2} ( \iota ) =}{}+\varPi _{2} (\iota , \int _{0}^{\phi _{ 2 } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{2}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{2} \end{cases} $$

in the generalized Banach space $\mathcal{{ C }} ( [0,1], E_{1} )\times \mathcal{{ C }} ( [0,1], E_{2} )$.

2 Preliminaries

This section deals with basic notions and results of generalized Banach spaces, G–weak topology, generalized measures of weak noncompactness, and fixed point theory, which are needed in sections to come. We begin by defining on $\mathcal{M}_{m\times n}(\mathbb{R}_{+})$, the set of all $m \times n$ matrices with nonnegative entries, the partial order relation as follows: Let $\varLambda , \varUpsilon \in \mathcal{M}_{m\times n}( \mathbb{R}_{+})$, $m\geq 1$, and $n\geq 1$. Put $\varLambda =( \varLambda _{i,j})_{1\leq j\leq m \atop 1\leq i\leq n}$ and $\varUpsilon =(\varUpsilon _{i,j})_{1\leq j\leq m \atop 1\leq i\leq n}$. Then

$$ \begin{aligned} &\varLambda \preccurlyeq \varUpsilon \quad \text{if } \varUpsilon _{i,j} \geq \varLambda _{i,j} \quad \text{for all } j=1, \ldots , m, i=1, \ldots , n, \\ & \varLambda \prec \varUpsilon\quad \text{if } \varUpsilon _{i,j} > \varLambda _{i,j}\quad \text{for all } j=1,\ldots , m, i=1,\ldots , n, \end{aligned} $$

and we write I for the identity $n \times n$ matrix. Let $\varOmega =\prod_{i=1}^{n}\varOmega _{i}$ be a bounded set in $\mathbb{R}^{n}$. We denote by the supremum bound (resp. the infimum bound) of Ω the vector

$$\begin{aligned}& \operatorname{\widehat{sup}}\{\lambda :\lambda \in \varOmega \} \\& \quad := \begin{pmatrix} \sup \{\lambda _{1}:\lambda _{1}\in \varOmega _{1}\} \\ \vdots \\ \sup \{\lambda _{n}:\lambda _{n}\in \varOmega _{n}\} \end{pmatrix} ,\quad \left ( \text{resp. } \operatorname{ \widehat{inf}}\{\lambda : \lambda \in \varOmega \} := \begin{pmatrix} \inf \{\lambda _{1}:\lambda _{1}\in \varOmega _{1}\} \\ \vdots \\ \inf \{\lambda _{n}:\lambda _{n}\in \varOmega _{n}\} \end{pmatrix} \right ) . \end{aligned}$$

Definition 2.1

Let $\mathcal{E}$ be a vector space on $\mathbb{K} = \mathbb{R} \text{ or } \mathbb{C}$. A generalized norm on $\mathcal{E}$ is a map defined by

$$\begin{aligned} \Vert . \Vert _{G} :\quad &\mathcal{E} \longrightarrow \mathbb{R}^{n}_{+}, \\ & \zeta \longrightarrow \Vert \zeta \Vert _{G}= \begin{pmatrix} \Vert \zeta \Vert _{1} \\ \vdots \\ \Vert \zeta \Vert _{n} \end{pmatrix} \end{aligned}$$

which fulfills the following properties:

• (i) $\|\zeta \|_{G} \succcurlyeq 0_{\mathbb{R}_{+}^{n}}$ for all $\zeta \in \mathcal{E}$; if $\|\zeta \|_{G} = 0_{\mathbb{R}_{+}^{n}}$, then $\zeta = 0_{\mathcal{E}}$;

• (ii) $\|\alpha \zeta \|_{G}= |\alpha |\|\zeta \|_{G}$ for all $\zeta \in \mathcal{E}$ and $\alpha \in \mathbb{K}$; and

• (iii) $\| \zeta + \eta \|_{G}\preccurlyeq \|\zeta \|_{G} + \|\eta \|_{G}$ for all $\zeta , \eta \in \mathcal{E}$.

The pair $(\mathcal{E},\|.\|_{G})$ is called a generalized normed space. If the generalized metric generated by the map $\|.\|_{G}$ (i.e., $\delta _{G}(\zeta , \eta ) = \|\zeta - \eta \|_{G}$) is complete, then the space $(\mathcal{E},\|.\|_{G})$ is called a generalized Banach space (in short, GBS).

Proposition 2.2

[12] In GBS in the sense of Perov, the notions of convergence sequence, continuity, open subset, and closed subset are similar to those for the usual Banach spaces.

Now, let $(\mathcal{E},\|.\|_{G})$ be a GBS. The space

$$ \tilde{\mathcal{E}} = \bigl\{ \underbrace{(\zeta , \ldots , \zeta )}_{n \text{ times}} : \zeta \in \mathcal{E} \bigr\} , $$

endowed with the following norm

$$ \bigl\Vert (\zeta ,\ldots , \zeta ) \bigr\Vert _{*} =\sum _{i=1}^{n} \Vert \zeta \Vert _{i} $$

for all $\zeta \in \mathcal{E}$, is clearly a Banach space.

Throughout this article, for $r = (r_{1}, \ldots , r_{n}) \in \mathbb{R}^{n}_{+}$ and $\zeta _{0}\in \mathcal{E}$, we denote by

$$ B(\zeta _{0}, r) = \bigl\{ \zeta \in \mathcal{E} : \Vert \zeta - \zeta _{0} \Vert _{G} \prec r\bigr\} \quad \bigl(\text{resp. } B_{i}(\zeta _{0_{i}}, r_{i}) = \bigl\{ \zeta _{i} \in \mathcal{E}_{i} : \Vert \zeta _{0_{i}}- \zeta _{i} \Vert _{i} < r_{i}\bigr\} \bigr) $$

the open ball centered at $\zeta _{0}$ (resp. $\zeta _{0_{i}}$) with radius r (resp. $r{_{i}}$), and by

$$ \overline{B}(\zeta _{0}, r) = \bigl\{ \zeta \in \mathcal{E} : \Vert \zeta _{0}- \zeta \Vert _{G} \preccurlyeq r\bigr\} \quad \bigl( \text{resp. } \overline{B_{i}}( \zeta _{0_{i}}, r_{i}) = \bigl\{ \zeta _{i} \in \mathcal{E}_{i} : \Vert \zeta _{0_{i}}- \zeta _{i} \Vert _{i} \leq r_{i}\bigr\} \bigr) ) $$

the closed ball centered at $\zeta _{0}$ (resp. $\zeta _{0_{i}}$) with radius r (resp. $r{_{i}}$). Finally, we respectively denote by $\overline{\mathcal{K}}$ and $\operatorname{co}(\mathcal{K})$ the closure and the convex hull of an arbitrary set $\mathcal{K}$ of $\mathcal{E}$.

The following lemma plays an essential role in this paper.

Lemma 2.3

[12] Let $(\mathcal{E}, \|.\|_{G})$ be a GBS. Then the map

$$ \begin{aligned} h_{\mathcal{E}} :\quad & \mathcal{E}\longrightarrow \tilde{ \mathcal{E} }, \\ & \zeta \longrightarrow h_{\mathcal{E}}(\zeta )=(\zeta , \ldots , \zeta ) \end{aligned} $$

defines a homeomorphism.

Definition 2.4

Let $( \mathcal{E},\|.\|_{G})$ be a GBS and let $\mathcal{K}$ be a subset of $\mathcal{E}$. Then $\mathcal{K}$ is said to be G-bounded if there is a vector $V\in \mathbb{R}^{n}_{+}$ such that

$$ \text{ for all } \zeta \in \mathcal{K},\quad \Vert \zeta \Vert _{G} \preccurlyeq V. $$

Notation

We denote by $\mathcal{B}_{G}(\mathcal{E})$ the collection of all nonempty G–bounded subsets of $\mathcal{E}$.

Definition 2.5

Let $( \mathcal{E},\|.\|_{G_{\mathcal{E}}})$, $( \mathcal{F},\|.\|_{G_{\mathcal{F}}})$ be two GBSs with the generalized norms

$$ \Vert . \Vert _{G_{\mathcal{E}}}= \begin{pmatrix} \Vert .\|_{{\mathcal{E}}_{1}} \\ \vdots \\ \Vert .\|_{{\mathcal{E}}_{n}} \end{pmatrix} ,\qquad \Vert .\|_{G_{\mathcal{F}}}= \begin{pmatrix} \Vert .\|_{{\mathcal{F}}_{1}} \\ \vdots \\ \Vert .\|_{{\mathcal{F}}_{m}} \end{pmatrix} $$

respectively, and let $\mathbb{A}:\mathcal{E}\rightarrow \mathcal{F}$ be a linear operator. Then $\mathbb{A}$ is said to be G-bounded if there is a matrix $M\in \mathcal{\mathcal{M}}_{m\times n}(\mathbb{R}_{+})$ such that

$$ \Vert \mathbb{A}\zeta \Vert _{G_{\mathcal{F}}}\preccurlyeq M \Vert \zeta \Vert _{G_{ \mathcal{E}}} \quad \text{for all } \in \mathcal{E} . $$

Notation

We denote by $\mathcal{L}_{G}(\mathcal{E},\mathcal{F})$ the set of all G–bounded linear operators acting from $( \mathcal{E},\|.\|_{G_{\mathcal{E}}})$ into $( \mathcal{F},\|.\|_{G_{\mathcal{F}}})$.

Definition 2.6

Let $( \mathcal{E},\|.\|_{G_{\mathcal{E}}})$ and $( \mathcal{F},\|.\|_{G_{\mathcal{F}}})$ be two GBSs with the generalized norms

$$ \Vert . \Vert _{G_{\mathcal{E}}}= \begin{pmatrix} \Vert .\|_{{\mathcal{E}}_{1}} \\ \vdots \\ \Vert .\|_{{\mathcal{E}}_{n}} \end{pmatrix} ,\qquad \Vert .\|_{G_{\mathcal{F}}}= \begin{pmatrix} \Vert .\|_{{\mathcal{F}}_{1}} \\ \vdots \\ \Vert .\|_{{\mathcal{F}}_{m}} \end{pmatrix} $$

respectively. The generalized norm of $\mathcal{L}_{G}(\mathcal{E},\mathcal{F})$ is the matrix defined as follows:

$$ \begin{aligned} \Vert . \Vert _{\mathcal{L}_{G}(\mathcal{E},\mathcal{F})}: \quad & \mathcal{L}_{G}( \mathcal{E},\mathcal{F}) \longrightarrow \mathcal{M}_{m\times n}( \mathbb{R}_{+}), \\ & \mathbb{A}\longrightarrow \Vert \mathbb{A} \Vert _{\mathcal{L}_{G}(\mathcal{E}, \mathcal{F})}=\bigl( \Vert \mathbb{A} \Vert _{\mathcal{L}(\mathcal{E}_{i}, \mathcal{F}_{j})}\bigr)_{1\leq j\leq m\atop 1\leq i\leq n }.\end{aligned} $$

In the following, we give some definitions and properties related to the generalized weak topology extracted from [4].

Definition 2.7

[4] Let $( \mathcal{E},\|.\|_{G})$ be a GBS. The topology $\tau _{{\mathcal{E}}}^{G}$ of $\mathcal{E}$ generated by

$$ \bigl\lbrace h_{\mathcal{E}}^{-1}\bigl(O^{w}\bigr); O^{w}\in \sigma \bigl( \tilde{\mathcal{E}},\tilde{\mathcal{E}}^{*} \bigr) \bigr\rbrace $$

is called the generalized weak topology of $\mathcal{E}$, here $\sigma (\tilde{\mathcal{E}},\tilde{\mathcal{E}}^{*})$ denotes the weak topology of $\tilde{\mathcal{E}}$.

Proposition 2.8

[4] The generalized weak topology $\tau _{{\mathcal{E}}}^{G}$ of a GBS $\mathcal{E}$ is a Hausdorff space.

Definition 2.9

[4] Let $( \mathcal{E},\|.\|_{G})$ be a GBS. A sequence $(\zeta _{n})_{n \in \mathbb{N}}$ in $\mathcal{E}$ is called G-weakly convergent to an element $\zeta \in \mathcal{E}$, and we denote it by $\zeta _{n} \overset{G}{\rightharpoonup} \zeta$ if $(h_{\mathcal{E}}(\zeta _{n}))_{n\in \mathbb{N}}$ converges weakly to $h_{\mathcal{E}}(\zeta )$ in $\tilde{\mathcal{E}}$.

Definition 2.10

Let $( \mathcal{E},\|.\|_{G_{\mathcal{E}}})$, $( \mathcal{F},\|.\|_{G_{\mathcal{F}}})$ be two GBSs, and let $\mathbb{A}:\mathcal{E}\longrightarrow \mathcal{F}$ be an operator. Then $\mathbb{A}$ is said to be:

• (i) G-weakly sequentially continuous if for every sequence $(\zeta _{n})_{n\in \mathbb{N}}$ in $\mathcal{E}$ such that $\zeta _{n}\overset{G}{\rightharpoonup}\zeta$ in $\mathcal{E}$, then ${\mathbb{A}\zeta _{n}}\overset{G}{\rightharpoonup} \mathbb{A}\zeta$ in $\mathcal{F}$.

• (ii) G–ww-compact if $( \zeta _{ n } ) _{ n \in \mathbbm{ }\mathbb{N}\mathbbm{ } }$ is a G-weakly convergent sequence in $\mathcal{E}$, then $(\mathbb{A}\zeta _{ n } ) _{ n \in \mathbb{N}}$ has a G-weakly convergent subsequence in $\mathcal{F}$.

Lemma 2.11

[4] Let $\mathcal{E}$ and $\mathcal{F}$ be two GBSs, and let $\mathbb{A}:\mathcal{E}\longrightarrow \mathcal{F}$ be a linear operator. Then $\mathbb{A}$ is G–bounded if, and only if, $\mathbb{A}$ is G-weakly continuous.

Lemma 2.12

[4] Let $\mathcal{E}$ and $\mathcal{F}$ be two GBSs and $\mathbb{A}: \mathcal{E} \rightarrow \mathcal{F}$ be a mapping from $\mathcal{E}$ into $\mathcal{F}$. If $\mathbb{A}$ is G-weakly continuous, then $\mathbb{A}$ is G-weakly sequentially continuous.

For the definitions of G-weakly compact, sequentially G-weakly compact, countably G-weakly compact, relatively G–(compact, sequentially compact, and countably compact), we refer the reader to [4] and the references therein.

Notation

We denote by $\mathcal{W}_{\tau _{\mathcal{E}}^{G}}(\mathcal{E})$ the collection of all G-weakly compact subsets of $\mathcal{E}$ and by $\mathcal{W}(\tilde{\mathcal{E}})$ the collection of compact subsets on $\sigma (\tilde{\mathcal{E}},\tilde{\mathcal{E}}^{*})$.

Now, we define angelic space, which was established by Fremlin in [10].

Definition 2.13

A Hausdorff topological space $\mathcal{E}$ is called angelic if for every relatively countably compact subset $\mathcal{K}$ of $\mathcal{E}$ the following hold:

• (i) $\mathcal{K}$ is relatively compact;

• (ii) For each $\zeta \in \overline{\mathcal{K}}$, there is a sequence in $\mathcal{K}$ that converges to ζ.

The following theorem expresses the fundamental characteristic of angelic spaces.

Theorem 2.14

[23] If $\mathcal{E}$ is an angelic space, then we have the equivalence between compactness, countable compactness, and sequential compactness.

The next result plays an important role in this paper.

Lemma 2.15

[4] The GBS is angelic by its generalized norm topology and generalized weak topology $\tau _{\mathcal{E}}^{G}$.

Next, we present a helpful definition for the generalized measure of weak noncompactness, which will generalize the one introduced in 1988 by J. Banaś and J. Rivero [3].

Definition 2.16

Let $( \mathcal{E},\|.\|_{G})$ be a GBS. The following map

$$\begin{aligned} \mu _{G}^{\tau ^{G}_{\mathcal{E}}} :\quad &\mathcal{B}_{G}(\mathcal{E}) \longrightarrow [0,+ \infty )^{n}, \\ &\varDelta \longrightarrow \mu _{G}^{\tau ^{G}_{\mathcal{E}}} ( \varDelta )= \begin{pmatrix} \mu _{1}(\varDelta ) \\ \vdots \\ \mu _{n} (\varDelta ) \end{pmatrix} \end{aligned}$$

is called a generalized measure of weak noncompactness (for short G–MWNC) defined on $\mathcal{E}$ if the following requirements are met:

• (i) $\ker \mu _{G}^{\tau ^{G}_{\mathcal{E}}} = \{\varDelta \in \mathcal{B}_{G}(\mathcal{E}): \mu _{G}^{\tau ^{G}_{\mathcal{E}}}( \varDelta ) = 0_{\mathbb{R}^{n}}\} \neq \emptyset$ and $\ker \mu _{G}^{\tau ^{G}_{\mathcal{E}}} \subset \mathcal{W}_{\tau _{ \mathcal{E}}^{G}}(\mathcal{E})$.

• (ii) For all $\varDelta _{1}$, $\varDelta _{2} \in \mathcal{B}_{G}(\mathcal{E})$ with $\varDelta _{1}\subset \varDelta _{2}$, we have $\mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\varDelta _{1}) \preccurlyeq \mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\varDelta _{2})$.

• (iii) For all $\varDelta \in \mathcal{B}_{G}(\mathcal{E})$, we have $\mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\varDelta )= \mu _{G}^{\tau ^{G}_{ \mathcal{E}}} (\overline{\varDelta}^{\tau ^{G}_{\mathcal{E}}} )=\mu _{G}^{ \tau ^{G}_{\mathcal{E}}}(\operatorname{co}(\varDelta ))$.

• (iv) For all $\varDelta _{1}, \varDelta _{2} \in \mathcal{B}_{G}(\mathcal{E})$ and $\alpha \in [0, 1]$, we have $\mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\alpha \varDelta _{1}+ (1 - \alpha )\varDelta _{2} ) \preccurlyeq \alpha \mu _{G}^{\tau ^{G}_{ \mathcal{E}}} (\varDelta _{1}) + (1- \alpha )\mu _{G}^{\tau ^{G}_{ \mathcal{E}}}(\varDelta _{2})$.

• (v) Generalized Cantor intersection property, i.e., if $(\varDelta _{ m } ) _{ n \geq 1 }$ is a sequence of nonempty, weakly closed subsets of $\mathcal{E}$ with $\varDelta _{ 1 }$ is G–bounded and $\varDelta _{ 1 } \supseteq \varDelta _{ 2 } \supseteq \cdots \supseteq \varDelta _{ m } \ldots$ and such that ${\lim_{ m \rightarrow + \infty } } \mu _{G}^{ \tau ^{G}_{\mathcal{E}}} (\varDelta _{ m } ) = 0_{ \mathbb{R}^{n}}$, then the set $\varDelta _{ \infty } : = {\bigcap_{ m = 1 } ^{ \infty }}\varDelta _{ m }$ is nonempty and G-weakly compact.

A G-MNWC is called:

• (vi) subadditive if $\mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\varDelta _{1} + \varDelta _{2} ) \preccurlyeq \mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\varDelta _{1}) + \mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\varDelta _{2})$ for all $\varDelta _{1}, \varDelta _{2} \in \mathcal{B}_{G}(\mathcal{E})$;

• (vii) regular if $\ker \mu _{G}^{\tau ^{G}_{\mathcal{E}}} = \mathcal{W}_{\tau _{ \mathcal{E}}^{G}}(\mathcal{E})$.

Example 2.17

A typical example of a generalized measure of weak noncompactness that satisfies properties (vi) and (vii) is the Deblasi measure $\omega _{G}^{\tau ^{G}_{\mathcal{E}}}$ defined for all G–bounded subset $\varOmega \subset \mathcal{E}$ by

$$ \begin{aligned} \omega _{G}^{\tau ^{G}_{\mathcal{E}}}(\varOmega )&:= \operatorname{\widehat{inf}} \bigl\{ \varepsilon \in \mathbb{R}_{+}^{n}: \text{ there exists } Q\in \mathcal{W}_{\tau _{\mathcal{E}}^{G}}( \mathcal{E})\text{ such that }\varOmega \subseteq Q+ \varepsilon B (0,1 ) \bigr\} , \\ &= \begin{pmatrix} \inf \{\varepsilon _{1}>0 : \text{ there exists } Q_{1}\in \mathcal{W}(\tilde{\mathcal{E}})\text{ such that }\varOmega \subseteq Q_{1}+ \varepsilon _{1} B (0,1 ) \} \\ \vdots \\ \inf \{ \varepsilon _{n}>0 : \text{ there exists } Q_{n}\in { \mathcal{W}(\tilde{\mathcal{E}})} \text{ such that }\varOmega \subseteq Q_{n}+ \varepsilon _{n} B (0,1 ) \} \end{pmatrix} \\ &= \begin{pmatrix} \omega _{1}(\varOmega ) \\ \vdots \\ \omega _{n} (\varOmega ) \end{pmatrix} . \end{aligned} $$

Definition 2.18

A matrix $M\in \mathcal{\mathcal{M}}_{n\times n}(\mathbb{R})$ is called convergent to zero if

$$ M^{k} \longrightarrow 0, \quad \text{as } k \longrightarrow \infty . $$

Lemma 2.19

[28] Let M be a square matrix of nonnegative numbers. The following assertions are equivalent:

• (i) $M^{k} \longrightarrow 0 \textit{ as } k \longrightarrow \infty$;

• (ii) $I -M$ is invertible and

  $$ (I -M)^{-1} = I +M +M^{2} + \cdots +M^{k} + \cdots ; $$

• (iii) The eigenvalues of M lie in the open unit disc of $\mathbb{C}$

.

Remark 2.20

From assertion (ii) of Lemma 2.19, it is easy to verify that if there is $p\in \mathbb{N}$ such that $M^{p}$ converges to zero, then $(I-M)^{-1}$ exists and

$$ (I -M)^{-1} = \bigl(I-M^{p} \bigr)^{-1}\sum_{k=0}^{p-1} M^{k} . $$

(2.1)

Definition 2.21

Let $(\mathcal{E}, \delta _{G})$ be a complete generalized metric space with $\delta _{G} : \mathcal{E} \times \mathcal{E} \longrightarrow \mathbb{R}^{n}$ and $\mathbb{A}$ be an operator from $\mathcal{E}$ into itself. $\mathbb{A}$ is called G-Lipschitz with matrix ϒ if there is a square matrix of nonnegative numbers, and

$$ \delta _{G}\bigl(\mathbb{A}(\zeta ),\mathbb{A}(\nu )\bigr) \preccurlyeq \varUpsilon \delta _{G}(\zeta , \nu ) \quad \text{for all } \zeta , \nu \in \mathcal{E} . $$

If the matrix ϒ converges to zero, then $\mathbb{A}$ is called ϒ-contraction.

Definition 2.22

Let $( \mathcal{E},\|.\|_{G})$ be a GBS, and let $\mu _{G}^{\tau ^{G}_{\mathcal{E}}}$ be a G-MWNC. A self-mapping $\mathbb{A}: \mathcal{E}\longrightarrow \mathcal{E}$ is said to be $(M, \mu _{G}^{\tau ^{G}_{\mathcal{E}}})$-G-weakly set contractive if $\mathbb{A}$ is G–bounded, and there exists a matrix M converging to zero such that

$$ \mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\mathbb{A} \varOmega ) \preccurlyeq M \mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\varOmega )\quad \text{for all } \varOmega \in \mathcal{B}_{G}(\mathcal{E}). $$

Theorem 2.23

(Perov, [21]) Let $(\mathcal{E}, \delta _{G})$ be a complete generalized metric space, and let $\mathbb{A} : \mathcal{E} \longrightarrow \mathcal{E}$ be an M-contraction operator. Then $\mathbb{A}$ has a unique fixed point $\zeta ^{*} \in \mathcal{E}$.

The next result is a consequence of Perov’s fixed point theorem.

Lemma 2.24

[22] Let $( \mathcal{E},\|.\|_{G})$ be a GBS and $\mathbb{A}: \mathcal{E} \longrightarrow \mathcal{E}$ be a contraction. Then $\mathbb{I}_{d} -\mathbb{A}$ is a homeomorphism, where $\mathbb{I}_{d}$ denotes the identity operator on $\mathcal{E}$.

In the next, we generalize the previous result as follows.

Lemma 2.25

Let $(\mathcal{E},\|.\|_{G})$ be a GBS and $\mathbb{A} : \mathcal{E}\rightarrow \mathcal{E}$ be G–Lipschitzian with matrix M. Assume that there is $p \in \mathbbm{ }\mathbb{N}\mathbbm{ }$ such that the $p^{th}$ power of the operator $\mathbb{A} _{ \nu} : \mathcal{E} \rightarrow \mathcal{E}$ defined by $\mathbb{A} _{ \nu} \zeta =\mathbb{A}\zeta + \nu$ for each $\nu \in \mathcal{E}$ is an $N_{\nu}$-contraction. Then the operator $( \mathbb{I}_{d} -\mathbb{A} )$ is surjective on $\mathcal{E}$. Furthermore, $F : = \mathbb{I}_{d} -\mathbb{A} : \mathcal{E} \rightarrow \mathcal{E}$ is invertible and its inverse satisfies

$$ \bigl\Vert F ^{ - 1 } \zeta - F ^{ - 1 } \eta \bigr\Vert _{G} \preccurlyeq \varUpsilon _{ p } \Vert \zeta - \eta \Vert _{G},\quad \zeta , \eta \in \mathcal{E}, $$

(2.2)

where

$$ \varUpsilon _{ p } = \textstyle\begin{cases} { { p }.(I-N)^{-1} , } & \textit{if } M = I, \\ (I - M)^{-1}, & \textit{if } M \textit{ converges to zero}, \\ { ( I-N )^{-1}({ I-M ^{ p } }). (I-M )^{-1}}, & \textit{otherwise}. \end{cases} $$

(2.3)

Proof

Let $\nu \in \mathcal{E}$ be an arbitrary point. Because $\mathbb{A} _{ \nu} ^{ p }$ is $N_{\nu}$-contraction, then

$$ \bigl\Vert \mathbb{A}_{ \nu} ^{ p } \zeta - \mathbb{A}_{ \nu} ^{ p } z \bigr\Vert _{G} \preccurlyeq N_{\nu} \Vert \zeta - z \Vert _{G}, \quad \forall \zeta , z \in \mathcal{E}. $$

Now, we claim that $( \mathbb{I}_{d} -\mathbb{A} )$ maps $\mathcal{E}$ onto $\mathcal{E}$. Indeed, from the contraction of $\mathbb{A} _{ \nu} ^{ p }$ and an application of Perov’s theorem, we deduce that there is unique $\zeta ^{ * } \in \mathcal{E}$ such that $\mathbb{A} _{ \nu } ^{ p } \zeta ^{ * } = \zeta ^{ * }$. Hence,

$$ \mathbb{A} _{ \nu }\zeta ^{ * }=\mathbb{A} _{ \nu }\bigl(\mathbb{A} _{ \nu } ^{ p } \zeta ^{ * }\bigr) = \mathbb{A} _{ \nu } ^{ p }\bigl( \mathbb{A} _{ \nu }\zeta ^{ * }\bigr). $$

(2.4)

According to (2.4), the point $\mathbb{A} _{ \nu }\zeta ^{ * }$ is a fixed point of the operator $\mathbb{A} _{ \nu } ^{ p }$, and thus, by the uniqueness of $\zeta ^{ * }$, we conclude that $\zeta ^{ * }$ is the unique fixed point of $\mathbb{A} _{ \nu}$, too. Hence, we have

$$ ( \mathbb{I}_{d} -\mathbb{A} ) \zeta ^{ * } = \nu , $$

which gives that $\mathbb{I}_{d} -\mathbb{A} : \mathcal{E} \rightarrow \mathcal{E}$ is onto. Now, the operator $\mathbb{A} ^{ p }$ is N-contractive. Then, by using Lemma 2.24, we conclude that $(\mathbb{I}_{d} -\mathbb{A}^{p})$ is a homeomorphism. Thus, the operator $( \mathbb{I}_{d} -\mathbb{A} ) ^{ - 1 }$ exists on $\mathcal{E}$ because

$$ ( \mathbb{I}_{d} -\mathbb{A} ) ^{ - 1 } = \bigl( \mathbb{I}_{d}- \mathbb{A}^{ p } \bigr) ^{ - 1 }\sum_{ k = 0 } ^{ p - 1 } \mathbb{A}^{ k }. $$

(2.5)

Taking into account the fact that $\mathbb{A}^{p }$ is an N-contraction, hence for each $\zeta , \eta \in \mathcal{E}$ we get

$$\begin{aligned} \begin{aligned} \bigl\Vert \bigl( \mathbb{I}_{d} -\mathbb{A} ^{ p } \bigr) \zeta - \bigl( \mathbb{I}_{d} -\mathbb{A} ^{ p } \bigr) \eta \bigr\Vert _{G}&= \bigl\Vert (\zeta -\eta ) -\bigl(\mathbb{A} ^{ p } \zeta -\mathbb{A} ^{ p } \eta \bigr) \bigr\Vert _{G} \\ &\succcurlyeq \bigl\Vert (\zeta -\eta ) \bigr\Vert _{G}- \bigl\Vert \mathbb{A} ^{ p }\zeta -\mathbb{A} ^{ p }\eta \bigr\Vert _{G} \\ & \succcurlyeq (I- N ) \Vert \zeta - \eta \Vert _{G},\end{aligned} \end{aligned}$$

(2.6)

and consequently, by using Lemma 2.19, the matrix $(I-N)$ is invertible, then

$$ \bigl\Vert \bigl( \mathbb{I}_{d} -\mathbb{A} ^{ p } \bigr) ^{ - 1 } \zeta - \bigl( \mathbb{I}_{d} -\mathbb{A} ^{ p } \bigr) ^{ - 1 } \eta \bigr\Vert _{G}\preccurlyeq (I-N)^{-1} \Vert \zeta - \eta \Vert _{G}, \quad \forall \zeta , \eta \in \bigl( \mathbb{I}_{d} - \mathbb{A}^{ p } \bigr) ( \mathcal{E} ). $$

(2.7)

On the other hand, a series of induction calculations yields that

$$\begin{aligned} \begin{aligned} \bigl\Vert \mathbb{A}^{ k } \zeta -\mathbb{A}^{ k } \eta \bigr\Vert _{G} & \preccurlyeq M \bigl\Vert \mathbb{A}^{ k-1 } \zeta - \mathbb{A} ^{ k-1 } \eta \bigr\Vert _{G} \\ & \vdots \\ &\preccurlyeq M^{k} \Vert \zeta - \eta \Vert _{G},\quad \forall \zeta , \eta \in \mathcal{E} \text{ and } k \in \mathbbm{ }\mathbb{N}\mathbbm{ }. \end{aligned} \end{aligned}$$

(2.8)

Going back to (2.5), (2.7), and (2.8), we conclude that

• (1) If $M =\mathbb{I}_{d}$, ${ \sum_{k=0}^{p-1}}M ^{ k }=p.\mathbb{I}_{d}$, and

  $$ \varUpsilon _{ p }= (I- N)^{-1} \sum _{ k = 0 } ^{ p - 1 } M ^{ k } = { p }.(I-N) ^{-1} . $$

• (2) If M converges to zero, then $N=M^{ p }$, and using Eq. (2.1) we have ${\sum_{k=0}^{p-1}}M ^{ k }={(I-M^{p}})({I-M})^{-1}$, hence

  $$ \varUpsilon _{ p }=(I - M)^{-1}. $$

• (3) Else, ${\sum_{k=0}^{p-1}}M ^{ k }={(I-M^{p}})({I-M})^{-1}$, and

  $$ \varUpsilon _{ p }= (I-N ) ^{-1}\bigl({ I-M ^{ p } } \bigr). (I-M )^{-1} . $$

In conclusion, (2.3) is verified, and this proves the desired estimate (2.2). □

Lemma 2.26

[4] Let $( \mathcal{E},\|.\|_{G})$ be a GBS and $\mathbb{A}: \mathcal{E} \longrightarrow \mathcal{E}$ be a G–bounded linear operator. If $\|\mathbb{A} \|_{\mathcal{L}_{G}}$ converges to zero, then the operator $(\mathbb{I}_{d} -\mathbb{A})$ is invertible and

$$ (\mathbb{I}_{d} -\mathbb{A})^{-1} = \mathbb{I}_{d} +\mathbb{A} + \mathbb{A}^{2} + \cdots +\mathbb{A}^{k} + \cdots \in \mathcal{L}_{G}( \mathcal{E}). $$

In [4], the authors presented and proved the following theorems.

Theorem 2.27

[4] Let $\mathcal{K}$ be a nonempty, convex, and G-weakly compact subset of a GBS $\mathcal{E}$. If $\mathbb{A}$ is a G-weakly continuous map and transfers $\mathcal{K}$ into itself, then $\mathbb{A}$ has, at least, a fixed point.

Theorem 2.28

[4] Let $\mathcal{E}$ be a GBS, and let $\mathcal{K}$ be a G-weakly compact and convex subset of $\mathcal{E}$. Then any G-weakly sequentially continuous map $\mathbb{A}:\mathcal{K}\longrightarrow \mathcal{K}$ has, at least, a fixed point.

3 Fixed point results

Our first purpose in this section is to give the noncompact type of Theorem 2.27 and Theorem 2.28.

Theorem 3.1

Let $\mathcal{E}$ be a GBS and let $\mu _{G}^{\tau ^{G}_{\mathcal{E}}}$ be an arbitrary G-MWNC. Then every nonempty, G–bounded, closed, convex subset $\mathcal{K}$ of $\mathcal{E}$ has the fixed point property for G-weakly continuous mapping, which is a $( M,\mu _{G}^{\tau ^{G}_{\mathcal{E}}})$-G-weakly set contractive mapping.

Proof

Defining the following sequence of sets:

$$ K_{n} = \textstyle\begin{cases} \mathcal{K} & \text{if } n = 0, \\ \overline{\operatorname{co}}(\mathbb{A}K_{n-1}) & \text{otherwise.} \end{cases} $$

Obviously, the sequence $(K_{ n } ) _{ n \in \mathbbm{ }\mathbb{N}\mathbbm{ } }$ is of nonempty closed convex decreasing subsets of $\mathcal { K}$. Taking into consideration that $\mathbb{A}$ is $( M,\mu _{G}^{\tau ^{G}_{\mathcal{E}}})$-G-weakly set contractive, we have

$$ \mu _{G}^{\tau ^{G}_{\mathcal{E}}} (K_{ 2 } ) = \mu _{G}^{ \tau ^{G}_{\mathcal{E}}} \bigl( \overline { \operatorname{ c o} } (\mathbb{A}K_{ 1 } ) \bigr) = \mu _{G}^{\tau ^{G}_{ \mathcal{E}}} (\mathbb{A}K_{ 1 } ) \preccurlyeq M \mu _{G}^{ \tau ^{G}_{\mathcal{E}}} (K_{ 1 } ). $$

Continuing this process, we obtain

$$ \mu _{G}^{\tau ^{G}_{\mathcal{E}}} (K_{ n } ) \preccurlyeq M^{ n } \mu _{G}^{\tau ^{G}_{\mathcal{E}}} ( \mathcal { K} ) \quad \text{for each } n\in \mathbb{N}. $$

Since M converges to zero, we conclude that ${\lim_{ n \rightarrow \infty }} \mu _{G}^{\tau ^{G}_{ \mathcal{E}}} (K_{ n } ) = 0_{\mathbb{R}^{n}}$. Using property (v) of $\mu _{G}^{\tau ^{G}_{\mathcal{E}}} (\cdot )$, we conclude that $\mathcal { Q } : = {\bigcap_{ n = 1 } ^{ \infty }}K_{ n }$ is a nonempty closed convex G-weakly compact subset of $\mathcal { K}$. Furthermore, it is easily seen that $\mathbb{A}\mathcal { Q } \subset \mathcal { Q }$. Now, Theorem 2.27 completes the proof. □

Theorem 3.2

Let $\mathcal{E}$ be a GBS, $\mu _{G}^{\tau ^{G}_{\mathcal{E}}}$ be an arbitrary G-MWNC, and let $\mathcal{K}$ be a nonempty, G–bounded, closed, and convex subset of $\mathcal{E}$. Assume that $\mathbb{A}: \mathcal{K}\longrightarrow \mathcal{K}$ is G-weakly sequentially continuous and $(M,\mu _{G}^{\tau ^{G}_{\mathcal{E}}})$-G-weakly set contractive mapping, then $\mathbb{A}$ has, at least, a fixed point in $\mathcal{K}$.

Proof

By using the same ideas applied in Theorem 3.1, we find that all the hypotheses of Theorem 2.28 are fulfilled. □

We now prove certain fixed point theorems of Krasnoselskii type.

Theorem 3.3

Let $\mathcal{K}$ be a nonempty, G–bounded, closed, and convex subset of a GBS $\mathcal{E}$, and let $\mu _{G}^{\tau ^{G}_{\mathcal{E}}}$ be an arbitrary G-MWNC. Suppose that $\mathbb{B}: \mathcal{K} \longrightarrow \mathcal{E}$ and $\mathbb{A}: \mathcal{E} \longrightarrow \mathcal{E}$ are such that:

• (i) $\mathbb{B}$ is G-weakly sequentially continuous;

• (ii) There exists a matrix M converging to zero such that $\mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\mathbb{B}(\varOmega )+ \mathbb{A}(\varOmega )) \preccurlyeq M\mu _{G}^{\tau ^{G}_{ \mathcal{E}}}(\varOmega )$ for all $\varOmega \subset \mathcal{K}$;

• (iii) $\mathbb{A}$ is a contraction with a matrix N and G-weakly sequentially continuous; and

• (iv) $(\zeta = \mathbb{A}\zeta + \mathbb{B}\nu , \nu \in \mathcal{K}) \Longrightarrow \zeta \in \mathcal{K}$.

Then the sum of $\mathbb{A}$ and $\mathbb{B}$ has, at least, a fixed point in $\mathcal{K}$.

Proof

On account of the fact that $\mathbb{A}$ is an N-contraction, it comes as a consequence of Lemma 2.24 that the map $\mathbb{I}_{d} -\mathbb{A}$ is a homeomorphism from $\mathcal{E}$ into $\mathcal{E}$. Taking now $\nu \in \mathcal{K}$, the map $\mathbb{A}\cdot +\mathbb{B}\nu$ defines a contraction from $\mathcal{E}$ into itself. Hence, by the Perov fixed point Theorem 2.23, the equation $\zeta = \mathbb{A}\zeta + \mathbb{B}\nu$ has a unique solution $\zeta \in \mathcal{E}$. By hypothesis (iv) we have $\zeta \in \mathcal{K}$. So, $\zeta = (\mathbb{I}_{d} -\mathbb{A})^{-1}\mathbb{B}\nu \in \mathcal{K}$; in other words, the mapping $( \mathbb{I}_{d} -\mathbb{A})^{-1}\mathbb{B}$ maps $\mathcal{K}$ into itself.

Presently, we define the following sequence of sets:

$$ K_{n} = \textstyle\begin{cases} \mathcal{K} & \text{if } n = 0, \\ \overline{\operatorname{co}}(( \mathbb{I}_{d} -\mathbb{A})^{-1} \mathbb{B}K_{n-1}) & \text{otherwise.} \end{cases} $$

We have already seen that $(K_{n})_{n \in \mathbb{N}}$ is a decreasing sequence of nonempty closed convex subsets of $\mathcal{K}$. Moreover, for each $n \in \mathbb{N}$, we get

$$ \begin{aligned}( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}(K_{n } ) &= ( \mathbb{I}_{d} -\mathbb{A}+\mathbb{A}) ( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}( K_{n } ) \\ & = \mathbb{B}( K_{n } ) +\mathbb{A}( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}( K_{n } ), \end{aligned}$$

so

$$ \begin{aligned}(\mathbb{I}_{d}-\mathbb{A})^{-1} \mathbb{B} (K_{n } ) &\subset \mathbb{B} (K_{n } )+\mathbb{A} \bigl( \overline{\operatorname{co}} \bigl((\mathbb{I}_{d}- \mathbb{A})^{-1} \mathbb{B} (K_{n } ) \bigr) \bigr) \\ &\subset \mathbb{B} (K_{n } )+\mathbb{A} (K_{n } ). \end{aligned}$$

Moreover, the use of assumption (ii) leads to

$$ \begin{aligned} \mu _{G}^{\tau ^{G}_{\mathcal{E}}}\bigl(( \mathbb{I}_{d}-\mathbb{A})^{-1} \mathbb{B} (K_{n } )\bigr) &\preccurlyeq \mu _{G}^{\tau ^{G}_{ \mathcal{E}}}\bigl(\mathbb{B} (K_{n } )+\mathbb{A} (K_{n } )\bigr) \\ &\preccurlyeq M\mu _{G}^{\tau ^{G}_{\mathcal{E}}}(K_{n }) \\ & \vdots \\ &\preccurlyeq M^{n+1}\mu _{G}^{\tau ^{G}_{\mathcal{E}}}(\mathcal{K}), \end{aligned} $$

but M converges to zero, thus $\mathcal { Q } : = {\bigcap_{ n = 1 } ^{ \infty }}K_{ n }$ is a nonempty closed convex G-weakly compact subset of $\mathcal { K}$ and $(\mathbb{I}_{d}-\mathbb{A})^{-1}\mathbb{B} (\mathcal { Q } ) \subset \mathcal { Q }$.

Next, we verify that $(\mathbb{I}_{d}-\mathbb{A})^{-1} \mathbb{B}: \mathcal { Q } \rightarrow \mathcal { Q }$ is G-weakly sequentially continuous. Indeed, let $(\zeta _{n})_{n \in \mathbb{N}}$ be a sequence in $\mathcal { Q }$ with $\zeta _{n}\overset{G}{\rightharpoonup}\zeta$. Set $\nu _{n} = (\mathbb{I}_{d} -\mathbb{A})^{-1}\mathbb{B}\zeta _{n} \in \mathcal { Q }$ for all $n \in \mathbb{N}$, then by Lemma 2.15 the sequence $\{\nu _{n}\}_{n\in \mathbb{N}}$ has a subsequence G-weakly convergence to some ν in $\mathcal { Q }$. Evidently, by the G–weak sequential continuity of the maps $\mathbb{A}$ and $\mathbb{B}$ and the equation

$$ \begin{aligned}\nu _{n_{k}}&=( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{n_{k}} \\ &= \mathbb{B}\zeta _{n_{k}} +\mathbb{A}( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{n_{k}}\quad \text{for all } k \in \mathbb{N}, \end{aligned}$$

we have $\nu = \mathbb{A}\nu + \mathbb{B}\zeta$, and thus $\nu =(\mathbb{I}_{d} -\mathbb{A})^{-1}\mathbb{B}\zeta$.

We next claim that

$$ ( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n } \overset{G}{\rightharpoonup} ( \mathbb{I}_{d} - \mathbb{A}) ^{ - 1 } \mathbb{B}\zeta . $$

Assume the opposite; hence there exists a neighborhood of $( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta$ in the sense of $\tau _{\mathcal{E}}^{G}$, let us denote it by $U^{\tau _{\mathcal{E}}^{G}}$, and there is a subsequence $\{ \zeta _{ n _{j}} \}_{j \in \mathbb{N}}$ of $\{\zeta _{ n } \}_{n \in \mathbb{N}}$ such that $( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ j} } \notin U^{\tau _{\mathcal{E}}^{G}}$ for all $j \geq 1$. The sequence $\{ \zeta _{ n _{j} } \}_{j \in \mathbb{N}}$ converges to ζ in the sense of $\tau _{\mathcal{E}}^{G}$; then, reasoning as before, we can extract a subsequence $\{ \zeta _{ n_{j _{ k }} }\}_{k \in \mathbb{N}}$ of $\{ \zeta _{ n _{ j } } \}_{j \in \mathbb{N}}$ so that $( \mathbb{I}_{d} - \mathbb{A} ) ^{ - 1 } \mathbb{B}\zeta _{ n _{ j _{ k } } } \overset{G}{\rightharpoonup}( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta$. But this is a contradiction with $( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{j } } \notin U^{\tau _{\mathcal{E}}^{G}}$ for all $j \geq 1$. Our claim is hence verified. Finally, the fixed point theorem, Theorem 2.28, ensures the existence of the fixed point of the operator $( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 }\mathbb{B}$ in $\mathcal { Q }$. Thus, the proof of the theorem is completed. □

Theorem 3.4

Let $\mathcal{K}$ be a nonempty, G–bounded, closed, and convex subset of a GBS $\mathcal{E}$. Suppose that $\mathbb{A} : \mathcal{E} \rightarrow \mathcal{E}$ and $\mathbb{B}: \mathcal{K} \rightarrow \mathcal{E}$ are G-weakly sequentially continuous mappings such that:

• (i) $\mathbb{A}$ satisfies the conditions of Lemma 2.25and $(\mathbb{I}_{d}-\mathbb{A})^{-1}$ is G–ww–compact;

• (ii) $\mathbb{B}$ is a $(\Gamma ,\omega _{G}^{\tau ^{G}_{\mathcal{E}}})$-G–set contractive map; and

• (iii) $[ \zeta =\mathbb{A}\zeta + \mathbb{B}\nu , \nu \in \mathcal{K} ] \Longrightarrow \zeta \in \mathcal{K}$.

Then the sum $\mathbb{A}+\mathbb{B}$ admits at least one fixed point in $\mathcal{K}$ provided that the matrix $\varLambda = \Gamma \cdot \varUpsilon _{ p }$ converges to zero.

Proof

Since $\mathbb{A} : \mathcal{E} \rightarrow \mathcal{E}$ verifies all the hypotheses of Lemma 2.25, the operator $(\mathbb{I}_{d} -\mathbb{A})$ maps $\mathcal{E}$ onto $\mathcal{E}$. Keeping in mind that $\mathbb{B}: \mathcal{K} \rightarrow \mathcal{E}$, for each $\zeta \in \mathcal{K}$, there exists $\nu \in \mathcal{E}$ such that

$$ y -\mathbb{A}\nu = \mathbb{B}\zeta\quad \Longleftrightarrow\quad ( \mathbb{I}_{d}-\mathbb{A}) \nu = \mathbb{B}\zeta . $$

(3.1)

Using Lemma 2.25 one more time, we infer that $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 }$ exists on $\mathcal{E}$, and thus, from the third condition and (3.1), we get $\nu = (\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta \in \mathcal{K}$. From (2.2), $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 }$ is $\varUpsilon _{ p }$–G–Lipschitz.

Next, let $\varOmega \subset \mathcal{K}$ and $r\succ \omega _{G}^{\tau ^{G}_{\mathcal{E}}} (\varOmega )$. There exist $0_{\mathbb{R}^{n}} \preccurlyeq r _{ 0 } \preccurlyeq r$ and a G-weakly compact subset $\mathcal{Q}$ of $\mathcal{E}$ such that $\varOmega \subseteq \mathcal{Q} + r_{0}B(0,1)$.

Let $\iota \in \varOmega$. Then there is $\varsigma \in \mathcal{Q}$ such that $\| \varsigma - \iota \|_{G} \preccurlyeq r _{ 0 }$. Since $(\mathbb{I}_{d}-\mathbb{A})^{-1}$ is $\varUpsilon _{p}$-G-Lipschitzian, then $\|(\mathbb{I}_{d}-\mathbb{A})^{-1}\varsigma - (\mathbb{I}_{d}- \mathbb{A})^{-1} \iota \|_{G} \preccurlyeq \varUpsilon _{p} \| \varsigma - \iota \|_{G} \preccurlyeq \varUpsilon _{p} r _{ 0 }$, then

$$ (\mathbb{I}_{d}-\mathbb{A})^{-1}A \subseteq (\mathbb{I}_{d}- \mathbb{A})^{-1}\mathcal{Q} + { \varUpsilon _{p} r _{ 0 } } {B} (0,1) \subseteq \overline { ( \mathbb{I}_{d}-\mathbb{A})^{-1}\mathcal{Q} }^{ \tau ^{G}_{\mathcal{E}} } + { \varUpsilon _{p} r _{ 0 } } {B} (0,1) . $$

(3.2)

Since the operator $(\mathbb{I}_{d}-\mathbb{A})^{-1}$ is ww–G–compact, if $( \xi _{ n } ) _{ n \in \mathbbm{ }\mathbb{N}\mathbbm{ } }$ is a G-weakly convergent sequence in $\mathcal{Q}$, then $(\sigma _{n})_{n\in \mathbb{N}}:=((\mathbb{I}_{d}-\mathbb{A})^{-1} \xi _{ n } ) _{ n \in \mathbb{N}}$ has a G-weakly convergent subsequence; which means $\overline { (\mathbb{I}_{d}-\mathbb{A})^{-1}\mathcal{Q} }^{ \tau ^{G}_{ \mathcal{E}} }$ is G-weakly sequentially continuous, hence Lemma 2.15 implies that $\overline { (\mathbb{I}_{d}-\mathbb{A})^{-1}\mathcal{Q} }^{ \tau ^{G}_{ \mathcal{E}} }$ is G-weakly compact. Consequently, by using (3.2) and the subadditivity of $\omega _{G}^{\tau ^{G}_{\mathcal{E}}}$, we get

$$ \omega _{G}^{\tau ^{G}_{\mathcal{E}}} \bigl( (\mathbb{I}_{d}- \mathbb{A})^{-1}A \bigr) \preccurlyeq \varUpsilon _{p} r _{ 0 } \prec \varUpsilon _{p} r. $$

Letting $r \rightarrow \omega _{G}^{\tau ^{G}_{\mathcal{E}}} (\varOmega )$, we get

$$ \omega _{G}^{\tau ^{G}_{\mathcal{E}}} \bigl((\mathbb{I}_{d}- \mathbb{A})^{-1} \varOmega \bigr) \preccurlyeq \varUpsilon _{p}\omega _{G}^{\tau ^{G}_{ \mathcal{E}}} (\varOmega ). $$

Using now condition (ii), we get

$$ \omega _{G}^{\tau ^{G}_{\mathcal{E}}} \bigl( \bigl( (\mathbb{I}_{d}- \mathbb{A}) ^{ - 1 } \mathbb{B} \bigr) (\varOmega ) \bigr) \prec M \omega _{G}^{\tau ^{G}_{\mathcal{E}}}(\varOmega ). $$

In other words, $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}: \mathcal{K} \rightarrow \mathcal{K}$ is an $( M,\mu _{G}^{\tau ^{G}_{\mathcal{E}}})$-G-weakly set contractive map, thus (in view of the proof of Theorem 3.1) there is a subset $\mathcal{Q} \subset \mathcal{K}$ invariant by $(\mathbb{I}_{d}-\mathbb{A})^{ - 1 }\mathbb{B}$ and G-weakly compact. Now we show that $(\mathbb{I}_{d}-\mathbb{A}): \mathcal{Q}\rightarrow \mathcal{Q}$ is G– weakly sequentially continuous. To this end, let $\zeta , \zeta _{ n } \in \mathcal{Q}$ such that $\zeta _{ n } \overset{G}{\rightharpoonup}\zeta$ and set ${M} = \{ \zeta _{ n } : n \in \mathbb{N} \}$. Clearly, $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}( {M})$ is relatively G-weakly compact. Thus, by Lemma 2.15, there is a subsequence $( \zeta _{ n _{ k } } )_{ k \in \mathbb{N}}$ of $( \zeta _{ n } )_{ n \in \mathbb{N}}$ such that

$$ (\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ k } } \overset{G}{\rightharpoonup} u . $$

Using the equality

$$ (\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ k } } = \mathbb{B}\zeta _{ n _{ k } } +\mathbb{A}( \mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ k } } $$

together with the G–weak sequential continuity of $\mathbb{B}$ and $\mathbb{A}$, we deduce $u =\mathbb{A}u + \mathbb{B}\zeta$, and thus $u = ( \mathbb{I}_{d} -\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta = ( \mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta$. Accordingly,

$$ (\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ k } } \overset{G}{\rightharpoonup} (\mathbb{I}_{d}- \mathbb{A}) ^{ - 1 } \mathbb{B}\zeta . $$

Now, we are going to prove the following convergence:

$$ (\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n } \overset{G}{\rightharpoonup} (\mathbb{I}_{d}- \mathbb{A}) ^{ - 1 } \mathbb{B}\zeta . $$

Suppose the opposite, then there is a G-weak neighborhood $U ^{\tau ^{G}_{\mathcal{E}}}$ of $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta$ and a subsequence $( \zeta _{ n _{ j } } )_{ j\in \mathbb{N}}$ of $( \zeta _{ n } )_{ n\in \mathbb{N}}$ such that $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ j } } \notin U ^{\tau ^{G}_{\mathcal{E}}}$ for all $j \geq 1$. The sequence $( \zeta _{ n _{ j } } )_{ j\in \mathbb{N}}$ converges G-weakly to ζ. By reasoning as before, we may then extract a subsequence $( \zeta _{ n _{ j _{k} } } )_{ k \in \mathbb{N}}$ of $( \zeta _{ n _{ j } } )_{ j \in \mathbb{N}}$ such that $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ j _{ k } } } \overset{G}{\rightharpoonup}(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta$, which is absurd since $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 } \mathbb{B}\zeta _{ n _{ j _{ k } } } \notin U ^{\tau ^{G}_{\mathcal{E}}}$ for all $k \geq 1$. Finally, $(\mathbb{I}_{d}-\mathbb{A}) ^{ - 1 }\mathbb{B}$ is G-weakly sequentially continuous. Applying Theorem 3.2, we infer that the sum $\mathbb{A}+\mathbb{B}$ has a fixed point. □

Let us now state the following consequence of Theorem 3.4.

Corollary 3.5

Let $\mathcal{K}$ be a nonempty, G–bounded, closed, and convex subset of a GBS $\mathcal{E}$. Suppose that $\mathbb{A} : \mathcal{E} \rightarrow \mathcal{E}$ and $\mathbb{B}: \mathcal{K} \rightarrow \mathcal{E}$ such that:

• (i) $\mathbb{A}$ is linear, G–bounded and there exists $p \geq 1$ such that $\mathbb{A}^{p}$ is a contraction;

• (ii) $\mathbb{B}$ is a G-weakly sequentially continuous mapping and $(\Gamma ,\omega _{G}^{\tau ^{G}_{\mathcal{E}}})$-G–set contractive; and

• (iii) $[ \zeta =\mathbb{A}\zeta + \mathbb{B}\nu , \nu \in \mathcal{K} ] \Longrightarrow \zeta \in \mathcal{K}$.

Then $\mathbb{A}+\mathbb{B}$ admits at least one fixed point in $\mathcal{K}$ whenever the matrix $\varLambda = \Gamma \cdot \varUpsilon _{ p }$ converges to zero.

Proof

We are going to see that $\mathbb{A}$ verifies all the conditions of Theorem 3.4. Indeed, because $\mathbb{A}$ is a G–bounded linear operator, it is G-Lipschitzian with matrix $M:= \|\mathbb{A}\|_{\mathcal{L}_{G}}$. Let $\nu \in \mathcal{E}$ be arbitrary. One may conclude from induction that

$$\begin{aligned}& \mathbb{A} _{ \nu} \zeta =\mathbb{A}\zeta + \nu, \\& \mathbb{A} _{ \nu} ^{ 2} \zeta =\mathbb{A} _{ \nu}( \mathbb{A} \zeta + \nu ) =\mathbb{A}(\mathbb{A} \zeta + \nu ) +\nu = \mathbb{A}^{ 2 } \zeta +\mathbb{A}\nu + \nu, \\& \vdots \\& \mathbb{A} _{ \nu} ^{ k } \zeta =\mathbb{A}^{ k } \zeta + \mathbb{A}^{ k - 1 } \nu + \cdots +\mathbb{A}\nu + \nu\quad \text{for all } k \in \mathbbm{ }\mathbb{N}\mathbbm{ }. \end{aligned}$$

This shows

$$ \bigl\Vert \mathbb{A}_{ \nu} ^{ k } \zeta - \mathbb{A}_{ \nu} ^{ k } z \bigr\Vert _{G}= \bigl\Vert \mathbb{A}^{ k} \zeta -\mathbb{A}^{ k } z \bigr\Vert _{G}\quad \text{for all } k\in \mathbb{N}\text{ and for all } \zeta , z \in \mathcal{E}. $$

In particular, for $k=p$,

$$ \bigl\Vert \mathbb{A}_{ \nu} ^{ p } \zeta - \mathbb{A}_{ \nu} ^{ p } z \bigr\Vert _{G}= \bigl\Vert \mathbb{A}^{ p } \zeta -\mathbb{A}^{ p } z \bigr\Vert _{G} \preccurlyeq M^{p} \Vert \zeta - z \Vert _{G} \quad \text{for all } \zeta , z \in \mathcal{E}. $$

Consequently, $\mathbb{A} _{ \nu} ^{ p }$ is a contraction, and so all the conditions of Lemma 2.25 are verified. On the other hand, it follows by Lemma 2.26 that $(\mathbb{I}_{d} -\mathbb{A}^{p})^{-1}$ exists on $\mathcal{E}$ and is G–bounded, hence

$$ ( \mathbb{I}_{d} -\mathbb{A} ) ^{ - 1 } = \bigl( \mathbb{I}_{d}- \mathbb{A}^{ p } \bigr) ^{ - 1 }\sum _{ k = 0 } ^{ p - 1 } \mathbb{A}^{ k } \in \mathcal{L}_{G}(\mathcal{E}). $$

When combining Eq. (2.2) and Lemma 2.11, we conclude that $( \mathbb{I}_{d} -\mathbb{A} ) ^{ - 1 }$ is G-weakly continuous. In view of Lemma 2.12, $( \mathbb{I}_{d} -\mathbb{A} ) ^{ - 1 }$ is G-weakly sequentially continuous, thus it is a G–ww–compact operator. Now, Theorem 3.4 completes the proof. □

4 An application

Let $E_{1}$ and $E_{2}$ be two reflexive Banach spaces. Consider the following system of integral equations (SIE):

$$ \textstyle\begin{cases} \zeta _{1} ( \iota ) = ( \int _{ 0 } ^{ \iota }\mathbb{H} _{1}( \varsigma ,\iota )\varXi _{1} ( \iota ,\varsigma , \zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma ) )\,d\varsigma )\cdot u_{1} \\ \hphantom{\zeta _{1} ( \iota ) =}{}+ \varPi _{1} (\iota , \int _{0}^{\phi _{ 1 } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{1}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{1}, \\ \zeta _{2} (\iota ) = ( \int _{ 0 } ^{ \iota }\mathbb{H} _{2}( \varsigma ,\iota ) \varXi _{2} ( \iota ,\varsigma , \zeta _{1} ( \varsigma ), \zeta _{2} (\varsigma ) )\,d\varsigma ) \cdot u_{2} \\ \hphantom{\zeta _{2} (\iota ) =}{}+\varPi _{2} (\iota , \int _{0}^{\phi _{ 2 } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{2}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{2} , \end{cases} $$

(4.1)

where $u_{1},v_{1} \in E_{1} \backslash \{ 0 \}$ and $u_{2},v_{2} \in E_{2} \backslash \{ 0 \}$. We will prove that system (4.1) has a solution in the GBS $\mathcal{E}= \mathcal{{ C }} ( [0,1], E_{1} )\times \mathcal{{ C }} ( [0,1], E_{2} )$ of all couple of continuous functions on $[0,1]$ equipped with the generalized norm

$$ \begin{aligned} \Vert . \Vert _{G} : \quad &\mathcal{E} \longrightarrow \mathbb{R}^{2}_{+} \\ & \zeta =(\zeta _{1},\zeta _{2}) \mapsto \bigl\Vert ( \zeta _{1},\zeta _{2}) \bigr\Vert _{G}= \begin{pmatrix} {\sup_{\iota \in [0,1]}} \Vert \zeta _{1}(\iota ) \Vert _{E_{1}} \\ {\sup_{\iota \in [0,1]}} \Vert \zeta _{2}(\iota ) \Vert _{E_{2}} \end{pmatrix} . \end{aligned} $$

We recall that problem (SIE) (4.1) can be written in the following form:

$$ \zeta =(\mathbb{A}+\mathbb{B})\zeta , $$

where

$$ \mathbb{A}\zeta (\iota )= \begin{pmatrix} \mathbb{A}_{1}\zeta (\iota ) \\ \mathbb{A}_{2}\zeta (\iota ) \end{pmatrix} = \begin{pmatrix} ( \int _{ 0 } ^{ \iota }\mathbb{H} _{1}(\varsigma ,\iota ) \varXi _{1} ( \iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ) )\,d\varsigma ) \cdot u_{1} \\ ( \int _{ 0 } ^{ \iota }\mathbb{H} _{2}(\varsigma ,\iota ) \varXi _{2} ( \iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ) )\,d\varsigma ) \cdot u_{2} \end{pmatrix} $$

and

$$ \mathbb{B}\zeta (\iota )= \begin{pmatrix} \mathbb{B}_{1}\zeta (\iota ) \\ \mathbb{B}_{2}\zeta (\iota ) \end{pmatrix} = \begin{pmatrix} \varPi _{1} (\iota , \int _{0}^{\phi _{ 1 } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{1}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{1} \\ \varPi _{2} (\iota , \int _{0}^{\phi _{ 2} ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{2}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))\,d\varsigma ) \cdot v_{2} \end{pmatrix} . $$

Problem (4.1) will be discussed under the following assumptions:

$(\mathcal{H}_{1})$:

The functions $\varXi _{1}, \varXi _{2},: [0,1] \times [0,1] \times E_{1} \times E_{2} \longrightarrow \mathbbm{ }\mathbb{R}\mathbbm{ }$ such that

• (a) $\varXi _{i}$, $i\in \{1,2\}$ are linear on $\mathcal{E}$, and there are constants $a_{i} \in \mathbb{R_{+}}$ such that

  $$ \bigl\vert \varXi _{i}\bigl(\iota ,\varsigma ,\zeta _{1}(\iota ),\zeta _{2}(\iota )\bigr) \bigr\vert \leq a_{i} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}},\quad i=1,2. $$

• (b) $\varXi _{i}$, $i\in \{1,2\}$ are continuous on $[0,1]$ with respect to the first variable.

$(\mathcal{H}_{2})$:

$\phi _{1}, \phi _{2} : [0,1] \longrightarrow [0,1]$ are continuous and nondecreasing,

$(\mathcal{H}_{3})$:

The functions $\varTheta _{1}, \varTheta _{2},: [0,1] \times [0,1] \times \mathbb{R}\times \mathbb{R}\longrightarrow \mathbbm{ }\mathbb{R}\mathbbm{ }$ such that:

• (a) For arbitrary fixed $\varsigma \in [0,1]$ and $\zeta \in \mathcal{E}$, the partial function $\iota \rightarrow \varTheta _{i} ( \iota ,\varsigma , \zeta _{1}, \zeta _{2} )$, $i =1,2$, is continuous on $[0,1]$,

• (b) There exist functions $\theta _{i} \in \mathcal{C}([0,1],\mathbb{R}_{+})$, $i=1,2$, and a vector $r \in \mathbb{R}^{2}_{+}$ such that $| \varTheta _{i} ( \iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2} ( \varsigma ) ) | \leq \theta _{ i}(\varsigma )$, $i =1,2$, $\text{ for } \zeta \in \mathcal{E} \text{ such that } \| \zeta \|_{ G} \preccurlyeq r$ with

  $$ \int _{0}^{1} \frac{1}{\iota +\varsigma} \theta (\varsigma ) \,\mathrm{d}\varsigma < \infty , $$

• (c) The functions $\varTheta _{1}$, $\varTheta _{2}$ are weakly sequentially continuous.

$(\mathcal{H}_{4})$:

The mappings $\varPi _{i} : [0,1]\times \mathbb{R}\longrightarrow \mathbb{R}$, $i \in \{1,2\}$ such that:

• (a) $\varPi _{1}$, $\varPi _{2}$ are continuous with respect to the first variable and $L_{i}$-Lipschitz with respect to the second variable $i=1,2$.

• (b) $\varPi _{1}$, $\varPi _{2}$ are weakly sequentially continuous with respect to the second variable.

$(\mathcal{H}_{5})$:

The functions $\mathbb{H}_{1}$, $\mathbb{H}_{2}$ defined on $\Delta =\{(\iota , \varsigma ):0\leq \iota \leq 1 , 0\leq \varsigma \leq \iota \}$ in $\mathbb{R}$ are essentially bounded, measurable, and continuous with respect to the second variable.

Theorem 4.1

Suppose that assumptions $(\mathcal{H}_{1})$–$(\mathcal{H}_{5})$ are satisfied, then (SIE) (4.1) has a solution in $\mathcal{E}$ provided that for $i =1,2$

$$ 0\leq \frac {L_{ i } \delta +\sup_{\iota \in [0,1]} \vert \varPi _{i}(\iota ,0) \vert ) \Vert v_{i} \Vert _{E_{i}}}{1-\beta _{i}a_{i} \cdot \Vert u_{i} \Vert _{E_{i}}} \leq r_{i}, $$

(4.2)

where

$$ \delta \geq \int _{0}^{1} \theta _{i}(\varsigma ) \frac {1}{\iota +\varsigma}\,d\varsigma . $$

Proof

Let $\mathcal{K} = \overline{B}({0}, r)$ on $\mathcal{E}$, where r above-mentioned in $(\mathcal{H}_{3})$(b) and satisfies the inequality in (4.2).

To determine a fixed point in $\mathcal{E}$ for the operator $\mathbb{A}+\mathbb{B}$, we focus on applying Corollary 3.5. There will be numerous steps to complete the proof.

Claim 1: It should be highlighted that the operators involved in (4.1) are well defined. First, we show the continuity of the mapping $\mathbb{A}\zeta$ on $[0, 1]$ for all $\zeta \in \mathcal{E}$. To this end, let $\zeta \in \mathcal{E}$ and $\{ \iota _{ n } \}_{n\in \mathbb{N}}$ be a convergent sequence in $[0,1]$ with limit ι in $[0,1]$. Then, for any $i=1,2$, we get

$$\begin{aligned} \begin{aligned} &\bigl\Vert ( \mathbb{A}_{i} \zeta ) ( \iota _{n}) - ( \mathbb{A}_{i} \zeta ) ( \iota ) \bigr\Vert _{E_{i}} \\ &\quad \leq \biggl( \int _{ 0 } ^{ \iota _{n}} \bigl\vert \mathbb{H} _{i}(\varsigma ,\iota _{n})\varXi _{i} \bigl( \iota _{n}, \varsigma , \zeta _{i} (\varsigma ) \bigr) - \mathbb{H} _{i}(\varsigma , \iota )\varXi _{i} \bigl( \iota ,\varsigma , \zeta _{i} (\varsigma ) \bigr) \bigr\vert d \varsigma \\ & \qquad {} + \int _{ \iota } ^{ \iota _{n}} \bigl\vert \mathbb{H} _{i}(\varsigma , \iota )\varXi _{i} \bigl( \iota ,\varsigma , \zeta _{i} (\varsigma ) \bigr) \bigr\vert d \varsigma \biggr) \Vert u_{i } \Vert _{E_{i}} \\ & \quad \leq \biggl( \int _{ 0 } ^{ 1} \bigl\vert \mathbb{H} _{i}(\varsigma ,\iota _{n}) \varXi _{i} \bigl( \iota _{n},\varsigma , \zeta _{i} (\varsigma ) \bigr) - \mathbb{H} _{i}(\varsigma ,\iota )\varXi _{i} \bigl( \iota , \varsigma , \zeta _{i} (\varsigma ) \bigr) \bigr\vert \,d\varsigma \\ &\qquad {} + \beta _{i}a_{i}{\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}} \vert \iota _{n}-\iota \vert \biggr) \Vert u_{i } \Vert _{E_{i}}. \end{aligned} \end{aligned}$$

(4.3)

In view of hypotheses $(\mathcal{H}_{1})$(b) and $(\mathcal{H}_{5})$, we have

$$ \mathbb{H} _{i}(\varsigma ,\iota _{n})\varXi _{i} \bigl( \iota _{n}, \varsigma , \zeta _{i} ( \varsigma ) \bigr) \to \mathbb{H} _{i}(\varsigma , \iota )\varXi _{i} \bigl( \iota ,\varsigma , \zeta _{i} (\varsigma ) \bigr) \quad \text{in } \mathbb{R} \text{ when } \iota _{n} \text{ goes to }\iota . $$

Moreover, the use of inequality $(\mathcal{H}_{1})$(a), the boundedness of $\mathbb{H} _{1}$, $\mathbb{H} _{2}$, and the dominated convergence theorem shows that

$$ \bigl\Vert ( \mathbb{A}_{i} \zeta ) ( \iota _{n}) - ( \mathbb{A}_{i} \zeta ) ( \iota ) \bigr\Vert _{E_{i}}\to 0 \quad \text{when } \iota _{n} \to \iota , $$

then the operator $\mathbb{A}_{i}\zeta \in \mathcal{C}(J,E_{i})$ for each $i \in \{1,2\}$; in other words, $\mathbb{A}$ is well defined.

Now, we are going to prove the continuity of the map $\mathbb{B}\zeta$ on $[0,1]$ for all $\zeta \in \mathcal{E}$. Indeed, let $\{ \iota _{ n } \}_{n\in \mathbb{N}}$ be a convergent sequence in $[0,1]$ with limit ι in $[0,1]$; and by setting $\varPsi _{i}(\iota ,\varsigma ,\zeta (\varsigma ) ):= \frac {\iota}{\iota +\varsigma} \varTheta _{i}(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ))$, we get for $i=1,2$

$$\begin{aligned} \begin{aligned} &\biggl\vert \int _{0}^{\phi _{i} ({{\iota}_{n}})}{\varPsi _{i}\bigl( \iota _{n},\varsigma ,\zeta (\varsigma )\bigr)\,d\varsigma - \int _{0}^{ \phi _{i} (\iota )}{\varPsi _{i}\bigl(\iota , \varsigma ,\zeta (\varsigma )\bigr)\,d\varsigma}} \biggr\vert \\ &\quad \leq \int _{0}^{\phi _{i} ({{\iota}_{n}})}{ \bigl\vert \varPsi _{i} \bigl(\iota _{n},\varsigma ,\zeta (\varsigma )\bigr)- \varPsi _{i}\bigl(\iota ,\varsigma ,\zeta (\varsigma )\bigr) \bigr\vert d \varsigma} \\ &\qquad {}+ \int _{\phi _{i} (\iota )}^{\phi _{i} ({{\iota}_{n}})}{ \bigl\vert \varPsi _{i}\bigl(\iota ,\varsigma ,\zeta (\varsigma )\bigr) \bigr\vert d \varsigma} \\ &\quad \leq \int _{0}^{1}{ \bigl\vert \varPsi _{i} \bigl(\iota _{n}, \varsigma ,\zeta (\varsigma )\bigr)-\varPsi _{i}\bigl(\iota ,\varsigma ,\zeta ( \varsigma )\bigr) \bigr\vert d \varsigma} \\ &\qquad {}+({{\theta}_{i}(\varsigma ) } | \phi _{i} ({{ \iota}_{n}})- \phi _{i} (\iota ) |. \end{aligned} \end{aligned}$$

(4.4)

Since $\iota _{n} \to \iota$, so $(\iota _{n},\varsigma ,\zeta _{1}(\varsigma ),\zeta _{2}(\varsigma )) \to (\iota ,\varsigma ,\zeta _{1}(\varsigma ),\zeta _{2}(\varsigma ))$ for all $\varsigma \in [0,1]$. By using hypothesis $(\mathcal{H}_{3})$(a), we get

$$ \frac{\iota _{n}}{\iota _{n}+\varsigma} \varTheta _{i}\bigl(\iota _{n}, \varsigma ,\zeta _{1}(\varsigma ),\zeta _{2}(\varsigma ) \bigr) \to \frac{\iota}{\iota +\varsigma}\varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1}( \varsigma ),\zeta _{2}(\varsigma )\bigr) \quad \text{in } \mathbb{R}. $$

Moreover, the use of the first inequality $(\mathcal{H}_{3})$(b) and the dominated convergence theorem and $(\mathcal{H}_{4})$(a) shows that $\mathbb{B}_{i}\zeta \in \mathcal{C}([0,1],\mathbb{R})$ for each $i \in \{1,2\}$, hence $\mathbb{B}$ is well defined.

Claim 2: Proving that $\mathbb{A}$ is G–bounded and there is $p \in \mathbb{N}$ such that $\mathbb{A}^{p}$ is a contraction. In fact, from $(\mathcal{H}_{1})$(a) the first part is obvious, now let $\zeta \in \mathcal{E}$, then

$$\begin{aligned} \begin{aligned} \bigl\Vert ( \mathbb{A}_{i} \zeta ) ( \iota ) \bigr\Vert _{E_{i}} &\leq \biggl( \int _{ 0 } ^{ \iota} \bigl\vert \mathbb{H} _{i}(\varsigma ,\iota ) \bigr\vert \bigl\vert \varXi _{i} \bigl( \iota ,\varsigma , \zeta _{i} (\varsigma ) \bigr) \bigr\vert \,d\varsigma \biggr) \Vert u_{i } \Vert _{E_{i}} \\ & \leq \biggl( \beta _{i} \int _{ 0 } ^{ \iota } a_{i} \bigl\Vert \zeta _{i}( \varsigma ) \bigr\Vert _{E_{i}}\,d\varsigma \biggr) \Vert u_{i } \Vert _{E_{i}} \\ & \leq \Bigl( \beta _{i}a_{i} {\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}} \iota \Bigr) \Vert u_{i } \Vert _{E_{i}}, \end{aligned} \end{aligned}$$

(4.5)

where $\beta _{i}= \operatorname { ess} { \sup_{ ( \iota ,\varsigma ) \in \Delta }} | \mathbb{H}_{i} ( \iota , \varsigma ) | < \infty$. Again we have

$$\begin{aligned} \begin{aligned} \bigl\Vert \bigl( \mathbb{A}_{i}^{2} \zeta \bigr) ( \iota ) \bigr\Vert _{E_{i}} &\leq \bigg( \int _{ 0} ^{ \iota} \bigl\vert \mathbb{H}_{i}( \iota , \varsigma ) \bigr\vert | \varXi _{i} \biggl( \iota , \varsigma , \int _{ 0 } ^{ \varsigma} \mathbb{H}_{ i } ( \varsigma ,\sigma ) \varXi _{i} \bigl(\varsigma , \sigma , \zeta _{i} (\sigma ) { d }\sigma \bigr) |{ d }s \biggr) \Vert u_{i } \Vert _{E_{i}} \\ & \leq \biggl( \beta _{i} \int _{ 0 } ^{ \iota} a_{i} \biggl\vert \int _{ 0 } ^{ \varsigma} \mathbb{H}_{ i } ( \varsigma ,\sigma ) \varXi _{i} \bigl( \varsigma ,\sigma , \zeta _{i} (\sigma ),\bigr){ d }\sigma \biggr\vert \biggr) \Vert u_{i } \Vert _{E_{i}} \\ & \leq \frac{ (\beta _{i}a_{i}\iota )^{2}}{2!} \Vert u_{i } \Vert _{E_{i}} { \sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}}. \end{aligned} \end{aligned}$$

(4.6)

By induction, one can deduce from (4.6) and (4.5) that

$$ \bigl\Vert \bigl( \mathbb{A}_{i} ^{ n } \zeta \bigr) ( \iota ) \bigr\Vert _{E_{i}} \leq \frac { (\beta _{i}a_{i}\iota )^{n} }{ n ! } \Vert u_{i } \Vert _{E_{i}} {\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}}. $$

Hence,

$$ {\sup_{\iota \in [0,1]}} \bigl\Vert \bigl( \mathbb{A}_{i} ^{ n } \zeta \bigr) ( \iota ) \bigr\Vert _{E_{i}} \leq \frac { (\beta _{i}a_{i} )^{ n } }{ n ! } \Vert u_{i } \Vert _{E_{i}} {\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}}. $$

(4.7)

Notice that

$$ \lim_{ n \rightarrow \infty } \frac { (\beta _{i}a_{i} )^{ n } }{ n ! } \Vert u_{i } \Vert _{E_{i}} = 0. $$

And we set

$$ p = \min \biggl\{ n \in \mathbbm{ }\mathbb{N}\mathbbm{ } : \max \biggl\{ i=1,2: \frac {(\beta _{i}a_{i}) ^{ n } }{ n ! } \Vert u_{i } \Vert _{E_{i}}< 1 \biggr\} \biggr\} . $$

Clearly, p is finite, then

$$ \bigl\Vert \mathbb{A}^{p}\zeta \bigr\Vert _{G}= \begin{pmatrix} \Vert \mathbb{A}_{1}^{p}\zeta \Vert _{\infty } \\ \Vert \mathbb{A}^{p}_{2}\zeta \Vert _{\infty } \end{pmatrix} \preccurlyeq M\cdot \Vert \zeta \Vert _{G}. $$

In other words, there is $p \in \mathbb{N}$ such that $\mathbb{A}^{p}$ is an M-contraction with

$$ M= \begin{pmatrix} \frac { (\beta _{1}a_{1} )^{ p } }{ p ! } \Vert u_{1 } \Vert _{E_{1}} 0 \\ 0 \frac { (\beta _{2}a_{2} )^{ p } }{ p ! } \Vert u_{2 } \Vert _{E_{2}} \end{pmatrix} . $$

As result, our claim is verified.

Claim 3: Next, let us show that $\mathbb{B}$ is G-weakly compact. It suffices us to prove that $\mathbb{B}({\overline{B}({0}, r)} )$ is relatively G-weakly compact. By definition, for all $\iota \in (0, 1)$, we have

$$ \begin{aligned}&\mathbb{B}_{i}\bigl({\overline{B}({0}, r)} \bigr) (\iota ) \\ &\quad = \biggl\{ \varPi _{i} \biggl(\iota , \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr)\,d\varsigma \biggr) \cdot v_{i}, \Vert \zeta \Vert _{G} \preccurlyeq r \biggr\} , \quad \iota \in [0,1]. \end{aligned}$$

Proving now that for each $i=1,2$, $\mathbb{B}_{i}(\overline{B}({0}, r))(\iota )$ is weakly sequentially relatively compact in $E_{i}$. To this end, let $\{ \zeta _{ n } \}_{n=0}^{\infty}= \{( \zeta _{1_{ n}},\zeta _{2_{ n} }) \}_{n=0}^{\infty}$ be any sequence in $\overline{B}({0}, r)$. From assumptions $( \mathcal{H}_{ 4} )$(a) and $( \mathcal{H}_{ 3 } )$(b), it follows that for all $\iota \in [0, 1]$

$$\begin{aligned} \bigl\Vert \mathbb{B}_{i} \zeta _{n}(\iota ) \bigr\Vert _{E_{i}} \leq{}& \biggl[ \biggl\vert \varPi _{i} \biggl(\iota , \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota , \varsigma ,\zeta _{1_{n}} (\varsigma ), \zeta _{2_{n}}( \varsigma )\bigr)\,d\varsigma \biggr)-\varPi _{i}(\iota ,0) \biggr\vert \\ &{}+ \bigl\vert \varPi _{i}( \iota ,0) \bigr\vert \biggr] \cdot \Vert v_{i} \Vert _{E_{i}} \\ \leq{}& \biggl[ L_{ i } \biggl\vert \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1_{n}} (\varsigma ), \zeta _{2_{n}}( \varsigma )\bigr)\,d\varsigma \biggr\vert + \bigl\vert \varPi _{i}(\iota ,0) \bigr\vert \biggr]\cdot \Vert v_{i} \Vert _{E_{i}} \\ \leq{}& \biggl[ L_{ i } \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \bigl\vert \varTheta _{i}\bigl(\iota , \varsigma ,\zeta _{1_{n}} ( \varsigma ), \zeta _{2_{n}}( \varsigma )\bigr) \bigr\vert \,d\varsigma + \sup_{\iota \in [0,1]} \bigl\vert \varPi _{i}(\iota ,0) \bigr\vert \biggr] \\ &{}\cdot \Vert v_{i} \Vert _{E_{i}} \\ \leq{}& \biggl[ L_{ i } \int _{0}^{1} \theta _{i}(\varsigma ) \frac{1}{\iota +\varsigma}\,d\varsigma +\sup_{\iota \in [0,1]} \bigl\vert \varPi _{i}( \iota ,0) \bigr\vert \biggr]\cdot \Vert v_{i} \Vert _{E_{i}} \\ \leq{}& \Bigl(L_{ i } \delta +\sup_{\iota \in [0,1]} \bigl\vert \varPi _{i}(\iota ,0) \bigr\vert \Bigr) \Vert v_{i} \Vert _{E_{i}}, \end{aligned}$$

(4.8)

where $\delta \geq \int _{0}^{1} \theta _{i}(\varsigma ) \frac{1}{\iota +\varsigma}\,d\varsigma$; this shows that $\{\mathbb{B}_{i}\zeta _{n}, n \in \mathbb{N}\}$ is a uniformly bounded sequence in $\mathbb{B}_{i}(\overline{B}({0}, r))$. As a result, $\mathbb{B}_{i}(\overline{B}({0}, r))(\iota )$ is sequentially relatively weakly compact. Next, we will show that $\mathbb{B}_{i} ( \overline{B}({0}, r))$ is a weakly equicontinuous set for $i = 1,2$. If we take $\varepsilon > 0$, $\zeta \in \overline{B}({0}, r)$, $\zeta _{i}^{*} \in E_{i}^{*}$, and $\iota , \iota ^{ \prime } \in [0,1]$ such that $\iota \leq \iota ^{ \prime }$, $\iota ^{ \prime } - \iota \leq \varepsilon$,

$$\begin{aligned}& \bigl\Vert \zeta _{i}^{*} \bigl(\mathbb{B}_{i} \zeta (\iota )-\mathbb{B}_{i} \zeta \bigl(\iota ^{ \prime } \bigr)\bigr) \bigr\Vert _{E_{i}} \\& \quad \leq \biggl\vert \varPi _{i} \biggl(\iota , \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr)\,d\varsigma \biggr) \\& \qquad {}- \varPi _{i} \biggl(\iota ^{ \prime }, \int _{0}^{\phi _{ i } ( \iota ^{ \prime } )} \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma )\bigr)\,d\varsigma \biggr) \biggr\vert \cdot \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \quad \leq L_{i} \biggl\vert \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr)\,d\varsigma \\& \qquad {}- \int _{0}^{\phi _{ i } ( \iota ^{ \prime } )} \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma )\bigr)\,d\varsigma \biggr\vert \cdot \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \quad \leq L_{i} \biggl[ \int _{ 0 } ^{ \phi _{ i } ( \iota ) } \biggl\vert \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) - \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma )\bigr) \biggr\vert \,d\varsigma \biggr] \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \qquad {}+ L_{i} \biggl[ \int _{ \phi _{ i } ( \iota ) } ^{ \phi _{ i } ( \iota ^{ \prime } ) } \biggl\vert \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) \biggr\vert \,d\varsigma \biggr] \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \quad \leq L_{i} \biggl( {\sup_{ \iota , \iota ^{ \prime },\varsigma \in [0,1], \vert \iota -\iota ' \vert < \varepsilon ,\atop (\zeta _{1}, \zeta _{2} )\in \overline{B}({0}, r)}} \biggl\vert \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl( \iota ,\varsigma ,\zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) \\& \qquad {}- \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) \biggr\vert \biggr) \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \qquad {}+L_{i} \biggl( \int _{ \phi _{ i } ( \iota ) } ^{ \phi _{ i } ( \iota ^{ \prime } ) } \biggl\vert \theta _{i}(\varsigma ) \frac{1}{\iota ^{\prime}+\varsigma} \biggr\vert \,d\varsigma \biggr) \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \quad \leq L_{i} \biggl( {\sup_{ \iota , \iota ^{ \prime },\varsigma \in [0,1], \vert \iota -\iota ' \vert < \varepsilon ,\atop (\zeta _{1}, \zeta _{2} )\in \overline{B}({0}, r)}} \biggl\vert \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl( \iota ,\varsigma ,\zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) \\& \qquad {}- \frac{\iota ^{ \prime }}{\iota ^{ \prime }+\varsigma} \varTheta _{i}\bigl( \iota ^{ \prime },\varsigma ,\zeta _{1} (\varsigma ), \zeta _{2}( \varsigma )\bigr) \biggr\vert \biggr) \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert \\& \qquad {}+ L_{i} \Bigl( {\sup_{ \iota , \iota ^{ \prime } \in [0,1],\atop \vert \iota -\iota ' \vert < \varepsilon }} \bigl\{ \bigl\vert \phi _{ i } ( \iota ) - \phi _{ i } \bigl( \iota ^{ \prime } \bigr) \bigr\vert \bigr\} \cdot {\sup_{ \varsigma \in [0,1]\atop }} \bigl\vert \theta _{i}(\varsigma ) \bigr\vert \Bigr) \bigl\vert \zeta _{i}^{*}(v_{i}) \bigr\vert . \end{aligned}$$

(4.9)

Remembering that the functions $\varTheta _{i}(.,\varsigma ,\zeta _{1} , \zeta _{2} )$ and $\phi _{i}$ are uniformly continuous on $[0,1]$, for each $i=1,2$, so $| \zeta _{i}^{*}((\mathbb{B}_{i}\zeta )(\iota )- (\mathbb{B}_{i} \zeta )(\iota '))|\rightarrow 0$ when ι goes to $\iota ^{\prime}$. By applying Arzelà–Ascoli’s theorem [30], we infer that $\mathbb{B}_{i} ( \overline{B}({0}, r) )$ is weakly sequentially relatively compact in $E_{i}$ for $i=1,2$, hence $\mathbb{B}$ is G-weakly compact on $\mathcal{E}$.

Claim 4: Next, we show that $\mathbb{B}$ is G-weakly sequentially continuous. To this end, let $\{\xi _{n}, n \in \mathbb{N}\}$ be a converging sequence of $\overline{B}({0}, r)$ to a point ξ in $\tau _{{\mathcal{E}}}^{G}$ settings, then

$$ \xi _{i_{n}}\rightharpoonup \xi _{i}\quad \text{in } \mathcal{{ C }} \bigl( [0,1],E_{i} \bigr), i=1,2. $$

By the boundedness of $\overline{B_{i}}(0, r_{i})$ and Dobrakov’s theorem [7], we have

$$ \xi _{i _{n} } ( \iota ) \rightharpoonup \xi _{i} ( \iota ) \quad \text{in } E_{i}, i=1,2 . $$

(4.10)

Combining (4.10), assumptions $(\mathcal{H}_{ 3 } )$(b), $(\mathcal{H}_{ 3 } )$(c), and Dobrakov’s theorem, we obtain

$$ \frac{\iota}{\iota +\varsigma} \varTheta _{i} \bigl( \iota ,\varsigma , \xi _{1 _{n} } (\varsigma ),\xi _{2 _{n} } (\varsigma ) \bigr) \rightharpoonup \frac{\iota}{\iota +\varsigma} \varTheta _{i} \bigl( \iota , \varsigma , \xi _{1 } (\varsigma ),\xi _{2 } (\varsigma ) \bigr) \quad \text{in } \mathbb{R}. $$

Now, by using $(\mathcal{H}_{ 3 } )$(b) and the dominated convergence theorem [16], we infer that

$$ \lim_{ n \rightarrow \infty } \int _{ 0 } ^{ \phi _{ i} ( \iota ) } \frac{\iota}{\iota +\varsigma} \varTheta _{ i } \bigl( \iota ,s, \xi _{ n } ( \varsigma ) \bigr)\,d\varsigma = \int _{ 0 } ^{ \phi _{ i } ( \iota ) } \frac{\iota}{\iota +\varsigma} \varTheta _{ i } \bigl(\varsigma ,\iota , \xi (\varsigma ) \bigr)\,d\varsigma . $$

The use of assumption $(\mathcal{H}_{ 4} )$(b) and Dobrakov’s theorem allows us to obtain

$$ \varPi _{ i} \bigl( \iota , \xi _{ n } ( \iota ) \bigr) \rightharpoonup \varPi _{ i } \bigl( \iota , \xi ( \iota ) \bigr) \quad \text{in }\mathbbm{ }\mathbb{R}\mathbbm{ }, i=1,2. $$

So,

$$ \mathbb{B}_{i}\xi _{n}(\iota )\rightharpoonup \mathbb{B}_{i}\xi ( \iota )\quad \text{in } E_{i}, i=1,2. $$

In view of Eq. (4.8), we deduce that $(\mathbb{B}_{i}\xi _{{n}})_{n\in \mathbb{N}}$, $i=1,2$, is bounded by $(L_{ i } \delta +\sup_{\iota \in [0,1]}|\varPi _{i}(\iota , 0)|) \|v_{i}\|_{E_{i}}$. Then, by using Dobrakov’s theorem again, we get that $\mathbb{B}_{i} \xi _{{ n }} \rightharpoonup \mathbb{B}_{i} \xi$, hence $\mathbb{B}$ is G-weakly sequentially continuous on $\overline{B}({0}, r)$.

Claim 5: Proving that ($\zeta =\mathbb{A}\zeta + \mathbb{B}\nu$, $\nu \in \overline{B}({0}, r)$) implies $\zeta \in \overline{B}({0}, r)$

$$ \begin{aligned} \Vert \zeta \Vert _{G} &= \Vert \mathbb{A}\zeta + \mathbb{B}\nu \Vert _{G} \\ &= \begin{pmatrix} {\sup_{\iota \in [0,1]}} \Vert \mathbb{B}_{1}\nu ( \iota )+\mathbb{A}_{1}\zeta (\iota ) \Vert _{E_{1}} \\ { \sup_{\iota \in [0,1]} } \Vert \mathbb{B}_{2}\nu ( \iota )+\mathbb{A}_{2}\zeta (\iota ) \Vert _{E_{2}} \end{pmatrix} . \end{aligned} $$

And we have

$$ \begin{aligned} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}} ={}& \biggl\Vert \biggl( \int _{ 0 } ^{ \iota }\mathbb{H} _{i}(\varsigma ,\iota )\varXi _{i} \bigl( \iota , \varsigma , \zeta _{1} ( \varsigma ), \zeta _{2}( \varsigma ) \bigr)\,d\varsigma \biggr)\cdot u_{i} \\ & {}+\varPi _{i} \biggl(\iota , \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota ,\varsigma ,\nu _{1} (\varsigma ), \nu _{2}( \varsigma )\bigr)\,d\varsigma \biggr) \cdot v_{i} \biggr\Vert _{E_{i}} \\ \leq{}& \int _{ 0 } ^{ \iota } \bigl\vert \mathbb{H} _{i}(\varsigma ,\iota ) \bigr\vert \bigl\vert \varXi _{i} \bigl( \iota ,\varsigma , \zeta _{1} (\varsigma ), \zeta _{2}( \varsigma ) \bigr) \bigr\vert \,d\varsigma \cdot \Vert u_{i} \Vert _{E_{i}} . \\ &{}+ \biggl\vert \varPi _{i} \biggl(\iota , \int _{0}^{\phi _{ i } ( \iota )} \frac{\iota}{\iota +\varsigma} \varTheta _{i}\bigl(\iota , \varsigma ,\nu _{1} (\varsigma ), \nu _{2}( \varsigma )\bigr)\,d\varsigma \biggr) \biggr\vert \cdot \Vert v_{i} \Vert _{E_{i}} \\ \leq{}& \Bigl(\beta _{i}a_{i} {\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}} \Bigr) \cdot \Vert u_{i} \Vert _{E_{i}}+\Bigl(L_{ i } \delta +\sup_{\iota \in [0,1]} \bigl\vert \varPi _{i}(\iota ,0) \bigr\vert \Bigr) \Vert v_{i} \Vert _{E_{i}}; \end{aligned} $$

so

$$ \begin{aligned} {\sup_{\iota \in [0,1]}} \bigl\Vert \zeta _{i}(\iota ) \bigr\Vert _{E_{i}} \leq \frac {L_{ i } \delta +\sup_{\iota \in [0,1]} \vert \varPi _{i}(\iota ,0) \vert ) \Vert v_{i} \Vert _{E_{i}}}{1-\beta _{i}a_{i} \cdot \Vert u_{i} \Vert _{E_{i}}} \leq r_{i}, \end{aligned} $$

to put it simply,

$$ \Vert \zeta \Vert _{G}\preccurlyeq r. $$

By applying Corollary 3.5, we get that problem (4.1) has a solution in $\mathcal{E}$, and thus the proof is completed. □