Abstract
We introduce a class of stochastic matrix control functions and apply them to stabilize pseudo stochastic κ-random operator inequalities in matrix MB-algebras. We obtain an approximation for stochastic κ-random operator inequalities and calculate the maximum error of the estimate.
Similar content being viewed by others
1 Introduction
In this paper, we study distribution functions with the ranges in a class of matrix algebras [1–3] and introduce the concept of a matrix Menger normed algebra using the generalized triangular norm which is a generalization of an MB-algebra [4], i.e., a Menger normed space with algebraic structures [5–8]. This concept helps us to study intuitionistic spaces and their generalization, i.e., neutrosophic spaces introduced by Smarandache [9, 10]. We define a stochastic matrix control function and stabilize pseudo-stochastic κ-random operator inequalities, and this process leads to best approximation of a κ-random operator inequality.
2 Preliminaries
Let
We denote \({\mathbf{t}}:=\operatorname{diag}[t_{1},\dots ,t_{n}]\preceq {\mathbf{s}}:= \operatorname{diag}[s_{1},\dots ,s_{n}]\) if and only if \(t_{i}\leq s_{i}\) for all \(i=1,\dots ,n\), also \({\mathbf{1}}=\operatorname{diag}[1,\dots ,1]\) and \({\mathbf{0}}=\operatorname{diag}[0,\dots ,0]\).
Now, we extend the concept of triangular norms [11, 12] on \(\operatorname{diag} M_{n}([0,1])\).
Definition 2.1
A generalized triangular norm (GTN) on \(\operatorname{diag} M_{n}([0,1])\) is an operation  satisfying the following conditions:
satisfying the following conditions:
-
(a)
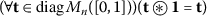 (boundary condition);
(boundary condition); -
(b)
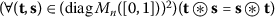 (commutativity);
(commutativity); -
(c)
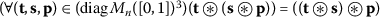 (associativity);
(associativity); -
(d)
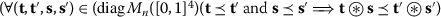 (monotonicity).
(monotonicity).
If for every \(\mathbf{t}, \mathbf{s} \in \operatorname{diag} M_{n}([0,1])\) and every sequences \(\{\mathbf{t}_{k}\}\) and \(\{\mathbf{s}_{k}\}\) converging to t and s we have

then  on \(\operatorname{diag} M_{n}([0,1])\) will be continuous (in short, CGTN). Now we present some examples of CGTN.
on \(\operatorname{diag} M_{n}([0,1])\) will be continuous (in short, CGTN). Now we present some examples of CGTN.
(1) Define  such that
such that

then  is CGTN (product CGTN);
is CGTN (product CGTN);
(2) Define  such that
such that

then  is CGTN (minimum CGTN);
is CGTN (minimum CGTN);
(3) Define  such that
such that

then  is CGTN (Lukasiewicz CGTN).
is CGTN (Lukasiewicz CGTN).
Now, we present some numerical examples:

Also, since
we get

We consider the set of matrix distribution functions (MDF) \(\Xi ^{+}\) which are left-continuous and increasing maps \(\Theta :{\mathbb{R}} \cup \{-\infty ,\infty \} \to \operatorname{diag} M_{n}([0,1])\) such that \(\Theta _{0}={\mathbf{0}}\) and \(\Theta _{+\infty }={\mathbf{1}}\). Now \(O^{+}\subseteq \Xi ^{+}\) are all (proper) mappings \(\Theta \in \Xi ^{+}\) for which \(\ell ^{-}\Theta _{+\infty }={\mathbf{1}}\) (\(\ell ^{-}\Theta _{\tau }=\lim_{\sigma \to \tau ^{-}}\Theta _{\sigma }\)). Note proper MDFs are the MDFs of real random variables (i.e., of those random variables g that a.s. take real values (\(P(|g|=\infty )=0\))).
In \(\Xi ^{+}\), we define “⪯” as follows:
Also
belongs to \(\Xi ^{+}\), and for every MDF Θ we have \(\Theta \preceq \nabla ^{0}\) [11, 13–16]. For example,
is an MDF in \(\operatorname{diag} M_{3}([0,1])\). Note that \(\Theta _{\tau }=\operatorname{diag}[\theta _{1,\tau },\dots ,\theta _{n, \tau }]\), in which \(\theta _{i,\tau }\) are distribution functions, is an MDF.
Definition 2.2
Consider the CGTN  , a linear space W, and MDF \(\Theta :W\to O^{+}\). In this case, we call a matrix Menger normed space (MMN-space) the triple
, a linear space W, and MDF \(\Theta :W\to O^{+}\). In this case, we call a matrix Menger normed space (MMN-space) the triple  if the following conditions are satisfied:
if the following conditions are satisfied:
-
(MMN1)
\(\Theta ^{w}_{\tau }=\nabla ^{0}_{\tau }\) for all \(\tau >0\) if and only if \(w=0\);
-
(MMN2)
\(\Theta ^{\alpha w}_{\tau }=\Theta ^{w}_{\frac{\tau }{|\alpha |}}\) for all \(w\in W\) and \(\alpha \in \mathbb{C}\) with \(\alpha \neq 0\);
-
(MMN3)
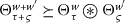 for all \(w,w'\in W\) and \(\tau ,\varsigma \geq 0\).
for all \(w,w'\in W\) and \(\tau ,\varsigma \geq 0\).
For example, the MDF Θ given by
is a matrix Menger norm and  is an MMN-space; here \((W,\|\cdot \|)\) is a normed linear space.
is an MMN-space; here \((W,\|\cdot \|)\) is a normed linear space.
Note that in neutrosophic set theory we need three norms to describe an object (probability, improbability, undecidability), while in intuitionistic random normed spaces we need two norms to describe an object, so MDFs on \(\operatorname{diag} M_{3}([0,1])\) and \(\operatorname{diag} M_{2}([0,1])\) are suitable for these theories, respectively.
Definition 2.3
Consider the CGTN’s  ,
,  and the MMN-space
and the MMN-space  . If
. If
-
(MMN-5)
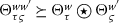 for all \(w,w'\in W\) and all \(\tau ,\varsigma >0\),
for all \(w,w'\in W\) and all \(\tau ,\varsigma >0\),
we say that  is a matrix Menger normed algebra (in short, MMN-algebra).
is a matrix Menger normed algebra (in short, MMN-algebra).
If
then
is an MMN-algebra  , and vice versa. A Menger Banach algebra (MMB-algebra) is a complete MMN-algebra. Consider the complete MMN-spaces U and V. Consider the probability measure space \((\Gamma , \Pi , \Theta )\) with the Borel measurable spaces \((U,{\mathfrak{B}}_{U})\) and \((V,{\mathfrak{B}}_{V})\). A random operator is a map \(\Lambda :\Gamma \times U\to V\) such that \(\{\gamma : \Lambda (\gamma ,u)\in B\}\in \Pi \) for all u in U and \(B\in {\mathfrak{B}}_{V}\). If
, and vice versa. A Menger Banach algebra (MMB-algebra) is a complete MMN-algebra. Consider the complete MMN-spaces U and V. Consider the probability measure space \((\Gamma , \Pi , \Theta )\) with the Borel measurable spaces \((U,{\mathfrak{B}}_{U})\) and \((V,{\mathfrak{B}}_{V})\). A random operator is a map \(\Lambda :\Gamma \times U\to V\) such that \(\{\gamma : \Lambda (\gamma ,u)\in B\}\in \Pi \) for all u in U and \(B\in {\mathfrak{B}}_{V}\). If
then Λ is linear, and if we can find a \(H(\gamma )>0\) such that
then Λ is bounded.
In MMB-algebras, we study κ-random operator inequalities
where \(0\neq \kappa \in \mathbb{C}\) is fixed and \(|\kappa |<1\). We stabilize the pseudo-stochastic biadditive κ-random operator in MMB-algebras by a stochastic control function. This process is said to be Hyers–Ulam–Rassias (HUR) stable for additive κ-random operator inequalities in MMB-algebras.
3 Best approximation of the κ-random operator inequality (2.1)
We improve Park et al. results [17, 18] and [15, 19–23] to get a better approximation.
Lemma 3.1
Let \(\Lambda : \Gamma \times U^{2} \rightarrow V\) be a random operator satisfying (2.1) and \(\Lambda (\gamma ,0, w) = \Lambda (\gamma ,u,0)=0\) for each \(u,w,r\in U\) and \(\gamma \in \Gamma \). Then \(\Lambda : \Gamma \times U^{2} \rightarrow V\) is biadditive.
Proof
Putting \(u=v\) and \(r=0\) in (2.1), we obtain (note \(\Lambda (\gamma ,0, w) = \Lambda (\gamma ,u,0)=0\)) \(\Lambda (\gamma ,2u, w) = 2\Lambda (\gamma ,u, w)\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Thus
and
for all \(u, v, w, r \in U\), \(\gamma \in \Gamma \), \(\tau >0\).
Putting \(r=0\) in (3.1), we have \(\Lambda (\gamma ,u+v, w) +\Lambda (\gamma ,u-v, w) = 2\Lambda ( \gamma ,u, w) \) and \(\Lambda (\gamma ,u_{1}, w) + \Lambda (\gamma ,v_{1}, w) = 2\Lambda (\gamma ,\frac{u_{1} + v_{1}}{2}, p ) =\Lambda (\gamma ,u_{1} + v_{1}, p)\) for all \(u_{1} : = u+v\), \(v_{1} : = u-v\), \(w \in U\), since \(|\kappa |\le 1\) and \(\Lambda (\gamma ,0, w) =0\) for all \(w\in U\). Thus \(\Lambda : \Gamma \times U^{2} \to V\) is additive in the second variable.
By a similar method, we can show that \(\Lambda :\Gamma \times U^{2} \to V\) is additive in the last variable. Then \(\Lambda : \Gamma \times U^{2} \to V\) is a random biadditive operator. □
Theorem 3.2
Let  be an MMB-algebra, let \(\psi :U^{4}\rightarrow O^{+} \) be an MDF such that there exists a \(\beta <1\) with \(\psi ^{\frac{u}{2},\frac{v}{2},w,0}_{\tau }\succeq \psi ^{u,v,w,0}_{ \frac{2\tau }{\beta }}\) for all \(u,v,w,r\in U\) and \(\tau >0\), and
be an MMB-algebra, let \(\psi :U^{4}\rightarrow O^{+} \) be an MDF such that there exists a \(\beta <1\) with \(\psi ^{\frac{u}{2},\frac{v}{2},w,0}_{\tau }\succeq \psi ^{u,v,w,0}_{ \frac{2\tau }{\beta }}\) for all \(u,v,w,r\in U\) and \(\tau >0\), and
for all \(u,v\in U\), \(\tau >0\). Suppose the random operator \(\Lambda :\Gamma \times U^{2}\rightarrow V\) satisfies \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\), \(\gamma \in \Gamma \) and

for all \(u,v,w,r\in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
Putting \(r=0\) and \(v =u\) in (3.3), we get
for all \(u,w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Thus
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Replacing u by \(\frac{u}{2^{n}}\) in (3.6), we obtain
It follows from
and (3.7) that

for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0\). That is,
Replacing u with \({\frac{u}{2^{m}}}\) in (3.8), we get
Since \(\psi ^{u,u,w,0}_{ \frac{\tau }{\sum _{k=m+1}^{n+m}\frac{\beta ^{k}}{2}}}\) tends to \(\nabla ^{0}_{\tau }\) as \(m,n\to \infty \), it follows that the sequence \(\{2^{n} \Lambda (\gamma ,\frac{u}{2^{n}}, w )\}\) is Cauchy for all \(u, w \in U\), \(\gamma \in \Gamma \). Since V is an MMB-algebra, \(\{2^{n} \Lambda (\gamma ,\frac{u}{2^{n}}, w )\}\) is a convergent sequence. Now, we define a random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) by
for all \(u,w \in U\), \(\gamma \in \Gamma \). Putting \(m =0\) and letting \(n \to \infty \) in (3.9), we conclude that
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Now, (3.3) implies that

for all \(u,v,w,r\in T\), \(\gamma \in \Gamma \), \(\tau >0\), since \(\psi ^{\frac{u}{2^{n}},\frac{u}{2^{n}},w,0}_{\frac{\tau }{2^{n}}} \) tends to \(\nabla ^{0}_{\tau }\) as \(n \to \infty \). Thus
for all \(u,v,w,r\in U\), \(\gamma \in \Gamma \), \(\tau >0\). From Lemma 3.1, the random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) is stochastic biadditive.
Now, to show that the random operator Δ is unique, assume that there exists a stochastic biadditive random operator \(\Omega :\Gamma \times U^{2} \rightarrow V\) which satisfies (3.4). Thus,

Since \(\lim_{n\to \infty }\frac{2(1-\beta )}{\beta ^{n+1}}=\infty \), we get that \(\psi ^{u,u,w,0}_{\frac{2(1-\beta )\tau }{\beta ^{n+1}}}\) tends to \(\nabla ^{0}_{\tau }\) as \(n \to \infty \).
Therefore, it follows that \(\Theta ^{ 2^{n}\Delta (\gamma ,\frac{u}{2^{n}}, w ) - 2^{n} \Omega (\gamma ,\frac{u}{2^{n}} w )}_{\tau }=1\), for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0\). Thus we can conclude that \(\Delta (\gamma ,u, w)=\Omega (\gamma ,u, w)\), for all \(u, w \in U\) and \(\gamma \in \Gamma \). □
Corollary 3.3
Let  be an MMB-algebra. Assume that \(\iota > 1\), ς is a nonnegative real number, and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying \(\Lambda (\gamma ,u, 0)= \Lambda (\gamma ,0, w)=0\) and
be an MMB-algebra. Assume that \(\iota > 1\), ς is a nonnegative real number, and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying \(\Lambda (\gamma ,u, 0)= \Lambda (\gamma ,0, w)=0\) and

for all \(u,v, w, r \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Then we can find a unique biadditive random operator \(\Delta : \Gamma \times T^{2} \rightarrow S\) such that
for all \(u,w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
The result follows from Theorem 3.2 by putting
for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0\), and \(\beta =2^{1-\iota }\). □
Theorem 3.4
Let  be an MMB-algebra, let \(\psi :U^{4}\rightarrow O^{+} \) be an MDF such that there exists a \(\beta <1\) with \(\psi ^{u,v,w,0}_{\tau }\succeq \psi ^{\frac{u}{2},\frac{v}{2},w,0}_{ \frac{\tau }{2\beta }}\) for all \(u,v,w\in U\), \(\lim_{n\to \infty }\psi ^{2^{n}u,2^{n}v,w,0}_{2^{n}\tau }=1\) for all \(u,v,w\in U\), \(\tau >0\). Suppose that a random operator \(\Lambda :\Gamma \times U^{2}\rightarrow V\) satisfies (3.3) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,v\in U\) and \(\gamma \in \Gamma \). Then, there is a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
be an MMB-algebra, let \(\psi :U^{4}\rightarrow O^{+} \) be an MDF such that there exists a \(\beta <1\) with \(\psi ^{u,v,w,0}_{\tau }\succeq \psi ^{\frac{u}{2},\frac{v}{2},w,0}_{ \frac{\tau }{2\beta }}\) for all \(u,v,w\in U\), \(\lim_{n\to \infty }\psi ^{2^{n}u,2^{n}v,w,0}_{2^{n}\tau }=1\) for all \(u,v,w\in U\), \(\tau >0\). Suppose that a random operator \(\Lambda :\Gamma \times U^{2}\rightarrow V\) satisfies (3.3) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,v\in U\) and \(\gamma \in \Gamma \). Then, there is a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
Putting \(r=0\) and \(v = u\) in (3.3), we have
for all \(u,w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Thus
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Changing u by \(2^{n}u\) in (3.15), we have
From
and (3.16), we get
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). That is,
Replacing u with \({2^{m}u}\) in (3.17), we get
Since \(\psi ^{u,u,w,0}_{ \frac{\tau }{\sum _{k=m}^{n+m}\frac{(2\beta )^{k}}{2\times 2^{k}}}}\) tends to \(\nabla ^{0}_{\tau }\) as \(m,n\to \infty \), it follows that \(\{\frac{1}{2^{n}} \Lambda (\gamma ,2^{n}u, w )\}\) is a Cauchy sequence for all \(u,w \in U\) and \(\gamma \in \Gamma \). Since V is an MMB-algebra, the sequence \(\{\frac{1}{2^{n}}\Lambda (\gamma ,2^{n}u, w )\}\) converges. Now, we define the random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) by
for all \(u, w \in U\) and \(\gamma \in \Gamma \). Putting \(m =0\) and letting \(n \to \infty \) in (3.18), we have
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). The proof is finished by using Theorem 3.2. □
Corollary 3.5
Let  be an MMB-algebra. Assume that \(\iota < 1\), \(\varsigma \geq 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying (3.11) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
be an MMB-algebra. Assume that \(\iota < 1\), \(\varsigma \geq 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying (3.11) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
The result follows from Theorem 3.4 by putting
for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0 \), and \(\beta =2^{\iota -1}\). □
4 Best approximation of the κ-random operator inequality (2.2)
Lemma 4.1
Let the random operator \(\Lambda : \Gamma \times U^{2} \rightarrow V\) satisfy \(\Lambda (\gamma ,0, w) = \Lambda (\gamma ,u,0)=0\) and
for all \(u, v, w,r \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Then \(\Lambda : \Gamma \times U^{2} \rightarrow V\) is biadditive.
Proof
Putting \(v=r=0\) in (4.1), we get \(4 \Lambda (\gamma ,\frac{u}{2}, w ) = 2\Lambda (\gamma ,u,w) \) for all \(u, w\in U\) and \(\gamma \in \Gamma \). Thus
and
for all \(u,v, w,r \in U\) and \(\gamma \in \Gamma \).
The proof is completed by using a similar method as in Lemma 3.1. □
Theorem 4.2
Let  be an MMB-algebra. Assume that \(\psi :U^{4}\rightarrow O^{+} \) is an MDF in which there is a \(\beta <1\) with \(\psi ^{\frac{u}{2},\frac{v}{2},w,0}_{\tau }\geq \psi ^{u,v,w,0}_{ \frac{2\tau }{\beta }}\) for all \(u,v,w\in U\). Let \(\Lambda :\Gamma \times U^{2}\rightarrow V\) be a random operator satisfying \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\), \(\gamma \in \Gamma \) and
be an MMB-algebra. Assume that \(\psi :U^{4}\rightarrow O^{+} \) is an MDF in which there is a \(\beta <1\) with \(\psi ^{\frac{u}{2},\frac{v}{2},w,0}_{\tau }\geq \psi ^{u,v,w,0}_{ \frac{2\tau }{\beta }}\) for all \(u,v,w\in U\). Let \(\Lambda :\Gamma \times U^{2}\rightarrow V\) be a random operator satisfying \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\), \(\gamma \in \Gamma \) and

for all \(u, v, w, r \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u,w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
Putting \(v=r=0\) in (4.2), we have
for all \(u, w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Thus
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Replacing u by \(\frac{u}{2^{n}}\) in (4.5), we get
It follows from
and (4.6) that
for all \(u, w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\). That is,
Replacing u with \({\frac{u}{2^{m}}}\) in (4.7), we get
Since \(\psi ^{u,0,w,0}_{\frac{\tau }{\sum _{k=m}^{n+m}\frac{\beta ^{k}}{2}}}\) tends to \(\nabla ^{0}_{\tau }\) as \(m,n\to \infty \), it follows that the sequence \(\{2^{n} \Lambda (\gamma ,\frac{u}{2^{n}}, w )\}\) is Cauchy for all \(u,w \in U\) and \(\gamma \in \Gamma \). Since V is an MMB-algebra, \(\{2^{n} \Lambda (\gamma ,\frac{u}{2^{n}}, w )\}\) is a convergent sequence. Now, we define the random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) by
for all \(u,w \in U\) and \(\gamma \in \Gamma \). Putting \(m =0\) and letting \(n \to \infty \) in (4.8), we have
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). The proof is completed by a similar method as in Theorem 3.2. □
Corollary 4.3
Let  be an MMB-algebra. Assume that \(\iota > 1\), \(\varsigma \geq 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying \(\Lambda (\gamma ,u,0)= \Lambda (\gamma ,0,w) =0\) and
be an MMB-algebra. Assume that \(\iota > 1\), \(\varsigma \geq 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying \(\Lambda (\gamma ,u,0)= \Lambda (\gamma ,0,w) =0\) and

for all \(u, v, w, r \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Then we can find a unique biadditive random operator \(\Delta : \Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w \in U\), \(\gamma \in \Gamma \). and \(\tau >0\).
Proof
The result follows from Theorem 4.2 by putting
for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0\), and \(\beta =2^{1-\iota }\). □
Theorem 4.4
Let  be an MMB-algebra. Assume that \(\psi :U^{4}\rightarrow O^{+} \) is an MDF such that there exists a \(\beta <1\) with \(\varphi ^{u,v,w,0}_{\tau } \geq \psi ^{\frac{u}{2},\frac{v}{2},w,0}_{ \frac{\tau }{2\beta }}\) for all \(u,v,w\in U\). Let \(\Lambda :\Gamma \times U^{2}\rightarrow V\) be a random operator satisfying (4.2) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
be an MMB-algebra. Assume that \(\psi :U^{4}\rightarrow O^{+} \) is an MDF such that there exists a \(\beta <1\) with \(\varphi ^{u,v,w,0}_{\tau } \geq \psi ^{\frac{u}{2},\frac{v}{2},w,0}_{ \frac{\tau }{2\beta }}\) for all \(u,v,w\in U\). Let \(\Lambda :\Gamma \times U^{2}\rightarrow V\) be a random operator satisfying (4.2) and \(\Lambda (\gamma ,u,0)=\Lambda (\gamma ,0,w)=0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
Letting \(v=r=0\) in (4.3), we have
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Thus
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). Replacing u by \(2^{n}u\) in (4.12), we get
From
and (4.13), we conclude that
for all \(u, w\in U\), \(\gamma \in \Gamma \), and \(\tau >0\). That is,
Replacing u with \({2^{m}u}\) in (4.14), we get
Since \(\psi ^{u,0,u,0}_{ \frac{\tau }{\sum _{k=m+1}^{n+m}\frac{\beta ^{k}}{2}}}\) tends to \(\nabla ^{0}_{\tau }\) as \(m,n\to \infty \), it follows that the sequence \(\{\frac{1}{2^{n}} \Lambda (\gamma ,2^{n}u, w )\}\) is Cauchy for all \(u, w \in U\), \(\gamma \in \Gamma \). Since V is an MMB-algebra, \(\{\frac{1}{2^{n}} F(\gamma ,2^{n}u, w )\}\) is a convergent sequence. Now, we define the random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) by
for all \(u, w \in U\) and \(\gamma \in \Gamma \). Putting \(m =0\) and letting \(n \to \infty \) in (4.15), we get
for all \(u, w \in U\), \(\gamma \in \Gamma \), and \(\tau >0\). The proof is completed by a similar method as in Theorem 4.2. □
Corollary 4.5
Let  be an MMB-algebra. Assume that \(\iota < 1\), \(\varsigma \ge 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying (4.9) and \(\Lambda (\gamma ,u,0) = \Lambda (\gamma ,0,w) =0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
be an MMB-algebra. Assume that \(\iota < 1\), \(\varsigma \ge 0\), and \(\Lambda :\Gamma \times U^{2} \rightarrow V\) is a random operator satisfying (4.9) and \(\Lambda (\gamma ,u,0) = \Lambda (\gamma ,0,w) =0\) for all \(u,w\in U\) and \(\gamma \in \Gamma \). Then we can find a unique biadditive random operator \(\Delta :\Gamma \times U^{2} \rightarrow V\) such that
for all \(u, w \in T\), \(\gamma \in \Gamma \), and \(\tau >0\).
Proof
The result follows from Theorem 4.4 by putting
for all \(u, w \in U\), \(\gamma \in \Gamma \), \(\tau >0\), and \(\beta =2^{\iota -1}\). □
5 Conclusions
In this paper, we introduce distribution functions and a triangular norm with the ranges in a class of matrix algebras, and we introduce the concept of a matrix Menger normed algebra. We apply the HUR stability process to get best approximation of stochastic κ-random operator inequalities.
Availability of data and materials
Not applicable.
References
Longstaff, W.E.: On minimal sets of \((0,1)\)-matrices whose pairwise products form a basis for \(M_{n}(\mathbb{F})\). Bull. Aust. Math. Soc. 98(3), 402–413 (2018)
Collins, B., Osaka, H., Sapra, G.: On a family of linear maps from \(M_{n}(\mathbb{C})\) to \(M_{n^{2}}(\mathbb{C})\). Linear Algebra Appl. 555, 398–411 (2018)
Dolinar, G., Kuzma, B., Marovt, J.: Lie product preserving maps on \(M_{n}(\mathbb{F})\). Filomat 31(16), 5335–5344 (2017)
Madadi, M., Saadati, R., Park, C., Rassias, J.M.: Stochastic Lie bracket (derivation, derivation) in MB-algebras. J. Inequal. Appl. 2020, Paper No. 141, 15 pp. (2020)
Jang, S.Y., Saadati, R.: Approximation of an additive \((\varrho _{1},\varrho _{2})\)-random operator inequality. J. Funct. Spaces 2020, Article ID 7540303 (2020)
Saadati, R., Park, C.: Approximation of derivations and the superstability in random Banach ∗-algebras. Adv. Differ. Equ. 2018, Paper No. 418, 12 pp. (2018)
Wang, Sh., Qian, D.: Common fixed point theorems in Menger probabilistic metric spaces using the CLRg property. J. Nonlinear Sci. Appl. 12(1), 48–55 (2019)
Wang, Zh., Rassias, Th.M., Eshaghi Gordji, M.: Stability of quadratic functional equations in Sherstnev probabilistic normed spaces. Sci. Bull. “Politeh.” Univ. Buchar., Ser. A, Appl. Math. Phys. 77(4), 79–92 (2015)
Smarandache, F.: Neutrosophic set, a generalisation of the intuitionistic fuzzy sets. Int. J. Pure Appl. Math. 24, 287–297 (2005)
Al-Omeri, W.F., Jafari, S., Smarandache, F.: Φ, Ψ-weak contractions in neutrosophic cone metric spaces via fixed point theorems. Math. Probl. Eng., 2020, Article ID 9216805 (2020)
Schweizer, B., Sklar, A.: Probabilistic Metric Spaces. North-Holland Series in Probability and Applied Mathematics. North-Holland, New York (1983)
Hadzic, O., Pap, E.: Fixed Point Theory in Probabilistic Metric Spaces. Mathematics and Its Applications, vol. 536. Kluwer Academic, Dordrecht (2001)
Saadati, R.: Random Operator Theory. Elsevier, London (2016)
Ns̆dăban, S., Bînzar, T., Pater, F.: Some fixed point theorems for φ-contractive mappings in fuzzy normed linear spaces. J. Nonlinear Sci. Appl. 10(11), 5668–5676 (2017)
Lee, Y.-H., Jung, S.-M.: A fixed point approach to the stability of a general quartic functional equation. J. Math. Comput. Sci. 20(3), 207–215 (2020)
Rishi, N., Matloob, A.: Weighted Jessen’s functionals and exponential convexity. J. Math. Comput. Sci. 19, 171–180 (2019)
Park, C., Jin, Y., Zhang, X.: Bi-additive s-functional inequalities and quasi-multipliers on Banach algebras. Rocky Mt. J. Math. 49(2), 593–607 (2019)
Park, C., Lee, J.R., Zhang, X.: Additive s-functional inequality and hom-derivations in Banach algebras. J. Fixed Point Theory Appl. 21(1) Art. 18, 14 pp. (2019)
Fechner, W.: Stability of a composite functional equation related to idempotent mappings. J. Approx. Theory 163(3), 328–335 (2011)
Brzdek, J., Ciepliński, K.: A fixed point theorem in n-Banach spaces and Ulam stability. J. Math. Anal. Appl. 470(1), 632–646 (2019)
Cădariu, L., Găvruţa, L., Găvruţa, P.: On the stability of an affine functional equation. J. Nonlinear Sci. Appl. 6(2), 60–67 (2013)
Isac, G., Rassias, Th.M.: Stability of Ψ-additive mappings: applications to nonlinear analysis. Int. J. Math. Math. Sci. 19(2), 219–228 (1996)
Rätz, J.: On inequalities associated with the Jordan-von Neumann functional equation. Aequ. Math. 66(1–2), 191–200 (2003)
Acknowledgements
The authors are thankful to the area editor and referees for giving valuable comments and suggestions.
Funding
No funding.
Author information
Authors and Affiliations
Contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Madadi, M., O’Regan, D., Rassias, T.M. et al. Best approximation of κ-random operator inequalities in matrix MB-algebras. J Inequal Appl 2021, 13 (2021). https://doi.org/10.1186/s13660-021-02548-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-021-02548-4



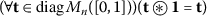 (boundary condition);
(boundary condition);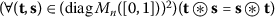 (commutativity);
(commutativity);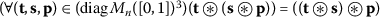 (associativity);
(associativity);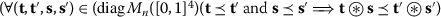 (monotonicity).
(monotonicity).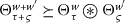 for all
for all 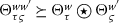 for all
for all