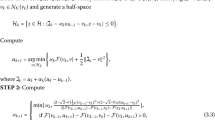Weak convergence of explicit extragradient algorithms for solving equilibirum problems

Abstract

This paper aims to propose two new algorithms that are developed by implementing inertial and subgradient techniques to solve the problem of pseudomonotone equilibrium problems. The weak convergence of these algorithms is well established based on standard assumptions of a cost bi-function. The advantage of these algorithms was that they did not need a line search procedure or any information on Lipschitz-type bifunction constants for step-size evaluation. A practical explanation for this is that they use a sequence of step-sizes that are updated at each iteration based on some previous iterations. For numerical examples, we discuss two well-known equilibrium models that assist our well-established convergence results, and we see that the suggested algorithm has a competitive advantage over time of execution and the number of iterations.

1 Introduction

Equilibrium problem (shortly, EP) can be considered as a general problem in the sense that it comprises many mathematical models such as variational inequality problems (shortly, VIP), optimization problems, fixed point problems, complementarity problems, Nash equilibrium of noncooperative games, saddle point, vector minimization problem and the Kirszbraun problem (see e.g., [1,2,3,4]). To the best of our knowledge, the term “equilibrium problem” was initiated in 1992 by Mu and Oettli [5] and has been further strengthened by Blum and Oettli [1]. The equilibrium problem (EP) is also seen as the Ky Fan inequality, since Fan [6] gives the first existence result regarding the solution of the EP. Many results about the existence of the solution of equilibrium problems have been accomplished and generalized by several authors (e.g., see [7, 8]). One of the most useful research directions in the equilibrium problem theory is to develop the iterative methods to find a numerical solution of the equilibrium problems. The research in this direction is continuing to develop new methods, leading weak convergence to strong convergence, providing modification and extension of existing algorithms which are suitable for a specific subclass of equilibrium problems. In recent years, many methods have been developed to solve equilibrium problems in finite and infinite-dimensional spaces (for instance, [9,10,11,12,13,14,15,16,17,18,19,20]).

In this direction, two approaches are very well known, one of them is the proximal point method (shortly, PPM) [21] and the other one is an auxiliary problem principle [22]. The PPM was introduced by Martinet [23] for monotone variational inequality problems, and later it was continued by Rockafellar [24] for monotone operators. Moudafi [21] extended the PPM to EPs involving monotone bifunction. The PPM method is implemented to monotone EPs, i.e. the bifunction of an equilibrium problem has to be monotone. Thus, each regularized subproblem becomes strongly monotone, and a unique solution exists. This method will not guarantee the existence of the solution if the bifunction is more general monotone, like pseudomonotone. However, the auxiliary problem principle is based on the idea to develop a new problem that is identical and usually simpler to solve compared to the initial problem. This principle was early established by Cohen [25] for optimization problems and later extended for variational inequality problems [26]. Moreover, Mastroeni [22] uses the auxiliary problem principle for strongly monotone equilibrium problems.

In this paper, we focus on the second direction, including projection methods that are well known and practically easy to implement due to their easier numerical computation. As is well known, the earliest well-known projection method for VIPs is the gradient projection method. After that, many other projection methods were developed such as the extragradient method [27], the subgradient extragradient method [28], Popov’s extragradient method [29], Tseng’s extragradient method [30], projection and contraction schemes [31] and other hybrid and projected gradient methods [32,33,34,35]. In recent years, the equilibrium problem theory has become an attractive field for many researchers and a lot of numerical methods for solving equilibrium problems have been developed and analyzed by many authors in Hilbert spaces. Thus, Quoc [20] and Flam [36] extended the extragradient method for equilibrium problems. Recently, Hieu [37] extended the Halpern subgradient extragradient method for variational inequality problem to an equilibrium problem and also many other methods were extended and modified for variational inequality problems to equilibrium problems (see [38, 39]).

On the other hand, let us point out inertial-type algorithms, depending on the heavy ball methods of the two-order time dynamical system, Polyak [40] firstly proposed an inertial extrapolation as an acceleration process to solve the smooth convex minimization problem. The inertial method is a two-step iterative method, and the next iteration is determined by the use of two previous iterates and it can be considered as a procedure of speeding up an iterative sequence (for more details, see [40, 41]). Various inertial-like algorithms previously developed for special classes of the problem (EP) can be found (for instance, in [42,43,44]). For the problem (EP), Moudafi [45] has done work in this direction and proposed a new inertial-type method, namely the second-order differential proximal method. This algorithm can be taken as a combination of the relaxed PPM [21] and inertial effect [40]. Recently, another type of inertial algorithm has also been introduced by Chbani and Riahi [46], by choosing a suitable inertial term and incorporating a viscosity-like technique in their algorithm.

This paper proposes two modifications of Algorithm 1 (see [47]) for a class of pseudomonotone equilibrium problems motivated from some recent results (see [28, 48, 49]). These resulting algorithms combine the explicit iterative extragradient method with the subgradient method and the inertial term that is used to speed-up the iterative sequence towrads the solution. The major advantage of these methods is that they are independent of line search procedures and also there is no need to have a prior knowledge of Lipschitz-type constants of a bifunction. Instead of that, they use a sequence of step-sizes which is updated at each iteration, based on some previous iterates. We establish the weak convergence of the resulting algorithm under standard assumptions on a cost bifunction.

We organize the rest of this paper in the following manner: In Sect. 2, we give some definitions and preliminary results that will be used throughout the paper. Section 3 comprises our first subgradient algorithm and provides the weak convergence theorem for the proposed algorithm. Section 4 deals with proposing and analyzing the convergence of the inertial subgradient algorithm, involving a pseudomonotone bifunction. Finally, in Sect. 5, we study the numerical experiments to illustrate the computational performance of our suggested algorithms on test problems, which are modeled from a Nash–Cournot oligopolistic equilibrium model and Nash–Cournot equilibrium models of electricity markets.

2 Preliminaries

Let C be a closed and convex subset of a Hilbert space $\mathbb{H}$ with an inner product $\langle\cdot , \cdot\rangle$ and norm $\|\cdot\|$, respectively. Let $\mathbb{R}$ be the set of all real numbers and $\mathbb{N}$ be the set all positive integers. While $\{x_{n}\}$ is a sequence in $\mathbb{H}$, we denote the strong convergence by $x_{n} \rightarrow x$ and weak convergence by $x_{n} \rightharpoonup x$ as $n\rightarrow\infty$. Also, $[t]_{+}= \max\{0, t\}$ and $\mathit{EP}(f, C)$ denote the solution set of the equilibrium problem inside C and p is an element of $\mathit{EP}(f, C)$.

Definition 2.1

(Equilibrium problem [1])

Let C be a nonempty closed convex subset of $\mathbb{H}$. Let f be a bifunction from $C \times C$ to the set of real numbers $\mathbb{R}$ such that $f (x, x) = 0$ for all $x \in C$. The equilibrium problem (EP) for the bifunction f on C is to

$$ \textrm{Find } p\in C \quad\textrm{such that} \quad f(p, y) \geq 0, \quad\forall y \in C. $$

Definition 2.2

([50])

Let C be a closed convex subset in $\mathbb{H}$ and we denote the metric projection on C by $P_{C}(x)$, $\forall x \in\mathbb{H}$, i.e.

$$ P_{C}(x) = \arg \min \bigl\{ \Vert y - x \Vert : y \in C \bigr\} . $$

Lemma 2.1

([51])

Let $P_{C} : \mathbb{H} \rightarrow C$be the metric projection from $\mathbb{H}$ontoC. Then

• (i) For all $x \in C$, $y \in\mathbb{H}$,

  $$\bigl\Vert x - P_{C}(y) \bigr\Vert ^{2} + \bigl\Vert P_{C}(y) - y \bigr\Vert ^{2} \leq \Vert x - y \Vert ^{2}. $$

• (ii) $z = P_{C}(x)$if and only if

  $$\langle x - z, y - z \rangle\leq0. $$

Now, we define concepts of monotonicity for a bifunction (see [1, 52] for more details).

Definition 2.3

A bifunction $f : \mathbb{H} \times\mathbb{H} \rightarrow\mathbb{R}$ is said to be

• (i) strongly monotone on C if there exists a constant $\gamma> 0$ such that

  $$f (x, y) + f (y, x) \leq-\gamma \Vert x - y \Vert ^{2}, \quad \forall x, y \in C; $$

• (ii) monotone on C if

  $$f (x, y) + f (y, x) \leq0, \quad\forall x, y \in C; $$

• (iii) strongly pseudomonotone on C if there exists a constant $\gamma> 0$ such that

  $$f (x, y) \geq0 \quad\Longrightarrow\quad f (y, x) \leq -\gamma \Vert x - y \Vert ^{2}, \quad\forall x, y \in C; $$

• (iv) pseudomonotone on C if

  $$f (x, y) \geq0 \quad\Longrightarrow\quad f (y, x) \leq0, \quad\forall x, y \in C; $$

• (v) a Lipschitz-type condition on C if there exist two positive constants $c_{1}$, $c_{2}$ such that

  $$f(x, z) \leq f(x, y) + f(y, z) + c_{1} \Vert x - y \Vert ^{2} + c_{2} \Vert y - z \Vert ^{2}, \quad \forall x, y, z \in C. $$

Remark 2.1

From Definition 2.3, the following implications hold:

$$\text{(i)} \Longrightarrow\text{(ii)} \Longrightarrow \text{(iv)} \quad\text{and} \quad \text{(i)} \Longrightarrow\text{(iii)} \Longrightarrow\text{(iv)}. $$

Remark 2.2

The converse of the above implications is not true in general.

Remark 2.3

If $F : C \rightarrow\mathbb{H}$ is a Lipschitz continuous operator, then the bifunction $f (x, y) = \langle F(x), y - x \rangle$ satisfies Lipschitz-type condition with $c_{1} = c_{2} = \frac{L}{2}$ (see [53], Lemma 6(i)).

Further, we recall that the subdifferential of a convex function $g : C \rightarrow\mathbb{R}$ at $x \in C$ is defined by

$$\partial g(x) = \bigl\{ w \in C : g(y) - g(x) \geq\langle w, y - x \rangle, \forall y \in C \bigr\} , $$

and the normal cone of C at $x \in C$ is defined by

$$N_{C}(x) = \bigl\{ w \in \mathbb{H} : \langle w, y - x \rangle\leq0, \forall y \in C \bigr\} . $$

Lemma 2.2

([54], p. 97)

LetCbe a nonempty closed convex subset of a real Hilbert space $\mathbb{H}$and $g : C \rightarrow\mathbb{R}$be a convex, subdifferentiable, lower semicontinuous function onC. Thenzis a solution to the following convex optimization problem $\min\{ g(x) : x \in C \}$if and only if $0 \in\partial g(z) + N_{C}(z)$, where $\partial g(z)$and $N_{C}(z)$denote the subdifferential ofgatzand the normal cone ofCatz, respectively.

Lemma 2.3

([55], p. 31)

For all $x, y \in\mathbb{H}$with $\mu\in\mathbb{R}$the following relation holds:

$$\bigl\Vert \mu x + (1 - \mu)y \bigr\Vert ^{2} = \mu \Vert x \Vert ^{2} + (1 - \mu) \Vert y \Vert ^{2} - \mu (1 - \mu) \Vert x - y \Vert ^{2}. $$

Lemma 2.4

([56])

Let $\phi_{n}$, $\delta_{n}$and $\beta_{n}$be sequences in $[0, +\infty)$such that

$$\phi_{n+1} \leq\phi_{n} + \beta_{n} ( \phi_{n} - \phi_{n-1}) + \delta _{n}, \quad\forall n \geq1, \sum_{n=1}^{+\infty} \delta_{n} < +\infty, $$

and there exists a real numberβwith $0 \leq\beta_{n} \leq \beta< 1$for all $n \in\mathbb{N}$. Then the following relations hold:

• (i) $\sum_{n=1}^{+\infty} [\phi_{n} - \phi_{n-1}]_{+} < \infty$, where $[t]_{+} := \max\{t, 0\}$.

• (ii) There exists $\phi^{*} \in[0, +\infty)$such that $\lim_{n \rightarrow+\infty} \phi_{n} = \phi^{*}$.

Lemma 2.5

([57])

LetCbe a nonempty set of $\mathbb{H}$and $\{x_{n}\}$be a sequence in $\mathbb{H}$such that the following two conditions hold:

• (i) For every $x \in C$, $\lim_{n\rightarrow\infty} \|x_{n} - x \|$exists.

• (ii) Every sequentially weak cluster point of $\{x_{n}\}$is inC.

Then $\{x_{n}\}$converges weakly to a point inC.

Assumption 2.1

We have the following assumptions on the bifunction $f: \mathbb{H} \times\mathbb{H} \rightarrow\mathbb{R}$ which are useful to prove the weak convergence of the iterative sequence $\{x_{n}\}$ generated by our proposed algorithms.

$(A_{1})$:

$f (x, x) = 0$, $\forall x \in C$ and f is pseudomonotone on C.

$(A_{2})$:

f satisfies the Lipschitz-type conditions on $\mathbb {H}$ with two constants $c_{1}$ and $c_{2}$.

$(A_{3})$:

$\lim_{n\rightarrow\infty} \sup f(x_{n}, y) \leq f(z, y)$ for each $y \in C$ and $\{x_{n}\} \subset C$ with $x_{n} \rightharpoonup z$.

$(A_{4})$:

$f (x, \cdot)$ is convex and subdifferentiable on C for every fixed $x \in C$.

3 Subgradient explicit iterative algorithm for a class of pseudomonotone EP

In this section, we suggest our first algorithm for finding a solution to a pseudomonotone problem (EP). This algorithm comprises two convex optimization problems with a subgradient technique, used to make the computation easier, the so-called “subgradient explicit iterative algorithm” for a class of pseudomonotone EP. The detailed algorithm is given below.

Remark 3.1

From the definition of $\lambda_{n}$, we can see that this sequence is bounded, non-increasing, and converges to some positive number $\lambda > 0$ (for more details see [47]).

Remark 3.2

It is definite that $H_{n}$ is a half-space and $C \subset H_{n}$ (see [37]). If we restrict our constraint set to C in the above convex minimization problem then we have the same algorithm (see Algorithm 1 [47]).

Lemma 3.1

From Algorithm 1, we have the following useful inequality:

$$\lambda_{n} f(y_{n}, y) - \lambda_{n} f(y_{n}, x_{n+1}) \geq\langle x_{n} - x_{n+1}, y - x_{n+1} \rangle,\quad\forall y \in H_{n}. $$

Algorithm 1

Subgradient explicit iterative algorithm for pseudomontone EP

Proof

It follows from Lemma 2.2 and the definition of $x_{n+1}$ that we have

$$0 \in\partial_{2} \biggl\{ \lambda_{n} f(y_{n}, y) + \frac{1}{2} \Vert x_{n} - y \Vert ^{2} \biggr\} (x_{n+1}) + N_{H_{n}}(x_{n+1}). $$

Thus, for $\upsilon\in\partial f(y_{n}, x_{n+1})$ there exists $\overline{\upsilon} \in N_{H_{n}(}x_{n+1})$ such that

$$\lambda_{n} \upsilon+ x_{n+1} - x_{n} + \overline{\upsilon} = 0, $$

which implies that

$$\langle x_{n} - x_{n+1}, y - x_{n+1} \rangle= \lambda_{n} \langle \upsilon, y - x_{n+1} \rangle+ \langle \overline{\upsilon}, y - x_{n+1} \rangle, \quad\forall y \in H_{n}. $$

Since $\overline{\upsilon} \in N_{H_{n}}(x_{n+1})$ we have $\langle \overline{\upsilon}, y - x_{n+1} \rangle\leq0$ for all $y \in H_{n}$. This implies that

$$ \langle x_{n} - x_{n+1}, y - x_{n+1} \rangle\leq\lambda_{n} \langle \upsilon, y - x_{n+1} \rangle, \quad\forall y \in H_{n}. $$

(1)

From $\upsilon\in\partial f(y_{n}, x_{n+1})$ and the definition of the subdifferential, we have

$$ f(y_{n}, y) - f(y_{n}, x_{n+1}) \geq\langle\upsilon, y - x_{n+1} \rangle, \quad\forall y \in\mathbb{H}. $$

(2)

Combining (1) and (2) we obtain

$$ \lambda_{n} f(y_{n}, y) - \lambda_{n} f(y_{n}, x_{n+1}) \geq\langle x_{n} - x_{n+1}, y - x_{n+1} \rangle,\quad\forall y \in H_{n}. $$

(3)

 □

Lemma 3.2

Let $\{x_{n}\}$and $\{y_{n}\}$be generated from the Algorithm 1, then the following relation holds:

$$\lambda_{n} \bigl\{ f(x_{n}, x_{n+1}) - f(x_{n}, y_{n}) \bigr\} \geq \langle x_{n} - y_{n}, x_{n+1} - y_{n} \rangle. $$

Proof

It follows from the definition of $x_{n+1}$ in Algorithm 1 and by the definition of the hyperplane $H_{n}$ that $\langle x_{n} - \lambda_{n}\upsilon_{n} - y_{n}, x_{n+1} - y_{n} \rangle\leq0$. Thus, we get

$$ \lambda_{n} \langle\upsilon_{n}, x_{n+1} - y_{n} \rangle\geq\langle x_{n} - y_{n}, x_{n+1} - y_{n} \rangle. $$

(4)

Further, $\upsilon_{n} \in\partial f(x_{n}, y_{n})$ and due to definition of the subdifferential, we have

$$f(x_{n}, y) - f(x_{n}, y_{n}) \geq\langle \upsilon_{n}, y - y_{n} \rangle, \quad \forall y \in \mathbb{H}. $$

Substitute $y = x_{n+1}$ in the above expression

$$ f(x_{n}, x_{n+1}) - f(x_{n}, y_{n}) \geq\langle\upsilon_{n}, x_{n+1} - y_{n} \rangle, \quad\forall y \in\mathbb{H}. $$

(5)

Combining (4) and (5) we obtain

$$\lambda_{n} \bigl\{ f(x_{n}, x_{n+1}) - f(x_{n}, y_{n}) \bigr\} \geq \langle x_{n} - y_{n}, x_{n+1} - y_{n} \rangle. $$

 □

Next, we prove an important inequality that is useful for understanding the pattern and converging analysis of the sequence generated by Algorithm 1.

Lemma 3.3

Let $f: \mathbb{H} \times\mathbb{H} \rightarrow\mathbb{R}$be a bifunction satisfying the conditions $(A_{1})$–$(A_{4})$ (Assumption 2.1). Assume that the solution set $\mathit{EP}(f, C)$is nonempty. Then for all $p \in \mathit{EP}(f , C)$we have

$$\Vert x_{n+1} - p \Vert ^{2} \leq \Vert x_{n} - p \Vert ^{2} - \biggl(1 - \frac{\mu\lambda _{n}}{\lambda_{n+1}} \biggr) \Vert x_{n} - y_{n} \Vert ^{2} - \biggl(1 - \frac{\mu \lambda_{n}}{\lambda_{n+1}} \biggr) \Vert x_{n+1} - y_{n} \Vert ^{2}. $$

Proof

By Lemma 3.1 and replacing $y=p$ we obtain

$$ \lambda_{n} f(y_{n}, p) - \lambda_{n} f(y_{n}, x_{n+1}) \geq\langle x_{n} - x_{n+1}, p - x_{n+1} \rangle. $$

(6)

Since $f(p, y_{n}) \geq0$ and from assumption $(A_{1})$ we have $f(y_{n}, p) \leq0$, which implies that

$$ \langle x_{n} - x_{n+1}, x_{n+1} - p \rangle\geq\lambda_{n} f(y_{n}, x_{n+1}). $$

(7)

From the definition of $\lambda_{n+1}$ we get

$$ f(x_{n}, x_{n+1}) - f(x_{n}, y_{n}) - f(y_{n}, x_{n+1}) \leq \frac{\mu ( \Vert x_{n} - y_{n} \Vert ^{2} + \Vert x_{n+1} - y_{n} \Vert ^{2})}{2 \lambda_{n+1}}. $$

(8)

From Eqs. (7) and (8) we get the following:

$$ \begin{aligned}[b] \langle x_{n} - x_{n+1}, x_{n+1} - p \rangle&\geq\lambda_{n} \bigl\{ f(x_{n}, x_{n+1}) - f(x_{n}, y_{n}) \bigr\} \\ &\quad- \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n} - y_{n} \Vert ^{2} - \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n+1} - y_{n} \Vert ^{2}. \end{aligned} $$

(9)

Next, by Lemma 3.2 and Eq. (9) we obtain

$$ \begin{aligned}[b] \langle x_{n} - x_{n+1}, x_{n+1} - p \rangle&\geq \langle x_{n} - y_{n}, x_{n+1} - y_{n} \rangle \\ &\quad- \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n} - y_{n} \Vert ^{2} - \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n+1} - y_{n} \Vert ^{2}. \end{aligned} $$

(10)

We have the following facts:

$$\begin{gathered} \|a \pm b \|^{2} = \|a\|^{2} + \|b\| ^{2} \pm2 \langle a, b \rangle , \\ - 2 \langle x_{n} - x_{n+1}, x_{n+1} - p \rangle= - \Vert x_{n} - p \Vert ^{2} + \Vert x_{n+1} - x_{n} \Vert ^{2} + \Vert x_{n+1} - p \Vert ^{2}, \\ 2 \langle y_{n} - x_{n}, y_{n} - x_{n+1} \rangle= \Vert x_{n} - y_{n} \Vert ^{2} + \Vert x_{n+1} - y_{n} \Vert ^{2} - \Vert x_{n} - x_{n+1} \Vert ^{2}.\end{gathered} $$

Through the above expressions and Eq. (10) we have

$$\Vert x_{n+1} - p \Vert ^{2} \leq \Vert x_{n} - p \Vert ^{2} - \biggl(1 - \frac{\mu\lambda _{n}}{\lambda_{n+1}} \biggr) \Vert x_{n} - y_{n} \Vert ^{2} - \biggl(1 - \frac{\mu \lambda_{n}}{\lambda_{n+1}} \biggr) \Vert x_{n+1} - y_{n} \Vert ^{2}. $$

 □

Let us formulate the first main convergence result of this work.

Theorem 3.1

Under the hypotheses $(A_{1})$–$(A_{4})$ (Assumption 2.1) the sequences $\{x_{n}\}$, $\{y_{n}\}$generated from Algorithm 1 converge weakly to an elementpof $\mathit{EP}(f, C)$. Moreover, $\lim_{n\rightarrow\infty} P_{\mathit{EP}(f, C)} (x_{n}) = p$.

Proof

By the definition of $\lambda_{n+1}$ the sequence $\frac{\lambda _{n}}{\lambda_{n+1}} \rightarrow1$ and $\mu\in(0, 1)$, which implies that

$$\biggl(1 - \frac{\mu\lambda_{n}}{\lambda_{n+1}} \biggr) \rightarrow1 - \mu> 0. $$

Next, we can easily choose $\epsilon\in(0, 1 - \mu)$ such that $(1 - \frac{\mu\lambda_{n}}{\lambda_{n+1}} ) > \epsilon$, $\forall n \geq n_{0}$. Due to this fact and Lemma 3.3, we obtain

$$ \Vert x_{n+1} - p \Vert ^{2} \leq \Vert x_{n} - p \Vert ^{2}, \quad\forall n\geq n_{0}. $$

(11)

Furthermore, we fix an arbitrary number $m \geq n_{0}$ and consider Lemma 3.3, for all numbers $n_{0}, n_{0} + 1, \ldots, m$. Summing, we obtain

$$ \begin{aligned}[b] \Vert x_{m+1} - p \Vert ^{2} &\leq \Vert x_{n_{0}} - p \Vert ^{2} - \sum _{k=n_{0}}^{m} \biggl(1 - \frac{\mu\lambda_{k}}{\lambda_{k+1}} \biggr) \Vert x_{k} - y_{k} \Vert ^{2} \\ &\quad- \sum_{k=n_{0}}^{m} \biggl(1 - \frac{\mu\lambda_{k}}{\lambda _{k+1}} \biggr) \Vert x_{k+1} - y_{k} \Vert ^{2} \\ &\leq \Vert x_{n_{0}} - p \Vert ^{2}. \end{aligned} $$

(12)

Taking $k \rightarrow\infty$ in Eq. (12), we can deduce the following results:

$$ \sum_{n} \Vert x_{n} - y_{n} \Vert ^{2} < +\infty\quad\Longrightarrow\quad\lim _{n\rightarrow\infty} \Vert x_{n} - y_{n} \Vert = 0 $$

(13)

and

$$ \sum_{n} \Vert x_{n+1} - y_{n} \Vert ^{2} < +\infty\quad\Longrightarrow\quad\lim _{n\rightarrow\infty} \Vert x_{n+1} - y_{n} \Vert = 0. $$

(14)

Further, Eqs. (11) and (12) imply that

$$ \lim_{n\rightarrow\infty} \Vert x_{n} - p \Vert = b, \quad\text{for some finite } b > 0. $$

(15)

Moreover, from Eqs. (13), (14) and the Cauchy inequality, we get

$$ \lim_{n\rightarrow\infty} \Vert x_{k+1} - x_{k} \Vert \Longrightarrow0. $$

(16)

Next, we show that a very sequential weak cluster point of the sequence $\{x_{n}\}$ is in $\mathit{EP}(f, C)$. Assume that z is a weak cluster point of $\{x_{n}\}$, i.e. there exists a subsequence, denoted by $\{ x_{n_{k}}\}$ of $\{x_{n}\}$, weakly converging to z. Then $\{ y_{n_{k}}\}$ also weakly converges to z and $z \in C$. Let us show that $z \in \mathit{EP}(f, C)$. By Lemma 3.1, the definition of $\lambda_{n+1}$ and Lemma 3.2, we have

$$ \begin{aligned}[b] \lambda_{n_{k}} f(y_{n_{k}}, y) & \geq \lambda_{n_{k}} f(y_{n_{k}}, x_{n_{k}+1}) + \langle x_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle \\ & \geq \lambda_{n_{k}} f(x_{n_{k}}, x_{n_{k+1}}) - \lambda_{n_{k}} f(x_{n_{k}}, y_{n_{k}}) - \frac{\mu\lambda_{n_{k}}}{2 \lambda _{n_{k}+1}} \Vert x_{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad- \frac{\mu\lambda_{n_{k}}}{2 \lambda_{n_{k}+1}} \Vert y_{n_{k}} - x_{n_{k}+1} \Vert ^{2} + \langle x_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle \\ & \geq \langle x_{n_{k}} - y_{n_{k}}, x_{n_{k}+1} - y_{n_{k}} \rangle - \frac{\mu\lambda_{n_{k}}}{2 \lambda_{n_{k}+1}} \Vert x_{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad- \frac{\mu\lambda_{n_{k}}}{2 \lambda_{n_{k}+1}} \Vert y_{n_{k}} - x_{n_{k}+1} \Vert ^{2} + \langle x_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle, \end{aligned} $$

(17)

where y is any element in $H_{n}$. It follows from (13), (14), (16) and the boundedness of $\{x_{n}\}$ that the right-hand side of the last inequality tends to zero. Using $\lambda _{n_{k}} > 0$, condition $(A_{3})$ and $y_{n_{k}} \rightharpoonup z$ we have

$$0 \leq\limsup_{k \rightarrow\infty} f(y_{n_{k}}, y) \leq f(z, y), \quad \forall y\in C. $$

Since $C \subset H_{n}$ and $z \in C$ we have $f(z, y) \geq0$, $\forall y \in C$. This shows that $z \in \mathit{EP}(f, C)$. Thus Lemma 2.5, ensures that $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to p as $n \rightarrow\infty$.

Next, we show that $\lim_{n\rightarrow\infty} P_{\mathit{EP}(f, C)} (x_{n}) = p$. Define $t_{n} := P_{\mathit{EP}(f, C)} (x_{n})$ for all $n \in\mathbb{N}$. Since $p \in \mathit{EP}(f, C)$, we have

$$ \Vert t_{n} \Vert \leq \Vert t_{n} - x_{n} \Vert + \Vert x_{n} \Vert \leq \Vert p - x_{n} \Vert + \Vert x_{n} \Vert . $$

(18)

Thus, $\{t_{n}\}$ is bounded. In fact, by Lemma 3.3 for $n \ge n_{0}$, we deduce that

$$ \Vert x_{n+1} - t_{n+1} \Vert ^{2} \leq \Vert x_{n+1} - t_{n} \Vert ^{2} \leq \Vert x_{n} - t_{n} \Vert ^{2}, \quad\forall n \geq n_{0}. $$

(19)

Equations (18) and (19) imply the existence of the $\lim_{n \rightarrow\infty} \| x_{n} - t_{n} \|$. By using Lemma 3.3, for all $m > n \geq n_{0}$, we have

$$ \begin{aligned} \Vert t_{n} - x_{m} \Vert ^{2} \leq \Vert t_{n} - x_{m-1} \Vert ^{2} \leq \cdots \leq \Vert t_{n} - x_{n} \Vert ^{2}. \end{aligned} $$

(20)

Next, we show that $\{t_{n}\}$ is a Cauchy sequence. Let us take $t_{m}, t_{n} \in \mathit{EP}(f, C)$, for $m > n \geq n_{0}$, and Lemma 2.1(i) with (20) gives

$$ \Vert t_{n} - t_{m} \Vert ^{2} \leq \Vert t_{n} - x_{m} \Vert ^{2} - \Vert t_{m} - x_{m} \Vert ^{2} \leq \Vert t_{n} - x_{n} \Vert ^{2} - \Vert t_{m} - x_{m} \Vert ^{2}. $$

(21)

The existence of $\lim_{n\rightarrow\infty} \| t_{n} - x_{n} \|$ implies that $\lim_{m, n\rightarrow\infty} \| t_{n} - t_{m} \| = 0$, for all $m > n$. Consequently, $\{t_{n}\}$ is a Cauchy sequence. Since $\mathit{EP}(f, C)$ is closed, we find that $\{t_{n}\}$ converges strongly to $p^{*} \in \mathit{EP}(f, C)$. Now, we prove that $p ^{*} = p$. It follows from Lemma 2.1(ii) and $p, p ^{*} \in \mathit{EP}(f, C)$ that

$$ \langle x_{n} - t_{n}, p - t_{n} \rangle\leq0. $$

(22)

Since $t_{n} \rightarrow p^{*}$ and $x_{n} \rightharpoonup p$, we have

$$\bigl\langle p - p^{*}, p - p^{*} \bigr\rangle \leq0, $$

which implies that $p=p^{*}= \lim_{n\rightarrow\infty} P_{\mathit{EP}(f, C)} (x_{n})$. Further, $\|x_{n} - y_{n} \| \rightarrow0$, implies $\lim_{n\rightarrow\infty} P_{\mathit{EP}(f, C)} (y_{n}) = p$. □

Remark 3.3

In the case when the bifunction f is strongly pseudomonotone and satisfies the Lipschitz-type condition, the linear rate of convergence can be achieved for Algorithm 1 (for more details see [47]).

4 Modified subgradient explicit iterative algorithm for a class of pseudomonotone EP

In this section, we propose an iterative scheme that involves two strong convex optimization problems with an inertial term that is used to speed up the iterative sequence, so we refer to it as a “modified explicit iterative algorithm” for a class of pseudomonotone equilibrium problems. This algorithm is a modification of Algorithm 1 that performs better than the earlier algorithm due to the inertial term. The detailed Algorithm 2 is given belowthes.

Algorithm 2

Modified subgradient explicit iterative algorithm for pseudomontone EP

Lemma 4.1

From Algorithm 2 we have the following useful inequality:

$$\lambda_{n} f(y_{n}, y) - \lambda_{n} f(y_{n}, x_{n+1}) \geq\langle w_{n} - x_{n+1}, y - x_{n+1} \rangle,\quad\forall y \in H_{n}. $$

Proof

The proof is very similar to Lemma 3.1. □

Lemma 4.2

Let $\{x_{n}\}$and $\{y_{n}\}$generated from the Algorithm 2, then the following relation holds:

$$\lambda_{n} \bigl\{ f(w_{n}, x_{n+1}) - f(w_{n}, y_{n}) \bigr\} \geq \langle w_{n} - y_{n}, x_{n+1} - y_{n} \rangle. $$

Proof

The proof is similar to Lemma 3.2. □

Lemma 4.3

Let $f: \mathbb{H} \times\mathbb{H} \rightarrow\mathbb{R}$be a bifunction satisfying the conditions $(A_{1})$–$(A_{4})$as in Assumption 2.1. Assume that the solution set $\mathit{EP}(f, C)$is nonempty. Then for all $p \in \mathit{EP}(f , C)$we have

$$\Vert x_{n+1} - p \Vert ^{2} \leq \Vert w_{n} - p \Vert ^{2} - \biggl(1 - \frac{\mu\lambda _{n}}{\lambda_{n+1}} \biggr) \Vert w_{n} - y_{n} \Vert ^{2} - \biggl(1 - \frac{\mu \lambda_{n}}{\lambda_{n+1}} \biggr) \Vert x_{n+1} - y_{n} \Vert ^{2}. $$

Proof

By Lemma 4.1 and replacing $y=p$, we obtain

$$ \lambda_{n} f(y_{n}, p) - \lambda_{n} f(y_{n}, x_{n+1}) \geq\langle w_{n} - x_{n+1}, p - x_{n+1} \rangle. $$

(23)

Since $f(p, y_{n}) \geq0$ and from $(A_{1})$ we have $f(y_{n}, p) \leq 0$, which implies that

$$ \langle w_{n} - x_{n+1}, x_{n+1} - p \rangle\geq\lambda_{n} f(y_{n}, x_{n+1}). $$

(24)

From the definition of $\lambda_{n+1}$ we get

$$ f(w_{n}, x_{n+1}) - f(w_{n}, y_{n}) - f(y_{n}, x_{n+1}) \leq \frac{\mu ( \Vert w_{n} - y_{n} \Vert ^{2} + \Vert x_{n+1} - y_{n} \Vert ^{2})}{2 \lambda_{n+1}} . $$

(25)

Combining (24) and (25) we get

$$ \begin{aligned}[b] \langle w_{n} - x_{n+1}, x_{n+1} - p \rangle&\geq\lambda_{n} \bigl\{ f(w_{n}, x_{n+1}) - f(w_{n}, y_{n}) \bigr\} \\ &\quad- \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert w_{n} - y_{n} \Vert ^{2} - \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n+1} - y_{n} \Vert ^{2}. \end{aligned} $$

(26)

Next, by Lemma 4.2 and Eq. (26) we have

$$ \begin{aligned}[b] \langle w_{n} - x_{n+1}, x_{n+1} - p \rangle&\geq \langle w_{n} - y_{n}, x_{n+1} - y_{n} \rangle \\ &\quad- \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert w_{n} - y_{n} \Vert ^{2} - \frac{\mu\lambda_{n}}{2\lambda_{n+1}} \Vert x_{n+1} - y_{n} \Vert ^{2}. \end{aligned} $$

(27)

Furthermore, we have the following facts:

$$\begin{gathered} 2 \langle w_{n} - x_{n+1}, x_{n+1} - p \rangle= \Vert w_{n} - p \Vert ^{2} - \Vert x_{n+1} - w_{n} \Vert ^{2} - \Vert x_{n+1} - p \Vert ^{2}, \\ 2 \langle w_{n} - y_{n}, x_{n+1} - y_{n} \rangle= \Vert w_{n} - y_{n} \Vert ^{2} + \Vert x_{n+1} - y_{n} \Vert ^{2} - \Vert w_{n} - x_{n+1} \Vert ^{2}.\end{gathered} $$

Using the above facts and Eq. (27) after multiplying by 2, we get the desired result. □

Now, let us formulate the second main convergence result for Algorithm 2.

Theorem 4.1

The sequences $\{w_{n}\}$, $\{y_{n}\}$and $\{x_{n}\}$generated by Algorithm 2 converge weakly to the solutionpof the problem (EP), where

$$0 < \mu < \frac{\frac{1}{2} - 2\alpha- \frac{1}{2} \alpha^{2}}{\frac {1}{2} - \alpha+ \frac{1}{2} \alpha^{2} } \quad\textit{and} \quad 0 \leq \alpha_{n} \leq \alpha< \sqrt{5} - 2. $$

Proof

From Lemma 4.3, we have

$$ \begin{aligned}[b] \Vert x_{n+1} - p \Vert ^{2} &\leq \Vert w_{n} - p \Vert ^{2} - \biggl(1 - \frac{\mu \lambda_{n}}{\lambda_{n+1}} \biggr) \Vert w_{n} - y_{n} \Vert ^{2} - \biggl(1 - \frac {\mu\lambda_{n}}{\lambda_{n+1}} \biggr) \Vert x_{n+1} - y_{n} \Vert ^{2} \\ &\leq \Vert w_{n} - p \Vert ^{2} - \frac{1}{2} \biggl(1 - \frac{\mu\lambda _{n}}{\lambda_{n+1}} \biggr) \Vert x_{n+1} - w_{n} \Vert ^{2}. \end{aligned} $$

(28)

By the definition of $w_{n}$ in Algorithm 2, we get

$$ \begin{aligned}[b] \Vert w_{n} - p \Vert ^{2} &= \bigl\Vert x_{n} + \alpha_{n}(x_{n} - x_{n-1}) - p \bigr\Vert ^{2} \\ &= \bigl\Vert (1 + \alpha_{n}) (x_{n} - p) - \alpha_{n}(x_{n-1} - p) \bigr\Vert ^{2} \\ &= (1 + \alpha_{n}) \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} + \alpha_{n}(1 + \alpha_{n}) \Vert x_{n} - x_{n-1} \Vert ^{2}. \end{aligned} $$

(29)

Further, by the definition $w_{n}$ and using the Cauchy inequality, we have

$$\begin{aligned} \Vert x_{n+1} - w_{n} \Vert ^{2} &= \bigl\Vert x_{n+1} - x_{n} - \alpha_{n}(x_{n} - x_{n-1}) \bigr\Vert ^{2} \\ &= \Vert x_{n+1} - x_{n} \Vert ^{2} + \alpha_{n}^{2} \Vert x_{n} - x_{n-1} \Vert ^{2} - 2 \alpha_{n} \langle x_{n+1} - x_{n}, x_{n} - x_{n-1} \rangle \end{aligned}$$

(30)

$$\begin{aligned} &\geq \Vert x_{n+1} - x_{n} \Vert ^{2} + \alpha_{n}^{2} \Vert x_{n} - x_{n-1} \Vert ^{2} - 2 \alpha_{n} \Vert x_{n+1} - x_{n} \Vert \Vert x_{n} - x_{n-1} \Vert \\ &\geq \Vert x_{n+1} - x_{n} \Vert ^{2} + \alpha_{n}^{2} \Vert x_{n} - x_{n-1} \Vert ^{2} - \alpha_{n} \Vert x_{n+1} - x_{n} \Vert ^{2} - \alpha_{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\geq(1 - \alpha_{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} + \bigl(\alpha_{n}^{2} - \alpha_{n} \bigr) \Vert x_{n} - x_{n-1} \Vert ^{2}. \end{aligned}$$

(31)

Next, combining (28), (29) and (31), we obtain

$$\begin{aligned} \Vert x_{n+1} - p \Vert ^{2} &\leq (1 + \alpha_{n}) \Vert x_{n} - p \Vert ^{2} - \alpha _{n} \Vert x_{n-1} - p \Vert ^{2} + \alpha_{n}(1 + \alpha_{n}) \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\quad- \varrho_{n} (1 - \alpha_{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} - \varrho _{n}\bigl(\alpha_{n}^{2} - \alpha_{n} \bigr) \Vert x_{n} - x_{n-1} \Vert ^{2} \end{aligned}$$

(32)

$$\begin{aligned} &= (1 + \alpha_{n}) \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} - \varrho_{n} (1 - \alpha_{n}) \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\quad+ \bigl[ \alpha_{n}(1 + \alpha_{n}) - \varrho_{n} \bigl(\alpha_{n}^{2} - \alpha_{n} \bigr) \bigr] \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &= (1 + \alpha_{n}) \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} - Q_{n} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\quad+ R_{n} \Vert x_{n} - x_{n-1} \Vert ^{2}, \end{aligned}$$

(33)

where

$$\begin{gathered} \varrho_{n} := \frac{1}{2} \biggl(1 - \frac{\mu\lambda_{n}}{\lambda _{n+1}} \biggr), \\ Q_{n} := \varrho_{n} (1 - \alpha_{n}) ,\end{gathered} $$

and

$$R_{n} := \alpha_{n}(1 + \alpha_{n}) - \varrho_{n} \bigl(\alpha_{n}^{2} - \alpha_{n} \bigr). $$

Next, we take

$$\varLambda_{n} = \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} + R_{n} \Vert x_{n} - x_{n-1} \Vert ^{2}, $$

and compute

$$ \begin{aligned}[b] \varLambda_{n+1} - \varLambda_{n} &= \Vert x_{n+1} - p \Vert ^{2} - \alpha_{n+1} \Vert x_{n} - p \Vert ^{2} + R_{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\quad- \Vert x_{n} - p \Vert ^{2} + \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} - R_{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\leq \Vert x_{n+1} - p \Vert ^{2} - (1 + \alpha_{n}) \Vert x_{n} - p \Vert ^{2} + \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} \\ &\quad+ R_{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} - R_{n} \Vert x_{n} - x_{n-1} \Vert ^{2}. \end{aligned} $$

(34)

Using Eq. (33) in (34), we obtain

$$ \begin{aligned}[b] \varLambda_{n+1} - \varLambda_{n} &\leq- Q_{n} \Vert x_{n+1} - x_{n} \Vert ^{2} + R_{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &= -(Q_{n} - R_{n+1}) \Vert x_{n+1} - x_{n} \Vert ^{2}. \end{aligned} $$

(35)

Furthermore, we have to compute

$$ \begin{aligned}[b] Q_{n} - R_{n+1} &= \varrho_{n} (1 - \alpha_{n}) - \alpha_{n+1}(1 + \alpha_{n+1}) + \varrho_{n+1} \bigl(\alpha_{n+1}^{2} - \alpha_{n+1} \bigr) \\ &\geq \varrho_{n} (1 - \alpha_{n+1}) - \alpha_{n+1}(1 + \alpha_{n+1}) + \varrho_{n} \bigl(\alpha_{n+1}^{2} - \alpha_{n+1} \bigr) \\ &= \varrho_{n} (1 - \alpha_{n+1})^{2} - \alpha_{n+1}(1 + \alpha_{n+1}) \\ &\geq \varrho_{n} (1 - \alpha)^{2} - \alpha(1 + \alpha) \\ &= \bigl(\varrho_{n} - \alpha- \alpha^{2}\bigr) + \varrho_{n} \alpha^{2} - 2 \varrho_{n} \alpha \\ &= \biggl( \frac{1}{2} - \alpha- \alpha^{2} + \frac{\alpha^{2}}{2} -\alpha \biggr) - \mu \biggl( \frac{ \lambda_{n}}{2\lambda_{n+1}} + \frac{ \lambda_{n}}{2 \lambda_{n+1}} \alpha^{2} - \frac{ \lambda_{n}}{\lambda _{n+1}} \alpha \biggr) \\ &= \biggl( \frac{1}{2} - 2\alpha- \frac{1}{2} \alpha^{2} \biggr) - \mu \biggl( \frac{ \lambda_{n}}{2\lambda_{n+1}} - \frac { \lambda_{n}}{\lambda_{n+1}} \alpha+ \frac{ \lambda_{n}}{2 \lambda _{n+1}} \alpha^{2} \biggr) . \end{aligned} $$

(36)

We have

$$0 < \mu < \frac{\frac{1}{2} - 2\alpha- \frac{1}{2} \alpha^{2}}{\frac {1}{2} - \alpha+ \frac{1}{2} \alpha^{2} } \quad\text{and} \quad 0 \leq\alpha< \sqrt{5} - 2. $$

This implies that, for every $0 \leq\alpha< \sqrt{5} - 2$, there exist $n_{0} \geq1$ and a fixed number

$$\epsilon\in \biggl( 0, \frac{1}{2} - 2\alpha- \frac{1}{2} \alpha^{2} - \mu \biggl( \frac{1}{2} - \alpha+ \frac{1}{2} \alpha^{2} \biggr) \biggr), $$

such that

$$ Q_{n} - R_{n+1} \geq\epsilon, \quad\forall n \geq n_{0}. $$

(37)

Equations (35) and (37) imply that, for all $n \geq n_{0}$, we have

$$ \varLambda_{n+1} - \varLambda_{n} \leq - (Q_{n} - R_{n+1}) \Vert x_{n+1} - x_{n} \Vert ^{2} \leq0. $$

(38)

Hence the sequence $\{\varLambda_{n}\}$ is nonincreasing for $n\geq n_{0}$. Further, from the definition of $\varLambda_{n+1}$ we have

$$ \begin{aligned}[b] \varLambda_{n+1} &= \Vert x_{n+1} - p \Vert ^{2} - \alpha_{n+1} \Vert x_{n} - p \Vert ^{2} + R_{n+1} \Vert x_{n+1} - x_{n} \Vert ^{2} \\ &\geq - \alpha_{n+1} \Vert x_{n} - p \Vert ^{2}. \end{aligned} $$

(39)

Also, from $\varLambda_{n}$ we have

$$ \begin{aligned}[b] \varLambda_{n} &= \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} + R_{n} \Vert x_{n} - x_{n-1} \Vert ^{2} \\ &\geq \Vert x_{n} - p \Vert ^{2} - \alpha_{n} \Vert x_{n-1} - p \Vert ^{2}. \end{aligned} $$

(40)

Equation (40) implies that, for $n\geq n_{0}$, we have

$$ \begin{aligned}[b] \Vert x_{n} - p \Vert ^{2} &\leq\varLambda_{n} + \alpha_{n} \Vert x_{n-1} - p \Vert ^{2} \\ &\leq\varLambda_{n_{0}} + \alpha \Vert x_{n-1} - p \Vert ^{2} \\ &\leq\cdots \leq\varLambda_{n_{0}}\bigl(\alpha^{n-n_{0}} + \cdots+ 1 \bigr) + \alpha^{n-n_{0}} \Vert x_{n_{0}} - p \Vert ^{2} \\ &\leq \frac{\varLambda_{n_{0}}}{1 - \alpha} + \alpha^{n-n_{0}} \Vert x_{n_{0}} - p \Vert ^{2}. \end{aligned} $$

(41)

Combining (39) and (41) we obtain

$$ \begin{aligned}[b] - \varLambda_{n+1} &\leq \alpha_{n+1} \Vert x_{n} - p \Vert ^{2} \\ &\leq\alpha \Vert x_{n} - p \Vert ^{2} \\ &\leq \alpha\frac{\varLambda_{n_{0}}}{1 - \alpha} + \alpha^{n-n_{0}+1} \Vert x_{n_{0}} - p \Vert ^{2}. \end{aligned} $$

(42)

It follows from (38) and (42) that

$$ \begin{aligned}[b] \epsilon\sum _{n=n_{0}}^{k} \Vert x_{n+1} - x_{n} \Vert ^{2} &\leq\varLambda _{n_{0}} - \Delta_{k+1} \\ &\leq\varLambda_{n_{0}} + \alpha\frac{\Delta_{n_{0}}}{1 - \alpha} + \alpha^{k-n_{0}+1} \Vert x_{n_{0}} - p \Vert ^{2} \\ &\leq\frac{\varLambda_{n_{0}}}{1 - \alpha} + \Vert x_{n_{0}} - p \Vert ^{2}. \end{aligned} $$

(43)

Letting $k \rightarrow\infty$ in (43) we have $\sum_{n=1}^{\infty} \|x_{n+1} - x_{n}\|^{2} < +\infty$. This implies that

$$ \Vert x_{n+1} - x_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty. $$

(44)

From Eqs. (30) and (44) we have

$$ \Vert x_{n+1} - w_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty. $$

(45)

Moreover, by Lemma 2.4, Eq. (32) and $\sum_{n=1}^{\infty} \|x_{n+1} - x_{n}\|^{2} < +\infty$,

$$ \lim_{n \rightarrow\infty} \Vert x_{n} - p \Vert ^{2} = b. $$

(46)

Thus, from Eqs. (29), (44) and (46),

$$ \lim_{n \rightarrow\infty} \Vert w_{n} - p \Vert ^{2} = b, $$

(47)

also

$$ 0 \leq \Vert x_{n} - w_{n} \Vert = \Vert x_{n} - x_{n+1} \Vert + \Vert x_{n+1} - w_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty. $$

(48)

To show $\lim_{n \rightarrow\infty} \|y_{n} - p \|^{2} = b$, we use Lemma 4.3 for $n \geq n_{0}$, which gives

$$ \begin{aligned}[b] & \biggl(1 - \frac{\mu\lambda_{n}}{\lambda_{n+1}} \biggr) \Vert w_{n} - y_{n} \Vert ^{2} \\ &\quad\leq \Vert w_{n} - p \Vert ^{2} - \Vert x_{n+1} - p \Vert ^{2} \\ &\quad\leq \bigl( \Vert w_{n} - p \Vert + \Vert x_{n+1} - p \Vert \bigr) \bigl( \Vert w_{n} - p \Vert - \Vert x_{n+1} - p \Vert \bigr) \\ &\quad\leq \bigl( \Vert w_{n} - p \Vert + \Vert x_{n+1} - p \Vert \bigr) \Vert x_{n+1} - w_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty \end{aligned} $$

(49)

and

$$ 0 \leq \Vert x_{n} - y_{n} \Vert = \Vert x_{n} - w_{n} \Vert + \Vert w_{n} - y_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty. $$

(50)

Further, (44), (46) and (50) imply that

$$ \Vert x_{n+1} - y_{n} \Vert \rightarrow0 \quad\text{as } n \rightarrow\infty ,\quad\text{and} \quad \lim _{n \rightarrow\infty} \Vert y_{n} - p \Vert ^{2} = b. $$

(51)

This implies that the sequences $\{x_{n}\}$, $\{w_{n}\}$ and $\{y_{n}\}$ are bounded, and for every $p \in \mathit{EP}(f, C)$, the $\lim_{n\rightarrow \infty} \|x_{n} - p\|^{2}$ exists. Now, further we show that for very sequential weak cluster point of the sequence $\{x_{n}\}$ is in $\mathit{EP}(f, C)$. Assume that z is a weak cluster point of $\{x_{n}\}$, i.e., there exists a subsequence, denoted by $\{x_{n_{k}}\}$, of $\{x_{n}\}$ weakly converging to z. Then $\{y_{n_{k}}\}$ also weakly converges to z and $z \in C$. Let us show that $z \in \mathit{EP}(f, C)$. By Lemma 4.1, the definition of $\lambda_{n+1}$ and Lemma 4.2, we have

$$ \begin{aligned}[b] \lambda_{n_{k}} f(y_{n_{k}}, y) &\geq\lambda_{n_{k}} f(y_{n_{k}}, x_{n_{k}+1}) + \langle w_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle \\ &\geq\lambda_{n_{k}} f(w_{n_{k}}, x_{n_{k+1}}) - \lambda_{n_{k}} f(w_{n_{k}}, y_{n_{k}}) - \frac{\mu\lambda_{n_{k}}}{2 \lambda _{n_{k}+1}} \Vert w_{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad-\frac{\mu\lambda_{n_{k}}}{2 \lambda_{n_{k}+1}} \Vert y_{n_{k}} - x_{n_{k}+1} \Vert ^{2} + \langle w_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle \\ &\geq \langle w_{n_{k}} - y_{n_{k}}, x_{n_{k}+1} - y_{n_{k}} \rangle - \frac{\mu\lambda_{n_{k}}}{2 \lambda_{n_{k}+1}} \Vert w_{n_{k}} - y_{n_{k}} \Vert ^{2} \\ &\quad- \frac{\mu\lambda_{n_{k}}}{2 \lambda _{n_{k}+1}} \Vert y_{n_{k}} - x_{n_{k}+1} \Vert ^{2} + \langle w_{n_{k}} - x_{n_{k}+1}, y - x_{n_{k}+1} \rangle, \end{aligned} $$

(52)

where y is any element in $H_{n}$. It follows from (45), (49), (51) and the boundedness of $\{x_{n}\}$ that the right-hand side of the last inequality tends to zero. Using $\lambda_{n_{k}} > 0$, condition $(A_{3})$ and $y_{n_{k}} \rightharpoonup z$, we have

$$0 \leq\limsup_{k \rightarrow\infty} f(y_{n_{k}}, y) \leq f(z, y), \quad \forall y\in\mathbb{H}_{n}. $$

Since $C \subset H_{n}$ and $z \in C$, we have $f(z, y) \geq0$, $\forall y \in C$. This shows that $z \in \mathit{EP}(f, C)$. Thus Lemma 2.5, ensures that $\{w_{n}\}$, $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to p as $n \rightarrow\infty$. □

Remark 4.1

The knowledge of the Lipschitz-type constants is not mandatory to build up the sequence $\{x_{n}\}$ in Algorithm 2 and to get the convergence result in Theorem 4.1.

5 Computational experiment

In this section, some numerical results will be presented in order to test Algorithms 1 and 2 with the recent Heiu algorithm in [47]. The MATLAB codes run on a PC (with Intel(R) Core(TM)i3-4010U CPU @ 1.70 GHz 1.70 GHz, RAM 4.00 GB) under MATLAB version 9.5 (R2018b).

5.1 Nash–Cournot oligopolistic equilibrium model

We consider an extension of a Nash–Cournot oligopolistic equilibrium model [2]. Assume that there are m companies that are producing the same commodity. Let x denote the vector whose entry $x_{j}$ stands for the quantity of the commodity produced by company j. We suppose that the price $p_{j}(s)$ is a decreasing affine function of s with $s = \sum_{j=1}^{m} x_{j}$ i.e. $p_{j}(s) = \alpha_{j} - \beta_{j} s$, where $\alpha_{j} > 0$, $\beta_{j} > 0$. Then the profit made by company j is given by $f_{j}(x) = p_{j}(s)x_{j} - c_{j}(x_{j})$, where $c_{j}(x_{j})$ is the tax and fee for generating $x_{j}$. Suppose that $C_{j} = [x_{j}^{\min}, x_{j}^{\max }]$ is the strategy set of company j. Then the strategy set of the model is $C := C_{1} \times C_{2} \times\cdots\times C_{m}$. Actually, each company wants to maximize its profit by choosing the corresponding production level under the presumption that the production of the other companies is a parameter input. A frequently used approach to dealing with this model is based upon the well-known Nash equilibrium concept. We recall that a point $x^{*} \in C = C_{1} \times C_{2} \times\cdots\times C_{m}$ is an equilibrium point of the model if

$$f_{j}\bigl(x^{*}\bigr) \geq f_{j} \bigl(x^{*}[x_{j}]\bigr), \quad\forall x_{j} \in C_{j}, \forall j = 1, 2, \ldots, m. $$

where the vector $x^{*}[x_{j}]$ stands for the vector attain from $x^{*}$ by replacing $x_{j}^{*}$ with $x_{j}$. By taking $f(x, y) := \psi(x, y) - \psi(x, x)$ with $\psi(x, y) := - \sum_{j=1}^{m} f_{j}(x[y_{j}])$, the problem of finding a Nash equilibrium point of the model can be formulated as

$$\text{Find } x^{*} \in C : f\bigl(x^{*}, y\bigr) \geq0, \quad\forall y \in C. $$

Now, assume that the tax-fee function $c_{j}(x_{j})$ is increasing and affine for every j. This assumption means that both of the tax and fee for producing a unit are increasing as the quantity of the production gets larger. As in [20, 53], the bifunction f can be formulated in the form of $f(x, y) = \langle Px + Qy + q, y - x \rangle$, where $q \in\mathbb {R}^{m}$ and P, Q are two matrices of order m such that Q is symmetric positive semidefinite and $Q - P$ is symmetric negative semidefinite.

For Experiment 5.1 we take $x_{-1}=(10, 0, 10, 1, 10)^{T}$, $x_{0}=(1, 3, 1, 1, 2)^{T}$, $C=\{x : -2 \leq x_{i} \leq5 \}$ and y-axes represent for the value of $D_{n} = \|w_{n} - y_{n}\|$ while the x-axes represent for the number of iterations or elapsed time (in seconds).

5.1.1 Algorithm 2 nature in terms of different values of $\alpha_{n}$

Figures 1 and 2 illustrate the numerical results for the first 120 iterations of Algorithm 2 (shortly, MSgEIA) with respect to using different values of $\alpha_{n}$. For these results, we use parameters $\alpha_{n}=0.22, 0.16, 0.11, 0.07, 0.03$, $\lambda_{0}=1$ and $\mu=0.11$. These two figures are useful for choosing the best possible value of $\alpha_{n}$.

Figure 1

Experiment 5.1: Algorithm 2 behavior in terms of iterations relative to different values of $\alpha_{n}$

Figure 2

Experiment 5.1: Algorithm 2 behavior in terms of elapsed time relative to different values of $\alpha_{n}$

5.1.2 Algorithm 2 comparison with existing algorithms

Figures 3 and 4 describe the numerical results for the first 100 iterations of Algorithm 2 [Modified subgradient explicit iterative algorithm (shortly, MSgEIA)] compared with Algorithm 1 [Subgradient explicit iterative algorithm (shortly, SgEIA)] and explicit Algorithm 1 [Explicit iterative algorithm (shortly, EIA) [47]] in terms of no. of iterations and elapsed time in seconds.

• (i) For Explicit iterative algorithm (EIA) we use the parameters $\mu=0.11$, $\lambda_{0}=1$ and $D_{n}=\|x_{n} - y_{n}\|$.

• (ii) For Subgradient explicit iterative algorithm (SgEIA) we use the parameters $\mu=0.11$, $\lambda_{0}=1$ and $D_{n}=\|x_{n} - y_{n}\|$.

• (iii) For Modified subgradient explicit iterative algorithm (MSgEIA) we use the parameters $\alpha_{n}=0.12$, $\mu=0.11$, $\lambda _{0}=1$ and $D_{n}=\|w_{n} - y_{n}\|$.

Figure 3

Experiment 5.1: Algorithm 2 comparison in terms of iterations

Figure 4

Experiment 5.1: Algorithm 2 comparison in terms of elapsed time

5.2 Nash–Cournot equilibrium models of electricity markets

In this experiment, we apply our proposed algorithm to a Nash–Cournot equilibrium model of electricity markets as in [13]. In this model, it is considered that there are three electricity companies i ($i = 1, 2, 3$). Each company i has its own, several generating units with index set $I_{i}$. In this experiment, suppose that $I_{1} = \{1\}$, $I_{2} = \{2, 3\}$ and $I_{3} = \{4, 5, 6\}$. Let $x_{j}$ be the power generation of units j ($j = 1, \ldots, 6$) and suppose that the electricity price p can be expressed as by $p = 378.4 - 2 \sum_{j=1}^{6} x_{j}$. The cost of a generating unit j is illustrated by

$$c_{j}(x_{j}) := \max\bigl\{ \overset{\circ}{c_{j}}(x_{j}), \overset{\bullet }{c_{j}}(x_{j}) \bigr\} , $$

with

$$\overset{\circ}{c_{j}}(x_{j}) := \frac{\overset{\circ}{\alpha_{j}}}{2} x_{j}^{2} + \overset{\circ}{\beta_{j}} x_{j} + \overset{\circ}{\gamma _{j}} $$

and

$$\overset{\bullet}{c_{j}}(x_{j}) := \overset{\bullet}{ \alpha_{j}} x_{j} + \frac{\overset{\bullet}{\beta_{j}}}{\overset{\bullet}{\beta_{j}} + 1} \overset{\bullet}{ \gamma_{j}}^{\frac{-1}{\overset{\bullet}{\beta_{j}}}} (x_{j})^{\frac{(\overset{\bullet}{\beta_{j}} + 1)}{\overset{\bullet }{\beta_{j}} }}, $$

where the parameter values are given in $\overset{\circ}{\alpha_{j}}$, $\overset{\circ}{\beta_{j}}$, $\overset{\circ}{\gamma_{j}}$, $\overset {\bullet}{\alpha_{j}}$, $\overset{\bullet}{\beta_{j}}$ and $\overset {\bullet}{\gamma_{j}}$ are given in Table 1. Suppose the profit of company i is given by

$$f_{i}(x) := p \sum_{j \in I_{i}} x_{j} - \sum_{j \in I_{i}} c _{j} (x_{j}) = \Biggl(378.4 - 2 \sum_{l=1}^{6} x_{l} \Biggr) \sum_{j \in I_{i}} x_{j} - \sum_{j \in I_{i}} c_{j} (x_{j}), $$

where $x=(x_{1}, \ldots, x_{6})^{T}$ subject to the constraint $x\in C := \{x\in\mathbb{R}^{6} : x_{j}^{\min} \leq x_{j} \leq x_{j}^{\max} \}$, with $x_{j}^{\min}$ and $x_{j}^{\max}$ given in Table 2.

Table 1 The parameter values used in this experiment

Table 2 The parameter values used in this experiment

Next, we define the equilibrium function f by

$$f(x, y) := \sum_{i=1}^{3} \bigl( \phi_{i}(x, x) - \phi_{i}(x, y) \bigr), $$

where

$$\phi_{i}(x, y) := \biggl[ 378.4 - 2 \biggl( \sum _{j \notin I_{i}} x_{j} + \sum_{j \in I_{i}} y_{j} \biggr) \biggr] \sum_{j \in I_{i}} y_{j} - \sum_{j \in I_{i}} c_{j}(y_{j}). $$

The Nash–Cournot equilibrium models of electricity markets can be reformulated as an equilibrium problem (see [58]):

$$\text{Find } x^{*} \in C \quad\text{such that} \quad f \bigl(x^{*}, y\bigr) \geq0, \quad\forall y \in C. $$

For Experiment 5.2, we take $x_{-1}=(10, 0, 10, 1, 10, 1)^{T}$, $x_{0}=(48, 48, 30, 27, 18, 24)^{T}$, and the y-axes represent for the value of $D_{n}$ while the x-axes represent the number of iterations or elapsed time (in seconds).

5.2.1 Algorithm 2 nature in terms of different values of $\lambda_{0}$

Figures 5 and 6 describe the numerical results of Algorithm 2 (MSgEIA) with respect to using different values of $\lambda_{0}$, in terms of no. of iterations and elapsed time in seconds relative to $D_{n}=\|x_{n+1} - x_{n}\|$. For these results, we use the parameters $\alpha_{n}=0.20$ $\lambda_{0}=1, 0.8, 0.6, 0.4, 0.2$, $\mu=0.24$ and $\epsilon=10^{-2}$.

Figure 5

Experiment 5.2: Algorithm 2 behavior in terms of iterations relative to different values of $\lambda_{0}$

Figure 6

Experiment 5.2: Algorithm 2 behavior in terms of elapsed time relative to different values of $\lambda_{0}$

5.2.2 Algorithm 2 comparison with existing algorithms

Figures 7 and 8 describe the numerical results of Algorithm 2 [Modified subgradient explicit iterative algorithm (MSgEIA)] compared with Algorithm 1 [Subgradient explicit iterative algorithm (SgEIA)] and Algorithm 1 [Explicit iterative algorithm (EIA) [47]] in terms of no. of iterations and elapsed time in seconds.

• (i) For the Explicit iterative algorithm (EIA) we use the parameters $\mu=0.2$, $\lambda_{0}=0.6$ and $D_{n}=\|x_{n+1} - x_{n}\|$.

• (ii) For Subgradient explicit iterative algorithm (SgEIA) we use the parameters $\mu=0.2$, $\lambda_{0}=0.6$ and $D_{n}=\|x_{n+1} - x_{n}\|$.

• (iii) For Modified subgradient explicit iterative algorithm (MSgEIA) we use the parameters $\alpha_{n}=0.20$, $\mu=0.2$, $\lambda _{0}=0.6$ and $D_{n}=\|x_{n+1} - x_{n}\|$.

Figure 7

Experiment 5.2: Algorithm 2 compared in terms of iterations

Figure 8

Experiment 5.2: Algorithm 2 compared in terms of elapsed time

5.3 Two-dimensional (2-D) pseudomonotone EP

Let us consider the following bifunction:

$$f(x, y) = \bigl\langle F(x), y - x \bigr\rangle , $$

where

$$F(x) = \begin{pmatrix} ( x_{1}^{2} + (x_{2} - 1)^{2} )(1 + x_{2}) \\ - x_{1}^{3} - x_{1} (x_{2} - 1)^{2} \end{pmatrix} \quad\text{with } C = \bigl\{ x \in\mathbb{R}^{2} : -10 \leq x_{i} \leq10 \bigr\} . $$

The bifunction is not monotone on C but pseudomonotone (for more details see p. 10, [59, 60]). Figure 9 illustrates the numerical results of comparison of Algorithm 2 with two other algorithms, with $x_{-1}=(5, 5)^{T}$ and $x_{0}=(10, 10)^{T}$.

Figure 9

Algorithm 2 compared in terms of no. of iterations and elapsed time

6 Conclusion

In this paper, we propose two algorithms by incorporating the subgradient and inertial technique with an explicit iterative algorithm, which can solve the problem of a pseudomonotone equilibrium. The evaluation of the step-size did not require a line search procedure or information on the Lipchitz-type constants of the bifunction. Rather, one uses a step-size sequence that can be updated on each iteration with the help of previous iterations. We have presented various numerical results to show the computational performance of our algorithm in comparison with other algorithms. These numerical results have also explained that the algorithm with inertial effects seems to perform better than without inertial effects.