Abstract
In this paper, we introduce a new family of generalized Bernstein operators based on q integers, called \((\alpha,q)\)-Bernstein operators, denoted by \(T_{n,q,\alpha}(f)\). We investigate a Kovovkin-type approximation theorem, and obtain the rate of convergence of \(T_{n,q,\alpha}(f)\) to any continuous functions f. The main results are the identification of several shape-preserving properties of these operators, including their monotonicity- and convexity-preserving properties with respect to \(f(x)\). We also obtain the monotonicity with n and q of \(T_{n,q,\alpha}(f)\).
Similar content being viewed by others
1 Introduction
A generalization of Bernstein polynomials based on q-integers was proposed by Lupaş in 1987 in [1]. However, the Lupaş q-Bernstein operators are rational functions rather than polynomials. In 1997, Phillips [2] proposed the Phillips q-Bernstein polynomials, and for decades thereafter the application of q integers in positive linear operators became a hot topic in approximation theory, such as generalized q-Bernstein polynomials [3–6], Durrmeyer-type q-Bernstein operators [7–9], Kantorovich-type q-Bernstein operators [10–13], etc. As we know, q integers play important roles not only in approximation theory, but also in CAGD. Based on the Phillips q-Bernstein polynomials [2], which are generalizations of Bernstein polynomials, generalized Bézier curves and surfaces were introduced in [14–16]. In [14], Oruç and Phillips constructed q-Bézier curves using the basis functions of Phillips q-Bernstein polynomials. Dişibüyük and Oruç [15, 16] defined the q generalization of rational Bernstein–Bézier curves and tensor product q-Bernstein–Bézier surfaces. Moreover, Simeonov et al. [17] introduced a new variant of the blossom, the q blossom, which is specifically adapted to developing identities and algorithms for q-Bernstein bases and q-Bézier curves. In 2014, Han et al. [18] proposed a generalization of q-analog Bézier curves with one shape parameter, and established degree evaluation and de Casteljau algorithms and some other properties. In 2016, Han et al. [19] introduced a new generalization of weighted rational Bernstein–Bézier curves based on q integers, and investigated the generalized rational Bézier curve from a geometric point of view, obtaining degree evaluation and de Casteljau algorithms, etc.
Recently, Chen et al. [20] introduced a new family of α-Bernstein operators, and investigated some approximation properties, such as the rate of convergence, Voronovskaja-type asymptotic formulas, etc. They also obtained the monotonic and convex properties. For \(f(x)\in [0,1]\), \(n\in \mathbb{N}\), and any fixed real α, the α-Bernstein operators they introduced are defined as
where \(f_{i}=f ( \frac{i}{n} ) \). For \(i=0,1,\ldots,n\), the α-Bernstein polynomial \(p_{n,i}^{\alpha }(x)\) of degree n is defined by \(p_{1,0}^{(\alpha )}(x)=1-x\), \(p_{1,1}^{(\alpha )}(x)=x\) and
where \(n\geq 2\).
Motivated by above research, in this paper we propose the q analogue of α-Bernstein operators, called \((\alpha , q)\)-Bernstein operators, which are defined as
where \(q\in (0,1]\), \(f_{i}=f ( \frac{[i]_{q}}{[n]_{q}} ) \), \(i=0,1,2,\ldots,n\), \(p_{1,q,0}^{(\alpha )}(x)=1-x\), \(p_{1,q,1}^{(\alpha )}(x)=x\), and
By simple computations, we can also express the \((\alpha , q)\) operators (3) as
where
Here, we mention some definitions based on q integers, the details of which can be found in [21, 22]. For any fixed real number \(0< q\leq 1\) and each non-negative integer k, we denote q-integers by \([k]_{q}\), where
Also, q-factorial and q-binomial coefficients are defined as follows:
The q-analog of \((1+x)^{n}\) is defined by \((1+x)_{q}^{n}:=\prod_{s=0}^{n-1} ( 1+q^{s}x ) \). The q derivative and q derivative of the product are defined as \(D_{q}f(x):=\frac{d_{q}f(x)}{d _{q}x}=\frac{f(qx)-f(x)}{(q-1)x} \) and \(D_{q}(f(x)g(x)):=f(qx)D_{q}g(x)+g(x)D _{q}f(x)\), respectively. We also have \(D_{q}x^{n}=[n]_{q}x^{n-1}\) and \(D_{q}(1-x)_{q}^{n}=-[n]_{q}(1-qx)_{q}^{n-1}\).
The rest of this paper is organized as follows. In the next section, we give some basic properties of the operators \(T_{n,q,\alpha }(f)\), such as the moments and central moments for proving the convergence theorems, the forward difference form of \(T_{n,q,\alpha }(f)\) for proving shape-preserving properties, etc. In Sect. 3, we obtain the convergence property and the rate of convergence theorem. In Sect. 4, we investigate some shape-preserving properties, such as monotonicity- and convexity-preserving properties with respect to \(f(x)\), and also we study the monotonicity with n and q of \(T_{n,q,\alpha }(f)\).
2 Auxiliary results
For proving the main results, we require the following lemmas.
Lemma 2.1
We have the following equalities:
Proof
By (5), we have
However,
Lemma 2.1 is proved. □
Remark 2.2
From Lemma 2.1, we know that the \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) reproduce linear functions; that is,
for all real numbers a and b.
We immediately obtain Lemma 2.3 from (5) and Lemma 2.1.
Lemma 2.3
For all functions f and g defined in \([0,1]\), \(x\in [0,1]\), real numbers λ, μ defined in \([0,1]\), and \(q\in (0,1]\), the following statements hold true.
-
(i)
Endpoint interpolation: \(T_{n,q,\alpha }(f;0)=f(0)\) and \(T_{n,q,\alpha }(f;1)=f(1)\).
-
(ii)
Linearity: \(T_{n,q,\alpha }(\lambda f+\mu g;x)= \lambda T_{n,q,\alpha }(f;x)+\mu T_{n,q,\alpha }(g;x)\).
-
(iii)
Non-negative: For \(0\leq \alpha \leq 1\) and \(0< q<1\), if f is non-negative on \([0,1]\), so is \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\).
-
(iv)
Monotone: For fixed \(0\leq \alpha \leq 1\) and \(0< q<1\), if \(f\geq g\), then \(T_{n,q,\alpha }(f;x)\geq T_{n,q,\alpha }(g;x)\).
Lemma 2.4
-
(i)
The \((\alpha , q)\)-Bernstein operators may be expressed in the form
(8)where , \(\triangle_{q}^{r}f_{j}=\triangle_{q}^{r-1}f_{j+1}-q ^{r-1}\triangle_{q}^{r-1}f_{j}\), \(r\geq 1\), with \(\triangle_{q}^{0}f _{j}=f_{j}=f ( \frac{[j]_{q}}{[n]_{q}} ) \).
-
(ii)
The higher-order forward difference of \(g_{i}\) may be expressed in the form
$$\begin{aligned} \triangle_{q}^{r}g_{i}= \biggl( 1- \frac{q^{n-i-1}[i]_{q}}{[n-1]_{q}} \biggr) \triangle_{q}^{r}f_{i}+ \frac{q^{n-i-1-r}[i+r]_{q}}{[n-1]_{q}}\triangle _{q}^{r}f_{i+1}, \end{aligned}$$(9)where \(\triangle_{q}^{0}g_{i}=g_{i}\), which is defined in (6).
Proof
We can obtain (8) easily by [2]. Next, in order to prove (9), we use induction on r. It is clear that (9) holds for \(r=0\). Let us assume that (9) holds for some \(r=k\geq 0\). For \(r=k+1\), we have
This shows that (9) holds when k is replaced by \(k+1\), and this completes the proof of Lemma 2.4. □
Since \(f [ \frac{[j]_{q}}{[n]_{q}},\frac{[j+1]_{q}}{[n]_{q}},\ldots, \frac{[j+k]_{q}}{[n]_{q}} ] =\frac{[n]_{q}^{k}\triangle_{q}^{k}f _{j}}{q^{\frac{k(2j+k-1)}{2}}[k]_{q}!}=\frac{f^{(k)}(\xi )}{k!}\), where \(\xi \in ( \frac{[j]_{q}}{[n]_{q}},\frac{[j+k]_{q}}{[n]_{q}} ) \), the q differences of the monomial \(x^{k}\) of order greater than k are zero. We see from Lemma 2.4 that, for all \(n\geq k\), \(T_{n,q,\alpha } ( t^{k};x ) \) is a polynomial of degree k. Actually, the \((\alpha , q)\)-Bernstein operators are degree-reducing on polynomials; that is, if f is a polynomial of degree m, and then \(T_{n,q,\alpha }(f)\) is a polynomial of degree \(\leq \min\{m,n\}\). In particular, we have the following results.
Lemma 2.5
Letting \(f(t)=t^{k}\), \(n-1\geq k\geq 2\), we have
where \(a_{k}=\frac{q^{\frac{k(k-1)}{2}}[n-2]_{q}!}{[n-k]_{q}![n]_{q} ^{k}} \{ (1-\alpha )[n-k]_{q}[n-1+k]_{q}+\alpha [n]_{q}[n-1]_{q} \} \).
Proof
Indeed, from (9) and \(\triangle_{q}^{k}f_{j}=\frac{q^{ \frac{k(2j+k-1)}{2}}[k]_{q}!f^{(k)}(\xi )}{k![n]_{q}^{k}}\), we have
Thus, we obtain
Hence, using (8), we have
We then obtain the proof of Lemma 2.5 by simple computations. □
Lemma 2.6
The following equalities hold true:
Proof
For \(f(t)=t^{2}\), we have \(\triangle_{q}^{0}f_{0}=f_{0}=0\), \(\triangle_{q}^{1}f_{0}=f_{1}-f_{0}=\frac{1}{[n]_{q}^{2}}\), \(\triangle_{q}^{1}f_{1}=f_{2}-f_{1}=\frac{2q+q^{2}}{[n]_{q}^{2}}\), \(\triangle_{q}^{2}f_{0}=\triangle_{q}^{1}f_{1}-q\triangle_{q}^{1}f _{0}=f_{2}-[2]_{q}f_{1}+qf_{0}=\frac{q[2]_{q}}{[n]_{q}^{2}}\), and \(\triangle_{q}^{2}f_{1}=f_{3}-[2]_{q}f_{2}+qf_{1}=\frac{q^{3}+q^{4}}{[n]_{q} ^{2}}\). By (9), we have \(\triangle_{q}^{0}g_{0}=0\), and
From (8), we have
Hence, (10) is proved. Finally, using Lemma 2.1, we obtain
Then (11) is proved by (10). This completes the proof of Lemma 2.6. □
3 Convergence properties
We now state the well-known Bohman–Korovkin theorem, followed by a proof based on that given by Cheney [23].
Theorem 3.1
Let \(\{L_{n}\}\) denote a sequence of monotone linear operators that map a function \(f\in C[a,b]\) to a function \(L_{n}f\in C[a,b]\), and let \(L_{n}f\rightarrow f\) uniformly on \([a,b]\) for \(f=1, t\) and \(t^{2}\). Then \(L_{n}f\rightarrow f\) uniformly on \([a,b]\) for all \(f\in C[a,b]\).
Theorem 3.1 leads to the following theorem on the convergence of \((\alpha , q)\)-Bernstein operators.
Theorem 3.2
Let \(q:=\{q_{n}\}\) denote a sequence such that \(q_{n}\in (0,1)\) and \(\lim_{n\rightarrow \infty }q_{n}=1\). Then, for any \(f\in C[0,1]\) and \(\alpha \in [0,1]\), \(T_{n,q,\alpha }(f;x)\) converges uniformly to \(f(x)\) on \([0,1]\).
Proof
From Lemma 2.1, we see that \(T_{n,q,\alpha }(f;x)=f(x)\) for \(f(t)=1\) and \(f(t)=t\). Since \(\lim_{n\rightarrow \infty }q_{n}=1\), we see from (10) that \(T_{n,q,\alpha }(f;x)\) converges uniformly to \(f(x)\) for \(f(t)=t^{2}\) as \(n\rightarrow \infty \). It also follows that \(T_{n,q,\alpha }\) is a monotone operator by Lemma 2.3; the proof is then completed by applying the Bohman–Korovkin theorem 3.1. □
As we know, the space \(C{[0,1]}\) of all continuous functions on \([0,1]\) is a Banach space with sup-norm \(\Vert f \Vert :=\sup_{x\in [0,1]} \vert f(x) \vert \). Letting \(f\in C{[0,1]}\), the Peetre K functional is defined by \(K_{2}(f;\delta ):=\inf_{g\in C^{2}{[0,1]}} \{ \Vert f-g \Vert +\delta \Vert g'' \Vert \}\), where \(\delta >0\) and \(C^{2}{[0,1]}:=\{g \in C{[0,1]}: g', g''\in C{[0,1]}\}\). By [24], there exists an absolute constant \(C>0\), such that
where \(\omega_{2}(f;\delta ):=\sup_{0< h\leq \delta } \sup_{x,x+h,x+2h\in [0,1]} \vert f(x+2h)-2f(x+h)+f(x) \vert \) is the second-order modulus of smoothness of \(f\in C{[0,1]}\).
Theorem 3.3
For \(f\in C{[0,1]}\), \(\alpha \in [0,1]\), \(q\in (0,1)\), we have
where C is a positive constant.
Proof
Letting \(g\in C^{2}{[0,1]}\), \(x,t\in [0,1]\), by Taylor’s expansion we have
Using Lemma 2.1, we obtain
Thus, we have
However, using Lemma 2.1, we have
Hence, taking the infimum on the right-hand side over all \(g\in C^{2} {[0,1]}\), we obtain
By (12), we obtain
where C is a positive constant. Theorem 3.3 is proved. □
Remark 3.4
Letting \(q:=\{q_{n}\}\) denote a sequence such that \(q_{n}\in (0,1)\) and \(\lim_{n\rightarrow \infty }q_{n}=1\), we know that, under the conditions of theorem 3.3, the convergence rate of the operators \(T_{n,q, \alpha }(f)\) to f is \(1/\sqrt{[n]_{q}}\) as \(n\rightarrow \infty \). This convergence rate can be improved depending on the choice of q, at least as fast as \(1/\sqrt{n}\).
Example 3.5
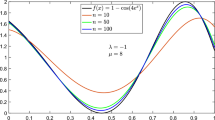
Letting \(f(x) = 1 - \cos(4e^{x})\), the graphs of \(f(x)\) and \(T_{n,q,0.9}(f;x)\) with different values of n and q are shown in Fig. 1. Figure 2 shows the graphs of \(f(x)\) and \(T_{10,0.9,\alpha }(f;x)\) with \(\alpha =0.6\) and \(\alpha =0.9\).
4 Shape-preserving properties
The \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) have a monotonicity-preserving property.
Theorem 4.1
Let \(f\in C{[0,1]}\). If f is a monotonically increasing or monotonically decreasing function on \([0,1]\), so are all its \((\alpha , q)\)-Bernstein operators for fixed \(q\in (0,1)\) and \(\alpha \in [0,1]\).
Proof
From (5), we have
where \(f_{i}=\frac{[i]_{q}}{[n+1]_{q}}\), \(g_{i}= ( 1- \frac{q^{n-i}[i]_{q}}{[n]_{q}} ) f_{i}+ \frac{q^{n-i}[i]_{q}}{[n]_{q}}f_{i+1}\). Then the q derivative of \(T_{n+1,q,\alpha }(f;x)\) is
and we denote the first and second parts of the right-hand side of the last equation by \(\Lambda_{1}\) and \(\Lambda_{2}\), respectively. We then have
Using (9), we obtain
Thus, we have
Similarly, we can obtain
Therefore, by using (15) and (16), the derivative of \(( \alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) may be expressed in the form
Since if f is monotonically increasing on \([0,1]\), the forward differences \(\triangle_{q}^{1}f_{i}\) and \(\triangle_{q}^{1}f_{i+1}\) are non-negative, and so is \(D_{q} [ T_{n,q,\alpha }(f;x) ] \). Hence, \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) are monotonically increasing on \([0,1]\) for fixed \(q\in (0,1)\) and \(\alpha \in [0,1]\). On the contrary, if f is monotonically decreasing on \([0,1]\), then operators \(T_{n,q,\alpha }(f;x)\) are monotonically decreasing on \([0,1]\) for fixed \(q\in (0,1)\) and \(\alpha \in [0,1]\). Theorem 4.1 is proved. □
The \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) have a convexity-preserving property
Theorem 4.2
Let \(f\in C{[0,1]}\). If f is convex on \([0,1]\), so are all of its \(( \alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\) for fixed \(q\in (0,1)\) and \(\alpha \in [0,1]\).
Proof
From (5), we obtain
where \(f_{i}=\frac{[i]_{q}}{[n+2]_{q}}\), \(g_{i}= ( 1- \frac{q^{n-i+1}[i]_{q}}{[n+1]_{q}} ) f_{i}+ \frac{q^{n-i+1}[i]_{q}}{[n+1]_{q}}f_{i+1}\). The q-derivative of \(T_{n+2,q,\alpha }(f;x)\) can easily obtained by the proof theorem 4.1, which may be expressed as
Then we have
By some easy computations, we obtain
where \(\triangle_{q}^{2}g_{i}= ( 1- \frac{q^{n-i+1}[i]_{q}}{[n+1]_{q}} ) \triangle_{q}^{2}f_{i}+\frac{q ^{n-i-1}[i+2]_{q}}{[n+1]_{q}}\triangle_{q}^{2}f_{i+1}\). By the connection between the second-order q differences and convexity, we know that \(\triangle_{q}^{2}f_{i}\) and \(\triangle_{q}^{2}f_{i+1}\) are all non-negative since f is convex on \([0,1]\). Hence, we obtain \(D_{q}^{2} [ T_{n+2,q,\alpha }(f;x) ] \geq 0\), and then the convexity-preserving property of \(T_{n,q,\alpha }(f;x)\). Theorem 4.2 is proved. □
Next, if \(f(x)\) is convex, the \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f;x)\), for n fixed, are monotonic in q.
Theorem 4.3
For \(0< q_{1}\leq q_{2}\leq 1\), \(\alpha \in [0,1]\) and for \(f(x)\) convex on \([0,1]\), then \(T_{n,q_{2},\alpha }(f;x)\leq T_{n,q_{1},\alpha }(f;x)\).
Proof
In the following main proof of our results, we must introduce a linear polynomial function:
where \(\frac{[i]_{q}}{[n]_{q}}\leq x<\frac{[i+1]_{q}}{[n]_{q}}\), \(f _{i}=f ( \frac{[i]_{q}}{[n]_{q}} ) \), \(i=0,\ldots,n-1\). Then it is straightforward to check that \(g_{i}=g ( \frac{[i]_{q}}{[n-1]_{q}} ) \). Since f is convex on \([0,1]\), the intrinsic linear polynomial function \(g(x)\) must be convex on \([0,1]\) as well. Therefore, by the classical results of q-Bernstein operators (see [3]), we note that
We have \(B_{n-1}^{q_{2}}(g;x)\leq B_{n-1}^{q_{1}}(g;x)\) and \(B_{n}^{q_{2}}(f;x)\leq B_{n}^{q_{1}}(f;x)\), and the desired result is obvious. Theorem 4.3 is proved. □
Finally, if \(f(x)\) is convex, we give the monotonicity of \((\alpha , q)\)-Bernstein operators \(T_{n,q,\alpha }(f; x)\) with n.
Theorem 4.4
If \(f(x)\) is convex on \([0,1]\), for fixed \(q\in (0,1)\) and \(\alpha \in [0,1]\), we have
Proof
Combining (17) and (18), and the fact that if f and g are convex on \([0,1]\), then
(see [25]). The desired result is obvious. □
Example 4.5
Letting the convex function \(f(x) = 1 - \sin(\pi x)\), \(x\in [0,1]\), the graphs of \(f(x)\) and \(T_{n,0.9,0.9}(f;x)\) with different values of \(n=10, 15, 20, 30\) are shown in Fig. 3. Figure 4 shows the graphs of \(f(x) = 1 - \sin(\pi x)\) and \(T_{10,q,0.9}(f;x)\) with \(q=0.6, 0.7, 0.8, 0.9\).
5 Conclusion
In this paper, we proposed a new family of generalized Bernstein operators, named \((\alpha , q)\)-Bernstein operators, and denoted by \(T_{n,q,\alpha }(f)\). We study the rate of convergence of these operators, investigate their monotonicity-, convexity-preserving properties with respect to \(f(x)\), and also obtain their monotonicity with n and q of \(T_{n,q,\alpha }(f)\).
References
Lupaş, A.: A q-analogue of the Bernstein operator. In: Seminar on Numerical and Statistical Calculus 9, University of Cluj-Napoca (1997)
Phillips, G.M.: Bernstein polynomials based on the q-integers. Ann. Numer. Math. 4, 511–518 (1997)
Goodman, T.N.T., Oruç, H., Phillips, G.M.: Convexity and generalized Bernstein polynomial. Proc. Edinb. Math. Soc. 42, 179–190 (1999)
Nowak, G.: Approximation properties for generalized q-Bernstein polynomials. J. Math. Anal. Appl. 350, 50–55 (2009)
Il’inskii, A.: Convergence of generalized Bernstein polynomial. J. Approx. Theory 116, 100–112 (2002)
Wang, H., Meng, F.: The rate of convergence of q-Bernstein polynomials. J. Approx. Theory 136, 151–158 (2005)
Gupta, V., Finta, Z.: On certain q-Durrmeyer type operators. Appl. Math. Comput. 209, 415–420 (2009)
Gupta, V.: Some approximation properties of q-Durrmeyer operators. Appl. Math. Comput. 197, 172–178 (2008)
Gupta, V., Wang, H.: The rate of convergence of q-Durrmeyer operators for \(0< q<1\). Math. Methods Appl. Sci. 31, 1946–1955 (2008)
Mursaleen, M., Khan, F., Khan, A.: Approximation properties for King’s type modified q-Bernstein–Kantorovich operators. Math. Methods Appl. Sci. 36(9), 1178–1197 (2015)
Agrawal, P.N., Finta, Z., Kumar, A.S.: Bernstein–Schurer–Kantorovich operators based on q-integers. Appl. Math. Comput. 256, 222–231 (2015)
Dalmanog̃lu, Ö., Dog̃ru, O.: On statistical approximation properties of Kantorovich type q-Bernstein operators. Math. Comput. Model. 52, 760–771 (2010)
Aral, A., Gupta, V., Agarwal, R.P.: Applications of q-Calculus in Operator Theory. Springer, New York (1993)
Oruç, H., Phillips, G.M.: q-Bernstein polynomials and Bézier curves. J. Comput. Appl. Math. 151, 1–12 (2003)
Dişibüyük, Ç., Oruç, H.: A generalization of rational Bernstein–Bézier curves. BIT Numer. Math. 47, 313–323 (2007)
Dişibüyük, Ç., Oruç, H.: Tensor product q-Bernstein polynomials. BIT Numer. Math. 48, 689–700 (2008)
Simeonov, P., Zafiris, V., Goldman, R.N.: q-Blossoming: a new approach to algorithms and identities for q-Bernstein bases and q-Bézier curves. J. Approx. Theory 164, 77–104 (2012)
Han, L.W., Chu, Y., Qiu, Z.Y.: Generalized Bézier curves and surfaces based on Lupaş q-analogue of Bernstein operator. J. Comput. Appl. Math. 261, 352–363 (2014)
Han, L.W., Wu, Y.S., Chu, Y.: Weighted Lupaş q-Bézier curves. J. Comput. Appl. Math. 308, 318–329 (2016)
Chen, X., Tan, J., Liu, Z., Xie, J.: Approximation of functions by a new family of generalized Bernstein operators. J. Math. Anal. Appl. 450, 244–261 (2017)
Gasper, G., Rahman, M.: Basic Hypergeometric Series. Encyclopedia of Mathematics and Its Applications, vol. 35. Cambridge University Press, Cambridge (1990)
Kac, V.G., Cheung, P.: Quantum Calculus. Universitext. Springer, New York (2002)
Cheney, E.W.: Introduction to Approximation Theory. McGraw-Hill, New York (1966)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation. Springer, Berlin (1993)
Oruç, H., Phillips, G.M.: A generalization of the Bernstein polynomials. Proc. Edinb. Math. Soc. 42, 403–413 (1999)
Acknowledgements
We thank Fujian Provincial Key Laboratory of Data Intensive Computing and Key Laboratory of Intelligent Computing and Information Processing of Fujian Province University.
Availability of data and materials
All data generated or analyzed during this study are included in this published article.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 11601266), the Natural Science Foundation of Fujian Province of China (Grant No. 2016J05017) and the Program for New Century Excellent Talents in Fujian Province University.
Author information
Authors and Affiliations
Contributions
The authors carried out the whole manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cai, QB., Xu, XW. Shape-preserving properties of a new family of generalized Bernstein operators. J Inequal Appl 2018, 241 (2018). https://doi.org/10.1186/s13660-018-1821-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-018-1821-9