Abstract
In this paper, we consider a kind of p-Laplacian neutral Rayleigh equation with singularity of attractive type,
By applications of an extension of Mawhin’s continuation theorem, sufficient conditions for the existence of periodic solution are established.
Similar content being viewed by others
1 Introduction
As is well known, the Rayleigh equation can be derived from many fields, such as physics, mechanics and engineering technique fields, and an important question is whether this equation can support periodic solutions. In 1977, Gaines and Mawhin [1] introduced some continuation theorems and applied this theorem to discussing the existence of solutions for the Rayleigh equation [1, p. 99]
Gaines and Mawhin’s work has attracted the attention of many scholars in the field of the Rayleigh equations. More recently, the existence of periodic solutions for Rayleigh equation was extensively studied (see [2–11] and the references therein). Some classical tools have been used to study Rayleigh equation in the literature, including the method of upper and lower solutions [6], the time map continuation theorem [7, 9], fixed point theory [4], the Manásevich–Mawhin continuation theorem [10, 11], and coincidence degree theory [2, 3, 5, 8].
Recently there have been published some results on singular Rayleigh equations [12–16]. In 2015, Wang and Ma [15] investigated the following singular Rayleigh equation:
where g had a repulsive singularity at the origin, i.e.,
By applications of the limit properties of the time map, the authors obtained the result of the existence of periodic solution for this equation. Afterwards, by using topological degree theory, Chen and Lu [12] discussed that the existence of periodic solution for the following singular Rayleigh equations:
The authors found new methods for estimating a lower priori bounds of periodic solutions to equation (1.2). Recently, Xin and Cheng [16] investigated a kind of neutral Rayleigh equation with singularity of repulsive type,
where \(g(t,u)=g_{1}(t,u)+g_{0}(u)\) and \(g_{0}\) had a strong singularity at \(u=0\), i.e.,
By applications of coincidence degree theory, the authors found the existence of positive periodic solution for equation (1.3).
All the aforementioned results are related to Rayleigh equation or neutral Rayleigh equation with singularity of repulsive type. Naturally, a new question arises: how p-Laplacian neutral Rayleigh equation works on singularity of attractive type? Besides practical interests, the topic has obvious intrinsic theoretical significance. To answer this question, in this paper, we consider a kind of p-Laplacian neutral Rayleigh equation with singularity of attractive type,
where \(p>1\), \(\varphi_{p}(u)=\vert u\vert ^{p-2}u\) for \(u\neq 0\) and \(\varphi _{p}(0)=0\); \(\vert c\vert \neq 1\) and δ is a constant with \(0\leq \delta <\omega \); \(e:\mathbb{R}\rightarrow \mathbb{R}\) is continuous periodic functions with \(e(t+\omega)-e(t)\equiv 0\) and \(\int^{T}_{0}e(t)\,dt=0\); f is for continuous functions defined on \(\mathbb{R}^{2}\) and periodic in t with \(f(t,\cdot)=f(t+\omega, \cdot)\) and \(f(t,0)=0\), \(g(t,u)=g_{0}(u)+g_{1}(t,u)\), here \(g_{1}:\mathbb{R}\times (0,+\infty)\to \mathbb{R}\) is an \(L^{2}\)-Carathéodory function, \(g_{1}(t,\cdot)=g_{1}(t+\omega, \cdot)\); \(g_{0}\in C((0,\infty);\mathbb{R})\) has an attractive singularity at the origin, i.e.,
Obviously, the attractive condition (1.6) is in contradiction with the repulsive singularity of (1.1) and (1.4). Therefore, the above methods of [12, 15, 16] are no long applicable to the proof of existence of a periodic solution for (1.5) with singularity of attractive type. So we need to find a new method to get over it.
In this paper, by applications of an extension of Mawhin’s continuation theorem in [17] and some analysis techniques, we see the existence of a positive periodic solution for (1.5). Our results improve and extend the results in [12, 15, 16].
2 Preliminary lemmas
For convenience, define
which is a Banach space endowed with the norm \(\Vert \cdot \Vert \) define by \(\Vert u\Vert =\max \{\Vert u\Vert _{\infty },\Vert u'\Vert _{\infty }\}\), for all x, and
Lemma 2.1
(see [18])
If \(\vert c\vert \neq 1\), then the operator \((Au)(t):=u(t)-cu(t- \delta)\) has a continuous inverse \(A^{-1}\) on the space \(C_{\omega }\), and satisfying
Lemma 2.2
If \(\vert c\vert \neq 1\), then operator \(A^{-1}\) satisfying
Proof
We first consider \(\vert c\vert <1\). From Lemma 2.1, we have
Similarly, for \(\vert c\vert >1\), we can get
Therefore, we have
□
Lemma 2.3
(see [19])
If \(u\in C^{1}_{\omega }(\mathbb{R},\mathbb{R})\), and there exists a point \(t^{*}\in [0,\omega ]\) such that \(\vert u(t^{*})\vert < d\), then
and
where \(1\leq p<\infty \), \(\pi_{p}=2\int^{(p-1)/p}_{0}\frac{ds}{(1-\frac{s ^{p}}{p-1})^{1/p}}=\frac{2\pi (p-1)^{1/p}}{p\sin (\pi /p)}\).
The following lemma involves the consequences of Theorem 3.1 of [17].
Lemma 2.4
Assume that condition \(\vert c\vert \neq 1\), Ω is an open bounded set in \(C^{1}_{\omega }\). If:
-
(i)
for each \(\lambda \in (0,1)\) the equation
$$ \bigl(\phi_{p}(Au)'(t) \bigr)'+\lambda f \bigl(t,u'(t) \bigr)+\lambda g \bigl(t,u(t) \bigr)=\lambda e(t) $$(2.1)has no solution on ∂Ω;
-
(ii)
the equation
$$F(a):=\frac{1}{\omega } \int^{\omega }_{0}g(t,a)\,dt=0 $$has no solution on \(\partial \Omega \cap \mathbb{R}\);
-
(iii)
the Brouwer degree
$$\deg \{F,\Omega \cap \mathbb{R},0\}\neq 0, $$then Eq. (2.1) has at least one periodic solution on Ω̄.
3 Main results: positive periodic solution for (1.5)
In this section, we will consider the existence of a positive periodic solution for (1.5) with singularity.
Theorem 3.1
Assume that the following conditions hold:
- \((H_{1})\) :
-
there exists a positive constant K such that \(\vert f(t,v)\vert \leq K\), for \((t,v)\in \mathbb{R}\times \mathbb{R}\);
- \((H_{2})\) :
-
there exist positive constants \(D_{1}\) and \(D_{2}\) with \(D_{1}>D_{2}>0\) such that \(g(t,u)<-K\) for \((t,u)\in \mathbb{R}\times (D_{1},+\infty)\) and \(g(t,u)>K\) for \((t,u)\in \mathbb{R}\times (0,D _{2})\);
- \((H_{3})\) :
-
there exist positive constants a, b such that
$$-g(t,u)\leq a u^{p-1}+b,\quad \textit{for all } u>0. $$
Then (1.5) has at least one positive solution with period ω if \(\frac{\omega (1+\vert c\vert )^{\frac{1}{p}}a^{\frac{1}{p}}}{\vert 1-\vert c\vert \vert }<2^{ \frac{p-1}{p}}\).
Proof
Firstly, we will claim that the set of all possible ω-periodic solutions of (2.1) is bounded. Let \(u(t)\in C^{1}_{\omega }\) be an arbitrary solution of (2.1) with period ω.
We claim that there exists a point \(t_{0}\in [0,\omega ]\) such that
Integrating both sides of (2.1) over \([0,\omega ]\), we have
Therefore, from \((H_{1})\), we have
From \((H_{2})\), we know that there exist two points \(t_{0}\), \(\tau \in (0,T)\), such that
Since \(u(t)>0\), \(t\in [0,\omega ]\), we get \(0< u(t_{0})\leq D_{1}\). Equation (3.1) is proved.
Then, from Lemma 2.3, we have
Multiplying both sides of (2.1) by \((Au)(t)\) and integrating over \([0,\omega ]\), we get
i.e.
From \((H_{1})\), we have
We get from \((H_{1})\), \((H_{3})\) and (3.2)
where \(g^{-}:=\min \{g(t,u),0\}\). Substituting (3.4) and (3.7) into (3.6), we have
where \(N_{1}:=2b\omega +2K\omega +\Vert e\Vert _{\infty }\omega \). For a given constant \(\zeta >0\), which is only dependent on \(k>0\), we have
Therefore, we have
By application of Lemma 2.1, we have
since \((Au')(t)=(Au)'(t)\) and \(\frac{1}{p}+\frac{1}{q}=1\). Apply the inequality
Substituting (3.8) into (3.9), we have
Since \(\frac{\omega (1+\vert c\vert )^{\frac{1}{p}}a^{\frac{1}{p}}}{\vert 1-\vert c\vert \vert }<2^{ \frac{p-1}{p}}\), it is easy to see that there exists a positive constant \(M_{1}'\) such that
From (3.4) and (3.10), we have
As \((Au)(0)=(Au)(\omega)\), there exists \(t_{1}\in [0,\omega ]\) such that \((Au)'(t_{1})=0\), while \(\phi_{p}(0)=0\), we have
where \(t\in [t_{1},t_{1} +\omega ]\). In view of \((H_{1})\), (3.7) and (3.12), we have
We claim that there exists a positive constant \(M_{2}>M_{2}'+1\) such that, for all \(t\in \mathbb{R}\),
In fact, if \(u'\) is not bounded, there exists a positive constant \(M_{2}''\) such that \(\Vert u'\Vert _{\infty }>M_{2}''\) for some \(u'\in \mathbb{R}\). Therefore, we have
Then it is a contradiction. So (3.14) holds.
On the other hand, it follows by (2.1) that
Multiplying both sides of (3.15) by \(u'(t)\) we get
Let \(\tau \in [0,\omega ]\) be as in (3.3), for any \(\tau \leq t\leq \omega\), we integrate (3.16) on \([\tau,t]\) and get
By (3.7), (3.11) and (3.14), we have
Moreover, from \((H_{1})\) and (3.14)
where \(g_{M_{1}}=\max_{0\leq u\leq M_{1}}\vert g_{1}(t,u)\vert \in L^{2}(0, \omega)\).
With these inequalities we can derive from (3.17) that
In view of (1.6), we know there exists \(M_{3}>0\) such that
The case \(t\in [0,\tau ]\) can be treated similarly.
Having in mind (3.11), (3.14) and (3.18), we define
where \(0< E_{1}< \min \{D_{2},M_{3}\}\), \(E_{2}>\max \{M_{1}, D_{1}\} \) and \(E_{3}>M_{2}\). We know that (2.1) has no solution on ∂Ω as \(\lambda \in (0,1)\) and when \(u(t)\in \partial \Omega \cap \mathbb{R}\), \(u(t)=E_{2}\) or \(u(t)=E_{1}\), from (3.4), we know that \(E_{2}+1>D_{1}\); therefore, from \((H_{2})\) we see that
and
So condition (ii) is also satisfied. Set
where \(x\in \partial \Omega \cap \mathbb{R}\), \(\mu \in [0,1]\), we have
and thus \(H(u,\mu)\) is a homotopic transformation and
So condition (iii) is satisfied. In view of Lemma 2.1, there exists a solution with period ω. □
4 Example
Example 4.1
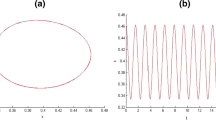
Consider the following p-Laplacian neutral Rayleigh equation with singularity:
where \(\mu \geq 1\) and \(p=4\), δ is a constant and \(0\leq \delta <\omega \).
It is clear that \(\omega =\frac{\pi }{2}\), \(c=\frac{1}{4}\), \(e(t)=\sin ^{2}(2t)\), \(f(t,v)=-\cos^{2}(2t)\sin v\), \(g(t,u)=-\frac{1}{3\pi^{3}}( \sin 4t+2)u^{4}(t)+\frac{1}{u^{\mu }(t)}\). Choose \(K=1\), \(D_{1}=2\), \(D_{2}=1\), \(a=\frac{1}{\pi^{4}}\), it is obvious that \((H_{1})\), \((H_{2})\) and \((H_{3})\) hold. Next, we consider
Therefore, by Theorem 3.1, (4.1) has at least one nonconstant \(\frac{\pi }{2}\)-periodic solution.
5 Conclusions
In this article we introduce the existence of a periodic solution for a p-Laplacian neutral Rayleigh equation with singularity of attractive type. Due to the attractive condition being in contradiction with the repulsive condition, the methods of [12, 15, 16] are no long applicable to the proof of a periodic solution for equation (1.5) with singularity of attractive singularity. In this paper, we give attractive conditions (1.6) and \((H_{3})\), and we see the existence of a periodic solution for (1.5) by applications of the extension of Mawhin’s continuation theorem [17]. Moreover, in view of the mathematical points, the results satisfying the conditions of an attractive singularity are valuable to understand the periodic solution for Rayleigh equations.
References
Gaines, R.E., Mawhin, J.L.: Coincidence Degree, and Nonlinear Differential Equations. Lecture Notes in Mathematics, vol. 568. Springer, Berlin (1977)
Cheng, Z.B., Ren, J.L.: Periodic solutions for a fourth-order Rayleigh type p-Laplacian delay equation. Nonlinear Anal. 70, 516–523 (2009)
Cheung, W., Ren, J.L.: Periodic solutions for p-Laplacian Rayleigh equations. Nonlinear Anal. 65, 2003–2012 (2006)
Cheung, W., Ren, J.L., Han, W.: Positive periodic solution of second-order neutral functional differential equations. Nonlinear Anal. 71, 3948–3955 (2009)
Du, B., Lu, S.P.: On the existence of periodic solutions to a p-Laplacian Rayleigh equation. Indian J. Pure Appl. Math. 40, 253–266 (2009)
Habets, P., Torres, P.: P: Some multiplicity results for periodic solutions of a Rayleigh differential equation. Dyn. Contin. Discrete Impuls. Syst., Ser. A Math. Anal. 8, 335–351 (2001)
Ma, T.: Periodic solutions of Rayleigh equations via time-maps. Nonlinear Anal. 75, 4137–4144 (2012)
Wang, L., Shao, J.: New results of periodic solutions for a kind of forced Rayleigh-type equations. Nonlinear Anal., Real World Appl. 11, 99–105 (2010)
Wang, Z.H.: On the existence of periodic solutions of Rayleigh equations. Z. Angew. Math. Phys. 56, 592–608 (2005)
Wang, Y., Dai, X.: Existence and stability of periodic solutions of a Rayleigh type equation. Bull. Aust. Math. Soc. 79, 377–390 (2009)
Xin, Y., Cheng, Z.B.: Existence and uniqueness of a positive periodic solution for Rayleigh type ϕ-Laplacian equation. Adv. Differ. Equ. 2014, 225 (2014)
Chen, L.J., Lu, S.P.: A new result on the existence of periodic solutions for Rayleigh equations with a singularity of repulsive type. Adv. Differ. Equ. 2017, 106 (2017)
Lu, S.P., Zhang, T., Chen, L.: Periodic solutions for p-Laplacian Rayleigh equations with singularities. Bound. Value Probl. 2016, 96 (2016)
Sun, X., Yu, P., Qin, B.: Global existence and uniqueness of periodic waves in a population model with density-dependent migrations and Allee effect. Int. J. Bifurc. Chaos Appl. Sci. Eng. 27, 1750192 (2017)
Wang, Z.H., Ma, T.: Periodic solutions of Rayleigh equations with singularities. Bound. Value Probl. 2015, 154 (2015)
Xin, Y., Cheng, Z.B.: Study on a kind of neutral Rayleigh equation with singularity. Bound. Value Probl. 2017, 92 (2017)
Lu, S.P.: Periodic solutions to a second order p-Laplacian neutral functional differential system. Nonlinear Anal. TMA 69, 4215–4229 (2008)
Zhang, M.R.: Periodic solutions of linear and quasilinear neutral functional differential equations. J. Math. Anal. Appl. 189, 378–392 (1995)
Xin, Y., Cheng, Z.B.: Positive periodic solution of p-Laplacian Liénard type differential equation with singularity and deviating argument. Adv. Differ. Equ. 2016, 41 (2016)
Acknowledgements
YX, HML and ZBC would like to thank the referee for invaluable comments and insightful suggestions. This work was supported by National Natural Science Foundation of China (No. 11501170), Education Department of Henan Province project (No. 16B110006) and Henan Polytechnic University Outstanding Youth Fund (J2016-03).
Author information
Authors and Affiliations
Contributions
YX, HML and ZBC worked together on the derivation of the mathematical results. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Xin, Y., Liu, H. & Cheng, Z. Positive periodic solution for p-Laplacian neutral Rayleigh equation with singularity of attractive type. J Inequal Appl 2018, 58 (2018). https://doi.org/10.1186/s13660-018-1654-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-018-1654-6