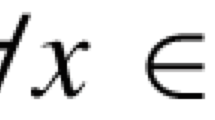Iterative algorithm for solving the multiple-sets split equality problem with split self-adaptive step size in Hilbert spaces

Abstract

The split equality problem is a generalization of the split feasibility problem, meanwhile it is a special case of multiple-sets split equality problems. In this paper, we propose an iterative algorithm for solving the multiple-sets split equality problem whose iterative step size is split self-adaptive. The advantage of the split self-adaptive step size is that it could be obtained directly from the iterative procedure without needing to have any information of the spectral norm of the related operators. Under suitable conditions, we establish the theoretical convergence of the algorithm proposed in Hilbert spaces, and several numerical results confirm the effectiveness of the algorithm proposed.

1 Introduction

There arise various linear inverse problems in phase retrieval, radiation therapy treatment, signal processing, and medical image reconstruction etc. Censor and Elfving [1] summarized one of these classes of problems and proposed a new concept which is called the split feasibility problem (SFP), and the SFP can be characterized mathematically as

$$\textit{finding } x\in C \textit{ which satisfies }Ax\in Q, $$

where C, Q are closed, convex, and nonempty subsets of the Hilbert spaces $H_{1}$ and $H_{2}$, respectively, and $A:H_{1}\mapsto H_{2}$ is a bounded and linear operator.

For solving it, Byrne [2, 3] presented the well-known CQ-algorithm, inspired by the idea of iterative scheme of fixed point theory. It is worth noting that the step size of the CQ-algorithm is fixed, depending upon the norm of the operator A. Later, Qu and Xiu [4] and Lopez et al. [5] revised the CQ-algorithm by using the Armijo-like search method and the self-adaptive step size, respectively. Both of the methods need not know the spectral norm of operator A. For more information as regards algorithms for solving the SFP, see [6, 7]. In 2005, Censor et al. [8] made an extension upon the form of SFP, replaced the convex set C with an intersection of a family of closed and convex sets, which is the original multiple-sets split feasibility problem (MSSFP), and introduced its applications for inverse problems.

Then Moudafi [9] generalized the content of SFP, to one called the split equality problem (SEP), which can be characterized mathematically as

$$ \textit{finding }x\in C, y\in Q\textit{ which satisfy }Ax=By, $$

(1.1)

where C, Q are closed, convex, and nonempty subsets of Hilbert spaces $H_{1}$ and $H_{2}$, respectively, and $H_{3}$ is also a Hilbert space, $A:H_{1}\mapsto H_{3}$, $B:H_{2}\mapsto H_{3}$ are two bounded and linear operators. When $B=I$, the SEP is just the SFP. Later, Byrne and Moudafi [10] presented the following algorithms to solve it.

Alternating CQ-algorithm:

$$ \left \{ \textstyle\begin{array}{l} x_{k+1}=P_{C}(x_{k}-\gamma_{k} A^{*}(Ax_{k}-By_{k})), \\ y_{k+1}=P_{Q}(y_{k}+\gamma_{k} B^{*}(Ax_{k}-By_{k})). \end{array}\displaystyle \right . $$

(1.2)

Relaxed alternating CQ-algorithm:

$$\left \{ \textstyle\begin{array}{l} x_{k+1}=P_{C_{k}}(x_{k}-\gamma_{k} A^{*}(Ax_{k}-By_{k})), \\ y_{k+1}=P_{Q_{k}}(y_{k}+\gamma_{k} B^{*}(Ax_{k}-By_{k})). \end{array}\displaystyle \right . $$

We know, in order to make the sequences generated above convergent, the values of step sizes $\gamma_{k}$ depend upon the norms of operators A, B. Then Shi et al. [11] improved Moudafi’s algorithms and obtained a strong convergent result:

$$\left \{ \textstyle\begin{array}{l} x_{k+1}=P_{C}[(1-\alpha_{k})(x_{k}-\gamma A^{*}(Ax_{k}-By_{k}))], \\ y_{k+1}=P_{Q}[(1-\alpha_{k})(y_{k}+\gamma B^{*}(Ax_{k}-By_{k}))]. \end{array}\displaystyle \right . $$

But the defect is the same as Moudafi’s: that the γ above also relies upon the norms of operators A, B. For more information as regards methods solving the split equality problem, see [12, 13].

In this paper, along with Censor’s idea, we consider the multiple-sets form of the split equality problem (MSSEP), which can be characterized mathematically as

$$ \textit{finding }x\in\bigcap^{r}_{i=1} C_{i}, y\in\bigcap^{t}_{j=1} Q_{j} \textit{ which satisfy } Ax=By, $$

(1.3)

where r, t are positive integers, $\{C_{i}\}^{r}_{i=1}$ and $\{Q_{j}\}^{t}_{j=1}$ are closed, convex, and nonempty subsets of Hilbert spaces $H_{1}$ and $H_{2}$, respectively; and $H_{3}$ is also a Hilbert space, $A:H_{1}\mapsto H_{3}$, $B:H_{2}\mapsto H_{3}$ are two bounded and linear operators. Obviously, when $r=t=1$, the MSSEP reduces to the SEP. We propose an iterative algorithm with split self-adaptive step size where we need not calculate or estimate the spectral norms of related operators.

The general structure of this paper is as follows. In the next section, we provide some lemmas and definitions as well as their properties which will be useful in succedent processes. In Section 3, we present an iterative algorithm with split self-adaptive step size and provide the proof of its convergence. In Section 4, several numerical results are showed to confirm the effectiveness of our algorithm. In the last section, there are some conclusions.

2 Preliminaries

As a matter of convenience, we introduce several notations first. Let H be a real Hilbert space with inner product $\langle\cdot,\cdot\rangle$ and norm $\|\cdot\|$; I denotes the unit operator on H. $x^{k}\rightarrow x$ and $x^{k}\rightharpoonup x$ represent sequences $\{x^{k}\}$ converging strongly and weakly to x, respectively. $\omega_{w}(x^{k})$ denotes the weak cluster point set of sequence $\{x^{k}\}$; $\operatorname{Fix}(T)$ and $T^{*}$ are the fixed points set and adjoint operator of operator T, respectively.

Next, there are several definitions and lemmas that will be available in the following proof process.

Definition 2.1

[14]

A mapping $T:H\mapsto H$ goes by the name of

• (i) non-expansive, if $\|Tx-Ty\|\leq\|x-y\|$, $\forall x,y\in H$;

• (ii) firmly non-expansive, if $\|Tx-Ty\|^{2}\leq\langle x-y,Tx-Ty\rangle$, $\forall x,y\in H$.

Review that $P_{C}$ is a mapping from H onto a closed, convex, and nonempty subset C of H, if

$$P_{C}(x)=\arg\min_{y\in C}\|x-y\|,\quad \forall x\in H, $$

then $P_{C}$ is called the orthogonal projection from H onto C.

Bauschke et al. presented the following properties of the orthogonal projection operator.

Lemma 2.2

[14]

Let C be a closed, convex, and nonempty subset of H, then for any $x,y\in H$ and $z\in C$,

• (i) $\langle x-P_{C}x,z-P_{C}x\rangle\leq0$;

• (ii) $\|P_{C}x-P_{C}y\|^{2}\leq\langle P_{C}x-P_{C}y,x-y\rangle$;

• (iii) $\|P_{C}x-z\|^{2}\leq\|x-z\|^{2}-\|P_{C}x-x\|^{2}$.

Remark 2.2′

Based on the Cauchy-Schwarz inequality, it is not hard to show that a firmly non-expansive mapping is non-expansive. It follows from Lemma 2.2 that $P_{C}$ is firmly non-expansive and non-expansive. It also can be deduced that $I-P_{C}$ is firmly non-expansive and non-expansive.

Definition 2.3

[14]

Let C be a nonempty subset of H, and let $\{x^{k}\}$ be a sequence in H. Then $\{x^{k}\}$ is Fejér monotone with respect to C, if

$$\bigl\Vert x^{k+1}-z\bigr\Vert \leq\bigl\Vert x^{k}-z \bigr\Vert ,\quad \forall z\in C. $$

Obviously, a Fejér monotone sequence $\{x^{k}\}$ is bounded and $\lim_{k\rightarrow\infty}\|x^{k}-z\|$ exists.

The demiclosedness principle is a perfect conclusion and plays a significant role in fixed point theory.

Lemma 2.4

[15, 16]

Let X be a Banach space, C be a closed and convex subset of X, and $T:C\mapsto C$ be a non-expansive mapping with $\operatorname{Fix}(T)\neq\emptyset$. If $\{x^{k}\}\rightharpoonup x$ and $\{(I-T)x^{k}\}\rightarrow y$, then $(I-T)x=y$.

The following lemma is a primarily used tool in the proof of our main results.

Lemma 2.5

[17]

Let K be a closed, convex, and nonempty subset of H, and $\{x^{k}\}$ be a sequence in H, if

• (i) $\lim_{k\rightarrow\infty}\|x^{k}-x\|$ exists for each $x\in K$;

• (ii) $\omega_{w}(x^{k})\subseteq K$,

then $\{x^{k}\}$ converges weakly to a point in K.

3 Main results

Recall the multiple-sets split equality problem (MSSEP), without loss of generality, we assume that $t>r$ in (1.3), and make $C_{r+1}=C_{r+2}=\cdots=C_{t}=H_{1}$, then the problem MSSEP (1.3) can be described equivalently as

$$ \textit{finding }x\in\bigcap^{t}_{i=1} C_{i}, y\in\bigcap^{t}_{j=1} Q_{j}\textit{ which satisfy } Ax=By. $$

(3.1)

Let $S_{i}=C_{i}\times Q_{i}\subseteq H=H_{1}\times H_{2}$, $i=1,2,\ldots,t$, $G=[A,-B]:H\mapsto H_{3}$, $G^{*}$ be the adjoint operator of G, then the original problem (1.3) can be modified as

$$ \textit{finding }w=(x,y)\in\bigcap_{i=1}^{t}S_{i} \textit{ which satisfies } Gw=0. $$

(3.2)

Theorem 3.1

Let $\Omega\neq\emptyset$ be the solution set of the problem MSSEP (3.2). Choose an initial point $w_{0}\in H$ arbitrarily, the iterative sequence $\{w^{k}\}$ with split self-adaptive step size is obtained by the following:

$$ w^{k+1}=w^{k}+\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum _{i=1}^{t}\alpha _{i}\bigl(P_{S_{i}}w^{k}-w^{k} \bigr)-\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}G^{*}Gw^{k}, $$

(3.3)

or component-wise

$$ \left \{ \textstyle\begin{array}{l} x^{k+1}=x^{k}+\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{C_{i}}x^{k}-x^{k}\| ^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{C_{i}}x^{k}-x^{k})\|^{2}}\sum_{i=1}^{t}\alpha _{i}(P_{C_{i}}x^{k}-x^{k}) \\ \hphantom{x^{k+1}={}}{}-\frac{\rho_{2}^{k}\|Ax^{k}-By^{k}\|^{2}}{\|A^{*}(Ax^{k}-By^{k})\| ^{2}}A^{*}(Ax^{k}-By^{k}), \\ y^{k+1}=y^{k}+\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{Q_{i}}y^{k}-y^{k}\| ^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{Q_{i}}y^{k}-y^{k})\|^{2}}\sum_{i=1}^{t}\alpha _{i}(P_{Q_{i}}y^{k}-y^{k}) \\ \hphantom{y^{k+1}={}}{}+\frac{\rho_{2}^{k}\|Ax^{k}-By^{k}\|^{2}}{\|B^{*}(Ax^{k}-By^{k})\| ^{2}}B^{*}(Ax^{k}-By^{k}), \end{array}\displaystyle \right . $$

(3.4)

where $0<\underline{\rho}_{1}\leq\rho_{1}^{k}\leq\bar{\rho}_{1}<1$, $0<\underline{\rho }_{2}\leq\rho_{2}^{k}\leq\bar{\rho}_{2}<1$, $\{\alpha_{i}\}_{i=1}^{t}>0$, then $\{w^{k}\}$ converges weakly to a solution of the problem MSSEP (3.2).

Proof

Since $\Omega\neq\emptyset$, taking a $\bar{w}\in\Omega$, $G\bar{w}=0$,

$$\begin{aligned}& \bigl\Vert w^{k+1}-\bar{w}\bigr\Vert ^{2} \\& \quad = \Biggl\Vert w^{k}+\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha _{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\| ^{2}}\sum _{i=1}^{t}\alpha_{i}\bigl(P_{S_{i}}w^{k}-w^{k} \bigr)-\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\| G^{*}Gw^{k}\|^{2}}G^{*}Gw^{k}-\bar{w}\Biggr\Vert ^{2} \\& \quad = \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}+2\Biggl\langle w^{k}-\bar{w},\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha _{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum _{i=1}^{t}\alpha_{i}\bigl(P_{S_{i}}w^{k}-w^{k} \bigr)\Biggr\rangle \\& \qquad {} -2\biggl\langle w^{k}-\bar{w},\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\| ^{2}}G^{*}Gw^{k} \biggr\rangle \\& \qquad {} +\Biggl\Vert \frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha _{i}\bigl(P_{S_{i}}w^{k}-w^{k}\bigr) \Biggr\Vert ^{2} \\& \qquad {} +\biggl\Vert \frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}G^{*}Gw^{k}\biggr\Vert ^{2} \\& \qquad {} -2\Biggl\langle \frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\| ^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha _{i}\bigl(P_{S_{i}}w^{k}-w^{k}\bigr), \frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\| ^{2}}G^{*}Gw^{k}\Biggr\rangle \\& \quad \leq \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}+2 \Biggl\langle w^{k}-\bar{w},\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha _{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum _{i=1}^{t}\alpha_{i}\bigl(P_{S_{i}}w^{k}-w^{k} \bigr)\Biggr\rangle \\& \qquad {} -2\biggl\langle w^{k}-\bar{w},\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\| ^{2}}G^{*}Gw^{k} \biggr\rangle \\& \qquad {} +2\Biggl\| \frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha _{i}\bigl(P_{S_{i}}w^{k}-w^{k}\bigr) \Biggr\| ^{2} \\& \qquad {} +2\biggl\| \frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}G^{*}Gw^{k}\biggr\| ^{2} \\& \quad = \bigl\| w^{k}-\bar{w}\bigr\| ^{2}+2\Biggl\langle w^{k}-\bar{w},\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha _{i}\bigl(P_{S_{i}}w^{k}-w^{k}\bigr) \Biggr\rangle \\& \qquad {} -2\biggl\langle w^{k}-\bar{w},\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}G^{*}Gw^{k} \biggr\rangle \\& \qquad {} +2\frac{(\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}+2\frac{(\rho_{2}^{k}\|Gw^{k}\| ^{2})^{2}}{\|G^{*}Gw^{k}\|^{2}}. \end{aligned}$$

(3.5)

Next, we prove that the iterative sequence $\{w^{k}\}$ is Fejér monotone with respect to Ω.

First, according to the property of the projection operator (Lemma 2.2) and the definition of an adjoint operator, we obtain the following estimations:

$$\begin{aligned}& \Biggl\langle w^{k}-\bar{w},\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\| P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum _{i=1}^{t}\alpha_{i} \bigl(P_{S_{i}}w^{k}-w^{k}\bigr)\Biggr\rangle \\& \quad = \frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha_{i}\bigl\langle w^{k}-\bar{w},P_{S_{i}}w^{k}-w^{k} \bigr\rangle \\& \quad = \frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha_{i}\bigl\langle w^{k}-P_{S_{i}}w^{k},P_{S_{i}}w^{k}-w^{k} \bigr\rangle \\& \qquad {} +\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha_{i}\bigl\langle P_{S_{i}}w^{k}- \bar{w},P_{S_{i}}w^{k}-w^{k}\bigr\rangle \\& \quad \leq -\frac{\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}\sum_{i=1}^{t} \alpha_{i}\bigl\Vert P_{S_{i}}w^{k}-w^{k} \bigr\Vert ^{2} \\& \quad = -\frac{\rho_{1}^{k}(\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}} \end{aligned}$$

(3.6)

and

$$\begin{aligned}& \biggl\langle w^{k}-\bar{w},\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\| ^{2}}G^{*}Gw^{k} \biggr\rangle \\& \quad = \frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}\bigl\langle Gw^{k}-G\bar {w},Gw^{k}\bigr\rangle \\& \quad = \frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\|^{2}}\bigl\Vert Gw^{k}\bigr\Vert ^{2} \\& \quad = \frac{\rho_{2}^{k}\|Gw^{k}\|^{4}}{\|G^{*}Gw^{k}\|^{2}} . \end{aligned}$$

(3.7)

Substituting (3.6) and (3.7) into (3.5), we get

$$\begin{aligned}& \bigl\Vert w^{k+1}-\bar{w}\bigr\Vert ^{2} \\& \quad \leq \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}-2 \frac{\rho_{1}^{k}(\sum_{i=1}^{t}\alpha_{i}\| P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\| ^{2}}-2\frac{\rho_{2}^{k}\|Gw^{k}\|^{4}}{\|G^{*}Gw^{k}\|^{2}} \\& \qquad {} +2\frac{(\rho_{1}^{k}\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\| \sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}+2\frac{(\rho_{2}^{k})^{2}\|Gw^{k}\| ^{4}}{\|G^{*}Gw^{k}\|^{2}} \\& \quad = \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}-2 \rho_{1}^{k}\bigl(1-\rho_{1}^{k}\bigr) \frac{(\sum_{i=1}^{t}\alpha _{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\| ^{2}} \\& \qquad {} -2\rho_{2}^{k}\bigl(1-\rho_{2}^{k} \bigr)\frac{\|Gw^{k}\|^{4}}{\|G^{*}Gw^{k}\|^{2}} . \end{aligned}$$

(3.8)

Based on the assumptions of $\{\rho_{1}^{k}\}$ and $\{\rho_{2}^{k}\}$, it follows from (3.8) that

$$\bigl\Vert w^{k+1}-\bar{w}\bigr\Vert \leq\bigl\Vert w^{k}-\bar{w}\bigr\Vert , $$

w̄ is taken arbitrarily in Ω, hence, the iterative sequence $\{w^{k}\}$ is Fejér monotone with respect to Ω. Therefore, $\lim_{k\rightarrow\infty}\|w^{k}-\bar{w}\|$ exists.

Since $\rho_{1}^{k}\in[\underline{\rho}_{1},\bar{\rho}_{1}]\subset(0,1)$, from (3.8) we have

$$\begin{aligned}& 2\underline{\rho}_{1}(1-\bar{\rho}_{1}) \frac{(\sum_{i=1}^{t}\alpha _{i}\|P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\| ^{2}} \\& \quad \leq 2\rho_{1}^{k}\bigl(1-\rho_{1}^{k} \bigr)\frac{(\sum_{i=1}^{t}\alpha_{i}\| P_{S_{i}}w^{k}-w^{k}\|^{2})^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}} \\& \quad \leq \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}-\bigl\Vert w^{k+1}-\bar{w}\bigr\Vert ^{2} . \end{aligned}$$

(3.9)

Letting $k\rightarrow\infty$ on both sides of the above inequality (3.9), we obtain

$$ \lim_{k\rightarrow\infty}\frac{(\sum_{i=1}^{t}\alpha_{i}\|P_{S_{i}}w^{k}-w^{k}\| ^{2})^{2}}{\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|^{2}}=0 . $$

(3.10)

The sequence $\{w^{k}\}$ is bounded, there exists a real number $M>0$ such that $\|\sum_{i=1}^{t}\alpha_{i}(P_{S_{i}}w^{k}-w^{k})\|\leq M$ for all $k\geq0$, and $P_{S_{i}}-I$ is non-expansive, consequently, it follows from (3.10) that

$$\lim_{k\rightarrow\infty}\sum_{i=1}^{t} \alpha_{i}\bigl\Vert P_{S_{i}}w^{k}-w^{k} \bigr\Vert ^{2}=0,\quad i=1,2,\ldots,t, $$

which is equal to

$$ \lim_{k\rightarrow\infty}\bigl\Vert P_{S_{i}}w^{k}-w^{k} \bigr\Vert =0,\quad i=1,2,\ldots,t. $$

(3.11)

Analogously, due to the fact $\rho_{2}^{k}\in[\underline{\rho}_{2},\bar {\rho}_{2}]\subset(0,1)$, from (3.8) one deduces that

$$\begin{aligned}& 2\underline{\rho}_{2}(1-\bar{\rho}_{2}) \frac{\|Gw^{k}\|^{4}}{\| G^{*}Gw^{k}\|^{2}} \\& \quad \leq 2\rho_{2}^{k}\bigl(1-\rho_{2}^{k} \bigr)\frac{\|Gw^{k}\|^{4}}{\|G^{*}Gw^{k}\|^{2}} \\& \quad \leq \bigl\Vert w^{k}-\bar{w}\bigr\Vert ^{2}-\bigl\Vert w^{k+1}-\bar{w}\bigr\Vert ^{2} , \end{aligned}$$

(3.12)

letting $k\rightarrow\infty$ in (3.12), we arrive at

$$\lim_{k\rightarrow\infty}\frac{\|Gw^{k}\|^{4}}{\|G^{*}Gw^{k}\|^{2}}=0. $$

Since $\{w^{k}\}$ is bounded, and by the boundedness of A, B, we know that $G^{*}G$ is also a bounded and linear operator, so there exists a real number $L>0$ such that $\|G^{*}Gw^{k}\|^{2}\leq L$, therefore,

$$ \lim_{k\rightarrow\infty}\bigl\Vert Gw^{k}\bigr\Vert =0. $$

(3.13)

Now, we prove that the weak cluster point set of the sequence $\{w^{k}\}$ lies in Ω, i.e., $\omega_{w}(w^{k})\subset\Omega$. In fact, $\{w^{k}\}$ is bounded, then $\omega_{w}(w^{k})\neq\emptyset$. Let $\{ w^{k_{n}}\}$ be a subsequence of $\{w^{k}\}$ which weakly converges to a point ŵ in $\omega_{w}(w^{k})$. According to Lemma 2.4, we infer from (3.11) that

$$ \hat{w}\in\bigcap_{i=1}^{t}S_{i}. $$

(3.14)

Since $w^{k_{n}}\rightharpoonup\hat{w}$, by the Fréchet-Riesz representation theorem, we have

$$ \|G\hat{w}\|^{2}=\langle G\hat{w},G\hat{w}\rangle=\bigl\langle \hat{w},G^{*}G\hat {w}\bigr\rangle =\lim_{n\rightarrow\infty}\bigl\langle w^{k_{n}},G^{*}G\hat{w}\bigr\rangle =\lim_{n\rightarrow\infty}\bigl\langle Gw^{k_{n}},G\hat{w}\bigr\rangle . $$

By virtue of (3.13), it follows that $\lim_{n\rightarrow\infty}\| Gw^{k_{n}}\|=0$. Hence,

$$\|G\hat{w}\|^{2}=\lim_{n\rightarrow\infty}\bigl\langle Gw^{k_{n}},G\hat{w}\bigr\rangle =0, $$

that is,

$$ G\hat{w}=0. $$

(3.15)

Combining (3.14) with (3.15), we conclude that $\hat{w}\in\Omega$. Due to the fact that $\hat{w},\bar{w}\in\Omega$ are taken arbitrarily in Ω, the conditions of Lemma 2.5 are satisfied, it follows that the iterative sequence $\{w^{k}\}$ weakly converges to a point in Ω. The proof of Theorem 3.1 is completed. □

When $t=1$ in Theorem 3.1, it is the iterative algorithm for solving the SEP (1.1).

Corollary 3.2

Assume that the solution set of SEP (1.1) is nonempty. For any initial point $w^{0}\in H$, the iterative sequence $\{w^{k}\}$ with split self-adaptive step size is obtained by

$$ w^{k+1}=w^{k}+\rho_{1}^{k} \bigl(P_{S}w^{k}-w^{k}\bigr)-\frac{\rho_{2}^{k}\|Gw^{k}\|^{2}}{\|G^{*}Gw^{k}\| ^{2}}G^{*}Gw^{k}, $$

(3.16)

or component-wise

$$ \left \{ \textstyle\begin{array}{l} x^{k+1}=x^{k}+\rho_{1}^{k}(P_{C}x^{k}-x^{k})-\frac{\rho_{2}^{k}\|Ax^{k}-By^{k}\|^{2}}{\| A^{*}(Ax^{k}-By^{k})\|^{2}}A^{*}(Ax^{k}-By^{k}), \\ y^{k+1}=y^{k}+\rho_{1}^{k}(P_{Q}y^{k}-y^{k})+\frac{\rho_{2}^{k}\|Ax^{k}-By^{k}\|^{2}}{\| B^{*}(Ax^{k}-By^{k})\|^{2}}B^{*}(Ax^{k}-By^{k}), \end{array}\displaystyle \right . $$

(3.17)

where $0<\underline{\rho}_{1}\leq\rho_{1}^{k}\leq\bar{\rho}_{1}<1$, $0<\underline {\rho}_{2}\leq\rho_{2}^{k}\leq\bar{\rho}_{2}<1$, the sequence $\{w^{k}\}$ converges weakly to a solution of the SEP (1.1).

4 Numerical experiments

In this section, we provide several numerical results and compare with Byrne’s algorithm (1.2) in [10] to confirm the effectiveness of our proposed algorithm. The whole program was written in Wolfram Mathematica (version 9.0). All the numerical results were carried out on a personal Lenovo Thinkpad computer with Intel(R) Core(TM) i5-4200M CPU 2.50 GHz and RAM 4.00 GB.

The SEP with $A=(a_{ij})_{P\times M}$, $B=(b_{ij})_{P\times N}$, $C=\{x\in R^{M}|\|x\|\leq1\}$, $Q=\{y\in R^{N}|\|y\|\leq2\}$, where $a_{ij}\in [0,1]$, $b_{ij}\in[0,1]$ are all generated randomly, P, M, N are positive integers. We take the initial points $x_{0}=(1,1,\ldots,1)\in R^{M}$, $y_{0}=(0,0,\ldots,0)\in R^{N}$, $\rho_{1}^{k}=\rho_{2}^{k}=0.1$ in Theorem 3.1, $\gamma_{k}=0.01$ in (1.2), and $\|Ax-By\|<\epsilon$ as the termination condition. For P, M, N and error value ϵ, we take two values, respectively. In Tables 1-4, n and t are the iterative steps and CPU time, respectively.

Table 1 $\pmb{\epsilon=10^{-5}}$ , $\pmb{P=5}$ , $\pmb{M=3}$ , $\pmb{N=2}$

Table 2 $\pmb{\epsilon=10^{-10}}$ , $\pmb{P=5}$ , $\pmb{M=3}$ , $\pmb{N=2}$

Table 3 $\pmb{\epsilon=10^{-5}}$ , $\pmb{P=10}$ , $\pmb{M=5}$ , $\pmb{N=5}$

Table 4 $\pmb{\epsilon=10^{-10}}$ , $\pmb{P=10}$ , $\pmb{M=5}$ , $\pmb{N=5}$

From Tables 1-4, we see that, under the same conditions, both the number of iterative steps and the CPU times of our algorithm are less than Byrne’s. So to some extent, the numerical results indicate that our algorithm is better than Byrne’s.

5 Conclusions

We propose a new iterative algorithm with split self-adaptive step size to solve the multiple-sets split equality problem, which ensures that we can leave out much work on the calculation or estimation of the spectral norms of related operators. Under proper conditions, the theoretical convergence of the algorithm proposed is presented. Several numerical results confirm the effectiveness of the algorithm proposed.