Abstract
In this paper, we give an upper bound for the Sugeno fuzzy integral of log-convex functions using the classical Hadamard integral inequality. We present a geometric interpretation and some examples in the framework of the Lebesgue measure to illustrate the results.
Similar content being viewed by others
1 Introduction
Aggregation is a process of combining several numerical values into a single one which exists in many disciplines, such as image processing [1], pattern recognition [2] and decision making [3, 4]. To obtain a consensus quantifiable judgments, some synthesizing functions have been proposed. For example, arithmetic mean, geometric mean and median can be regarded as a basic class, because they are often used and very classic. However, these operators are not able to model an interaction between criteria. For having a representation of interaction phenomena between criteria, fuzzy measures have been proposed [5].
The properties and applications of the fuzzy measures and fuzzy integrals have been studied by many authors. Ralescu and Adams [6] studied several equivalent definitions of fuzzy integrals. Román-Flores et al. [7–11] studied the level-continuity of fuzzy integrals, H-continuity of fuzzy measures and geometric inequalities for fuzzy measures and integrals, respectively. Wang and Klir [12] had a general overview on fuzzy measurement and fuzzy integration theory.
Two main classes of the fuzzy integrals are Choquet and Sugeno integrals. Choquet and Sugeno integrals are idempotent, continuous and monotone operators. Recently, many authors have studied the most well-known integral inequalities for fuzzy integral. Agahi et al. [13–15] proved general Minkowski type inequalities, general extensions of Chebyshev type inequalities and general Barnes-Godunova-Levin type inequalities for fuzzy integrals. Caballero and Sadarangani [16, 17] proved Chebyshev type inequalities and Cauchy type inequalities for fuzzy integrals. Kaluszka et al. [18] gave necessary and sufficient conditions guaranteeing the validity of Chebyshev type inequalities for generalized Sugeno fuzzy integrals in the case of functions belonging to a much wider class than the comonotone functions. Wu et al. [19] proved two inequalities for the Sugeno fuzzy integral on abstract spaces generalizing all previous Chebyshev’s inequalities. Mesiar et al. [20] discussed the integral inequalities known for the Lebesgue integral in the framework of the Choquet integral.
A stronger property of convexity is log-convexity. The arithmetic mean-geometric mean inequality easily yields that every log-convex function is also convex. The behavior of certain interference-coupled multiuser systems can be modeled by means of logarithmically convex (log-convex) interference functions [21]. In this paper, the main purpose is to estimate the upper bound of Sugeno fuzzy integral for log-convex functions using the classical Hadamard integral inequality.
The paper is organized as follows. Some necessary preliminaries and summarization of some previous known results are presented in Section 2. In Section 3, the upper bound of the Sugeno fuzzy integral for log-convex functions is investigated. In Section 4, a geometric interpretation is presented to illustrate the results. Convexity associated to means is discussed in Section 5. Finally, a conclusion is given in Section 6.
2 Preliminaries
In this section, we are going to review some well-known results from the theory of non-additive measures. Let X be a non-empty set and Σ be a σ-algebra of subsets of X.
Definition 2.1
(Ralescu and Adams [6]). Suppose that \(\mu: \Sigma\longrightarrow[0, \infty)\) is a set function. We say that μ is a fuzzy measure if it satisfies
-
1.
\(\mu(\emptyset)= 0\).
-
2.
\(E, F \in\Sigma\) and \(E \subset F\) imply \(\mu(E) \leq\mu(F)\).
-
3.
\(E_{n} \in\Sigma\) (\(n \in\mathbb{N}\)), \(E_{1} \subset E_{2} \subset \cdots\) imply \(\lim_{n \rightarrow\infty} \mu(E_{n})= \mu(\bigcup_{n= 1}^{\infty} E_{n})\) (continuity from below).
-
4.
\(E_{n} \in\Sigma\) (\(n \in\mathbb{N}\)), \(E_{1} \supset E_{2} \supset \cdots\) , \(\mu(E_{1}) < \infty\) imply \(\lim_{n \rightarrow\infty} \mu(E_{n})= \mu(\bigcap_{n= 1}^{\infty} E_{n})\) (continuity from above).
The triple \((X, \Sigma, \mu)\) is called a fuzzy measure space.
Let \((X, \Sigma, \mu)\) be a fuzzy measure space. By \(\mathcal{F}_{+}(X)\) we denote the set
For \(f \in\mathcal{F}_{+}(X)\) and \(\alpha> 0\), \(F_{\alpha}\) and \(F_{\tilde{\alpha}}\) we will denote the following sets:
Note that if \(\alpha\leq\beta\), then \(F_{\beta} \subset F_{\alpha}\) and \(F_{\tilde{\beta}} \subset F_{\tilde{\alpha}}\).
Definition 2.2
(Pap [22], Sugeno [5], Wang and Klir [12]). Let \((X, \Sigma, \mu)\) be a fuzzy measure space, \(f \in\mathcal {F}_{+}(X)\) and \(A \in\Sigma\), then the Sugeno fuzzy integral of f on A with respect to the fuzzy measure μ is defined by
where ∧ is just the prototypical t-norm minimum and ⋁ the prototypical t-conorm maximum. When \(A= X\), then
The following properties of the Sugeno fuzzy integral are well known and can be found in [12, 22].
Theorem 2.3
Let \((X, \Sigma, \mu)\) be a fuzzy measure space, \(A, B \in\Sigma\) and \(f, g \in\mathcal{F}_{+}(X)\) then
-
(1)
\(\fint _{A} f \,\mathrm{d}\mu\leq\mu(A)\).
-
(2)
\(\fint _{A} k\, \mathrm{d}\mu= k \wedge\mu(A)\), k non-negative constant.
-
(3)
If \(f \leq g\) on A. then \(\fint _{A} f \,\mathrm{d}\mu \leq \fint _{A} g\, \mathrm{d}\mu\).
-
(4)
If \(A \subset B\), then \(\fint _{A} f \,\mathrm{d}\mu\leq \fint _{B} f \,\mathrm{d}\mu\).
A t-norm [23] is a function \(T: [0, 1] \times[0, 1] \longrightarrow[0, 1]\) satisfying the following conditions:
- (T1):
-
\(T(x, 1)= T(1, x)= x\) for any \(x \in[0, 1]\).
- (T2):
-
For any \(x_{1}, x_{2}, y_{1}, y_{2} \in[0, 1]\) with \(x_{1} \leq x_{2}\) and \(y_{1} \leq y_{2}\), \(T(x_{1}, y_{1}) \leq T(x_{2}, y_{2})\).
- (T3):
-
\(T(x, y)= T(y, x)\) for any \(x, y \in[0, 1]\).
- (T4):
-
\(T (T(x, y), z )= T (x, T(y ,z) )\) for any \(x, y, z \in[0, 1]\).
A function \(S: [0, 1] \times[0, 1] \longrightarrow[0, 1]\) is called a t-conorm [24] if there is a t-norm T such that \(S(x, y)= 1- T(1- x, 1- y)\).
Example 2.4
The following functions are t-norms:
-
1.
\(T_{M} (x, y)= x \wedge y\),
-
2.
\(T_{P} (x, y)= x \cdot y\),
-
3.
\(T_{L} (x, y)= (x+ y- 1) \vee0\).
Remark 2.5
A binary operator T on \([0, 1]\) is called a t-seminorm [23] if it satisfies the above conditions (T1) and (T2). Notice that if T is a t-seminorm, for any \(x, y \in[0, 1]\), we have \(T(x, y) \leq T(x, 1)= x\) and \(T(x, y) \leq T(1, y)= y\), and consequently, \(T(x, y) \leq T_{M} (x, y)\).
By using the concept of t-seminorm, García and Álvarez [23] proposed the following family of fuzzy integrals.
Definition 2.6
Let T be a t-seminorm. Then the seminormed Sugeno fuzzy integral of a function \(f \in\mathcal{F}_{+}(X)\) over \(A \in\Sigma\) with respect to T and the fuzzy measure μ is defined by
Notice that the Sugeno fuzzy integral of \(f \in\mathcal{F}_{+}(X)\) over \(A \in\Sigma\) is the seminormed Sugeno fuzzy integral of f over \(A \in\Sigma\) with respect to the t-seminorm \(T_{M}\).
Proposition 2.7
(García and Álvarez [23])
Let \((X, \Sigma, \mu)\) be a fuzzy measure space and T be a t-seminorm. Then
-
1.
For any \(A \in\Sigma\) and \(f, g \in\mathcal{F}_{+}(X)\) with \(f \leq g\), we have
$$\int_{T, A} f \,\mathrm{d}\mu\leq\int_{T, A} g \,\mathrm{d}\mu. $$ -
2.
For \(A, B \in\Sigma\) with \(A \subset B\) and any \(f \in\mathcal {F}_{+}(X)\),
$$\int_{T, A} f \,\mathrm{d}\mu\leq\int_{T, B} f \,\mathrm{d}\mu. $$
A stronger property of convexity is log-convexity. A positive function f defined on a real interval \([a, b]\) (or, more generally, on a convex subset of some vector space) is called log-convex if logf is a convex function of x; equivalently, if for all \(x, y \in[a, b]\) and \(\lambda\in[0, 1]\) we have
It will be convenient to invoke the logarithmic mean \(L(x, y)\) of two positive numbers \(x, y\), which is given by
The following Hadamard inequality provides an upper bound for the mean value of a log-convex function \(f: [a, b] \longrightarrow\mathbb{R}\) (see [25]):
3 The main results
Hereafter, we assume that \((X, \Sigma, \mu)\) is a general fuzzy measure space. To simplify the calculation of the fuzzy integral, for a given \(f \in\mathcal{F}_{+}(X)\) and \(A \in\Sigma\), we write
It is easy to see that
The following example shows that the Hadamard inequality (2) is not valid in the fuzzy context.
Example 3.1
Let \(X= [0, 1]\) and μ be the Lebesgue measure on \(\mathbb{R}\). We take the positive and log-convex function \(f(x)= 2^{x^{2} - 3}\). We have
In this expression, \(1- \sqrt{\frac{\ln(\alpha)}{\ln(2)}+ 3}\) may be negative, but it is a decreasing continuous function of α when \(\alpha\geq0\). Hence, the supremum will be attained at the point which is one of the solutions of the equation
that is, at \(\alpha\approx0.196\). So, we have
On the other hand, \(L (f(0), f(1) ) \approx0.180\). This proves that the Hadamard inequality (2) is not satisfied in the fuzzy context.
In the sequel, we will establish an upper bound on the Sugeno fuzzy integral of log-convex functions. Some specific examples will be given to illustrate the results.
Theorem 3.2
Let \(f: [0, 1] \longrightarrow(0, \infty)\) be a log-convex function with \(f(0)\neq f(1)\). Then
where \(\Gamma= [f(0), f(1) )\) for \(f(1) > f(0)\) and \(\Gamma= [f(1), f(0) )\) for \(f(0) > f(1)\).
Proof
Using the log-convexity of f, for \(x \in[0, 1]\), we have
and by (3) of Theorem 2.3, we get
For calculating the integral in the right-hand part of the last inequality, we consider the distribution function G given by
If \(f(1)> f(0)\), then
Thus, \(\Gamma= [f(0), f(1) )\), and we only need to consider \(\alpha\in [f(0), f(1) )\).
If \(f(1)< f(0)\), then
Thus, \(\Gamma= [f(1), f(0) )\) and we only need to consider \(\alpha\in [f(1), f(0) )\).
Taking into account (1) of Theorem 2.3, we get
and the proof is completed. □
Remark 3.3
In the case \(f(0)= f(1)\) in Theorem 3.2, we have \(g(x)= f(0)\), and using (2) and (3) of Theorem 2.3, we get
Corollary 3.4
Let \(f: [0, 1] \longrightarrow(0, \infty)\) be a log-convex function with \(f(0)\neq f(1)\), Σ be the Borel field and μ be the Lebesgue measure on \(X= \mathbb{R}\). Then
Example 3.5
Let μ be the Lebesgue measure on \(\mathbb{R}\). Consider the function \(f(x)= 2^{x^{2} - \frac{1}{2}}\) on \(X= [0, 1]\). This function is, obviously, log-convex and positive on \([0, 1]\). As \(f(0)= \sqrt {2}/2\), \(f(1)= \sqrt{2}\), using Corollary 3.4 we can get the following estimate:
In this expression, \(\log_{2} \frac{\sqrt{2}}{\alpha}\) is a decreasing continuous function of α when \(\alpha\in [\sqrt{2}/2, \sqrt {2} )\). Hence, the supremum will be attained at the point which is one of the solutions of the equation
that is, at \(\alpha\approx0.808\). Consequently, we have
Proposition 3.6
Let \(f: [0, 1] \longrightarrow(0, 1]\) be a log-convex function with \(f(0)\neq f(1)\), Σ be the Borel field and μ be the Lebesgue measure on \(X= \mathbb{R}\). Then
Proof
For a log-convex function \(f: [0, 1] \longrightarrow(0, 1]\) with \(f(0)\neq f(1)\), according to (1) of Proposition 2.7 and Corollary 3.4 with t-norm \(T_{P}\), we have
□
Example 3.7
Let μ be the Lebesgue measure on \(\mathbb{R}\). Consider the function \(f(x)= 2^{x^{2} - 1}\) on \(X= [0, 1]\). This function is, obviously, log-convex and positive on \([0, 1]\). As \(f(0)= 1/2\) and \(f(1)= 1\), using Proposition 3.6, we can get the following estimate:
In the next theorem, we prove the general case of Theorem 3.2.
Theorem 3.8
Suppose that \(f: [a, b] \longrightarrow(0, \infty)\) is a log-convex function with \(f(a)\neq f(b)\). Then
where \(t= \frac{x- a}{b- a}\), \(\Gamma= [f(a), f(b) )\) for \(f(b) > f(a)\) and \(\Gamma= [f(b), f(a) )\) for \(f(a) > f(b)\).
Proof
As f is log-convex, for \(x \in[a, b]\), we have
where \(t= \frac{x- a}{b- a}\). By (3) of Theorem 2.3, we get
A similar argument as in the proof of Theorem 3.2 yields
where \(t= \frac{x- a}{b- a}\), \(\Gamma= [f(a), f(b) )\) for \(f(b) > f(a)\) and \(\Gamma= [f(b), f(a) )\) for \(f(a) > f(b)\). This completes the proof. □
Remark 3.9
In the case \(f(a)= f(b)\) in Theorem 3.8, we have \(g(x)= f(a)\) and using (2) and (3) of Theorem 2.3, we get
Corollary 3.10
Let \(f: [a, b] \longrightarrow(0, \infty)\) be a log-convex function with \(f(a)\neq f(b)\), Σ be the Borel field and μ be the Lebesgue measure on \(X= \mathbb{R}\). Then
Example 3.11
Let μ be the Lebesgue measure on \(\mathbb{R}\). Consider the function \(f(x)= x 2^{x^{2} - 2}\) on \(X= [1, 2]\). This function is, obviously, positive and log-convex on \([1, 2]\). As \(f(1)= 1/2\), \(f(2)= 8\), using Corollary 3.10, we may approximate the upper bound of the Sugeno fuzzy integral of f on \([1, 2]\) by
In this expression, \(\log_{16} \frac{8}{\alpha}\) is a decreasing continuous function of α when \(\alpha\in [1/2, 8 )\). Hence, the supremum will be attained at the point which is one of the solutions of the equation
that is, at \(\alpha\approx0.822\). Therefore,
It should be noted that the exact solution of \(\fint _{1}^{2} x 2^{x^{2} - 2} \,\mathrm{d}\mu\) cannot be easily calculated. But surely the exact solution is less than or equal to 0.822.
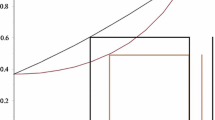
4 Geometric interpretation
Assume that \(X= \mathbb{R}\), Σ is the Borel field, μ is the Lebesgue measure and \(f: A \subseteq\mathbb{R} \longrightarrow(0, \infty)\) is a continuous function. Then the geometric significance of \(\fint _{A} f \,\mathrm{d}\mu\) is the edge’s length of the largest square between the curve of \(f(x)\) and the x-axis.
In Example 3.5, for the real log-convex function \(f(x)= 2^{x^{2} - \frac{1}{2}}\) on \([0, 1]\), there exists the real function
such that
Geometric interpretation of (4) is shown in Figure 1. The lengths of the lines 1 and 2 are the solutions of the integrals in left- and right-hand sides of (4), respectively. We have a similar geometric interpretation for Example 3.11.
Geometric interpretation of Example 3.5 .
5 Convexity associated to means
Let us recall the following means for two positive numbers:
-
The arithmetic mean
$$A= A(a, b):= \frac{a+ b}{2},\quad a, b > 0. $$ -
The geometric mean
$$G= G(a, b):= \sqrt{a b},\quad a, b > 0. $$
The inequality \(G \leq A\) is well known in the literature.
The definition of convexity and log-convexity can be embedded into a more general framework by taking two regular means M and N (on the intervals I and J respectively) and calling a function \(f: I \longrightarrow J\) to be \((M, N)\)-midpoint convex if it satisfies
for every \(x, y \in I\) (see [26–28]). If f is continuous, this yields the \((M, N)\)-convexity of f; that is,
for every \(x, y \in I\) and every \(\lambda\in[0, 1]\). For example, if f is continuous, the inequality (1) can be introduced as \((A, G)\)-convexity.
The following result provides an upper bound on the right-hand side of the inequality (3) (Theorem 3.8) in the case that f is continuous.
Theorem 5.1
Let \(f: [a, b] \longrightarrow(0, \infty)\) be a continuous and log-convex function with \(f(a)\neq f(b)\). Then
where \(t= \frac{x- a}{b- a}\), \(\Gamma= [f(a), f(b) )\) for \(f(b) > f(a)\) and \(\Gamma= [f(b), f(a) )\) for \(f(a) > f(b)\).
Proof
By the geometric mean-arithmetic mean inequality (\(G \leq A\)), we have
where \(t= \frac{x- a}{b- a}\), which yields
Hence, the assertion of this theorem is true in view of Definition 2.2 and Theorem 3.8. □
Corollary 5.2
Let \(f: [a, b] \longrightarrow(0, \infty)\) be a continuous and log-convex function with \(f(a)\neq f(b)\), Σ be the Borel field and μ be the Lebesgue measure on \(X= \mathbb{R}\). Then, for \(f(b)> f(a)\),
If \(f(b)< f(a)\), then
Example 5.3
Consider again the function \(f(x)= x 2^{x^{2} - 2}\) on \(X= [1, 2]\), see Example 3.11. In virtue of Corollary 5.2 and Example 3.11, we have
6 Conclusion
In this paper, we have established an upper bound on the Sugeno fuzzy integral of log-convex functions which is a useful tool to estimate unsolvable integrals of this kind. In many applications, assumptions about the log-convexity of a probability distribution allow just enough special structure to yield a workable theory. The log-concavity or log-convexity of probability densities and their integrals has interesting qualitative implications in many areas of economics, in political science, in biology, and in industrial engineering. As we know, fuzzy measures have been introduced by Sugeno in the early seventies in order to extend probability measures by relaxing the additivity property. Thus the study of the Sugeno fuzzy integral for log-convex functions is an important and interesting topic for further research.
References
Soria-Frisch, A: A new paradigm for fuzzy aggregation in multisensorial image processing. In: Computational Intelligence. Theory and Applications, pp. 59-67. Springer, Berlin (2001)
Soda, P, Iannello, G: Aggregation of classifiers for staining pattern recognition in antinuclear autoantibodies analysis. IEEE Trans. Inf. Technol. Biomed. 13, 322-329 (2009)
Merigó, JM, Casanovas, M: Decision-making with distance measures and induced aggregation operators. Comput. Ind. Eng. 60, 66-76 (2011)
Merigó, JM, Casanovas, M: Induced aggregation operators in the Euclidean distance and its application in financial decision making. Expert Syst. Appl. 38, 7603-7608 (2011)
Sugeno, M: Theory of Fuzzy Integrals and its applications. Ph.D. dissertation, Tokyo Institute of Technology (1974)
Ralescu, D, Adams, G: The fuzzy integral. J. Math. Anal. Appl. 75, 562-570 (1980)
Flores-Franulič, A, Román-Flores, H: A Chebyshev type inequality for fuzzy integrals. Appl. Math. Comput. 190, 1178-1184 (2007)
Román-Flores, H, Chalco-Cano, Y: H-Continuity of fuzzy measures and set defuzzification. Fuzzy Sets Syst. 157, 230-242 (2006)
Román-Flores, H, Chalco-Cano, Y: Sugeno integral and geometric inequalities. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 15, 1-11 (2007)
Román-Flores, H, Flores-Franulič, A, Chalco-Cano, Y: A Jensen type inequality for fuzzy integrals. Inf. Sci. 177, 3192-3201 (2007)
Román-Flores, H, Flores-Franulič, A, Chalco-Cano, Y: The fuzzy integral for monotone functions. Appl. Math. Comput. 185, 492-498 (2007)
Wang, Z, Klir, G: Fuzzy Measure Theory. Plenum Press, New York (1992)
Agahi, H, Mesiar, R, Ouyang, Y: General Minkowski type inequalities for Sugeno integrals. Fuzzy Sets Syst. 161, 708-715 (2010)
Agahi, H, Mesiar, R, Ouyang, Y, Pap, E, Strboja, M: General Chebyshev type inequalities for universal integral. Inf. Sci. 187, 171-178 (2012)
Agahi, H, Román-Flores, H, Flores-Franulič, A: General Barnes-Godunova-Levin type inequalities for Sugeno integral. Inf. Sci. 181, 1072-1079 (2011)
Caballero, J, Sadarangani, K: A Cauchy-Schwarz type inequality for fuzzy integrals. Nonlinear Anal. 73, 3329-3335 (2010)
Caballero, J, Sadarangani, K: Chebyshev inequality for Sugeno integrals. Fuzzy Sets Syst. 161, 1480-1487 (2010)
Kaluszka, M, Okolewski, A, Boczek, M: On Chebyshev type inequalities for generalized Sugeno integrals. Fuzzy Sets Syst. 244, 51-62 (2014)
Wu, L, Sun, J, Ye, X, Zhu, L: Hölder type inequality for Sugeno integral. Fuzzy Sets Syst. 161, 2337-2347 (2010)
Mesiar, R, Li, J, Pap, E: The Choquet integral as Lebesgue integral and related inequalities. Kybernetika 46, 1098-1107 (2010)
Boche, H, Schubert, M: A calculus for log-convex interference functions. IEEE Trans. Inf. Theory 54, 5469-5490 (2008)
Pap, E: Null-Additive Set Functions. Kluwer Academic, Dordrecht (1995)
García, FS, Álvarez, PG: Two families of fuzzy integrals. Fuzzy Sets Syst. 18, 67-81 (1986)
Klement, EP, Mesiar, R, Pap, E: Triangular Norms. Trends in Logic, Studia Logica Library, vol. 8. Kluwer Academic, Dordrecht (2000)
Gill, PM, Pearce, CEM, Pečarić, J: Hadamard’s inequality for r-convex functions. J. Math. Anal. Appl. 215, 461-470 (1997)
Dragomir, SS, Pearce, CEM: Selected Topics on Hermite-Hadamard Inequalities and Applications. RGMIA Monographs, Victoria University (2000). http://rgmia.vu.edu.au/monographs.html
Niculescu, CP: The Hermite-Hadamard inequality for log-convex functions. Nonlinear Anal. 75, 662-669 (2012)
Niculescu, C, Persson, LE: Convex Functions and Their Applications: A Contemporary Approach. Springer, New York (2006)
Acknowledgements
The authors are very grateful to the Spanish Government for its support of this research through Grant DPI2012-30651. The authors are also grateful to the Basque Government through Grant IT 378-10.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors confirm that this work is original and has not been published elsewhere nor is it currently under consideration for publication elsewhere and there are no known conflicts of interest associated with this publication.
Authors’ contributions
The authors confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. The authors further confirm that the order of authors listed in the manuscript has been approved by all of them. All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Abbaszadeh, S., Eshaghi, M. & de la Sen, M. The Sugeno fuzzy integral of log-convex functions. J Inequal Appl 2015, 362 (2015). https://doi.org/10.1186/s13660-015-0862-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-015-0862-6