A nonmonotone hybrid conjugate gradient method for unconstrained optimization

Abstract

A nonmonotone hybrid conjugate gradient method is proposed, in which the technique of the nonmonotone Wolfe line search is used. Under mild assumptions, we prove the global convergence and linear convergence rate of the method. Numerical experiments are reported.

1 Introduction

Let us take the following unconstrained optimization problem:

$$ \min_{x\in{R}^{n}} f(x), $$

(1)

where $f: {R}^{n}\rightarrow {R}$ is continuously differentiable. For solving (1), the conjugate gradient method generates a sequence $\{x_{k}\}$: $x_{k+1}=x_{k}+\alpha_{k}d_{k}$, $d_{0}= -g_{0}$, and $d_{k}=-g_{k}+\beta_{k}d_{k-1}$, where the stepsize $\alpha_{k}>0$ is obtained by the line search, $d_{k}$ is the search direction, $g_{k}=\nabla f{(x_{k})}$ is the gradient of $f(x)$ at the point $x_{k}$, and $\beta_{k}$ is known as the conjugate gradient parameter. Different parameters correspond to different conjugate gradient methods. A remarkable survey of conjugate gradient methods is given by Hager and Zhang [1].

Plenty of hybrid conjugate gradient methods were presented in [2–7] after the first hybrid conjugate algorithm was proposed by Touati-Ahmed and Storey [8]. In [5], Lu et al. proposed a new hybrid conjugate gradient method (LY) with the conjugate gradient parameter $\beta_{k}^{LY}$,

$$\begin{aligned} \beta_{k}^{LY}= \left \{ \begin{array}{@{}l@{\quad}l} \frac{g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}, & \mbox{if }|1-\frac{g_{k}^{T}d_{k-1}}{\|g_{k}\|^{2}}|\leq\mu,\\ \frac{\mu\|g_{k}\|^{2}}{d_{k-1}^{T}g_{k}-\lambda d_{k-1}^{T}g_{k-1}}, & \mbox{otherwise}, \end{array} \right . \end{aligned}$$

(2)

where $0<\mu\leq\frac{\lambda-\sigma}{1-\sigma}$, $\sigma<\lambda\leq1$. Numerical experiments show that the LY method is effective.

It is well known that the nonmonotone algorithms are promising methods for solving highly nonlinear large-scale and possibly ill-conditioned problems. The first nonmonotone line search framework was proposed by Grippo et al. in [9] for Newton’s methods. At each iteration, the current function value is defined as follows:

$$ f_{l(k)}=\max_{0\leq j \leq m(k)}f(x_{k-j}), $$

(3)

where $m(0)=0$, $0\leq m(k)\leq\min{\{m(k-1)+1,M\}}$, M is some positive integer. Zhang and Hager [10] proposed another nonmonotone line search technique, they adopted $C_{k}$ to replace the current function $f_{k}$, where

$$ C_{k}=\frac{\zeta_{k-1} Q_{k-1} C_{k-1}+f_{k}}{Q_{k}}, $$

(4)

$Q_{0}=1$, $C_{0}=f(x_{0})$, $\zeta_{k-1}\in[0,1]$, and

$$ Q_{k}=\zeta_{k-1} Q_{k-1}+1. $$

(5)

To obtain the global convergence (see [4, 11–14]) and implement the algorithms, the line search in the conjugate gradient is usually chosen by a Wolfe line search; the stepsize $\alpha_{k}$ satisfies the following two inequalities:

$$\begin{aligned}& f(x_{k}+\alpha_{k}d_{k})\leq f(x_{k})+ \rho\alpha_{k}g_{k}^{T} d_{k}, \end{aligned}$$

(6)

$$\begin{aligned}& g(x_{k}+\alpha_{k}d_{k})^{T}d_{k} \geq\sigma g_{k}^{T} d_{k}, \end{aligned}$$

(7)

where $0<\rho<\sigma<1$. In particular, a nonmonotone version line search can relax the choice of the stepsize. Therefore the nonmonotone Wolfe line search requires the stepsize $\alpha_{k}$ to satisfy

$$\begin{aligned} f(x_{k}+\alpha_{k}d_{k})\leq f_{l(k)}+ \rho\alpha_{k}g_{k}^{T} d_{k} \end{aligned}$$

(8)

and (7), or

$$\begin{aligned} f(x_{k}+\alpha_{k}d_{k})\leq C_{k}+ \rho \alpha_{k}g_{k}^{T} d_{k} \end{aligned}$$

(9)

and (7).

The aim of this paper is to propose a nonmonotone hybrid conjugate gradient method which combines the nonmonotone line search technique with the LY method. It is based on the idea that the larger values of the stepsize $\alpha_{k}$ may be accepted by the nonmonotone algorithmic framework and improve the behavior of the LY method.

The paper is organized as follows. A new nonmonotone hybrid conjugate gradient algorithm is presented and the global convergence of the algorithm is proved in Section 2. The line convergence rate of the algorithm is shown in Section 3. In Section 4, numerical results are reported.

2 Nonmonotone hybrid conjugate gradient algorithm and global convergence

Now we present a nonmonotone hybrid conjugate gradient algorithm.

Algorithm 1

• Step 1. Given $x_{0}\in R^{n}$, $\epsilon>0$, $d_{0}=-g_{0}$, $C_{0}=f_{0}$, $Q_{0}, \zeta_{0}, k:=0$.

• Step 2. If $\|g_{k}\|<\epsilon$, then stop. Otherwise, compute $\alpha_{k}$ by (9) and (7), set $x_{k+1}=x_{k}+\alpha_{k}d_{k}$.

• Step 3. Compute $\beta_{k+1}$ by (2), set $d_{k+1}=-g_{k+1}+\beta_{k+1}d_{k}$, $k:=k+1$, and go to Step 2.

Assumption 1

We make the following assumptions:

• (i) The level set ${\Omega_{0}}=\{x\in R^{n}:{f{(x)}\leq f{(x_{0})}}\}$ is bounded, where $x_{0}$ is the initial point.

• (ii) The gradient function $g(x)=\nabla f(x)$ of the objective function f is Lipschitz continuous in a neighborhood $\mathcal{N}$ of level set ${\Omega_{0}}$, i.e. there exists a constant $L\geq0$ such that

  $$\bigl\| g{(x)}-g{(\bar{x})}\bigr\| \leq L\|x-\bar{x}\|, $$

  for any ${x,\bar{x}}\in\mathcal{N}$.

Lemma 2.1

Let the sequence $\{x_{k}\}$ be generated by Algorithm 1. Then $d_{k}^{T}g_{k}<0$ holds for all $k\geq1$.

Proof

From Lemma 2 and Lemma 3 in [5], the conclusion holds. □

Lemma 2.2

Let Assumption  1 hold and the sequence $\{x_{k}\}$ be obtained by Algorithm 1, $\alpha_{k}$ satisfies the nonmonotone Wolfe conditions (9) and (7). Then

$$ \alpha_{k}\geq\frac{\sigma-1}{L}\frac{g_{k}^{T}d_{k}}{\|d_{k}\|^{2}}. $$

(10)

Proof

From (7), we have

$$\begin{aligned} (g_{k+1}-g_{k})^{T}d_{k}\geq( \sigma-1)g_{k}^{T}d_{k} \end{aligned}$$

and by (ii) of Assumption 1 it implies that

$$\begin{aligned} (g_{k+1}-g_{k})^{T}d_{k}\leq \alpha_{k} L\|d_{k}\|^{2}. \end{aligned}$$

By combining these two inequalities, we obtain

$$\alpha_{k}\geq\frac{\sigma-1}{L}\frac{g_{k}^{T}d_{k}}{\|d_{k}\|^{2}}. $$

 □

Lemma 2.3

Let the sequence $\{x_{k}\}$ be generated by Algorithm 1 and $d_{k}^{T}g_{k}<0$ hold for all $k\geq1$. Then

$$ f_{k}\leq C_{k}. $$

(11)

Proof

See Lemma 1.1 in [10]. □

Lemma 2.4

Let Assumption  1 hold, and the sequence $\{x_{k}\}$ be obtained by Algorithm 1, where $d_{k}$ satisfies $d_{k}^{T}g_{k}<0$, $\alpha_{k}$ is obtained by the nonmonotone Wolfe conditions (9) and (7). Then

$$ \sum_{k\geq0}\frac{1}{Q_{k+1}} \frac{{(d_{k}^{T}g_{k})}^{2}}{\|d_{k}\|^{2}}< +\infty. $$

(12)

Proof

By (9) and (10), we have

$$ f_{k+1}\leq C_{k}-c_{0} \frac{(d_{k}^{T}g_{k})^{2}}{\|d_{k}\|^{2}}, $$

(13)

where $c_{0}=\rho(1-\sigma)/L$.

From (4), (5), and (13), we have

$$\begin{aligned} C_{k+1} =&\frac{\zeta_{k} Q_{k} C_{k}+f(x_{k+1})}{ Q_{k+1}} \leq\frac{\zeta_{k} Q_{k} C_{k}+C_{k}-c_{0}\frac {{(d_{k}^{T}g_{k})}^{2}}{\|d_{k}\|^{2}}}{ Q_{k+1}} \leq C_{k}-\frac{c_{0}}{Q_{k+1}}\frac{(d_{k}^{T}g_{k})^{2}}{\|d_{k}\|^{2}}. \end{aligned}$$

(14)

Since $f(x)$ is bounded from below in the level set $\Omega_{0}$ and by (11) for all k, we know that $C_{k}$ is bounded from below. It follows from (14) that (12) holds. □

Theorem 2.1

Suppose that Assumptions  1 hold and the sequence $\{x_{k}\}$ is generated by the Algorithm 1. If $\zeta_{\max}<1$, then either $g_{k}=0$ for some k or

$$ \lim_{k\rightarrow\infty}\inf\|g_{k}\|=0. $$

(15)

Proof

We prove by contradiction and assume that there exists a constant $\epsilon>0$ such that

$$ \|g_{k}\|^{2}\geq\epsilon, \quad k=0,1,2,3, \ldots. $$

(16)

By Lemma 4 in [5], we have $|\beta_{k}|^{LY}\leq\frac{\mu\|g_{k}\| ^{2}}{d_{k-1}^{T}g_{k}-\lambda d_{k-1}^{T}g_{k-1}}$. Then we have ${\|d_{k}\|}^{2}=(\beta^{LY})^{2} \|d_{k-1}\|^{2}-2g_{k}^{T}d_{k}-\|g_{k}\|^{2} \leq(\frac{\mu\|g_{k}\|^{2}}{d_{k-1}^{T}g_{k}-\lambda d_{k-1}^{T}g_{k-1}})^{2}\|d_{k-1}\|^{2}-2g_{k}^{T}d_{k}-\|g_{k}\|^{2}$. The rest of the proof is similar to Theorem 2 and Theorem 1 in [5], and we also conclude

$$\frac{(g_{k}^{T}d_{k})^{2}}{\|d_{k}\|^{2}}\geq\frac{\epsilon}{k}. $$

Furthermore, by $\zeta_{\max}<1$ and (5), we have

$$ Q_{k}=1+\sum_{j=0}^{k-1} \prod_{i=0}^{j}\zeta_{k-1-i}\leq \frac{1}{1-\zeta_{\max}}, $$

(17)

then

$$\frac{1}{Q_{k+1}}\frac{(g_{k}^{T}d_{k})^{2}}{\|d_{k}\|^{2}}\geq(1-\zeta_{\max }) \frac{\epsilon}{k}, $$

which indicates

$$\sum_{i=1}^{\infty}\frac{1}{Q_{k+1}} \frac {{(g_{k}^{T}d_{k})}^{2}}{\|d_{k}\|^{2}}=+\infty. $$

This contradicts (12). Therefore (15) holds. □

3 Linear convergence rate of algorithm

We analyze the linearly convergence rate of the nonmonotone hybrid conjugate gradient method under the uniform convex assumption of $f(x)$. The nonmonotone strong Wolfe line search is adopted in this section, given by (9) and

$$\begin{aligned} \bigl|g(x_{k}+\alpha_{k}d_{k})^{T}d_{k} \bigr|\leq-\sigma g_{k}^{T} d_{k}. \end{aligned}$$

(18)

We suppose that the object function $f(x)$ is twice continuously differentiable and uniformly convex on the level set $\Omega_{0}$. Then the point $x^{*}$ denotes a unique solution of the problem (1); there exists a positive constant τ such that

$$ f(x)-f \bigl(x^{*} \bigr)\leq\bigl\| \nabla f(x)\bigr\| \bigl\| x-x^{*}\bigr\| \leq\tau\bigl\| \nabla f(x)\bigr\| ^{2}, \quad\mbox{for all } x \in R^{n}. $$

(19)

The above conclusion (19) can be found in [10].

To analyze the convergence of the nonmonotone line search hybrid conjugate gradient method, the main difficulty is that the search directions do not usually satisfy the direction condition:

$$ g_{k}^{T}d_{k}\leq-c \|g_{k}\|^{2}, $$

(20)

for some constant $c>0$ and all $k\geq1$. The following lemma has proven that the direction generated by Algorithm 1 with the strong Wolfe line search (9) and (18) in this paper satisfies the direction condition (20) by the observation for $g_{k}^{T}d_{k-1}$.

Lemma 3.1

Suppose that the sequence $\{x_{k}\}$ is generated by Algorithm 1 with the strong Wolfe line search (9) and (18), $0<\sigma <\frac{\lambda}{1+\mu}$. Then there exists some constant $c>0$ such that the direction condition (20) holds.

Proof

According to the choice of the conjugate gradient parameter $\beta _{k}^{LY}$, the result is discussed by two cases. In the first case,

$$ \biggl|1-\frac{g_{k}^{T}d_{k-1}}{\|g_{k}\|^{2}}\biggr|\leq\mu, \quad \textit{i.e. } 1-\mu\leq \frac{g_{k}^{T}d_{k-1}}{\|g_{k}\|^{2}}\leq1+\mu, $$

(21)

then $\beta_{k}=\frac{g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}$. If $\beta_{k}\geq0$, then, by (21) and $d_{k-1}^{T}g_{k-1}<0$, $d_{k-1}^{T}g_{k}\geq0$ and $g_{k}^{T}(g_{k}-d_{k-1})\geq0$. Furthermore, we have, by (18),

$$\begin{aligned} g_{k}^{T}d_{k}&=-\|g_{k} \|^{2}+\frac {g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}g_{k}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}-\sigma\frac {g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}g_{k-1}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}-\sigma\frac {g_{k}^{T}(g_{k}-d_{k-1})}{-d_{k-1}^{T}g_{k-1}}g_{k-1}^{T}d_{k-1} \\ &= -\|g_{k}\|^{2}+\sigma \bigl(\|g_{k} \|^{2}-g_{k}^{T}d_{k-1} \bigr) \\ &=-(1-\sigma)\|g_{k}\|^{2}-\sigma g_{k}^{T}d_{k-1} \\ &\leq-(1-\sigma)\|g_{k}\|^{2}-\sigma(1-\mu) \|g_{k}\|^{2} \\ &=-(1-\sigma\mu)\|g_{k}\|^{2}. \end{aligned}$$

(22)

If $\beta_{k}<0$, we have, by (18) and (21),

$$\begin{aligned} g_{k}^{T}d_{k}&=-\|g_{k} \|^{2}+\frac {g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}g_{k}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}+\sigma\frac {g_{k}^{T}(g_{k}-d_{k-1})}{d_{k-1}^{T}(g_{k}-g_{k-1})}g_{k-1}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}+\sigma\frac {g_{k}^{T}(g_{k}-d_{k-1})}{-d_{k-1}^{T}g_{k-1}}g_{k-1}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}-\sigma \bigl(\|g_{k} \|^{2}-g_{k}^{T}d_{k-1} \bigr) \\ &=-(1+\sigma)\|g_{k}\|^{2}+\sigma g_{k}^{T}d_{k-1} \\ &=-(1+\sigma)\|g_{k}\|^{2}+\sigma(1+\mu) \|g_{k} \|^{2} \\ &=-(1-\sigma\mu)\|g_{k}\|^{2}. \end{aligned}$$

(23)

In the second case,

$$ \biggl|1-\frac{g_{k}^{T}d_{k-1}}{\|g_{k}\|^{2}}\biggr|>\mu, $$

(24)

then $\beta_{k}=\frac{\mu\|g_{k}\|^{2}}{d_{k-1}^{T}g_{k}-\lambda d_{k-1}^{T}g_{k-1}}>0$. By (18), we have

$$\begin{aligned} g_{k}^{T}d_{k}&=-\|g_{k} \|^{2}+{\frac{\mu\|g_{k}\|^{2}}{{d^{T}_{k-1}}g_{k}-\lambda d^{T}_{k-1}g_{k-1}}} g_{k}^{T}d_{k-1} \\ &\leq-\|g_{k}\|^{2}-{\frac{\sigma\mu\|g_{k}\|^{2}}{(\sigma-\lambda) d^{T}_{k-1}g_{k-1}}} g_{k-1}^{T}d_{k-1} \\ &=- \biggl(1-\frac{\mu\sigma}{\lambda-\sigma} \biggr)\|g_{k}\|^{2}. \end{aligned}$$

(25)

From (23) and (25), we obtain (20), where $c=\min\{1-\sigma\mu, 1-\frac{\mu\sigma}{\lambda-\sigma}\}>0$. The proof is completed. □

Lemma 3.2

Suppose the assumptions of Lemma  2.2 hold and, for all k,

$$ \|d_{k}\|\leq c_{1}\|g_{k}\|, $$

(26)

then there exists a constant $c_{2}>0$ such that

$$ \alpha_{k}\geq c_{2}, \quad\textit{for all } k. $$

(27)

Proof

By Lemma 2.2 and Lemma 3.2, we have

$$\alpha_{k}\geq\frac{\sigma-1}{L}\frac{g_{k}^{T}d_{k}}{\|d_{k}\|^{2}}\geq- \frac {\sigma-1}{L}\frac{c\|g_{k}\|^{2}}{c_{1}\|g_{k}\|^{2}}\geq c_{2}, $$

where $c_{2}=\frac{c(1-\sigma)}{c_{1}L}$. □

Theorem 3.1

Let $x^{*}$ be the unique solution of problem (1) and the sequence $\{ x_{k}\}$ be generated by Algorithm 1 with the nonmonotone Wolfe conditions (9) and (18), $0<\sigma<\frac{\lambda}{1+\mu }$. If $\alpha_{k}\leq\nu$ and $\zeta_{\max}<1$, then there exists a constant $\vartheta\in(0,1)$ such that

$$ f_{k}-f \bigl(x^{*} \bigr)\leq\vartheta^{k} \bigl(f_{0}-f \bigl(x^{*} \bigr) \bigr). $$

(28)

Proof

The proof is similar to that Theorem 3.1 given in [10]. By (9), (20), and (27), we have

$$\begin{aligned} f_{k+1}&\leq C_{k}+\rho\alpha_{k}g_{k}^{T}d_{k} \leq C_{k}-cc_{2}\rho\|g_{k}\|^{2}. \end{aligned}$$

(29)

By (ii) in Assumption 1, $x_{k+1}=x_{k}+\alpha_{k}d_{k}$ and (27), we have

$$ \|g_{k+1}\|\leq\|g_{k+1}-g_{k}\|+ \|g_{k}\|\leq\alpha_{k}L\|d_{k}\|+\|g_{k} \|\leq (1+c_{1}\nu L)\|g_{k}\|. $$

(30)

In the first case, $\|g_{k}\|^{2}\geq\beta(C_{k}-f(x^{*}))$, where

$$ \beta=1/ \bigl(cc_{2}\rho+\tau(1+c_{1}\nu L)^{2} \bigr). $$

(31)

By (4) and (29), we have

$$\begin{aligned} C_{k+1}-f \bigl(x^{*} \bigr)&=\frac{\zeta_{k}Q_{k}(C_{k}-f(x^{*}))+(f_{k+1}-f(x^{*}))}{1+\zeta _{k} Q_{k}} \\ &\leq\frac{\zeta_{k}Q_{k}(C_{k}-f(x^{*}))+(C_{k}-f(x^{*}))-cc_{2}\rho\|g_{k}\| ^{2}}{1+\zeta_{k} Q_{k}} \\ &=C_{k}-f \bigl(x^{*} \bigr)-\frac{cc_{2}\rho\|g_{k}\|^{2}}{Q_{k+1}}. \end{aligned}$$

(32)

Since $Q_{k+1}\leq\frac{1}{1-\zeta_{\max}}$ by (17), we have

$$C_{k+1}-f \bigl(x^{*} \bigr)\leq C_{k}-f \bigl(x^{*} \bigr)-cc_{2}\rho(1-\zeta_{\max})\|g_{k} \|^{2}. $$

By $\|g_{k}\|^{2}\geq\beta(C_{k}-f(x^{*}))$, we have

$$ C_{k+1}-f \bigl(x^{*} \bigr)\leq\vartheta \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr), $$

(33)

where $\vartheta=1-cc_{2}\rho\beta(1-\zeta_{\max})\in(0, 1)$.

In the second case, $\|g_{k}\|^{2}< \beta(C_{k}-f(x^{*}))$. By (19) and (30), we have

$$f_{k+1}-f \bigl(x^{*} \bigr)\leq\tau(1+c_{1}\nu L)^{2} \|g_{k}\|^{2}\leq\tau\beta(1+c_{1} \nu L)^{2} \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr). $$

By combining the equality, the first equation of (32), and $Q_{k+1}\leq\frac{1}{1-\zeta_{\max}}$, $\zeta_{\max}<1$ and (31), we obtain

$$\begin{aligned} C_{k+1}-f \bigl(x^{*} \bigr)&\leq\frac{\zeta_{k}Q_{k}(C_{k}-f(x^{*}))+\tau\beta(1+c_{1}\nu L)^{2}(C_{k}-f(x^{*}))}{1+\zeta_{k} Q_{k}} \\ &= \biggl(1-\frac{1-\tau\beta(1+c_{1}\nu L)^{2}}{Q_{k+1}} \biggr) \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr) \\ &= \bigl(1-{ \bigl(1-\tau\beta(1+c_{1}\nu L)^{2} \bigr)} {(1- \zeta_{\max})} \bigr) \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr) \\ &= \bigl(1-cc_{2}\rho\beta(1-\zeta_{\max}) \bigr) \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr) \\ &\leq\vartheta \bigl(C_{k}-f \bigl(x^{*} \bigr) \bigr). \end{aligned}$$

(34)

By (11), (33), and (34), we have

$$f_{k}-f \bigl(x^{*} \bigr)\leq C_{k}-f \bigl(x^{*} \bigr)\leq \vartheta \bigl(C_{k-1}-f \bigl(x^{*} \bigr) \bigr)\leq\cdots\leq \vartheta^{k} \bigl(C_{0}-f \bigl(x^{*} \bigr) \bigr). $$

The proof is completed. □

4 Numerical experiments

In this section, we report numerical results to illustrate the performance of hybrid conjugate gradient (LY) in [5], Algorithm 1 (NHLYCG1) and Algorithm 2 (NGLYCG2), in which (8) replaces only (9) in Step 2 of Algorithm 1. All codes are written with Matlab R2012a and are implemented on a PC with CPU 2.40 GHz and 2.00GB RAM. We select 12 small-scale and 28 large-scale unconstrained optimization test functions from [15] and the CUTEr collection [16, 17] (see Table 1). All algorithms implement the stronger version of the Wolfe condition with $\rho=0.45$ and $\sigma=0.39$, and $\mu=0.5$, $\lambda=0.6$, $C_{0}=f_{0}$, $Q_{0}=1$, $\zeta _{0}=0.08$, $\zeta_{1}=0.04$, $\zeta_{k+1}=\frac{\zeta_{k}+\zeta_{k-1}}{2}$, and the terminated condition

$$\|g_{k}\|_{2}\leq10^{-6} \quad\mbox{or}\quad |f_{k+1}-f_{k}|\leq10^{-6}\max\bigl\{ 1.0,|f_{k}|\bigr\} . $$

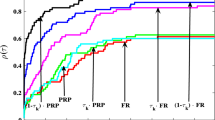
Table 2 lists all the numerical results, which include the order numbers and dimensions of the tested problems, the number of iterations (it), the function evaluations (nf), the gradient evaluations (ng), and the CPU time (t) in seconds, respectively. We presented the Dolan and Moré [18] performance profiles for the LY, NHLYCG1, and NGLYCG2. Note that the performance ratio $q(\tau)$ is the probability for a solver s for the tested problems with the factor τ of the smallest cost. As we can see from Figure 1 and Figure 2, NHLYCG1 is superior to LY and NGLYCG2 for the number of iterations and CPU time. Figure 3 shows that NGLYCG1 is slightly better than LY and NGLYCG2 for the number of function value evaluations. Figure 4 shows the performance of NGLYCG1 is very much like that of LY for the number of gradient evaluations. However, the performance of NGLYCG2 with the nonmonotone framework (3) is less than satisfactory.

Figure 1

Performance profile comparing the number of iterations.

Figure 2

Performance profile comparing the CPU time.

Figure 3

Performance profile comparing the number of function evaluations.

Figure 4

Performance profile comparing the number of gradient evaluations.

Table 1 Test problems

Table 2 Numerical comparisons of LY, NMLY1, and NMLY2