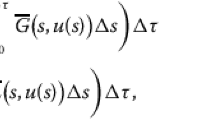Abstract
The objective of this paper is to study some dynamic integral inequalities on time scales, which provide explicit bounds on unknown functions. Our results include many known ones in the literature and can be used as tools in the study of qualitative theory of certain classes of dynamic equations with mixed nonlinearities on time scales.
Similar content being viewed by others
1 Introduction
The theory of time scales was introduced and developed by Hilger [1] and Bohner and Peterson [2, 3] in order to unify continuous and discrete analysis. It has been applied to various fields of mathematics. In particular, many authors have extended some integral inequalities used in the theory of differential, difference, and integral equations to an arbitrary time scale; see, for instance, the papers [4–16] and the references cited therein.
In what follows, let us briefly comment on a number of closely related results which motivated our study. Li and Sheng [8] established several integral inequalities and studied the boundedness properties of some nonlinear dynamic equations, one of which we present below for convenience of the reader. In what follows, we use the following notation (some other concepts related to the notion of time scales; see Bohner and Peterson [2]):
ℝ denotes the set of real numbers, \(\mathbb{R}_{+}=[0,\infty)\), \(\mathbb{T}\) is an arbitrary time scale, and the set \(\mathbb{T}^{k}\) is derived from \(\mathbb{T}\) as follows: if \(\mathbb{T}\) has a left-scattered maximum \(m_{0}\), then \(\mathbb{T}^{k}=\mathbb{T}-\{m_{0}\}\), otherwise \(\mathbb{T}^{k}=\mathbb{T}\).
Theorem 1.1
[8, Theorem 3.2]
Assume that \(u,a,b,f,g:\mathbb{T}^{k}\rightarrow\mathbb{R}_{+}\) are rd-continuous functions and let p and q be real constants satisfying \(p\geq q>0\). Then the inequality
implies that, for any \(K>0\),
where \(t\in\mathbb{T}^{k}\) and \(A(t)=b(t)(f(t)+qK^{(q-p)/p}g(t)/p)\).
Sun and Hassan [15] studied the following dynamic integral inequality with mixed nonlinearities.
Theorem 1.2
[15, Theorem 1]
Assume that \(u,a,b,g,h_{1},h_{2}:\mathbb{T}^{k}\rightarrow \mathbb{R}_{+}\) are rd-continuous functions and let \(\lambda_{1}\) and \(\lambda_{2}\) be real constants satisfying \(0<\lambda_{1}<1<\lambda_{2}\). Then, for any rd-continuous functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) on \(\mathbb{T}^{k}\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) and \(\mu(t)k(t)b(\sigma(t))<1\) for \(t\in\mathbb{T}^{k}\), the inequality
implies that
where
and
The aim of this paper is to further generalize some integral inequalities on time scales that have been reported in [7, 8, 15]. We consider the following dynamic integral inequalities with mixed nonlinearities
and
where \(p\geq q>0\), \(p\geq r>0\), \(0<\lambda_{1}<p<\lambda_{2}\), p, q, r, \(\lambda_{1}\), and \(\lambda_{2}\) are real constants, \(u,a,b,f,g,h_{1},h_{2},l,m:\mathbb{T}^{k}\rightarrow\mathbb{R}_{+}\) are rd-continuous functions, and \(w:\mathbb{T}\times \mathbb{T}^{k}\rightarrow\mathbb{R}\) is a continuous function.
2 Main results
In what follows, ℤ denotes the set of integers, \(\mathbb{N}_{0}\) denotes the set of nonnegative integers, \(\mathrm{C}_{\mathrm{rd}}\) denotes the set of rd-continuous functions. We say that a function \(p: \mathbb{T}\rightarrow\mathbb{R}\) is regressive provided \(1+\mu(t)p(t)\neq0\), for all \(t\in\mathbb{T}^{k}\). The set of all regressive and rd-continuous functions will be denoted in this paper by ℛ, and \(\mathcal{R}^{+}=\{p\in \mathcal{R}:1+\mu(t)p(t)>0, \mbox{for all } t\in\mathbb{T}\}\).
The following lemmas are very useful in the proof of our main results.
Lemma 2.1
[2, Theorem 6.1]
Let \(u, b\in\mathrm{C}_{\mathrm{rd}} \) and \(a\in\mathcal{R}^{+}\). Then
yields
Lemma 2.2
[2, Theorem 1.117]
Let \(t_{0}\in\mathbb {T}^{k}\) and \(w:\mathbb{T}\times\mathbb{T}^{k}\rightarrow\mathbb{R}\) be continuous at \((t,t)\), \(t\in\mathbb{T}^{k}\) with \(t>t_{0}\). Assume that \(w^{\Delta}(t,\cdot)\) is rd-continuous on \([t_{0},\sigma(t)]\). Suppose that, for each \(\varepsilon>0\), there exists a neighborhood \({\mathcal{U}}\) of t, independent of \(\tau\in[t_{0},\sigma(t)]\), such that
where \(w^{\Delta}\) denotes the derivative of w with respect to the first variable. Then
implies that
Lemma 2.3
[5, Lemma 2.1]
Assume that \(a\geq0\) and \(p\geq q>0\). Then
for any \(K>0\).
Lemma 2.4
Let u be a nonnegative function, \(0<\lambda_{1}<p<\lambda_{2}, c_{1}\geq0, c_{2}> 0\), \(k_{1}>0\), and \(k_{2}\geq0\). Then, for \(i=1,2\),
where
Proof
Set \(F_{i}(u)=(-1)^{i+1}c_{i}u^{\lambda _{i}}+(-1)^{i}k_{i}u^{p}\). It is not difficult to verify that \(F_{i}\) obtains its maximum at \(u=({\lambda_{i}c_{i}}/{(k_{i}p}))^{{1}/{(p-\lambda_{i})}}\) and
The proof is complete. □
Theorem 2.1
Assume that \(u,a,b,f,g,h_{1},h_{2},l,m:\mathbb{T}^{k}\rightarrow\mathbb{R}_{+}\) are rd-continuous functions. Then, for any rd-continuous functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) on \(\mathbb{T}^{k}\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) and \(\mu(t)k(t)b(\sigma(t))<1\) for \(t\in\mathbb{T}^{k}\), the inequality (I) implies that
where
and
Proof
Define a function y by
Then \(y(t_{0})=0\) and
On the basis of a straightforward computation and Lemma 2.4, we have
By virtue of Lemma 2.3, for any \(K > 0\), we obtain
Using inequalities (2.2)-(2.4), we conclude that
which implies that
that is,
where \(D(t)=[1+\mu(t)B(t)]C(t)\). Note that \(y,D\in\mathrm{C}_{\mathrm{rd}}\) and \(A\oplus B\in\Re^{+}\). By Lemma 2.1, we get the desired inequality (2.1). This completes the proof. □
Remark 2.1
If \(p=1\) and \(g(t)=m(t)=l(t)=0\), then (2.1) reduces to the inequality established in Theorem 1.2.
Remark 2.2
If \(m(t)=0\), \(l(t)=0\), and \(h_{i}(t)=0\) (\(i=1,2\)), then Theorem 2.1 reduces to Theorem 1.1.
Remark 2.3
Theorem 2.1 can be applied on an arbitrary time scale. Thus, we immediately obtain the following corollaries for some peculiar time scales.
Corollary 2.1
Let \(\mathbb{T}=\mathbb{R}\) and assume that \(u,a,b,f,g,h_{1},h_{2},l,m:[t_{0},\infty)\rightarrow\mathbb{R}_{+}\) are continuous. Then, for any continuous functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) on \([t_{0},\infty)\), the inequality (I) yields
where
and
Corollary 2.2
Let \(\mathbb{T}=\mathbb{Z}\) and \(u,a,b,f,g,h_{1},h_{2},l,m:\mathbb{N}_{0}\rightarrow \mathbb{R}_{+}\). Then, for any functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) and \(k(t)b(t+1)<1\) on \(\mathbb{N}_{0}\), the inequality (I) implies that
where
and
Theorem 2.2
Assume that \(u,a,b,f,g,h_{1},h_{2},l,m:\mathbb{T}^{k}\rightarrow\mathbb{R}_{+}\) are rd-continuous functions, \(w(t,s)\) is defined as in Lemma 2.2 such that \(w(\sigma(t),t)\geq0\) and \(w^{\Delta}(t,s)\geq0\) for \(t,s\in\mathbb{T}\) with \(s\leq t\). Then, for any rd-continuous functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) on \(\mathbb{T}^{k}\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) and \(\mu(t)\hat{B}(t)<1\) for \(t\in\mathbb{T}^{k}\) with
the inequality (II) implies that
where
A and C are defined as in Theorem 2.1.
Proof
Define a new function z by
Then \(z(t_{0})=0\) and
Using Lemmas 2.2-2.4 and combining (2.6) and (2.7), we deduce that
Similar to the proof of Theorem 2.1, we obtain (2.5). The proof is complete. □
Remark 2.4
The inequality established in Theorem 2.2 generalizes that reported in [7, Theorem 3.2].
On the basis of Theorem 2.2, the following two corollaries are easily obtained.
Corollary 2.3
Let \(\mathbb{T}=\mathbb{R}\) and assume that \(u,a,b,f,g,h_{1},h_{2},l,m:[t_{0},\infty)\rightarrow\mathbb{R}_{+}\) are continuous. Suppose further that \(w(t,s)\) and its partial derivative \(\partial w(t,s)/\partial t\) are real-valued nonnegative continuous functions for \(t,s\in[t_{0},\infty)\) with \(s\leq t\). Then, for any continuous functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) on \([t_{0},\infty)\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\), the inequality (II) implies that
where
\(A_{1}\) and \(C_{1}\) are the same as in Corollary 2.1.
Corollary 2.4
Let \(\mathbb{T}=\mathbb{Z}\) and \(u,a,b,f,g,h_{1},h_{2},l,m:\mathbb{N}_{0}\rightarrow \mathbb{R}_{+}\). Assume that \(w(t,s)\) and \(\Delta_{1}w(t,s)\) are real-valued nonnegative functions for \(t,s \in\mathbb{N}_{0}\) with \(s\leq t\). Then, for any functions \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) satisfying \(k(t)=k_{1}(t)-k_{2}(t)\geq0\) and \(\hat{B}_{2}(t)<1\) on \(\mathbb{N}_{0}\) with
the inequality (II) yields
where \(\Delta_{1}w(t,s)=w(t+1,s)-w(t,s)\) for \(t,s\in\mathbb{N}_{0}\) with \(s\leq t\),
\(A_{2}\) and \(C_{2}\) are defined as in Corollary 2.2.
Remark 2.5
By choosing possible values of \(k_{1}\) and \(k_{2}\), one can derive many explicit estimates for dynamic integral inequalities of types (I) and (II). For instance, if we let \(k_{1}=k_{2}>0\), then \(B(t)=\tilde{B}(t)=0\). In this case, Theorems 2.1 and 2.2 take simpler forms.
3 Example
The following example illustrates possible applications of our main results.
Example 3.1
Consider the following dynamic equation
where \(C_{0}\) is a real constant, \(F, U:\mathbb{T}^{k}\times \mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}\), \(H:\mathbb{T}^{k}\times\mathbb{R}\rightarrow\mathbb{R}\) are continuous functions. Assume that, for \(t\in\mathbb{T}^{k}\),
where \(p\geq q>0\), \(p\geq r>0\), \(0<\lambda_{1}<p<\lambda_{2}\), p, q, r, \(\lambda_{1}\), and \(\lambda_{2}\) are real constants, f, g, \(h_{1}\), \(h_{2}\), and m are nonnegative rd-continuous functions on \(\mathbb{T}^{k}\). Then every solution u of (3.1) satisfies, for any \(K>0\),
where
and
where \(k_{1}(t)>0\) and \(k_{2}(t)\geq0\) are any rd-continuous functions satisfying \(k(t)=k_{1}(t)-k_{2}(t)=0\) for \(t\in \mathbb{T}^{k}\).
As a matter of fact, the solution u of (3.1) satisfies the following equivalent equation
It follows now from (3.2) and (3.4) that
Using Theorem 2.1 in (3.5), we conclude that (3.3) is satisfied.
References
Hilger, S: Analysis on measure chains - a unified approach to continuous and discrete calculus. Results Math. 18, 18-56 (1990)
Bohner, M, Peterson, A: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston (2001)
Bohner, M, Peterson, A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston (2003)
Gu, J, Meng, FW: Some new nonlinear Volterra-Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 245, 235-242 (2014)
Jiang, FC, Meng, FW: Explicit bounds on some new nonlinear integral inequalities with delay. J. Comput. Appl. Math. 205, 479-486 (2007)
Li, LZ, Han, MA: Some new dynamic Opial type inequalities and applications for second order integro-differential dynamic equations on time scales. Appl. Math. Comput. 232, 542-547 (2014)
Li, WN: Some new dynamic inequalities on time scales. J. Math. Anal. Appl. 319, 802-814 (2006)
Li, WN, Sheng, WH: Some nonlinear integral inequalities on time scales. J. Inequal. Appl. (2007). doi:10.1155/2007/70465
Li, WN, Sheng, WH: Some nonlinear dynamic inequalities on time scales. Proc. Indian Acad. Sci. Math. Sci. 117, 545-554 (2007)
Ma, Q-H, Pečarić, J: The bounds on the solutions of certain two-dimensional delay dynamic systems on time scales. Comput. Math. Appl. 61, 2158-2163 (2011)
Peng, Y, Kang, Y, Yuan, M, Huang, R, Yang, L: Gronwall-type integral inequalities with impulses on time scales. Adv. Differ. Equ. 2011, 26 (2011)
Saker, SH: Applications of Opial inequalities on time scales on dynamic equations with damping terms. Math. Comput. Model. 58, 1777-1790 (2013)
Sarikaya, MZ: On weighted Iyengar type inequalities on time scales. Appl. Math. Lett. 22, 1340-1344 (2009)
Sun, YG: Some new integral inequalities on time scales. Math. Inequal. Appl. 15, 331-341 (2012)
Sun, YG, Hassan, TS: Some nonlinear dynamic integral inequalities on time scales. Appl. Math. Comput. 220, 221-225 (2013)
Yeh, C-C: Ostrowski’s inequality on time scales. Appl. Math. Lett. 21, 404-409 (2008)
Acknowledgements
This research was supported by the NNSF of China (Grant Nos. 11171178 and 11271225) and the NSF of Shandong Province (ZR2012AL03).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All four authors contributed equally to this work. They all read and approved the final version of the manuscript.
Rights and permissions
Open Access This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly credited.
About this article
Cite this article
Tian, Y., Cai, Y., Li, L. et al. Some dynamic integral inequalities with mixed nonlinearities on time scales. J Inequal Appl 2015, 12 (2015). https://doi.org/10.1186/s13660-014-0537-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-014-0537-8