1 Introduction

Recently, reconfigurable intelligent surface (RIS) is a potential technique to create dynamic and adaptable wireless radio propagation [1,2,3,4,5]. The low-cost RIS structure comprises multiple passive elements, which are smaller in size than the wavelength of the signal. RIS can be set up at critical sites such as building exteriors and highway poles, advertising displays, and car windows [6,7,8,9]. Every passive element of RIS can dynamically modify channels, either constructively or destructively, by changing the amplitude and phase shift of the radiated signal. So, RIS makes the wireless environment intelligent. In other words, by properly designing optimal RIS coefficients, signal beams can be configured to achieve diverse goals, including increasing the throughput of specific terminals, eliminating interference from other devices, or mitigating information leakage to potential eavesdroppers [10,11,12,13]. Considering the mentioned features of RIS result overcoming signal attenuation, more energy efficiency, improving spectral efficiency and data rates, and flexibility in network design, which is particularly valuable in dynamic environments with changing user requirements and network conditions.

A recently introduced type of RIS, the simultaneous transmission and reflection RIS (Star-RIS), has been announced. It can make full spatial coverage by simultaneously reflecting signals in front of the Star-RIS and transmitting behind it. In other words, the incoming signal is divided into two components referred to as the transmitted and reflected signals. So, Star-RIS can overcome the conventional RIS limitation, which achieves only half-space coverage because of the reflecting signal. Also, simultaneous control of transmitted and reflected signals enables more degrees-of-freedom than conventional RIS [14,15,16,17,18,19].

However, the security of wireless networks is a significant aspect. RIS can enhance the secrecy performance by dynamically adjusting wireless channels due to emitting waves constructively or destructively in proportion to system goals such as reducing leakage of information to eavesdroppers and enhancing the security rate [20,21,22,23,24]. The authors in [25] studied Star-RIS and UAV assisted secure communication in which optimized transmission beamforming vector consists of information and artificial noise components, RIS phase shift, and UAV trajectory to maximize the total secrecy rate. Existing work in [26] studied a secure communication system based on Star-RIS and AN. [27] investigated a Star-RIS-aided NOMA secure communication to guarantee full space secure transmission based on ES, MS, and TS. The authors in [28] investigated beamforming for Star-RIS-aided uplink NOMA secrecy communication by considering imperfect CSI for eavesdroppers and show performance improvement with the aide of Star-RIS compared to conventional RIS. The existing work in [29] studied secure communication assisted by Star-RIS-aided SWIPT and RSMA techniques. Also, a secure NOMA communication aided by Star-RIS, is studied in [30,31,32,33].

In practical scenarios, physical transceivers experience inherent hardware impairments, which cause distortions in both transmitted and received signals, with the ratio proportional to the transmitted and received signal power, unlike receiver noise, which is only added to the received signal and is independent of the signal. [34, 35]. Based on research findings, the distortion noise is modeled as an additive Gaussian distribution with variance proportional to the signal power [36]. In [37, 38], the authors studied the RSMA-assisted MIMO Star-RIS communication system while considering hardware impairments. [39] investigated the ergodic achievable rate of an uplink NOMA communication system with the assistance of Star-RIS by considering imperfect CSI and transceiver hardware impairments. The author in [40] investigated Star-RIS NOMA downlink communication under phase error and transceiver hardware impairment.

As shown in Table 1, few works have been devoted to Star-RIS assisted communication under hardware impairments [37,38,39,40,41]. The existing work in [37] investigates RSMA in MIMO RIS communication system and assumes that the transceivers may suffer from hardware imperfections such as I/Q imbalance, which arise due to mismatches in amplitude and phase between the in-phase and quadrature components transformation. It demonstrates that Star-RIS with MS improves the fairness rate, outperforming regular RIS. Also, the authors in [38] studied the spectral efficiency of a MIMO broadcast channel with transceiver I/Q imbalance and showed that Star-RIS outperforms RIS in fairness rate based on ES and MS protocols. [37, 38] proposed an optimization solution via majorization and minimization approaches and did not demonstrate the impact of the number of RIS elements and BS antennas on the performance. Authors in [39] have studied NOMA uplink communication assisted by Star-RIS. Firstly, they estimated the equivalent channel from user to BS using the LMMSE and then theoretically calculated ergodic sum rate by considering channel estimation errors and hardware impairments. They demonstrate saturation of the channel estimation and the ergodic sum rate by increasing transmit power due to distortion noise caused by hardware impairments. In [40], the ergodic rate behavior of Star-RIS assisted NOMA communications is evaluated based on MS protocol for Star-RIS under phase error and hardware impairment. It shows the degrading impact of hardware impairment on the ergodic sum rate and performance improvement by increasing transmission power and the number of RIS elements. The existing work in [41] minimized transmitted power consumption by optimizing active and passive beamforming in a symbiotic radio communication assisted by active Star-RIS under hardware impairments.

As a result of the above discussions based on Table 1, although the efforts in [37,38,39,40,41] studied the Star-RIS Communication under hardware impairments, the critical issue of secrecy communication has not been analyzed yet and remains an open issue. Also, none of them investigated the downlink achievable rate in the presence of Gaussian distortion noise for hardware impairment. We optimize active and passive beamforming based on Star-RIS ES and MS protocols to maximize the total secrecy rate under the constraints of limited transmission power consumption and hardware imperfections of BS and legitimate users. The proposed non-convex problem is solved by alternating optimization methods with semi-definite relaxation, successive convex approximation, penalty concave–convex procedure techniques, and slack variables. Our results show that Star-RIS outperforms conventional RIS and No-RIS in terms of performance. Between Star-RIS protocols, ES has higher performance than MS. The total secrecy rate increases by increasing the number of Star-RIS elements and BS antennas, but it saturates due to distortion noise caused by hardware impairments. A higher transceiver hardware impairment level leads to decreasing SSR, and the impact of receiver hardware impairment level is higher than transmitter hardware impairment level to decrease the SSR.

Table 1 Novelty comparison with the literatures related to STAR-RIS
Full size table

Notation: This paper uses the following mathematical notations and symbols. Boldface uppercase and lowercase demonstrate matrices and vectors, respectively. We use \({{\textbf{X}}^\mathrm{{*}}}\), \({{\textbf{X}}^\mathrm{{T}}}\), \({{\textbf{X}}^\mathrm{{H}}}\), \(\left\| {\textbf{X}} \right\| _2^2\) to represent conjugate, transpose, hermitian, and Frobenius norm of \({\textbf{X}}\), respectively. \(\mathrm{{Diag}}({\textbf{x}})\) demonstrates a diagonal matrix that \({\textbf{x}}\) is on its main diagonal. \(\mathrm{{diag}}({\textbf{X}})\) is a vector consists of main diagonal of \({\textbf{X}}\). \({\widetilde{Diag}}({\mathbf{X}})\) is a diagonal matrix with diagonal elements the same as the \(\textbf{X}\). \({[{\textbf{x}}]_m}\) is the \({m_{th}}\) element of vector \({\textbf{x}}\). \({\textbf{X}}\mathop \succ \limits _ - 0\) shows a positive semi-definite matrix. \({{\mathbb {C}}^{M \times N}}\) denotes complex value matrices space. \({{\mathcal {C}}}{{\mathcal {N}}}(\mu ,{\hspace{0.55542pt}} {\sigma ^2})\) shows complex Gaussian random variables with mean of \(\mu\) and variance of \({\sigma ^2}\).

2 Methods/experimental

The first part of this section explains the studied system model, and the second and third parts demonstrate the channel and signal model. Then, we explain the problem formulation for ES protocol and solve the problem for MS protocol. At the end of this part, we propose convergence and complexity analysis.

2.1 System model

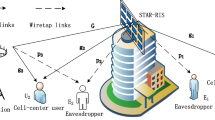
As shown in Fig. 1  , we study a Star-RIS assisted secure communications consisting of an N-antenna transmitter, a Star-RIS with M elements, two single-antenna eavesdroppers, and two legitimate receivers. Star-RIS has established two separate spaces within the spatial vicinity of itself. The initial space, denoted as the ’R space’, is where the reflected signal from RIS is directed back into the same space as the incident signal and the opposite space, referred to as ’T space’, away from the incident signal source and the transmitter. Star-RIS concurrently can serve both ’T’ and ’R’ spaces. The receiver and eavesdropper in the i-th space are the i-th receiver and i-th eavesdropper. Every element of Star-RIS transmits and reflects signal \({p_m} = \sqrt{\beta _m^p} {e^{j\phi _m^p}}{s_m}\), based on changing amplitude and phase shift of incident signal (\({s_m}\)), which \(\sqrt{\beta _m^p} \in [0,1]\) and \(\phi _m^p \in [0,2\pi )\) are the amplitude and phase shift of the m-th element of Star-RIS, \(p = r\) and \(p = t\) specify reflection or transmission mode. It should be noted that the \(\phi _m^r\) and \(\phi _m^t\) in each element are independent of each other, but \(\sqrt{\beta _m^r}\) and \(\sqrt{\beta _m^t}\) due to the conservation of energy principle should satisfy \({\left| {{t_m}} \right| ^2} + {\left| {{r_m}} \right| ^2} = {\left| {{s_m}} \right| ^2}\) that leads to \(\beta _m^r + \beta _m^t = 1\), which means that the total energy of the radiated signal on an element should be equal to the sum of the energies of signals in both T and R modes [42].

We employ ES and MS in the proposed problem. In ES, each element should operate in both T and R modes, and the ratio of transmitted energy at mode T to mode R is \(\beta _m^t:\beta _m^r\). So, the ES mode has the highest degree of freedom among other methods due to design transmission and reflection coefficients simultaneously, which are modeled as

$$\begin{aligned} {\varvec{\Phi }}_p^{ES} = \mathrm{{Diag}} \left(\sqrt{\beta _1^p} {e^{j\phi _1^p}},\sqrt{\beta _2^p} {e^{j\phi _2^p}},\ldots ,\sqrt{\beta _M^p} {e^{j\phi _M^p}} \right), \end{aligned}$$
(1)

where \(p = r\) and \(p = t\) specify the reflection or transmission coefficient, respectively, and \(\phi _m^p \in [0,2\pi )\), \(\sqrt{\beta _m^p} \in [0,1]\), \(\beta _m^t + \beta _m^r = 1\), \(m \in M \buildrel \Delta \over = \{ \mathrm{{1}},\mathrm{{2}},\ldots ,\mathrm{{M}}\}\) [43].

In MS mode, all elements of Star-RIS form two sets of \({M_t}\) and \({M_r}\) elements work in T and R modes, respectively, where \({M_t} + {M_r} = M\). In other words, MS mode is a particular case of ES mode with binary amplitude of the coefficients, which leads to lower degrees of freedom than ES. The MS transmission and reflection coefficients are modeled as

$$\begin{aligned} {\mathbf {\Phi }}_p^{MS} = \mathrm{{Diag}}\left(\sqrt{\beta _1^p} {e^{j\phi _1^p}},\sqrt{\beta _2^p} {e^{j\phi _2^p}},\ldots ,\sqrt{\beta _M^p} {e^{j\phi _M^p}} \right), \end{aligned}$$
(2)

where \(p = r\) and \(p = t\) specify the reflection and transmission coefficient, respectively, and \(\phi _m^p \in [0,2\pi )\), \(\sqrt{\beta _m^p} \in \{ 0,1\}\), \(m \in M \buildrel \Delta \over = \{ \mathrm{{1}},\mathrm{{2}},\ldots ,\mathrm{{M}}\}\) [43].

2.2 Channel model

Let \(\textbf{h}_i^H \in {{\mathbb {C}}^{1 \times N}}\), \(\textbf{g}_i^H \in {{\mathbb {C}}^{1 \times N}}\), \(\textbf{v}_i^\mathrm{{H}} \in {{\mathbb {C}}^{1 \times M}}\), \(\textbf{r}_i^\mathrm{{H}} \in {{\mathbb {C}}^{1 \times M}}\), and \({\textbf{G}} \in {{\mathbb {C}}^{M \times N}}\) denote the channels corresponding to communication paths from BS to i-th legitimate receiver, BS to i-th eavesdropper, RIS to i-th legitimate receiver, RIS to i-th eavesdropper, and BS to RIS, respectively, where \(i \in \{ t,r\}\). It is assumed that the perfect CSI of these links is known at the BS, and all channels are independent quasi-static block fading. Let, \(\textbf{h}_i\), and \({\textbf{g}}_i\) are Rayleigh fading, \(\textbf{G}\), \({\textbf{v}}_i\), and \({\textbf{r}}_i\) follow Rician distribution with Rician factor k, in which \({{\textbf{G}}^{\text{{LoS}}}}\), \({{\textbf{v}}_i^{\text{{LoS}}}}\) and \({{\textbf{r}}_i^{\text{{LoS}}}}\) are modeled by the product of steering vector of receiver and transmitter in each channel while \({\textbf{v}}_i^\mathrm{{NLoS}}\), \({\textbf{r}}_i^\mathrm{{NLoS}}\), \({\textbf{G}^\mathrm{{NLoS}}}\) follow Rayleigh distribution. These channels are expressed as

$$\begin{aligned} {\textbf{G}}&= \sqrt{{{{\rho _0}} \over {d_{\text{{BS\_RIS}}}^\alpha }}} \left(\sqrt{{k \over {1 + k}}} {{\textbf{G}}^{\text{{LoS}}}} + \sqrt{{1 \over {1 + k}}} {{\textbf{G}}^{NLoS}} \right), \end{aligned}$$
(3)
$$\begin{aligned} {{\textbf{v}}_i}&= \sqrt{{{{\rho _0}} \over {d_{RIS\_U_i}^{{\alpha _i}}}}} \left(\sqrt{{k \over {1 + k}}} {{\textbf{v}}_i^{\text{{LoS}}}} + \sqrt{{1 \over {1 + k}}} {{\textbf{v}}_i^{NLoS}} \right),\end{aligned}$$
(4)
$$\begin{aligned} {{\textbf{r}}_i}&= \sqrt{{{{\rho _0}} \over {d_{RIS\_E_i}^{{\alpha _i}}}}} \left(\sqrt{{k \over {1 + k}}} {{\textbf{r}}_i^{\text{{LoS}}}} + \sqrt{{1 \over {1 + k}}} {{\textbf{r}}_i^{NLoS}} \right), \end{aligned}$$
(5)
$$\begin{aligned} {{\textbf{h}}_i}&= \sqrt{{{{\rho _0}} \over {d_{BS\_U_i}^{{\alpha _i}}}}} {\textbf{h}}_i^{\mathrm{{NLOS}}}, \end{aligned}$$
(6)
$$\begin{aligned} {{\textbf{g}}_i}&= \sqrt{{{{\rho _0}} \over {d_{BS\_E_i}^{{\alpha _i}}}}} {\textbf{g}}_i^{\mathrm{{NLOS}}}, \end{aligned}$$
(7)

Where, \({\rho _0}\) is the path loss at the reference distance of 1 m. The symbols \({d_{BS - RIS}}\), \({d_{RIS - U_i}}\), \({d_{RIS - E_i}}\), \({d_{BS - U_i}}\), and \({d_{BS - E_i}}\) indicate distances between BS and RIS, RIS and i-th user, RIS and i-th eavesdropper, BS and i-th user, BS and i-th eavesdropper, respectively. \(\alpha \ge 2\) represents the path loss exponent.

2.3 Signal model

The BS simultaneously broadcasts the signal to Star-RIS and two legitimate users, placed in reflection and transmission regions where an eavesdropper attempts to wiretap the signal in each region. Furthermore, Star-RIS conveys signals to legitimate users. Since, in a practical scenario, the transmitter and receiver experience inherent hardware impairments, we suppose that BS and legitimate receivers suffer from residual hardware impairments. We consider direct and indirect links from BS to legitimate receivers, and eavesdroppers. Let \(s\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,{\hspace{0.55542pt}} 1)\) as the transmitted signal, \({\textbf{w}} \in {{\mathbb {C}}^{N \times 1}}\) as active beamforming vector, \({{\textbf{m}}_T} \in {{\mathbb {C}}^{N \times 1}}\) as independent Gaussian transmit distortion noise with power distortion \({{\textbf{m}}_T} \sim {{\mathcal {C}}}{{\mathcal {N}}}(0,{\mu _t}{\widetilde{Diag}}({\textbf{w}}{{\textbf{w}}^H}))\) by ratio of \({\mu _t} \ge 0\) to transmitted signal power due to BS hardware impairment. So, BS transmits the signal as below

$$\begin{aligned} {\textbf{x}} = {\textbf{w}}s + {{\textbf{m}}_T}, \end{aligned}$$
(8)

then received baseband signals at legitimate users and eavesdroppers are calculated as below

$$\begin{aligned} {y_i}&= ({{\textbf{h}}_i^H} + {\textbf{v}}_i^H{\mathbf {\Phi }}_i^H{\textbf{G}}){\textbf{x}} + {n_i} + {m_i},&\forall i \in \{ r,t\}, \end{aligned}$$
(9)
$$\begin{aligned} {y_{{e_i}}}&= ({{\textbf{g}}_i^H} + {\textbf{r}}_i^H{\mathbf {\Phi }}_i^H{\textbf{G}}){\textbf{x}} + {n_{{e_i}}},&\forall i \in \{ r,t\}, \end{aligned}$$
(10)

where \({m_i}\) is an independent Gaussian distortion noise at i-th legal receiver with distribution of \({{\mathcal {C}}}{{\mathcal {N}}}(0,{\mu _r}\{ |{y_i} - {m_i}{|^2}\} )\) by the ratio of \({\mu _r} \ge 0\) to received signal power. The additive white Gaussian noises (AWGN) at each receiver and eavesdropper are represented by \({n_i}\), and \({n_{{e_i}}}\), respectively, with mean of zero and variance of \(\sigma _i^2\) and \(\sigma _e^2\) where \({n_i}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,{\hspace{0.55542pt}} \sigma _i^2)\) and \({n_{{e_i}}}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,{\hspace{0.55542pt}} \sigma _e^2)\).

BS feeds back Star-RIS’s coefficients to the RIS controller through dedicated feedback channels. Let \({{\varvec{\theta }}_i} = diag({{\mathbf {\Phi }}_i}) \in {{\mathbb {C}}^{M \times 1}}\) and convert to \({{\varvec{\theta }}_i} = [{{\varvec{\theta }}_i};1] \in {{\mathbb {C}}^{(M + 1) \times 1}}\), then the equivalent channels from RIS to users and eavesdroppers i.e. \(\{{{\textbf{H}}_i}, {{\textbf{F}}_i}\} \in {{\mathbb {C}}^{(M + 1) \times N}}\) are formulated by

$$\begin{aligned} {{\textbf{H}}_i}= & {} \begin{bmatrix} \mathrm{{Diag}}({\textbf{v}}_i^H){\textbf{G}}\\ {{\textbf{h}}_i^H} \end{bmatrix},\forall i \in \{ r,t\}, \end{aligned}$$
(11)
$$\begin{aligned} {{\textbf{F}}_i}= & {} \begin{bmatrix} \mathrm{{Diag}}({\textbf{r}}_i^H){\textbf{G}}\\ {{\textbf{g}}_i^H} \end{bmatrix},\forall i \in \{ r,t\}, \end{aligned}$$
(12)

then the Eqs. 9 and 10 can be rewritten as below

$$\begin{aligned} {y_i}&= {\varvec{\theta }}_i^H{{\textbf{H}}_i}({\textbf{x}}) + {n_i} + {m_i},&\forall i \in \{ r,t\} \end{aligned}$$
(13)
$$\begin{aligned} {y_{{e_i}}}&= {\varvec{\theta }}_i^H{{\textbf{F}}_i}({\textbf{x}}) + {n_{{e_i}}},&\forall i \in \{ r,t\} \end{aligned}$$
(14)

then, the data rate that can be attained at user i is modeled as

$$\begin{aligned} {R_i}\mathrm{{ = log}}\left(\mathrm{{1 + }}{{{\textbf{w}}^H{\textbf{H}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{\textbf{H}_i\textbf{w}}} \over {{\mu _r}({\textbf{w}}^H{\textbf{H}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({\varvec{\theta }_i}^H{{\textbf{H}}_i}{\widetilde{\mathrm{{Diag}}}}({\textbf{w}}{{\textbf{w}}^H}){\textbf{H}}_i^H{\varvec{\theta }_i}) + (1 + {\mu _r})\sigma _i^2}} \right), \end{aligned}$$
(15)

with using \({y^H}{\widetilde{\mathrm{{Diag}}}}(x{x^H})y = {x^H}{\widetilde{\mathrm{{Diag}}}}(y{y^H})x\), Eq. 15 is rewritten as below

$$\begin{aligned} {R_i}\mathrm{{ = lo}}{\mathrm{{g}}_2}\left(\mathrm{{1 + }}{{{{\textbf{w}}^H}{\textbf{H}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{H}}_i}{\textbf{w}}} \over {{\mu _r}({{\textbf{w}}^H}{\textbf{H}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{H}}_i}){\textbf{w}}) + (1 + {\mu _r})\sigma _i^2}} \right), \end{aligned}$$
(16)

and the data rate that can be attained at Eve i is provided by

$$\begin{aligned} {R_{e,i}}\mathrm{{ = lo}}{\mathrm{{g}}_2}\left(\mathrm{{1 + }}{{{{\textbf{w}}^H}{\textbf{F}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{F}}_i}{\textbf{w}}} \over {{\mu _t}({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{{\varvec{\theta }}_i}{\varvec{\theta }}_i^H}{{\textbf{F}}_i}){\textbf{w}}) + \sigma _{e,i}^2}}\right), \end{aligned}$$
(17)

2.4 Problem formulation

In this part, we design optimized active beamforming and transmission and reflection beamforming based on ES protocol to maximize the total secrecy rate under the impact of transmitter and legitimate receivers hardware impairments subject to limited transmission power. Our objective is to solve the subsequent problem mathematically

$$\begin{aligned} \mathop \mathrm{{{Max}}}_{{{\textbf {w}}_i},{\varvec{\theta }}_i}&\quad{} & {} \sum \limits _{i = r,t} {{R_i}} - {R_{{e_i}}}{} & {} \end{aligned}$$
(18a)
$$\begin{aligned} \text {Subject to}&\quad{} & {} {\left\| {\textbf{w}} \right\| ^2} \le {P_{\max }} \end{aligned}$$
(18b)
$$\begin{aligned}&\quad{} & {} \mathrm{{ }}\sum \limits _{i = r,t} {\mathrm{{diag}}({{\varvec{\theta }}_i}} {\varvec{\theta }}_i^H) = [{{\textbf{1}}_{1 \times M}};2]. \end{aligned}$$
(18c)

Constraint 18b denotes the limited transmission power consumption, and constraint 18c is added due to the ES coefficient. Problem 18 is not-convex due to non-concave objective function 18a and non-convex ES coefficient constraint 18c.

To solve problem 18, the SCA method is implemented, which converges to a local solution [44] and alternating optimization that converts the proposed problem into convex sub-problems, which is solved via conventional optimization tools like CVX. So, we solve the proposed problem based on optimizing \({\textbf{w}}\) and \({{\varvec{\theta }}_i}\) in an iterative manner. We implement alternating optimization based on auxiliary variables, first-order Taylor approximation, and the equality Eq. 19 to reformulate the proposed problem into a convex problem. We implement sequential rank-one constraint relaxation (SROCR) for decoupling the hardly coupled variables and non-convex rank one Star-RIS coefficients constraint. For simplicity we solve the problem based on assuming \({\textbf{E}_i} = {{\varvec{\theta }}_i}{\varvec{\theta }}_i^H\) where \({\textbf{E}_i} \in {{\mathbb {C}}^{(M + 1) \times (M + 1)}}\), and also we use Eq. 19 in our solution.

$$\begin{aligned} {y^H}{\widetilde{\mathrm{{Diag}}}}(x{x^H})y = {x^H}{\widetilde{\mathrm{{Diag}}}}(y{y^H})x. \end{aligned}$$
(19)

For solving problem 18, the first step toward converting Eq. 18a into concave form is using auxiliary variables \({{\textbf{P}}_i} = [{p_{1,i}},{p_{2,i}},{p_{3,i}},{p_{4,i}}]\) as below [36]

$$\begin{aligned}&{\log _2}((1 + {\mu _r})({{\textbf{w}}^H}{\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}){\textbf{w}}) + (1 + {\mu _r})\sigma _i^2) \ge {p_{1,i}}, \end{aligned}$$
(20a)
$$\begin{aligned}&\quad {\log _2}({\mu _r}({{\textbf{w}}^H}{\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}){\textbf{w}}) + (1 + {\mu _r})\sigma _i^2) \le {p_{2,i}}, \end{aligned}$$
(20b)
$$\begin{aligned}&\quad {\log _2}({\textbf{wF}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}{\textbf{w}} + {\mu _t}({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}){\textbf{w}}) + \sigma _{e,i}^2) \le {p_{3,i}}, \end{aligned}$$
(20c)
$$\begin{aligned}&\quad {\log _2}({\mu _t}({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}){\textbf{w}}) + \sigma _{e,i}^2) \ge {p_{4,i}}, \end{aligned}$$
(20d)

so that, \(\sum \limits _{i = r,t} {({R_i}} - {R_{{e_i}}}) \ge \sum \limits _{i = r,t} {({p_{1,i}}} - {p_{2,i}} - {p_{3,i}} + {p_{4,i}})\).

For optimizing problem based on \({\textbf{w}}\) with given \({{\textbf{E}} _i}\), we introduce an auxiliary variable \({{\textbf{r}}_{f,i}} = [{r_{f,i,1}},{r_{f,i,2}},{r_{f,i,3}},{r_{f,i,4}}]\), so that the equivalent of Eq. 20a is given below [36]

$$\begin{aligned}&{\log _2}({r_{f,i,1}}) \ge {p_{1,i}}, \end{aligned}$$
(21a)
$$\begin{aligned}&\quad (1 + {\mu _r})({{\textbf{w}}^H}{\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}){\textbf{w}}) + (1 + {\mu _r})\sigma _i^2 \ge {r_{f,i,1}}, \end{aligned}$$
(21b)

the equivalent of Eq. 20b is given below

$$\begin{aligned}&{\log _2}({r_{f,i,2}}) \le {p_{2,i}}, \end{aligned}$$
(22a)
$$\begin{aligned}&\quad {\mu _r}({{\textbf{w}}^H}{\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}{\textbf{w}}) + {\mu _t}(1 + {\mu _r})({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i}){\textbf{w}}) + (1 + {\mu _r})\sigma _i^2 \le {r_{f,i,2}}, \end{aligned}$$
(22b)

the equivalent of Eq. 20c is given below

$$\begin{aligned}&{\log _2}({r_{f,i,3}}) \le {p_{3,i}}, \end{aligned}$$
(23a)
$$\begin{aligned}&\quad {\textbf{wF}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}{\textbf{w}} + {\mu _t}({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}){\textbf{w}}) + \sigma _{e,i}^2 \le {r_{f,i,3}}, \end{aligned}$$
(23b)

the equivalent of Eq. 20d is given below

$$\begin{aligned}&{\log _2}({r_{f,i,4}}) \ge {p_{4,i}}, \end{aligned}$$
(24a)
$$\begin{aligned}&\quad {\mu _t}({{\textbf{w}}^H}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i}){\textbf{w}}) + \sigma _{e,i}^2 \ge {r_{f,i,4}}. \end{aligned}$$
(24b)

The Eqs. 21a, 22b, 23b, and 24a are convex but the Eqs. 21b, 22a, 23a, and 24b are concave. By using the first-order Taylor approximation and equality 19, the non-convex equations are, respectively, equivalent as below

$$\begin{aligned}{} & {} 2{\mathop {\textrm{ Re}}\nolimits } \{ {{\textbf{w}}^{n,H}}{{\textbf{A}}_{1,i}}{\textbf{w}}\} - {\textbf{w}^{n,H}}{{\textbf{A}}_{1,i}}{{\textbf{w}}^n} + (1 + {\mu _r})\sigma _i^2 \ge {r_{f,i,1}}, \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \quad {\log _2}(r_{f,i,2}^n) + {{({r_{f,i,2}} - r_{f,i,2}^n)} \over {r_{f,i,2}^n\ln (2)}} \le {p_{2,i}}, \end{aligned}$$
(26)
$$\begin{aligned}{} & {} \quad {\log _2}(r_{f,i,3}^n) + {{({r_{f,i,3}} - r_{f,i,3}^n)} \over {r_{f,i,3}^n\ln (2)}} \le {p_{3,i}}, \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \quad 2{\mathop {\textrm{ Re}}\nolimits } \{ {{\textbf{w}}^{n,H}}{{\textbf{A}}_{2,i}}{\textbf{w}}\} - {{\textbf{w}}^{n,H}}{{\textbf{A}}_{2,i}}{{\textbf{w}}^n} + \sigma _e^2 \ge {r_{f,i,4}}, \end{aligned}$$
(28)

where \({{\textbf{A}}_{1,i}} = (1 + {\mu _r}){\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i} + {\mu _t}(1 + {\mu _r}){\widetilde{\mathrm{{Diag}}}}({\textbf{H}}_i^H{{\textbf{E}}_i}{{\textbf{H}}_i})\) and \({{\textbf{A}}_{2,i}} = {\mu _t}{\widetilde{\mathrm{{Diag}}}}({\textbf{F}}_i^H{{\textbf{E}}_i}{{\textbf{F}}_i})\), and \({\textbf{w}}^n\) is obtained at iteration n. Please refer to Appendix 1 for the proof of Eqs. (25) and (28). The optimization problem 18 for optimizing \({\textbf{w}}\) by fixing \({{\textbf{E}} _i}\) is reformulated as

$$\begin{aligned} \mathop \mathrm{{{Max}}}_{{\textbf{w}},{\textbf{P}},{{\textbf{r}}_{f,i}}}&\quad{} & {} \sum \limits _{i = r,t} (p_{1,i} - p_{2,i} - p_{3,i} + p_{4,i}) \end{aligned}$$
(29a)
$$\begin{aligned} \text {subject to:}&\quad{} & {} 18b, 21a, 22b, 23b, 24a, 25, 26, 27, 28 . \ \end{aligned}$$
(29b)

For optimizing the problem based on \({\textbf{E} _i}\) where \({\textbf{E}_i} = {{\varvec{\theta }}_i}{\varvec{\theta }}_i^H\) with given \({\textbf{w}}\), we use semi-definite relaxation (SDR). The subproblem of optimizing \({\textbf{E} _i}\) by fixing \({\textbf{w}}\) is proposed as

$$\begin{aligned} \mathop \mathrm{{{Max}}}_{{{\textbf {E}}_i}}&\quad{} & {} \sum _{i=r,t} {(p_{1,i} - p_{2,i} - p_{3,i} + p_{4,i}) }{} & {} &\end{aligned}$$
(30a)
$$\begin{aligned} \text {subject to:}&\quad{} & {} Rank({{\textbf{E}}_i}) = 1\mathrm{{ }},&\quad&\forall i \in \{ r,t\}, \end{aligned}$$
(30b)
$$\begin{aligned}&\quad{} & {} \mathrm{{diag}}({{\textbf{E}}_t}) + \mathrm{{diag}}({{\textbf{E}}_r}) = [{{\textbf{1}}_{1 \times M}};2], \end{aligned}$$
(30c)
$$\begin{aligned}&\quad{} & {} {{\textbf{E}}_i}\mathop \succ \limits _ - 0\mathrm{{ }},&\quad&\forall i \in \{ r,t\}, \end{aligned}$$
(30d)

We introduce an auxiliary variable \({{\textbf{r}}_{e,i}} = [{r_{e,i,1}},{r_{e,i,2}},{r_{e,i,3}},{r_{e,i,4}}]\), so that the equivalent of Eq. 20a is given below

$$\begin{aligned} {\log _2}({r_{e,i,1}})&\ge {p_{1,i}}, \end{aligned}$$
(31a)
$$\begin{aligned} Tr({{\textbf{B}}_{1,i}}{{\textbf{E}}_i}) + (1 + {\mu _r})\sigma _i^2&\ge {r_{e,i,1}}, \end{aligned}$$
(31b)

the equivalent of Eq. 20b is given below

$$\begin{aligned} {\log _2}({r_{e,i,2}})&\le {p_{2,i}}, \end{aligned}$$
(32a)
$$\begin{aligned} Tr({{\textbf{B}}_{2,i}}{{\textbf{E}}_i}) + (1 + {\mu _r})\sigma _i^2&\le {r_{e,i,1}}, \end{aligned}$$
(32b)

the equivalent of Eq. 20c is given below

$$\begin{aligned} {\log _2}({r_{e,i,3}})&\le {p_{3,i}}, \end{aligned}$$
(33a)
$$\begin{aligned} Tr({{\textbf{B}}_{3,i}}{{\textbf{E}}_i}) + \sigma _e^2&\le {r_{e,i,3}}, \end{aligned}$$
(33b)

the equivalent of Eq. 20d is given below

$$\begin{aligned} {\log _2}({r_{e,i,4}})&\ge {p_{4,i}}, \end{aligned}$$
(34a)
$$\begin{aligned} Tr({{\textbf{B}}_{4,i}}{{\textbf{E}}_i}) + \sigma _e^2&\ge {r_{e,i,4}}, \end{aligned}$$
(34b)

where \({{\textbf{B}}_1} = (1 + {\mu _r}){{\textbf{H}}_i}{\textbf{w}}{{\textbf{w}}^H}{\textbf{H}}_i^H + {\mu _t}(1 + {\mu _r}){{\textbf{H}}_i}{\widetilde{\mathrm{{Diag}}}}({\textbf{w}}{{\textbf{w}}^H}){\textbf{H}}_i^H\), \({{\textbf{B}}_2} = {\mu _r}{{\textbf{H}}_i}{\textbf{w}}{{\textbf{w}}^H}{\textbf{H}}_i^H + (1 + {\mu _r}){\mu _t}{{\textbf{H}}_i}{\widetilde{\mathrm{{Diag}}}}({\textbf{w}}{{\textbf{w}}^H}){\textbf{H}}_i^H\), \({{\textbf{B}}_3} = {\mu _t}{{\textbf{F}}_i}{\widetilde{\mathrm{{Diag}}}}({\textbf{w}}{{\textbf{w}}^H}){\textbf{F}}_i^H + {{\textbf{F}}_i}{\textbf{w}}{{\textbf{w}}^H}{\textbf{F}}_i^H\) and \({{\textbf{B}}_4} = {\mu _t}{{\textbf{F}}_i}{\widetilde{\mathrm{{Diag}}}}({\textbf{w}}{{\textbf{w}}^H}){\textbf{F}}_i^H\).

We approximate the non-convex constraints 32a and 33a based on the first-order Taylor approximation as below

$$\begin{aligned}{} & {} {\log _2}(r_{e,i,2}^n) + {{({r_{e,i,2}} - r_{e,i,2}^n)} \over {r_{e,i,2}^n\ln (2)}} \le {p_{2,i}}, \end{aligned}$$
(35)
$$\begin{aligned}{} & {} \quad {\log _2}(r_{e,i,3}^n) + {{({r_{e,i,3}} - r_{e,i,3}^n)} \over {r_{e,i,3}^n\ln (2)}} \le {p_{3,i}}. \end{aligned}$$
(36)

The rank-one constraint 30b is relaxed by implementing sequential rank-one constraint relaxation (SROCR) as below,

$$\begin{aligned} {\mathrm{{\varepsilon }}_{\max }}({{\textbf{E}}_i}) \ge {\mathrm{{\varepsilon }}^{[l]}}Tr({{\textbf{E}}_i}), \end{aligned}$$
(37)

where \({\mathrm{{\varepsilon }}_{\max }}({{\textbf{E}}_i})\) represents maximum eigenvalue of \({\textbf{E}}_i\), and \({\mathrm{{\varepsilon }}^{[l]}} \in [0,1]\) is relaxation parameter in \(\mathrm{{l}}\)-th iteration. Since the maximum eigenvalue of a rank-one matrix is equal to the trace of that matrix, so \({\mathrm{{\varepsilon }}^{[l]}} = 1\) means that the matrix is rank one but \({\mathrm{{\varepsilon }}^{[l]}} = 0\) leads to dropped rank-one constraint. \({\mathrm{{\varepsilon }}_{\max }}({{\textbf{E}}_i})\) is approximated by the following

$$\begin{aligned} {\mathrm{{\varepsilon }}_{\max }}({{\textbf{E}}_i}) \approx e_{\max }^H({\textbf{E}}_i^{[l]}){{\textbf{E}}_i}{e_{\max }}({\textbf{E}}_i^{[l]}), \end{aligned}$$
(38)

where \(e_{\max }^H({\textbf{E}}_i^{[l]})\) denotes the largest eigenvector associated with the maximum eigenvalue of \({\textbf{E}}_i^{[l]}\). It should be noted that \({\mathrm{{\varepsilon }}^{[l]}}\) can be updated with the following formula in each iteration

$$\begin{aligned} {\mathrm{{\varepsilon }}_i^{[l]}} = \min \left(1,{{{\varepsilon _{\max }}({\textbf{E}}_i^{[l]})} \over {Tr({\textbf{E}}_i^{[l]})}} + {\Delta ^l} \right), \end{aligned}$$
(39)

where \({\Delta ^l}\) is the step size. So finally, the optimization subproblem of optimizing \({{\textbf{E}}_i}\) by fixing \({\textbf{w}}\) is reformulated as

$$\begin{aligned} \mathop \mathrm{{{Max}}}_{{{\textbf{E}}_i},{\textbf{P}},{{\textbf{r}}_{e,i}}}&\quad{} & {} \sum \limits _{i = r,t} {({p_{1,i}}} - {p_{2,i}} - {p_{3,i}} + {p_{4,i}}) \end{aligned}$$
(40a)
$$\begin{aligned} \text {subject to:}&\quad{} & {} e_{\max }^H({\textbf{E}}_i^{[l]}){{\textbf{E}}_i}{e_{\max }}({\textbf{E}}_i^{[l]}) \ge {\mathrm{{\varepsilon }}_i^{[l]}}Tr({{\textbf{E}}_i}), \end{aligned}$$
(40b)
$$\begin{aligned}&\quad{} & {} 30c, 30d, 31a, 31b, 32b, 33b, 34a, 34b, 35, 36. \ \end{aligned}$$
(40c)

Finally, we proposed iterative Algorithm 1 to solve problem (18) for ES protocol. This algorithm involves an alternating optimization of active beamforming in problem (29) and passive beamforming in problem (40). Hear, \(\mathrm{{\varepsilon }}_i\) denotes the rank-one relaxation parameter mentioned in Eq. (35).

Algorithm 1
figure a

Proposed algorithm in ES mode

Full size image
Fig. 1
figure 1

System model

Full size image
Fig. 2
figure 2

Sum secrecy rate versus transmission power consumption

Full size image
Fig. 3
figure 3

Sum secrecy rate versus the number of RIS elements

Full size image
Fig. 4
figure 4

Sum secrecy rate versus the number of BS’s antennas

Full size image
Fig. 5
figure 5

Sum Secrecy rate versus hardware impairment level, where \(\mu =\mu _t=\mu _r\)

Full size image

2.5 Investigating MS

Compared to energy splitting mode, for mode switching (MS), with given \({{\textbf{E}}_i}\), the optimization of transmitter beamforming vector \({\textbf{w}}\) is the same as ES mode while in optimization of passive beamforming \({{\textbf{E}}_i}\) with given \({\textbf{w}}\), transmission and reflection coefficients are always between 0 and 1, so constraint \(\beta _m^i - {(\beta _m^i)^2} \ge 0\) always holds but the equality holds in MS mode that \(\beta _m^i\) is only 0 or 1. So the optimization problem with given \({\textbf{w}}\) has non-convex binary constraints, and to tackle these non-convex binary terms, we add a penalty term to the objective function based on the Eq. 41

$$\begin{aligned} -\sum \limits _{i \in \{ r,t\} } {\sum \limits _{m \in \{ 1,2,\ldots ,M\} } {\beta _m^i - {{(\beta _m^i)}^2}} } \ge 0. \end{aligned}$$
(41)

Since the objective function should be maximum, the penalty term is non-concave due to \({(\beta _m^i)^2}\). By using \(\beta _m^{i,n}\), which is calculated in the last iteration of the SCA algorithm, based on the first-order Taylor approximation, the lower bound for Eq. 41 is obtained as below [45, 46]

$$\begin{aligned} -\sum \limits _{i \in \{ r,t\} } {\sum \limits _{m \in \{ 1,2,\ldots ,M\} } {(1 - 2\beta _m^{i,n})\beta _m^i + {{(\beta _m^{i,n})}^2}} } \le -\sum \limits _{i \in \{ r,t\} } {\sum \limits _{m \in \{ 1,2,\ldots ,M\} } {\beta _m^i - {{(\beta _m^i)}^2}} }. \end{aligned}$$
(42)

In addition, the equivalent of \(\beta _m^i\) is \({\textbf{E}}_{m,m}^i\). So, the optimization problem in MS mode is given below

$$\begin{aligned} \mathop \mathrm{{{Max}}}_{{{\textbf{E}}_i},{\textbf{P}},{{\textbf{r}}_{e,i}}}&\quad{} & {} \mathrm{{ }}\sum \limits _{i = r,t} {({p_{1,i}}} - {p_{2,i}} - {p_{3,i}} + {p_{4,i}}) - \chi \sum \limits _{i \in \{ r,t\} } {\sum \limits _{M \in \{ 1,\ldots ,M\} } {[(1 - 2{\textbf{E}}_{m,m}^{i,n}} } ){\textbf{E}}_{m,m}^i + {\textbf{E}}_{m,m}^{i,n}{\textbf{E}}_{m,m}^{i,n}] \end{aligned}$$
(43a)
$$\begin{aligned} \text {Subject to}&\quad{} & {} 30c, 30d, 31a, 31b, 32b, 33b, 34a, 34b, 35, 36, 40b. \ \end{aligned}$$
(43b)
Algorithm 2
figure b

Proposed algorithm in MS

Full size image

Where \(\mathrm{{\chi }} > 0\) is a penalty factor that imposes a penalty to the objective function. We should notice that, unlike ES protocol, in MS protocol, we use an outer loop to guarantee binary STAR-RIS coefficients with predefined accuracy \(\varepsilon _\mathrm{{{out}}}\). In the outer loop, we increase the penalty factor proportionally by \(\kappa \ge 1\) in each iteration, when \(\mathrm{{\chi }} \rightarrow + \infty\), the solution of problem 43 is satisfied the equality constraint 41 [42, 47].

Finally, we develop two-layer iterative algorithm (2) to tackle problem (18) in MS protocol. In the inner layer, we alternatively optimize active beamforming in problem (29) and passive beamforming in problem (43). In the outer layer, we ensure the binary MS Star-RIS coefficients meet the predefined accuracy \({\varepsilon _\mathrm{{{out}}}} > 0\).

2.6 Convergence analysis

The convergence behavior of the implemented solution is guaranteed based on the following details. Since the optimization problem 18 is solved based on the alternating manner and SCA, and also due to non-decreasing objective function 18a in each iteration while having a finite upper bound for objective function due to limited transmission power, i.e., constraint 18b, therefor the convergence of AO algorithm is ensured. So, let \({R_{secure}}({\textbf{w}}_i^k,{\textbf{E}}_i^k)\), \({R_{secure}}({\textbf{w}}_i^{k+1},{\textbf{E}}_i^k)\), \({R_{secure}}({\textbf{w}}_i^{k+1},{\textbf{E}}_i^{k+1})\) represent the objective of 18 and 29 and 40, respectively, then we have the following inequality

$$\begin{aligned} R_{secure}({{\textbf{w}}_i^k},{{\textbf{E}}_i^k}) \le R_{secure}({{\textbf{w}}_i^{k+1}},{{\textbf{E}}_i^k}) \le R_{secure}({\textbf{w}}_i^{k + 1},{\textbf{E}}_i^{k + 1}), \end{aligned}$$
(44)

so due to bounded objective function, \(R_{\textrm{secure}}({{\textbf{w}}_i^k},{{\textbf{E}}_i^k})\) is converged to an optimal point limit \(R_{secure}({{\textbf{w}}_i^\mathrm{{{opt}}}},{{\textbf{E}}_i^\mathrm{{{opt}}}})\) [48, 49].

2.7 Complexity analysis

The complexity of SOCP active beamforming (29) is \(\mathcal {O}(N^3)\) [36], and the complexity of SDP passive beamforming (40), and (43) is \(\mathcal {O}(M^{3.5})\) [50], Thus, the overall complexity of Algorithm 1 for ES protocol is \(\mathcal {O}(I_l(N^3+M^{3.5}))\), where \(I_l\) represents the iteration number needed for convergence. The total complexity of Algorithm (2) for MS is \(\mathcal {O}(I_\mathrm{{{out}}}I_{in}(N^3+M^{3.5}))\), where \(I_\mathrm{{{out}}}\) and \(I_{in}\) representing the iteration numbers of the outer and inner layers required for convergence.

Table 2 System parameters
Full size table

3 Results and discussion

The advantages of deploying Star-RIS in the proposed secure wireless communications system are evaluated in this section. We assume that users are at (50 m,2 m) and (50 m, -2 m), and eavesdroppers are at (45 m,2 m) and (45 m, -2 m). We compare the performance of Star-RIS with M elements and No-RIS system, and conventional RIS that contains two reflection and transmission surfaces, each one with M/2 elements. For more details, the simulation parameters are written in Table 2.

In Fig. 2, we plot total secrecy rate versus transmitted power consumption across all deployments of RIS. Since Star-RIS simultaneously reflects and transmits signals, it has more degrees of freedom than conventional RIS, which results in higher performance for Star-RIS than conventional RIS and No-RIS systems. Also, we demonstrate the performance of the No-RIS system, which has the lowest performance since RIS and Star-RIS can create dynamic and adaptable wireless radio propagation. In the two operating protocols of Star-RIS, ES mode has higher performance than MS due to more degrees of freedom. It should be noted that the secrecy rate trends to an upper bound with increasing maximum transmission power due to distortion noise.

The SSR versus the number of RIS elements is shown in Fig. 3. It can be observed that RIS can obtain more signal power and enable beamforming with more elements. Hence, the sum secrecy rate improves with increasing M. It should be noted that hardware impairment degrades the sum secrecy rate due to distortion noise. So, the SSR saturates for hardware impairment by an increase in M. Also, in curves with more transmit power, it can be observed that SSR reaches the saturation and largest value with the lower number of RIS elements since the transceiver hardware impairments are power dependent. Also, Star-RIS outperforms conventional RIS due to more degrees of freedom. Among ES and MS modes in Star-RIS, ES has better performance due to the continuous altitude of RIS coefficients in contrast to MS, which can operate with a binary altitude of coefficients. This figure validates the impact of optimization over passive beamforming vectors, which refers to both transmission and reflection.

The SSR versus number of BS antennas is shown in Fig. 4, where \(p_\mathrm{{{Max}}}=15dBm\), and \(M=16\). Since more antennas in BS enable higher active beamforming gain, the total secrecy rate increases for all methods, but, increasing transmitter or receiver hardware impairment levels, i.e., \(\mu _t\) or \(\mu _r\) leads to a decrease in sum secrecy rate. In each deployment method, the SSR with simulation parameters \(\mu _t = 0.05, \mu _r= 0.01\) has higher performance than with \(\mu _t = 0.01, \mu _r= 0.05\) since the receiver distortion noise power is larger than the transmit distortion noise. Also, similar to the previous figure, Star-RIS outperforms conventional RIS (CRIS) and No-RIS systems. ES has the highest performance, and the No-RIS scenario has the lowest performance. This figure confirms the impact of active beamforming optimization. So, the effect of optimizing joint active and passive beamforming together is confirmed in Figs. 4 and  3.

Figure 5 shows the SSR versus the receiver and transmitter hardware impairment level (i.e., \(\mu _r\) and \(\mu _t\)). Since more hardware impairment levels in BS and legitimate receivers result in more distortion noise, it leads BS to use some of available transmission power for compensating the hardware impairments, and hence sum secrecy rate of legitimate users decreases with increasing \(\mu _r\) and \(\mu _t\).

It should be noted that with large \(\mu\), distortion noise in equation 16 becomes noticeable with respect to receiver noise. Also, the algorithm with more degrees of freedom receives more distortion noise, so the distortion noise in ES is larger than in the MS and conventional RIS, respectively. Due to these two reasons, and based on equation 16, with large \(\mu\), three algorithms perform the same, But with small \(\mu\), ES outperforms MS, and MS outperforms conventional RIS. So, finally, ES, MS, and conventional algorithms gradually perform the same when the hardware impairment levels increase.

4 Conclusion

This paper investigates robust beamforming designs for secure MISO downlink communication systems aided by Star-RIS under residual transceiver hardware impairments that lead to distortion noise. We aimed to maximize the total secrecy rate subject to limited power consumption by optimizing beamforming at BS and Star-RIS with two practical protocols named ES and MS. Based on our simulation results, Star-RIS outperforms conventional RIS and No-RIS systems in terms of performance. In Star-RIS, the ES performs better than MS. The total secrecy rate increases with more Star-RIS elements and BS antennas, but residual transceiver hardware impairment reduces SSR. It should be noted that the impact of the receiver hardware impairment level is higher than the transmitter hardware impairment level. Our results show that the sum secrecy rate trends to an upper bound with increasing maximum transmission power and number of RIS elements due to distortion noise.