Multi-armed bandit approach for mean field game-based resource allocation in NOMA networks

Abstract

Facing the exponential demand for massive connectivity and the scarcity of available resources, next-generation wireless networks have to meet very challenging performance targets. Particularly, the operators have to cope with the continuous prosperity of the Internet of things (IoT) along with the ever-increasing deployment of machine-type devices (MTDs). In this regard, due to its compelling benefits, non-orthogonal multiple access (NOMA) has sparked a significant interest as a sophisticated technology to address the above-mentioned challenges. In this paper, we consider a hybrid NOMA scenario, wherein the MTDs are divided into different groups, each of which is allocated an orthogonal resource block (RB) so that the members of each group share a given RB to simultaneously transmit their signals. Firstly, we model the densely deployed network using a mean field game (MFG) framework while taking into consideration the effect of the collective behavior of devices. Then, in order to reduce the complexity of the proposed technique, we apply the multi-armed bandit (MAB) framework to jointly address the resource allocation and the power control problem. Thereafter, we derive two distributed decision-making algorithms that enable the users to autonomously regulate their transmit power levels and self-organize into coalitions based on brief feedback received from the base station (BS). Simulation results are given to underline the equilibrium properties of the proposed resource allocation algorithms and to reveal the robustness of the proposed learning process.

1 Introduction

Driven by the pervasiveness and inclusiveness of Internet of things (IoT) services, cellular communication networks have witnessed a drastic expansion of the number of wireless devices and the proliferation of new emerging applications. Particularly, machine-type communications (MTC), also known as machine-to-machine communications (M2M) have been a high-demanding scenario that can support the ubiquity of IoT systems and meet the massive access requirements. Generally, MTC refer to automated communications among machine-type devices (MTDs) that occur without any specific human intervention. These connections are mainly characterized by prominent properties of sparse and small packet transmissions with low data rates. Despite the sporadic nature of MTC, the traffic generated by massive MTC (mMTC) network is rather challenging. On the other hand, due to the scarcity of available resources, scheduling an entire resource block (RB) to each connection is neither efficient nor feasible. Consequently, designing sophisticated multiple access techniques is required to handle the above-mentioned challenges. Interestingly, non-orthogonal multiple access (NOMA) techniques have been spotlighted as eye-catching schemes that can serve as fuel for the evolution of wireless communication systems towards the future sixth-generation (6 G) networks. The advantage of the NOMA technique lies in its ability to allow multiple devices to access common resources where either power domain [1, 2] or code domain [3, 4] is exploited to perform multiplexing of different users’ signals. Then, the base station (BS) processes successive interference cancellation (SIC) to separate and decode the superimposed messages, which yields a substantial improvement in the spectral efficiency and the network capacity.

Attracted by the appealing features of NOMA, plenty of research has investigated the uplink as well as the downlink NOMA systems. In [5], the authors have studied the performance of the NOMA network in terms of overall system throughput in both downlink and uplink transmissions. The authors in [6] have investigated the resource allocation problem of power domain-NOMA (PD-NOMA) in the context of downlink transmission where different transmit power levels are assigned to the different users. In [7], the authors have evaluated the system performance of an uplink NOMA system taking into account the imperfect SIC process in order to minimize the overall power consumption. Indeed, the performance of a PD-NOMA scheme is particularly based on the way the power is partitioned among the users. More precisely, the BS can successfully decode and recover the interfering signals from different transmitters by exploiting the disparity in power levels among them. Consequently, an improper power assignment yields an important interference impact, which impairs the effectiveness of the SIC at the BS and results in high energy consumption at MTDs. As a result, it is of the utmost significance to thoroughly focus on studying the power control problem to suitably deal with the inter-user interference and thus further boost the NOMA network gain.

As well as the power control, the user grouping constitutes a fundamental pillar for the design of NOMA schemes. Indeed, despite its distinctive characteristics, we can not turn a blind eye to the limitations of NOMA. Ideally, multiple users are admitted to share a particular RB to reach a high spectral efficiency [8]. However, accommodating a huge number of users comes at the cost of emerging co-channel interference and thus an increased computational complexity of the SIC, which in turn may spoil the system performance. Thereafter, it is neither feasible nor efficient to jointly superimpose all the users’ signals using one RB [9]. Hybrid NOMA network represents an alternative approach, in which users are divided into multiple NOMA groups. Orthogonal RBs are assigned to these groups so that the members of each group share a given RB to simultaneously transmit their signals. Obviously, establishing hybrid NOMA networks relies heavily on the user grouping strategy, which seeks to strike a meaningful trade-off between NOMA gains and interference effects. With this in mind, we consider PD-NOMA scheme in the context of a hybrid NOMA network and we investigate the user grouping problem intertwined with the power allocation issue. Therefore, such combined problems need to be solved through joint optimization.

Game theory has emerged as an analytical framework to provide interesting solution concepts to efficiently deal with the selfish nature of wireless devices and provide flexible solutions to critical optimization problems such as power management, user grouping and wireless channel allocation. [10]. Typically, game theory studies the interaction between each player and every other player in the system. By doing so, to address densely deployed networks, a large number of equations must be solved, which leads to an inherent mathematical complexity. To deal with this burdensome task, mean field game (MFG) has received a significant attention as an advanced tool that can cope with the presence of a large population and alleviate the mathematical complexity of the game analysis [11]. Indeed, in such a game, each device is called upon to focus on how to cope with the collective behavior of its opponents, rather than being concerned with the specific individual strategy of each. Here, the collective effect faced by the devices represents the mean field and stands for the distribution of the system state over the user set [12]. In this way, MFG can simplify the resolution of the power control problem by drastically reducing the mathematical complexity to a two-body complexity rooted in two tractable combined equations, the Hamilton-Jacobi-Bellman (HJB) and the Fokker-Planck-Kolmogorov (FPK) equations. In fact, the HJB characterizes the interactions between the players and the mean field, and then allows each player to make its own decision, whereas the FPK equation rules the evolution of the mean field based on the players’ decisions. Afterward, the mean field equilibrium (MFE) is obtained by iteratively solving these coupled equations.

Conventionally, the finite difference method is invoked to approach the MFE and solve the MFG [13]. Nevertheless, when the game is characterized by large state and action spaces, the finite difference method requires a higher computational burden. Meanwhile, as an alternative method, the reinforcement learning (RL) techniques have been exploited to solve the MFG [14,15,16,17]. Particularly, the multi-armed bandit (MAB) framework [18], which represents a class of RL algorithms, has been specifically adopted to optimize the resource allocation problems in the context of wireless networks. In this paper, we propose a RL approach based on the mean field theory in order to jointly solve the resource allocation and power control problem in a hybrid NOMA scenario. We more specifically investigate the MAB algorithm to model the competitive behaviors of the players over the set of arms, i.e., set of available RBs, with an eye toward maximizing their rewards.

Reference [19] is a conference version of this paper. Indeed, the present work extends the previous work by providing two resource allocation algorithms based on the combination of MAB approaches and MFG framework. Different from the conference version, we delve into the calculation of total expected regret accumulated during the learning process by adding more regret analysis to this work. In addition, we included extensive system-level simulation results to reveal the robustness of the proposed approaches and demonstrate their performance in very dense networks. The significant contributions of this paper include the following:

• We propose a NOMA system where the BS is not concerned by allocating power levels to MTDs, rather it only broadcasts limited feedback to users. Thereby, we are able to alleviate the performance drop observed with almost all existing grant-free approaches.

• We derive two developed MFG-based MAB approaches in which the MAB technique is invoked to enable the MTDs to self-organize into coalitions. Then, the MFG is applied such that MTDs can adjust their transmit power levels based on the received MFI.

• Our proposed algorithms are designed with the aid of the $\epsilon$-decreasing greedy and the upper confidence bounds (UCB) methods in order to allow the devices to decide which coalition it is better to belong to.

• Regret analysis is presented to evaluate the performance of the proposed MFG-based MAB techniques. We show that the regret incurred during the learning process evolves logarithmically.

• We provide numerical simulations that underline the features of the combined MFG and MAB frameworks under several scenarios made up of different numbers of devices and RBs.

In light of the above, we construct the rest of this paper as follows. The discussion of related work and contributions is presented in the next section. We introduce our system model and the considered assumptions in Sect. 3. The MFG approach is investigated in Sect. 3.2 to model the power control problem. Section 4 is devoted to deriving two distributed MFG-aided MAB algorithms in order to address the joint problems of RB selection and power allocation. To assess the performance of the proposed approaches, numerical results are provided in Sect. 5. Finally, Sect. 6 concludes the paper.

2 Related work and contributions

Usually, wireless communication networks are characterized by an important level of interference encountered by each user. In an effort to alleviate the interference effects, numerous research contributions have been devoted to modeling the power control problem under game theory setting. For instance, the authors in [20] have formulated a hierarchical game approach to illustrate the performance of multi-carrier systems in terms of energy efficiency. In [21], a game-theoretic approach has been proposed for the Aloha-based NOMA (NM-ALOHA) scheme in order to enable the users to organize their transmissions by selecting appropriate transmission probabilities. A cooperative coalitional game has been investigated in [22] to derive a user clustering algorithm with the aim of optimizing power allocation in hybrid NOMA-based cognitive radio networks. In contrast, while a non-cooperative game has been applied in [23] to address the joint user selection and power allocation issues for MTC underlying NOMA heterogeneous networks taking into account the energy efficiency requirements. In our prior work [24], we have established a hybrid NOMA network upon invoking a bi-level game theoretical framework made of a Hedonic game on top of a non-cooperative game. The proposed bi-level game enables the devices to first organize themselves into NOMA coalitions, and then autonomously determine the transmit power levels to use in order to deliver their messages.

Meanwhile, Bayesian optimization has been widely invoked as a promising mathematical framework to effectively identify solutions to black-box optimization problems. It has been applied to handle hyperparameters resource allocation problems by improving decentralized performance and effectively balancing exploration and exploitation [25]. For instance, in [26], the Bayesian optimization has been used to enhance uplink power allocation performance by modeling a black-box objective function with continuous variables as a Gaussian process. The authors in [27] have proposed Bayesian optimization-based technique for online dynamic management in time-varying systems. They have focused on jointly optimizing the wireless devices’ decisions on the binary computation task offloading and analog-amplitude resource allocation policies while taking into account the constraint of energy-delay cost. In [28], the authors have applied the Bayesian optimization to improve the learning efficiency in Unmanned Aerial Vehicles(UAV)-assisted networks by guiding UAVs’ trajectory to more rewarding action allowing each of which to deviate from fruitless action explorations. Generally, Bayesian-based approaches use Gaussian processes (GP) to provide flexible solutions for desired objective functions while optimizing the GP’s hyperparameters. However, the major limitation of Bayesian optimization is its inability to scale to high-dimensional optimization problems, especially in dense networks. Indeed, although Bayesian optimization is an advantageous method for the black-box optimization of low dimension, it requires sampling a large number of hyperparameters in order to model the posterior prediction distribution, resulting in an increased computational complexity and an inefficient optimization problem at high network loads. Thus, Bayesian optimization-based approaches struggle with high-dimensional functions and are therefore restricted to moderate-dimensional problems. [29, 30]. Consequently, invoking such a method for real-world problems of dense wireless networks is costly and prohibitive, as it is computationally unaffordable for low-power IoT devices and represents an overwhelming burden for mMTC scenarios. [31].

Alternatively, MFG has sparked a considerable interest in suitably designing distributed power control for densely deployed wireless networks. Some contributions have mainly focused on the interplay between NOMA approach and the mean field theory. For example, in [32], MFG has been exploited in order to meet the trade-off between quality of service requirements and the energy consumption for a code domain NOMA scheme in an mMTC scenario, while in [33], the authors have adopted MFG to derive a distributed power control policy for NOMA-assisted UAV networks. In our previous contribution [34], we have leveraged the features of MFG in the context of MTDs underlying uplink NOMA network by conducting the analysis of the proposed approach through only two combined equations HJB and FPK. Interestingly, the formulated game has modeled the mass behavior of the devices as a mean field interference (MFI) that each user has to interact with in order to make its decision. Particularly, we have derived a distributed power control policy to iteratively achieve the MFE using the finite difference method. However, we have been interested only in the case where each user is unable to choose the most appropriate RB to use or the best coalition to join, it can only adjust its power level to the network load. Now, we aim to make each user able to choose its RB at each time slot so that it can deviate from its current coalition. Such a decision requires usually more information about the other coalitions. In other words, in this paper, we seek to make the devices autonomous in their choice of groups while modeling their behavior in each group as the mean field, so that each device can adapt its transmission strategy to the system load. In this case, we are dealing with the joint optimization problems of the user grouping and the power control. In contrast to [34] in which we have applied the finite difference method to solve the power control problem, invoking such a method to jointly deal with the user grouping and the power control problems is not practically affordable, especially for high-dimensional state and action spaces. To overcome this issue, we turn our attention to MAB-based approaches in this paper.

Recently, RL algorithms have been adopted as an advanced tool to solve the MFG. Indeed, the amalgam of MFG and RL algorithms has garnered a substantial attention, as it provides useful insights into how to effectively deal with the resource allocation problems. The authors in [14] have designed RL-based MFG algorithm with the intention of maximizing the sum rate among users in the context of UAV-enabled mmWave systems. Shi et al. have considered in [15] a cooperative multi-access edge computing framework and resorted to the deep RL to learn the optimal policy in order to achieve the Nash equilibrium of MFG. [17] and [16] have first applied the MFG framework to model the collective behavior of multi-user NOMA scenarios in mobile edge computing systems. Then, deep RL algorithms have been proposed to solve the game and optimize the resource allocation between users in NOMA clusters. Concomitantly, within the MAB framework, there are some contributions that have examined the NOMA approach, such as [35,36,37]. In fact, authors of [35] have been interested in organizing the user transmissions as well as their power allocation coefficients by invoking the MAB framework. In [36], a distributed MAB algorithm has been proposed in order to handle the channel access and power control issues, whereas in [37] a MAB learning approach has been conceived to address the scheduling problem for fast-grant MTDs.

At the time of writing, although the literature provides some contributions that have combined the MFG and the RL techniques and others that have applied the MAB algorithm in NOMA-based networks, there is no published literature that has investigated the combination of the MFG framework and the MAB approach underlying NOMA networks. To the best of our knowledge, our proposed approach is the first work that focuses on jointly solving the user grouping and power control problems using MFG-based MAB approaches for NOMA systems.

3 Methods

3.1 Network model

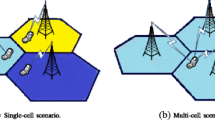
Consider an uplink NOMA network, as depicted in Fig. 1, where a single BS is located at the center of the network, whereas a set of N MTDs are independently scattered throughout the coverage area. The positions of the devices are modeled using homogeneous Poisson point processes (PPP) $\Phi _N$ with density $\lambda _N$ [38]. It is noteworthy that PPP model can conveniently abstract the network in which the MTDs are randomly distributed and each device generates its own traffic according to its position without any need for particular human intervention. Throughout this paper, we consider a hybrid NOMA scenario consisting of K groups, each of which is called a coalition. The available bandwidth is split up into K RBs, $N>>K$, which are orthogonally assigned to the groups so that each group of MTDs uses one RB for non-orthogonal communication with the BS. More precisely, when a device i is a part of a given coalition, to which the k-th RB is allocated, the channel coefficient between this device and the BS is represented by $h_{k,i}=\frac{g_{k,i}}{l_i}$, where $g_{k,i}$ and $l_i$ denote the Rayleigh fading and the path loss, respectively. We adopt the free-space path loss model [39] to define the path loss.

In this way, the devices belonging to each coalition transmit their messages through the associated RB. Hence, the received overlapped signals at the BS from the k-th group can be given as:

$$\begin{aligned} y_k=\sum \limits _{i=1}^{N} h_{k,i}\sqrt{p_{k,i}}s_{k,i} + b_k, \end{aligned}$$

(1)

where $s_{k,i}$ and $p_{k,i}$ represent the transmit symbol and the power coefficient of the device i through the k-th RB, respectively. The transmit power of user i is constrained by the maximum transmit power $P^{max}$. In addition, $b_k$ denotes the additive noise of variance $\sigma ^2$ over the RB k. Once the BS receives the superimposed signals, it applies the SIC procedure to detect and recover each user’s signal.

Consider a particular coalition consisting of a number of MTDs that are allowed to access one RB in order to transmit their signals non-orthogonally. In order to enable the BS to effectively decode the signals from the devices, the signal-to-interference-plus-noise ratio (SINR) of each MTD should be greater than the SINR threshold $\gamma _{th}$. Since we investigate a hybrid NOMA scenario, the BS applies the SIC concept to the combined signals received from each coalition on the allocated RB. Thus, each MTD faces an interference level only from the devices in the same coalition and there is no co-interference between the users belonging to different groups.

In order to differentiate the users sharing the same coalition, we have defined in [24], target signal-to-noise ratio (SNR) coefficients $\Gamma =\{\gamma _1,\cdots ,\gamma _{\alpha }\}$ where $\alpha$ is the maximum number of MTDs that can be allocated and allowed to simultaneously transmit using one RB at each time slot. Therefore, with the aim of handling the access of the MTDs to the same RB and managing their activities, we use an access probability denoted by $p_t$. In [34], we have proven that the probability of successfully decoding a user’s signal, given as $P_{s}={p_t}(1-\frac{p_t}{\alpha })^{N-1}$, is maximized when the access probability is $p_t=\frac{\alpha }{N}$.

Now, we consider a dense deployment scenario in which a large number of users are involved. Thus, it becomes increasingly challenging to ensure the successful transmission of different devices, especially at high network loads. Therefore, in an effort to handle the massive connectivity of the devices, we model the resource allocation problem as a MFG framework in the next section. Note that in what follows, the RB index k is omitted to simplify the notation.

3.2 Mean field game for power control

With the aim of deriving a distributed algorithm based on the MFG framework, we first pose the power allocation problem in the context of the differential game theory.

Definition 1

Let G be the differential game for the power control problem of the proposed approach, where $G=(\mathcal {N},\{\mathcal {P}_i\}_{i\in \mathcal {N}},\{\mathcal {S}_i\}_{i\in \mathcal {N}},\{\mathcal {Q}_i\}_{i\in \mathcal {N}},\{\ U_i\}_{i\in \mathcal {N}})$ and

• Set of players $\mathcal {N}=\{1 \dots N\}$: the set of devices, considered as the players of our proposed game.

• Set of transmit power $\{\mathcal {P}_i\}_{i\in \mathcal {N}}$: denotes set of power levels of device i.

• State space $\{\mathcal {S}_i\}_{i\in \mathcal {N}}$: for each device, $s_i(t)=\{h_i(t),k_i\}$ is its state at each time t, which is the combination of its channel gain $h_i$ and the RB $k_i$ on which this device transmits its signals.

• Control policy $\{\mathcal {Q}_i\}_{i\in \mathcal {N}}$: represents the control strategy to be determined by the device to make its decision with the aim of maximizing its own utility over a period of time T.

• Utility function $\{U_i\}_{i\in \mathcal {N}}$: each user seeks to deliver its packets successfully while consuming less energy. For this reason, our utility function can be given as the Eq. (2), which has units of bits/joule, to measure the energy efficiency.

3.2.1 Utility function

In game theory, the design of the utility function is crucial, as it catches how satisfied a user is when playing the game. Indeed, a packet is successfully decoded when the device achieves an SINR higher than $\gamma _{th}$. On the other hand, in the context of MTDs having limited energy budgets, if a given device reaches a high SINR, it obviously consumes a lot of energy uselessly. In this regard, in our work, the objectives of the players are to meet their SINR requirements and to reduce their power consumption as much as possible. With this in mind, we adopt the following utility function to adequately address the above trade-off:

$$\begin{aligned} U_i(p_i,\textbf{p}_{-i})=\frac{f(\gamma _i)}{p_i}, \end{aligned}$$

(2)

where $\textbf{p}_{-i}$ denotes the transmit power of all the MTDs excluding the i-th device and $\gamma _i$ represents the SNR value for the device i. The efficiency function, which is represented by $f(\cdot )$, reflects the packet success rate. It is an increasing and continuous function that has a sigmoidal shape. We assume that $f(0)=0$ and $f(\gamma _{th})=f(\infty )=1$. In addition, we have an efficiency of 1 if the SINR is greater than $\gamma _{th}$ which means that the packet is successfully received by the BS. More details on the efficiency function can be found in [24].

Indeed, each user seeks to find the optimal power control strategy $\mathcal {Q}_i^*(t)$ that enables it to reach its maximum utility value at time $t \in [0, T]$. To this end, the user has to determine the value function that maximizes its utility as follows:

$$\begin{aligned} v_i(t)=\max \limits _{p_i(t)} \textrm{E}\left[ \int _{t}^{T} U_i(p_i(\tau )) \,d\tau \right] ,\quad t\in [0,T]. \end{aligned}$$

(3)

Once each user has calculated its value function and determined its optimal power control, the differential game is solved. However, this leads to an inherent mathematical complexity, especially for a large population. On the other hand, when a densely deployed network is investigated, a single user’s strategy has a negligible impact on the entire network. In contrast, the effect of the mass on each device is significant. Henceforth, each player is no longer interested in the specific individual strategy of each of its opponents but it is more concerned with the effect of their collective behavior in making its decision. For example, in the case of a densely deployed Wireless Sensor Network (WSN), it is more important for a device to know how many devices sharing the same RB it is going to use rather than having complete knowledge about all the users. In this regard, when a large number of devices are involved in the game, the differential game can be shifted towards the MFG.

3.2.2 Mean field

Mean field definition is one of the essential ingredients of the MFG framework. It represents the state dynamics over the set of devices and reflects their collective behavior. Thus, the mean field for every state s and at any time t is defined as follows:

$$\begin{aligned} m(t,s)=\underset{N \rightarrow +\infty }{lim}\frac{1}{N} \sum _{i=1}^{N}\mathbbm {1}_{\{s_i(t)=s\}}, \end{aligned}$$

(4)

where the $\mathbbm {1}$ is an indicator function which returns 1 when ${\{s_i(t)=s\}}$ holds and zero, otherwise. Generally, the MFG game is characterized by the fulfillment of some assumptions. Firstly, the rationality of the players is required, i.e., each of them seeks to optimize its own utility. Secondly, the interactions between the devices are no longer one-to-one interactions. Instead, each player is asked to interact with the mean field. Then, when a dense network is envisaged, a large population can be modeled as a continuum of players. Finally, the last assumption relies on the interchangeability of the states, which means that the MFG game’s outcome is not impacted by any permutation of states between players and that the state evolution of the players does not depend on a particular device [40].

3.2.3 Mean field interference

In the context of the MFG framework, each player is called upon to interact with the mass behavior of its opponents in order to make its own decision. In our case, this mass behavior is captured by the MFI. Thus, the latter can be defined as the weighted sum of active players sharing the RBs. Since the activity of each device is controlled by the access probability $p_t=\frac{\alpha }{N}$, the aggregated interference perceived by any device can be expressed as:

$$\begin{aligned} I_i(t)=\frac{\alpha }{N}\sum \limits _{j\ne i}|h_j(t)|^2 p_j(t). \end{aligned}$$

(5)

Furthermore, we have proven in [34] that mean interference term can be given as follows:

$$\begin{aligned} I^{mean}(t)=\underset{N \rightarrow +\infty }{lim}\ I_i(t) = \alpha \int |h(t)|^2 p(t) m(t,s) ds. \end{aligned}$$

(6)

Indeed, the BS collects the information from different devices when they upload their local information, namely their states and their transmit power levels. Then, it determines the mean field (4) and the MFI (6). This MFI can also be estimated by the BS using the received superimposed signals if it does not have perfect knowledge of users’ Channel State Information (CSI) for example. Then, the BS broadcasts the MFI to the devices participating in the game. Once each of them receives interference information, it estimates the interference level that it perceives. In fact, by performing the SIC procedure, the BS cancels part of the interference perceived by each device depending on the distance to this device before decoding its signal. Hence, each user can estimate the interference level from its perspective as:

$$\begin{aligned} \tilde{I}_i(t)= \left( 1-\frac{r_i}{R}\right) I^{mean}(t), \end{aligned}$$

(7)

where $r_i$ represents the distance between the ith-MTD and the BS, whereas R is the cell radius. Consequently, in response to this estimated interference, each user calculates its SINR value as well as its utility as follows:

$$\begin{aligned} \gamma ^{mean}(t)= & {} \frac{p(t) |h(t)|^2}{\sigma ^2+\tilde{I}_i(t)}, \end{aligned}$$

(8)

$$\begin{aligned} U^{mean}(t)= & {} \frac{f( \gamma ^{mean}(t))}{p(t)}. \end{aligned}$$

(9)

3.2.4 Mean field game equations

The formulated MFG is expressed as a combination of two fundamental equations, namely the HJB and the FPK. We have derived these equations in our previous work [34] as (10) and (11), respectively.

$$\begin{aligned}{} & {} -\frac{\partial v(t)}{\partial t}= \max \limits _{p(t)}[ U(t,p(t))+\nabla _{s}{v(t,s(t))}.\frac{\partial s(t)}{\partial t}], \end{aligned}$$

(10)

$$\begin{aligned}{} & {} \frac{\partial m(t,s)}{\partial t}+\nabla _s (m(t,s).\frac{\partial s}{\partial t})=0. \end{aligned}$$

(11)

Indeed the HJB equation allows each player to deal with the mean field, while the FPK equation governs the evolution of the mean field in response to the players’ decisions. The interaction between these coupled equations leads to the convergence point, namely the MFE. In [34], we have adopted the finite difference method to numerically solve the MFG. Upon invoking this method, we end up with an optimal power strategy given by:

$$\begin{aligned} p(t)=\gamma ^{*} \frac{\tilde{I}(t)+\sigma ^2}{|h(t)|^2} \end{aligned}$$

(12)

where $\gamma ^{*}$ is the solution to

$$\begin{aligned} \gamma f^{\prime }(\gamma )-f(\gamma )=0. \end{aligned}$$

(13)

The aforementioned approach relies on the fact that each user, at each time t, joins the cluster that corresponds to its best channel. Now, if a device aims to deviate from its current coalition, it needs to choose which coalition is preferable to be part of. Such a decision requires usually more information about the other coalitions. In other words, in this paper, we seek to make the devices autonomous in their choice of groups while modeling their behavior in each group as the mean field, so that each device can regulate its transmit power in response to the mean field. In this case, we are dealing with the joint optimization problems of the user grouping and the power control. Therefore, applying the finite difference method to solve these combined problems is not practically affordable, especially for high-dimensional state and action spaces. With this in mind, we spotlight MAB-based approaches in the following.

4 Multi-armed bandit framework

In this section, we model the user grouping problem intertwined with the power control issue as MFG-based technique underlying a multi-user MAB approach. Firstly, the players adopt the MAB tool to arrange themselves into several NOMA groups. Then, within each group, the devices apply the MFG with the aim of autonomously regulating their power levels based on feedback information received from the BS.

We propose two MFG-based MAB algorithms using the $\epsilon$-decreasing greedy and UCB techniques in order to enable each user to make a move upon selecting an arm with the aim of maximizing its own utility. In this direction, we define the set of devices as the set of learners and the set of available RBs as the arms to be chosen by the learners. Let $\mathcal {A}_{i}=\{a_1 \dots a_K \}$ denotes the set of possible arms for each device i. Indeed, at time slot t, the device i first pulls an arm $a_i$, then it joins the coalition corresponding to this chosen RB. After transmission, the BS informs each device whether its packet was received and decoded successfully or not by sending back a reward value $r_i(t,a_i)$, allowing it in turn to determine its utility value $U_i(t,a_i)$. In fact, we assume that upon picking its arm $a_i$, the device determines the appropriate transmit power $p_i(t,a_i)$ to be used by being part of the chosen coalition based on the MFI received from the BS. Then, the device transmits its message to the BS. The latter applies the SIC procedure to separate the superimposed signals. Thus, if the packet of the device i is successfully decoded, it receives $r_i(t,a_i)=1$ and its utility is calculated as in the Eq. (9). Otherwise, it receives $r_i(t,a_i)=0$ which implies that the user has no utility by choosing the arm $a_i$ at time t.

4.1 $\epsilon$ - decreasing greedy

The $\epsilon$-greedy method is widely used as one of the most prominent solution concepts for the arm selection problem in the MAB framework [18]. It allows users to explicitly manage an exploration-exploitation trade-off with an exploration rate $\epsilon$. Indeed, at each time slot, each device decides either to explore or exploit. In other words, it arbitrarily picks an arm with a probability of $\epsilon$ or it selects with a probability of $1-\epsilon$, the optimal arm which gives it the highest average reward $Q_t(i,:)$ considering the past observations. Nevertheless, if the exploration parameter $\epsilon$ is constant for the entire process, we end up with a sub-optimal allocation and a linear regret which in turn affects the overall system performance. In order to overcome this issue, the exploration coefficient $\epsilon$ has to be adjusted over time. Thus, in our paper, we apply the $\epsilon$-decreasing proposed by [41] whose key idea is outlined in the Algorithm (1). By doing so, we define the adaptation of time-dependent exploration parameter as follows:

$$\begin{aligned} \epsilon _t=\min (1,\frac{\epsilon _0}{t}), \end{aligned}$$

(14)

where $\epsilon _0 > 0$ is the initial exploration parameter. In this way, at the beginning of the learning process, more exploration is performed, allowing each user to discover the arm space as much as possible. Then, $\epsilon _t$ is dynamically regulated as a function of the learning time. Thus, the user can now properly select its best arm according to its acquired experience.

Algorithm 1

$\epsilon$-decreasing greedy

4.2 Upper confidence bounds algorithm

UCB algorithm was first proposed by [41] and broadly adopted to deal with the arm selection problem in MAB setting. Unlike the $\epsilon$-decreasing greedy method, UCB implicitly distinguishes between exploration and exploitation phases by selecting the arm associated with the highest average reward given the past observations. This arm is known as the UCB index and is given by the following equation for each user $i \in \mathcal {N}$:

$$\begin{aligned} a_i(t)=\mathop {\textrm{argmax}}\limits \limits _{ a \in \mathcal {A}} \left[ u_i(t,a) \right] \end{aligned}$$

(15)

with $u_i(t,a)$ is UCB of a given arm a, given as:

$$\begin{aligned} u_i(t,a)= \hat{Q_i}(t,a)+\sqrt{\frac{2\log (t)}{n_{i}(t,a)}}, \end{aligned}$$

(16)

where $n_{i}(t,a_i)$ is the number of times the arm $a_i$ and has been played during the previous time slots. In fact, the UCB at time slot t gathers two components, the upper confidence bias $\psi _t(a_i)=\sqrt{\frac{2\log (t)}{n_{i}(t,a_i)}}$ and empirical average of the observed rewards $\hat{Q_i}(t,:)$ of playing the arm $a_i$ up to time t. Particularly, $\psi _t(a_i)$ which depends on $n_{i}(t,a_i)$, is used to encourage the exploration and serves as an interval around the average reward. Thus, the more the arm is played, the more this interval is shrunken, which in turn reduces the probability of discarding this arm in future observations. Consequently, UCB concept tends to effectively meet the trade-off between the exploration and exploitation phases.

4.3 Distributed learning algorithms with multi-armed bandit

In this section, we derive two distributed MFG-based MAB algorithms to solve the joint problems of user grouping and power control in a hybrid NOMA network. The first algorithm, illustrated in Algorithm (3), adopts the $\epsilon$-decreasing greedy method, whereas the second algorithm, depicted in Algorithm (4), resorts to the UCB method with the aim of efficiently performing the decision-making process. For the two proposed methods, we assume that a device can only belong to one coalition at a time. At each time slot t, each learner i pulls an arm $a_i$ that represents the RB to use in order to deliver its packets. Then, it joins the coalition associated with this chosen RB.

Algorithm 2

Parameters update

Algorithm 3

$\epsilon$-decreasing MFG-based MAB method for joint user grouping and power control: $\epsilon$-decreasing MFG

Algorithm 4

UCB MFG-based MAB method for joint user grouping and power control: UCB-based MFG

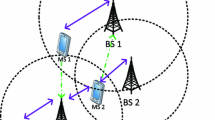
In fact, when the user i attempts to access the channel, it implicitly uploads to the BS information about its state $s_i$ and its selected arm $a_i$. Subsequently, the BS broadcasts feedback information about the MFI $I^{mean}(t)$. Then, by being part of the chosen coalition, each device estimates its interference level $\tilde{I}(t,a_i)$, according to its distance from the BS and calculates its power level $p_i(t,a_i)$ in response to the estimated interference. After the transmission, the BS processes the SIC procedure and sends back a reward $r_i(t,a_i)$ to the device i to inform it whether its packet was successfully decoded or not, enabling it to update its parameters as indicated in the Algorithm (2). At the end of time slot t, the BS updates the mean field m as well as the MFI $I^{mean}$ for time slot $t+1$. This interaction between each user and the BS is illustrated in Fig. 2.

4.4 Regret analysis

The performance measure of the MAB-based techniques is commonly related to the calculation of total expected regret accumulated during the learning process. Generally, it is defined as the difference between the actually obtained reward and the one that would have been obtained if the optimal arm had been selected. Hence, for the single device’s case, the expected regret over a period of T time slots can be expressed as follows

$$\begin{aligned} R_i=TQ_i^*-\sum _{t=1}^{T} \mathbb {E}[r_i(a_i(t))], \end{aligned}$$

(17)

where $r_i(a_i(t))$ is the received reward by the i-th device at time t by pulling the arm $a_i(t)$ and $Q_i^*$ is its average reward by selecting the optimal armi.

Since the scenario under consideration is composed of N users, the total expected regret is given by:

$$\begin{aligned} \begin{aligned} R_{MAB}&=\sum _{i=1}^{N}R_i\\&=T\sum _{i=1}^{N}Q_i^*-\sum _{i}\sum _{t=1}^{T} \mathbb {E}[r_i(a_i(t))]. \end{aligned} \end{aligned}$$

(18)

4.4.1 Regret of the $\epsilon$- decreasing MFG algorithm

Now, we analyze the regret incurred when the $\epsilon$-decreasing MFG Algorithm (3) is invoked. In doing so, we start by showing that learning the best arm can be performed in finite time as Lemma 1:

Lemma 1

The proposed $\epsilon$-decreasing MFG algorithm identifies an $\epsilon$-best arm with at least probability $1-{\delta }$ when an arm sampling is carried out l times, where:

$$\begin{aligned} l=\frac{1}{2\epsilon ^2}\log (\frac{2K}{\delta }). \end{aligned}$$

(19)

where ${\delta } \in [0,1]$ denotes the probability of failure.

Proof

Denote by $\epsilon$-best arm $a{'}$ an arm whose reward $r{'}$ is different from the best reward $r^*$ by less than $\epsilon$, that is: $|r^*-r{'}| \le \epsilon$. Indeed, the user needs to sample each arm l times in order to obtain an $\epsilon$-best arm with a probability of $1-\frac{\delta }{K}$. Thus, we have

$$\begin{aligned} P(|r^*-r{'}| > \epsilon ) \le \frac{\delta }{K}. \end{aligned}$$

(20)

On the other hand, according to Hoeffding inequality, we obtain:

$$\begin{aligned} P(|r^*-r{'}| > \epsilon ) \le 2e^{-2l\epsilon ^2}. \end{aligned}$$

(21)

Consequently, we end up with:

$$\begin{aligned} l=\frac{1}{2\epsilon ^2}\log (\frac{2K}{\delta }). \end{aligned}$$

(22)

Henceforth, when a device samples an arm l times, $\epsilon$-best reward is obtained with a probability of $1-\frac{\delta }{K}$. $\square$

Lemma 2

All the devices can learn their best arms with a high probability, at least $1-{\delta }$, by adopting the $\epsilon$-decreasing MFG algorithm $T^*$ rounds, where

$$\begin{aligned} T^*=\frac{l}{\alpha (1-\frac{1}{N})^{(N-1)}}. \end{aligned}$$

(23)

Proof

We have shown in Sect. 3 that the probability of successfully decoding the user’s packet can be defined as $P_{s}=\frac{\alpha }{N}(1-\frac{1}{N})^{(N-1)}$. Therefore, the collision probability $P_{c}$ of the set of N players over K RBs can be given as:

$$\begin{aligned} \begin{aligned} P_{c}&=1-\sum _{n=1}^{N}\sum _{k=1}^{K} \frac{\alpha }{N}(1-\frac{1}{N})^{(N-1)}\\&=1-N.K.\frac{\alpha }{N} (1-\frac{1}{N})^{(N-1)} \\&=1-\alpha K(1-\frac{1}{N})^{(N-1)}. \end{aligned} \end{aligned}$$

(24)

Hence, the number of successful samples for a given arm over a period of time t is expressed as follows:

$$\begin{aligned} \begin{aligned} N_{s}&=(1-P_{c})\frac{t}{K}\\&=\alpha t (1-\frac{1}{N})^{(N-1)}, \end{aligned} \end{aligned}$$

(25)

For a period of $T^{*}$ time slots, we have $N_{s}=l$, where l given in (19), which in turn results in:

$$\begin{aligned} T^{*}=\frac{l}{\alpha (1-\frac{1}{N})^{(N-1)}}. \end{aligned}$$

(26)

$\square$

Lemma 3

The expected regret incurred over a horizon T by N devices employing the $\epsilon$-decreasing MFG algorithm over K arms is upper bounded as follows:

$$\begin{aligned} R_{\epsilon -decreasing MFG}=\mathcal {O}(\log {}T). \end{aligned}$$

(27)

Proof

The regret accumulated during a period of duration t can be analyzed as the sum of the regret incurred during the two phases, i.e., exploitation phase $R_1(t)$ and exploration phase $R_2(t)$. According to Algorithm (1), when a given user pulls a random variable x that allows it to explore, i.e., $x>=\epsilon _t$, and choose its best-learned arm over a period of t time slots, it will not regret. Hence $R_2(t)=0$. On the other hand, the exploration probability for our proposed approach at time t is given as $\epsilon _t=\min (1, \frac{\epsilon _0}{t})$. Subsequently, for each device, the expected regret accumulated during the exploration phase over a period of time t can be given as

$$\begin{aligned} R_{2,i}(t) \le \sum \limits _{t'=1}^{t} \epsilon _{t'}=\epsilon _0+ \sum \limits _{t'=\epsilon _0+1}^{t} \epsilon _{t'}. \end{aligned}$$

(28)

The discrete sum can be approximated using an integral:

$$\begin{aligned} R_{2,i}(t) \le \epsilon _0+\epsilon _0 \int _{\epsilon _0}^{t-1} \frac{1}{x} \,dx =\epsilon _0+\epsilon _0 \log (\frac{t-1}{\epsilon _0}). \end{aligned}$$

(29)

Then the total expected regret incurred by all devices is bounded by:

$$\begin{aligned} \begin{aligned} R_2(t)&\le N \epsilon _0+N\epsilon _0 \log (\frac{t-1}{\epsilon _0}) \\&\le N \epsilon _0+N\epsilon _0\log (t) \\&=\mathcal {O}(\log {}t). \end{aligned} \end{aligned}$$

(30)

$\square$

4.4.2 Regret of UCB-based MFG algorithm

Lemma 4

the expected regret accumulated when the UCB-based Algorithm (4) is invoked by N devices over a time period of T is upper bounded by:

$$\begin{aligned} R_{UCB-based MFG} \le 8 N \log (T) \sum _{k=1}^{K} \frac{1}{\Delta _k}+4 N \sum _{k=1}^{K} \Delta _k, \end{aligned}$$

(31)

therefore

$$\begin{aligned} R_{UCB-based MFG}=\mathcal {O}(\log {}T), \end{aligned}$$

(32)

where $\Delta _k=Q(k^{*})-Q(k)$ is the deviation function that measures the instantaneous loss of playing an arm $a_k$.

Proof

Let $c_{k_t}(t)=\sqrt{\frac{2\log (t)}{s_k}}$ be the confidence interval of a given arm $k_t$ at time slot t when it is played $s_k$ times. Note that throughout this proof the user index i is omitted to simplify the notation. According to [41], the cumulative regret of a single user after T rounds can be defined as

$$\begin{aligned} R_{UCB}(T)= \sum _{k=1}^{K} \Delta _k n(t,k). \end{aligned}$$

(33)

where $\Delta _k=Q(k^{*})-Q(k)$ and n(t, k) is the number of times the k-th arm has been played. Therefore, in order to bound the regret incurred by the UCB-based algorithm during T rounds, we can upper bound the number of pulls of every arm k up to T given as:

$$\begin{aligned} n(T,k)=1+\sum _{t=K+1}^{T}\mathbbm {1}{\{k_t=k\}}, \end{aligned}$$

where the $\mathbbm {1}$ is an indicator function that is equal 1 when ${\{k_t=k\}}$ holds and zero, otherwise. Generally, during the first K time slots, each arm is played once in order to compute a non-zero UCB index for each arm. Then, the algorithm pulls the arm with the highest UCB index at every $t \ge K + 1$. Consider a positive integer l, the above equation can be rewritten:

$$\begin{aligned} n(T,k)\le l+\sum _{t=l}^{T}\mathbbm {1}{\{k_t=k,~n(t-1,k)\ge l\}}, \end{aligned}$$

(34)

if $k_t=k$ then $u(t,k^{*})<u(t,k)$ which means:

$$\begin{aligned} \hat{Q}_{n_{t-1,k^{*}}}(t-1,k^{*}) +c_{n_{t-1,k^{*}}}(t-1)< \hat{Q}_{n_{t-1,k}}(t-1,k) +c_{n_{t-1,k}}(t-1). \end{aligned}$$

Thus, the inequality (34) can be written as:

$$\begin{aligned} \begin{aligned} n(T,k)&\le l+\sum _{t=l}^{T}\mathbbm {1}{\{\hat{Q}_{n_{t-1,k^{*}}}(k^{*}) +c_{n_{t-1,k^{*}}}(t-1)< \hat{Q}_{n_{t-1,k}}(k) +c_{n_{t-1,k}}(t-1),~n(t-1,k)\ge l\}}\\&\le l+\sum _{t=l}^{T}\mathbbm {1} {\{ \min \limits _{0<s^{*}< t} \hat{Q}_{s^{*}}(k^{*}) +c_{s^{*}}(t-1)< \max \limits _{l<s_k< t} \hat{Q}_{s_k}(k) +c_{s_k}(t-1)\}}\\&\le l+\sum _{t=l}^{T}\sum _{s^{*}=1}^{t-1}\sum _{s_k=l}^{t-1}\mathbbm {1} {\{ \hat{Q}_{s^{*}}(k^{*}) +c_{s^{*}}(t)< \hat{Q}_{s_k}(k) +c_{s_k}(t)\}}. \end{aligned} \end{aligned}$$

(35)

Then $\hat{Q}_{s^{*}}(k^{*}) +c_{s^{*}}(t)< \hat{Q}_{s_k}(k) +c_{s_k}(t)$ implies that at least one of the following events must hold

$$\begin{aligned}{} & {} \hat{Q}_{s^{*}}(k^{*}) \le Q(k^{*}) -c_{s^{*}}(t) \end{aligned}$$

(36)

$$\begin{aligned}{} & {} \hat{Q}_{s_k}(k) \ge Q(k)-c_{s_{k}}(t) \end{aligned}$$

(37)

$$\begin{aligned}{} & {} Q(k^{*}) < Q(k) +2c_{s_{k}}(t). \end{aligned}$$

(38)

Using Hoeffding’s inequality, the probability of the events in (36) and (37) can be bounded as:

$$\begin{aligned}{} & {} P( \hat{Q}_{s^{*}}(k^{*}) \le Q(k^{*}) -c_{s^{*}}(t))\le e^{-4 \log (t)} \le t^{-4}. \end{aligned}$$

(39)

$$\begin{aligned}{} & {} P(\hat{Q}_{s_k}(k) \ge Q(k)-c_{s_{k}}(t) )\le e^{-4 \log (t)} \le t^{-4}. \end{aligned}$$

(40)

Consider $\Delta _k=Q(k^{*})-Q(k)$, since $c_{s_{k}}(t)=\sqrt{\frac{2\log (t)}{s_k}}$ then the equation (38) can be rewritten as:

$$\begin{aligned} Q(k^{*})-Q(k)-2c_{s_{k}}(t)= \Delta _k-2\sqrt{\frac{2\log (t)}{s_k}} < 0, \end{aligned}$$

(41)

if $s_k \ge \frac{8\log (t)}{\Delta _k^2}$ then

$$\begin{aligned} P(\Delta _k-2\sqrt{\frac{2\log (t)}{s_k}}<0 )=0. \end{aligned}$$

(42)

Thus l can be chosen as $l=\frac{8 log(T)}{\Delta _k^2}$. Consequently, in this case, we end up with:

$$\begin{aligned} \begin{aligned} n(T,k)&\le \frac{8 log(T)}{\Delta _k^2}+\sum _{t=\frac{8 log(T)}{\Delta _k^2}}^{T}\sum _{s^{*}=1}^{t-1}\sum _{s_k=\frac{8 log(T)}{\Delta _k^2}}^{t-1}\mathbbm {1} {\{ \hat{Q}_{s^{*}}(k^{*}) +c_{s^{*}}(t)< \hat{Q}_{s_k}(k) +c_{s_k}(t)\}}\\&\le \frac{8 log(T)}{\Delta _k^2}+\sum _{t=\frac{8 log(T)}{\Delta _k^2}}^{T}\sum _{s^{*}=1}^{t}\sum _{s_k=\frac{8 log(T)}{\Delta _k^2}}^{t} 2t^{-4}\\&\le \frac{8 log(T)}{\Delta _k^2}+\sum _{t=\frac{8 log(T)}{\Delta _k^2}}^{\infty }\sum _{s^{*}=1}^{t}\sum _{s_k=\frac{8 log(T)}{\Delta _k^2}}^{t} 2t^{-4}\\&\le \frac{8 log(T)}{\Delta _k^2}+1+\frac{\pi ^2}{3} \approx \frac{8 log(T)}{\Delta _k^2}+4. \end{aligned} \end{aligned}$$

(43)

By substituting the last inequality into Eq. (33), we upper bound the expected regret of a single user as follows:

$$\begin{aligned} R_{UCB}(T) \le 8 \log (T) \sum _{k=1}^{K} \frac{1}{\Delta _k}+4 \sum _{k=1}^{K} \Delta _k. \end{aligned}$$

(44)

The total expected regret incurred by all users is given as:

$$\begin{aligned} R_{UCB-based MFG} = \sum _{i=1}^{N}R_{UCB,i}(T). \end{aligned}$$

(45)

Then

$$\begin{aligned} R_{UCB-based MFG} \le N R_{UCB,i}(T), \end{aligned}$$

(46)

and

$$\begin{aligned} R_{UCB-based MFG} = \mathcal {O}(\log {}T), \end{aligned}$$

(47)

which concludes the proof. $\square$

In the next section, we present numerical results to analyze the equilibrium behaviors of the proposed MFG-based MAB approaches, i.e., the $\epsilon$-decreasing MFG Algorithm (3) and the UCB-based MFG Algorithm (4), and to demonstrate their effectiveness against the interference impact.

5 Results and discussion

In this section, we use extensive Matlab-based simulations to validate the proposed algorithms. Particularly, we consider a hybrid NOMA system made up of N devices occupying K RBs. At each time t, each user belongs to only one coalition and communicates with the BS via the RB assigned to that coalition. Simulation parameters are introduced in Table 1.

Firstly, we assess the performance of the proposed UCB-based MFG Algorithm (4) by illustrating its convergence properties. Then, we provide comparisons between the two proposed approaches, i.e., the $\epsilon$-decreasing MFG Algorithm (3) and the UCB-based MFG Algorithm (4), and other existing techniques in the literature.

Table 1 Numerical parameters

Table 2 Parameters for energy consumption

5.1 Performance metrics

In order to spotlight the features of our MFG-based MAB techniques, we adopt the following metrics:

• Number of active devices per coalition: is the average number of devices that can transmit simultaneously in each group at each time slot.

• Packet success rate: is the ratio between the number of MTDs whose packets have been successfully decoded and the number of active MTDs that decided to transmit.

• Average transmission rate: is calculated as the ratio of the number of users whose packets have been successfully decoded to the total number of MTDs in the system.

• Average utility: we assume that the utility function is calculated only when the user satisfies the SINR requirement which means when its SINR is higher than SINR threshold $\gamma _{th}$. In other words, the user has a utility value if the BS succeeds in decoding its signal upon executing the SIC, otherwise, it has no utility. Thereby, the average utility is the ratio between the utility values of users whose signals have been successfully retrieved by the BS and the total number of devices.

• Average energy: Similar to the calculation of the average utility, the average energy is calculated by considering the energy consumed when a device achieves a successful transmission.

5.2 Behavior of the UCB-based MFG approach at the equilibrium

Throughout this section, we evaluate our proposed UCB-based MFG technique for multiple hybrid NOMA scenarios in which we have N users, i.e., $N=2000$, $N=4000$, $N=6000$, $N=8000$ and $N=10000$, transmitting over $K=20$ RBs.

First, we start by showing the packet success rate over time slots in Fig. 3. It is significantly interesting to observe that the rate settles at $t=10$ ms to about 0.78 (78% of success rate). Furthermore, we can clearly see that this rate stagnates at the same value for the different cases. Thus, each MTD has the same chance of successfully sending its message regardless of the network size. Interestingly, the proposed UCB-based MFG approach provides significant interference management by allowing devices to adapt their transmission strategies to the system load. By doing so, the proposed algorithm can reduce the performance drop witnessed by almost all existing grant-free schemes, especially in dense scenarios.

In Fig. 4, we depict the average transmission rate with respect to the time slots. In contrast to Fig. 3, this rate stagnates at different values for the different network sizes, since it reflects the successful transmissions of the the total number of users in the system. Thus, the highest value is reached when the network is the most sparse, i.e., $N=2000$. Then, the average transmission rate decreases as the network becomes denser. This is mainly due to the fact that the interference effects become more challenging in the denser network.

Now, we measure the average utility as well as the average energy in Figs. 5 and 6, respectively. It is interesting to note that these figures have a similar equilibrium behavior to what we have shown in Fig. 4, which emphasizes the convergence of the UCB-based MFG approach. Hence, the proposed technique settles down at the point where the players that achieve successful transmissions, meet their desired goal of maximizing their utilities with less energy consumption. Interestingly, the highest utility value is achieved when $N = 2000$, but this also results in higher energy consumption than what can be observed in the other cases. These behaviors are achieved since the average utility and the average energy consumption are, respectively, obtained by averaging the utility values and the consumed energy of the devices that have successfully transmitted over the total number of devices in the system.

In other words, the results shown in Figs. 5 and 6 are obtained when we consider respectively the utility and the energy consumption of the successful transmission cases reflected by Fig. 4. It is worth noting that we use the model of [42] to evaluate the energy consumption of the different approaches. According to this model, a user i consumes the following energy to transmit an L-bit message :

$$\begin{aligned} {\left\{ \begin{array}{ll} L\times E_{elec}+L\times \epsilon _{fs}r_i^2 &{} \text {if}~ r_i< r_{0},\\ L\times E_{elec}+L\times \epsilon _{amp}r_i^4 &{} \text {if}~ r_i\ge r_{0}. \end{array}\right. } \end{aligned}$$

Table 2 lists the energy consumption parameters proposed by [42].

5.3 Comparison

Now, we provide a comparison between the $\epsilon$-decreasing MFG algorithm, the second proposed learning approach, i.e., UCB-based MFG algorithm, and the basic deterministic algorithm of MFG approach developed in [34]. The simulation results obtained for this comparison are devoted to the case where $N=2000$ devices sharing $K=20$ RBs over a training period of $T=500$ time slots.

In Fig. 7, we illustrate the average number of active devices that can transmit simultaneously per group with respect to the time slots. Upon comparing the $\epsilon$-decreasing MFG and UCB-based MFG algorithms, we observe that the former yields a higher value than the latter. However, this number reaches its highest value when the MFG is adopted. This is mainly due to the fact that the MFG is a deterministic approach, which means that each device has no choice but to join the cluster corresponding to its best channel. In contrast, the proposed MFG-based MAB approaches allow each device to choose its coalition using either the $\epsilon$-decreasing greedy or UCB algorithms.

Indeed, after making its choice, each user first estimates its interference level $\tilde{I}$ according to the Eq. (7) based on the MFI received from the BS. Then, the user calculates its power level as in the Eq. (12), in response to the estimated interference. Since the MFG technique requires each user to join the coalition that corresponds to its highest channel gain, its transmit power is likely to be less than the maximum transmit power, meaning that the user is able to cope with the estimated interference level $\tilde{I}$ by having an acceptable power level. On the other hand, by invoking the MFG-based MAB algorithms, the user may deviate from the coalition associated with its best channel gain and join another coalition that corresponds to a lower channel gain. Hence, facing an interference level while having a lower channel gain may require much more power than the device can handle, i.e., a power level higher than the maximum transmit power. Therefore, this device withdraws to play this arm. Consequently, the proposed algorithms result in a lower number of active devices per coalition than the MFG approach.

Figures 8 and 9 display, respectively the packet success rate and the average transmission rate for the different techniques. Interestingly, as shown in Fig. 8, UCB-based MFG achieves the highest value of the packet success rate, about 78% of success compared to the other techniques. Nevertheless, the MFG outperforms the MFG-based MAB algorithms in terms of the average transmission rate, as depicted in Fig. 9.

These results are somehow intuitive since the packet success rate is calculated as the ratio of the number of devices that successfully transmitted to the number of users that transmitted. By contrast, the average transmission rate is measured as the ratio between the number of devices that have succeeded in transmitting and the total number of devices in the system. Indeed, as shown in Fig. 7, the number of active users per cluster reaches its highest value when MFG is invoked, which means that we have more devices playing the MFG than the other techniques, allowing it to achieve the highest value in terms of average transmission rate as in Fig. 9. On the other hand, the $\epsilon$-decreasing MFG results in a higher number of active users per cluster than the UCB-based MFG algorithm, as represented in Fig. 7, which enables it to achieve a greater average transmission rate than UCB-based MFG algorithm as in Fig. 9. But, in terms of the packet success rate, the UCB-based MFG approach guarantees higher values than the $\epsilon$-decreasing MFG algorithm and the MFG approach, as shown in Fig. 8. Therefore we can conclude that, when a device transmits its packet, it has more chance to achieve a successful transmission by adopting the UCB-based MFG algorithm than invoking the other approaches. However, the MFG algorithm allows more users to successfully transmit their packets than the MFG-based MAB approaches.

Now, we are interested in comparing the different approaches in terms of the average utility and the average energy consumption depicted in Figs. 10 and 11, respectively. It can be concluded from these figures that although the MFG approach outperforms the two proposed MFG-based MAB algorithms in terms of the average utility, it requires much more energy consumption to reach this higher utility. Furthermore, it can be clearly observed that the behaviors of these figures follow that of the average transmission rate illustrated in Fig. 9. Unsurprisingly, upon comparing the two MFG-based MAB algorithms, we clearly observe that the UCB-based MFG achieves a higher average utility and a lower average energy consumption than the $\epsilon$-decreasing MFG algorithm.

The latest simulation results reveal the performance comparison of the proposed UCB-based MFG approach with the MFG technique [34] as well as the Bi-level theoretical framework developed in [24] and the NM-ALOHA game investigated in [21]. In Fig. 12, we display the packet success rate as a function of the number of RBs K and the number of users N. Clearly, this rate decreases as the network becomes denser for both the Bi-level game and the NM-ALOHA game, while it remains stable for the UCB-based MFG algorithm and the MFG framework. As explained above, by invoking the MFG algorithm, the devices are able to cope with the system load by adapting their transmission strategies in response to the mean field information. Hence, we achieve effective interference management that in turn results in mitigating the performance drop faced by almost all the proposed grant-free techniques, especially in very dense networks. Besides, this performance comparison in terms of the packet success rate is highly spotlighted in Fig. 13 which represents the case where the N devices share $K=20$ RBs. As we can clearly observe, the proposed UCB-based MFG algorithm results in a considerable improvement in terms of the packet success rate over the MFG approach and the other schemes. Consequently, it is interesting to highlight that facing the interference effects, the UCB-based MFG technique provides much more robustness than the MFG approach, which accentuates the benefit of adopting the proposed MAB-based approach.

Finally, Fig. 14 is devoted to illustrating the variation of the average utility for the scenario of $N=2000$ devices as the number of RBs K increases. As we can clearly see, the proposed UCB-based MFG algorithm yields a performance enhancement on the average utility over the Bi-level game and the NM-ALOHA game. Nevertheless, the MFG approach outperforms all other techniques. The reason behind this is mainly related to the choice of the coalition. Indeed, it has been investigated in [20] that the utility function for a given user is maximized when it transmits on its best channel. Since the MFG algorithm requires each user to join the coalition corresponding to its best channel and then transmit over the associated RB, it is unsurprisingly that the MFG approach achieves a higher average utility than the UCB-based MFG algorithm, wherein each device can choose another RB rather than its best RB.

6 Conclusion

In this paper, a hybrid NOMA network has been investigated in a dense deployment context in which a large population of MTDs is split up into independent coalitions. We derived a bi-level learning to jointly address the user grouping and power control problems. Firstly, we modeled dense scenarios using the MFG framework while taking into consideration the effect of the collective behavior of devices. Then, we exploited the MAB-based approach with the aim of paving the way for an autonomous decision-making process for the players involved in the formulated MFG. Thereafter, we derived two MFG underlying MAB algorithms that allow the MTDs to arrange themselves into coalitions and regulate their power levels based on brief feedback received from the BS. Our simulation results have emphasized the equilibrium behaviors of proposed MFG-based MAB approaches. More precisely, we have shown that the proposed UCB-based MFG algorithm can not only handle the high access load more efficiently, but also result in more robustness against the interference impacts with lower energy consumption than the other techniques.

Fig. 1

The System model

Fig. 2

The interaction process between the BS and each user at each time t

Fig. 3

Packet success rate as a function of time T when the number of RBs $K = 20$. The blue dash-dotted line represents the case when the system is composed of 2000 devices; The solid orange line represents the case when the system is composed of 4000 devices; The yellow dash-dotted line represents the case when the system is composed of 6000 devices; The purple dash-dotted line represents the case when the system is composed of 8000 devices; The green dashed line represents the case when the system is composed of 10000 devices

Fig. 4

Average transmission rate as a function of time T when the number of RBs $K = 20$. The blue dash-dotted line represents the case when the system is composed of 2000 devices; The solid orange line represents the case when the system is composed of 4000 devices; The yellow dash-dotted line represents the case when the system is composed of 6000 devices; The purple dash-dotted line represents the case when the system is composed of 8000 devices; The green dashed line represents the case when the system is composed of 10000 devices

Fig. 5

Average utility as a function of time T when the number of RBs $K = 20$. The blue dash-dotted line represents the case when the system is composed of 2000 devices; The solid orange line represents the case when the system is composed of 4000 devices; The yellow dash-dotted line represents the case when the system is composed of 6000 devices; The purple dash-dotted line represents the case when the system is composed of 8000 devices; The green dashed line represents the case when the system is composed of 10000 devices

Fig. 6

Average energy as a function of time T when the number of RBs $K = 20$. The blue dash-dotted line represents the case when the system is composed of 2000 devices; The solid orange line represents the case when the system is composed of 4000 devices; The yellow dash-dotted line represents the case when the system is composed of 6000 devices; The purple dash-dotted line represents the case when the system is composed of 8000 devices; The green dashed line represents the case when the system is composed of 10000 devices

Fig. 7

Number of active users per cluster as a function of time T when the number of RBs $K = 20$ and the system is composed of 2000 devices. The blue dotted line represents the case when the MFG algorithm is invoked; The solid orange line represents the case when the $\epsilon$-decreasing MFG algorithm is applied; The purple dash-dotted line represents the case when the UCB-based MFG algorithm is used

Fig. 8

Packet success rate as a function of time T when the number of RBs $K = 20$ and the system is composed of 2000 devices. The blue dotted line represents the case when the MFG algorithm is invoked; The solid orange line represents the case when the $\epsilon$-decreasing MFG algorithm is applied; The purple dash-dotted line represents the case when the UCB-based MFG algorithm is used

Fig. 9

Average transmission rate as a function of time T when the number of RBs $K = 20$ and the system is composed of 2000 devices. The blue dotted line represents the case when the MFG algorithm is invoked; The solid orange line represents the case when the $\epsilon$-decreasing MFG algorithm is applied; The purple dash-dotted line represents the case when the UCB-based MFG algorithm is used

Fig. 10

Average utility as a function of time T when the number of RBs $K = 20$ and the system is composed of 2000 devices. The blue dotted line represents the case when the MFG algorithm is invoked; The solid orange line represents the case when the $\epsilon$-decreasing MFG algorithm is applied; The purple dash-dotted line represents the case when the UCB-based MFG algorithm is used

Fig. 11

Average energy consumption as a function of time T when the number of RBs $K = 20$ and the system is composed of 2000 devices. The blue dotted line represents the case when the MFG algorithm is invoked; The solid orange line represents the case when the $\epsilon$-decreasing MFG algorithm is applied; The purple dash-dotted line represents the case when the UCB-based MFG algorithm is used

Fig. 12

Packet success rate for different number of users N and number of RBs K. The orange curve represents the case when the UCB-based MFG algorithm is applied; The blue curve represents the case when the MFG algorithm is invoked; The red curve represents the case when the Bi-Level game NOMA is used; The purple curve represents the case when the NM-ALOHA game is invoked

Fig. 13

Packet success rate versus the number of users N sharing $K=20$ RBs. The orange line represents the case when the UCB-based MFG algorithm is applied; The blue line represents the case when the MFG algorithm is invoked; The red line represents the case when the Bi-Level game NOMA is used; The purple line represents the case when the NM-ALOHA game is invoked

Fig. 14

Average utility versus the number of RBs K when the system is composed of $N=2000$. The orange line represents the case when the UCB-based MFG algorithm is applied; The blue line represents the case when the MFG algorithm is invoked; The red line represents the case when the Bi-Level game NOMA is used; The purple line represents the case when the NM-ALOHA game is invoked