1 Introduction

The Internet of Things (IoT) has become one of the emerging technologies as the development of next-generation networks. It is recognized as the ultimate infrastructure to connect everything anytime and anywhere [1]. However, the energy limitation and high costs make the deployment of IoT face some challenges. Therefore, backscatter communication technology is proposed to solve these problems [2,3,4]. The sensor can use backscatter communication technology to convert the surrounding signals into energy available for its work through internal wireless acquisition modules. Thus, it can use backscatter communication technology to realize the information transmission of the target node. Backscatter communication technology modulates the data that need to be sent to the input signal to achieve data transmission [5, 6].

Usually, a backscatter communication system includes three structures: excitation source, backscatter device, and backscatter receiver. A typical application of backscatter communication for IoT is in radio frequency identification (RFID) scenarios [7]. The radio frequency (RF) reader (which contains excitation source and backscatter receiver) first transmits the RF signals to the passive tag which contains backscatter device. The tag harvests energy from the RF reader signal to power its circuit, and then forwards the bits of information carried on the received RF sinusoidal signal back to the reader by adjusting its load impedance to change the amplitude and phase of its backscattered signal [8,9,10]. The modulated signal backscattered from the tag may suffer two-path losses (e.g., from base station (BS) to BD and from BD to BR) [11]. Therefore, the backscatter communication network is mainly used for short-range wireless communication applications. However, when the signal transmitting base station is damaged, it cannot provide RF signals. In this case, we can use UAV as a signal transmitting base station when facing these problems [12, 13].

As the demands for global cellular network coverage increase, UAV combined with cellular networks can support UAV communications in a cost-effective and highly mobile, while also offering the possibility of establishing new dedicated ground networks. When the coverage of traditional cellular base stations cannot meet the demand [14], UAV has some advantages such as high mobility, flexible deployment and low terrain constraints, especially reliable data collection and real-time data transmission [15,16,17]. UAV as Aerial base station (ABS), we can determine the deployment location of the UAV based on the time-space distribution characteristics of the ground user. Compared to the ground base stations, ABS is more adaptable to environmental changes, so it can be deployed to provide emergency communication connections in areas without infrastructure coverage. When natural disasters such as earthquakes, tsunamis and flash floods occur, ground base stations are often destroyed to the point that they cannot provide communication services, which hinders the rescue operations. UAV as aerial base stations is not limited by the basic communication facilities in the disaster area, and can quickly provide reliable communication over a large area for the disaster area [18, 19]. In [20], the authors propose a multi-UAV-assisted data collection scenario. A UAV can fly close to a backscatter sensor node (BSN) to activate it and collect data. After the collection task is completed, minimize the total flight time of the rechargeable UAV. In [21], the author investigated a resource optimization scheme for uplink data transmission in U-IoT networks, considering statistical QoS and outage probability requirements for IoT devices. However, this paper does not consider the impact of the UAV flying trajectory on resource allocation. In [22], the authors only considered a single backscatter device on the ground and did not consider multiple backscatter devices and scheduling issues. In [23], the authors designed a fly-by-wire communication scheme to maximize the system’s energy efficiency by jointly optimizing the trajectory of UAVs, the scheduling of BDs and the transmission power of CEs. However, [23] did not consider optimizing the reflection coefficient. In [24], the authors studied a UAV-assisted backscatter secure communication system to maximize the uplink fair secrecy rate of BDs. In [25], the authors designed a UAV-assisted backscatter communication system to improve the system performance by considering BD scheduling, reflection coefficient and fairness constraints among BDs. However, [25] did not consider optimizing the transmit power. Only reasonable consideration of transmit power allocation can effectively improve the survival time of BDs nodes in the whole network.

In this paper, we study a UAV-assisted backscatter communication network. The UAV acts as an airborne mobile BS and broadcasts signals to the ground BDs, which transmit the data signals to the BR in a backscattered manner. The ground BDs use TDMA protocol to communicate with the BR, considering the dynamicity of the UAV broadcast signal, which requires data transmission scheduling to maximize the availability of RF signals in the BDs.

Based on the above motivations, we aim to maximizing the minimum rate of the proposed network by jointly optimizing backscatter device scheduling, reflection coefficient, UAV’s power control, and UAV’s trajectory. The main contributions of this paper are summarized as follows:

  • First, we propose a communication-while-flying scheme for this UAV-assisted backscatter communication network. The BDs harvest energy from the incident sinusoidal signals emitted by UAV using TDMA protocol, backscatter the information to the BR.

  • Second, we formulate the maximizing the minimum (max–min) rate problem of the proposed network by jointly optimizing backscatter device scheduling, reflection coefficient, UAV’s power control and UAV’s trajectory. However, the problem is non-convex and challenging to solve optimally.

  • Finally, we propose an efficient iterative algorithm to solve the max–min resource allocation problem. The optimization problem is transformed into four subproblems using block coordinate descent (BCD) [26, 27], and then equivalently transformed into a convex optimization problem using a first-order Taylor expansion using the successive convex approximation (SCA) algorithm [28]. Simulation results show that the proposed algorithm has a better performance than other benchmark schemes.

The rest of the paper is organized as follows. Section 2 presents the system model and the proposed optimization problem. Section 3 formulates the resource allocation problem with joint optimization of backscatter device scheduling, reflection coefficient, UAV’s power control, and UAV’s trajectory. Section 4 shows the simulation results to verify the performance of the designed algorithm scheme. Finally, Sect. 5 gives a conclusion of the paper.

2 System model

Fig. 1
figure 1

UAV-assisted backscatter communication system

Full size image

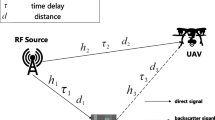
As shown in Fig. 1, we consider a UAV-assisted backscatter communication network, UAV is used as a mobile base station in the air to transmit signals to K \((K \ge 1)\) BDs on the ground and the receiver receives the modulated signals from BD k through backscattering and also receives signals transmitted from the UAV. The set of all BDs are denoted by \(\mathcal{K} \buildrel \Delta \over = \{ 1,2,\ldots ,K\}\). The ground-based BDs communicate with the BR using a dynamic protocol based on TDMA. Each operation time is denoted by T. To facilitate the problem, we assume that each period is discretized and divided into N equal time slots, i.e., \(T=Nt\). Thus the UAV trajectory q(t) at time t can be approximated by the sequence as \(q[n] \in {R^{2 \times 1}}, n \in \mathcal{N} \buildrel \Delta \over = \{ 1,2,\ldots ,N\}\). The maximum speed of the UAV is denoted by \({V_{\max }}\). Then, we obtain the maximum flight distance of each time slot, i.e., \({D_{\max }} = {V_{\max }}t\). Thus, the UAV trajectory should satisfy the following constrains.

$$\begin{aligned} q [1]= & {} q[N], \end{aligned}$$
(1)
$$\begin{aligned} \parallel q[n + 1] - q[n]\parallel\le & {} {{V_{\max }}t}{ ,\quad }n{\mathrm{= 1,}}\ldots {\mathrm{,}}N - 1. \end{aligned}$$
(2)

where (1) devotes the constraint that the UAV flies back to its initial location by the time period T, and (2) imposes UAV’s maximum flying speed constraint.

We assume that the positions of all BDs and receiver are known. A Cartesian coordinate system is considered where BD k and receiver respectively located in the horizontal plane at \({w_k}\) and \({w_r}\), \({w_k} \in {R^{2 \times 1}}\) and \({w_r} \in {R^{2 \times 1}}\). The UAV has a fixed height H and the distance from the UAV to BD k, the distance from BD k to the receiver at the time slot n are denoted as \({d_k}[n] = \sqrt{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}} ,{\forall k,n}\) and \({d_{br}} = \parallel {w_k} - {w_r}\parallel ,{\forall k}\), respectively.

Assume an A2G (air-to-ground) model, i.e., a free-space path loss model, which is used between the UAV and the BD k [29]. In [30], it is proved by the validation that the communication channel from the UAV to the BD k is mainly controlled by line of sight (LoS) propagation. The channel gain at time slot n from the UAV to the BD k can be expressed as \({\beta _k}[n] = \frac{{{\beta _0}}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}},{\forall k,n}\), where \({\beta _0}\) represents the reference channel gain at \(d= 1\) m. The UAV and the receiver channel can be expressed as \({\beta _r}[n] = \frac{{{\beta _0}}}{{\parallel q[n] - {w_r}{\parallel ^2} + {H^2}}},{\forall n}\) [23].

Moreover, we assume that the channel model between the BD and the receiver is modeled as a Rayleigh channel with distance-dependent large-scale fading coefficients [31]. Thus, the channel gain between the BD k and the receiver is \({\beta _{br}} = \frac{{{\beta _0}}}{{\parallel {w_k} - {w_r}{\parallel ^2}}},{\forall k}\).

Let \(P{\mathrm{[n]}}\) be the transmit power of the UAV at time slot n. Then, the following constraints should be satisfied.

$$\begin{aligned}&0 \le P{\mathrm{[n]}} \le {P_{\max }},\quad{\forall n}, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{1}{N}\sum \limits _{n = 1}^N {P[n] \le {\overline{P}} }, \end{aligned}$$
(4)

where \({P_{\max }}\) denotes the maximum power that can be transmitted by the UAV and \({\overline{P}}\) denotes the average power constraint of the UAV. We use the above two constraints to limit the UAV’s transmit power through constraints (3) and (4).

Considering that the UAV works in TDMA protocol, each time slot can schedule at most one BD to communicate with the UAV. We define a binary variable \({a_k}[n]\), where \({a_k}[n] = 1\) denotes that the UAV scheduling BD k at time slot n, otherwise denoted as \({a_k}[n] = 0\). As [24], a maximum of one BD can be activated during one-time slot in order to avoid any conflicts in data transmission. Thus the following constraints are generated according to the above scheduling scheme

$$\begin{aligned}&\sum \limits _{k = 1}^K {{a_k}} [n] \le 1,\quad{\forall n}, \end{aligned}$$
(5)
$$\begin{aligned}&{a_k}[n] \in \{ 0,1\} ,\quad{\forall k,n}. \end{aligned}$$
(6)

As we know, each BD also separates the received  RF signals, one part of which is used to harvest energy for the operation of the BD k circuit and the rest is used for backscattering [32, 33]. Let \({b_k}[n] (0 \le {b_k}[n] \le 1)\) be the reflection coefficient of the BD k at time slot n. Because a maximum of one BD can be activated during one time slot, we can obtain the energy harvested by BD k for the power supply as follows.

$$\begin{aligned} {E_k}[n]{\mathrm{= }}{\eta _k}\sum \limits _{n = 1}^N {\frac{T}{N}(1 - {b_k}[n]} ){\beta _k}[n]P[n], \end{aligned}$$
(7)

where \({\eta _k}\) denotes the BD k energy harvesting efficiency. In the downlink, at time slot n, the signal received at the BD k from the UAV is written as follows

$$\begin{aligned} \begin{aligned} {y_{bk}}[n] =\sqrt{{\beta _k}[n]} \sqrt{P[n]} x[n] , \end{aligned} \end{aligned}$$
(8)

Thus, we can write the signal at the receiver at time slot n as

$$\begin{aligned} \begin{aligned} {y_k}[n]&= \sqrt{{\beta _k}[n]} \sqrt{{\beta _{br}}} \sqrt{P[n]} \sqrt{{b_k}[n]} x[n]{c_k}[n] \\&\quad +\sqrt{{\beta _r}[n]}\sqrt{P[n]} x[n] + z[n], \\ \end{aligned} \end{aligned}$$
(9)

x[n] denotes the transmitted signal of the UAV at the time slot \(n, {c_k}[n]\) denotes its signal of BD k at the time slot n, where \(\parallel x[n]{\parallel ^2} = 1,\parallel {c_k}[n]{\parallel ^2} = 1, z[n]\) denotes the noise power of the receiver with \({\sigma ^2}\). We assume that the receiver either knows the broadcast signal of the UAV or uses interference cancellation techniques to decode and remove the UAV signal [34]. Thus, we can express the maximum achievable rate from UAV to the receiver at the time slot n as

$$\begin{aligned} {R_k}[n] = {\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}\right) , \end{aligned}$$
(10)

where \(D = \frac{{{\beta _{br}}}}{{{\sigma ^2}}}, {\sigma ^2}\) denotes the additive Gaussian white noise of the receiver. For the achievable average rate of the UAV-assisted backscatter communication network over N time slots are given by

$$\begin{aligned} {R_k} = \frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]{\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}\right) . \end{aligned}$$
(11)

Let A = \(\{ {a_k}[n],\forall k,n\}, \hbox {B} = \{{b_k}[n],\forall k,n\}\), \(\hbox {P} = \{ P[n],\forall n\}, \hbox {Q} = \{q[n],\forall n\}\). We jointly optimize BD k scheduling A, reflection coefficient B, transmit power P and UAV trajectory Q. Considering allocation user’s fairness, we maximize their minimum average rate. The max–min rate optimization problem can be formulated as follows.

$$\begin{aligned} ({\text {P1}}):&\mathop {\max \min }\limits _{A.Q.P.B} \,\,{R_k} \nonumber \\ {\text{s.t.}}\;\;\;&{\eta _k}\sum \limits _{n = 1}^N {\frac{T}{N}(1 - {b_k}[n]} ){\beta _k}[n]P[n] \ge {E_{\min }},\quad{\forall k} \end{aligned}$$
(12a)
$$\begin{aligned}&\sum \limits _{k = 1}^K {{a_k}} [n] \le 1{\mathrm{,}}{\forall n}\,\,{\mathrm{and }}\,\,{a_k}[n] \in \{ 0,1\} {\mathrm{,}}{\forall k,n} \end{aligned}$$
(12b)
$$\begin{aligned}&0 \le P{\mathrm{[n]}} \le {P_{\max }},{\forall n} \end{aligned}$$
(12c)
$$\begin{aligned}&\frac{1}{N}\sum \limits _{n = 1}^N {P[n] \le {\overline{P}} } \end{aligned}$$
(12d)
$$\begin{aligned}&0 \le {{\mathrm{b}}_k}[n] \le 1{\mathrm{,}}{\forall k,n} \end{aligned}$$
(12e)
$$\begin{aligned}&\parallel q[n + 1] - q[n]\parallel \le {V_{\max }t},\quad n{\mathrm{= 1,}}\ldots {\mathrm{,}}N - 1 \end{aligned}$$
(12f)
$$\begin{aligned}&q[1] = q[N] \end{aligned}$$
(12g)

where (12a) is the minimum harvest energy \({E_{\min }}\) required for each BD k constraint. (12b) means that in each time slot, at most one BD is scheduled for communication with UAV. (12c) and (12d) are the peak power constraint and the average power constraint to limit the UAV’s transmit power. (12e) is the BD k backscattering coefficient constraint. (12f) means that UAV return to its initial location at the time period of T. (12g) is the UAV speed is limited by \({V_{\max }}\).

3 Proposed method

As the P1 is a non-convex problem and the objective function is challenging to solve due to the optimal variables A for BD k scheduling and UAV trajectory variables Q. Thus, we first use an auxiliary variable and relaxation method to change P1 to the equivalent optimization problem [35]. Then, we propose an iterative algorithm by dividing the equivalent optimization problem into four subproblems, which are solved iteratively based on BCD and SCA technology.

3.1 BDs scheduling optimization

For given B, P, Q, introduce a slack variable \(\tau\), let \(\tau (\mathrm{A},{\mathrm{B,P,Q) = }}\mathop {\min }\limits _{k \in \mathrm{K}} {R_k}\) as a function of A, B, P, Q. To solve the problem (P1), we relax the binary variables in the problem (P1) to continuous variables and the problem (P1) can be rewritten in the following form

$$\begin{aligned} ({\text {P2}}):&\mathop {\max }\limits _{A.\tau } \,\,\tau \nonumber \\ {\text{s.t.}}\;\;\;&\frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]{\log _2}(1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}) \ge \tau ,{\forall k} \end{aligned}$$
(13a)
$$\begin{aligned}&\sum \limits _{k = 1}^K {{a_k}} [n] \le 1,{\forall n} \end{aligned}$$
(13b)
$$\begin{aligned}&0 \le {a_k}[n] \le 1,{\forall k,n} \end{aligned}$$
(13c)

Problem (P2) is a standard linear programming (LP) problem, and it can be solved by the interior point method [35]. Therefore, we can use optimization tools (e.g., CVX) to solve it [36].

3.2 Reflection coefficient optimization

Given A, P, Q, the backscattering coefficients of BD k can be optimized by solving the following problem.

$$\begin{aligned} ({\text {P3}}):&\mathop {\max }\limits _{B.\tau } \,\,\tau \nonumber \\ {\text{s.t.}}\;\;\;&\frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]{\log _2}(1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}) \ge \tau ,{\forall k} \end{aligned}$$
(14a)
$$\begin{aligned}&{\eta _k}\sum \limits _{n = 1}^N {\frac{T}{N}(1 - {b_k}[n]} ){\beta _k}[n]P[n] \ge {E_{\min }},\quad{\forall k} \end{aligned}$$
(14b)
$$\begin{aligned}&0 \le {{\mathrm{b}}_k}[n] \le 1{\mathrm{,}}{\forall k,n} \end{aligned}$$
(14c)

Note that problem (P3) is a convex optimization problem in terms of transmit power P of UAV, and all the (14a) (14b) (14c) are all convex. Thus, it can be solved with an efficient optimization tool (e.g., CVX).

3.3 UAV transmit power optimization

In this subsection, we conduct the optimization of the UAV transmit power, and given A, B and Q to solve for the power P, it can be written in the following form

$$\begin{aligned} ({\text {P4}}):&\mathop {\max }\limits _{P.\tau } \,\,\tau \nonumber \\ {\text{s.t.}}\;\;\;&\frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]{\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}\right) \ge \tau ,{\forall k} \end{aligned}$$
(15a)
$$\begin{aligned}&{\eta _k}\sum \limits _{n = 1}^N {\frac{T}{N}(1 - {b_k}[n]} ){\beta _k}[n]P[n] \ge {E_{\min }},\quad{\forall k} \end{aligned}$$
(15b)
$$\begin{aligned}&0 \le P{\mathrm{[n]}} \le {P_{\max }},{\forall n} \end{aligned}$$
(15c)
$$\begin{aligned}&\frac{1}{N}\sum \limits _{n = 1}^N {P[n] \le {\overline{P}} } \end{aligned}$$
(15d)

Problem (P4) is a convex optimization problem. Therefore, we can then use convex optimization tools to solve it, such as CVX. We conduct the average power constraint, which is not meaningless, and the constraint makes the distribution of power more fair and reasonable.

3.4 UAV trajectory optimization

For a given scheduling A, reflection coefficient B and power allocation P, we can use the SCA technique to optimize the trajectory of the UAV, so this subproblem can be written as

$$\begin{aligned} ({\text {P5}}):&\mathop {\max }\limits _{Q.\tau } \,\,\tau \nonumber \\ {\text{s.t.}}\;\;\;&\frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]{\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}\right) \ge \tau ,{\forall k} \end{aligned}$$
(16a)
$$\begin{aligned}&\parallel q[n + 1] - q[n]\parallel \le {V_{\max }t},\quad n{\mathrm{= 1,}}\ldots {\mathrm{,}}N - 1 \end{aligned}$$
(16b)
$$\begin{aligned}&q[1] = q[N] \end{aligned}$$
(16c)

Note (16a) is non-convex constraint with respect to q[n], but the left-han-side (LHS) of (16a) is convex with respect to \(\parallel q[n] - {w_k}{\parallel ^2}\). To solve the non-convexity of (16a), we use the SCA technique. From [37], we know that the first-order Taylor expansion of a convex function at any point is its global lower bound. Thus the first-order Taylor expansion of \({R_k}[n]\) with respect to q[n] on \({q_0}[n]\) obtains its lower bound

$$\begin{aligned} \begin{aligned} {R_k}[n]&= {\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel q[n] - {w_k}{\parallel ^2} + {H^2}}}\right) \\&\ge {\log _2}\left( 1 + \frac{{D{\beta _0}{b_k}[n]P[n]}}{{\parallel {q_0}[n] - {w_k}{\parallel ^2} + {H^2}}}\right) \\&\quad - \varphi \times (\parallel q[n] - {w_k}{\parallel ^2} - \parallel {q_0}[n] - {w_k}{\parallel ^2}) \buildrel \Delta \over = R_k^{lb}[n] \end{aligned} \end{aligned}$$
(17)

where \(\varphi = \frac{{D{\beta _0}{b_k}[n]P[n]{{\log }_2}e}}{{(\parallel {q_0}[n] - {w_k}{\parallel ^2} + {H^2})(D{\beta _0}{b_k}[n]P[n] + \parallel {q_0}[n] - {w_k}{\parallel ^2} + {H^2})}}\). We obtain a lower bound of \({R_k}[n]\), so we optimize the lower bound for (P5) as follow.

$$\begin{aligned} ({\text {P5}}{\text {.1}}):&\mathop {{\mathrm{max }}}\limits _{Q.\tau }\,\, {\tau ^{lb}} \nonumber \\ {\text{s.t.}}\;\;\;&\frac{1}{N}\sum \limits _{n = 1}^N {{a_k}} [n]R_k^{lb}[n] \ge {\tau ^{lb}},{\forall k} \end{aligned}$$
(18a)
$$\begin{aligned}&\parallel q[n + 1] - q[n]\parallel \le {V_{\max }t},\quad n{\mathrm{= 1,}}\ldots {\mathrm{,}}N - 1 \end{aligned}$$
(18b)
$$\begin{aligned}&q[1] = q[N] \end{aligned}$$
(18c)

Now that the objective function and constraints are convex, the problem (P5.1) can be solved using the optimization tool such as CVX.

3.5 Overall algorithm

Based on the solutions of the original problem (P1), which proposed an efficient iterative algorithm by the BCD method. We alternately optimize the four subproblems, and the locally optimal solution of the original problem (P1) can be updated in each iteration. The details of the algorithm for solving (P1) are summarized in Algorithm 1.

figure a

3.6 Convergence analysis

The convergence of Algorithm 1 is as follows. First, in step 3 of Algorithm 1, since the optimal solution of problem (P2) is obtained for given \({B^l}, {P^l}\) and \({Q^l}\), we have [38, 39]

$$\begin{aligned} \begin{aligned} \tau ({A^l},{B^l},{P^l},{Q^l}) \le \tau ({A^{l + 1}},{B^l},{P^l},{Q^l}) \end{aligned} \end{aligned}$$
(19)

Second, in step 4 of Algorithm 1, since the optimal solution of the problem (P3) is obtained for given \({A^{l + 1}}, {P^l}\) and \({Q^l}\), we have

$$\begin{aligned} \begin{aligned} \tau ({A^{l + 1}},{B^l},{P^l},{Q^l}) \le \tau ({A^{l + 1}},{B^{l + 1}},{P^l},{Q^l}) \end{aligned} \end{aligned}$$
(20)

Third, in step 5 of Algorithm 1, since the optimal solution of the problem (P4) is obtained for given \({A^{l + 1}}, {P^l}\) and \({Q^l}\), since it follow that

$$\begin{aligned} \begin{aligned} \tau ({A^{l + 1}},{B^{l + 1}},{P^l},{Q^l}) \le \tau ({A^{l + 1}},{B^{l + 1}},{P^{l+1}},{Q^l}) \end{aligned} \end{aligned}$$
(21)

Next, in step 6 of Algorithm 1, since the optimal solution of the problem (P5) is obtained for given \({A^{l + 1}}, {P^l}\) and \({Q^l}\), it follow that

$$\begin{aligned} \begin{aligned} \tau ({A^{l + 1}},{B^{l + 1}},{P^{l + 1}},{Q^l})&\mathop {=} \limits ^{(a)} {\tau _{lb}}({A^{l + 1}},{B^{l + 1}},{P^{l + 1}},{Q^l}) \\&\mathop {\le }\limits ^{(b)} {\tau _{lb}}({A^{l + 1}},{B^{l + 1}},{P^{l + 1}},{Q^{l + 1}}) \\&\mathop {\le }\limits ^{(c)} \tau ({A^{l + 1}},{B^{l + 1}},{P^{l + 1}},{Q^{l + 1}}) \\ \end{aligned} \end{aligned}$$
(22)

where (a) holds that fact since the first-order Taylar expansion in (17) is tight at given local point, which means that the problem (P5.1) has the same objective value of the problem (P5) at \({Q^l}\); (b) holds since \({Q^{l + 1}}\) is the optimal solution to the problem (P5.1); and (c) holds since the problem (P5.1) is lower bound of the problem (P5). The inequality in (22) implies that although the approximate problem (P5.1) of the original UAV trajectory optimization subproblem (P5) is locally optimal in each iteration. The objective value of the problem (P5) is always non-decreasing after each iteration.

Based on (19)–(22), we have

$$\begin{aligned} \begin{aligned} \tau ({A^l},{B^l},{P^l},{Q^l}) \le \tau ({A^{l + 1}},{B^{l + 1}},{P^{l + 1}},{Q^{l + 1}}) \end{aligned} \end{aligned}$$
(23)

which implies that the objective value of (P2) is non-decreasing after each iteration in Algorithm 1. Therefore, The proposed Algorithm 1 is guaranteed to converge due to the upper bound of the objective value of (P2) and monotonicity of iteration.

3.7 Complexity analysis

We analyze the complexity of Algorithm 1. In step 3 of Algorithm 1, the subproblem (P2) is a linear optimization problem. Thus, we can solve it by interior point method with complexity \(O({L_1}{(N)^{\frac{1}{2}}}\frac{1}{\varepsilon })\), where N denotes the number of variables, and \(\varepsilon\) is the iterative accuracy [40]. Where \({L_1}\) is the number of iterations require to update scheduling. In step 4 and 5 of Algorithm 1, the complexity is \(O({L_2}{N^{\frac{7}{2}}})\) and \(O({L_3}{N^{\frac{7}{2}}})\), respectively [41]. In step 6 of Algorithm 1, problem (P5) is a convex quadratic programming problem, the complexity is \(O({L_4}{(5N)^3})\) [42]. To sum up, the total computational complexity of Algorithm 1 is \(O(L({L_1}{(N)^{\frac{1}{2}}}\frac{1}{\varepsilon } + {L_2}{(N)^{\frac{7}{2}}} + {L_3}{(N)^{\frac{7}{2}}} + {L_4}{(5N)^3}))\), where L is the iteration number of Algorithm 1. This means that Algorithm 1 can obtain suboptimal solutions in polynomial time.

3.8 Trajectory initialization

In this paper, we propose the UAV-assisted backscatter communication network, which needs to find an effective trajectory initialization method. In [43], UAV trajectory is based on the circle packing scheme, so we define a trajectory initialization scheme for Algorithm 1. In particular, the initial UAV trajectory is set to a circular trajectory, we define the geometric center of all BDs on the ground as the center of the circle of the initial UAV trajectory, i.e., \(C = \frac{{\sum \nolimits _{k = 1}^K {{\omega _k}} }}{K}\). In order to cover all BDs on the ground, we take half the radius of the circle with C as the center, i.e., \({r_1} = \frac{1}{2} * \mathop {\max }\limits _{k \in K} \parallel {\omega _k} - C\parallel\). The maximum allowed radius is \({r_2} = \frac{{{V_{\max }}T}}{{2\pi }}\) for a given T. Thus, the radius of the initial UAV trajectory is \(r = \min ({r_1},{r_2})\). Based on C and r, the initial UAV trajectory in time slot n is denoted as \({q^0}[n] = {[C + r\cos {\theta _n},C + r\sin {\theta _n}]^T},\quad\forall n\), where \({\theta _n} \buildrel \Delta \over = 2\pi \frac{{(n - 1)}}{{N - 1}},\quad\forall n, n = 1,\ldots ,N\).

4 Simulation results and discussion

In this section, we demonstrate the effectiveness of the proposed algorithm based on simulation results. We consider a system of \(K=6\) terrestrial BDs, which are randomly and uniformly distributed within a geographic area of size \(70\times 70\,{{\mathrm{m}}^2}\) and the locations shown in Fig. 2, receiver located at \({[10,10]^T}\) m. The UAV altitude \(H = 10\) m. A maximum flight speed \({V_{\max }} = 5\) m/s, \(t = 1\) s. Maximum transmit power of UAV is set as \({P_{\max }} = 3\) W and an average power \({\overline{P}} = 10\) dBm. Set the channel gain \({\beta _0} = 0.1\), the noise power of the receiver \({\sigma ^2} = - 110\) dBm, \({\eta _k} = 0.8, {E_{\min }} = 0.26 \times {10^{ - 6}}\) J [44], and the threshold value \(\varepsilon\) equals \({10^{ - 4}}\) in Algorithm 1.

Fig. 2
figure 2

Optimized trajectories of UAV with different flying times T (circles represent BDs, triangles represent sampling points)

Full size image

Figure 2 shows the optimized trajectory of the UAV for different time T. When T is 10 s, the trajectory of the UAV is limited by the short distance. As T increases, the UAV uses its mobility to adaptively expand and adjust the trajectory path to be closer to the backscatter devices on the ground. When T is 60 s, we can observe that the UAV can stay above all backscatter devices and fly for a period of time, the UAV trajectory becomes a closed-loop, which connects all points directly above the BD position. In this way, a better max–min average rate can be obtained due to the better channel gain can be obtained. We can also observe that the trajectory sampling points around each BD are denser than the sampling points far away from the BDs. It means that the UAV will slow down when approaching the BD and spend more time using the LoS channel to transmit more information with the BDs.

Fig. 3
figure 3

The UAV speed versus time for \(T = 60\) s

Full size image

It is observed from Fig. 3 that the best LoS channel can be obtained for communication at a maximum \(T = 60\) s. When the UAV is flying at the top of each BD, the speed will drop to zero. When T is 10 s and 20 s, the UAV is flying at the maximum speed to avoid wasting time and get as those to each BD as possible within a limited time to obtain the best channel for information transmission.

Fig. 4
figure 4

The max–min average rate versus period T

Full size image

Figure 4 shows the max–min average obtained by different trajectory desig algorithms. The proposed algorithm is compared with two other algorithms named the circular trajectory and static UAV schemes. The circular trajectory algorithm is optimizing max–min rate by circular trajectory. The static UAV algorithm is optimizing max–min rate by fixing the UAV’s location. We can see that the proposed algorithm is much better than the other two compared algorithms. The max–min average rate of the receiver stabilizes after reaching a peak for the circular trajectory algorithm because the circular trajectory increases as time T starts to increase. The UAV can establish better channel gains with more ground BDs as T increases, the max–min average rate increases with T until it is convergent to optimal circular trajectory. For static scheme, the max–min average rate is independent of time T because the channel between UAV and BDs is constant due to the fixed UAV location design. Therefore, our algorithm is better than the two algorithms as it can take full advantage of UAV’s mobility for trajectory design.

Fig. 5
figure 5

\({{\overline{P}}}\) versus T

Full size image

In Fig. 5, we have compared the variation of the max–min average rate with time T for different values of constraint \({{\overline{P}} }\). It can be seen that the max–min average rate increase as time T increases. When \({{\overline{P}} }\) increases from 5 to 15 dBm, the max–min average rate also increases. When \({{\overline{P}} }\) is 15 dBm, compared with the other two schemes, the max–min average rate has a performance gain of 19% and 39%, respectively.

Fig. 6
figure 6

BD scheduling (\(T= 60\) s)

Full size image
Fig. 7
figure 7

Convergence of proposed algorithm

Full size image

In Fig. 6, when T is 60 s, we can observe that the UAV schedules only one backscatter device at each time slot under the TDMA protocol, and the order of scheduling backscatter devices is 4, 5, 6, 1, 2 and 3, respectively. The running time of the proposed algorithm in the paper decreases with the UAV trajectory path or the increasing number of line segment indexes, as the number of optimization variables decreases as the UAV flies to its destination. It is verified in [45] that the computation time required by the proposed algorithm to move the distance between two BDs is all around 1 s, which is a tolerable result. Figure 7 illustrates the convergence performance of the proposed algorithm when \(T= 60\) s, 80 s and 100 s. We observe that the algorithm converges within six iterations and the throughput increases significantly in the first three iterations, verifying the fast convergence of the algorithm. And the throughput finally converges to 1.1293 bps/Hz, 1.1518 bps/Hz and 1.1605 bps/Hz for \(T=60\) s, 80 s and 100 s, respectively.

5 Conclusion

In this paper, we study the resource allocation for a UAV-assisted backscatter communication network. Considering the user’s fairness, the minimum average rate of the proposed network is maximized by jointly optimizing BD scheduling, backscatter coefficient, UAV’s power control, and trajectory. An iterative algorithm is proposed which utilizes the interior point method and SCA technique to solve the resource allocation problem. Simulation results verify the convergence of the proposed algorithm. Moreover, the proposed algorithm achieves a better max–min rate than the circular and static trajectory algorithms.