Abstract
The evolution of non-orthogonal multiple access (NOMA) has raised many opportunities for massive connectivity with less latency in signal transmissions at great distances. We aim to integrate NOMA with a satellite communications network to evaluate system performance under the impacts of imperfect channel state information and co-channel interference from nearby systems. In our considered system, two users perform downlink communications under power-domain NOMA. We analyzed the performance of this system with two modes of shadowing effect: heavy shadowing and average shadowing. The detailed performance was analyzed in terms of the outage probability and ergodic capacity of the system. We derive closed-form expressions and performed a numerical analysis. We discover that the performance of two destinations depends on the strength of the transmit power at the satellite. However, floor outage occurs because the system depends on other parameters, such as satellite link modes, noise levels, and the number of interference sources. To verify the authenticity of the derived closed-form expressions, we also perform Monte-Carlo simulations.
Similar content being viewed by others
1 Introduction
Satellite communications are especially able to provide radio access in difficult areas [1]. Because satellite networks can provide higher quality of services (QoS) for comparatively less cost, they can also attain significant improvements in the efficiency of fixed and mobile satellite services. In the evolution of fifth generation (5 G) networks, satellite communications have been viewed as a potential addition to many technologies such as the internet of things (IoT), sensor networks and relaying communications [2]. The future of satellite networks is expected to support services of massive connectivity and reduce operational costs. Therefore, they can be deployed through their integration with various geostationary and non-geo-stationary orbital satellites by applying cooperative transmission or cognitive radio networks to increase the spectrum efficiency. To date, most satellite networks have adopted the orthogonal multiple access (OMA) technique for the transmission and reception of data [3].
The major disadvantage of OMA is that it cannot meet the growing requirements of communications networks. Under OMA, efficient spectrum use and limitations on the number of users have become major challenges which diminish system performance. In the present paper, we consider non-orthogonal multiple access (NOMA) to tackle the challenges raised by OMA. Of the two NOMA categories, we applied Power-Domain NOMA since much of the research has proved this system as having promising features. In NOMA, signals are transmitted superimposed in the same resource block by varying the power level of each user according to their channel gain. To identify the required user signal at the receiver, the system applies successive interference cancellation (SIC) and thereby extracts the required signal. As mentioned, NOMA uses the same resource block for multiple users and thus increases the efficiency of spectrum use at a reasonable level of implemented complexity [4, 5]. The NOMA technique has achieved significant attention from researchers around the globe and is a promising technology with advantages which can be exploited in 5 G communications. Numerous studies have been performed to compare the performance of the NOMA system to OMA. The main finding is that NOMA is efficient [6, 7]. With an increase in spectrum efficiency, the benefits of NOMA performance can be more prevalent if NOMA is integrated with other techniques.
Various studies have introduced the NOMA technique in satellite communications [8,9,10,11,12,13,14,15,16]. In [11], the authors studied integration of the NOMA technique with multi-beam satellite networks, while in [12], the authors investigated integration of NOMA with cognitive satellite networks to increase ergodic performance of the system. The performance of NOMA-hybrid satellite relay networks (HSRN) was studied in [13, 14]. NOMA integrated cognitive HSRN has been studied to analyze outage performance [15]. The performance of a similar system studied in [13] was investigated with the effect of hardware impairments [16]. The work in [17,18,19] considered NOMA-based satellite-terrestrial networks to increase the efficiency of the spectrum by beamforming. In [20], a cooperative NOMA-HSRN was considered in which the user with better channel gain acted as a relay to the remaining users in the cluster. In [21], the authors studied the effect of imperfect channel state information (CSI) and channel impairments (CI) in a NOMA-based terrestrial mobile communications network (TMCN) which functioned with multiple relays. In [22], the authors considered NOMA-based integrated terrestrial satellite networks (ISTN) to study the effect of relaying configurations such as Amplify and Forward (AF) and Decode and Forward (DF). The authors in [29] investigated a system similar to the study in [22] and explored the effect of CI under a DF relay configuration.
In the context of NOMA-HSRN, the effect of co-channel interference (CCI) in all system models has rarely been addressed. In practice, NOMA-HSRN might experience a rich CCI situation, which is an important consideration in the deployment of NOMA and HSRN in wireless communications. It can be demonstrated that the aggressive reuse of spectrum resources leads to degraded performance because of the effect of CCI. As a result, it is more than simply an important priority consideration, as the performance of NOMA-HSRN is guaranteed only if CCI is taken into account. To the best of the authors’ knowledge, the performance of NOMA-HSRN under the impact of CCI has not been solved yet. Aiming to overcome the effect of CCI, which is unavoidable in practical scenarios, the authors in [23] reported degraded performance in a single-user hybrid satellite-terrestrial amplify-and-forward relay network (HSTAFRN) with multiple Rayleigh-faded interference sources. The performance metrics of a downlink multi-user HSTAFRN were examined using a fixed-gain relaying protocol under the effect of CCI [24]. The authors in [25] employed dual-hop relay networks which assumed interference-limited relays and noisy destinations. These may arise from cell-edge or frequency-division relaying [26], although the NOMA-HSRN still experiences worse performance under the effect of CCI. In [27], the authors analysis the performance of millimeter-wave in multi-user HSRN system and using the shadowed-Rician for the link from satellite to relay. The authors in [28] deployed a single-antenna satellite for a multi-user HSTAFRN system and evaluated its outage performance under the effect of both CCI and outdated CSI.
Satellite networks have been designed to replace terrestrial communications systems, but challenges still exist in some aspects of signal processing. The referred studies suggest that integrating NOMA with satellite systems will extend the efficiency of communication between users. Although satellite systems have numerous advantages, challenges such as fading effect and interference require solutions. The majority of research has studied the effect of various scenarios, including imperfect SIC, imperfect CSI and channel impairments, but none has mentioned the effect on system performance from CCI. Therefore, in the present paper, we studied the effect of interference by considering shadowing and interference links in dual-user communications occurring under a NOMA-assisted satellite network. We studied the shadowing effect in two modes: heavy shadowing (HS) and average shadowing (AS). We also investigated the effect of interference links on communications channels in HS mode. In contrast to similar studies listed in Table 1 and to highlight the superiority of NOMA-aided satellite systems, performance was analyzed completely in terms of outage probability (OP) and ergodic capacity (EC).
The primary contributions of the paper are manifold:
-
In contrast to other studies, our study focus on a complex NOMA-based terrestrial satellite relay network with two users on the ground and a relay which encounters interference from nearby sources. We provide system performance metrics by considering a Shadowed-Rician channel between the satellite and relay, and a Nakagami-m channel between the relay and destination.
-
The system encounters HS and AS effects as a result of the shadowing channel links. We analyzed and compared the system’s performance under these two shadowing modes.
-
We derived the closed-form expressions for outage probability and ergodic capacity of both users in a dedicated NOMA user group. A performance gap is expected for these users depending on their demands and the portion of power allocated to each user.
-
Finally, we performed a numerical analysis and Monte-Carlo simulations for the derived expressions to verify their authenticity and analyze the system’s performance. We illustrate the system’s performance in HS mode by varying the interference links and mean square error of the channels.
The paper is organized as follows. Section 2 explains the system model and types of signal received from the users. Section 3 provides a performance analysis and describes the mathematical expressions for outage probability, ergodic capacity and diversity order of the system. Section 4 provides an analysis and simulations of the expressions obtained in Sect. 3. Section 5 concludes the paper with the attained results.
2 System model
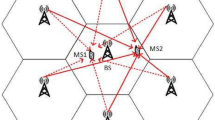
In this section, we assume a satellite (S), a relay (R) and two users \(D_i,i\in (1,2)\) as in Fig. 1. All nodes are equipped with a single antenna, and the relay operates with the DF protocol. The relay node is also affected by N co-channel interference sources \(\{I_n\}^N_{n=1}\). The link from S to \(D_i\) is not available because of heavy shadowing [30]. \(h_{R}\) denotes the channel coefficient from S to R and follow a Shadowed-Rician channel, \(h_{i}\) denotes the channel coefficients from R to \(D_i\) and follow a Nakagami-m channel, \(h_{nR}\) denotes the channel coefficient of the link between the n-th interference source and relay and follows independent and non-identically distributed (i.ni.d.) Nakagami-m random variable (RVs). Under these conditions, the CSI procedure exhibits error. The estimation channel is expressed as [31]
where \(j\in \{R,1,2\}\), \(e_j\) is the error term for \(CN(0,\sigma _{e_j}^2)\) [32].
The power-domain assisted NOMA signal from the source transmits user signals superimposed in the same resource block by varying the power coefficient of each user according to their channel state information (CSI). At the receiver’s end, perfect successive interference cancellation (SIC) is assumed to extract the desired signal from the superimposed signal. Imperfect CSI should therefore be studied in practical scenario. Satellite-terrestrial networks needs relay to empower signals before forwarding them to mobile users. The main reason of design a relay is to deal with signal transmission at long distances. The satellite needs to allocate suitable power level to expected users. The first user \(D_1\) is assumed to be located at far distance and such weak signal needs higher power allocation. Meantime, the near user \(D_2\) just acquire lower level of transmit power. In the first phase, S transmits the signal \(\sqrt{P_S A_1 } x_1\) + \(\sqrt{P_SA_2 } x_2\) to R, where \(P_S\) is the transmit power, \(A_1\) and \(A_2\) are power allocation such that \(A_1 + A_2 = 1\) and \(A_1>A_2\) assumed under the NOMA scheme. Then, the signal received at R is given as
where \(P_{Cn}\) is the transmit power of the n-th interference source and \(n_R\) is the additive white Gaussian noise (AWGN) at R for \(CN(0,N_0)\). The signal to interference plus noise ratio (SINR) is then used to decode \(x_1\) and given as
where \(\rho _S = \frac{{P_S }}{{N_0 }}\) is the transmit SNR, \(\rho _{Cn} = \frac{{P_{Cn} }}{{N_0 }}\) and \(\gamma _C = \sum \limits _{n = 1}^N {\rho _{Cn} \left| {h_{nR} } \right| ^2 }\). Then, the SINR decoded \(x_2\) is given as
In the second phase, relay R forwards the signals to the ground users. The signal received at \(D_i\) is given as
where \(P_R\) is the transmit power at R and \(n_{D_i}\) AWGN for \(CN(0,N_0)\). It is noted that the other main parameters are listed in Table 2. The SINR which decodes \(x_1\) at \(D_1\) is given as
where \(\rho _R = \frac{{P_R }}{{N_0 }}\), the SINR which decodes signal \(x_1\) at \(D_2\) is given as [32]
Applying SIC, the SINR which decodes its own signal \(x_2\) at \(D_2\) is computed according to
For performance analysis, these SINRs provide important information which allows us to compute probabilities.
3 Performance analysis
In this section, we analyze the two main system metrics with the assumed channel models below.
3.1 Channel model
Following the results in [33], the probability density function (PDF) of \(|\hat{h}_{\rm{R}}|^2\) is formulated by
where \(\alpha _{\rm{R}} = \frac{{\left( {\frac{{2b_{\rm{R}} m_{\rm{R}} }}{{2b_{\rm{R}} m_{\rm{R}} + \varOmega _{\rm{R}} }}} \right) ^{m_{\rm{R}} } }}{{2b_{\rm{R}} }}\), \(\beta _{\rm{R}} = ({{2b_{\rm{R}} }})^{-1}\), \(\delta _{\rm{R}} = \frac{{\varOmega _{\rm{R}} }}{{2b_{\rm{R}} \left( {2b_{\rm{R}} m_{\rm{R}} + \varOmega _{\rm{R}} } \right) }}\), \(m_{\rm{R}}\) is the fading severity parameter, \(2b_{\rm{R}}\) and \(\varOmega _{\rm{R}}\) denote multipath components and the average power of light of sight (LOS), respectively, and \({_1 F_1}\left( {.,.,.} \right)\) is the confluent hypergeometric function of the first kind [46, Eq. 9.210.1]. Using [34], we can rewrite the PDF of \(|h_{\rm{R}}|^2\) as
where \(\xi \left( k \right) = \frac{{\left( { - 1} \right) ^k \left( {1 - m_R } \right) _k \delta _R^k }}{{\left( {k!} \right) ^2 }}\), \(\varXi _R = \beta _R - \delta _R\) and \((.)_x\) denotes the Pochhammer symbol [46, p. xliii]. Based on [46, Eq.3.351.2], the the cumulative distribution function (CDF) of \(\left| {\hat{h}_R } \right| ^2\) can be obtained as
The PDF and CDF of \(|h_i|^2\) are then, respectively, given as [35]
and
where \(m_i\) and \(\varOmega _i\) are the fading severity parameter and the average power, respectively, and \(\varGamma (.,.)\) is the upper incomplete gamma function [46].
Moreover, the PDF of \(\gamma _C\) is calculated with corresponding severity parameters \(\{m_{Cn}\}^N_n\) and average powers \(\{\varOmega _{Cn}\}^N_n\). Therefore, we can express the PDF of \(\gamma _C\) as [36, 37] and [24]
where the parameters \(m_I\) and \(\varOmega _I\) are obtained from moment based estimators. For this, we define \(\varTheta = \sum \nolimits _{n = 1}^I {\left| {h_{nR} } \right| ^2 }\), and without loss of generality, we assume no power control is used, i.e., \(P_{Cn} = P_C\) or \(\rho _{Cn} = \rho _C\). Then, we have \(\varOmega _I = \rho _C \varOmega _C\), where \(\varOmega _C = E\left[ \varTheta \right] = \sum \nolimits _{n = 1}^N {\varOmega _{Cn} }\) and \(m_I = \frac{{\varOmega _C^2 }}{{E\left[ {\varTheta ^2 } \right] - \varOmega _C^2 }}\). From this, the exact moments of \(\varTheta\) can be obtained as
where \(E\left[ {\left| {h_{iR} } \right| ^n } \right] = \frac{{\varGamma \left( {m_{Cn} + \frac{n}{2}} \right) }}{{\varGamma \left( {m_{Cn} } \right) }}\left( {\frac{{m_{Cn} }}{{\varOmega _{Cn} }}} \right) ^{ - \frac{n}{2}}\).
3.2 Outage probability of \(D_1\)
An outage event of \(D_1\) is given when R and \(D_1\) cannot detect \(x_1\) correctly. Then, the outage probability of \(D_1\) is given as
where \(\gamma _{i } = 2^{2R_i } - 1\), and \(R_i\) is the target rate.
Proposition 1
Here, the closed-form of \(B_1\) is given as
Proof
See Appendix A.
Next, using (6), \(B_2\) is rewritten as
where \(\phi _2 = \frac{{\left( {\rho _R \sigma _{e_1 }^2 + 1} \right) \gamma _1 }}{{\left( {A_1 - A_2 \gamma _1 } \right) \rho _R }}\). Based on the CDF of \(\hat{h} _i\) in (13), \(B_2\) can be expressed as
Finally, substituting (17) and (19) into (16), \(P_{D_1}\) can be obtained by
3.3 Outage probability of \(D_2\)
The outage events of \(D_2\) occurs when R and \(D_2\) cannot detect \(x_2\) correctly. Therefore, the outage probability of \(D_2\) is given as
Proposition 2
The closed-form outage probability of \(P_{D_2}\) is obtained as
Proof
See Appendix B.
3.4 Diversity order
To gain some insight, we derive under the asymptotic outage probability of \(D_i\) under a high SNR \((\rho = \rho _S=\rho _R \rightarrow \infty )\). The diversity order is defined as [38]
where \({P_{D_i }^\infty }\) is the asymptotic outage probability of \(D_i\).
Proposition 3
The asymptotic outage probability of \(D_1\) is given as
Proof
See Appendix C.
Similarly, the asymptotic of \(D_2\) can be expressed by
The results in (24) and (25) refer to limits of outage performance in the region of high SNR. It can be predicted that the outage performance of two ground users encounters the lower bound even though we improve other system parameters. As discussed, the diversity is then zero.
3.5 Ergodic capacity of \(D_1\)
The ergodic capacity of \(x_i\) is expressed as [39]
where \(Q_1 = \min \left( {\varGamma _{R \rightarrow x_1 },\varGamma _{D_1 \rightarrow x_1 } } \right)\).
Proposition 4
The closed-form ergodic capacity of \(x_1\) is given as (27), where \(\varPsi _1 = \frac{{\left( {\rho _S \sigma _{e_R }^2 + 1} \right) \varXi _R \left( {1 + \theta _p } \right) }}{{A_2 \rho _S \left( {1 - \theta _p } \right) }} + \frac{{m_1 \left( {\rho _R \sigma _{e_1 }^2 + 1} \right) \left( {1 + \theta _p } \right) }}{{A_2 \varOmega _1 \rho _R \left( {1 - \theta _p } \right) }}\).
Proof
See Appendix D.
3.6 Ergodic capacity \(D_2\)
Similarly, the ergodic capacity of \(x_2\) is written as
where \(Q_2 = \min \left( {\varGamma _{R \rightarrow x_2 },\varGamma _{D_1 \rightarrow x_2 } } \right)\).
Proposition 5
The closed-form ergodic capacity of \(x_1\) is given as (29), where \(\varPsi _2 = \frac{{\varXi _R \left( {\rho _S \sigma _{e_R }^2 + 1} \right) }}{{\rho _R A_2 }} + \frac{{m_2 \left( {\rho _R \sigma _{e_2 }^2 + 1} \right) }}{{\varOmega _2 \rho _R A_2 }}\) and \(G_{1,\left[ {1:1} \right] ,0,\left[ {1:1} \right] }^{1,1,1,1,1}[.,.]\) denotes the Meijer-G function with two variables [42].
Proof
See Appendix E.
4 Consideration on case of multiple antenna relay
In this section, we consider how a multiple antennas relay makes influences to performance of two users \(D_i\). In particular, a DF relay can be equipped with \(K_R\) received antennas and \(K_T\) transmit antenna. To represent mathematical expressions from now on, \({\mathbf {h}}_{R} = [h^1_{R},h^2_{R},...,h^{K_R}_{R}]^T\) is denoted the \(K_R \times 1\) channel vector between and R, \({\mathbf {h}}_{i} = [h^1_{i},h^2_{i},...,h^{K_T}_{i}]^T\) denotes the \(K_T \times 1\) channel vector between R and \(D_i\). In this first phase, the signal received at R with help (1) is given by
where \(\mathbf {n}_R\) denote the vector of zero mean AWGN with variance \(N_0\) and \({\mathbf {w}}_{R}=\frac{\widehat{{\mathbf {h}}}_{R}}{\left\| {\hat{{\mathbf {h}}}_{R}} \right\| _F}\). Then, the SINR is then used to decode \(x_1\) and given as
where \(\eta _R = \rho _S \left\| {\hat{{\mathbf {h}}}_R } \right\| _F^2\). Then, the SINR decoded \(x_2\) is given as
In the second phase, the received at \(D_i\) is expressed as
where \({\mathbf {w}}_i = \frac{\hat{{\mathbf {h}}}_i}{\left\| {\hat{{\mathbf {h}}}}_i \right\| _F}\). The SINR which decodes \(x_1\) at \(D_1\) is given as
where \(\eta _i = \rho _R \left\| {\hat{{\mathbf {h}}}_i } \right\| _F^2\), the SINR which decodes signal \(x_1\) at \(D_2\) is given as
Similarly, the SINR which decodes its own signal \(x_2\) at \(D_2\) is computed according to
4.1 Statistical characterization
In this section, we consider \({\hat{{\mathbf {h}}}_R }\) and \({\hat{{\mathbf {h}}}_i }\) have independent and identically distributed (i.i.d.) entries as [43]. In addition, the PDF of \(\eta _R\) can be expressed by [44]
With the help of [46, Eq. 3.351.2], we have the CDF of \(\eta _R\) as
In addition, the CDF of \(\eta _I\) is given by [44]
4.2 Outage probability
Proposition 6
The outage probability of \(D_1\) is expressed as
Proof
See Appendix F.
Similarly, the outage probability of \(D_2\) can be expressed by
where \(\bar{\phi }_2 = \frac{\gamma _2}{A_2}\)
5 Simulation results and discussion
In this section, we set \(\rho _C= 1\) dB, \(\rho = \rho _S = \rho _R\) and the main parameters given in Table 3. The Shadowed-Rician fading parameters for the satellite link are taken from [40] and shown in Table 4. Additionally, the interference channels parameters were set and calculated according to the respective analytical curves in [24] and are shown in Table 5. Moreover, we using MATLAB for Monte Carlo simulations.
Figure 2 shows the outage performance versus the \(\rho\) (dB) for different shadowing satellite links. We can observe that the performance of the system under AS is superior to the system under HS. That means satellite channel conditions contribute significantly to system performance at the ground users. We can also observe the difference in performance of the NOMA and OMA systems. In the OMA system, the gap between the two curves shows that with increased SNR, system performance increases similarly to the NOMA system. The authenticity of the derived expressions is also evident from the strict match of the Monte Carlo simulations with the analytical simulations.
Figure 3 represents how multiple antennas at relay contribute to improve the system performance at ground users. Once we design the relay with \(K_T=K_R=3\), the big gap outage behavior can be observed compared with the case of the relay with \(K_T=K_R=2\). The reason is that higher diversity from multiple antennas design could be strengthen signal received at ground users and hence outage performance could be improved thoroughly.
Figure 4 indicates the impact of imperfect CSI on outage probability when we change value of \(\rho\) for case of HS. We can see how performance could be affected by such CSI error by varying \(\sigma ^2\). An increase in the value of \(\sigma ^2\) shows a reduction in the performance of the user, and for the lowest value of \(\sigma ^2\), both users demonstrate better performance. As the SNR increases, the performance of both users continues to increase, while in similar conditions in Fig. 5, we varied the number of interfering links for both users by keeping \(\sigma ^2\) constant. Considering impact of CCI concern, the simulation shows that with a greater number of interference links, the performance of both users decreases. However, in all the links, the curves for each user meet at a saturated point at high SNR. We conclude that in the high SNR region, interference links do not have a great effect on user performance.
Figure 6 shows the simulation for outage performance versus \(\rho\) (dB) with the different satellite links as in Fig. 2. The ergodic capacity rates of the message at \(D_1\) are almost similar in both HS and AS modes, but for messaging at \(D_2\), the gap between the curves of ergodic capacity in both modes is comparatively very high. With a simultaneous increase in the SNR, the gap increase is unlike \(D_1\).
Figures 7 and 8 indicate the several curves of ergodic capacity versus \(\rho\) (dB) under HS. We can see the impact of CSI error levels of \(\sigma ^2\) in Fig. 7 while Fig. 8 confirms how the number of CCI sources leads to degradation of performance in term of ergodic capacity. In Fig. 7, as we increase the value of \(\sigma ^2\), the gap between the curves increases simultaneously at high SNR values. Figure 8 shows the ergodic capacity versus \(\rho\) (dB) varying N with satellite link under HS. Although gaps between the curves are evident at medium SNR values, the curves for both the users meet at a single point at higher SNRs, suggesting that at higher SNRs, a greater number of interference links does not show much differential effect on ergodic capacity rates.
6 Conclusion
We described the use of the NOMA technique for communication between a satellite to a relay and the relay to users. We investigated performance of the system in terms of outage probability and ergodic capacity under the effect of CCI at the relay. The performance gap between two destinations can be explained by the differences in power level allocated to the destinations. We also derived the closed-form expressions for outage probability and ergodic capacity at both users. We observed that with an increase in the channel error, both the outage probability and ergodic capacity of the users were significantly affected. The effect of CCI on both outage probability and ergodic capacity is more prominent when the SNR falls in range of 20–30 dB, whereas a greater number of interference links shows little effect in the high SNR region. More specifically, if, for example, the number of interference sources is 5, the outage performance of the system experiences a decrease of approximately 40% at a signal-to-noise ratio (SNR) of 30 dB at the satellite. Outage probability and ergodic capacity became saturated at SNRs of 50 dB and 45 dB, respectively. We also simulated and compared system performance under AS and HS modes for both outage probability and ergodic capacity.
Availability of data and materials
Please contact the corresponding author for data requests.
Abbreviations
- NOMA:
-
Non-orthogonal multiple access
- CSI:
-
Channel state information
- SIC:
-
Successive interference cancellation
- CCI:
-
Co-channel interference
- HS:
-
Heavy shadowing
- AS:
-
Average shadowing
- SNR:
-
Signal-to-noise ratio
- QoS:
-
Quality of services
- 5 G:
-
Fifth generation
- IoT:
-
Internet of things
- OMA:
-
Orthogonal multiple access
- CI:
-
Channel impairments
- HSRN:
-
Hybrid satellite relay networks
- TMCN:
-
Terrestrial mobile communications network
- ISTN:
-
Integrated terrestrial satellite networks
- AF:
-
Amplify and forward
- DF:
-
Decode and forward
- HSTAFRN:
-
Hybrid satellite-terrestrial amplify-and-forward relay network
- OP:
-
Outage probability
- EC:
-
Ergodic capacity
- SND:
-
Simultaneous non-unique detection
- RVs:
-
Random variables
- AWGN:
-
Additive white Gaussian noise
- LOS:
-
Light of sight
- PDF:
-
Probability density function
- CDF:
-
Cumulative distribution function
References
G. Giambene, S. Kota, P. Pillai, Satellite-5G integration: a network perspective. IEEE Netw. 32(5), 25–31 (2018)
S. K. Sharma, S. Chatzinotas, P.-D. Arapoglou, Satellite communications in the 5G era. IET, (2018)
E. Lutz, M. Werner, A. Jahn, Satellite systems for personal and broadband communications (Springer-Verlag, Berlin, 2000)
X. Li, J. Li, Y. Liu, Z. Ding, A. Nallanathan, Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Trans. Wirel. Commun. 19(1), 680–695 (2020). https://doi.org/10.1109/TWC.2019.2947670
D.-T. Do, M.-S. Van Nguyen, M. Voznak, A. Kwasinski, J.N. de Souza, Performance analysis of clustering car-following V2X system with wireless power transfer and massive connections. IEEE Internet Things J. (2021). https://doi.org/10.1109/JIOT.2021.3070744
Dinh-Thuan. Do, M..-S. Van Nguyen, Device-to-device transmission modes in NOMA network with and without Wireless Power Transfer. Comput. Commun. 139, 67–77 (2019)
D.-T. Do, M.-S.V. Nguyen, F. Jameel, R. Jäntti, I.S. Ansari, Performance evaluation of relay-aided CR-NOMA for beyond 5G communications. IEEE Access 8, 134838–134855 (2020)
Z. Yang, Z. Ding, P. Fan, N. Al-Dhahir, A general power allocation scheme to guarantee quality of service in downlink and uplink NOMA systems. IEEE Trans. Wireless Commun. 15(11), 7244–7257 (2016)
M. Zeng, A. Yadav, O.A. Dobre, G.I. Tsiropoulos, H.V. Poor, On the sum rate of MIMO-NOMA and MIMO-OMA systems. IEEE Wirel. Commun. Lett. 6(4), 534–537 (2017)
Y. Liu, Z. Ding, M. Elkashlan, H.V. Poor, Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer. IEEE J. Sel. Areas Commun. 34(4), 938–953 (2016)
M. Caus, M.A. Vázquez, A. Pérez-Neira, NOMA and interference limited satellite scenarios. Proc. IEEE ACSSC 497–501 (2016)
X. Yan, H. Xiao, C.-X. Wang, K. An, On the ergodic capacity of NOMA-based cognitive hybrid satellite terrestrial networks. Proc, ICCC (2017)
S. Xie, B. Zhang, D. Guo, B. Zhao, Performance analysis and power allocation for NOMA-based hybrid satellite-terrestrial relay networks with imperfect channel state information. IEEE Access 9, 136279–136289 (2019)
S. Xie et al., Outage analysis and optimization of NOMA-based integrated satellite-terrestrial system with an AF relay, Proc. IEEE Int. Conf. Commun. in China (ICCC), (2019)
X. Zhang et al., Outage performance of NOMA-based cognitive hybrid satellite-terrestrial overlay networks by amplify-and-forward protocols. IEEE Access 7, 85372–85381 (2019)
X. Tang, K. An, K. Guo, Y. Huang, S. Wang, Outage analysis of non-orthogonal multiple access-based integrated satellite-terrestrial relay networks with hardware impairments. IEEE Access 7, 141258–141267 (2019)
Z. Lin, M. Lin, J.-B. Wang, T. de Cola, J. Wang, Joint beamforming and power allocation for satellite-terrestrial integrated networks with non-orthogonal multiple access. IEEE J. Sel. Top. Signal Process. 13(3), 657–670 (2019)
X. Zhu, C. Jiang, L. Kuang, N. Ge, J. Lu, Non-orthogonal multiple access based integrated terrestrial-satellite networks. IEEE J. Sel. Areas Commun. 35(10), 2253–2267 (2017)
M. Lin, C. Yin, Z. Lin, J.-B. Wang, T. de Cola and J. Ouyang, Combined beamforming with NOMA for cognitive satellite-terrestrial networks. Proc. IEEE Int. Conf. Commun. (ICC), (2019)
X. Yan, H. Xiao, K. An, G. Zheng, W. Tao, Hybrid satellite-terrestrial relay networks with cooperative non-orthogonal multiple access. IEEE Commun. Lett. 22(5), 978–981 (2018)
X. Li, M. Liu, D. Deng, J. Li, C. Deng, Q. Yu, Power beacon assisted wireless power cooperative relaying using NOMA with hardware impairments and imperfect CSI. Int. J. Electron. Commun. 108, 275–286 (2019)
S. Xie, B. Zhang, D. Guo, B. Zhao, Performance analysis and power allocation for NOMA-based hybird satellite-terrestrial relay networks with imperfect channelstate-iinformation. IEEE Access 7, 136279–136289 (2019)
K. An et al., Performance analysis of multi-antenna hybrid satellite terrestrial relay networks in the presence of interference. IEEE Trans. Commun. 63(11), 4390–4404 (2015)
V. Bankey, P.K. Upadhyay, Ergodic capacity of multiuser hybrid satellite-terrestrial fixed-gain AF relay networks with CCI and outdated CSI. IEEE Trans. Veh. Technol. 67(5), 4666–4671 (2018)
J. Hussein, S. Ikki, S. Boussakta, C. Tsimenidis, Performance analysis of opportunistic scheduling in dual-hop multi-user underlay cognitive network in the presence of co-channel interference. IEEE Trans. Veh. Technol. 65(10), 8163–8176 (2016)
D.B. da Costa, H. Ding, M.D. Yacoub, J. Ge, Two-way relaying in interference-limited AF cooperative networks over Nakagami-m fading. IEEE Trans. Veh. Technol. 61(8), 3766–3771 (2012)
X. Liang, J. Jiao, S. Wu, Q. Zhang, Outage analysis of multirelay multiuser hybrid satellite-terrestrial millimeter-wave networks. IEEE Wirel. Commun. Lett. 7(6), 1046–1049 (2018)
P.K. Upadhyay, P.K. Sharma, Multiuser hybrid satellite-terrestrial relay networks with co-channel interference and feedback latency, in Proc. Athens, Greece, Eur. Conf. Netw. Commun. pp. 174–178, (2016)
K. Guo, Z. Ji, B. Yang, and X. Wang, NOMA-based integrated satellite-terrestrial multi-relay networks with hardware impairments and partial relay selection scheme, in Proc. IEEE 19th international conference on communication technology, pp. 1099-1104 (2019)
V. Bankey, P.K. Upadhyay, Physical layer security of multiuser multirelay hybrid satellite-terrestrial relay networks. IEEE Trans. Veh. Technol. 68(3), 2488–2501 (2019)
S. Xie, B. Zhang, D. Guo, B. Zhao, Performance analysis and power allocation for NOMA-based hybrid satellite-terrestrial relay networks with imperfect channel state information. IEEE Access 7, 136279–136289 (2019)
X. Li et al., A unified framework for HS-UAV NOMA networks: performance analysis and location optimization. IEEE Access 8, 13329–13340 (2020)
M.K. Arti, M.R. Bhatnagar, Beamforming and combining in hybrid satellite-terrestrial cooperative systems. IEEE Commun. Lett. 18(3), 483–486 (2014)
G. Alfano, A. De Maio, Sum of squared Shadowed-Rice random variables and its application to communication systems performance prediction. IEEE Trans. Wirel.Commun. 6(10), 3540–3545 (2007)
D. Do, A. Le, B.M. Lee, NOMA in cooperative underlay cognitive radio networks under imperfect SIC. IEEE Access 8, 86180–86195 (2020)
D.B. da Costa, H. Ding, J. Ge, Interference-limited relaying transmissions in dual-hop cooperative networks over Nakagami-m fading. IEEE Commun. Lett. 15(5), 503–505 (2011)
D.B. da Costa, M.D. Yacoub, Outage performance of two hop AF relaying systems with co-channel interferers over Nakagami-m fading. IEEE Commun. Lett. 15(9), 980–982 (2011)
Y. Liu, Z. Ding, M. Elkashlan, J. Yuan, Non-orthogonal multiple access in large-scale underlay cognitive radio networks. IEEE Trans. Veh. Technol. 65(12), 10152–10157 (2016)
X. Yue, Y. Liu, S. Kang, A. Nallanathan, Y. Chen, Modeling and analysis of two-way relay non-orthogonal multiple access systems. IEEE Trans. Veh. Technol. 66(9), 3784–3796 (2018)
N.I. Miridakis, D.D. Vergados, A. Michalas, Dual-hop communication over a satellite relay and shadowed Rician channels. IEEE Trans. Veh. Technol. 64(9), 4031–4040 (2015)
V. S. Adamchik and O. I. Marichev, The algorithm for calculating integrals of hypergeometric type functions and its realization in reduce system, in Proc. Int. Symp. Symbolic and Algebraic Computation (ISSAC), Tokyo, pp. 212-224 (1990)
R. P. Agrawal, Certain transformation formulae and Meijer’s G function of two variables. Indian J. Pure Appl. Math. 1(4), 537–551 (1970)
P.K. Upadhyay, P.K. Sharma, Max-max user-relay selection scheme in multiuser and multirelay hybrid satellite-terrestrial relay systems. IEEE Commun. Lett. 20(2), 268–271 (2016)
L. Han, W.-P. Zhu, M. Lin, Outage analysis of NOMA-based multiple-antenna hybrid satellite-terrestrial relay networks. IEEE Commun. Lett. 25(4), 1109–1113 (2021)
A.M. Mathai, R.K. Saxena, The H-function with applications in statistics and other disciplines (Wiley Eastern, India, 1978)
I.S. Gradshteyn, I.M. Ryzhik, Table of integrals, series and products, 6th edn. (Academic Press, New York, 2000)
Acknowledgements
We are greatly thankful to Van Lang University, Vietnam, for providing the budget for this study.
Funding
The research leading to these results was supported by the Ministry of Education, Youth and Sports of the Czech Republic under the grant SP2022/5 and e-INFRA CZ (ID:90140)
Author information
Authors and Affiliations
Contributions
All authors equally contributed to the work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Using (3), \(B_1\) is written as
where \(\phi _1 = \frac{{\gamma _{1 } }}{{\left( {A_1 - A_2 \gamma _{1 } } \right) \rho }}\). \(B_1\) can therefore be expressed as
Substituting (11) and (12) into (43), \(B_1\) is rewritten as
Based on [46, Eq. 1.111] and [46, Eq. 3.381.4], the closed-form of \(B_1\) is obtained as
This completes the proof.
Appendix B
Let us denote the first and second terms of (21) as \(C_1\) and \(C_2\), respectively. Using (4), \(C_1\) can then be written as
where \(\psi _1 = \frac{{\gamma _2 }}{{\rho _S A_2 }}\). As in Proposition 1, we obtain \(C_1\) as
Next, \(C_2\) is calculated as
where \(\psi _2 = \frac{{\left( {{\rho _R \sigma _{e_2 }^2 + 1}} \right) \gamma _2 }}{{\rho _R A_2 }}\).
Using (47) and (48), the closed-form outage probability of \(D_2\) is obtained as (22).
This completes the proof.
Appendix C
In the high SNR region, the CDF of \(|\hat{h}_R|^2\) and \(|\hat{h}_i|^2\) are, respectively, given s
and
Next, the asymptotic outage probability of \(D_1\) is calculated as
Then, \(B_1^\infty\) is expressed by
Using (49) and (14), we can rewrite \(B_1^\infty\) as
\(B_1^\infty\) is thus obtained by
Then, the term \(B_2^\infty\) can be calculated by
Substituting (54) and (55) into (51), we obtain (24).
This completes the proof.
Appendix D
First, the CDF of \(Q_1\) is expressed as
Substituting (56) into (26), we obtain \(R_{x_1}\) as
Using the Gaussian–Chebyshev property and denoting \(\theta _p = \cos \left( {\frac{{2p - 1}}{{2P}}\pi } \right)\), the closed-form ergodic capacity of \(x_1\) (27) can be obtained.
This completes the proof.
Appendix E
Similarly, the CDF of \(Q_2\) is expressed as
where \(\varPsi _2 = \frac{{\varXi _R \left( {\rho _S \sigma _{e_R }^2 + 1} \right) }}{{\rho _R A_2 }} + \frac{{m_2 \left( {\rho _R \sigma _{e_2 }^2 + 1} \right) }}{{\varOmega _2 \rho _R A_2 }}\). Next, we can calculate \(R_{x_2}\) as
Using [41], we have
where \(G_{1,1}^{1,1} [.,.]\) is the Meijer G-function [46]. Substituting (60) into (59), \(R_{x_2 }\) is rewritten as
Based on [45, 2.6.2], (10) is obtained.
This completes the proof.
Appendix F
The outage probability of \(D_1\) can be expressed by
With the help of (31), the first term \(F_1\) is obtained by
where \(\bar{\phi }_1 = \frac{{\gamma _1 }}{{\left( {A_1 - A_2 \gamma _1 } \right) }}\). Based on (14) and (37), \(F_1\) can be calculated as
Then, the second term of (63) can be calculated by
Putting (64) and (14) into (62), we have expected result. The proof is completed.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen, NT., Nguyen, HN., Le, AT. et al. Impact of CCI on performance analysis of downlink satellite-terrestrial systems: outage probability and ergodic capacity perspective. J Wireless Com Network 2022, 70 (2022). https://doi.org/10.1186/s13638-022-02140-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-022-02140-4