1 Introduction

Angle of arrival (AOA) estimation in a low grazing angle is one of the most challenging problems in radar fields [1–3], where the multipath effect is the main problem. In this case, the detection and tracking performance severely deteriorated due to the random phase variation of indirect signals. The direct and reflected returns coherently combined at the receiver with the peaks (maxima) and nulls (minima) corresponding to complete constructive and destructive interference, respectively, depending upon the phase difference. It had been shown that multipath reflections affects categorized into two different aspects, namely, multipath suppression and multipath utilization. Some methods regard the multipath effect as a clutter component and try to suppress it [4–12]. Numerous methods, such as spatial smoothing techniques, proposed removing the coherency [13, 14]. It had been demonstrated in [15] that the detection performance could be enhanced via multipath utilization with a statistical multiple-input multiple-output (MIMO) radar. The authors have further investigated a hybrid MIMO radar for detecting low grazing angle targets in multipath propagation scenarios [16].

We know that the location of the multipath nulls is frequency-dependent in range and elevation angle. Some methods have shown that using the advantage of multipath propagation, which provides spatial diversity of radar systems and frequency diversity of orthogonal frequency division multiplexing (OFDM) waveforms, and a remarkable improvement will be achieved [17]. The authors presented an adaptive waveform design method based on maximizing the Mahalanobis distance to improve the target detection performance in low grazing angle situations. We consider the OFDM signaling scheme [18–25], which is one of the ways to accomplish the simultaneous use of several subcarriers. Furthermore, the monopulse method, which has been utilized in many studies for target detection and tracking [26–31], has been applied for the angle of arrival estimation. A new adaptive beamforming method has been investigated in [32] for low-angle target tracking under multipath scenarios. They proposed a new monopulse technique that utilizes an iterative interference cancellation algorithm to overcome performance degradation.

In this study, we have investigated a new recursive algorithm which provides an efficient spectrum that uses optimized OFDM waveform proposed in [33]. The angle of arrival for each distance of a target is estimated based on the signal error obtained by the amplitude monopulse method. Simulation results show that the proposed approach allows to intelligently selecting subcarriers to fill in the nulls caused by the corresponding destructive effect of multipath.

Our contributions can be summarised as follows:

  • Analogous to [17], a realistic multipath reflection model, is considered for the Earth’s curvature, while an idealistic model had been considered in the literature [12].

  • Our work is to improve the target tracking performance in a low grazing angle region by employing the optimized OFDM waveform. To do this, we have proposed a new recursive method for low grazing angle target tracking, which could fill in multipath nulls and have a good performance in low grazing angle scenarios.

The rest of this paper is organized as follows: in Section 2, the ray reflection model is described to obtain the formulas that will be used to represent the geometrical environment of the low-angle target. In Section 3, the model of OFDM measurement for an extended target case, including multipath effect, has been presented. An extended target model with multiple approximately fixed scattering centers has been considered and assumed that the target may have a bulk velocity. In Section 4, the frequency diversity of OFDM waveforms has been utilized, and a recursive low-angle target tracking method is presented to mitigate multipath nulls. Simulation results are presented in Section 5 for selected experiments to illustrate the excellent performance of the proposed target tracking algorithm for low grazing angle scenarios. Finally, we summarize and conclude the paper in Section 6.

Notation: throughout this correspondence, \(E[.], (.)^{H}, (.)^{T}, (\hat {.}),I_{M}, Re(.), Tr(.)\) and logdet denote expectation operator, conjugate transpose, transpose, estimate, M×M identity matrix, real part, trace, and logarithm-determinant, respectively.

2 Geometric background

The spherical-earth model geometry shown in Fig. 1 is used to solve for the path length difference ΔR, target elevation angle θd, reflection point depression angle θr. Then the grazing angle Φ given the radar antenna height ha, target altitude ht, and the target slant range Rd.

Fig. 1
figure 1

Spherical-earth model geometry [17]

Full size image

Firstly, obtain the effective Earth radius as [20]

$$ R_{e}=\frac{4}{3}r_{e} $$
(1)

where re stands for the actual radius of the earth. The target elevation angle θd can be derived from applying the law of cosine (LOC) as

$$ \theta_{d}=sin^{-1}\left(\frac{2R_{e}(h_{t}-h_{a})+h_{t}^{2}-h_{a}^{2}-R_{d}^{2}}{2(R_{e}+h_{a})R_{d}}\right) $$
(2)

The target ground range r=r1+r2 is defined as [20]

$$ r=2R_{e} sin^{-1}\sqrt{\frac{R_{d}^{2}-(h_{t}-h_{a})^{2}}{4(R_{e}+h_{a})(R_{e}+h_{t})}} $$
(3)

The ground range r1 is given by

$$\begin{array}{*{20}l} r_{1}=\frac{r}{2}-psin\left(\frac{\phi}{3}\right) \end{array} $$
(4)

where

$$\begin{array}{*{20}l} p=\frac{2}{\sqrt{3}}\sqrt{R_{e}(h_{t}+h_{a})+\left(\frac{r}{2}\right)^{2}} \end{array} $$
(5)

And

$$\begin{array}{*{20}l} \phi=sin^{-1}\left(\frac{2R_{e}r(h_{t}-h_{a})}{p^{3}}\right) \end{array} $$
(6)

Using the law of cosines, the reflected ray path length from the radar antenna to the reflection point can be computed as

$$\begin{array}{*{20}l} & R_{1}=\sqrt{h_{a}^{2}+4R_{e}(h_{a}+R_{e})sin^{2}\left(\frac{r_{1}}{2R_{e}}\right)}\\ & R_{2}=\sqrt{h_{t}^{2}+4R_{e}(h_{t}+R_{e})sin^{2}\left(\frac{r_{2}}{2R_{e}}\right)} \end{array} $$
(7)

The depression angle of the reflected leg is computed as

$$ \theta_{r}=sin^{-1}\left(\frac{2R_{e}h_{a}+h_{a}^{2}+R_{1}^{2}}{2(R_{e}+h_{a})R_{1}}\right) $$
(8)

And finally, the grazing angle at the reflection point is

$$ \psi=sin^{-1}\left(\frac{2R_{e}h_{a}+h_{a}^{2}-R_{1}^{2}}{2R_{e}R_{1}}\right) $$
(9)

The path length difference between the direct and reflected legs can now be written as

$$ \Delta R=(R_{1}+R_{2})-R_{d}=\frac{4R_{1}R_{2}sin^{2}(\psi)}{R_{1}+R_{2}+R_{d}} $$
(10)

3 Preliminaries

We consider a multicarrier OFDM signaling system consists of L active subcarriers, a pulse duration of T seconds, and a bandwidth of B Hz. The complex-valued baseband OFDM signal can be written as

$$ s(t)=\sum_{l=0}^{L-1}a_{l}{\text{exp}}(j2{\pi}l{\Delta}ft) $$
(11)

Δf=1/T represents the subcarrier spacing and al denotes the complex weights transmitted over different subcarriers, satisfying \(\sum _{l=0}^{L-1}|a_{l}|^{2}=1\). Now let fc be the carrier frequency, then the OFDM transmitted signal can be written as

$$ \tilde{s}(t)=2 Re\left\{\sum_{l=0}^{L-1}a_{l}{\text{exp}}(j2{\pi}f_{l}t)\right\} $$
(12)

where

$$ f_{l}=f_{c}+l{{\Delta}f} \quad \quad l=0,1,...,L-1 $$
(13)

The complex envelope of the return signal along the p-th path at the terminals of the lth subchannel is given by

$$\begin{array}{*{20}l} \tilde{r_{l}}(t)=x_{lp}\tilde{s_{l}}({\gamma_{p}}(t-\tau_{p}))+\tilde{e_{lp}}(t) \end{array} $$
(14)

where xlp denotes a complex quantity representing the scattering coefficient of the target between the lth subchannel and p path; γ=1+β represents the stretching in time of the reflected signal and \(\beta = \frac {2< v,u>}{c}\) is the Doppler spreading factor, u is direction-of-arrival (DOA) unit-vector and c is the speed of propagation. τp is the roundtrip delay according along the lth subchannel and p path. The complex envelope of the received signal consists of the direct path and specular paths corresponding to a specific range cell containing the target can be described as

$$\begin{array}{*{20}l} \tilde{r_{l}}(t)=\sum_{p=0}^{P-1}a_{l}x_{lp}\phi_{lp}(n)+\tilde{e_{l}}(t) \end{array} $$
(15)

where

$$\begin{array}{*{20}l} \phi_{lp}(n)= e^{-j2{\pi}f_{l}\tau_{p}} e^{j2{\pi}f_{l}\beta_{p}{n}T_{PRI}} \end{array} $$
(16)

We can rewrite 15 as a column vector of dimension L×1 and we have

$$\begin{array}{*{20}l} y_{{\text{OFDM}}}(n)=AX\phi(v,n)+e(n) \quad n=0,1,\ldots,N-1 \end{array} $$
(17)

where

  • \(\phantom {\dot {i}\!}y_{{\text {OFDM}}}(n)=[y_{0_{{\text {OFDM}}}}(n),y_{1_{{\text {OFDM}}}}(n),\ldots y_{L-1_{{\text {OFDM}}}}(n)]^{T}\);

  • A=diag(a) is an L×L complex diagonal matrix includes the transmitted subcarrier weights;

  • \(X={\text {blkdiag}}\left (x_{0}^{T}, x_{1}^{T},\ldots,x_{L-1}^{T}\right)\) is an L×LP matrix; xl=xl.ρ where ρ=[ρ0,ρ1,…,ρP−1]T denotes the reflection coefficients over different paths. The number of possible propagation paths P adopted in our scenario are three, namely, direct-direct path (ρp=1), direct-reflected path (ρp=ρejϕ), and reflect-reflect path (ρp=(ρejϕ)2).

  • ϕ(v,n) is an L×1 vector comprising the Doppler information of the target at the lth subchannel through the parameter v;

  • e(n)=[e0(n),e1(n),…,eL−1(n)]T is an L×1 vector of measurement noise;

Then, combining the data from N successive pulses columnwise into an L×N matrix, the OFDM measurement model is derived as follows:

$$\begin{array}{*{20}l} Y_{{\text{OFDM}}}=AX\Phi+E \end{array} $$
(18)

where

  • YOFDM=[yOFDM(0),yOFDM(1),…yOFDM(N−1)];

  • Φt=[Φ(0),Φ(1),…,Φ(N−1)] is an L×N matrix comprising the Doppler information of the target;

  • E=[e(0),e(1),…,e(N−1)] is an L×N is a complex matrix that consists of measurement noise;

We construct a decision problem to choose between two possible hypotheses. We also consider noise and clutter as parts of the whole interference in this paper. Assume the target statistics are known while the interference statistics are not known. This corresponds, for example, to the situation where the radar is investigating for specific targets with identified signatures. Noise is assumed to be white with zero-mean complex Gaussian distribution. Besides, we suppose that the clutter reflection has been modeled by a collection of scatterers and is considered to be a zero-mean complex WSS Gaussian random process with unknown positive definite covariance matrix Σc as

$$\begin{array}{*{20}l} X^{c}\phi^{c}\sim C\mathcal{N}_{L}(0,\Sigma_{c}) \end{array} $$
(19)

The clutter reflections are assumed to be temporally independent from pulse to pulse and vary with an unknown distribution from scan to scan. Therefore, we can rewrite (18) as

$$\begin{array}{*{20}l} Y_{{\text{OFDM}}}=A\tilde{\Phi}^{t}+\tilde{E} \end{array} $$
(20)

where

$$\begin{array}{*{20}l} & \tilde{\Phi}^{t}=X^{t}\Phi^{t} \\ & \tilde{E}=AX^{c}\Phi^{c}+E \end{array} $$
(21)

Based on these assumptions, the OFDM received measurements are distributed as

$$\begin{array}{*{20}l} Y_{{\text{OFDM}}}\sim C\mathcal{N}_{L,N}\left(0, AR_{\tilde{\Phi}}A^{H}+R_{\tilde{E}}\right) \end{array} $$
(22)

where \(R_{\tilde {\Phi }}\) is the target covariance matrix and \(R_{\tilde {E}}\) is the interference covariance matrix which is given by [36]

$$\begin{array}{*{20}l} R_{\tilde{E}}= I_{N} \otimes\left(A\Sigma_{c}A^{H}+\sigma^{2}I_{L}\right) \end{array} $$
(23)

The target recognition problem in radar is formulated by (24), which is considered as a binary hypothesis testing problem.

$$ \left\{\begin{array}{l} H_{0}:\ Y_{OFDM}=\tilde{E}, ~ No ~ Target\\ H_{1}:\ Y_{OFDM}=A\tilde{\Phi}^{t}+\tilde{E}, ~ Target \\ {Exists} \end{array}\right. $$
(24)

We use the generalized likelihood ratio test (GLRT) detector which, had been derived in [33] for the considered hypothesis testing problem.

4 Proposed method

In this section, we present a recursive low-angle target tracking method to mitigate multipath nulls. We show that using frequency diversity of OFDM waveforms, and we can fill multipath nulls.

4.1 Waveform optimization procedure

In this section, an adaptive waveform design approach has been presented for designing the spectrum of the OFDM signal so that its complex weights match with the target and interference PSD. The maximization of the mutual information between unknown target impulse response and the received echoes as a function of the transmitted signal. This criterion is applied in this paper to design the complex weights of the transmitted signal and consequently improve the target tracking in low grazing angle scenarios.

If the transmitted waveform weights matrix A in (18) is known, the conditional mutual information between Y and \(\tilde {\Phi }\) was given by [34]:

$$\begin{array}{*{20}l} &{\text{MI}}(Y_{{\text{OFDM}}};\tilde{\Phi}|A)=h(Y_{{\text{OFDM}}}|A)-h((Y_{{\text{OFDM}}}|\tilde{\Phi},A))\\ & =N\left[{\text{logdet}}(AR_{\tilde{\Phi}}A^{H}+R_{\tilde{E}})-{\text{logdet}}(R_{\tilde{E}})\right] \end{array} $$
(25)

where MI(x;y) descibes the mutual information between x and y, h(x) represents the entropy of x and Rx=E[xxH] is the covariance matrix. We consider the power constraint to make the optimization problem nontrivial and consequently the optimization problem is stated as follows:

$$\begin{array}{*{20}l} &A_{{\text{opt}}}=\underset{A}{\text{arg\,max}}\left(N[{{logdet}}\left(AR_{\tilde{\Phi}}A^{H}+\sigma^{2} I_{L\times L}\right)]\right)\\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad s.t \ AA^{H}\leq P_{t} \end{array} $$
(26)

where Pt is the total transmitted power in dBW. In this paper, we applied our waveform design approach [36] which the transmitted OFDM signal weights were optimized based on maximizing mutual information criterion. The optimized weights of the OFDM signal was driven as

$$\begin{array}{*{20}l} \beta_{l}={\text{max}}\left(-\frac{1}{\lambda}-\frac{\sigma^{2}_{u,l}}{(N+1)\sigma^{2}_{x,l}},0\right) \end{array} $$
(27)

where the parameter λ can be calculated from (28).

$$\begin{array}{*{20}l} \sum_{l=1}^{L}{\text{max}}\left(-\frac{1}{\lambda}-\frac{\sigma^{2}_{u,l}}{(N+1)\sigma^{2}_{x,l}},0\right)=P_{t} \end{array} $$
(28)

Figure 2 shows the flowchart of the proposed OFDM signaling scheme for low grazing angle target tracking scenarios. We will show that utilizing the optimized weights of the OFDM signal and using the proposed tracking algorithm, a more uniform detection coverage obtain in the presence of multipath propagation.

Fig. 2
figure 2

Flowchart of the proposed OFDM signaling scheme for low grazing angle target tracking

Full size image

4.2 Amplitude monopulse target tracking method

We use a closed-loop amplitude monopulse target tracking method that utilizes the frequency diversity of OFDM signals to fill in multipath nulls. The target elevation angle by the amplitude monopulse method can be estimated as

$$\begin{array}{*{20}l} \hat{\theta_{d}}=\frac{1}{k_{m}}Re\left(\frac{\Delta}{\Sigma}\right) \end{array} $$
(29)

where km is the monopulse slope constant. It was shown that when the phase difference between the direct signal and reflected signal are in phase or out of phase will lead to destructive interference and consequently severe angle error estimation in the monopulse method.

The path length difference between the direct and reflected paths is a function of radar antenna height and target range and altitude. For a fixed set of these parameters, the amount of constructive or destructive interference is a function of RF carrier frequency. Operational radars attempt to mitigate nulls by transmitting a different RF carrier frequency from scan to scan.

It was shown in [20] that a sufficient change in the frequency will lead to decorrelate the phase measurement and make the measurement independent. With this assumption, the frequency spacing should be equal to

$$\begin{array}{*{20}l} \Delta f (Hz)=\frac{c(m/s)}{2D(m)} \end{array} $$
(30)

where D is the depth of the target. In this paper, we propose a narrowband OFDM signal that by transmitting multiple, parallel RF subcarriers simultaneously in a single pulse succeeds in filling multipath nulls. In the simulations, we have assumed that D = 15 m and Δf = 10 MHz will be obtained. On the other hand, the distance between the sub-carriers is the same, so it can result in frequency autonomy and frequency diversion to eliminate the multipath nulls. By transmitting a multicarrier OFDM signal with a bandwidth of a least that given by (30) should ensure that some of the subcarriers experience constructive interference or a peak while some may experience a null.

The proposed procedure for low-angle target tracking under multipath scenarios is indicated in Algorithm 1.

5 Simulation results and discussions

In this section, we consider several numerical examples to illustrate the performance of the proposed low grazing angle target approach. First, a description of the simulation setup is provided. The stochastic extended target involves a large number of scatterer points that are considered to move toward the radar with constant velocity and height, and its range varies from 8 km to 30 km. The scattering coefficients of the target (i.e., the entries of X) are taken from a Gaussian ensemble with known PSD (\(C\mathcal {N}(0, C_{X})\)). Then the scattering coefficients will be scaled to satisfy the required SNR. In each iteration, 1000 runs of the Monte Carlo simulation are performed, and the root mean square error (RMSE) of the estimated target elevation angle is computed at every 500 meter intervals.

Simulation Parameters for radar and environment are chosen as follow:

  • Carrier frequency fc=3GHz.

  • Pulse repetition interval TPRI=1ms

  • Pulse width T=0.1μs

  • Subcarrier spacing Δf=10MHz

  • Available bandwidth B=170MHz

  • Number of coherent pulses with a given CPI N=20

  • Number of subcarriers L=16

  • Total transmitted power Pt=10dBW

  • Number of multipaths P=3

  • Antenna height ha=60

  • Target height ht=350

  • Sea RMS wave height σh=0.07

  • Temperature T=20C

  • Static Dielectric Constant εs=69.08

  • Relaxation Time τr=9.15×10−12

  • Ionic Conductivity σi=4.70×1010

We present a recursive low-angle target tracking method using OFDM waveforms. The various simultaneous subcarrier frequencies will ensure that at least several subcarriers will always be outside multipath nulls on a given detection attempt to provide near-constant target visibility. We evaluate the performance of the proposed tracking algorithm via several simulations in the white Gaussian noise condition. The estimation performance is examined over 1000 Monte Carlo trials, and the RMSE of the estimated AOAs can be given at different target distances.

The sum and delta pattern simulated for the proposed amplitude monopulse method are shown in Fig. 3. Figure 4 shows the monopulse ratio which determines the target elevation angle based on (29).

Fig. 3
figure 3

Sum and delta pattern

Full size image
Fig. 4
figure 4

Amplitude monopulse ratio

Full size image

Figure 5 shows the different power allocation schemes applied in the proposed low grazing angle target tracking algorithm. These power allocation schemes include single-carrier waveform [22], conventional equal-power multi-carrier waveform [35], the GLR-based multi-carrier waveform [12], and the proposed MI-based power allocation multi-carrier waveform.

Fig. 5
figure 5

Illustration of power allocation for different multicarrier waveforms. a Diagonal elements of target covariance matrix. b Diagonal elements of equal power waveform. c Diagonal elements of GLR-based waveform. d Diagonal elements of the proposed waveform (L=16,Pt=10 dBW)

Full size image

Figure 6 shows the propagation coefficient in each sub-carrier for a single-carrier and a multi-carrier waveform. As can be seen in this figure, at some tracking distances, the amplitude for the single-carrier waveform is close to 0, which is leading to a lower signal level and consequently, the more target estimation angle error. However, for distances that the propagation coefficient of the single-carrier waveform is close to 0, we have appropriate propagation coefficient amplitudes and it means that we have sufficient energies in some carriers. Therefore, the target angle estimation will be improved using a multicarrier phase-coded (MCPC) waveform.

Fig. 6
figure 6

Pattern propagation factor for single and MCPC waveform

Full size image

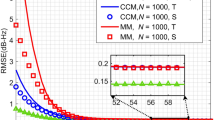
Figure 7 shows the RMSE curve of different approaches at different ranges. As shown in the figure, for the single-carrier waveform (red color), target return at the radar receiver due to different phase differences indicates the peaks (maxima) and nulls (minima) corresponding to complete the constructive and destructive effect. While using multicarrier waveforms, the destructive effect will be removed, and the proposed approach can track the target with reasonable angle measurement error. As indicated in this figure, the best performance for the MCPC waveforms is achieved by using the proposed MI-based approach compared to other MCPC waveform design approaches. Furthermore, in Table 1, we have summarized the comparison performance of different approaches in low grazing angle target tracking scenario.

Fig. 7
figure 7

RMSE versus range

Full size image
Table 1 Performance comparison of different approaches in low grazing angle target tracking scenario
Full size table

Operational radars attempt to mitigate nulls by transmitting a different RF carrier frequency from scan to scan. This solution comes at the expense of the potential increase in time to detect a target. This paper addresses the use of an OFDM radar waveform to provide a more uniform detection coverage in the presence of multipath propagation by transmitting multiple, parallel RF subcarriers simultaneously in a single pulse to fill in the nulls. Simulation results justify this issue and show the importance of adaptive OFDM waveform design in low gazing angle target tracking scenarios.

6 Conclusion

In this paper, we addressed an edge computing problem of target tracking in a low grazing angle with OFDM radar. First, to make the propagation model more accurate, we incorporated realistic physical and statistical effects. Then, based on the characteristic of the OFDM radar system and the multipath propagation model, we developed an OFDM measurement model and derived a GLRT detector. And then, an adaptive design algorithm was proposed based on maximizing mutual information to enhance the detection performance to design the complex weights of the transmitted waveform. And finally, we showed that the detection performance is improved due to the multipath utilization as well as the adaptive design method. We also demonstrated that the detection process of multicarrier radar waveforms outperforms the single-carrier OFDM radar waveform. Simulation results showed that by using the proposed OFDM waveform, the target tracking performance had been significantly improved in low grazing angle scenarios. In the future, we will explore other different criteria, e.g., ambiguity function, minimum mean square error, etc., to optimally design the transmit waveform to improve the tracking accuracy.