Abstract
Unmanned aerial vehicle (UAV)-enabled communication system provides flexibility and reliability compared to conventional ones. Millimeter wave (mmWave) and massive multiple-input–multiple-output (MIMO) have widely been researched since recent years, which are promising techniques for the next and even the later generation communication system. Hybrid precoding, as a method to reduce the high cost in hardware and power brought by massive antenna array, develops fiercely and is often combined to deep learning, a kind of popular optimization tool, which brings an overwhelming performance. On the other hand, there are not so many attentions about the hybrid precoding in time-varying mmWave massive MIMO, which is necessary to be considered in a UAV-enabled communication scenario because the performance will degrade seriously if the channel changed while the transmitter and receiver use the precoding matrix corresponding to the expired channel, yet. In this paper, we propose a double-pilot-based hybrid precoding system, which completes analog precoding and digital precoding separately—predicting the previous one using deep learning structure and updating equivalent channel frequently for the post one by enhancing the frequency of equivalent channel estimation.
Similar content being viewed by others
1 Introduction
With the development of remote controlling technique and the emergence of demand in wireless communications, UAV is considered to play an important role in next and beyond next-generation communication system, which brings the possibility of broadband seamless connectivity and flexibility of deployment equipped with multiple antennas and working in millimeter wave band [1]. Compared to conventional terrestrial platforms or high-altitude platforms, UAV-enabled platforms take the advantages of fast deployment, flexible reconfiguration and often more satisfying communication channels because UAV-enabled base station (BS) can dynamically coordinate its position to ensure the presence of short-range line-of-sight links [2]. References [2, 3] summarize three primary kinds of UAV-aided wireless communications, i.e., UAV-aided ubiquitous coverage, UAV-aided relaying, and UAV-aided information dissemination and data collection. The first one is often used to deal with the situation that the terrestrial BS is overloaded or just cannot serve normally due to natural damage where UAV-enabled BS can be flexibly deployed to support the terrestrial BS. The second one is typically used in areas where there are large blocks like mountains or something else to shadow wireless signal significantly, which degrades the performance of mmWave-based communication system [4]. In the last one, UAVs are used to exchange data with a large number of distributed UEs or sensors, in which time delay can be tolerated on a certain level.
MmWave is considered as an opportunity for the communication spectrum in 5G and beyond 5G. With being equipped with massive antennas in both transmitter and receiver, the strong path loss in mmWave can be overcome [5]. However, the massive antennas bring the need for precise channel state information (CSI) with high dimension and the pretty awesome cost in computation and hardware, especially in radio frequency chain (RF chain). Hybrid precoding, as a method to reduce the cost of RF chain and total transmitting power [6], is proposed, while it also needs an efficient algorithm because it is a NP-hard problem due to the constrains in phase shifters. Several efficient algorithms for hybrid precoding in mmWave massive MIMO or normal massive MIMO are proposed including OMP [7], RF iteration [8] and beam steering [9]. In addition, in recent years, more and more researchers pay attentions on the combination between hybrid precoding and deep learning, which often brings an inspiring design and excellent performance due to its powerful ability to mimic almost any relation and function, while we do not need to know what exactly the relation is, just like the hybrid precoding network proposed in [10].
By contrast to the exploring development in time-invariant mmWave massive MIMO, there are not proficient researches according to the time-varying system, such as the scenario of UAV-enabled communications and high-speed railway [11]. Although there are some researches about time-varying, we do a brief summary about existing researches and then introduce the necessity of our research. Reference [12] considers the scenario that the precoder acquired by singular value decomposition (SVD) is not corresponding to the current channel in a time-varying channel model, so the receiver needs to update it with some methods. A time-varying channel estimation method based on the Taylor expansion is presented in [13]. There is also a recent research [14] about time-varying precoding in MIMO-OFDM system, which uses an inverse extrapolation method to settle time-varying precoding problem. However, early researches consider the normal MIMO system and recent researches consider the problem of time-varying channel estimation or full digital precoding rather than hybrid precoding. In the next-generation communication system, it is necessary to research the time-varying hybrid precoding in a mmWave or normal massive MIMO scenario, especially in a UAV-enabled communication system due to the mobility of UAVs, which is both the advantage and new challenge for wireless communication. This is the motivation of our work, and the main contributions of this paper are listed in the following:
-
We propose a double-pilot-based time-varying hybrid precoding system based on the analysis that analog precoding and digital precoding vary in different speeds and the size of them is totally distinct, which determines the separate methods for them.
-
We leverage a beamforming index prediction net (BIP-Net) based on convolution 2D (Conv2D) LSTM, which is pretty efficient because we just predict the index of the beamforming from a codebook, which allows the fast training of net.
-
To the best of our knowledge, besides the different rate designs of the double-pilot hybrid precoding system, this is the first paper corresponding to the combination of beamforming prediction and deep learning in a UAV-enabled or time-varying system as well. In addition, the method proposed is flexible and feasible since it can be adopted in any beamforming methods based on a codebook.
Notation: We use the following notations throughout this paper: \({\mathbf {A}}\) is a matrix, \({\mathbf {a}}\) is a vector, \(a\) is a scalar and \({\mathbb {A}}\) is a set. \({\mathbf {A}}^ T\) and \({\mathbf {A}}^ H\) are, respectively, the transpose and conjugate transposes of \({\mathbf {A}}\). \(|{\mathbf {A}}|\) is the determinant of \({\mathbf {A}}\), and \(|\mathrm {a}|\) is the absolute value of \(\mathrm {a}\). \(\mathcal {C N}\left( m, \sigma ^{2}\right)\) means a complex Gaussian process with mean \(m\) and covariance \(\sigma ^{2}\). \(\left\| \cdot \right\| _{F}\) is Frobenius norm. \(\circ\) and \(*\) are Hadamard production and convolutional production, respectively.
2 System model and problem definition
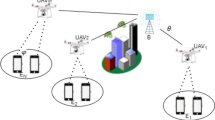
We consider such kind of scenario in which base station (BS) is deployed on a UAV and both BS and user equipment (UE) adopt the lens model [15], as shown in Fig. 1. It also presents the line-of-sight (LOS) and non-line-of-sight (NLOS) paths of mmWave. The time-varying mmWave channel is based on the time-varying geometry channel model. However, our proposed method is suitable for any hybrid precoding based on the certain kind of codebook. The following subsections will present: (1) the mmWave massive MIMO with lens model and the time-varying channel model and (2) the problem definition of hybrid precoding accompanying with the discussion of time-varying influence, respectively.
2.1 System model
2.1.1 Physical model
As illustrated in Fig. 2, the mmWave massive MIMO with lens is similar to the common one. It just substitutes a selector and a lens for the analog precoder and common antenna array. The lens is used to transform the channel into the beamspace, where the mmWave channel is sparse. The selector is used to select the beams which contain the most power.
\(N_s\) is the number of data streams, \({\mathbf {F}}_{BB}\)/\({\mathbf {W}}_{BB}\) is the digital precoding matrix with dimension \(N_{RF} \times N_s\), \(N_{RF}\) is the number of RF chains, \({\mathbf {S}}_t\)/\({\mathbf {S}}_r\) is the selecting matrix in transmitter and receiver with dimension \(N_t \times N_{RF}\)/\(N_r \times N_{RF}\) and \(N_t\)/\(N_r\) is the number of antennas corresponding to the transmitter/receiver.
The lenses in both sides are equal to a two-dimensional fast Fourier transformation (FFT) conducted on channel
where \({\mathbf {F}}_{N_t }\)/\({\mathbf {F}}_{N_r }\) is the 2D FFT matrix, H is the origin channel matrix and \({\mathbf {G}}\) is channel matrix in beamspace which is sparse and just mere points have nonnegligible value, as shown in Fig. 3.
The received signal in receiver can be expressed as
where \({\mathbf {x}}\) is the symbol to be transmitted, \({\mathbf {y}}\) is the received signal and \({\varvec{n}}\) is the noise satisfying the complex Gaussian distribution \(\mathcal {C N}\left( 0, 1\right)\). In a normal mmWave massive MIMO, \({\mathbf {F}}_{N_t } {\mathbf {S}}_t\)/\({\mathbf {F}}_{N_r } {\mathbf {S}}_r\) in the formula is \({\mathbf {F}}_{RF}\)/\({\mathbf {W}}_{RF}\) and called analog precoder/combiner.
So, the 2D FFT matrix \({\mathbf {F}}_{N_t }\)/\({\mathbf {F}}_{N_r }\) can be considered as the codebook \({\mathbb {F}}\)/ \({\mathbb {W}}\) for analog precoding, and the selector \({\mathbf {S}}_t\)/\({\mathbf {S}}_r\) is obligated to select the suitable vectors for beamforming.
2.1.2 Time-varying geometry channel
We adopt the geometry channel model, which depicts the channel matrix in a uniform linear array (ULA) and time-varying scenario as [16, 17].
where \(P\) is the number of multipath, \(\alpha _{\ell }(t)\) is the path loss of the \(\ell\)th path, \({\varvec{a}}_{r}\left( \phi _{r, \ell }(t)\right)\) and \({\varvec{a}}_{t}\left( \phi _{t, \ell }(t)\right)\) are the antenna array response of receiver and transmitter, respectively. \(\phi _{r, \ell }(t)\)/\(\phi _{t, \ell }(t)\) is angle of arrival (AoA) /angle of departure (AoD). \(f _{\ell }\) is the Doppler shift and \(T_s\) is the sampling period. In addition, \(\alpha _{\ell }(t)\) follows the first-order complex Gauss–Markov model and \(\phi _{r, \ell }(t)\)/\(\phi _{t, \ell }(t)\) varies by a low-speed following Gaussian distribution with zero mean and \({\sigma }^2\) variance (according to the position and velocity).
The antenna array response can be expressed as
where d is the antenna space and \({\varvec{a}}_{t}\left( \phi _{t, \ell }(t)\right)\) can also be expressed by the similar formulation just with substituting the AoD for AoA.
2.2 Problem definition and time-varying influence
2.2.1 Hybrid precoding problem definition
The hybrid precoding problem in the lens model can be defined as the following optimization problem [18]
where \({\mathbf {R}}_{n}=\frac{1}{S N R} {\mathbf {W}}^{H} {\mathbf {W}}\), SNR is signal-to-noise ratio and \({\mathbb {B}}^N\) is N-dimensional binary field.
We rewrite the optimization problem considering the suboptimal solution proposed in [19, 20], the coordinated optimization problem can be transformed to
The digital precoder and combiner can be solved by calculating the SVD of \({\mathbf {S}}_r^H {\mathbf {G}}{\mathbf {S}}_t\), considering the \({\mathbf {S}}_r^H {\mathbf {G}}{\mathbf {S}}_t\) as an equivalent channel.
Considering the sparse nature of mmWave channel, we can conduct the beamforming directly by selecting the largest several nonnegligible values in beamspace domain, just as shown in Fig. 3, and adopt the equivalent channel method to complete the hybrid precoding.
2.2.2 Time-varying influence
The following part of this subsection is dedicated to the discussion of the influence of time-varying in a mmWave massive MIMO.
Consider the following situation that the receiver calculates the precise CSI \({\mathbf {H}}(t_1)\) at time \(t_1\). However, when the transmitter and receiver prepare the perfect precoder and combiner for \({\mathbf {H}}(t_1)\), the channel just changes to \({\mathbf {H}}(t_2)\) and the previous precoder and combiner do not match the new channel, which degrades the performance of the system. Figure 4 depicts the aforementioned scenario.
To mitigate the influence, the transmitter and receiver need to frequently update CSI so that they can leverage the relatively recent channel to combat degradation of performance, which brings the problem of high consumption of pilot and computation time. Figure 5 illustrates this by the comparison between communication process diagram of time-invariant (the one above) and time-varying channel (the one below).
2.3 Analysis of analog precoding in time-varying channel
2.3.1 Solution space of analog precoding
Due to the quantification of phase and invariant norm of amplitude in analog precoding, the solution space of each element \(f_{BB}^{ij}\)/\(w_{BB}^{ij}\) (the element of analog precoder/combiner in row i and column j) is constrained into a discrete circuit, as Fig. 6 presents. In addition, in lens model, the analog precoding codebook is the columns of FFT matrix which in fact intends to quantify the AoA/AoD so that the precoder/combiner can only take the format of
where \(k=0,1,\ldots ,N-1\) and N equals to \(N_t\)/\(N_r\). Obviously, the elements of \({\mathbf {f}}_k\) are absolutely determined by k, so the solution space of \({\mathbf {f}}_k\) can be expressed as the same format of element solution space, i.e., Fig. 6.
Only when the deviation of the channel is large enough, the beam selector \({\mathbf {S}}_t\)/\({\mathbf {S}}_r\) needs to change the selected beam, which is shown as Fig. 7.
2.3.2 Robustness of analog precoding
As the final part of this section, we discuss the influence of time-varying on analog precoding, and we can see the robustness of analog precoding against Doppler shifting and the deviation of path gain loss in mmWave channel, which enhances the gap between the deviating speed of analog precoding and digital precoding. Consider the process of beam selection in lens model. The selector selects the closest analog codewords according to the first \(N_{RF}\) largest antenna responses in both sides.
Rewrite the formula of channel model to
It is obvious that Doppler shifting and the deviation of path gain loss do not influence the selection of beamforming because they can be seen as the part of new path gain loss \({\beta }_{\ell }(t)={\alpha }_{\ell }(t)e^{j2\pi f_{\ell }T_st}\).
Thus, we analyze the influence of time-varying mmWave massive MIMO in which digital precoding needs frequent updating so that it can trace the as recent channel as possible, contrary to analog precoding, which can combat Doppler shifting and small deviation of AoA/AoD. In the next section, we present the double-pilot-based hybrid system according to this fact.
3 Methods
In this section, we present the double-pilot-based hybrid precoding system, which is composed of two steps—beam sampling step and prediction step, as Fig. 8, the time axis diagram (the one above), shows. Figure 8 also provides the comparison between the proposed method (the one above) and the common method (the one below)—increasing the sampling rate directly. There are two kinds of pilots with different colors and densities used for, respectively, sampling the equivalent and original channels in the time axis of proposed method, meaning different sampling rates in the aforementioned two steps, which is based on the fact described in Sect. 2. We present the benefits of this double-rate sampling in Sect. 5. Subsection 1 is dedicated to the explanation of beam sampling step and beam prediction step, and subsection 2 explains the digital precoding under having acquired the appreciate beamforming. The ratio of sampling rate of the equivalent channel (yellow pilots) to that of original channel (blue pilots) is notated as \(R _{\mathrm{smpl}}\).
3.1 Analog precoding sampling and prediction
3.1.1 Beam sampling step
As shown in Fig. 8, the blue pilots are used to estimate the mmWave massive MIMO channel and only exist in the period of beam sampling step so that the system can acquire the selector by selecting the coordinate of first \(N_{RF}\) largest elements of the channel in beamspace during each time slot (\([t_{iR_{\mathrm{smpl}}},t_{(i+1)R_{\mathrm{smpl}}}),i=0,1,\ldots\)) in beam sampling step.

According to the enlarged drawing of blue time slot in Fig. 8, the blue pilot using precoding takes a large cost of time (long red block) due to the reality that it needs to transfer \(N_t \times N_t\) pilots and calculate the high-dimension channel matrix to acquire high-dimension analog precoding and low-dimension digital precoding, which is also the process of common precoding presented in the time axis below. After the whole process—including pilots transferring, channel estimation, precoding and feedback being done, data streams can be exchanged between BS and UE (green block).
3.1.2 Beam prediction step
Considering the time correlation showed in Equ. 3, we can try to use the first \(L-1\) selectors to predict the next one so that the transmitter and the receiver can use the precise selectors corresponding to time L rather than the previous ones. The relation of selectors in different times can be expressed as a state transfer equation
where f is the predictor, and we introduce our deep learning-based predictor in the next section.
With the utility of beam prediction, UAV-enabled BS and UE do not need to transfer blue pilots to conduct hybrid precoding and the analog precoding can be acquired directly from the predictor according to the previous \(L-1\) selectors, which saves pretty much time for conventional precoding. Of course, yellow pilots are necessary to complete digital precoding yet.
Obviously, in the beam prediction step, the system only needs a very low cost (short red block in Fig. 8) for digital beamforming, which is presented with details in the next subsection.
3.2 Low complexity digital precoding
This subsection depicts the process of digital precoding after acquiring analog precoding. We consider the parts including selectors and lens in both sides and mmWave massive MIMO channel itself as a whole, a new low-dimension channel \({\mathbf {H}}_{eq}={\mathbf {S}}_r^H{\mathbf {G}}{\mathbf {S}}_t\) and take the assumption that CSI does not change in an interval of \(T_s\), i.e., block fading or at least does not change as large as it does between intervals. Thanks to analog precoding for reducing the channel dimension significantly, we can achieve the equivalent channel with negligible cost before transferring message officially.
As Fig. 8 illustrates, the yellow pilots are used to estimate equivalent channel \({\mathbf {H}}_{eq}\) and the frequency of pilot transmitting should be pretty high due to that digital precoding shifts fast because it is influenced by small scale shading and Doppler shifting. However, thanks to the fact that the dimension of \({\mathbf {H}}_{eq}\) is very low (\(N_{RF} \times N_{RF}\)) so it is possible to update digital precoding frequently, which endows digital precoding the ability of following the time-varying channel smoothly. In each instance (the instance equals to \(T_s\)), transmitter and receiver update their digital precoding via equivalent channel except at the time of \(t_{iR_{\mathrm{smpl}}}\) in beam sampling step when digital precoding can be calculated together with selector, which can be expressed as Algorithm 2:

4 Beamforming index prediction-net in beam prediction step
This section presents the deep learning architecture used to predict the beamforming during the period of beam prediction step proposed in the previous section. Also, it is possible to utilize other methods to conduct the beam prediction. It is necessary to note that, for simplification, we use t to replace \(R_{\mathrm{smpl}}t\), and this notation method is just valid within this section because our deep neural network takes part in only the analog precoding so that there is only one kind of sampling rate for it.
Firstly, setting the time relevance length \(L\), the transmitter successively transfers pilot to the receiver in \(L-1\) slots (time slot equals to \(R _{\mathrm{smpl}} T_s\)) to estimate the channel and generate the beamforming selector by selecting the beams which accumulate most power. We get the first \(L-1\) beamforming selectors in beam sampling step according to the previous section, and we can consider a selector matrix as \(N_{RF}\) one-hot labels, which is widely used in classification problems, and this makes the net easy to be trained [21]. One-hot labels are illustrated in Fig. 9.
Here, we adopt the Conv2D LSTM structure to construct our deep learning net due to the assumption that the beamforming vectors for the specific channel are related and beamforming matrices at different times are related as well. Conv2D LSTM combines the characteristics of convolution net and LSTM net (Fig. 10). The previous one takes advantage of grasping the feature spatially, and the post one is good at analyzing time sequence. Conv2D LSTM uses tensor rather than sequence as input and can use former information at the same time. In Fig. 11, we present the structure of Conv2D LSTM block according to [22], which is pretty similar to the common LSTM block, and Fig. 12 explains the counterparts to the three gates in common LSTM block. The blue block in Fig. 11 means convolutional multiplication, which is the most difference between Conv2D LSTM and common LSTM. This structure is also adopted by [23] to predict the downlink CSI.
According to the second reviewer’s comment, we removed the original Fig. 12 and replaced it by the current Fig. 12.
The explicit relationship of the variables in Fig. 11. can be expressed as follows:
where the subscripts of \({\mathbf {W}}\) mean the operand according to the specific gate.
Figure 10 illustrates the proposed beamforming index prediction network (BIP-Net) with explicit explanations. \({\mathbf {X}}(t-1)\) in Fig. 10 is the selector \({\mathbf {S}}_t\) or \({\mathbf {S}}_r\) in time \(t-1\) and \(\widehat{{\mathbf {Y}}}(t)\) is the prediction of the beamforming index in time t and can be expressed as
where \(f_{C 2 L i}(\cdot )\) notes the Conv2D LSTM block i and \(\Phi _{i}\) means the parameters in the previous one. In addition, the red box in the diagram represents 1 in the input matrix and the yellow one means predicted 1 in the output selector.
We use binary cross-entropy as loss function, which in this net can be expressed as
where y/\({\hat{y}}\) is the element of \({\mathbf {Y}}(t)\)/\(\hat{{\mathbf {Y}}}(t)\), \({\mathbb {P}}=\{\Phi _i |i=1,2,\ldots ,n\}\) is the set of parameters. \({\mathbf {Y}}(t)={\mathbf {X}}(t)\) is label, the precise selector in the next time.
5 Results and discussion
In this section, the simulation results are demonstrated to confirm the feasibility and efficiency of our proposed BIP-Net from the term of achievable rate.
We present the achievable rate of BIP-Net with the research of the influence of time relevance length L in the network. The parameters of our simulated system are as follows. The number of antennas in both transmitter and receiver is 64, i.e., \(N_t=N_r=64\), the RF chain is 3, equals to data streams, and \(P=3\). \(T_s=10\) ms and \(f_{\ell } \in \left[ 0, f_{\max }\right]\), where \(f_{\max }\) can be calculated by Doppler shift formulation. \(R_{\mathrm{smpl}}\) is set to 500 and the velocity is set to 72 km/h, which is an easily achievable speed [24].
Firstly, as illustrated in Fig. 13, the influence of time-varying on normal beamforming methods is significant, where there is a gap between the red line (time-invariant situation) and green line (time-varying situation without BIP-Net). By contrast, with the equipment of BIP-Net, the transmitter and the receiver can transfer messages with almost the same rate of time-invariant situation. Figure 14 takes an example that BIP-Net predicts the correct beamforming, eliminating the influence of time-varying. All these three methods adopt the enumerate way to achieve beamforming due to the fact that we concentrate on the effect of erasing the influence of time-varying rather than beamforming itself. Again, our proposed BIP-Net actually can be leveraged in any beamforming methods to combat the degeneration of the performance as if the methods based on a certain codebook.
Secondly, we take research of the hyper-parameter, the time relevance length L of the Conv2D LSTM, and the result is shown in Fig. 15. Accompanying with the length increasing, the BIP-Net can grasp the precise feature of beamforming indices gradually. In addition, it is also widely known that the process of back-propagation algorithm is slow and hardware-consuming [25], which mobile stations cannot afford. The complicated and large-scale network will extremely constrain the usage of them in different scenarios because developers need to consider any situation and train the network completely in advance. We also execute the experiment of researching the influence of \(T_s\), as Fig. 16 shows.
Finally, it is worth noticing that we use the digital sampling rate during prediction step for the Taylor expansion method, which means that it needs much more pilots for Taylor expansion to achieve this performance since we just need to estimate the equivalent channel rather than the whole channel matrix by our proposed method. What is more, it also brings the huge cost to estimate the channel matrix in the period of beam sampling step with such high frequency. Table 1 explicitly depicts the pilot cost of both of the proposed method and Taylor expansion method.
6 Conclusion
In this paper, we propose an easy-implementable double-pilot-based using deep learning method in UAV-enabled mmWave massive MIMO, which is suitable in various antenna structures and can be trained pretty fast because we transform the precoding prediction problem into the prediction of the sequence with the end-to-end structure. By exploiting the time correlation of channel matrix, the BIP-Net fits the correlation between beamforming vectors.
In addition, the method is flexible because we do not constrain the specific source of the codebook and different kinds of channel estimation methods, codebook-based hybrid precoding methods and prediction methods can be combined to double-pilot-based hybrid precoding method just with the guarantee of the existence of the temporal correlation between CSI in different times. We believe this ideology of double-pilot-based time-varying hybrid precoding method can improve the performance of UAV-enabled communications or other time-varying communication systems significantly.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Abbreviations
- UAV:
-
Unmanned aerial vehicle
- mmWave:
-
Millimeter wave
- MIMO:
-
Multiple-input–multiple-output
- LSTM:
-
Long- and short-term memory
- CSI:
-
Channel state information
- RF:
-
Radio frequency
- SVD:
-
Singular value decomposition
- BIP-Net:
-
Beamforming index prediction net
- Conv2D:
-
Convolution 2D
- BS:
-
Base station
- UE:
-
User equipment
- LOS:
-
Line of sight
- NLOS:
-
Non-line-of-sight
- ULA:
-
Uniform linear array
- AoA:
-
Angle of arrival
- AoD:
-
Angle of departure
References
Z. Pi, F. Khan, An introduction to millimeter-wave mobile broadband systems. IEEE Commun. Mag. 49(6), 101–107 (2011)
Y. Zeng, R. Zhang, T.J. Lim, Wireless communications with unmanned aerial vehicles: opportunities and challenges. IEEE Commun. Mag. 54(5), 36–42 (2016)
A. Osseiran, F. Boccardi, V. Braun, K. Kusume, P. Marsch, M. Maternia, O. Queseth, M. Schellmann, H. Schotten, H. Taoka et al., Scenarios for 5g mobile and wireless communications: the vision of the metis project. IEEE Commun. Mag. 52(5), 26–35 (2014)
M. Mezzavilla, M. Zhang, M. Polese, R. Ford, S. Dutta, S. Rangan, M. Zorzi, End-to-end simulation of 5g mmwave networks. IEEE Commun. Surv. Tutor. 20(3), 2237–2263 (2018)
B. Yang, Z. Yu, J. Lan, R. Zhang, J. Zhou, W. Hong, Digital beamforming-based massive MIMO transceiver for 5g millimeter-wave communications. IEEE Trans. Microwave Theory Tech. 66(7), 3403–3418 (2018)
S.S. Ioushua, Y.C. Eldar, A family of hybrid analog–digital beamforming methods for massive MIMO systems. IEEE Trans. Signal Process. 67(12), 3243–3257 (2019)
O. El Ayach, S. Rajagopal, S. Abu-Surra, Z. Pi, R.W. Heath, Spatially sparse precoding in millimeter wave MIMO systems. IEEE Trans. Wirel. Commun. 13(3), 1499–1513 (2014)
M. Li, Z. Wang, X. Tian, Q. Liu, Joint hybrid precoder and combiner design for multi-stream transmission in mmwave MIMO systems. IET Commun. 11(17), 2596–2604 (2017)
Y. Ahn, T. Kim, C. Lee, A beam steering based hybrid precoding for MU-MIMO mmwave systems. IEEE Commun. Lett. 21(12), 2726–2729 (2017)
H. Huang, Y. Song, J. Yang, G. Gui, F. Adachi, Deep-learning-based millimeter-wave massive MIMO for hybrid precoding. IEEE Trans. Veh. Technol. 68(3), 3027–3032 (2019)
Y. Cui, X. Fang, L. Yan, Hybrid spatial modulation beamforming for mmwave railway communication systems. IEEE Trans. Veh. Technol. 65(12), 9597–9606 (2016)
G. Lebrun, J. Gao, M. Faulkner, MIMO transmission over a time-varying channel using SVD. IEEE Trans. Wirel. Commun. 4(2), 757–764 (2005)
W. Peng, M. Zou, T. Jiang, Channel prediction in time-varying massive MIMO environments. IEEE Access 5, 23938–23946 (2017)
S. Wu, E. Björnson, C. Mollén, X. Tao, E.G. Larsson, Inverse extrapolation for efficient precoding in time-varying massive MIMO-OFDM systems. IEEE Access 7, 91105–91119 (2019)
L. Dai, X. Gao, S. Han, I. Chih-Lin, X. Wang, Beamspace channel estimation for millimeter-wave massive mimo systems with lens antenna array, in 2016 IEEE/CIC International Conference on Communications in China (ICCC) (IEEE, 2016), pp. 1–6
L. Cheng, G. Yue, D. Yu, Y. Liang, S. Li, Millimeter wave time-varying channel estimation via exploiting block-sparse and low-rank structures. IEEE Access 7, 123355–123366 (2019)
H. Liu, T. Zhang, Z. Hu, J. Loo, Y. Wang, Channel tracking for uniform rectangular arrays in mmwave massive mimo systems, in 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP) (IEEE, 2018), pp. 1–6
A. Alkhateeb, R.W. Heath, Frequency selective hybrid precoding for limited feedback millimeter wave systems. IEEE Trans. Commun. 64(5), 1801–1818 (2016)
L. Zhao, D.W.K. Ng, J. Yuan, Multi-user precoding and channel estimation for hybrid millimeter wave systems. IEEE J. Sel. Areas Commun. 35(7), 1576–1590 (2017)
J.P. González-Coma, J. Rodriguez-Fernandez, N. González-Prelcic, L. Castedo, R.W. Heath, Channel estimation and hybrid precoding for frequency selective multiuser mmwave MIMO systems. IEEE J. Sel. Top. Signal Process. 12(2), 353–367 (2018)
T.-H. Chan, K. Jia, S. Gao, J. Lu, Z. Zeng, Y. Ma, Pcanet: a simple deep learning baseline for image classification? IEEE Trans. Image Process. 24(12), 5017–5032 (2015)
S. Xingjian, Z. Chen, H. Wang, D.-Y. Yeung, W.-K. Wong, W.-c. Woo, Convolutional LSTM network: a machine learning approach for precipitation nowcasting, in Advances in Neural Information Processing Systems (2015), pp. 802–810
J. Wang, Y. Ding, S. Bian, Y. Peng, M. Liu, G. Gui, UL-CSI data driven deep learning for predicting DL-CSI in cellular FDD systems. IEEE Access 7, 96105–96112 (2019)
L. Yang, W. Zhang, Beam tracking and optimization for UAV communications. IEEE Trans. Wirel. Commun. 18(11), 5367–5379 (2019)
A. Shrestha, A. Mahmood, Review of deep learning algorithms and architectures. IEEE Access 7, 53040–53065 (2019)
Funding
This work was supported by the National Natural Science Foundation of China under Grant No. 61771254 and No. 61871238.
Author information
Authors and Affiliations
Contributions
ZH is the main author of the current paper. ZH contributed to the development of the ideas, design of the study, theory, result analysis, and article writing. FL and TL contributed to the development of the ideas, design of the study, the theory and article writing. ZH and TL conceived, designed and performed the experiments. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hong, Z., Li, T. & Li, F. Deep double-pilot-based hybrid precoding in UAV-enabled mmWave massive MIMO. J Wireless Com Network 2020, 229 (2020). https://doi.org/10.1186/s13638-020-01854-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-020-01854-7