1 Introduction

With high mobility deployment flexibility and cost-effectiveness, the application of unmanned aerial vehicles (UAVs) in wireless communication has drawn wide attention in academia, research industries, and government [1–3]. UAV-enabled wireless network is recognized as a potential technique to provide communication service in natural disasters such as flood or earthquake [4]. To further enhance coverage and connectivity in some particular cases, many research efforts about UAV-enabled communication system have been made from the perspective of UAVs’ different roles, i.e., as a fixed base source and a demand relay [5].

As substitution of static relay, UAV can adjust its position dynamically according to the current environment so that performance gain of system is improved [6–8]. In [6], the author considered amplify-and-forward (AF) UAV-assisted relaying system in terms of outage probability. In [7], UAV is regarded as the relay to help communication between nodes in device-to-device network. The [8] proposed scheme maximized the end-to-end throughput by jointly optimizing power and UAV trajectory in UAV-assisted relaying system. However, the aforementioned literatures focus on half-duplex (HD) relaying, which leads to the loss of spectral efficiency due to extra cooperative transmission time [9].

As two potential techniques in next generation communication systems, full-duplex relaying [10, 11]and non-orthogonal multiple access (NOMA) [12, 13] are devoted to improving spectral efficiency. On the one hand, FD relaying allows a relay node to transmit and receives simultaneously at the same band different from HD mode. However, severe self-interference (SI) brings great challenge to the feasibility of FD relaying systems. To overcome this problem, the researchers have proposed some effective approaches, such as antenna isolation and analog/digital cancelation [14, 15]. As for FD relaying, there are two types of transmission protocols, namely decode-and-forwarding (DF) and amplify-and-forwarding (AF) [16, 17]. Recently, many literatures are proposed to further improve spectral efficiency [19–21]. Yu et al. [18] further studied outage probability minimization by optimizing the location of relay in full-duplex relaying system. Afterwards, the author considered the joint optimization of transmit power at source/relay and the location of relay in terms of outage probability [20]. Moreover, [21] demonstrated that the full-duplex monitor can significantly improve eavesdropping rate. However, in [19–21], the position of the relay is fixed, which is not suitable for the UAV mobile relay. Inspired by this, [22] considered a more general case where the static relay is replaced by UAV for cooperative communication. A novel UAV-enabled full-duplex scheme for the minimizing sum outage probability in relaying system is proposed. In [23], a UAV-enabled full-duplex relaying system was studied. The authors verified the superiority of the proposed scheme in terms of instantaneous data rate and outage probability.

On the other hand, non-orthogonal multiple access (NOMA) can not only significantly improve the spectrum efficiency but also allow more users or devices to access the network [24–29]. Different from the conventional orthogonal multiple access (OMA), the core of NOMA is to utilize superposed coding (SC) at the transmitter and successive interference cancelation (SIC) at the receivers [24]. The NOMA users are served on the same resource block, such as time/frequency/code [26, 27]. The superior performance of NOMA has stimulated many scholars’ interests, especially cooperative NOMA schemes [28, 29]. In [28], a novel full-duplex cooperative NOMA system was investigated, where the user in good channel condition was regarded as the relay to help communication between the source and the user in poor channel condition. Additionally, the authors maximized the data rate of relay user under quality-of-service (QoS) requirement of the user in poor channel condition. Liu et al. [29] induced a dedicated relay to assist the BS for data transmission. The paper is dedicated to maximizing energy efficiency of system by the joint optimization of transmit power at the source/relay. Wu et al. [28] and [29] both showed the superiority of the proposed cooperative schemes by simulation.

Motivated by the advantage of NOMA, more and more scholars are trying to apply the NOMA to UAV-enabled network for better performance [30]. Sun et al. [31] proposed a novel iterative algorithm to maximize minimum throughput by jointly optimizing multiuser communication scheduling with cyclical NOMA and UAV trajectory. To improve user fairness, [32] integrated NOMA and UAV into the satellite network. The authors proposed a power allocation scheme to improve outage performance. Qi et al. [33] considered sum rate maximization problem as a function of power allocation and UAV altitude. Simulation results verified that the UAV-enabled network with NOMA scheme can bring more performance gain over the existing schemes.

UAV-enabled wireless networks are facing some challenges while bringing significant performance gain. One of critical issues is the energy-constrained battery of UAV which would not support wireless communication constantly. Moreover, the lifetime of network would not be prolonged insufficiently by adjusting the UAV’s locations and the power allocation. Instead of decreasing energy consumption by maximizing energy efficiency [34, 35], simultaneous wireless information and power transfer (SWIPT) is recognized as a more effective approach to alleviate energy consumption problem [36–38]. The core of SWIPT is to enable the wireless devices to harvest energy from the radio frequency signal while receiving the signal. The existing receiver architecture of SWIPT is divided into two categories, i.e., time switching (TS) and power splitting (PS) [39, 40]. Motivated by this, some literatures about the application of SWIPT to UAV-enabled wireless network are studied [41–43]. Yin et al. [41] investigated the end-to-end throughput maximization for UAV-assisted cooperative communication system, where the UAV act as a dedicated relay to help data transmission between the BS and the destination by employing PS protocol. To solve this problem, the author alternately solved the two subproblems by the joint optimization of the UAV’s power profile, power-splitting ratio profile, and trajectory. In [42], the wireless powered UAV-assisted cooperative communication system was studied. The author verified the effectiveness of proposed scheme in terms of outage probability and throughput of system. Xu et al. [43] studied UAV-assisted wireless communication system where the UAV is charged by two energy receivers on the ground. By jointly optimizing the altitude, trajectory, and transmit beam-width of the UAV, the energy harvested from two energy receivers was maximized.

Different from the above literatures, we consider the application of NOMA and full-duplex relaying to UAV-assisted wireless network. On the one hand, the BS employs the NOMA protocol for data transmission and UAV operates in FD mode to implement the relaying behavior so that spectral efficiency is enhanced. On the other hand, we pay attention to the time switching mechanism to enable the UAV to harvest energy and relay data in two phases respectively such that communication reliability is improved.

The contributions of this paper are summarized as follows:

∙ A UAV-enabled cooperative NOMA system with application of SWIPT is studied in this paper, where the wireless powered UAV files along the fixed circle at the fixed height. Under power constraints at the BS and UAV as well as QoS requirement of two NOMA users, we formulate two optimization problems such that sum throughput of system and the harvested energy at UAV are maximized.

∙ Given the circular trajectory of UAV’s fight, we propose an iterative algorithm to tackle such problem by the joint optimization of transmit beamforming vectors and time allocation coefficient. With low complexity and fast convergence, the algorithm guarantees to reach at least local optimum within few iterations.

∙ We demonstrate that the proposed scheme is superior to other baseline schemes by simulation results in terms of sum throughput of system. We also consider the impact of location of UAV on the harvested energy at UAV. In addition, the optimal azimuth angle of UAV’s fight can be obtained by simulation.

Organization: The rest of the paper is organized as follows. Section 2 describes the UAV-enabled cooperative NOMA system with the application of SWIPT in detail and formulates the optimization problem mathematically. In Section 3, a low-complexity iterative algorithm is proposed to solve the highly non-convex problem by the joint optimization of beamforming vectors and time allocation ratio. Simulation results and conclusion are presented in Sections 4 and 5, respectively.

Notations: In this paper, the bold capital and lower-case letters are used to denote matrices and vectors, respectively. R{∙} stands for the real part of a variable. ε{·},(·)H,Tr(·),and rank(·) indicate the expectation, Hermitian transpose, trace, and rank, respectively. IN denotes the N×N identity matrix; \({\mathbb {C}^{N \times M}}\) and \(\mathbf {\mathbb {H}}_ +^{N}\) denote the N×M complex matrices and N×N Hermitian matrices, respectively. ∥ ·∥2 means the Euclidean norm of a vector while ∥ ·∥F means the Frobenius norm of a matrix; null(·) denotes the null space of a vector or matrix. \(\mathbf {x} \sim \mathcal {C}\mathcal {N}\left ({{\boldsymbol {\mu }}, {\Lambda }}\right)\) means the vector x is a complex Gaussian variable with mean μ and covariance Λ.

2 System model and problem formulation

2.1 System model

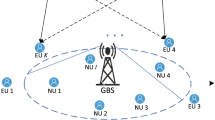
Figure 1 illustrates a wireless powered UAV-enabled relaying communication system with a full-duplex (FD) UAV, a base station (BS), and two downlink users. Using NOMA, the BS is intended to serve two users with different levels of power. Assume that the BS is unable to deliver the superimposed signals to two NOMA users owing to severe blockage. As shown in Fig. 1, high mobility UAV acts as a decode and forward (DF) relay to help data transmission between the BS and two users. In addition, the UAV can harvest energy from the BS and self-interference with utilization of time-splitting (TS) protocol to support relaying behavior. Assume that the BS is equipped with M>1 transmit antennas and two NOMA users are both single-antenna devices. The UAV operates in FD mode with a set of one receive antenna and N>1 transmit antenna. Assume that all channel state information is perfectly known [44].

Fig. 1
figure 1

Full-duplex wireless powered UAV-aided cooperative NOMA network

Full size image

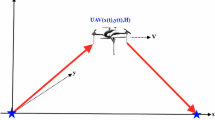
As shown in Fig. 2, the whole communication block T is divided into two slots. In the first time slot αT, the UAV harvests the energy from the BS. In the second time slot (1−α)T, the UAV receives the signal from the BS and transmits the superposed signal to two NOMA users. For simplicity, T is set as 1. In addition, the UAV would harvest energy from self-interference during the second period. The harvested energy at UAV is used for relaying behavior.

Fig. 2
figure 2

An illustration of time block diagram of the energy harvesting and information transmission in TS protocol

Full size image

2.2 Channel model

Without loss of generality, we consider a three-dimensional (3D) Cartesian coordinate system model. As illustrated in Fig. 1, the BS, NOMA near user, and far NOMA user are located at (−ds,0,0),(−d1,0,0), and (−d2,0,0) respectively, where d2>d1=ds=d>0. UAV is deployed at fixed height h and flies in circular domain with radius of r, whose center is located at (0,0,h). In addition, the corresponding azimuth angle while UAV is flying along the circular trajectory is denoted by 0≤θ≤2π. Hence, the fight trajectory of UAV can be written as (r cosθ,r sinθ,h). In practice, the channels between UAV and two users as well as the BS the channel contain two components, i.e., line-of-sight (LoS) and the non-LoS (NLoS), where LoS channel is dominant [45]. Thus, all channels can be modeled as

$$ {\mathbf{h}_{i}}{\mathrm{=}}\beta {\tilde{\mathbf{h}}_{i}}/d_{i}^{{\tau_{i}}\left(\theta\right)}\left(\theta\right)i \in \left\{{SR,R1,R2}\right\}, $$
(1)

where β stands for the channel power gain at the reference distance 1m; hSR,hR1, and hR2 denote channel BS-UAV, channel UAV-U1, and UAV-U2, respectively. Note that hSR,hR1, and hR2 are denoted by

$$ {\tilde{\mathbf{h}}_{i}} \,=\, \sqrt{\frac{{{K_{i}}\left(\theta\right)}}{{{K_{i}}\left(\theta\right) + 1}}} \tilde{\mathbf{h}}_{i}^{LoS} + \sqrt{\frac{1}{{{K_{i}}\left(\theta\right) + 1}}} \tilde{\mathbf{h}}_{i}^{NLoS},i \in \left\{ {SR,R1,R2} \right\} $$
(2)

where \(\tilde {\mathbf {h}}_{i}^{LoS}\) represents LoS component which satisfies \({\text {Tr}}\left \{ {\tilde {\mathbf {h}}_{SR}^{LoS}{{\left ({\tilde {\mathbf {h}}_{SR}^{LoS}} \right)}^{H}}} \right \}{\mathrm { = }}M, {\text {Tr}}\left \{ {\tilde {\mathbf {h}}_{R1}^{LoS}{{\left ({\tilde {\mathbf {h}}_{R1}^{LoS}} \right)}^{H}}} \right \}{\mathrm { = }}N, {\text {Tr}}\left \{ {\tilde {\mathbf {h}}_{R2}^{LoS}{{\left ({\tilde {\mathbf {h}}_{R2}^{LoS}} \right)}^{H}}} \right \}{\mathrm { = }}N\). And a Rayleigh fading channel component, which \(\tilde {\mathbf {h}}_{i}^{NLoS}\) is assumed to be independently circularly symmetric complex Gaussian (CSCG), is distributed with zero mean and unit variance, i.e., \(\tilde {\mathbf {h}}_{i}^{NLoS} \sim {\mathcal {C}}{\mathcal {N}}\left ({{\bf {0}},\mathbf {I}}\right)\). The Rician factor Ki(θ) can be given by \({K_{i}}\left (\theta \right){\mathrm { = }}{\nu _{1}}{e^{{\mu _{1}}{\varpi _{i}}\left (\theta \right)}}\), where ν1andμ1 are constant coefficients and ϖi(θ) is fight angle of UAV relative to communication devices, i.e., ϖi(θ)= arcsin(h/di),i∈{SR,R1,R2}. di,i∈{SR,R1,R2} represents the distances between UAV and all nodes, which are given by

$$ {d_{SR}} = \sqrt{{h^{2}} + {{\left({{d_{SR}} + r\cos \theta}\right)}^{2}}}, $$
(3)
$$ {d_{R1}} = \sqrt{{h^{2}} + {{\left({{d_{R1}}{\mathrm{ - }}r\cos \theta}\right)}^{2}}}, $$
(4)
$$ {d_{R2}} = \sqrt{{h^{2}} + {{\left({{d_{R2}}{\mathrm{ - }}r\cos \theta}\right)}^{2}}} $$
(5)

In addition, τi(θ) is path loss exponent which is written as τi(θ)=ν2PLoS(ϖi(θ))+ν3 with LoS probability \({P_{LoS}}\left ({{\varpi _{i}}\left (\theta \right)}\right) = {\left ({1 + {v_{4}}{e^{- {u_{2}}{\varpi _{i}}\left (\theta \right)}}}\right)^{- 1}}\). Herein, ν2,ν3,ν4, and μ2 are environment constants.

2.3 Signal model

According to NOMA principle, the BS transmits the superimposed signal x(n)=w1x1(n)+w2x2(n) to UAV, where \({\mathbb E}\left \{{{{\left | {{x_{1}}} \right |}^{2}}} \right \} = {\mathbb E}\left \{ {{{\left | {{x_{2}}} \right |}^{2}}} \right \} = 1\) and ∥w1∥2+∥w2∥2≤Ps. Then, the UAV forwards the decoded mixed signal \(\mathbf {s}\left (n\right) = {\mathbf {s}_{1}}{\hat x_{1}}\left ({n + \kappa } \right) + {\mathbf {s}_{2}}{\hat x_{2}}\left ({n + \kappa } \right)\) to two users using NOMA, where κ is time delay; \({\hat x_{1}}\left ({n + \kappa } \right), {\hat x_{2}}\left ({n + \kappa }\right)\) are the decoded versions of x1(n),x2(n), and ∥s1∥2+∥s2∥2 is no more than the maximum transmission power at UAV.

In the first phase αT, the harvested energy at UAV from the BS can be expressed as

$$ {E_{1}} = \eta {\phi_{1}}\left(\theta\right)\left({{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{2}}} \right|}^{2}} + {{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}}} \right)\alpha T $$
(6)

where η∈[0,1] is the energy conversion efficiency at UAV and \({\phi _{1}}\left (\theta \right) = \frac {\beta }{{d_{SR}^{{\tau _{SR}}\left (\theta \right)}\left (\theta \right)}}\).

In the second time phase (1−α)T, the received signal from the BS at the UAV is expressed as

$$ {{\mathrm{y}}_{r}} = {\phi_{2}}\left(\theta\right)\mathbf{h}_{SR}^{H}\mathbf{x}\left(n\right) + \sqrt \rho \mathbf{h}_{rr}^{H}\mathbf{s}\left(n\right) + {n_{r}} $$
(7)

where \({\phi _{2}}\left (\theta \right){\mathrm { = }}\sqrt {\frac {\beta }{{d_{SR}^{{\tau _{SR}}\left (\theta \right)}\left (\theta \right)}}}, \rho \) represents the SI cancelation level and \({n_{r}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,\sigma _{r}^{2}}\right)\) is the noise at UAV.

Meanwhile, the UAV forwards the decoded signals to two NOMA users. Then, the received signal at U1 and U2 can be denoted by

$$ {y_{1}} = {\phi_{3}}\left(\theta\right)\mathbf{h}_{R1}^{H}\mathbf{s}\left(n\right) + {n_{1}} $$
(8)

and

$$ {y_{2}} = {\phi_{4}}\left(\theta\right)\mathbf{h}_{R2}^{H}\mathbf{s}\left(n\right) + {n_{2}}, $$
(9)

respectively, where \(\sqrt {\frac {\beta }{{d_{R1}^{{\tau _{R1}}\left (\theta \right)}\left (\theta \right)}}}, \sqrt {\frac {\beta }{{d_{R2}^{{\tau _{R2}}\left (\theta \right)}\left (\theta \right)}}}, {n_{1}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,\sigma _{1}^{2}} \right)\), and \({n_{2}} \sim {\mathcal {C}}{\mathcal {N}}\left ({0,\sigma _{2}^{2}} \right)\) are noise at U1 and U2 respectively.

According to [11], the portion of SI filtered by the receiver filter proposed can be utilized for energy harvesting; we have

$$ {E_{SI}} = \eta \left({{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{2}}} \right|}^{2}} + {{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{1}}} \right|}^{2}}} \right)\left({1{\mathrm{ - }}\alpha} \right)T $$
(10)

Thus, the maximum transmit power for relaying at UAV is expressed as

$$ {P_{r}} = \frac{{{E_{1}} + {E_{SI}}}}{{\left({1 - \alpha} \right)T}}{\mathrm{ = }}\frac{{\eta {\phi_{1}}\left(\theta\right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}} \alpha }}{{1 - \alpha}}{\mathrm{ + }}\eta \sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{i}}} \right|}^{2}}} $$
(11)

The received SINR to detect the signal x2(n) and x1(n) at the UAV are respectively written as

$$ \gamma_{2}^{\mathrm{R}} = \frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{2}}} \right|}^{2}}}}{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}} + \rho \sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{i}}} \right|}^{2}}} + \sigma_{r}^{2}}}, $$
(12)
$$ \gamma_{1}^{\mathrm{R}} = \frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{\rho \left({{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{1}}} \right|}^{2}} + {{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{2}}} \right|}^{2}}} \right) + \sigma_{r}^{2}}} $$
(13)

The received SINR to detect the signal s2(n) at the U1 is expressed as

$$ \gamma_{2}^{{\mathrm{U1}}}{\mathrm{ = }}\frac{{{\phi_{2}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\phi_{2}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right|}^{2}} + \sigma_{1}^{2}}}. $$
(14)

The received signal to detect its own signal at U1 is represented by

$$ \gamma_{1}^{{\mathrm{U1}}}{\mathrm{ = }}\frac{{{\phi_{2}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right|}^{2}}}}{{\sigma_{1}^{2}}} $$
(15)

The received signal to detect the message s2(n) at U2 is expressed as

$$ \gamma_{2}^{{\mathrm{U2}}}{\mathrm{ = }}\frac{{{\phi_{3}}\left(\theta \right){{\left| {\mathbf{h}_{R2}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\phi_{3}}\left(\theta \right){{\left| {\mathbf{h}_{R2}^{H}{\mathbf{s}_{1}}} \right|}^{2}} + \sigma_{2}^{2}}} $$
(16)

Hence, the available rate of U1 can be written as

$$ R1{\mathrm{ = }}\min \left\{{\ln\left({1 + \gamma_{1}^{\mathrm{R}}} \right),\ln \left({1 + \gamma_{1}^{{\mathrm{U1}}}} \right)} \right\}. $$
(17)

The available rate of U2 can be written as

$$ R2{\mathrm{ = }}\min \left\{{\ln\left({1 + \gamma_{2}^{\mathrm{R}}}\right),\ln \left({1 + \gamma_{2}^{{\mathrm{U1}}}} \right),\ln \left({1 + \gamma_{2}^{{\mathrm{U2}}}}\right)} \right\}. $$
(18)

According to [46], the sum data rate of the whole system can be calculated as

$$ {R_{{\text{sum}}}} = R1 + R2. $$
(19)

2.4 Problem formulation

2.4.1 Sum data rate maximization

Given the trajectory of UAV, we aim at maximizing sum throughput of system by the joint optimization of four beamforming vectors (w1,w2,s1,s2) and time allocation coefficient α in this paper. The problem can be formulated as

$$ \underset{\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha}{\max} {R_{\text{sum}}} $$
(20a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~ {R_{1}} \ge \bar R,{R_{2}} \ge \bar R, \end{array} $$
(20b)
$$ \begin{array}{l} ~~~~~~~~~~~~~~~~~~~{\left\| {{\mathbf{w}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{w}_{2}}} \right\|^{2}} \le {P_{s}}, \end{array} $$
(20c)
$$ ~~~~~~~~~~~~~~~~~~~~~{\left\| {{\mathbf{s}_{1}}} \right\|^{2}} + {\left\| {{\mathbf{s}_{2}}} \right\|^{2}} \le {P_{r}}, $$
(20d)
$$ \begin{array}{l} ~~~~~~~~~~~~~~~~~~~0 < \alpha < 1, \end{array} $$
(20e)

where the target data rate is set for two NOMA users in constraint (20b); constraint (20c) represents the power constraint at the BS, i.e., the transmission power should not be above the maximum Ps; constraint (20d) denotes that transmit power at UAV completely depends on the harvested power Pr; the range of time allocation ratio is given by constraint (20e).

2.4.2 Harvested energy maximization

Under QoS requirement of two NOMA users as well as power constraints at the BS and the relay, the harvested energy maximization can be written as

$$ \underset{\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha}{\max} {E_{1}} + {E_{SI}} $$
(21a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~ (20b)-(20e), \end{array} $$
(21b)

3 The proposed beamforming design

3.1 Sum data rate maximization

By simple transformation, the problem (20) can be rewritten as

$$ \underset{\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha}{\max} {R_{\text{sum}}} $$
(22a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~\min \left\{{\frac{{{\phi_{2}}\left(\theta\right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right|}^{2}}}}{{\sigma_{1}^{2}}},\frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{{\varphi_{1}}\left({{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)}}} \right\} \ge \bar \gamma, \end{array} $$
(22b)
$$ \begin{array}{l} \min \left\{{\frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{2}}} \right|}^{2}}}}{{{\varphi_{2}}\left({{\mathbf{w}_{1}},{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)}},\frac{{{\phi_{2}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\varphi_{3}}\left({{\mathbf{s}_{1}}} \right)}},\frac{{{\phi_{3}}\left(\theta\right){{\left| {\mathbf{h}_{R2}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\varphi_{4}}\left({{\mathbf{s}_{1}}} \right)}}} \right\} \ge \bar \gamma, \end{array} $$
(22c)
$$ \frac{{{{\left\| {{\mathbf{s}_{1}}} \right\|}^{2}} + {{\left\| {{\mathbf{s}_{2}}} \right\|}^{2}}}}{\alpha} \le \frac{{{\eta_{1}}{\phi_{1}}\left(\theta \right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}} }}{{1 - \alpha }}{\mathrm{ + }}\frac{{{\eta_{2}}\sum\limits_{j = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{j}}} \right|}^{2}}} }}{\alpha }, $$
(22d)
$$ \begin{array}{l} (20c), (20e) \end{array} $$
(22e)

where \({\varphi _{2}}\left ({{\mathbf {w}_{1}},{\mathbf {s}_{1}},{\mathbf {s}_{2}}} \right) = {\phi _{1}}\left (\theta \right){\left | {\mathbf {h}_{SR}^{H}{\mathbf {w}_{1}}} \right |^{2}} + \rho {P_{r}}\left ({{{\left | {\mathbf {h}_{rr}^{H}{\mathbf {s}_{1}}} \right |}^{2}} + {{\left | {\mathbf {h}_{rr}^{H}{\mathbf {s}_{2}}} \right |}^{2}}} \right) + \sigma _{r}^{2}, {\varphi _{1}}\left ({{\mathbf {s}_{1}},{\mathbf {s}_{2}}} \right) = \rho {P_{r}}\left ({{{\left | {\mathbf {h}_{rr}^{H}{\mathbf {s}_{1}}} \right |}^{2}} + {{\left | {\mathbf {h}_{rr}^{H}{\mathbf {s}_{2}}} \right |}^{2}}} \right) + \sigma _{r}^{2}, {\varphi _{3}}\left ({{\mathbf {s}_{1}}} \right){\mathrm { = }}{\phi _{2}}\left (\theta \right){\left | {\mathbf {h}_{R1}^{H}{\mathbf {s}_{1}}} \right |^{2}} + \sigma _{1}^{2}, {\varphi _{4}}\left ({{\mathbf {s}_{1}}} \right) = {\phi _{3}}\left (\theta \right){\left | {\mathbf {h}_{R2}^{H}{\mathbf {s}_{1}}} \right |^{2}} + \sigma _{2}^{2}\) and \(\bar \gamma {\mathrm { = }}{{\mathrm {e}}^{\bar R}}{\mathrm { - }}1\).

Apparently, the constraint (22e) is convex. However, the formulated problem is highly non-convex due to the non-convex objective (22a) and constraints (22b)–(22d). Next, let us cope with non-convex terms by using inner approximation method.

According to the inequality (45), five non-convex terms of the objective and two non-convex terms of the right side of (22b) can be bounded respectively around \(\left ({\left \{{\mathbf {w}_{i}^{k}}\right \}_{i = 1}^{2},\left \{{s_{j}^{k}}\right \}_{j = 1}^{2},{\alpha ^{k}}} \right)\) by

$$ {\begin{aligned} \frac{{{\phi_{2}}\left(\theta\right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right|}^{2}}}}{{\sigma_{1}^{2}}}& \ge \frac{{2{\phi_{2}}\left(\theta\right)R\left\{ {{{\left({\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right)}^{*}}\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right\}}}{{\sigma_{1}^{2}}} \\ &- \frac{{{\phi_{2}}\left(\theta\right){{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}}}}{{\sigma_{1}^{2}}}{\mathrm{ = }}{\lambda_{1}}\left({{\mathbf{s}_{1}}} \right), \end{aligned}} $$
(23)
$$ {\begin{aligned} \frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{{\varphi_{1}}\left({{\mathbf{w}_{1}},{\mathbf{s}_{1}},{\mathbf{s}_{2}}}\right)}} &\ge \frac{{2{\phi_{1}}\left(\theta \right)R\left\{{{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{2}}} \right\}}}{{{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}} \\ &- \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right|}^{2}}}}{{{{\left({{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)} \right)}^{2}}}}{\varphi_{1}}\left({{\mathbf{w}_{1}},{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)\\ &={\lambda_{2}}\left({\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{{{s_{j}}} \right\}_{j = 1}^{2}} \right), \end{aligned}} $$
(24)
$$ {\begin{aligned} \frac{{{\phi_{1}}\left(\theta\right){{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right|}^{2}}}}{{\sigma_{1}^{2}}} &\ge \frac{{2{\phi_{1}}\left(\theta\right)R\left\{{{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right\}}}{{\sigma_{1}^{2}}}\\ & - \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}}\right|}^{2}}}}{{\sigma_{1}^{2}}}{\mathrm{ = }}{\lambda_{3}}\left({{\mathbf{w}_{1}}}\right) \end{aligned}} $$
(25)
$$ {\begin{aligned} \frac{{{\phi_{2}}\left(\theta\right){{\left| {\mathbf{h}_{R1}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\varphi_{2}}\left({{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)}} &\ge \frac{{2{\phi_{2}}\left(\theta \right)R\left\{{{{\left({\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right)}^{*}}\mathbf{h}_{R1}^{H}{\mathbf{s}_{2}}} \right\}}}{{{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}} \\ &- \frac{{{{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{{\left({{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}\right)}^{2}}}}{\varphi_{2}}\left({{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right) ={\chi_{4}}\left({\left\{ {\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2}} \right) \end{aligned}} $$
(26)
$$ \begin{array}{l} \frac{{{\phi_{3}}\left(\theta\right){{\left| {\mathbf{h}_{R2}^{H}{\mathbf{s}_{2}}} \right|}^{2}}}}{{{\varphi_{3}}\left({{\mathbf{s}_{1}}} \right)}} \ge \frac{{2{\phi_{3}}\left(\theta\right)R\left\{ {{{\left({\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right)}^{*}}\mathbf{h}_{R2}^{H}{\mathbf{s}_{2}}} \right\}}}{{{\varphi_{3}}\left({\mathbf{s}_{1}^{k}}\right)}} - \frac{{{\phi_{3}}\left(\theta\right){{\left| {\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{{\left({{\varphi_{3}}\left({\mathbf{s}_{1}^{k}} \right)} \right)}^{2}}}}{\varphi_{3}}\left({{\mathbf{s}_{1}}} \right)\\ ~~~~~~~~~~~~{\mathrm{ = }}{\chi_{5}}\left({\left\{{{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}} \right) \end{array} $$
(27)
$$ {\begin{array}{l} \frac{{{\eta_{1}}{\phi_{1}}\left(\theta \right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}} }}{{1 - \alpha }} \ge {\eta_{1}}{\phi_{1}}\left(\theta \right)\sum\limits_{i = 1}^{2} {\left({\frac{{2R\left\{ {{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{i}^{k}} \right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right\}}}{{1 - {\alpha^{k}}}} - \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{i}^{k}} \right|}^{2}}\left({1 - \alpha} \right)}}{{{{\left({1 - {\alpha^{k}}} \right)}^{2}}}}} \right)} \\ ~~~~~~~~~~~~~~~~~~~~~~{\mathrm{ = }}{\chi_{6}}\left({\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\alpha} \right) \end{array}} $$
(28)

Thus, the constraints (22b)–(22d) can be innerly approximated by these convex ones, which are represented by

$$ \frac{{{{\left\| {{\mathbf{s}_{1}}} \right\|}^{2}} + {{\left\| {{\mathbf{s}_{2}}} \right\|}^{2}}}}{\alpha} \le {\chi_{6}}\left({\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\alpha} \right){\mathrm{ + }}{\chi_{7}}\left({\left\{ {{\mathbf{s}_{i}}} \right\}_{i = 1}^{2},\alpha} \right) $$
(29)
$$ \min \left\{{{\lambda_{1}}\left({{\mathbf{s}_{1}}}\right),{\lambda_{3}} \left({{\mathbf{w}_{1}}} \right)} \right\} \ge \bar \gamma $$
(30)
$$ {\begin{aligned} \min \left\{ {{\lambda_{2}}\left({\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2}} \right),{\chi_{4}}\left({\left\{{\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2}} \right),{\chi_{5}}\left({\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}} \right)} \right\} \ge \bar \gamma \end{aligned}} $$
(31)

Then, using the inequality (47), \(\ln \left ({1 + \gamma _{1}^{\mathrm {R}}}\right), \ln \left ({1 + \gamma _{1}^{{\mathrm {U1}}}}\right),\ln \left ({1 + \gamma _{2}^{\mathrm {R}}} \right),\ln \left ({1 + \gamma _{2}^{{\mathrm {U1}}}}\right), \ln \left ({1 + \gamma _{2}^{{\mathrm {U2}}}}\right)\) of the objective can be innerly approximated by

$$ {\begin{aligned} \ln \left({1 + \gamma_{1}^{\mathrm{R}}} \right) &\ge \ln \left({1{\mathrm{ + }}\frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right|}^{2}}}}{{\sigma_{1}^{2}}}} \right) - \frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right|}^{2}}}}{{\sigma_{1}^{2}}}\\ &+ \frac{{2{\phi_{1}}\left(\theta \right)R\left\{ {{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{1}}} \right\}}}{{\sigma_{1}^{2}}}\\ & - \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right|}^{2}}\left({{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right|}^{2}} + \sigma_{1}^{2}} \right)}}{{\sigma_{1}^{2}\left({\sigma_{1}^{2} + {{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{1}^{k}} \right|}^{2}}} \right)}}{\mathrm{ = }}{\Omega_{1}}\left({{\mathbf{w}_{1}}} \right) \end{aligned}} $$
(32)
$$ {\begin{aligned} \ln \left({1 + \gamma_{1}^{{\mathrm{U1}}}} \right) &\ge \ln \left({1{\mathrm{ + }}\frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}}}}{{\sigma_{1}^{2}}}} \right) - \frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}}}}{{\sigma_{1}^{2}}}\\ &+ \frac{{2{\phi_{1}}\left(\theta \right)R\left\{ {{{\left({\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right)}^{*}}\mathbf{h}_{R1}^{H}{\mathbf{s}_{1}}} \right\}}}{{\sigma_{1}^{2}}}\\ &- \frac{{{{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}}\left({{{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}} + \sigma_{1}^{2}} \right)}}{{\sigma_{1}^{2}\left({\sigma_{1}^{2} + {{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{1}^{k}} \right|}^{2}}} \right)}}{\mathrm{ = }}{\Omega_{2}}\left({{\mathbf{s}_{1}}} \right) \end{aligned}} $$
(33)
$$ {\begin{aligned} \ln \left({1 + \gamma_{2}^{\mathrm{R}}} \right) &\ge \ln \left({1 + \frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}}} \right) - \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}}\\ & + \frac{{2{\phi_{1}}\left(\theta \right)R\left\{ {{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{2}}} \right\}}}{{{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}}\\ &- \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right|}^{2}}{\varphi_{1}}\left({{\mathbf{w}_{1}},{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)}}{{{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)\left({{\varphi_{1}}\left({\mathbf{w}_{1}^{k},\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right) + {{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{2}^{k}} \right|}^{2}}} \right)}}\\ &={\Omega_{3}}\left({\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}} \right) \end{aligned}} $$
(34)
$$ {\begin{aligned} \ln \left({1 + \gamma_{2}^{{\mathrm{U1}}}} \right) &\ge \ln \left({1 + \frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}}} \right) - \frac{{{{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}} \\ &+ \frac{{2{\phi_{2}}\left(\theta \right)R\left\{ {{{\left({\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right)}^{*}}\mathbf{h}_{R1}^{H}{\mathbf{s}_{2}}} \right\}}}{{{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)}}\\ &- \frac{{{{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}{\varphi_{2}}\left({{\mathbf{s}_{1}},{\mathbf{s}_{2}}} \right)}}{{{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right)\left({{\varphi_{2}}\left({\mathbf{s}_{1}^{k},\mathbf{s}_{2}^{k}} \right) + {{\left| {\mathbf{h}_{R1}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}} \right)}}\\ &={\Omega_{4}}\left({\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}} \right) \end{aligned}} $$
(35)
$$ {\begin{aligned} \ln \left({1 + \gamma_{2}^{{\mathrm{U2}}}} \right) &\ge \ln \left({1 + \frac{{{\phi_{1}}\left(\theta \right){{\left| {\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{4}}\left({\mathbf{s}_{1}^{k}} \right)}}} \right) - \frac{{{{\left| {\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}}}{{{\varphi_{4}}\left({\mathbf{s}_{1}^{k}} \right)}} \\ &+ \frac{{2{\phi_{2}}\left(\theta \right)R\left\{{{{\left({\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right)}^{*}}\mathbf{h}_{R2}^{H}{\mathbf{s}_{2}}} \right\}}}{{{\varphi_{4}}\left({\mathbf{s}_{1}^{k}} \right)}}\\ &- \frac{{{{\left| {\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}{\varphi_{4}}\left({{\mathbf{s}_{1}}} \right)}}{{{\varphi_{4}}\left({\mathbf{s}_{1}^{k}} \right)\left({{\varphi_{4}}\left({\mathbf{s}_{1}^{k}}\right) + {{\left| {\mathbf{h}_{R2}^{H}\mathbf{s}_{2}^{k}} \right|}^{2}}} \right)}}={\Omega_{5}}\left({\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}} \right) \end{aligned}} $$
(36)

For kth iteration, the feasible points of the original problem can be generated by solving the convex problem

$$ \mathop {\max }\limits_{\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha} {f_{k}}\left({\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha} \right) $$
(37a)
$$ ~~~~~~~{s.t.}~~~~~~~ (22e),(29)-(31) $$
(37b)

where \({f_{k}}\left ({\left \{ {{\mathbf {w}_{i}}} \right \}_{i = 1}^{2}\!,\!\left \{ {{\mathbf {s}_{j}}} \right \}_{j = 1}^{2}\!,\!\alpha } \right){\mathrm { = }}{\Omega _{1}}\left ({{\mathbf {w}_{1}}} \right){\mathrm {\! +\! }}{\Omega _{2}}\left ({{\mathbf {s}_{1}}} \right){\mathrm {\! +\! }}{\Omega _{3}} \left ({\left \{ {{\mathbf {w}_{i}}} \right \}_{i = 1}^{2}\!,\!\left \{ {{\mathbf {s}_{j}}} \right \}_{j = 1}^{2}} \right){\mathrm {\! +\! }}{\Omega _{4}}\left ({\left \{ {{\mathbf {s}_{j}}} \right \}_{j = 1}^{2}} \right) {\mathrm { + }}{\Omega _{5}}\left ({\left \{ {{\mathbf {s}_{j}}} \right \}_{j = 1}^{2}} \right)\) is the approximation of the objective of original problem.

Convergence analysis: The convergence performance of the proposed scheme can be presented in the following proposition.

Proposition 1

Algorithm 1 can generate the feasible points by iteration to make the objective value of (22) become bigger and finally converge to the Karush-Kuhn-Tucker point of (22) after finitely many iterations.

Proof

Refer to Appendix 5 for the detailed proof. □

Complexity analysis: The computational cost of problem (22) at each iteration is O(m2n2.5+n3.5), where the optimization problem (22) involves m=2M+2N+1 the scalar real variables and n=4 quadratic and linear constraints [47].

Given the initial point \(\left ({\left \{ {\mathbf {w}_{i}^{0}} \right \}_{i = 1}^{2},\left \{ {s_{j}^{0}} \right \}_{j = 1}^{2},{\alpha ^{0}}} \right)\), we can achieve the feasible point of the problem (22) by iterating the following problem

$$ {\begin{aligned} &\underset{\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{{{s_{j}}}\right\}_{j = 1}^{2}}{\min} \\ &\left\{ {\frac{{\min \left\{{{\lambda_{1}}\left({{\mathbf{s}_{1}}} \right),{\lambda_{3}}\left({{\mathbf{w}_{1}}} \right)} \right\}}}{{\bar \gamma}},\frac{{\min \left\{ {{\lambda_{2}}\left({\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{{{s_{j}}} \right\}_{j = 1}^{2}}\right),{\chi_{4}}\left({\left\{ {\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2}} \right),{\chi_{5}}\left({\left\{{{\mathbf{s}_{j}}} \right\}_{j = 1}^{2}}\right)} \right\}}}{{\bar \gamma }}} \right\} \\ &~~~~~~s.t. ~~~~~~(22e),(29) \end{aligned}} $$
(38)

until the objective is greater than or equals 1.

3.2 Harvested energy maximization

For convenient treatment, the problem can be rewritten as

$$ \underset{\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha}{\max} {\eta_{1}}{f_{1}}\left(\theta \right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}} \alpha {\mathrm{ + }}{\eta_{2}}{f_{1}}\left(\theta \right)\sum\limits_{j = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{j}}} \right|}^{2}}} \left({1{\mathrm{ - }}\alpha} \right) $$
(39a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~ (22b)-(22e), \end{array} $$
(39b)

By introducing auxiliary variable λ1,λ2, we have

$$ \alpha {\lambda_{1}} \le 1{\mathrm{ ~~~~and ~~~~ }}\left({1 - \alpha} \right){\lambda_{2}} \le 1 $$
(40)

Hence, the problem (39) can be expressed equivalently as

$$ \underset{\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{{{s_{j}}}\right\}_{j = 1}^{2},\alpha,{\lambda_{1}},{\lambda_{2}}}{\max} \frac{{{\eta_{1}}{f_{1}}\left(\theta\right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}\alpha}}}{{{\lambda_{1}}}}{\mathrm{ + }}\frac{{{\eta_{1}}{f_{1}}\left(\theta \right)\sum\limits_{j = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{j}}} \right|}^{2}}} \left({1{\mathrm{ - }}\alpha} \right)}}{{{\lambda_{2}}}} $$
(41a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~ (22b)-(22d), \end{array} $$
(41b)
$$ \begin{array}{l} ~~~~~~~~~~~~~~~~~~~(22e),(40). \end{array} $$
(41c)

It is easily found that the constraints (41c) are convex. As for non-convex constraints (41b), we can approximate these into convex ones by referring to sum throughput maximization part, which can be expressed as (29)–(31).

Next, let us cope with the non-convex objective using (41a). Two terms of the objective can be bounded respectively by

$$ {\begin{aligned} \frac{{{\eta_{1}}{f_{1}}\left(\theta\right)\sum\limits_{i = 1}^{2} {{{\left| {\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right|}^{2}}}}}{\lambda_{1}}&\ge {\eta_{1}}{f_{1}}\left(\theta\right)\sum\limits_{i = 1}^{2} {\left({\frac{{2R\left\{{{{\left({\mathbf{h}_{SR}^{H}\mathbf{w}_{i}^{k}}\right)}^{*}}\mathbf{h}_{SR}^{H}{\mathbf{w}_{i}}} \right\}}}{{\lambda_{1}^{k}}} - \frac{{{{\left| {\mathbf{h}_{SR}^{H}\mathbf{w}_{i}^{k}} \right|}^{2}}{\lambda_{1}}}}{{{\left({\lambda_{1}^{k}}\right)}^{2}}}}\right)}\\ &= {{\mathrm{g}}_{1}}\left({\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},{\lambda_{1}}} \right) \end{aligned}} $$
(42)
$$ \begin{array}{l} \frac{{\eta_{2}}\sum\limits_{j = 1}^{2} {{{\left| {\mathbf{h}_{rr}^{H}{\mathbf{s}_{j}}} \right|}^{2}}}}{\lambda_{2}} \ge {\eta_{2}}\sum\limits_{j = 1}^{2} {\left({\frac{{2R\left\{{{{\left({\mathbf{h}_{rr}^{H}\mathbf{s}_{j}^{k}} \right)}^{*}}\mathbf{h}_{rr}^{H}{\mathbf{s}_{j}}} \right\}}}{{\lambda_{2}^{k}}} - \frac{{{{\left| {\mathbf{h}_{rr}^{H}\mathbf{s}_{j}^{k}}\right|}^{2}}{\lambda_{2}}}}{{{{\left({\lambda_{2}^{k}} \right)}^{2}}}}} \right)} \\ {\mathrm{ ~~~~~~~~~~~~~~~~ = }}{{\mathrm{g}}_{2}}\left({\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2},{\lambda_{2}}} \right) \end{array} $$
(43)

In result, at kth iteration, the feasible point of (41) can be generated by solving the following problem:

$$ \underset{\left\{{{\mathbf{w}_{i}}}\right\}_{i = 1}^{2},\left\{{{s_{j}}} \right\}_{j = 1}^{2},\alpha,{\lambda_{1}},{\lambda_{2}}}{\max} g\left({\left\{{{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{s_{j}}} \right\}_{j = 1}^{2},\alpha,{\lambda_{1}},{\lambda_{2}}} \right) $$
(44a)
$$ \begin{array}{l} ~~~~~~~{s.t.}~~~~~~~ (29)-(31), (41c), (42)-(43). \end{array} $$
(44b)

where \(g\left ({\left \{{{\mathbf {w}_{i}}} \right \}_{i = 1}^{2},\left \{ {{s_{j}}} \right \}_{j = 1}^{2},\alpha,{\lambda _{1}},{\lambda _{2}}} \right){\mathrm { = }}{{\mathrm {g}}_{1}}\left ({\left \{ {{\mathbf {w}_{i}}} \right \}_{i = 1}^{2},{\lambda _{1}}} \right)+{{\mathrm {g}}_{2}}\left ({\left \{ {{\mathbf {s}_{j}}} \right \}_{j = 1}^{2},{\lambda _{2}}} \right)\).

Convergence analysis: Algorithm 2 produces non-decreasing sequence and finally converges to the KKT point of (39) after finitely many iterations, whose proof can refer to Appendix 5.

Complexity analysis: The computational cost of problem (22) at each iteration is O(m2n2.5+n3.5), where the optimization problem (22) involves m=2M+2N+1 the scalar real variables and n=6 quadratic and linear constraints.

Given the λ1 and λ2, the initial feasible point of (41) can be generated by iterating optimization problem (38).

4 Simulation results

This section validates the proposed beamforming design for the UAV-enabled cooperative NOMA network by simulation results. Herein, the channel power gain at the reference distance d0=1m is up to β=−65 dB. The other environment coefficients related with channel model are set by \({\nu _{1}}{\mathrm { = }}5, {\nu _{2}}{\mathrm { = - }}1, {\nu _{2}}{\mathrm { = - }}1, {\nu _{4}}{\mathrm { = }}42, {\mu _{1}}{\mathrm { = }}\frac {2}{\pi }\ln 3\) and μ2=9. The distances from all nodes on the ground to central point are assumed to be ds=50m, d1=50m, and d2=65m. Unless otherwise stated, the default values of other parameters are displayed in Table 1.

Table 1 Default values of other parameters
Full size table

For comparison, we present three baseline transmission schemes as below:

∙ “FD+NOMA+SWIPT with fixed α=0.5”: the only difference between this scheme and the proposed scheme is that the scheme does not take adopts fixed time allocation coefficient α.

∙ “HD+NOMA+SWIPT”: different from the proposed scheme, the strategy adopts HD mode.

∙“FD+OMA+SWIPT”: in this scheme, traditional time division multiple access technique is employed, which separates the bandwidth equally for BS-UAV-U1 and BS-UAV-U2, respectively.

4.1 Convergence behavior

Figure 3 depicts the behaviors of the proposed Algorithm 1. We can observe that two algorithms can both converge to at least local optimum in fifteen steps, which has demonstrated the superiority of the proposed algorithms.

Fig. 3
figure 3

Convergence of Algorithm 1

Full size image

4.2 Comparison of schemes

In Fig. 4, we plot the sum throughput of the system in terms of transmission power at BS Ps with fixed time allocation ratio α=0.5 and fixed position of UAV, i.e., (r cosθ, sinθ,h). As expected, the sum throughput of the system increases with Ps. The proposed scheme yields the best among all schemes. Clearly, FD mode brings more performance gain than the HD one. What is more, it is seen that NOMA schemes can achieve higher spectral efficiency compared to OMA scheme, which can verify the advantage of NOMA in improving spectral efficiency.

Fig. 4
figure 4

Sum throughput of system versus transmission power at BS

Full size image

Figure 5 shows the impact of azimuth angle θ of UAV’s fight trajectory on the sum throughput of system for two different schemes. Clearly, the throughput performance first increases with θ and decreases with θ for the proposed scheme and “FD+OMA+SWIPT” scheme. However, the optimal azimuth angles for two schemes are different. The optimum θ is located at 90∘ in proposed scheme while the optimum θ is located at 120∘ in the “FD+OMA+SWIPT” scheme. In addition, it is observed that the proposed scheme outperforms the “FD+OMA+SWIPT” scheme whatever the value of θ is, which implied the advantage of using NOMA in improving spectral efficiency.

Fig. 5
figure 5

Sum throughput of system versus azimuth angle

Full size image

Figure 6 plots the sum throughput of the system versus time allocation coefficient for different circle radius of UAV’s fight. As shown in Fig. 6, the sum throughput of system reaches to peak when the value of time allocation coefficient is up to 0.38 probably. Furthermore, with the decreasing of the circular radius, the sum throughput of system degrades, which demonstrates that the better throughput performance prefers bigger range of UAV’s fight.

Fig. 6
figure 6

Sum throughput of system versus time allocation coefficient α

Full size image

We also investigated the sum throughput of system versus the UAV’s altitude in Fig. 7. As expected, the proposed scheme yields the best among all transmission schemes. Apparently, with the increase of altitude of UAV, the performance gain degrades for all strategies due to bigger channel fading.

Fig. 7
figure 7

Sum throughput of system versus the altitude of UAV

Full size image

Additionally, the performance gap becomes smaller between the proposed scheme and two baseline strategies with the increase of altitude of UAV. Therefore, the proposed scheme is more approximate to mid- and low-altitude mountainous region.

Figure 8 illustrates the sum throughput of system versus SI cancelation level. As shown in this figure, the sum throughput of system decreases with the decrease of SI cancelation level in the proposed scheme. Apparently, the performance of the proposed scheme is superior to ones in the HD scheme when ρ≤−25 dB, and the performance of the proposed scheme is inferior to ones in HD scheme when ρ≥−25 dB.

Fig. 8
figure 8

Sum throughput of system versus SI cancelation level

Full size image

Finally, we present the harvested energy at UAV versus the azimuth angle θ of UAV’s fight trajectory for the two schemes. Obviously, the harvested energy at UAV is increasingly improved when the UAV is getting closer to the BS (Fig. 9). Moreover, we can find that the proposed scheme outperforms the fixed α scheme, which can imply the importance of dynamically changing α.

Fig. 9
figure 9

Harvested energy at UAV versus azimuth angle

Full size image

5 Conclusion

We have considered a UAV-enabled cooperative NOMA system with application of SWIPT, where the UAV harvests the energy from the BS in the first phase and relay signals in FD mode with the harvested energy. To maximize the sum throughput of system, we have proposed a low-complexity algorithm to solve the joint optimization problem of beamforming vectors and time allocation ratio. Numerical results imply that the proposed scheme achieves more performance gain than other strategies.

6 Appendix 1

Since \(\varphi \left ({x,y} \right) = \frac {{{x^{2}}}}{y}\) is convex, thus, it is true that

$$ \frac{{{x^{2}}}}{y} \ge 2\frac{{{{\bar x}^{*}}x}}{{\bar y}} - \frac{{{{\left| {\bar x} \right|}^{2}}}}{{{{\bar y}^{2}}}}y $$
(45)

Following from [39], we have the below inequalities

$$ \ln \left({1 + \frac{{{{\left| x \right|}^{2}}}}{y}} \right) \ge \ln \left({1{\mathrm{ + }}\frac{{{{\left| {\bar x} \right|}^{2}}}}{{\bar y}}} \right){\mathrm{ - }}\frac{{{{\left| {\bar x} \right|}^{2}}}}{{\bar y}}{\mathrm{ + }}\frac{{2R\left\{ {{{\bar x}^{*}}x} \right\}}}{{\bar y}} - \frac{{{{\left| {\bar x} \right|}^{2}}\left({{{\left| {\bar x} \right|}^{2}} + y} \right)}}{{\bar y\left({\bar y + {{\left| {\bar x} \right|}^{2}}} \right)}} $$
(46)
$$ \frac{{\ln \left({1 + \omega} \right)}}{v} \ge \frac{{2\ln \left({1 + \bar \omega} \right)}}{{\bar v}} + \frac{{\bar \omega }}{{\left({\bar \omega + 1} \right)\bar v}} - \frac{{{{\bar \omega }^{2}}}}{{\left({\bar \omega + 1} \right)\bar v}}\frac{1}{\omega} - \frac{{\ln \left({1 + \bar \omega} \right)}}{{{{\bar v}^{2}}}}v $$
(47)

for all \(x \in {\mathbb C}, \bar x \in {\mathbb C}, y > 0\) and \(\bar y > 0\) and over the feasible region 2x∗x−|x∗|2>0.

7 Appendix 2

It is easily found that

$$ f\left({\left\{ {{\mathbf{w}_{i}}} \right\}_{i = 1}^{2},\left\{ {{\mathbf{s}_{j}}} \right\}_{j = 1}^{2},\alpha} \right) \ge {f_{k}}\left({\left\{ {\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right) $$
(48)

and

$$ f\left({\left\{ {\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right) = {f_{k}}\left({\left\{ {\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right). $$
(49)

Moreover, Algorithm 1 produces non-decreasing sequence provided that \(\left ({\left \{{\mathbf {w}_{i}^{k}}\right \}_{i = 1}^{2},\left \{{\mathbf {s}_{j}^{k}}\right \}_{j = 1}^{2},{\alpha ^{k}}} \right) \ne \left ({\left \{{\mathbf {w}_{i}^{k{\mathrm { + }}1}} \right \}_{i = 1}^{2},\left \{{\mathbf {s}_{j}^{k{\mathrm { + }}1}} \right \}_{j = 1}^{2},{\alpha ^{k{\mathrm { + }}1}}} \right)\), i.e.,

$$ {\begin{aligned} f\left({\left\{{\mathbf{w}_{i}^{k{\mathrm{ + }}1}}\right\}_{i = 1}^{2},\left\{{\mathbf{s}_{j}^{k{\mathrm{ + }}1}} \right\}_{j = 1}^{2},{\alpha^{k{\mathrm{ + }}1}}}\right) = {f_{k}}\left({\left\{{\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{{\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right). \end{aligned}} $$
(50)

Thus, we can derive that the feasible point generated by Algorithm 1 can make objective value of (22) become bigger due to that

$$ {\begin{aligned} f\left({\left\{{\mathbf{w}_{i}^{k{\mathrm{ + }}1}}\right\}_{i = 1}^{2},\left\{{\mathbf{s}_{j}^{k{\mathrm{ + }}1}} \right\}_{j = 1}^{2},{\alpha^{k{\mathrm{ + }}1}}}\right) &\ge {f_{k}}\left({\left\{ {\mathbf{w}_{i}^{k{\mathrm{ + }}1}} \right\}_{i = 1}^{2},\left\{ {\mathbf{s}_{j}^{k{\mathrm{ + }}1}} \right\}_{j = 1}^{2},{\alpha^{k{\mathrm{ + }}1}}} \right)\\ & \ge {f_{k}}\left({\left\{{\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{{\mathbf{s}_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right)\\ & = f\left({\left\{{\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {\mathbf{s}_{j}^{k}}\right\}_{j = 1}^{2},{\alpha^{k}}} \right) \end{aligned}} $$
(51)

The inequality (51) demonstrated that the feasible point \(\left ({\left \{{\mathbf {w}_{i}^{k{\mathrm { + }}1}} \right \}_{i = 1}^{2},\left \{{s_{j}^{k{\mathrm { + }}1}} \right \}_{j = 1}^{2},{\alpha ^{k{\mathrm { + }}1}}} \right)\) for (k+1)th iteration is better than the feasible point \(\left ({\left \{{\mathbf {w}_{i}^{k{\mathrm { }}}} \right \}_{i = 1}^{2},\left \{ {s_{j}^{k{\mathrm { }}}} \right \}_{j = 1}^{2},{\alpha ^{k{\mathrm { }}}}} \right)\) for kth iteration. According to Cauchy’s theorem, the bounded sequence \(\left ({\left \{ {\mathbf {w}_{i}^{k{\mathrm { }}}}\right \}_{i = 1}^{2},\left \{ {s_{j}^{k{\mathrm { }}}} \right \}_{j = 1}^{2},{\alpha ^{k{\mathrm { }}}}}\right)\) would converge to the limited point \(\left ({\left \{ {{{\bar {\mathbf {w}}}_{i}}} \right \}_{i = 1}^{2},\left \{ {{{\bar s}_{j}}} \right \}_{j = 1}^{2},{{\bar \alpha }}} \right)\), i.e.,

$$ \underset{\upsilon \to \infty}{\lim} \left[{f\left({\left\{{\mathbf{w}_{i}^{{k_{\upsilon} }}} \right\}_{i = 1}^{2},\left\{ {s_{j}^{{k_{\upsilon}}}}\right\}_{j = 1}^{2},{\alpha^{{k_{\upsilon} }}}} \right) - f\left({\left\{ {{{\bar{\mathbf{w}}}_{i}}} \right\}_{i = 1}^{2},\left\{ {{{\bar s}_{j}}} \right\}_{j = 1}^{2},{{\bar \alpha }^{k}}} \right)} \right] = 0 $$
(52)

Motivated by this, we can derive that

$$ \underset{k \to \infty}{\lim} f\left({\left\{{\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {s_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}} \right) = f\left({\left\{ {{{\bar{\mathbf{w}}}_{i}}} \right\}_{i = 1}^{2},\left\{ {{{\bar s}_{j}}} \right\}_{j = 1}^{2},\bar \alpha} \right) $$
(53)

due to that

$$ {\begin{aligned} 0 &= \underset{\upsilon \to \infty}{\lim} \left[{f\left({\left\{{\mathbf{w}_{i}^{{k_{\upsilon} }}}\right\}_{i = 1}^{2},\left\{{s_{j}^{{k_{\upsilon}}}}\right\}_{j = 1}^{2},{\alpha^{{k_{\upsilon} }}}} \right) - f\left({\left\{ {{{\bar{\mathbf{w}}}_{i}}} \right\}_{i = 1}^{2},\left\{ {{{\bar s}_{j}}}\right\}_{j = 1}^{2},{{\bar \alpha }^{k}}} \right)}\right]\\ &\quad \le \underset{k \to \infty}{\lim}\left[{f\left({\left\{{\mathbf{w}_{i}^{k}} \right\}_{i = 1}^{2},\left\{ {s_{j}^{k}} \right\}_{j = 1}^{2},{\alpha^{k}}}\right) - f\left({\left\{{{{\bar{\mathbf{w}}}_{i}}} \right\}_{i = 1}^{2},\left\{{{\bar s}_{j}}\right\}_{j = 1}^{2},\bar \alpha} \right)}\right]\\ &\quad \le \underset{\upsilon \to \infty}{\lim} \left[ {f\left({\left\{ {\mathbf{w}_{i}^{{k_{\upsilon + 1}}}} \right\}_{i = 1}^{2},\left\{ {s_{j}^{{k_{\upsilon + 1}}}} \right\}_{j = 1}^{2},{\alpha^{{k_{\upsilon + 1}}}}} \right) \,-\, f\left({\left\{ {{{\bar{\mathbf{w}}}_{i}}} \right\}_{i = 1}^{2},\left\{{{{\bar s}_{j}}} \right\}_{j = 1}^{2},\bar \alpha} \right)}\!\right]\\ &= 0. \end{aligned}} $$
(54)

where kυ≤k≤kυ+1. Thus, each accumulation point \({\left ({\left \{{{\bar {\mathbf {w}}}_{i}}\right \}_{i = 1}^{2},\left \{{{\bar s}_{j}}\right \}_{j = 1}^{2},\bar \alpha }\right)}\) of the feasible point \({\left ({\left \{{\mathbf {w}_{i}^{k}} \right \}_{i = 1}^{2},\left \{ {s_{j}^{k}} \right \}_{j = 1}^{2},{\alpha ^{k}}}\right)}\) generated by Algorithm 1 satisfies the KKT condition [48]. Proposition 1 has been proved.