1 Introduction

Designs of antennas have been paid more attention in the last few years [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Also, pattern synthesis of antenna arrays has become a traditional problem [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. Moreover, much attention has been paid to the position-only synthesis of uniformly excited antenna arrays [6,7,8,9,10,11,12,13,14]. There are two kinds of uniformly excited antenna arrays. One is thinned array [6,7,8,9,10], which is to delete some array elements from a uniform array. These kinds of arrays can easily constrain the spacing of the adjacent elements. The other one is sparse antenna array which means that the array elements are randomly distributed along the antenna array [11,12,13,14]. Compared with thinned antenna arrays, sparse antenna arrays can obtain better simulation results. However, in the design of sparse antenna arrays, it is hard to constrain the size of the array aperture, number of the array elements, and the minimum spacing of adjacent elements at the same time.

In recent years, as the development of modern military and defense application, circular and elliptical antenna arrays have become more popular in wireless communication [15,16,17,18,19,20]. Compared with linear antenna arrays, the radiation patterns of the circular and elliptical antenna arrays can cover the entire space. In the design of circular and elliptical antenna arrays, synthesis of non-uniform arrays has been paid more attention [15,16,17,18,19,20]. In [15], genetic algorithms are proposed to determine optimum weights and element separations that provided a radiation pattern with peak side lobe level reduction with a fixed beam width. As is introduced in [16], Hierarchical Dynamic Local Neighborhood Based PSO (HDLPSO) algorithm is introduced into the design of non-uniform circular antenna arrays. Invasive weed optimization (IWO) is presented in [17] for the design of non-uniform, planar, and circular antenna arrays that can achieve minimum side lobe levels for a specific first null beam width. Biogeography-based optimization (BBO) is presented in [18] for the optimization of non-uniform circular antenna arrays, and the optimization results show that the synthesis of non-uniform circular antenna arrays using the BBO algorithm provides a SLL reduction better than that obtained by using a genetic algorithm, simulated annealing, and particle swarm optimization. In [20], synthesis of elliptical antenna arrays is introduced by using three different optimization algorithms (self-adaptive differential evolution method, biogeography-based optimization method, and firefly algorithm).

In order to avoid the overlap of the array elements, the space of the adjacent elements must be constrained in the design of elliptical antenna arrays. So, the purpose of this paper is to reduce the peak side lobe level of the radiation pattern by optimizing the positions of array elements that fulfil the minimum space constraint. The element positions are optimized by differential invasive weed optimization (DIWO), and low PSLLs of the radiation patterns are obtained. IWO has been widely used in the design of antennas [17, 21, 22]. Usually, IWO has better optimization results than the other optimization methods in the final error level. The rest of the paper is organized as follows: Method and experiment are introduced in Section 2. In Section 3, the mathematical formulation is given. The used optimization algorithms and the optimization steps are briefly described in Section 4. In Section 5, numerical results and comparisons are given. Finally, the paper is concluded in Section 6.

2 Method and experiment

The study of the paper is to introduce a new design method of non-uniform elliptical antenna arrays. First, the design of antenna arrays is expressed as an optimization problem. The structure of an elliptical antenna array is depicted, and the fitness function is given. Also, the formulations of the element positions that can constrain the minimum element spacing are deduced. Second, a modified invasive weed optimization is introduced. Then, it is used to solve the introduced optimization problems. The experiment is based on numerical simulations. To verify the effectiveness of the proposed method, synthesis results and comparisons are made by taking three different antenna arrays. Comparisons show that the proposed algorithm is more efficient than other algorithms. The analysis shows that the proposed method is useful and effective to solve the design of non-uniform elliptical antenna arrays.

3 Mathematical formulation

3.1 Structure and array factor of elliptical antenna array

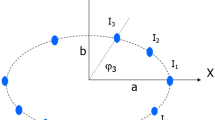
The structure of an elliptical antenna array with N elements placed in the x-y plane is given in Fig. 1. The original point is at the center of the ellipse. The semi-major axis and semi-minor axis lengths are depicted by a and b, respectively. The eccentricity of the ellipse is e which is calculated by

$$ e=\sqrt{1-\frac{b^2}{a^2}} $$
(1)
Fig. 1
figure 1

Structure of elliptical antenna array

Full size image

The array factor of this elliptical antenna array is given by

$$ AF\left(\theta, \phi \right)=\sum \limits_{n=1}^N{I}_n\exp \left[j\left(k\sin \theta \left( acos{\phi}_n cos\phi + bsin{\phi}_n sin\phi \right)\right)+j{\alpha}_n\right] $$
(2)

where k = 2π/λ is the wave number. In and αn represent the excitation amplitude and phase of the nth element. ϕn is the angular position of the nth element in the x-y plane. ϕ is the azimuth angle which is measured from the positive x-axis. θ is the elevation angle measured from the positive z-axis. In the following design, the array factor in the x-y plane, i.e., θ = 90o, is considered. So, the array factor of the elliptical antenna array can be depicted by

$$ AF\left(\phi \right)=\sum \limits_{n=1}^N{I}_n\exp \left[j\left(k\left( acos{\phi}_n cos\phi + bsin{\phi}_n sin\phi \right)\right)+j{\alpha}_n\right] $$
(3)

If the direction of the main beam is φ0, the phase excitation of the nth array element can be given by

$$ {\alpha}_n=-k\left( acos{\phi}_n\mathit{\cos}{\varphi}_0+ bsin{\phi}_n\mathit{\sin}{\varphi}_0\right) $$
(4)

3.2 Fitness function

In order to obtain radiation patterns with minimum side lobe levels and a specific first null beam width (FNBW), the element positions of elliptical antenna arrays are optimized. The desired function can be given by

$$ E={w}_1{\left.\frac{\left| AF\left(\phi \right)\right|}{A{F}_{\mathrm{max}}}\right|}_{\phi \in S}+{w}_2\left|{\mathrm{FNBW}}_{\mathrm{c}}-{\mathrm{FNBW}}_{\mathrm{d}}\right| $$
(5)

where w1 and w2 are the weighting factors. AFmax is the maximum value of |AF(ϕ)|. S is the side lobe area of the radiation pattern. The calculated first null beam width is defined by FNBWc, and the desired first null beam width is depicted by FNBWd.

In order to avoid the overlap of array elements, the minimum spacing of the adjacent elements is depicted by de. So, the objective function can be given by

$$ \left\{\begin{array}{c}\min \left\{E\right\}\\ {}s.t.\sqrt{{\left({x}_i-{x}_j\right)}^2+{\left({y}_i-{y}_j\right)}^2}\ge {d}_e\\ {}i,j=1,2,\cdots N;i\ne j\end{array}\right. $$
(6)

where (xn, yn) is the position of the nth element which can be calculated by

$$ \left\{\begin{array}{c}{x}_n=a\cos {\phi}_n\\ {}{y}_n=b\sin {\phi}_n\end{array}\right. $$
(7)

In the following procedure, the problem is changed into a maximum problem. So, the fitness function can be defined by

$$ f=\frac{1.0}{1+E} $$
(8)

3.3 Optimization of element positions

As is shown in Fig. 1, the length of the elliptical antenna array can be calculated by

$$ L=a{\int}_0^{2\pi}\sqrt{1-{e}^2{\cos}^2\phi } d\phi $$
(9)

The length that can allocate array elements is L − de. If array elements are allocated by the minimum spacing constraint de, the length of (N − 1)de is occupied. So, the remaining region over the array aperture to be optimized is given by [11]

$$ SP=L-{d}_e-\left(N-1\right){d}_e=L-N{d}_e $$
(10)

In the determination of element positions, the position of the first element must be determined. The first element should be allocated in the area of [0, SP]. As is shown in Fig. 2, the length from O to the first element position along the ellipse can be depicted by

$$ {l}_1= SP\times {r}_1 $$
(11)

where r1 is the random number among the rang of [0, 1]. Then, N − 1 real random numbers among the range of [0, SP] are calculated by

Fig. 2
figure 2

Elements distribution of elliptical antenna array

Full size image

\( {c}_{i-1}^{\prime }= SP\times {r}_i \), i = 2, 3, ⋯, N (12).

where ri, i = 2, 3, ⋯, N are real random numbers among the range of [0, 1]. Then, \( {c}_i^{\prime } \) are sorted in ascending order and a new vector C = [c1, c2, ⋯, cN − 1] is obtained, where c1 ≤ c2 ≤ ⋯ ≤ cN − 1. The length from O to the nth element position along the ellipse can be calculated by

$$ \left[\begin{array}{c}{l}_2\\ {}{l}_3\\ {}\cdots \\ {}{l}_N\end{array}\right]={l}_1+\left[\begin{array}{c}{c}_1\\ {}{c}_2\\ {}\cdots \\ {}{c}_{N-1}\end{array}\right]+\left[\begin{array}{c}{d}_e\\ {}2{d}_e\\ {}\cdots \\ {}\left(N-1\right){d}_e\end{array}\right]={l}_1+\left[\begin{array}{c}{c}_1+{d}_e\\ {}{c}_2+2{d}_e\\ {}\cdots \\ {}{c}_{N-1}+\left(N-1\right){d}_e\end{array}\right] $$
(13)

If ln > L, ln is updated by

$$ {l}_n={l}_n-L,\kern0.33em n=2,3,\cdots, N $$
(14)

Then, ln is sorted in ascending order and the ultimate ln is obtained. It can be proved that the element spacing between nth element and (n + 1)th element is de + (cn + 1 − cn), n = 1, 2, ⋯, N − 1 which satisfies the minimum spacing constraint of (6).

After ln, n = 1, 2, ⋯, N are calculated, the angular position ϕn of the nth array element can be calculated by

$$ \left\{\begin{array}{c}{l}_n-a{\int}_0^{\phi_n}\sqrt{1-{e}^2{\cos}^2\phi } d\phi =0\\ {}n=1,2,\cdots, N\end{array}\right. $$
(15)

4 Optimization algorithm

IWO and DE are intelligent algorithms which have been used in various kinds of optimization problems [21,22,23,24]. In order to improve the synthesis results, invasive weed optimization and differential evolution algorithm are combined for parallel computation. The IWO and DE has data exchange after m iteration steps. The newly introduced algorithm is called DIWO. The flowchart of this optimization method is given by Fig. 3. The optimization procedure can be expressed as follows:

  • Step 1. The parameter values of the antenna arrays and DIWO are given. A N × P–dimensional matrix r _ I and a N × d_max–dimensional matrix r _ D are chosen as the initial population for IWO and DE, respectively. Let iter = 1.

  • Step 2. The angular position of the array elements is calculated by (15).

  • Step 3. The radiation patterns of the antenna arrays are calculated by (3). The fitness value is defined by (8) which increases with the decrease of PSLL. The optimized element positions that can produce the best fitness value are preserved as the ultimate result.

  • Step 4. The optimization parameters r _ I and r _ D are updated by IWO and DE.

  • Step 5. If iter = 1 or iter = iter_max or mod (iter, m) = 0, go to step 6; otherwise, go to step 7. Where mod( ) is the modulus after division.

  • Step 6. Combine all the optimization population of IWO and DE. Choose the best p_max population as the new population of IWO. Choose the best d_max population as the new population of DE.

  • Step 7. Let iter = iter + 1, if iter < iter_max, go to step 2; otherwise, terminate iteration.

Fig. 3
figure 3

Flowchart representation of DIWO

Full size image

5 Results and discussion

In this section, several simulation results are given to show the feasibility and effectiveness of the proposed method. The parameters used in DIWO are given in Table 1. The minimum spacing constraint for the adjacent array elements is chosen as de = 0.15λ. The direction of the main beam is φ0 = 0o. The weighting factor w1 = 1, w2 = 3. The positions of the array elements are optimized to get radiation patterns with low side lobe levels. The algorithm is calculated 10 times, and the best result is preserved as the ultimate result.

Table 1 DIWO parameter values
Full size table

5.1 Optimization result of 8-element antenna array

In the first example, pattern synthesis of elliptical antenna array that has 8 elements is introduced. The semi-major axis length a and eccentricity e of the ellipse are 0.5λ and 0.5, respectively. The desired first null beam width is chosen as FNBWd = 111o. The same array is optimized in [20] using self-adaptive differential evolution (SADE) technique, biogeography-based optimization (BBO) and firefly algorithm (FA). The PSLLs of the radiation patterns optimized by these three methods are − 19.12 dB, − 19.40 dB and − 19.43 dB, respectively. When the elements are uniformly placed on the ellipse, the PSLL of the radiation pattern is − 8.02 dB. Using the method proposed in this paper, the best PSLL of 10 calculation times obtained by DIWO is − 19.91 dB which is 0.48 dB lower than that optimized by FA. The beam width of the radiation pattern is 111.5°. The minimum spacing of the adjacent elements is 0.18λ which fulfils the minimum spacing constraint of (6). When the same array is optimized by DE and IWO, the best PSLLs are − 19.82 dB and − 19.89 dB, respectively. The radiation patterns synthesized by different algorithms are given in Fig. 4. Table 2 shows the element positions of the best synthesis result optimized by different algorithms. The worst PSLL of 10 calculation times optimized by DIWO is − 19.72 dB while the average PSLL is − 19.81 dB.

Fig. 4
figure 4

Radiation pattern of elliptical antenna array with 8 elements

Full size image
Table 2 Positions of elliptical antenna array with 8 elements
Full size table

5.2 Optimization result of 12-element antenna array

In this example, synthesis result of elliptical antenna array that has 12 elements is given. The semi-major axis length and eccentricity of the ellipse are chosen as 1.15λ and 0.5, respectively. The desired first null beam width is 49°. The best PSLL optimized in [20] is − 10.37 dB by using SADE. The PSLL of the radiation pattern is − 3.82 dB when the elements are uniformly distributed. Using the method proposed in this paper, the best PSLL obtained by DIWO is − 10.65 dB. The beam width of the radiation pattern is 49.8°. The minimum spacing of the adjacent elements is 0.15λ. When the same array is optimized by DE and IWO, the best PSLLs are − 10.56 dB and − 10.58 dB, respectively. Figure 5 is the radiation patterns with minimum PSLL synthesized by different algorithms. Table 3 is the element positions of the elliptical antenna array optimized by different algorithms. In this example, the worst PSLL of 10 calculation times obtained by DIWO is − 10.36 dB and the average PSLL is − 10.56 dB.

Fig. 5
figure 5

Radiation pattern of elliptical antenna array with 12 elements

Full size image
Table 3 Positions of elliptical antenna array with 12 elements
Full size table

5.3 Optimization result of 20-element antenna array

In [20], the 20-element elliptical antenna array is optimized by SADE, BBO, and FA. The semi-major axis length and eccentricity of the ellipse are chosen as 1.6λ and 0.5, respectively. The best PSLL is − 11.27 dB obtained by FA. In this paper, the same array is optimized by DIWO. The desired beam width of the radiation pattern is – 34°. The best PSLL of the radiation pattern is − 12.21 dB synthesized by DIWO. The beam width of the radiation pattern is 34.8°. The minimum spacing of the adjacent elements is 0.15λ. When the same array is optimized by DE and IWO, the best PSLLs are − 11.93 dB and − 11.96 dB, respectively. The radiation patterns synthesized by different algorithms are given in Fig. 6. Table 4 gives the element positions of the elliptical antenna array optimized by different optimization algorithms. In this synthesis example, the worst PSLL of 10 calculation times obtained by DIWO is − 11.77 dB and the average PSLL is − 11.87 dB.

Fig. 6
figure 6

Radiation pattern of elliptical antenna array with 20 elements

Full size image
Table 4 Positions of elliptical antenna array with 20 elements
Full size table

6 Conclusions

Position-only synthesis of uniformly excited elliptical antenna arrays with minimum element spacing constraint has rarely been studied. When the array size and element number are given, it is hard to constrain the minimum spacing of the adjacent elements which is important in the design of antenna arrays. For the first time, pattern synthesis of non-uniform elliptical antenna arrays with minimum spacing constraint is introduced. The comparisons show that the design of non-uniform elliptical antenna arrays using the proposed method presents a good side lobe reduction in the radiation pattern for the optimized problem. Also, according to the real requirement of antenna array design, the minimum element spacing constraint can be set to other values.