Abstract
In this journal, we investigate the beam-domain channel estimation and power allocation in hybrid architecture massive multiple-input and multiple-output (MIMO) communication systems. First, we propose a low-complexity channel estimation method, which utilizes the beam steering vectors achieved from the direction-of-arrival (DOA) estimation and beam gains estimated by low-overhead pilots. Based on the estimated beam information, a purely analog precoding strategy is also designed. Then, the optimal power allocation among multiple beams is derived to maximize spectral efficiency. Finally, simulation results show that the proposed schemes can achieve high channel estimation accuracy and spectral efficiency.
Similar content being viewed by others
1 Introduction
Massive multiple-input and multiple-output (MIMO) has been envisioned as a crucial technology for the next-generation cellular systems, due to its high energy efficiency and spectral efficiency [1–3]. To exploit the benefits of massive antennas, a large number of radio frequency (RF) chains are needed so that each antenna can own one dedicated RF chain. Combating the expensive cost, hybrid architecture has been a promising scheme which combines cost-effective phase shifters and limited RF chains. For hybrid architecture, there are two most common precoding techniques: hybrid precoding and analog precoding [4, 5].
1.1 Related work
Hybrid analog/digital precoding has been investigated extensively including precoding design and channel estimation strategy [4–7], discrete Fourier transform (DFT)-based hybrid architecture [8–10], angle domain hybrid precoding and channel tracking [11, 12], and performance analysis on hybrid architecture [13–15]. Most of the existing hybrid precoding designs heavily rely on the perfect knowledge of the channel, which brings a great challenge because only limited RF chains are available at base station (BS) and user equipment (UE). An adaptive channel estimation algorithm was proposed in [6] for hybrid architecture millimeter wave (mmWave) systems, which applies the compressive sensing (CS) technology based on the poor scattering nature of mmWave. With the CS method, the channel estimation algorithm in [6] yields a limited accuracy and a high computational complexity. For analog precoding, an RF beam search method was proposed in [16, 17], where the channel estimation was obtained by sweeping all beam directions over the spatial region. However, the beam search algorithm in [16] is time-consuming due to the exhaustive beam searching. Besides, orthogonal training sequences have also been widely used to obtain the angle information for channel estimation in the DFT-based hybrid architecture [8, 9], which caused high computational complexity and feedback cost. Therefore, our objective is to design a simple and effective signal processing scheme for hybrid architecture massive MIMO systems.
1.2 Summary of contributions
In this journal, we investigate low-complexity beam-domain channel estimation, precoding, and power allocation in hybrid architecture massive MIMO systems. The major contributions of this journal are summarized as follows:
(1) A low-complexity channel estimation algorithm is proposed, which avoids high pilot overhead by utilizing estimated beams and beam gains.
(2) The RF precoder and combiner are designed based on estimated beam information.
(3) The power allocation among multiple beams is optimized to maximize spectral efficiency.
(4) Simulation results demonstrate high channel estimation accuracy and comparable spectral efficiency achieved by our proposed channel estimation and power allocation schemes.
2 System model
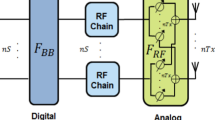
We consider a multi-path massive MIMO systemFootnote 1 with its forward-link scenario as shown in Fig. 1. The transmitter is equipped with an Mt×Nt uniform rectangular array (URA) and Kt≤min(Mt,Nt) RF chains, while the receiver is equipped with an Mr×Nr URA and Kr≤min(Mr,Nr) RF chains. Let L be the number of paths between the transmitter and receiver. We assume L≤min {Kt,Kr} due to the sparsity of channel [8], and L RF chains can be selected randomly from all RF chains for usage.
In a massive MIMO system with URAs, the forward-link channel matrix with L paths can be written as
where \(\gamma _{l}\sim \mathcal {CN}(0,\sigma _{l}^{2})\) is the complex gain of the lth path, \(\mathbf a_{t}(\theta _{l}^{t}, \phi _{l}^{t})\in \mathbb C^{M_{t}N_{t}\times 1}\) and \(\mathbf a_{r}(\theta _{l}^{r}, \phi _{l}^{r})\in \mathbb C^{M_{r}N_{r}\times 1}\) denote the array steering vectors of the lth path at the transmitter and receiver, respectively. \(\theta _{l}^{t}, \theta _{l}^{r}\in [0,\pi)\) are the azimuth angles and \(\phi _{l}^{t}, \phi _{l}^{r}\in [0,\frac {\pi }{2})\) are the elevation angles of the lth path. In general, the steering vector a(θl,ϕl) can be written as
where ⊗ denotes the Kronecker product, ax(θl,ϕl) is an M×1 vector with the mth element being \(e^{j\frac {2\pi }{\lambda }d(m-1)\cos \theta _{l}\sin \phi _{l}}\), and ay(θl,ϕl) is a N×1 vector with the nth element being \(e^{j\frac {2\pi }{\lambda }d(n-1)\sin \theta _{l}\sin \phi _{l}}, d=\frac {\lambda }{2}\) is the distance between two adjacent antennas, and λ is the wavelength. M and N are the numbers of antennas in the horizontal direction and vertical direction of the URA, respectively.
Lemma 1: The steering vectors of different paths are asymptotically orthogonal for sufficient large MN. That is, \(\mathop {\lim }\limits _{M, N\rightarrow \infty }\mathbf a^{H}(\theta _{l_{1}}, \phi _{l_{1}})\mathbf a(\theta _{l_{2}}, \phi _{l_{2}})=0\) (l1≠l2).
Proof 1.
: See Appendix 6.
In Fig. 1, the transmit processing includes power allocation and RF precoding. The post processing at the receiver consists of RF combining and baseband processing. The digital precoding is not considered due to the asymptotical orthogonality of different paths as shown in Lamme 1. Assuming a flat-fading channel, the discrete-time received signal at the receiver is given by [6]
where \(\mathbf {s}\in \mathbb {C}^{L\times 1}\) is the transmitted signal with \(\mathbb E\{\mathbf {s}\mathbf {s}^{H}\}=\sigma _{s}^{2}\mathbf I_{L}, \mathbb E\{\cdot \}\) is the expectation operator, \(\mathbf P\in \mathbb {R}^{L\times L}\) is the power allocation matrix, \(\mathbf F_{t}\in \mathbb C^{M_{t}N_{t}\times L}\) denotes the RF precoder, \(\mathbf F_{r}\in \mathbb C^{M_{r}N_{r}\times L}\) denotes the RF combiner, and \(\mathbf {n}\sim \mathcal {CN}(\mathbf {0},\sigma _{n}^{2}\mathbf {I}_{M_{r}N_{r}})\) denotes additive white Gaussian noise (AWGN) vector. Let [F]i,j denote the (i,j)th element of a matrix F. The RF precoder and RF combiner control phase changes by employing phase shifters with the magnitude \(|[\mathbf F_{t}]_{i,j}|=\frac {1}{\sqrt {M_{t}N_{t}}}\) and \(|[\mathbf F_{r}]_{i,j}|=\frac {1}{\sqrt {M_{r}N_{r}}}\), respectively.
3 Methods of beam-Domain channel estimation and power allocation
In this section, we present the beam-domain signal processing in hybrid architecture massive MIMO systems. First, we discuss the DOA estimation based on the hybrid architecture with limited RF chains. Then, low-complexity channel estimation is proposed based on the estimated beam information. Finally, we study the power allocation to improve the system performance.
3.1 Beam information estimation
Due to the angle reciprocity, the direction-of-departure (DOD) of the forward-link channel is the same as the DOA of the reverse-link channel, even for the frequency division duplex (FDD) systems [8].
The DOA information \(\theta _{l}^{t}\) and \(\phi _{l}^{t}\) can be estimated using the limited RF chains in two time slots, respectively. For the reverse link, Kt contiguous antennas in a row at the receiver (which is the transmitter in the forward link) are first chosen in the horizontal direction as in Fig. 1, and then linked with Kt RF chains to estimate the azimuth angle \(\theta _{l}^{t}\) in the first time slot. Similarly, the elevation angle \(\phi _{l}^{t}\) can be estimated by employing Kt antennas in a column in the second time slot. Here, the estimated angles are defined as (\(\theta _{l}^{t}, \phi _{l}^{t}\)).
By using only a small number of antennas, this estimation strategy has a low complexity and a high accuracy, which have been analyzed in our previous work [18]. For example, while Kt=16, the root mean square error (RMSE) of the estimated DOA has been less than 1∘ by costing only 32 snapshots [18]. Many DOA estimation algorithms can be adopted in this proposed estimation strategy, such as the well-known MUltiple SIgnal Classification (MUSIC) and Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [19–21]. In each time slot, there are a number of snapshots to obtain approximate covariance information for DOA estimation with MUSIC or ESPRIT algorithm.
Practically, considering the low-cost, finite-resolution phase shifters are implemented at the transmitter and receiver for RF processing. For the Mt×Nt URA, there are Mt and Nt phase shifters with finite-resolution in the horizontal and vertical directions, respectively. When all the phase shifters have the same resolution \(\frac {1}{P}\pi \), for the azimuth angle θ∈[0,π) in the horizontal direction, the beam codebook consists of P basic beams by sampling the angle space [0,π) as \(G_{M}=\left \{0,\frac {1}{P}\pi,\cdots,\frac {P-1}{P}\pi \right \}\); for the elevation angle \(\phi \in [0,\frac {\pi }{2})\) in the vertical direction, the beam codebook consists of \(\left (\left \lfloor \frac {P}{2}\right \rfloor +1\right)\) basic beams by sampling the angle space \([0,\frac {\pi }{2})\) as \(G_{N}=\left \{0,\frac {1}{P}\pi,\cdots,\frac {\left \lfloor \frac {P}{2}\right \rfloor }{P}\pi \right \}\). Thus, for an Mt×Nt URA, the beam codebook consists of \(P\left (\left \lfloor \frac {P}{2}\right \rfloor +1\right)\) basic 2-D beams (θ,ϕ).
Finally, the estimated angles (\(\theta _{l}^{t}, \phi _{l}^{t}\)) should be mapped to the beam codebooks for practical transmission. The DOA information can be easily estimated as \((\hat {\theta }_{l}^{t},\hat {\phi }_{l}^{t})=\text {arg} \mathop {\text {min}}\limits _{\theta \in G_{M},\\ \phi \in G_{N}}\left \{|\theta \,-\,\theta _{l}^{t}|\,+\,|\phi \,-\,\phi _{l}^{t}|\right \}\) for practical RF processing. Notably, the DOA estimation strategy can also be directly applied at the receiver in forward link to obtain \((\hat {\theta }_{l}^{r}, \hat {\phi }_{l}^{r})\).
With the estimated beams, RF precoder at the transmitter and RF combiner at the receiver are given as
3.2 Channel estimation
Channel estimation is crucial but intractable in massive MIMO systems [22, 23]. In this subsection, we propose a low-complexity channel estimation method in the beam domain. The proposed method includes the following three steps.
First, the magnitude of the channel gain \(|\hat {\gamma }_{l}|\) and DOAs \((\hat {\theta }_{l}^{t},\hat {\phi }_{l}^{t})\) mentioned above are simultaneously derived. In the reverse link, the received signal as the output of the URA at the receiver, which is the transmitter in the forward link, is expressed as [20, 21]
where X1 is the transmitted signal matrix from one antenna for DOA estimation with \(\mathbb E\left \{\mathbf {X}_{1}\mathbf {X}_{1}^{H}\right \}=\sigma _{X}^{2}\mathbf {I}_{L}, \mathbf {H}_{1}=\mathbf A_{t}\mathbf {G}\) is the reverse-link channel matrix, \(\mathbf A_{t}=\left [\mathbf a_{t}\left (\hat {\theta }_{1}^{t}, \hat {\phi }_{1}^{t}\right) \cdots \mathbf a_{t}\left (\hat {\theta }_{L}^{t}, \hat {\phi }_{L}^{t}\right)\right ]\) is obtained from the estimated beam information, G=diag(γ1,⋯,γL) is a L×L diagonal matrix with beam gains {γ1,⋯,γL} on the main diagonal, and \(\mathbf {W}_{1}\sim \mathcal {CN}\left (\mathbf {0},\sigma _{W}^{2}\mathbf {I}_{M_{t}N_{t}}\right)\) denotes the AWGN matrix. From (6), the covariance matrix of the received signal can be written as
Based on (7), the magnitude of the beam gain is obtained as
where \(\mathbf A_{t}^{\dag }=\left (\mathbf A_{t}^{H}\mathbf A_{t}\right)^{-1}\mathbf A_{t}^{H}\) is the pseudo-inverse of At, and \(\left (\mathbf A_{t}^{H}\right)^{\dag }=\mathbf A_{t}\left (\mathbf A_{t}^{H}\mathbf A_{t}\right)^{-1}\) is the pseudo-inverse of \(\mathbf A_{t}^{H}\). By using the statistic characteristic, the estimated magnitude of the beam gain will have higher accuracy than the pilot-based estimation method.
Second, the phase of beam gain is estimated through a channel estimation algorithm with low pilot overhead and complexity. While the training signal is transmitted in reverse link, the received signal is given by
where φl denotes the phase of \(\hat {\gamma }_{l}, \mathbf {X}_{2}\in \mathbb {C}^{L \times n_{s}}\) is the training signal consisting of ns bits pilots, and W2 is the AWGN matrix. Using (9), the phase of the beam gain is estimated as
where \(\mathbf X_{2}^{\dag }=\mathbf X_{2}^{H}\left (\mathbf X_{2}\mathbf X_{2}^{H}\right)^{-1}\) is the pseudo-inverse of X2. With L beams, there only needs ns= log2L bits pilots to estimate the phase of the beam gain. Due to the pseudo-inverse in (10), there is a significant complexity reduction by using ns bits pilots.
Finally, with the estimated beam gain \(\hat {\gamma }_{l}=|\hat {\gamma }_{l}|e^{j\hat {\varphi }_{l}}\), the forward-link channel matrix in (1) can be estimated as
In summary, the proposed channel estimation strategy has a low complexity for three reasons: (1) It directly uses the results of DOA estimation to obtain the magnitude of the channel gain as an additional product; (2) the DOA estimation strategy has a low complexity; (3) the L beam gains are estimated with short training pilots. Furthermore, the proposed channel estimation strategy has a high accuracy. The reason is that the magnitude of channel gain is estimated from the statistic characteristic as shown in (8), which has a higher accuracy than that of the conventional pilot-based channel estimation.
The proposed channel estimation method can also be adopted for multi-user systems, resulting in a great degradation of pilot overhead. When multiple users have similar DOAs and bring in multi-user interference, the proposed channel estimation method is still available. The reason is that the channel estimation of all users is obtained from the DOA estimation which needs to be implemented in a time-division method. As a result, the interference caused by the similar DOAs does not affect the time-division channel estimation of multiple users.
3.3 Power allocation
In this subsection, the power allocation problem is studied to improve the spectral efficiency of the hybrid architecture massive MIMO system. Let us denote the power allocation matrix \(\mathbf P=\text {diag}(\sqrt {p_{1}},\cdots,\sqrt {p_{L}})\). The power allocation problem can be formulated as
where Pt is the total transmit power.
Theorem
The optimal power allocation for the lth beam is derived as
where u+=max{u,0}, and λ is the Lagrange multiplier satisfying
□
Proof 2.
: Using (4)-(5) and (11), we obtain
and
where (a) and (c) follow from the Lemma 1 that the basis beams are asymptotically orthogonal for sufficiently large MrNr,(b) and (d) are due to \(\mathbf a_{r}^{H}(\hat {\theta }_{l}^{r}, \hat {\phi }_{l}^{r})\mathbf a_{r}(\hat {\theta }_{l}^{r}, \hat {\phi }_{l}^{r})=M_{r}N_{r}\), and all results are proved in Appendix 6.
where (e) and (f) follow the Lemma 1 and \(\mathbf a_{t}^{H}\left (\hat {\theta }_{l}^{t}, \hat {\phi }_{l}^{t}\right)\mathbf a_{t}\left (\hat {\theta }_{l}^{t}, \hat {\phi }_{l}^{t}\right)=M_{t}N_{t}\), respectively, and all proofs are shown in Appendix 6.
Combining (15) and (18), the product \(\left (\hat {\mathbf {F}}_{r}^{H}\hat {\mathbf {F}}_{r}\right)^{-1}\left (\hat {\mathbf {F}}_{r}^{H}\hat {\mathbf H}\hat {\mathbf {F}}_{t}\mathbf {P}\right)\left (\hat {\mathbf {F}}_{r}^{H}\hat {\mathbf H}\hat {\mathbf {F}}_{t}\mathbf {P}\right)^{H}\) in (12a) is derived as
The objective function in (12a) can be formulated as
Problem (12) with the simplified objective function (20) is a convex problem, and admits a water-filling solution as Theorem 1.
To sum up, the main steps of the low-complexity beam-domain signal processing are summarized as follows:
The low-complexity beam-domain signal processing
-
In forward link, the receiver estimates beams \((\hat {\theta }_{l}^{r},\hat {\phi }_{l}^{r})\).
-
Estimate the beams \((\hat {\theta }_{l}^{t},\hat {\phi }_{l}^{t})\) and the magnitude of beam gain \(|\hat {\gamma }_{l}|\) by (8) in reverse link.
-
With the estimated beams, RF precoder at the transmitter and RF combiner at the receiver are derived from (4) and (5), respectively.
-
Perform the power allocation only with \(|\hat {\gamma }_{l}|\) according to Theorem 1.
4 Numerical results and discussion
In this section, we present the numerical results to evaluate the performance of the proposed signal processing methods in hybrid architecture massive MIMO systems. In the simulations, both the transmitter and receiver are equipped with 16 ×16 URA and 16 RF chains. The channel fading coefficients are generated from the urban micro model in the 3GPP standard [24]. The path loss is given by PL(dB)=36.7log10(d)+22.7+26log10(fc), where d=50 m is the distance between the transmitter and receiver, and fc=1 GHz. All simulation results are obtained by averaging over 1000 channel realizations.
Figure 2 illustrates the normalized mean square error (MSE) of the proposed channel estimation scheme and the scheme in [8], as a function of SNR with L=2,4,6,8. We see that the proposed channel estimation algorithm provides a much higher estimation accuracy than the method in [8]. The higher accuracy is for the reason that the magnitude of the beam gain is estimated from the statistic characteristic of all signal as shown (8). By using the statistic characteristic, the accuracy of the estimation is much higher than that of using the one-time training pilots. Moreover, in Fig. 2, the MSE increases with the number of beams L. The reason is that the channel estimation depends on the estimated DOAs, as shown in (8)-(11). As L increases, the error of DOA estimation increases, resulting in larger MSE.
MSE of the proposed channel estimation scheme and the method in [8] with L=2,4,6,8
The channel capacity (CC) of the MIMO system can be obtained from the singular value decomposition (SVD) processing. To evaluate the optimality of the proposed power allocation, Fig. 3 presents the SVD-based channel capacity with the water-filling power allocation and the spectral efficiency (SE) of the proposed optimal power allocation, while the URA with the different number of antennas is employed and 6 beams are considered. It can be seen that the spectral efficiency is getting close to the channel capacity with the antenna number increasing from 4×4 to 16×16. The reason is that the proposed power allocation is approximated from the asymptotical orthogonality of basis beams for sufficient large antenna number M×N in Lemma 1. Furthermore, Fig. 3 shows that the URA with 8×8 antennas can ensure the asymptotical results, which indicates the proposed power allocation is available for the massive MIMO system.
Figure 4 compares the spectral efficiency of the proposed optimal power allocation (OPA) and equal power allocation (EPA) among multiple beams. It is observed that the spectral efficiency of the OPA is higher than that of EPA, especially in the SNR region of 0–15 dB. Besides, it is interesting to find that when SNR is relatively low, the spectral efficiency decreases with L, as shown in the enlarged view. In contrast, the spectral efficiency increases with L at high SNR. The reason is that, at low SNR, the transmit power is low, and the water-filling algorithm only allocates the power to one beam, resulting in spectral efficiency degradation after the channel is normalized by L. At high SNR, the transmit power is filling to all beams, which brings in higher spectral efficiency when L increases.
Figure 5 shows the spectral efficiency comparison of the proposed OPA and random power allocation (RPA) among multiple beams. It is observed that the spectral efficiency of the OPA is higher than that of RPA in the entire SNR region. The performance results of the OPA and RPA in Fig. 5 are similar to that of the OPA and EPA in Fig. 4, except that the spectral efficiency gap between the OPA and RPA is larger than that between the OPA and EPA.
5 Conclusion
In this journal, we have investigated the beam-domain channel estimation and precoding for hybrid architecture massive MIMO systems. We have proposed a low-complexity channel estimation algorithm based on the estimated beam information. The RF processing has been derived from the beam steering as well. Furthermore, we have optimized the power allocation to maximize the spectral efficiency. Simulation results have shown that the proposed signal processing methods can achieve high channel estimation accuracy and spectral efficiency.
6 Appendix
6.1 Proof of Lemma 1
According to (2), it can be derived that
where \(D=\frac {2\pi }{\lambda }d, \alpha _{1,2}=\sin \theta _{l_{2}}\sin \phi _{l_{2}}-\sin \theta _{l_{1}}\sin \phi _{l_{1}}\), and \(\beta _{1,2}=\cos \theta _{l_{2}}\sin \phi _{l_{2}}-\cos \theta _{l_{1}}\sin \phi _{l_{1}}\).
Since \(\theta _{l_{1}}\neq \theta _{l_{2}}\) and \(\phi _{l_{1}}\neq \phi _{l_{2}}\) for l1≠l2,α1,2 and β1,2 are not equal to 0 for l1≠l2. Therefore, \(\mathbf a^{H}(\theta _{l_{1}}, \phi _{l_{1}})\mathbf a(\theta _{l_{2}}, \phi _{l_{2}})\) is bounded as M,N→∞, and there exists
Thus, it is proved that the basis beams are asymptotically orthogonal for sufficiently large MN.
From direct calculation, it is derived that
Notes
For example, the communication between two BSs, the communication between BS and UE, the system of mmWave communications, etc.
Abbreviations
- AWGN:
-
Additive white gaussian noise
- BS:
-
Base station
- CC:
-
Channel capacity
- CS:
-
Compressive sensing
- DFT:
-
Discrete fourier transform
- DOA:
-
Direction-of-arrival
- DOD:
-
Direction-of-departure
- EPA:
-
Equal power allocation
- ESPRIT:
-
Estimation of signal parameters via rotational invariance techniques
- FDD:
-
Frequency division duplex
- MIMO:
-
Multiple-input and multiple-output
- mmWave:
-
Millimeter wave
- MSE:
-
Mean square error
- MUSIC:
-
Multiple signal classification
- OPA:
-
Optimal power allocation
- RF:
-
Radio frequency
- RMSE:
-
Root mean square error
- RPA:
-
Random power allocation
- SE:
-
Spectral efficiency
- SVD:
-
Singular value decomposition
- UE:
-
User equipment
- URA:
-
Uniform rectangular array
References
F. Rusek, D. Persson, B. K. Lau, E. G. Larsson, T. L. Marzetta, O. Edfors, F. Tufvesson, Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag.30(1), 40–60 (2013).
E. G. Larsson, O. Edfors, F. Tufvesson, T. L. Marzetta, Massive MIMO for next generation wireless systems. IEEE Commun. Mag.52(2), 186–195 (2014).
L. Lu, G. Y. Li, A. L. Swindlehurst, A. Ashikhmin, R. Zhang, An overview of massive mimo: Benefits and challenges. IEEE J. Sel. Topics Signal Process.8(5), 742–758 (2014).
F. Sohrabi, W. Yu, Hybrid digital and analog beamforming design for large-scale antenna arrays. IEEE J. Sel. Topics Signal Process.10(3), 501–513 (2016).
V. Raghavan, S. Subramanian, J. Cezanne, A. Sampath, O. H. Koymen, J. Li, Single-user versus multi-user precoding for millimeter wave MIMO systems. IEEE J. Sel. Areas Commun.35(6), 1387–1401 (2017).
A. Alkhateeb, O. E. Ayach, G. Leus, R. W. Heath, Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Topics Signal Process.8(5), 831–846 (2014).
R. W. Heath, N. Gonz ález-Prelcic, S. Rangan, W. Roh, A. M. Sayeed, An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Topics Signal Process.10(3), 436–453 (2016).
H. Lin, F. Gao, S. Jin, G. Y. Li, A new view of multi-user hybrid massive MIMO: Non-orthogonal angle division multiple access. IEEE J. Sel. Areas Commun.35(10), 2268–2280 (2017).
W. Tan, M. Matthaiou, S. Jin, X. Li, Spectral efficiency of DFT-based processing hybrid architectures in massive MIMO. IEEE Wirel. Commun. Lett.6(5), 586–589 (2017).
W. Tan, G. Xu, E. Carvalho, M. Zhou, C. Li, Low cost and high efficiency hybrid architecture massive MIMO systems based on DFT processing. Wirel. Commun. Mobile Comput.2018(10), 1–11 (2018).
D. Fan, F. Gao, G. Wang, Z. Zhong, A. Nallanathan, Angle domain signal processing-aided channel estimation for indoor 60-ghz TDD/FDD massive MIMO systems. IEEE J. Sel. Areas Commun.35(9), 1948–1961 (2017).
J. Zhao, F. Gao, W. Jia, S. Zhang, S. Jin, H. Lin, Angle domain hybrid precoding and channel tracking for millimeter wave massive MIMO systems. IEEE Trans. Wireless Commun.16(10), 6868–6880 (2017).
W. Tan, D. Xie, J. Xia, W. Tan, L. Fan, S. Jin, Spectral and energy efficiency of massive MIMO for hybrid architectures based on phase shifters. IEEE Access. 6:, 11751–11759 (2018).
W. Tan, S. Jin, C. Wen, T. Jiang, Spectral efficiency of multi-user millimeter wave systems under single path with uniform rectangular arrays. EURASIP J. Wirel. Commun. Netw.181:, 458–472 (2017).
W. Tan, W. Huang, X. Yang, Z. Shi, W. Liu, L. Fan, Multiuser precoding scheme and achievable rate analysis for massive MIMO system. EURASIP J. Wirel. Commun. Netw. 1:, 1–15 (2018).
J. Wang, Beam codebook based beamforming protocol for multi-gbps millimeter-wave WPAN systems. IEEE J. Sel. Areas Commun.27(8), 1390–1399 (2009).
Z. Xiao, T. He, P. Xia, X. G. Xia, Hierarchical codebook design for beamforming training in millimeter-wave communication. IEEE Trans. Wireless Commun.15(5), 3380–3392 (2016).
X. Chen, Z. Zhang, L. Wu, J. Dang, P. S. Lu, C. Sun, in 9th IEEE Proc. Int. Conf. Wireless Commun. Signal Process. (WCSP). Robust beam management scheme based on simple 2-D DOA estimation (Nanjing, China, 2017), pp. 1–6.
R. O. Schmidt, A SIGNAL SUBSPACE APPROACH TO MULTIPLE EMITTER LOCATION AND SPECTRAL ESTIMATION (Stanford Univ. Press, Stanford, CA, USA, 1982).
R. Schmidt, Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag.34(3), 276–280 (1986).
R. Roy, T. Kailath, ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech, Signal Process. 37(7), 984–995 (1989).
Y. Ding, S. E. Chiu, B. D. Rao, Bayesian channel estimation algorithms for massive MIMO systems with hybrid analog-digital processing and low resolution ADCs. IEEE J. Sel. Topics Signal Process.99:, 1–1 (2018).
L. Wu, Z. Zhang, J. Dang, J. Wang, H. Liu, Y. Wu, Channel estimation for multicell multiuser massive MIMO uplink over rician fading channels. IEEE Trans. Veh. Technol.66(10), 8872–8882 (2017).
ETSI TR, Universal Mobile Telecommunications System (UMTS); Spacial Channel Model for Multiple Input Multiple Output (MIMO) simulations (3GPP TR 25.996 version 13.0.0 Release 13) (2016).
Acknowledgements
We would like to thank the anonymous reviewers for their insightful comments on the paper, as these comments led us to an improvement of the work.
Funding
This work was supported by the National Natural Science Foundation of China projects (61501109, 61571105, and 61601119), National Key Research and Development Plan (2016YFB0502202), Scientific Research Foundation of Graduate School of Southeast University (YBJJ1816), and the Scholarship from China Scholarship Council (201806090072).
Author information
Authors and Affiliations
Contributions
XC and LW designed the proposed channel estimation and power allocation algorithms. XC also implemented the simulation environment for experiments and completed the analyses of experimental results. ZZ and JD gave some advice on this manuscript and proofread it. All authors read and approved this submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chen, X., Zhang, Z., Wu, L. et al. Low-complexity beam-domain channel estimation and power allocation in hybrid architecture massive MIMO systems. J Wireless Com Network 2019, 245 (2019). https://doi.org/10.1186/s13638-019-1546-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-019-1546-6