1 Introduction

Over the past decades, the H∞ filtering technique has attracted considerable research attention and fruitful results have appeared, see for example [1–13] and the references therein. This is mainly due to the following two reasons. Firstly, in a lot of practical engineering, it is hard to get the probabilistic information of disturbance and the H∞ technique could well deal with this kind of noise signals. Secondly, no matter how precise the system model is, there is also some error between the physical plant and its model. And the robustness of the H∞ filtering approach may tolerate such error in system model. From the above analysis, we could find that investigating the H∞ filtering technique has not only theoretically importance but also engineering significance. As such, we will employ the H∞ approach to design the filter for a class of sensor network systems.

It is well known that the limited network channel bandwidth and limited power are significant factors constraining the performance of industrial sensor network systems [14–19]. In traditional time-triggered communication mechanism, the signal of sensor is transmitted to the filter or controller at every time, which does not consider the limited bandwidth of communication channel and therefore increases the burden of industrial sensor network channel. To avoid the unnecessary frequent communication and save limited energy, an effective method is adopting event-triggered strategy [20–24], in which sensor measurement output is transmitted only when an event-triggered condition is satisfied. If only the event-triggered condition is suitably constructed, the transmission frequency of measurement will decrease while maintaining the prescribed filtering performance. During recent years, the event-triggered communication mechanism has been successfully applied to controller design for various engineer systems, such as networked systems [25, 26] and multi-agent systems [27–29]. Also, some results about event-based filter design have appeared, see for example [30–34]. However, when it comes to the industrial sensor network systems, considering the inevitable network-induced phenomena, the event-based filter design approach has not been adequately investigated and still has many problems needed to be solved. Therefore, the event-triggered communication mechanism will be adopted in the filtering problem for the proposed industrial sensor network systems.

Noting that, nonlinear control and filtering have attracted much interest [4, 35–41], due to the popular existence of nonlinearity in a lot of practical systems and its important effectiveness to systems. In [4], a sector-bounded approach is proposed to handle with a class of nonlinearities. It is pointed out that many plants may be modeled by systems with multiplicative noises and some characteristics of nonlinear systems can be closely approximately by models with multiplicative noises rather than by linearized models [42, 43]. Therefore, in this paper, the nonlinearity of addressed systems is described by a nonlinear function and state-multiplicative noises, which could better present the practical nonlinearity.

As a main source of system instability, time-delay widely exists in practical industrial sensor network systems and should be taken into the analysis process of systems. As such, the H∞ filtering for various time-delay plants has attracted much interest, see [35, 44–46] and the reference therein. For example, the robust filter is designed for systems with packet dropout and constant delay in [44]. In [35], a delay-dependent H∞ filtering method is proposed for delay systems whose postpone is time-varying. Very recently, in [30], the event-triggered strategy is adopted to address distributed H∞ filtering problem for industrial sensor networks with time-invarying delay. Unfortunately, up to now, when event-triggered communication is adopted, the relative investigation about event-based H∞ filter design problem has seldom taken time-varying delay into account. Therefore, we will investigate the event-based H∞ filtering problem for industrial sensor networks whose postpone is time-varying.

Summarizing the above discussions, the event-based H∞ filtering problem will be investigated for a class of nonlinear industrial sensor network systems with packet dropouts, multiplicative noises and time-varying delay. The main contributions are highlighted as follows:

1. During the design of filter for a class of discrete-time sensor network systems with time-varying delay, the event-triggered communication mechanism is adopted.

2. A comprehensive model of nonlinear sensor network systems is proposed which subjects to packet dropouts, multiplicative noises, and time-varying delay.

3. Sufficient conditions are built which could ensure proposed filter and corresponding event-based filtering algorithm is addressed.

Section 2 introduces the methods utilized for the energy-efficient filter. In Section 3, the delay sensor network with packet dropouts and multiplicative noises is introduced. The results and discussions are given in Section 4, where sufficient condition is derived for the H∞ filter and the filtering method is addressed. A numerical example is given in Section 5. Finally, we conclude in Section 6.

2 Methods

In this paper, the energy-efficient filter is designed based on Lyapunov theory method and linear matrix inequality method. The simulation experiment is based on the LMI toolbox of MATLAB R2014a.

3 Problem formulation and preliminaries

Here, the following discrete nonlinear sensor network system with time-varying delay and multiplicative noise is considered:

$$ {} \left\{ {\begin{aligned} x(k+1)&=\left[A+\sum\limits_{i=1}^{\alpha}\tilde{w}_{i(k)}A_{i}\right]x(k)+\left[A_{d}+\sum\limits_{j=1}^{\beta}\tilde{v}_{j}(k)A_{dj}\right]x(k-\tau(k))\\ & \quad +f(x(k))+Bw(k)\\ y(k)&=Cx(k)+Dv(k)\\ z(k)&=Lx(k)\\ x(l)&=\varphi(l), \quad l=-d_{M}, -d_{M+1},\, ...,\, 0, \end{aligned}} \right. $$
(1)

where \(x(k)\in {\mathbb {R}}^{n}\) represents the state vector, \(y(k) \in {\mathbb {R}}^{r}\) is sensor output, \(z(k) \in {\mathbb {R}}^{m}\) is the signal to be estimated, \(w(k)\in {\mathbb {R}}^{p}\) and \(v(k)\in {\mathbb {R}}^{q}\) are disturbance belonging to l2[0,∞],f(·):Rn→Rn is nonlinear vector function, \(\tilde {w}_{i}(k)(i=1, 2,..., \alpha)\) and \(\tilde {v}_{j}(k)(i=1, 2,..., \beta)\) are zero mean Gaussian white noise with \({\mathbb E}\{\tilde {w}_{i}(k)\}=0, {\mathbb E}\{\tilde {w}^{2}_{i}(k)\}=1, {\mathbb E}\{\tilde {w}_{i}(k)\tilde {w}_{j}(k)\}=0(i\neq j), {\mathbb E}\{\tilde {v}_{j}(k)\}=0, {\mathbb E}\{\tilde {v}^{2}_{j}(k)\}=1, {\mathbb E}\{\tilde {v}_{i}(k)\tilde {v}_{j}(k)\}=0(i\neq j), {\mathbb E}\{\tilde {w}_{i}(k)\tilde {v}_{j}(k)\}=0\). The time-varying delay τ(k)∈[dm,dM]. A, Ai, Ad, Adj, B, C, L, andD are known, real matrices with appropriate dimensions.

f(x(k)) is assumed to satisfy the following condition:

$$ \parallel f(x(k))\parallel^{2}\leq \theta \parallel Gx(k)\parallel^{2}, $$
(2)

where θ>0 is a known scalar and G is a known matrix.

Remark 1

As an essential characteristic for many practical networked systems, time-delay should be considered, due to it is a main source of system instability. Although, for the purpose of decreasing the difficulty of filter design, in many filter design algorithm, time-delay is assumed to be constant. But, the fact is that time-delay is almost time-variant. Therefore, it is more practical significant to design filter for network systems with time-varying delay.

Remark 2

The addressed system (1) is a comprehensive model for industrial sensor network systems which includes the multiple noises, nonlinearity, and time-varying delay. As far as we know, due to the complexity of the addressed system (1), the relevant research results are few. This motivates our research interest.

Different from traditional filter design, the event-triggered strategy is considered, which could reduce communication frequency. As such, a event generator function g(·,·) is defined as follows:

$$ g(\sigma(k), \delta)=\sigma^{T}(k)\sigma(k)-\delta^{2}y^{T}(k)y(k), $$
(3)

where σ(k)=y(ki)−y(k) with y(ki) being the measurement at the latest event time ki and y(k) is the current measurement. δ∈[0,1] is the threshold. In practical engineering, δ can be determined on the basis of the filtering requirement. When a smaller filtering error is needed, δ is set to be smaller.

The current measurement y(k) of the sensor is transmitted if only the following condition

$$ g(\sigma(k),\delta)>0 $$
(4)

is met. Thus, the event-triggered sequence 0≤k0≤k1≤···≤ki≤··· is determined iteratively by

$$ k_{i+1}=\text{inf}\{k \in N\mid k>k_{i}, f(\sigma(k),\delta)>0\}. $$
(5)

Remark 3

The event-triggered strategy is adopted in the networked filter design for industrial sensor network. As is well known, in time-triggered communication mechanism, the measurement output of sensor is transmitted by network communication channel with limited bandwidth at every sampling time, even though the measurement output changes slightly in the next instant, which increases the burden of network channel and wastes a lot of source of industrial sensor network. However, in event-triggered communication mechanism, only when the designed condition is met, then measurement signal of sensor is transmitted. And a suitable threshold in the event generator function could not only reduce the measurement communication frequency but also make sure prescribed filtering performance.

As is well known, the measurement of sensor transmitted by network may encounter packet dropouts. When the phenomenon of packet dropouts is considered, the real measurement obtained by filter can be depicted as

$$ \tilde{y}(k_{i})=\alpha(k_{i})y(k_{i}). $$
(6)

Here, stochastic variable α(ki) is employed to govern the phenomenon of packet dropouts in industrial sensor network. It is assumed to be Bernoulli-distributed white sequence with

$${}{\begin{aligned} \text{Prob}\{\alpha(k)=1\}={\mathbb{E}}\{\alpha(k)\}=\bar{\alpha}, \text{Prob}\{\alpha(k)=0\}=1-\bar{\alpha}. \end{aligned}} $$

For system (1), construct the following filter:

$$ \left\{ \begin{aligned} x_{f}(k+1)=&A_{f}x_{f}(k)+B_{f}\tilde{y}(k_{i})\\ z_{f}(k)=&C_{f}x_{f}(k), \end{aligned}\right. $$
(7)

where \(x_{f}(k)\in {\mathbb {R}}^{n}\) is the estimate of the state \(x(k), z_{f}(k) \in {\mathbb {R}}^{m}\) represents the estimate of z(k), and Af,Bf, and Cf is the filter gain matrix to be designed.

By letting \(\eta (k) = [x^{T}(k) \quad e^{T}(k)]^{T}, \tilde {z}(k)=z(k)-z_{f}(k), e(k)=x(k)-x_{f}(k), \bar {w}=[w^{T}(k) \quad v^{T}(k)]^{T}, h(\eta (k))=[f^{T}(x(k))\ f^{T}(x(k))]^{T}\), and \(\tilde {\alpha }(k)=\alpha (k)-\bar {\alpha }\), we could get the augmented system:

$$ {}\left\{ {\begin{aligned} \eta(k+1)=&\bar{A}\eta(k)+\tilde{\alpha}(k_{i})\bar{A}_{0}\eta(k)+\sum\limits_{i=1}^{\alpha}\tilde{w}_{i}(k)\bar{A}_{i}\eta(k)\\ &+\bar{A}_{d}\eta(k-\tau(k))+\sum\limits_{j=1}^{\beta}\tilde{v}_{j}(k)\bar{A}_{dj}\eta(k-\tau(k))+h(\eta(k))\\ &+\alpha(k_{i})\bar{B}_{f}\sigma(k)+\bar{B}_{1}\bar{w}(k)+\tilde{\alpha}(k_{i})\bar{B}_{2}\bar{w}(k)\\ \tilde{z}(k)=&\bar{L}\eta(k), \end{aligned}} \right. $$
(8)

where,

$${\begin{aligned} \bar{A}&= \left[ \begin{array}{cc} A & 0\\ A-A_{f}-\bar{\alpha}B_{f}C & A_{f} \end{array} \right], \bar{A}_{0}= \left[ \begin{array}{cc} 0 & 0\\ -B_{f}C & 0 \end{array} \right],\\&\quad \bar{A}_{i}= \left[ \begin{array}{cc} A_{i} & 0\\ A_{i} & 0 \end{array} \right],\ \bar{A}_{d}= \left[ \begin{array}{cc} A_{d} & 0\\ A_{d} & 0 \end{array} \right],\\ \bar{A}_{dj}&= \left[ \begin{array}{cc} A_{dj} & 0\\ A_{dj} & 0 \end{array} \right],\ \bar{B}_{f}= \left[ \begin{array}{cc} 0 \\ -B_{f} \end{array} \right], \bar{B}_{1}= \left[ \begin{array}{cc} B & 0\\ B & -\bar{\alpha}B_{f}D \end{array} \right],\\&\quad \bar{B}_{2}= \left[ \begin{array}{cc} 0 & 0\\ 0 & -B_{f}D \end{array} \right],\\ \bar{L}&= \left[ \begin{array}{cc} L-C_{f} & C_{f} \end{array} \right]. \end{aligned}} $$

Definition 1

[13]: The augmented system (8) with \(\bar {w}(k)=0\) is exponentially mean-square if there exist constant ε>0 and 0<κ<1 thus

$$ {\mathbb E}\left\{\parallel\eta(k)\parallel^{2}\right\}\!\leq\!\varepsilon\kappa^{k}\max_{i\in [-d_{m},0]}{\mathbb E}\left\{\parallel\eta(i)\parallel^{2}\right\},\ \ \ k\in [0,\infty). $$

Our aim is to design a filter satisfying the following requirements: (Q1) the filtering error system (8) is exponentially mean-square stable, and (Q2) under the zero initial condition, for given scalar γ>0, filtering error \(\tilde {z}(k)\) satisfies

$$ \sum\limits_{k=0}^{\infty}{\mathbb E}\left\{\parallel \tilde{z}(k)\parallel^{2}\right\}<\gamma^{2}\sum\limits_{k=0}^{\infty}{\mathbb E}\left\{\parallel \bar{w}(k)\parallel^{2}\right\} $$
(9)

for all nonzero \(\bar {w}(k)\).

4 Results and discussions

The main results and some discussions are presented in this section.

4.1 Analysis of H ∞ performance

First of all, we introduce the following lemma.

Lemma 1

(Schur complement) Given constant matrices S1,S2, and S3, where \(S_{1}=S_{1}^{T}\) and \(0<S_{2}=S_{2}^{T}\), then \(S_{1}+S_{3}^{T} S_{2}^{-1}S_{3}<0\) if and only if

$$ \left[ \begin{array}{cc} S_{1} & S_{3}^{T} \\ S_{3} & -S_{2}\\ \end{array} \right]<0 \quad \text{or} \quad \left[ \begin{array}{cc} -S_{2} & S_{3} \\ S_{3}^{T} & S_{1}\\ \end{array} \right]<0. $$
(10)

Theorem 1

:Consider the sensor network system(1) and let the filter parameters Af,Bf, and Cf be given. Thus, the filtering error system(8) with \(\bar {w}(k)=0\) is exponentially stable in mean-square, if there exist positive definite matrixes P>0,Q>0 and positive constant scalars ε1, satisfying

$$ {\begin{aligned} \Phi_{1}\,=\,\left[ \begin{array}{cccc} \begin{array}{c}\varphi_{11}+2\varepsilon_{1}\theta \bar{G}^{T}\bar{G}\\\!+\delta^{2}\bar{C}^{T}C\end{array} & \bar{A}^{T}P\bar{A}_{d} & \bar{A}^{T}P & \begin{array}{c} \bar{\alpha}\bar{A}^{T}P\bar{B_{f}}\\\!+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{B}_{f} \end{array}\\ * & \varphi_{22} & \bar{A}_{d}^{T}P & \bar{\alpha}\bar{A}_{d}^{T}P\bar{B}_{f} \\ * & * & P-\varepsilon_{1}I & \bar{\alpha}P\bar{B}_{f} \\ * & * & * & \bar{\alpha}\bar{B}_{f}^{T}P\bar{B}_{f}-I \\ \end{array}\! \right]<0, \end{aligned}} $$
(11)

where

$${\begin{aligned} \varphi_{11}&=\bar{A}^{T}P\bar{A}+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{A}_{0}+\sum\limits_{i=1}^{\alpha}\bar{A}_{i}^{T}P\bar{A}_{i} \\&\quad-P+(d_{M}-d_{m}+1)Q,\\ \varphi_{22}&=\bar{A}_{d}^{T}P\bar{A}_{d}+\sum\limits_{j=1}^{\beta}\bar{A}_{dj}^{T}P\bar{A}_{dj}-Q,\\ \bar{G}&=\left[ \begin{array}{cc} G & 0 \\ \end{array} \right],\ \bar{C}=\left[ \begin{array}{cc} C & 0 \\ \end{array} \right]. \end{aligned}} $$

Proof

: Choose the following Lyapunov function

$$ V(k)=V_{1}(k)+V_{2}(k)+V_{3}(k), $$
(12)

where

$$\begin{array}{*{20}l} V_{1}(k)&=\eta^{T}(k)P\eta(k),\ V_{2}(k)=\sum\limits_{i=k-\tau(k)}^{k-1}\eta^{T}(i)Q\eta(i), \\ V_{3}(k)&=\sum\limits_{j=k-d_{M}+1}^{k-d_{m}}\sum\limits_{i=j}^{k-1}\eta^{T}(i)Q\eta(i). \end{array} $$

□

Then, according to (8) with \(\bar {w}(k)=0\), there is

$$ {{} \begin{aligned} & {\mathbb{E}}\{\Delta V_{1}(k)\}\\ =& {\mathbb{E}}\{V_{1}(k+1)-V_{1}(k)\}\\ =&{\mathbb{E}}\left\{\eta^{T}(k+1)P\eta(k+1)-\eta^{T}(k)P\eta(k) \right\}\\ =&{\mathbb{E}}\left\{\left[\bar{A}\eta(k)+\tilde{\alpha}(k_{i})\bar{A}_{0}\eta(k)+\sum\limits_{i=1}^{\alpha}\tilde{w}_{i}(k)\bar{A}_{i}\eta(k)\right.\right.\\&\quad+\bar{A}_{d}\eta(k-\tau(k))\\ &\left.+\sum\limits_{j=1}^{\beta}\tilde{v}_{j}(k)\bar{A}_{dj}\eta(k\,-\,\tau(k))\,+\,h(\eta(k))+\alpha(k_{i})\bar{B}_{f}\sigma(k)\!\right]^{T}P\\ &\left[\!\bar{A}\eta(k)\,+\,\tilde{\alpha}(k_{i})\bar{A}_{0}\eta(k)\,+\,\sum\limits_{i=1}^{\alpha}\tilde{w}_{i}(k)\bar{A}_{i}\eta(k)\,+\,\bar{A}_{d}\eta(k\,-\,\tau(k))\right.\\ &\left.+\sum\limits_{j=1}^{\beta}\tilde{v}_{j}(k)\bar{A}_{dj}\eta(k-\tau(k))+h(\eta(k))+\alpha(k_{i})\bar{B}_{f}\sigma(k)\right]\\&\left.-\eta^{T}(k)P\eta(k)\right\}\\ \end{aligned}} $$
$$ {}\begin{aligned} =&{\mathbb E}\{\eta^{T}(k)\bar{A}^{T}P\bar{A}\eta(k)+2\eta^{T}(k)\bar{A}^{T}P\bar{A}_{d}\eta(k-\tau(k))\\ &+\!2\eta^{T}(k)\bar{A}^{T}Ph(\eta(k))+2\bar{\alpha}\eta^{T}(k)\bar{A}^{T}P\bar{B}_{f}\sigma(k)\\ &+\!\bar{\alpha}(1\,-\,\bar{\alpha})\eta^{T}(k)\bar{A}_{0}^{T}P\bar{A}_{0}\eta(k)\,+\,2\bar{\alpha}(1\,-\,\bar{\alpha})\eta^{T}\!(k)\bar{A}_{0}^{T}P\bar{B}_{f}\sigma\!(k)\\ &+\!\sum\limits_{i=1}^{\alpha}\eta^{T}(k)\bar{A}_{i}^{T}P\bar{A}_{i}\eta(k)\,+\,\eta^{T}(k\,-\,\tau(k))\bar{A}^{T}_{d}P\bar{A}_{d}\eta(k\,-\,\tau(k))\\ &+\!2\eta^{T}(k\,-\,\tau(k))\bar{A}^{T}_{d}Ph(\eta(k))\,+\,2\bar{\alpha}\eta^{T}\!(k\,-\,\tau(k))\bar{A}^{T}_{d}P\bar{B}_{f}\sigma\!(k)\\ &+\!\sum\limits_{j=1}^{\beta}\!\eta^{T}\!(k\,-\,\tau(k))\bar{A}_{dj}^{T}P\bar{A}_{dj}\eta(k\,-\,\tau(k))\,+\,h^{T}\!(x(k))Ph(\eta(k))\\ &+\!2\bar{\alpha}h^{T}(x(k))P\bar{B}_{f}\sigma(k)+\bar{\alpha}\sigma^{T}(k)\bar{B}_{f}^{T}P\bar{B}_{f}\sigma(k)\\ &-\eta^{T}(k)P\eta(k) \}. \end{aligned} $$
(13)

Next, it can be derived that

$$ {}\begin{aligned} {\mathbb E}\{\Delta V_{2}(k)\}=& {\mathbb E}\{V_{2}(k+1)-V_{2}(k)\}\\ \leq &{\mathbb E}\{\sum\limits_{i=k+1-d_{M}}^{k-d_{m}}\eta^{T}(i)Q\eta(i)+\eta^{T}(k)Q\eta(k)\\ & \quad\quad\quad\quad\quad\quad -\eta^{T}(k-\tau(k))Q\eta(k\,-\,\tau(k))\}\\ \end{aligned} $$
(14)

and

$$ {}\begin{aligned} {\mathbb E}\{\!\Delta \!V_{3}(k)\}\!=& {\mathbb E}\{V_{3}(k\,+\,1)\,-\,V_{3}(k)\}\\ = &{\mathbb E}\{\!(d_{M}\,-\,d_{m})\eta^{T}\!(k)Q\eta(k)\,-\,\!\sum\limits_{i=k+1-d_{M}}^{k-d_{m}}\!\!\eta^{T}\!(\!i)Q\eta(i)\}.\\ \end{aligned} $$
(15)

Let

$$ \zeta(k) = \left[ \begin{array}{cccc} \eta^{T}(k) & \eta^{T}(k-\tau(k)) & h^{T}(x(k)) & \sigma^{T}(k) \\ \end{array} \right]^{T}. $$

It follows from (13)–(15) that

$$ \begin{aligned} {\mathbb E}\{\Delta V(k)\}=&{\mathbb E}\{V(k+1)-V(k)\}\\ =&\sum\limits_{i=1}^{3} {\mathbb E}\{\Delta V_{i}(k)\}\\ \leq& {\mathbb E}\{\zeta^{T}(k)\tilde{\Phi}_{1}\zeta(k)\}, \end{aligned} $$
(16)

where

$$\begin{array}{@{}rcl@{}} \tilde{\Phi}_{1}=&\left[ \begin{array}{cccc} \begin{array}{c} \bar{A}^{T}P\bar{A}+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{A}_{0}\\ +\sum\nolimits_{i=1}^{\alpha}\bar{A}_{i}^{T}P\bar{A}_{i} -P\\ +(d_{M}-d_{m}+1)Q \end{array} & \bar{A}^{T}P\bar{A}_{d} \\ * & \bar{A}_{d}^{T}P\bar{A}_{d}+\sum\nolimits_{j=1}^{\beta}\bar{A}_{dj}^{T}P\bar{A}_{dj}-Q \\ * & * \\ * & * \\ \end{array} \right.\\ &\left.\begin{array}{cccc} & \bar{A}^{T}P & \bar{\alpha}\bar{A}^{T}P\bar{B_{f}}+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{B}_{f} \\ & \bar{A}_{d}^{T}P & \bar{\alpha}\bar{A}_{d}^{T}P\bar{B}_{f} \\ & P & \bar{\alpha}P\bar{B}_{f} \\ & * & \bar{\alpha}\bar{B}_{f}^{T}P\bar{B}_{f} \\ \end{array} \right]<0. \end{array} $$

Moreover, if follows from (2) that

$$ h^{T}(\eta(k))h(\eta(k))\leq 2\theta \eta^{T}(k)\bar{G}^{T}\bar{G}\eta(k). $$
(17)

Furthermore, it follows from (16) and (17) that

$$ \begin{aligned} {\mathbb E}\{\Delta V(k) \}\leq& {\mathbb E}\{\zeta^{T}(k)\tilde{\Phi}_{1}\zeta(k)-\varepsilon_{1}[h^{T}(\eta(k))h(\eta(k))\\&- 2\theta \eta^{T}(k)\bar{G}^{T}\bar{G}\eta(k)]\}. \end{aligned} $$
(18)

Considering the event-triggered condition (3), we have

$$ {}\begin{aligned} {\mathbb E}\{\!\Delta\! V\!(k) \}\!\leq& {\mathbb E}\{\zeta^{T}(k)\tilde{\Phi}_{1}\zeta(k)-\varepsilon_{1}[h^{T}(\eta(k))h(\eta(k))\\&- \!2\theta \eta^{T}\!(k)\bar{G}^{T}\!\bar{G}\eta(k)]\!-\sigma^{T}\!(k)\sigma(k)\,+\,\delta^{2}y^{T}\!(k)y(k) \}\\ =&{\mathbb E}\{\zeta^{T}(k)\Phi_{1}\zeta(k)\}. \end{aligned} $$
(19)

According to Theorem 1, we have Φ1<0. Thus, for all \(\zeta (k)\neq 0, {\mathbb E}\{\Delta V(k)\}\leq {\mathbb E}\{\zeta ^{T}(k)\tilde {\Phi }_{1}\zeta (k)\}<0\). Furthermore, similar to [13], system (8) can be proved to be exponentially mean-square stable. The proof is complete.

Then, the H∞ index will be analyzed.

Theorem 2

: Let Af,Bf, and Cf and γ be given. Then, system(8) is exponentially stable in the mean-square and satisfies the H∞ performance constraint (9) for any nonzero \(\bar {w}(k)\)under zero initial condition, if there exist matrices P>0,Q>0 and positive constant scalar ε1 satisfying

$$ \Phi_{2}<0, $$
(20)

where

$$\begin{array}{@{}rcl@{}} \begin{aligned} \Phi_{2}=&\left[ \begin{array}{ccccc} \varphi_{11}+2\varepsilon_{1}\theta \bar{G}^{T}\bar{G}+\delta^{2}\bar{C}^{T}C+\bar{L}^{T}\bar{L} & \bar{A}^{T}P\bar{A}_{d} & \bar{A}^{T}P\\ * & \varphi_{22} & \bar{A}_{d}^{T}P\\ * & * & P-\varepsilon_{1}I\\ * & * & *\\ * & * & * \end{array} \right.\\ &\left. \begin{array}{ccccc} & \begin{array}{c} \bar{\alpha}\bar{A}^{T}P\bar{B_{f}}\\+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{B}_{f}\end{array} & \bar{A}^{T}P\bar{B_{1}}+\bar{\alpha}(1-\bar{\alpha})\bar{A}_{0}^{T}P\bar{B}_{2}+\delta^{2}\bar{C}^{T}\bar{D}\\ & \bar{\alpha}\bar{A}_{d}^{T}P\bar{B}_{f} & \bar{A}_{d}^{T}P\bar{B}_{1}\\ & \bar{\alpha}P\bar{B}_{f} & P\bar{B}_{1}\\ & \bar{\alpha}\bar{B}_{f}^{T}P\bar{B}_{f}-I & \bar{\alpha}\bar{B}_{f}^{T}P\bar{B}_{1}+\bar{\alpha}(1-\bar{\alpha})\bar{B}_{f}^{T}P\bar{B}_{2}\\ & * & \bar{B}_{1}^{T}P\bar{B}_{1}+\bar{\alpha}(1-\bar{\alpha})\bar{B}_{2}^{T}P\bar{B}_{2}-r^{2}I+\delta^{2}\bar{D}^{T}\bar{D} \end{array} \right]<0, \end{aligned} \end{array} $$

\(\bar {D}=[0 \ \ \ D]\).

Proof

: It is clear that (20) implies (11). From Theorem 1, system (8) is exponentially stable. □

Then, we will analysis the H∞ performance.

$$ {\mathbb E}\{\Delta V(k) \}\leq \bar{\zeta}^{T}(k)\tilde{\Phi}_{2}\bar{\zeta}(k), $$
(21)

where

$$ \bar{\zeta}(k)=[\zeta^{T}(k)\ \ \ \bar{w}^{T}(k)]^{T}, $$
$$ \tilde{\Phi}_{2}=\left[ \begin{array}{cc} \Phi_{1} & U^{T} \\ * & \bar{B}_{1}^{T}P\bar{B}_{1}+\bar{\alpha}(1-\bar{\alpha})\bar{B}_{2}^{T}P\bar{B}_{2}+\delta^{2}\bar{D}^{T}\bar{D} \\ \end{array} \right], $$
$$\begin{aligned} U=\left[ \begin{array}{cccc} \bar{B}_{1}^{T}P\bar{A}+\bar{\alpha}(1-\bar{\alpha})\bar{B}_{2}^{T}P\bar{A}_{0}+\delta^{2}\bar{D}^{T}\bar{C} & \bar{B}_{1}^{T}P\bar{A}_{d} \end{array}\right. \\ \left. \begin{array}{cccc} \bar{B}_{1}^{T}P & \bar{\alpha}\bar{B}_{1}^{T}P\bar{B}_{f}+\bar{\alpha}(1-\bar{\alpha})\bar{B}_{2}^{T}P\bar{B}_{f} \\ \end{array} \right]. \end{aligned} $$

To handle with H∞ performance, the following index is introduced:

$$ J(n)=E\sum\limits_{k=0}^{n}\{\parallel\tilde{z}(k)\parallel^{2}-\gamma^{2}\parallel\bar{w}(k)\parallel^{2}\}, $$
(22)

where n is a nonnegative integer.

Under the zero initial condition, we have

$$ {}\begin{aligned} J(n)&=E\!\sum\limits_{k=0}^{n}\{\parallel\tilde{z}(k)\!\!\parallel^{2}\!\!-\gamma^{2}\!\!\parallel\!\!\bar{w}(k)\!\!\parallel^{2}\!\,+\,\Delta V(k) \}\,-\,{\mathbb E}\{\!\Delta\! V(n\,+\,1)\}\\ &\leq E\sum\limits_{k=0}^{n}\{\parallel\tilde{z}(k)\parallel^{2}-\gamma^{2}\parallel\bar{w}(k)\parallel^{2}+\Delta V(k) \}\\ &\leq E\!\sum\limits_{k=0}^{n}\{\eta^{T}\!(k)\bar{L}^{T}\bar{L}\eta(k)\,-\,\gamma^{2}\bar{w}^{T}\!(k)\bar{w}(k)\,+\,\bar{\zeta}^{T}\!(k)\tilde{\Phi}_{2}\bar{\zeta}(k) \}\\ &=E\sum\limits_{k=0}^{n}\{\bar{\zeta}^{T}(k)\Phi_{2}\bar{\zeta}(k) \}. \end{aligned} $$
(23)

According to Theorem 2, we have Φ2<0,J(n)<0. When n→∞, there is

$$ \sum\limits_{k=0}^{n}{\mathbb E}\{\parallel\tilde{z}(k)\parallel^{2} \}<\gamma^{2}\sum\limits_{k=0}^{\infty}\parallel\bar{w}(k)\parallel^{2}. $$
(24)

The proof is complete.

4.2 Event-based H ∞ filter design

Here, the H∞ filtering algorithm will be solved in Theorem 3.

Theorem 3

Let the disturbance attention level γ>0 be given. Then, for sensor network system (1) and filter (7), the H∞ performance constraints (9) and exponential stability are guaranteed, if there exist positive matrices P>0,Q>0, and ε1>0 and matrices X and Cf satisfying

$$ \Lambda=\left[ \begin{array}{ccc} \Lambda_{11} & \Lambda_{12} & \Lambda_{13} \\ * & \Lambda_{22} & \Lambda_{23}\\ * & * & \Lambda_{33} \\ \end{array} \right]<0, $$
(25)

where

$$\begin{array}{*{20}l} {}\Lambda_{11}&\,=\,\sum\limits_{i=1}^{\alpha}\bar{A}_{i}^{T}\!P\bar{A}_{i}\,+\,(d_{M}\,-\,d_{m}\,+\,1)Q\,+\,\varepsilon_{1}2\theta\!\bar{G}^{T}\!\bar{G}\,+\,\delta^{2}\bar{C}^{T}\bar{C}\,-\,P,\\ {}\Lambda_{12}&\,=\,\left[ \begin{array}{cccc} 0 & 0 & 0 & \delta^{2}\bar{C}^{T}\bar{D} \\ \end{array} \right],\\ {}\Lambda_{13}&\,=\,\left[ \begin{array}{ccc} \hat{A}^{T}P+\bar{\alpha}\hat{C}^{T}X^{T} & \sqrt{\bar{\alpha}(1-\bar{\alpha})}R^{T}X^{T} & \hat{L}^{T}-H_{2}^{T}C_{f}^{T} \\ \end{array} \right], \end{array} $$
$$\begin{array}{*{20}l} \Lambda_{22}&=\text{diag}\{\sum\limits_{j=1}^{\beta}\bar{A}_{dj}^{T}P\bar{A}_{dj}\,-\,Q,\ \!\!-\varepsilon_{1}I,\ \!\!-I,\ \!\!-\gamma^{2}I\,+\,\delta^{2}\bar{D}^{T}\bar{D}\},\\ \Lambda_{23}&=\left[ \begin{array}{ccc} \bar{A}_{d}^{T}P & 0 & 0 \\ P & 0 & 0 \\ \bar{\alpha}H_{1}^{T}X^{T} & \sqrt{\bar{\alpha}(1-\bar{\alpha})}H_{1}^{T}X^{T} & 0 \\ \hat{B}_{1}^{T}P+\bar{\alpha}\hat{D}^{T}X^{T} & \sqrt{\bar{\alpha}(1-\bar{\alpha})}\hat{D}^{T}X^{T} & 0\\ \end{array} \right],\\ \Lambda_{33}&=\text{diag}\{-P,\ -P,\ -I \}, \\ \hat{A}&=\left[ \begin{array}{cc} A & 0 \\ 0 & 0 \\ \end{array} \right], \ H_{0}=\left[ \begin{array}{c} 0 \\ I \\ \end{array} \right], \ K=\left[ \begin{array}{cc} B_{f} & A_{f} \\ \end{array} \right], \\ \hat{C}&=\begin{bmatrix} C & 0 \\ 0 & \frac{1}{\bar{\alpha}}I \\ \end{bmatrix},\ R=\begin{bmatrix} C & 0 \\ 0 & 0 \\ \end{bmatrix},\ H_{1}=\begin{bmatrix} I \\ 0 \\ \end{bmatrix},\\ \hat{B}_{1}&=\begin{bmatrix} B & 0 \\ 0 & 0 \\ \end{bmatrix},\ \hat{D}=\begin{bmatrix} 0 & D \\ 0 & 0 \\ \end{bmatrix},\\ \hat{L}&=\begin{bmatrix} L & 0 \\ \end{bmatrix},\ H_{2}=\begin{bmatrix} 0 & I \\ \end{bmatrix}. \end{array} $$

Furthermore, if (P, Q, X, Cf,ε1) is a feasible solution of (25), then the filter matrices (Af,Bf,Cf) could be obtained by means of matrices X and Cf, where

$$ \left[ \begin{array}{cc} B_{f} & A_{f} \\ \end{array} \right]=K=(H_{0}^{T}PH_{0})^{-1}H_{0}^{T}X. $$
(26)

Proof

: Rewrite Φ2 as follows:

$$ \Phi_{2}=\hat{\Phi}_{2}+V_{1}^{T}P^{-1}V_{1}+V_{2}^{T}P^{-1}V_{2}+V_{3}^{T}V_{3}, $$
(27)

where

$$\begin{array}{*{20}l} {} V_{1}&=\!\left[\! \begin{array}{ccccc} P\bar{A} & P\bar{A}_{d} & P & \bar{\alpha}P\bar{B}_{f} & P\bar{B}_{1} \\ \end{array} \right], \\ {}V_{2}&=\!\left[\! \begin{array}{ccccc} \sqrt{\bar{\alpha}(1\,-\,\bar{\alpha})}P\bar{A}_{0} & 0 & 0 &\! \sqrt{\bar{\alpha}(1\,-\,\bar{\alpha})}P\bar{B}_{f} & \!\sqrt{\bar{\alpha}(1\,-\,\bar{\alpha})}P\bar{B}_{2} \\ \end{array} \right], \\ {}V_{3}&=\!\left[\! \begin{array}{ccccc} \bar{L} & 0 & 0 & 0 & 0 \\ \end{array} \right], \\ \end{array} $$
$${} \hat{\Phi}_{2}=\left[\!\! \begin{array}{ccccc} \Lambda_{11} & 0 & 0 & 0 & \delta^{2}\bar{C}^{T}\bar{D} \\ * & \sum\nolimits_{j=1}^{\beta}\!\bar{A}_{dj}^{T}P\bar{A}_{dj}\,-\,Q & 0 & 0 & 0 \\ * & * & -\varepsilon_{1}I & 0 & 0 \\ * & * & * & -I & 0 \\ * & * & * & * & -\gamma^{2}I\,+\,\delta^{2}\bar{D}^{T}\bar{D} \\ \end{array} \!\right]. $$

□

According to Lemma 1, (27) is equivalent to

$$ \left[ \begin{array}{cccc} \hat{\Phi}_{2} & V_{1}^{T} & V_{2}^{T} & V_{3}^{T} \\ V_{1} & -P & 0 & 0 \\ V_{2} & 0 & -P & 0 \\ V_{3} & 0 & 0 & -I \\ \end{array} \right]<0. $$
(28)

Moreover, rewrite the parameters in (8):

$$ {}\begin{aligned} \bar{A}&=\hat{A}\,+\,\bar{\alpha}H_{0}K\hat{C},\ \bar{A}_{0}\,=\,H_{0}KR,\ \bar{B}_{f}\,=\,H_{0}KH_{1},\\ \bar{B}_{1}&=\hat{B}_{1}\,+\,\bar{\alpha}H_{0}K\hat{D},\ \bar{B}_{2}\,=\,H_{0}K\hat{D},\ \bar{L}\,=\,\hat{L}\,-\,C_{f}H_{2},\ PH_{0}K\,=\,X.\\ \end{aligned} $$
(29)

Thus, (28) is equivalent to (25). Then, from Lemma 2, we obtain (9), and system (8) is exponentially stable. The proof is complete.

Remark 4

The sufficient conditions guaranteeing the event-based filter satisfy Q1 and Q2 are proposed in Theorem 2. The design problem of desired filter is addressed in Theorem 3. It is easy to find that all the relevant information is contained in the LMI, such as system parameters, nonlinearity, and the threshold of event-triggered function.

5 Numerical simulations

The system (1) is as follows:

$${}\begin{aligned} A&\,=\,\left[\!\! \begin{array}{ccc} 0.3 & -0.2 & 0 \\ 0 & 0.4 & -0.1 \\ -0.2 & 0.1 & 0.25 \\ \end{array} \!\!\right],\ A_{1}\,=\,\left[\!\! \begin{array}{ccc} 0.1 & 0.05 & 0 \\ 0 & 0.15 & 0.1 \\ 0 & -0.1 & -0.01 \\ \end{array} \!\!\right],\ A_{2}\,=\,\left[\!\! \begin{array}{ccc} 0.1 & -0.05 & 0 \\ 0 & 0.15 & 0.05 \\ 0.05 & -0.05 & 0.1 \\ \end{array} \!\!\right],\\ A_{d}&=\left[\!\! \begin{array}{ccc} 0.05 & 0 & 0 \\ 0.1 & 0.1 & -0.1 \\ 0 & 0 & -0.1 \\ \end{array} \!\!\right],\ A_{d1}=\left[\!\! \begin{array}{ccc} 0.1 & 0.05 & 0 \\ 0.02 & 0.05 & 0 \\ 0 & 0 & 0.1 \\ \end{array} \!\!\right],\ A_{d2}=\left[\!\! \begin{array}{ccc} 0.1 & 0 & 0 \\ 0 & 0.05 & 0.05 \\ 0 & 0 & 0 \\ \end{array} \!\!\right],\\ C&=\left[\!\! \begin{array}{ccc} 0.3 & -0.2 & 0.1 \\ 0 & 0.35 & 0.2 \\ \end{array} \!\!\right],\ B=\left[\!\! \begin{array}{c} 0.2 \\ 0.15 \\ 0.4 \\ \end{array} \!\!\right],\ D=\left[\!\! \begin{array}{c} 0.3 \\ 0.1 \\ \end{array} \!\!\right],\ L=\left[\!\! \begin{array}{ccc} 0.5 & 0.2 & 0.3 \\ \end{array} \!\!\right]. \end{aligned} $$

f(k,x(k)) and disturbance w(k)andv(k) are chosen as

$$\begin{array}{@{}rcl@{}} \begin{aligned} f(k,x(k))&=\left[ \begin{array}{c} \frac{(0.1x_{1})}{1+2x_{3}^{2}} \\ \frac{0.1\sin{(x_{2})}}{\sqrt{x_{1}^{2}+2}} \\ 0.2x_{3} \end{array} \right],\\ w(k)&=\left[\! \begin{array}{c} \frac{5}{k+14}\!*\!cos(k) \\ \end{array} \!\!\right], v(k)\,=\,\left[\! \begin{array}{c} \exp(-0.05k)\sin{(k)} \\ \end{array} \!\right]. \end{aligned} \end{array} $$

where xi(i=1,2,3) denotes the ith element of the system state x(k). Then, the constraint (2) can be met with

$$\begin{array}{@{}rcl@{}} G(k)=\left[ \begin{array}{ccc} 0.1 & 0 & 0\\ 0 & 0.1 & 0\\ 0 & 0 & 0.2 \end{array} \right], \theta=1. \end{array} $$

The initial value of state is x(0)=[0.3 0.25 −0.5]T.The initial value of state estimation is \(\hat {x}(0)=[0\quad 0\quad 0]^{T}\). The probability of stochastic variable α(k) is taken as \(\bar {\alpha }=0.9\). Delay is dM=3,dm=1. Choose the event threshold δ=0.3. The disturbance attenuation level is γ=0.95.

The filter parameters can be obtained as follows:

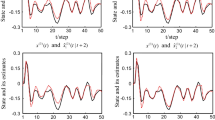
$$\begin{array}{@{}rcl@{}} A_{f}=\left[ \begin{array}{ccc} -0.0846 & 0.0548 & 0.0444 \\ 0.0025 & -0.1229 & 0.1027 \\ 0.0952 & -0.0107 & -0.0516 \end{array} \right], B_{f}=\left[ \begin{array}{cc} 0.4851 & 0.1995 \\ 0.2279 & 0.4215 \\ 0.2858 & 0.3967 \end{array} \right],\\ C_{f}=\left[ \begin{array}{ccc} 0.2714 & 0.1160 & 0.1708 \end{array} \right]. \end{array} $$

Figures 1, 2, 3, 4, 5, 6, and 7 show the simulation results. When setting the threshold δ=0.3, the results are described in Figs. 1, 2, 3, and 4. Figure 1 depicts the state variables x3(k) and its estimate \(\hat {x}_{3}(k)\), and Fig. 2 plots the output z(k) and its estimation \(\hat {z}(k)\), whereas the estimation error \(z(k)-\hat {z}(k)\) is shown in Fig. 3. Event-triggered times are plotted in Fig. 4, whereas one represents the times that event-triggered condition is satisfied and sensor signal is transmitted and zero represents times that event-triggered condition is not satisfied. It follows from Fig. 4 that the event-triggered communication mechanism can reduce the transmission frequency of the measurement output, which is energy efficient. According to Figs. 1, 2, and 3, it is easy to find that the proposed filter can estimate the state of the system well, and the energy-efficient filtering strategy has satisfying filtering performance. Next, we will compare the event-triggered mechanism with the time-triggered mechanism. When setting the threshold δ=0, e.g., the time-triggered mechanism, the corresponding results are depicted in Figs. 5, 6, and 7. Corresponding to Figs. 1, 2, and 3, Fig. 5 describes x3(k) and its estimate \(\hat {x}_{3}(k)\), and Fig. 6 plots z(k) and its estimation \(\hat {z}(k)\), whereas the estimation error \(z(k)-\hat {z}(k)\) is shown in Fig. 7. Compared with the simulation results between δ=0 and δ=0.3, we conclude that, with suitable threshold δ, the event-triggered mechanism could reduce the network burden while ensuring certain system performance. The results confirm the proposed filter design method which could well achieve the desired filtering requirement.

Fig. 1
figure 1

State x3(k) and its estimate (δ=0.3)

Full size image
Fig. 2
figure 2

Output z(k) and its estimate (δ=0.3)

Full size image
Fig. 3
figure 3

Estimation error \(z(k)-\hat {z}(k)\) (δ=0.3)

Full size image
Fig. 4
figure 4

The event-triggered times (δ=0.3)

Full size image
Fig. 5
figure 5

State x3(k) and its estimate (δ=0)

Full size image
Fig. 6
figure 6

Output z(k) and its estimate (δ=0)

Full size image
Fig. 7
figure 7

Estimation error \(z(k)-\hat {z}(k)\) (δ=0)

Full size image

6 Conclusions

In this paper, based on the event-triggered mechanism, we have designed the energy efficiency H∞ filter for a class of industrial sensor network system with time-varying delay, packet dropouts, and multiplicative noises. The event-triggered communication mechanism is adopted to improve energy efficiency. It could not only reduce the transmission frequency of the measurement output, but also guarantee the prescribed filtering performance. The time-varying delay is considered with event-triggered strategy, which has seldom been studied. Sufficient conditions are found through stochastic analysis technique. The filter parameters could be obtained by solving the certain LMI. Finally, the simulation confirms the proposed method.