1 Introduction

Nowadays, Energy harvesting has appeared as a promising approach to prolong lifetime of energy constrained wireless communication system [1–4], which is usually equipped with replacing or recharging batteries. For example, in wireless sensor networks, if a sensor is depleted of energy, it will be out of work. And replacing or recharging energy may be unavailable, especially when a sensor is embedded in building structures or inside human bodies. Earlier, the energy harvesting technologies mostly relied on external and traditional energy sources such as solar, wind, and vibration. However, the application range of the traditional energy harvesting technologies is limited because of the environment uncertainty, weather dependence.

Very recently, simultaneous wireless information and power transfer (SWIPT) has been an exciting new way to provide stale energy to wireless communication where the receiver is able to harvest energy and decode information from the received signals [5–11]. In [5], the authors described the basic idea about the wireless information and power transfer from information theoretical perspective, and in [6], the authors proposed a general receiver architecture with separated information decoding and energy harvesting receiver for SWIPT for practical applications.

Following these pioneering works, plenty of works have been done for various wireless networks, including cooperative relaying network [12–16], power allocation strategies [17–19], resource scheduling [20, 21], and multiple-input multiple-out (MIMO) system [22–24] or multiple-input single-output (MISO) [25, 26]. In [12], the authors analyzed the system maximal throughput for the time switching and power splitting protocols in AF relaying networks. The authors in [13] investigated the outage performance of the relay network over rayleigh fading channels where both AF and DF protocols were considered. In [14], the authors investigated the relay selection for SWIPT systems. In [17], the authors investigated the multi-user cooperative networks where how to distribute the harvested energy among the multiple users was studied. In [18], the authors discussed two types of power allocation policies for non-orthogonal multiple access (NOMA) system. In [20], the author proposed a greedy clustering algorithms to reduce the hardware cost of the PS scheme. In [22], a non-regenerative MIMO orthogonal frequency-division multiplexing (OFDM) relaying system was investigated, and the maximal achievable information rates of two protocols, time swithing-based relaying and power splitting-based relaying, were explored. In [23], the authors focused on quality-of-service-constrained energy efficient optimization in MIMO SWIPT systems via joint antenna selection and spatial switching. In [25] and [26], the secrecy performance of channel uncertainties and imperfect channel state information was studied for multiple-input and multiple-output SWIPT system.

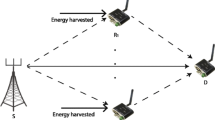
In this paper, we focus on a two-way relay SWIPT system over Nakagami-m fading, which consists of a source-destination (S-D) pair and a relay node R embedded power splitting (PS) (see Fig. 1). We investigate the effect of SWIPT on the outage probability and the impact of the ambient environment energy harvesting and the RF energy harvesting on the system outage probability. In detail, a closed-form expression of outage probability considering AF/DF relaying schemes at node R to decode and forward the received signals to node D is derived.

Fig. 1
figure 1

A system structure for energy harvesting relay-aided cooperative network with a power splitter relay node

Full size image

The contributions are expressed as below: at first, we derive a closed-form expressions of outage probability at two-way relay cooperation group for AF and DF relaying schemes with Nakagami-m fading channels respectively. Secondly, we simulate the outage probability of two-way relay SWIPT systems with Monte Carlo method; at the same time, we consider the impact of power splitting fraction, the position of the relay node between the source node and destination node, the buffer energy capacity of relay node harvesting from ambient environment, etc. Finally, we give the comparison of system operation time of numerical analysis and Monte Carlo method.

The rest of the paper is organized as follows. Section 2 reports about model of the system. Section 3 presents the outage probability analysis. Section 4 presents our numerical result and validates the analytical result through Monte Carlo simulations. Finally, a conclusion will be drawn in Section 5.

2 System model

In the first section, we assumed a simplest cooperation group including a source-destination (S-D) pair, and a relay node R. All links experience independent and identically Nakagami-m fading. In the first phase, the received signals at the information receiver of R and D in downlink phase are expressed as

$$\begin{array}{@{}rcl@{}} y_{R}= \sqrt\rho \left(\sqrt{P_{s}} h_{sr}X + n_{R} \right) + z_{R} \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}}{} y_{D1}= \sqrt{P_{s}} h_{sd}x + n_{D} \end{array} $$
(2)

where P i (i∈(S,R)) is the transmit power at node i, x denotes the transmitted symbols from node S, h i j (i,j∈S,R,D) is the link channel gain between node i and j, n i (i∈D,R) denotes the independent complex Gaussian noise at the information receiver of node R and Dwith zero means and a same variance, and N0 and z R are the signal processing noise by the information decoder at node R followed by additional white Gaussian noise with zero means and variance σ2.

So, the SNR of the received signal at information receiver of R and Dcan be expressed as

$$\begin{array}{@{}rcl@{}} \gamma_{sr}= \frac{\rho P_{s} |h_{sr}|^{2}}{\left.\left(\rho N_{0}+\sigma^{2}\right)\left(\alpha d\right)^{2}\right)} \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}}{} \gamma_{sd}= \frac{P_{s} |h_{sd}|^{2}}{N_{0}d^{2}} \end{array} $$
(4)

where ρ denotes the ratio of power splitter, α denotes the ratio of the distance of the relay node position departing from the source node S to the distance d between the source node S and the destination node D.

The probability density function (PDF) of |h s r |2 and |h s d |2 can be given as

$$ p\left(|h_{sr}|^{2}\right)=\frac{{m_{sr}}^{m_{sr}}{\gamma_{sr}}^{m_{sr}-1}}{\bar{\gamma_{sr}}^{m_{sr}} \Gamma(m_{sr})}\exp\left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{sr}\right) $$
(5)
$$ p\left(|h_{sd}|^{2}\right)=\frac{{m_{sd}}^{m_{sd}}{\gamma_{sd}}^{m_{sd}-1}}{\bar{\gamma_{sd}}^{m_{sd}} \Gamma(m_{sd})}\exp\left(-\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{sd}\right) $$
(6)

where m s d and m s r denote that the Nakagami-m fading parameter at the respective hop. Γ(.) stands for the Gamma function [27], and average SNR (\(\bar {\gamma _{sr}} \ and\ \bar {\gamma _{sd}}\)) of received signal at relay and destination [28, 29] can be written as

$$\begin{array}{@{}rcl@{}}{} \bar{\gamma_{sr}}=\rho P_{s} \frac{E\left(|h_{sr}|^{2} \right)}{\left(\rho N_{0}+\sigma^{2}\right)\left(\alpha d\right)^{2}}\! =\!\rho P_{s} \frac{E_{h1}}{\left.\left(\rho N_{0}+\sigma^{2}\right)\left(\alpha d\right)^{2}\right)} \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \bar{\gamma_{sd}}=P_{s} \frac{E\left(|h_{sd}|^{2} \right)}{N_{0}} =P_{s} \frac{E_{h2}}{N_{0}d^{2}} \end{array} $$
(8)

3 Outage analysis

3.1 DF scheme outage analysis

In this second phase, if R decides to forward the detected symbols, X r , to D after regenerating, the received signal at D is

$$\begin{array}{@{}rcl@{}} y_{D2df}= \sqrt{P_{r}} h_{rd}X_{r} + n_{D} \end{array} $$
(9)

where P r =(1−ρ)P R F +Emax, where P R F denotes the energy harvested by relay node through RF and Emax denotes the natural energy harvested by relay node from ambient environment (e.g., solar energy, wind energy).

Accordingly, the SNR of the received signal at D can be expressed as

$$\begin{array}{@{}rcl@{}} \gamma_{rd}= \frac{P_{r} |h_{rd}|^{2}}{N_{0}(1-\alpha d)^{2}} \end{array} $$
(10)

The probability density function (PDF) of |h r d |2 can be given as

$$ p(|h_{rd}|^{2})=\frac{{m_{rd}}^{m_{rd}}{\gamma_{rd}}^{m_{rd}-1}}{\bar{\gamma_{rd}}^{m_{rd}}\Gamma(m_{rd})}\exp \left(-\frac{m_{rd}}{\bar{\gamma_{rd}}}\gamma_{rd}\right) $$
(11)

where the average SNR of the received signal at destination can be written as

$$\begin{array}{@{}rcl@{}} \bar{\gamma_{rd}}=P_{r} \frac{E\left(|h_{rd}|^{2} \right)}{N_{0}\left(1-\alpha d\right)^{2}} =P_{r} \frac{E_{h3}}{N_{0}\left(1-\alpha d\right)^{2}} \end{array} $$
(12)

The outage probability of the consider system for the DF scheme can be expressed as

$$\begin{array}{@{}rcl@{}} P_{\text{out}}(\gamma_{th}) &= P{\left[\gamma_{sr}>\gamma_{th}\right]}P{\left[\gamma_{d}\leq \gamma_{th}|\gamma_{sr}>\gamma_{th}\right]} \\ & + P{\left[\gamma_{sr} \leq \gamma_{th}\right]}P{\left[\gamma_{D1}\leq \gamma_{th}\right]} \end{array} $$
(13)

The probability with the SNR of S-R link γ s r can be expressed as

$$ {{}\begin{aligned} P\left[\gamma_{sr}\leq \gamma_{th}\right] &=\int_{0}^{\gamma_{th}}\frac{{m_{sr}}^{m_{sr}}{\gamma_{sr}}^{m_{sr}-1}}{\bar{\gamma_{sr}}^{m_{sr}}\Gamma(m_{sr})}\exp \left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}{\gamma_{sr}}\right)d\gamma_{sr}\\ &=1-\exp{\left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sr}-1} \left(\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)^{n}\frac{1}{n!} \end{aligned}} $$
(14)

Similarly, the probability with the SNR of S-D link γ s d can be expressed as

$$ {{}\begin{aligned} P\left[\gamma_{sd}\leq \gamma_{th}\right] &=\int_{0}^{\gamma_{th}}\frac{{m_{sd}}^{m_{sd}}{\gamma_{sd}}^{m_{sd}-1}}{\bar{\gamma_{sd}}^{m_{sd}} \Gamma(m_{sd})}\exp \!\left(\! -\frac{m_{sd}}{\bar{\gamma_{sd}}}{\gamma_{sd}}\! \right)d\gamma_{sd} \\ &=1-\exp{\left(-\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sd}-1} \left(\frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}}\right)^{n}\frac{1}{n!} \end{aligned}} $$
(15)

The probability with the SNR of the combined signal at D, γ D , can be expressed as

$$ \begin{aligned} P{\left[\gamma_{d}\leq \gamma_{th}|\gamma_{sr}>\gamma_{th}\right]}&=P{\left[\gamma_{D}\leq \gamma_{th}\right]}= P{\left[{\max}{\{\gamma_{D1},\gamma_{D2}\}}\leq \gamma_{th}\right]} \\ &=\left[1-\exp{\left(-\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sd}-1} \left(\frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}}\right)^{n}\frac{1}{n!} \right] \\ &\quad \times \left[\! 1-\exp{\left(\! -\frac{m_{rd}}{\bar{\gamma_{rd}}}\gamma_{th}\! \right)}\sum_{n=0}^{m_{rd}-1} \left(\frac{m_{rd}\gamma_{th}}{\bar{\gamma_{rd}}}\right)^{n}\frac{1}{n!}\right] \end{aligned} $$
(16)

Therefore, the outage probability can be obtained by substituting (14), (15), and (16) into (13) as

$$ {{}\begin{aligned} P_{\text{out}}^{(df)}(\gamma_{th})&=\exp{\left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sr}-1} \left(\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)^{n}\frac{1}{n!}\\ &\quad \times\left[\! 1-\exp{\left(\! -\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\! \right)}\sum_{n=0}^{m_{sd}-1} \left(\!\frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}}\! \right)^{n}\frac{1}{n!}\! \right]\\ &\quad \times\left[\! 1-\exp{\left(\! -\frac{m_{rd}}{\bar{\gamma_{rd}}}\gamma_{th}\! \right)}\sum_{n=0}^{m_{rd}-1} \left(\! \frac{m_{rd}\gamma_{th}}{\bar{\gamma_{rd}}}\! \right)^{n}\frac{1}{n!}\! \right]\\ &\quad +\left[\! 1-\exp{\left(\! -\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{th} \!\right)}\sum_{n=0}^{m_{sr}-1} \left(\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)^{n}\frac{1}{n!}\right]\\ &\quad \times\left[\! 1-\exp{\left(\! -\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\! \right)}\sum_{n=0}^{m_{sd}-1} \left(\! \frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}} \!\right)^{n}\frac{1}{n!}\! \right] \end{aligned}} $$
(17)

3.2 AF scheme outage analysis

In this second phase, if the node R decides to forward the detected symbols, X r , to the node D after amplifying, the received signal at node D can be expressed as

$$\begin{array}{@{}rcl@{}} y_{D2af}&=&Gh_{rd}y_{R}+n_{D}\\ &=&Gh_{rd}\left[\sqrt\rho \left(\sqrt{P_{s}} h_{sr}X + n_{R} \right) + z_{R}\right]+n_{D} \end{array} $$
(18)

where \(G=\frac {\sqrt {P_{r}}}{\sqrt {P_{s}|h_{sr}|^{2}+N_{0}}}\) is the amplifying factor at R. Therefore, the SNR of the received signal at D can be expressed as

$$\begin{array}{@{}rcl@{}} \gamma_{rd2}&=&\frac{\frac{{P_{s}P_{r}}\rho|h_{rd}|^{2}|h_{sr}|^{2}}{{P_{s}|h_{sr}|^{2}+N_{0}}}} {\frac{P_{s}|h_{rd}|^{2}}{P_{s}|h_{sr}|^{2}+N_{0}}\left(\rho N_{0}+\sigma^{2}\right)+N_{0}}\\ &=&\frac{\frac{\rho P_{s}{|h_{sr}|^{2}}}{\rho N_{0}+\sigma^{2}}\frac{P_{r}|h_{rd}|^{2}}{N_{0}}}{\frac{1}{\rho}\frac{\rho P_{s}|h_{sr}|^{2}}{\rho N_{0}+\sigma^{2}}+\frac{P_{r}|h_{rd}|^{2}}{N_{0}}+\frac{N_{0}}{\rho N_{0}+\sigma^{2}}}\\ &=&\frac{\gamma_{sr}\gamma_{rd}}{a\gamma_{sr}+\gamma_{rd}+b}=\frac{\gamma_{1}\gamma_{2}}{a\gamma_{1}+\gamma_{2}+b} \end{array} $$
(19)

where \(a=\frac {1}{\rho }\), \(b=\frac {N_{0}}{\rho N_{0}+\sigma ^{2}}\), γ s r =γ1, and γ r d =γ2. Let \(P_{srd}^{(\text {out})}\) denotes the outage probability of γrd2, so it can be expressed as

$$ \begin{aligned} P_{srd}^{(\text{out})}&=P\left[\gamma_{rd2}\leq\gamma_{th}\right]=\int_{0}^{\gamma_{th}} P\left[\gamma_{2}\geq\frac{(ax+b)\gamma_{th}}{x-\gamma_{th}}|\gamma_{1}\right]\cdot {f}_{\gamma_{1}}(x)dx \\ & \quad+\int_{\gamma_{th}}^{\infty} P\left[\gamma_{2}\leq\frac{(ax+b)\gamma_{th}}{x-\gamma_{th}}|\gamma_{1}\right]\cdot {f}_{\gamma_{1}}(x)dx \\ &=1-\frac{2(m_{rd}-1)!m_{sr}^{m_{sr}}}{\bar{\gamma_{sr}}^{m_{sr}}\Gamma(m_{sr})\Gamma(m_{rd})} \exp{\left(-\frac{am_{rd}\gamma_{th}}{\bar{\gamma_{rd}}}-\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)} \\ &\quad \times\sum_{n=0}^{m_{sr}-1}\sum_{k=0}^{m_{rd}-1}\sum_{l=0}^{k}\left(\begin{array}{c} k\\ l \end{array}\right)\left(\begin{array}{l} {m_{sr}-1}\\ n \end{array}\right)a^{u}\left(a\gamma_{th}+b\right)^{v} \left(\frac{m_{sr}}{\bar{\gamma_{sr}}}\right)^{\frac{w}{2}}\\ &\quad \times\left(\frac{m_{rd}}{\bar{\gamma_{rd}}}\right)^{p}K_{-w}\left(2\sqrt{\frac{m_{sr}m_{rd}\gamma_{th}\left(a\gamma_{th}+b\right)}{\bar{\gamma_{sr}} \bar{\gamma_{rd}}}}\right)\gamma_{th}^{q}\frac{1}{k!} \end{aligned} $$
(20)

where u=k−l, \(v=\frac {n+l+1}{2}\), w=l−n−1, \(p=\frac {2k+n-l+1}{2}\), \(q=\frac {2k+2m_{sr}-n-l-1}{2}\).

Therefore, the outage probability of system can be obtained by substituting (14), (15), and (20) into (13) as

$$ \begin{aligned} P_{\text{out}}^{(af)}\left(\gamma_{th}\right)&=\exp{\left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sr}-1} \left(\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)^{n}\frac{1}{n!}\\ &\times\left[1-\exp{\left(-\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sd}-1} \left(\frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}}\right)^{n}\frac{1}{n!}\right]\\ &\times\left[1-\frac{2\left(m_{rd}-1\right)!m_{sr}^{m_{sr}}}{\bar{\gamma_{sr}}^{m_{sr}}\Gamma(m_{sr}) \Gamma(m_{rd})}\exp{\left(-\frac{am_{rd}\gamma_{th}}{\bar{\gamma_{rd}}}-\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)}\right.\\ &\times\sum_{n=0}^{m_{sr}-1}\sum_{k=0}^{m_{rd}-1}\sum_{l=0}^{k}\left(\begin{array}{l} k\\ l \end{array}\right)\left(\begin{array}{l} {m_{sr}-1}\\ {n} \end{array}\right)a^{u}\left(a\gamma_{th}+b\right)^{v} \left(\frac{m_{sr}}{\bar{\gamma_{sr}}}\right)^{\frac{w}{2}}\\ &\left.\times\left(\frac{m_{rd}}{\bar{\gamma_{rd}}}\right)^{p}K_{-w}\left(2\sqrt{\frac{m_{sr}m_{rd}\gamma_{th}\left(a\gamma_{th}+b\right)} {\bar{\gamma_{sr}}\bar{\gamma_{rd}}}}\right)\gamma_{th}^{q}\frac{1}{k!}\right]\\ &+\left[1-\exp{\left(-\frac{m_{sr}}{\bar{\gamma_{sr}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sr}-1} \left(\frac{m_{sr}\gamma_{th}}{\bar{\gamma_{sr}}}\right)^{n}\frac{1}{n!}\right]\\ &\times\left[1-\exp{\left(-\frac{m_{sd}}{\bar{\gamma_{sd}}}\gamma_{th}\right)}\sum_{n=0}^{m_{sd}-1} \left(\frac{m_{sd}\gamma_{th}}{\bar{\gamma_{sd}}}\right)^{n}\frac{1}{n!}\right] \end{aligned} $$
(21)

4 Numerical and simulation results

This section studies how the outage probability changes as a function of the system parameters in different situations under both AF and DF schemes. Unless otherwise explicitly specified, the main parameters adopted in our experiments and simulations are set as P S =P R =1, σ2=0.01, γ t h =0dB, ρ=0.5, and Eh1=Eh2=Eh3=1.

In Fig. 2, the outage probability curves under DF schemes are presented where Eh1=Eh2=1 and ρ={0.1, 0.3, 0.5, 0.7, 0.9}. Clearly, the outage probability for a lower ρ outperforms the one for a higher ρ at the lower Eh3/Eh1 and outperforms on the contrary with the increase of the value of Eh3/Eh1. This is because a lower ρ means a lower portion of the received signal power split to the ID at R, resulting in a higher received SNR at R, which leads to a higher capacity, but with the increment of Eh3/Eh1, the relay link channel will be worse, so the outage probability will become greater when the ρ increases at the same value of Eh3/Eh1. In Fig. 3, the outage probability curves under AF schemes are presented where Eh1=Eh2=1 and ρ={0.1, 0.3, 0.5, 0.7, 0.9}. We can get that the outage probability for a higher ρ outperforms the one for a lower ρ when ρ is smaller than 0.5 and on the contrary with the increase of the value of ρ. This is because a lower ρ means a lower portion of the received signal power split to the ID at R, resulting in a higher received SNR at R. Yet with the continuous increment of ρ when ρ is greater than 0.5, the outage probability will be larger than the lower ρ system at the same value of Eh3/Eh1; this is because of the transmission information becoming more and more small. In Fig. 4, the outage probability curves for the disposition of R between the S node and the D node. The best outage probability occurs at 0.3, which is the disposition of the relay-aided node R departing from S node. In Fig. 5, the outage probability curves under DF and AF schemes are depicted where the value of Emax={0.1, 0.3, 0.5, 0.7, 0.9} and Eh1=Eh3=1. Obviously, the outage probability for a higher Emax outperforms that for a lower Emax. That is to say, when the relay node harvests the more energy from ambient environment, the better system performance will be obtained.

Fig. 2
figure 2

Outage probability versus Eh1 for ρ with DF

Full size image
Fig. 3
figure 3

Outage probability versus Eh1 for ρ with AF

Full size image
Fig. 4
figure 4

Outage probability versus d with DF and AF

Full size image
Fig. 5
figure 5

Outage probability versus Eh1 for E max with DF and AF

Full size image

In Figs. 6 and 7, the outage probability curves under AF and DF schemes are depicted where Eh1=Eh2 and Eh1={1, 2, 3, 4, 5}. We can get that the outage probability for a lower Eh1 outperforms the one for a higher Eh1. Because a lower Eh1 means a lower probability, the SNR at each receriver falls below the threshold. It can also be observed that outage probability becomes worse when the value of Eh1/Eh3 increases. This is because the increasement of the value of Eh1/Eh3 means the worse of the R-D link, resulting in an increasing outage probability over the R-D link.

Fig. 6
figure 6

Outage probability versus Eh1 for Eh2=Eh3 with DF

Full size image
Fig. 7
figure 7

Outage probability versus Eh1 for Eh2=Eh3 with AF

Full size image

In Figs. 8 and 9, the outage probability curves under DF and AF schemes are depicted where Eh1=Eh3=1 and γ t h ={0, 1, 2, 3, 4}. It is clearly that the outage probability for a lower γ t h ourperforms than that for a higher γ t h . Because a lower γ t h means a lower probability, the SNR at each receiver falls below the threshold. Further, outage probability becomes worse when the value of Eh1/Eh2 increases, because the increasing value of Eh1/Eh2 means the S-D link becoming worse too, resulting in a lower diversity gain at node D.

Fig. 8
figure 8

Outage probability versus γ t h for Eh2=Eh3 with DF

Full size image
Fig. 9
figure 9

Outage probability versus γ t h for Eh2=Eh3 with AF

Full size image

In Fig. 10, the outage probability curves under DF and AF schemes are depicted where Eh2=Eh3=1. It is obviously that the outage probability for a higher m outperforms the one for a lower m. It means that the greater m, the more energy the relay node can receive, so the lower the probability of system interruption.

Fig. 10
figure 10

Outage probability versus m=m s r =m r d =m s d for Eh2=Eh3 with DF and AF

Full size image

5 Conclusions

In this paper, we presented the outage probability of power splitting SWIPT two-way relay networks in Nakagami-m fading. With the help of some approximations, we got the explicit closed-form expression of outage probability of cooperative system over Nakagami-m fading. And the numerical results proposed by the present work were validated by the Monte Carlo method. From the numerical analysis and simulation results, we found that the system parameters have great impact on both AF and DF relay systems.

6 Method

This paper mainly studies a two-way relay SWIPT system over Nakagami-m fading, which consists of a source-destination (S-D) pair and a relay node R embedded power-splitting (PS). In this wireless network system, we consider the protocols of AF and DF and the power splitting energy receiver. In the part of experimental designment, we analyze the outage probability of the traditional energy harvesting technique, the RF energy harvesting technique, and the outage probability of this kind of relay wireless network under different parameters. At last, we verify the outage probability of the explicit closed-form expressions with the Monte Carlo statistical method. From the simulation results, we can observe that the expressions obtained in this paper are correct and effective.