1 Introduction

Orthogonal frequency division multiplexing (OFDM) is a very promising modulation technique to achieve high spectral efficiency. However, the inter-carrier interference (ICI) will be introduced by the non-orthogonality between subcarriers that interfere with each other. A large number of different algorithms have been studied in the last decade for ICI cancellation, e.g., [1–3], which take advantage of the banded channel matrix to remove the ICI from neighbouring subcarriers sequentially. Additionally, some techniques in [4, 5] exploit the sparsity of the banded matrix to design the OFDM block equalizers. Also, several pre-equalized methods have been proposed in [6–10] to reduce the time variations and obtain a quasi-diagonal channel matrix as convectional OFDM systems over the slowly time-varying channels. Some decision feedback equalization techniques are also compatible with OFDM systems [11–16]. According to the previous literature, we can observe that the equalizers with the banded channel matrix can be efficiently performed in sequential or block manners. Additionally, the overall complexity will approximately scale with O(D 2) [2–4]. Note that the algorithm proposed in [9, 17] can reach a very low complexity, which linearly increases with the number of subcarriers. But the performance loss is too significant at high normalized Doppler frequency regime. After the equalization, the power of the desired subcarrier that spreads across the neighbouring subcarrier are aggregated, and the ICI is also mitigated.

In this paper, we proposed a multi-segmental OFDM signal equalization method in rapidly time-varying channels. Unlike the methods in [3, 4, 15, 16, 18], the conventional banded channel matrix is not adopted for equalization. Motivated by [8, 19–21], a new form of multi-segmental OFDM signals equalizer with the PLM is derived for ICI suppression. Unlike the previous literature, we do not assume that the channels remain constant during each sample duration and neither exploit real oversampling benefits as in [19], in which more samples are obtained around each subcarrier. Additionally, we approximate the time variations by the PLM between two segments rather than that between two OFDM blocks in [20]. Although the multi-segmental operations can effectively reduce the time variations, the additional irreducible interference will be introduced with the large segments number M. In other words, the SIR performance will be gradually saturated with the increasing number of segments M. In [21], the authors proposed a similar method to approximate the time variations by the differences between real channel coefficients in each symbol duration and the midpoint channel coefficients in each segment. However, it is very difficult to obtain the accurate channel coefficients in each symbol duration for the rapidly time-varying channels. Furthermore, the authors in [22] approximate the time variations of OFDM systems by a Taylor expansion. In [23], a simple and efficient polynomial surface channel estimation technique is exploited to reduce ICI in a low complexity. The algorithm proposed in [24] decomposes the ICI caused by the time variations into a simple inter-symbol interference and a low ICI. Although these methods can substantially improve the performance of OFDM systems in high Doppler scenarios with lower complexity, the requirement of the relatively large matrix inversion operations and addition memory is still unavoidable. In contract, the proposed algorithm is more flexible in terms of complexity with different segment numbers and can save a large amount of memory compared to the methods that use the matrix inversion.

The contribution of this paper is summarized as (1) a new system model of multi-segmental OFDM signals with PLM is formulated, (2) a MMSE equalizer for the system model is presented, (3) an alternative MMSE method with the iterative rank-1 matrix updates is proposed, (4) efficient computation of the channel coefficients for the equalizers is presented, and (5) the theoretical performance on pre-equalized and equalized SIR is derived.

The paper is organized as follows. Section 2 states the new system model for multi-segmental OFDM signals with PLM. Section 3 presents the proposed equalization methods for multi-segmental OFDM signals and their complexity is also discussed. In Section 4, the SIR performance is analyzed. The simulation results are given in Section 5, and Section 6 draws the conclusions.

2 System model

2.1 Conventional model

We consider a OFDM system with N s subcarriers over rapidly time-varying channels modelled by the the Jakes’ model [25], the normalized Doppler frequency of which is defined as F d T s . Where the quantity F d denotes the maximum Doppler frequency, and the symbol duration is T s . The subcarrier spacing between two consecutive subcarriers is defined as \(\Delta f = \frac {1}{N_{s}T_{s}} = \frac {1}{T}\), so the frequency of the kth subcarrier denotes f k =f c +(k−1)Δ f, and the bandwidth of the OFDM system is B w =N s Δ f The information bit sequence are mapped into the finite constellation points, the vector of which is expressed as \(\mathbf {s} = \left [s_{1},s_{2},\ldots,s_{N_{s}}\right ]^{T}\). For brevity, the notation of the symbol duration T s =1 is omitted in the following otherwise specified. The modulated baseband OFDM signals transmitted is given as:

$$ u(n) = \sqrt{\frac{1}{N_{s}}}\sum^{N_{s}-1}_{k=0}s_{k}e^{j2\pi f_{k}n}, n \in \left[-L, N_{s}-1\right], $$
(1)

where the quantity L denotes the length of multipath channels. The guard interval is assumed to be equal to the maximum delay spread in the sense that the multipath effects is perfectly removed for the conventional OFDM systems.

The receive signals of the passband can be expressed as

$${} \begin{aligned} r(n) = \sqrt{\frac{1}{N_{s}}}\sum^{L-1}_{l=0}\sum_{k=0}^{N_{s}-1}h_{l}(n)s_{k}e^{j2\pi f_{k}(n-l)}+z(n), n \in \left[-L, N_{s}-1\right], \end{aligned} $$
(2)

where the channel impulse response (CIR) for the lth channel path and the nth symbol duration is defined as h l (n). The quantity z(n) is the additive white Gaussian noise (AWGN) with the variance \(\sigma _{z}^{2}\). After the removal of the guard interval, the truncated receive signal in (2) with the fast Fourier transform (FFT) becomes:

$${} \begin{aligned} y_{d} &= \sqrt{\frac{1}{N_{s}}}\sum^{N_{s}-1}_{n=0}r(n)e^{-j2\pi f_{d}n}\\ &=\frac{1}{N_{s}}\sum_{k=0}^{N_{s}-1}s_{k}\sum^{N_{s}-1}_{n=0}\underbrace{\left(\sum^{L-1}_{l=0}h_{l}(n)e^{-j2\pi f_{k}l}\right)}_{H_{k}(n)}e^{-j2\pi f_{d-k}n}+v_{d}, \end{aligned} $$
(3)

where the channel frequency response (CFR) for the kth subcarrier at the nth symbol duration is denoted as H k (n). Motivated by [8], we rewrite (3) in a multi-segmental form as follows:

$${} \begin{aligned} y_{d}(m) =\frac{1}{N_{s}}\sum_{k=0}^{N_{s}-1}s_{k}\sum^{m_{2}}_{n=m_{1}}\underbrace{\left(\sum^{L-1}_{l=0}h_{l}(n)e^{-j2\pi f_{k}l}\right)}_{H_{k}(n)}e^{-j2\pi f_{d-k}n}+v_{d}(m), \end{aligned} $$
(4)

where the quantities m 1 and m 2 denote the start and the end symbol duration at the mth segment, respectively. If the CFR H k (n) in (3) is constant over time, the equation can be reduced to the conventional receive OFDM signal model over the very slowly time-varying channel, i.e., y d =s d H d +v d . Otherwise, the desired subcarrier s d will be interfered by the other subcarriers s k,k≠d due to the time variation of the channels. Thus, we employ the piecewise linear model (PLM) that approximates time variation by the channel slopes in each segment.

2.2 Piecewise linear model

To design a simple equalizer, the Eq. (4) can be approximated by the partial FFT model with the midpoint CIR. However, the additional approximation error will be introduced if the channel time variations is severe. For a more accurate model, the received signals can be given by

$${} \begin{aligned} & y_{d}(m) \approx \frac{1}{N_{s}}\sum_{k=0}^{N_{s}-1}s_{k} \sum^{m_{2}}_{n=m_{1}} \left(\vphantom{\dot{\left(m_{1}+\frac{m_{2}-m_{1}}{2}\right)}\!}H_{k}(n)+\alpha_{k}(n)\right. \\ & \qquad\quad \times \left.\left(n-\left(m_{1}+\frac{m_{2}-m_{1}}{2}\right)\right)\right) e^{j2\pi f_{k-d}n}+v_{d}(m), \end{aligned} $$
(5)

where the quantity α k (n) denotes the slope of the CFR of the kth subcarrier, and the midpoint CFR H k (n)=H k (m) in the mth segment. Defining \(m_{2}=\frac {mN_{s}}{M}\) and \(m_{1}=\frac {(m-1)N_{s}}{M}\), the expanded form of (5) can be equivalently given by

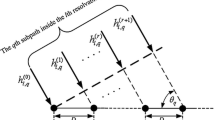
$${} \begin{aligned} y_{d}(m) &\approx \frac{1}{N_{s}}\sum_{k=0}^{N_{s}-1}s_{k} \cdot\left(H_{k}(m)\sum^{\frac{mN_{s}}{M}}_{n=\frac{(m-1)N_{s}}{M}}e^{j2\pi f_{k-d}n} \right.\\ &\quad+\alpha_{k}(m_{0})\sum^{\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}}_{n=\frac{(m-1)N_{s}}{M}} \left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi f_{k-d}n}\\ & \left. \quad+\alpha_{k}(m_{1})\sum^{\frac{mN_{s}}{M}}_{n=\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}} \left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi f_{k-d}n}\right) \\&\quad+v_{d}(m),\\ \end{aligned} $$
(6)

Note that we further split the mth segment into two regions 0 and 1 in the time domain, i.e., \(\left [\frac {(m-1)N_{s}}{M}, \frac {(m-1)N_{s}}{M}+\frac {N_{s}}{2M}\right)\) and \(\left [\frac {(m-1)N_{s}}{M}+\frac {N_{s}}{2M},\frac {mN_{s}}{M}\right ]\), the constant slopes of which are defined as α k (m 0) and α k (m 1), respectively. The diagram of the PLM is shown in Fig. 1, in which the time variations of the channels between the (m−1)th segment and the mth segment are modeled by the slopes as in (5). Additionally, the slopes α k (m i ) for the kth subcarrier are computed by the FFT as

$$ \alpha_{k}(m_{i})=\sum_{l=0}^{L-1} \alpha_{l}(m_{i}) e^{-j2\pi f_{k}l}, i=0,1 $$
(7)
Fig. 1
figure 1

The diagram of the piecewise linear model for the time-varying channels

Full size image

Note that the channel slopes are computed with the perfect CSI. Although the perfect CSI is used, the channel coefficients mismatch between the PLM and the perfect channel coefficients still exists and will be more significant with the increasing normalized Doppler frequency. However, the proposed model will be more accurate than the ones used in [8, 20], which approximate the channels by the midpoint CIR with the slopes between two consecutive OFDM symbols rather than the two segments or only the midpoint CIR in one particular segment.

With the exact derivation in Appendix A, the approximation of multi-segmental signals with the PLM can be given as

$${} \begin{aligned} y_{d}(m) &\approx \sum_{k=0}^{N_{s}-1}s_{k}\cdot\left(H_{k}(m)I_{k-d}(m) +\alpha_{k}(m_{0})\nu_{k-d}(m) \right.\\ &\quad \left.+\alpha_{k}(m_{1})\nu'_{k-d}(m)\right)+v_{d}(m)\\ \end{aligned} $$
(8)

where

$$\begin{array}{@{}rcl@{}} \nu_{i}(m) &=&\frac{-jN_{s}}{8M^{2}} e^{j 2\pi i \frac{4m-3}{4M}}J'_{1}\left(\frac{i\pi}{2M}\right) \end{array} $$
(9)
$$\begin{array}{@{}rcl@{}} \nu'_{i}(m)&=& \frac{-jN_{s}}{8M^{2}}e^{j2 \pi i \frac{4m-1}{4M}}J'_{1}\left(\frac{i\pi}{2M}\right) \end{array} $$
(10)

and i=−(N s −1),…,(N s −1). Note that the autocorrelation of the noise is defined as the same as [8]. The matrix form of the PLM with multi-segmental signals is expressed as

$$ \mathbf{y}_{d} \approx \sum_{k=0}^{N_{s}-1}s_{k}\left(\mathbf{H}_{k}\boldsymbol{\epsilon}_{k-d} +\boldsymbol{\Phi}_{k}(0)\boldsymbol{\nu}_{k-d} +\boldsymbol{\Phi}_{k}(1)\boldsymbol{\nu}'_{k-d}\right)+\mathbf{v}_{d} $$
(11)

where the diagonal matrix of the CFR is defined as \(\mathbf {H}_{k} = \mathcal {D}\left (\left [H_{k}(1),H_{k}(2),\ldots,H_{k}(M)\right ]^{T}\right)\), ε k =[I k (1),I k (2),…,I k (M)]T, \(\boldsymbol {\nu }_{k}=\left [\nu _{k}(1),\nu _{k}(2),\ldots,\nu _{k}(M)\right ]^{T}\!, \boldsymbol {\Phi }_{k}(0)=\mathcal {D}\left ([\alpha _{k}(1_{0}), \alpha _{k}(2_{0}),\ldots,\alpha _{k}(M_{0})]^{T}\right)\) for the first region, and the vector ν k′ the second slope matrix Φ k (1) are defined accordingly.

3 Equalization of multi-segmental OFDM signals with piecewise linear model

Firstly, we will present two equalization methods including the conventional minimum mean square error (MMSE) equalizer and the modified one with iterative rank-1 matrix updates (IRU). Secondly, an appropriate rank value selection will be discussed to further reduced the complexity of the MMSE equalizers.

3.1 Convectional MMSE equalizer

Let us define the coefficients of the MMSE equalizer as w d =[w d (1),w d (2),…,w d (M)]T and assume that the perfect CIRs and the channel slopes of the PLM are known to the receivers. The following optimization problem needs to be solved:

$$ \mathbf{w}^{\star}_{d} = \operatornamewithlimits{argmin}_{\mathbf{w}_{d}} \mathbb{E}\left\lbrace \Vert s_{d}-\mathbf{w}_{d}^{H}\mathbf{y}_{d}\Vert^{2}\right\rbrace $$
(12)

The optimum linear solution to the above problem is expressed as

$$\begin{array}{@{}rcl@{}} \mathbf{R}_{\mathbf{y}_{d}s_{d}} &=&= \mathbb{E}\lbrace \mathbf{y}_{d}s^{\ast}_{d} \rbrace =\mathbf{u}_{d} = \mathbf{H}_{d}\boldsymbol{\epsilon}_{0} +\boldsymbol{\Phi}_{k}(0)\boldsymbol{\nu}_{0} +\boldsymbol{\Phi}_{k}(1)\boldsymbol{\nu}'_{0} \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \mathbf{C} &=& \mathbb{E}\left\lbrace \sum_{k=0}^{N_{s}-1}\mathbf{u}_{k}\mathbf{u}_{k}^{H}\right\rbrace \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} \mathbf{R}_{\mathbf{y}_{d}}&=&\mathbf{C}+ \frac{\sigma_{v}^{2}}{M}\mathbf{I}_{M} \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} \mathbf{w}_{d}^{\star}&=&\mathbf{R}^{-1}_{\mathbf{y}_{d}}\mathbf{R}_{\mathbf{y}_{d}s_{d}} \end{array} $$
(16)

where

$$ \mathbf{H}_{k}\boldsymbol{\epsilon}_{k-d} +\boldsymbol{\Phi}_{k}(0)\boldsymbol{\nu}_{k-d} +\boldsymbol{\Phi}_{k}(1)\boldsymbol{\nu}'_{k-d} $$
(17)

3.2 Modified MMSE equalizer with iterative rank-1 matrix updates

Intuitively, the rank of the matrix \(\mathbf {u}_{k}\mathbf {u}_{k}^{H}\) is one. This is because the all the rows and columns are linear combinations of u k . In order to avoid the matrix inversion introduced in (16), the matrix inversion can be replaced by the iterative matrix updates as follows:

$$ \mathbf{R}_{\mathbf{y}_{d}}^{-1}=\left(\frac{\sigma^{2}}{M}\mathbf{I}_{M}+\mathbf{C}\right)^{-1} $$
(18)

As described above, the matrix C can be decomposed into the summation of multiple rank-1 matrices, and the matrices \(\left (\frac {\sigma ^{2}}{M}\mathbf {I}_{M}+\mathbf {C}\right)\) and C are invertible. Thus, we can obtain

$$ \left(\frac{\sigma^{2}}{M}\mathbf{I}_{M}+\mathbf{C}\right)^{-1} =\mathbf{B}^{-1}_{N_{s}}-g_{N_{s}}\mathbf{B}^{-1}_{N_{s}}\mathbf{u}_{N_{s}} \mathbf{u}_{N_{s}}^{H}\mathbf{B}^{-1}_{N_{s}} $$
(19)

and the matrix B k+1 can be iteratively updated as

$$ \mathbf{B}^{-1}_{k+1} = \mathbf{B}^{-1}_{k}-g_{k}\mathbf{B}^{-1}_{k}\mathbf{u}_{k}\mathbf{u}_{k}^{H} \mathbf{B}^{-1}_{k} $$
(20)

where \(g_{k} = \frac {1}{1+\text {tr}\left (\mathbf {B}^{-1}_{k}\mathbf {u}_{k} \mathbf {u}_{k}^{H}\right)}\), and the symbol tr(·) denotes the trace of the matrix. Additionally, \(\mathbf {B}^{-1}_{0}=\left (\frac {\sigma ^{2}}{M}\mathbf {I}_{M}\right)^{-1}\). It can be observed that the only direct computation of the matrix inversion is \(\mathbf {B}^{-1}_{0}\) for the initialization of (20). However, the complexity of the larger number of iterative updates will be higher than the conventional matrix inversion using Cholesky factorization [26]. Note that the performance modified MMSE equalizer is not comparable to the convectional one, but its performance will be significantly improved with ICI cancellation and the complexity is still very low. More details about the exact complexity can be found in subsection 3.5.

3.3 Efficient computation of u k

Because the FFT can be performed more efficiently with a large number of subcarriers, the vector u k for k=0,1,…,N s −1 required for the matrix inversion can be obtained via the FFT. Defining \(\mathbf {h}_{L}(m)=\left [h_{0}(m),h_{1}(m),\ldots,h_{L-1}(m),0,\ldots,0\right ]^{T} \in \mathbb {C}_{N_{s}\times 1}\), \(\boldsymbol {\phi }_{L}(m_{0})=\left [\alpha _{0}(m_{0}),\alpha _{1}(m_{0}),\ldots,\alpha _{L-1}(m_{0}),0,\ldots,0\right ]^{T} \in \mathbb {C}_{N_{s}\times 1}\) and ϕ L (m 1) accordingly, the matrix form of u k for k=0,1,…,N s −1 can be represented as

$$ \mathbf{U} = \mathbf{F}\mathbf{H}_{L}\odot\boldsymbol{\Upsilon}+\mathbf{F} \boldsymbol{\Phi}_{L}(0)\odot\boldsymbol{\Psi}+\mathbf{F}\boldsymbol{\Phi}_{L}(1) \odot\boldsymbol{\Psi}' $$
(21)

where the matrix F and F H are defined as FFT and inverse FFT (IFFT), respectively. \(\mathbf {U}=\left [\mathbf {u}^{T}_{0},\mathbf {u}^{T}_{1},\ldots,\mathbf {u}^{T}_{N_{s}-1}\right ]^{T}\), H L =[h L (1),h L (2),…,h L (M)], \(\boldsymbol {\Upsilon } =\left [\boldsymbol {\epsilon }^{T}_{0-d},\boldsymbol {\epsilon }^{T}_{1-d},\ldots, \boldsymbol {\epsilon }^{T}_{N_{s}-1-d}\right ]^{T}\), Φ L (0)=[ϕ L (10),ϕ L (20),…,ϕ L (M 0)], \(\boldsymbol {\Psi }=\left [\boldsymbol {\nu }^{T}_{0-d},\boldsymbol {\nu }^{T}_{1-d},\ldots,\boldsymbol {\nu }^{T}_{N_{s}-1-d}\right ]^{T}\). The matrices Φ L (1) and Ψ ′ are similarly defined as Φ L (0) and Ψ. After some linear algebra manipulations, the Eq. (21) can be written as

$${} \mathbf{U} = \mathbf{F}\left(\mathbf{H}_{L}\odot\mathbf{F}^{H}\boldsymbol{\Upsilon}+ \boldsymbol{\Phi}_{L}(0)\odot\mathbf{F}^{H}\boldsymbol{\Psi}+\boldsymbol{\Phi}_{L}(1) \odot\mathbf{F}^{H}\boldsymbol{\Psi}'\right) $$
(22)

The notation ⊙ denotes the element-wise multiplication. Note that the IFFT of Υ, Ψ, and Ψ ′ can be pre-computed before the transmission, and C=U H U.

3.4 Low-rank approximation of the matrix inversion

An appropriate subcarrier selection scheme can reduce the number of matrices summation and the updates. We have shown the interference power of interfering subcarriers (k≠d) and the desired subcarrier in Fig. 2, each of which contributes to the matrices summation in the above equation. The dth subcarrier (k=d) is the desired one. It can be observed that the main power comes from the desired and the corresponding neighbour subcarriers. Furthermore, the subcarriers which experience the deepest fading are located in these indices \(\mathcal {F}_{0} =\{\ldots,d-2M,d-M,d+M,d+2M,\ldots \}\), and the counterparts which have the peak power are located in \(\mathcal {F}_{1} =\{\ldots,d-\frac {5M}{2},d-\frac {3M}{2},d+\frac {3M}{2},d+\frac {5M}{2},\ldots \}\). The power of undesired subcarriers with large M becomes significant, because the more segments M implies the less orthogonality between subcarriers.

Fig. 2
figure 2

The power comparison of the desired subcarrier and other interfering subcarriers with the midpoint model with d=511, N s =1024, and F d T s =0.005

Full size image

Hence, the subcarrier selection scheme can be performed as follows:

  1. 1.

    Select the subcarriers with the peak power P(f k ) and \(k \in \mathcal {F}_{1}\).

  2. 2.

    Extract the main lobes and side lobes according to \(\mathcal {F}_{1}\), so the extracted indices for one particular lobe are \(\mathcal {L}_{0}=\{d-(i+1)M,d-(i+1)M+1,\ldots,d-iM\}\) for k<d and \(\mathcal {L}_{1}=\{d+iM,d+iM+1,\ldots,d+(i+1)M\}\) for k>d.

  3. 3.

    Set the minimum target power \(P^{\ast }_{f}\).

  4. 4.

    Search the subcarrier, the power \(P_{f_{k}}\) of which is larger than the minimum target power \(P^{\ast }_{f}\) in the zig-zag manner within \(\mathcal {L}_{0}\) or \(\mathcal {L}_{1}\). Put the desired subcarrier index in \(\mathcal {R}\).

  5. 5.

    Repeat step (4) for other lobes.

Hence, the autocorrelation matrix C in (14) can be approximately evaluated by

$$ \mathbf{C} = \mathbb{E}\left\lbrace \sum_{k\in \mathcal{R}}\mathbf{u}_{k}\mathbf{u}_{k}^{H}\right\rbrace $$
(23)

In other words, the number of matrices summation and the number of updates required in (14) and (19) are reduced.

3.5 Complexity analysis

In this part, we have discussed the complexity of the algorithms required in each step, which is evaluated by the complex multiplications (CMs).

3.5.1 MMSE equalizer with efficient computation of u k and low-rank approximation

The computational complexity of MMSE equalizer for the dth subcarrier is primarily determined by the computation of autocorrelation matrix \(\phantom {\dot {i}\!}\mathbf {R}_{\mathbf {y}_{d}}\) and its inversion, whose complexity scale with \(O(M^{3})+O(\log N_{s}+3ML)+O\left (\frac {\vert \mathcal {R}\vert }{2}(M^{2}-M)\right)\). For each subcarrier equalization, the matrix inversion using Cholesky factorization requires O(M 3) CMs. The computation of u k needs one FFT and three matrix vector multiplications, whose complexity is upper bounded by O(logN s +3ML) CMs. To obtain the autocorrelation matrix \(\phantom {\dot {i}\!}\mathbf {R}_{\mathbf {y}_{d}}\), the complexity is determined by the size of chosen subcarriers \(\vert \mathcal {R} \vert \) and the autocorrelation matrix \(\mathbf {u}_{k}\mathbf {u}^{H}_{k}\), which is around \(O\left (\frac {\vert \mathcal {R}\vert }{2}\right)\).

3.5.2 Modified MMSE equalizer with iterative rank-1 matrix updates

As discussed in [26], the computational complexity of the modified matrix inversion will be significantly increasing with the number of dimensions, i.e., \(\vert \mathcal {R}\vert \). Hence, the size of \(\mathcal {R}\) is limited to 3. In other words, the autocorrelation matrices \(\mathbf {u}_{k}\mathbf {u}^{H}_{k}, k = d,d-1,d+1\) are used to yield the approximate matrix inversion, whose complexity scales with \(O\left (\vert \mathcal {R}\vert ^{3} M^{2}\right)\). For further complexity reduction, k=d. Its complexity reduces to O(M 2).

3.5.3 Complexity comparison between different equalization algorithms

The overall complexity required by the equalizers for each subcarrier is summarized as follows. Note that the complexity of FFT is not considered (Table 1).

Table 1 Complexity comparison between different equalization algorithms
Full size table

4 Performance analysis in signal to interference ratio

In this section, we will present signal to interference ratio (SIR) analysis for the pre-equalized and equalized cases, which indicate the different behaviours of the different segment numbers on the SIR. The first case is the upper bound, which is based on the pre-equalized SIR at low normalized Doppler frequencies. The other case is for the equalized SIR with different M at a wide range of normalized Doppler frequencies.

4.1 Case I: pre-equalized signal to interference ratio analysis for multi-segmental OFDM signals

In this part, the theoretical pre-equalized SIR is derived for the slowly time-varying channels.

4.1.1 Derivation of the power of subcarriers

Given (8) and (23), the signal to interference ratio (SIR) of the dth subcarrier can be evaluated by

$$ \gamma_{d}(M) = \frac{\mathbb{E}\left\lbrace\mathbf{u}^{H}_{d}\mathbf{u}_{d}\right\rbrace} {\sum_{k=0,k\neq d}^{N_{s}-1}\mathbb{E}\left\lbrace\mathbf{u}^{H}_{k}\mathbf{u}_{k}\right\rbrace} $$
(24)

Hence, the autocorrelation function of u k (m) needs to be obtained for theoretical evaluation and can be expressed as

$$ \begin{aligned} u_{k}(m) &= \sum^{L-1}_{l=0}h_{l}(m)e^{-j2\pi f_{k}l}I_{k-d}(m)\\&\quad+\sum^{L-1}_{l=0}\alpha_{l}(m_{0})e^{-j2\pi f_{k}l}\nu_{k-d}(m)\\&\quad+\sum^{L-1}_{l=0}\alpha_{l}(m_{1})e^{-j2\pi f_{k}l}\nu'_{k-d}(m) \end{aligned} $$
(25)

where

$$\begin{array}{@{}rcl@{}} \alpha_{l}(m_{0}) &=& \frac{h_{l}(m)-h_{l}(m-1)}{N_{s}/M} \end{array} $$
(26)
$$\begin{array}{@{}rcl@{}} \alpha_{l}(m_{1}) &=& \frac{h_{l}(m+1)-h_{l}(m)}{N_{s}/M} \end{array} $$
(27)

For the theoretical analysis of the SIR, the following autocorrelation function is evaluated by

$${} \begin{aligned} \mathbb{E}\left\lbrace u_{k}u^{\ast}_{k} \right\rbrace &= \mathbb{E}\left\lbrace \sum^{L-1}_{l=0}h_{l}h^{\ast}_{l}I_{k-d}I^{\ast}_{k-d} +\sum^{L-1}_{l=0}\alpha_{l}(0)h^{\ast}_{l}\nu_{k-d}I^{\ast}_{k-d}\right. \\&\left.\quad+\sum^{L-1}_{l=0}\alpha_{l}(1)h^{\ast}_{l}\nu'_{k-d}I^{\ast}_{k-d}\right.\\ &\left.\quad+\sum^{L-1}_{l=0}\alpha_{l}(0)\alpha^{\ast}_{l}(0)\nu_{k-d}\nu^{\ast}_{k-d} +\sum^{L-1}_{l=0}h_{l}\alpha^{\ast}_{l}(0)I_{k-d}\nu^{\ast}_{k-d}\right. \\&\left.\quad+\sum^{L-1}_{l=0}\alpha_{l}(1)\alpha^{\ast}_{l}(0)\nu'_{k-d}\nu^{\ast}_{k-d}\right.\\ &\left.\quad+\sum^{L-1}_{l=0}\alpha_{l}(1)\alpha^{\ast}_{l}(1)\nu'_{k-d}\nu^{'\ast}_{k-d} +\sum^{L-1}_{l=0}h_{l}\alpha^{\ast}_{l}(1)I_{k-d}\nu^{'\ast}_{k-d}\right. \\&\left.\quad+\sum^{L-1}_{l=0}\alpha_{l}(0)\alpha^{\ast}_{l}(1)\nu_{k-d}\nu^{'\ast}_{k-d} \right\rbrace \end{aligned} $$
(28)

The notation m is omitted for simplicity, owing to the computation of the power of signals in (24). Using the symmetric properties of the autocorrelation function, we can obtain these as follows:

$$\begin{array}{@{}rcl@{}} {} \mathbb{E}\left\lbrace h_{l}h_{l}^{\ast} \right\rbrace &\,=\,& \mathbb{E}\left\lbrace h_{l}^{\ast}h_{l} \right\rbrace =\sigma^{2}_{l} \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} {} \mathbb{E}\left\lbrace \alpha_{l}(0)h_{l}^{\ast} \right\rbrace &\,=\,& \mathbb{E}\left\lbrace h_{l}\alpha^{\ast}_{l}(0) \right\rbrace= \frac{\sigma_{l}^{2}}{N_{s}/M}\left(1-r_{l}\left(N_{s}/M\right)\right) \end{array} $$
(30)
$$\begin{array}{@{}rcl@{}} {} \mathbb{E}\left\lbrace \alpha_{l}(1)h_{l}^{\ast} \right\rbrace &\,=\,& \mathbb{E} \left\lbrace h_{l}\alpha^{\ast}_{l}(1) \right\rbrace =\frac{\sigma_{l}^{2}}{N_{s}/M}\left(r_{l}\left(N_{s}/M\right)-1\right) \end{array} $$
(31)
$$\begin{array}{@{}rcl@{}} \mathbb{E}\left\lbrace \alpha_{l}(0)\alpha_{l}(0)^{\ast} \right\rbrace &=& \mathbb{E}\left\lbrace \alpha_{l}(1)\alpha^{\ast}_{l}(1) \right\rbrace\\ &=&\frac{\sigma^{2}_{l}}{(N_{s}/M)^{2}}\left(2-2r_{l}\left(N_{s}/M\right)\right) \end{array} $$
(32)
$$\begin{array}{@{}rcl@{}} \mathbb{E}\left\lbrace \alpha_{l}(0)\alpha_{l}(1)^{\ast}\! \right\rbrace &=& \mathbb{E}\left\lbrace \alpha_{l}(1)\alpha^{\ast}_{l}(0) \right\rbrace\\ &=&\!\!\frac{\sigma^{2}_{l}}{(N_{s}/M)^{2}}\!\left(2r_{l}\left(N_{s}/M\right)-r_{l}\left(2N_{s}/M\right)\,-\,1\!\right) \\ \end{array} $$
(33)

where r l (·) denotes the autocorrelation function of the lth channel path. We assume that \(\sum _{l=0}^{L-1}\sigma ^{2}_{l} = 1\) and the probability density function (PDF) and the autocorrelation function of each path is identical. Substituting (29), (30), (31), (32), and (33) into (28), the autocorrelation function can be given as

$$ \begin{aligned} \mathbb{E}\left\lbrace u_{k}u^{\ast}_{k} \right\rbrace &= I_{k-d}I^{\ast}_{k-d} +\frac{\left(1-r_{l}\left(N_{s}/M\right)\right)}{N_{s}/M} \nu_{k-d}I^{\ast}_{k-d} \\&\quad+\frac{\left(r_{l}\left(N_{s}/M\right)-1\right) }{N_{s}/M} \nu'_{k-d}I^{\ast}_{k-d} \\&\quad+\frac{2\left(1-r_{l}\left(N_{s}/M\right)\right)}{(N_{s}/M)^{2}}\nu_{k-d}\nu^{\ast}_{k-d} \\&\quad+\frac{\left(1-r_{l}\left(N_{s}/M\right)\right)}{N_{s}/M}I_{k-d}\nu^{\ast}_{k-d} \\&\quad+\frac{1}{(N_{s}/M)^{2}}\left(2r_{l}\left(N_{s}/M\right)\right. \\&\left.\quad-r_{l}\left(2N_{s}/M\right)-1\right)\nu'_{k-d}\nu^{\ast}_{k-d} \\&\quad+\frac{2\left(1-r_{l}\left(N_{s}/M\right)\right)}{(N_{s}/M)^{2}}\nu'_{k-d}\nu^{'\ast}_{k-d} \\&\quad+\frac{\left(r_{l}\left(N_{s}/M\right)-1\right)}{N_{s}/M}I_{k-d}\nu^{'\ast}_{k-d} \\&\quad+\frac{1}{(N_{s}/M)^{2}}\left(2r_{l}\left(N_{s}/M\right)\right. \\&\left.\quad-r_{l}\left(2N_{s}/M\right)-1\right)\nu_{k-d}\nu^{'\ast}_{k-d} \end{aligned} $$
(34)

Equation (34) can be written in a compact form as

$${} \begin{aligned} \mathbb{E}\left\lbrace u_{k}u^{\ast}_{k} \right\rbrace &\approx \frac{1}{M^{2}}J^{'2}_{0}\left(\frac{i\pi}{M}\right) +\frac{1-r_{l}(N_{s}/M)}{2M^{2}}\left(J^{'2}_{1}\left(\frac{i\pi}{2M}\right)\right)\\ \end{aligned} $$
(35)

where i=k−d. Hence, Eq. (35) yields the power of the desired subcarrier and the interference caused by the other subcarriers with k=d, k≠d, respectively.

For a simple analysis, we firstly assume that the number of subcarriers N s and the number of segments M are very large, and the noise term is omitted. Based on the assumptions above, Eq. (35) can be further simplified as follows:

$$ \begin{aligned} \mathbb{E}\left\lbrace u_{k}u^{\ast}_{k} \right\rbrace &\approx \frac{1}{M^{2}}J^{'2}_{0}\left(\frac{i\pi}{M}\right) =\frac{1}{M^{2}}\frac{\sin^{2}\left(\frac{i\pi}{M}\right)}{\left(\frac{i\pi}{M}\right)^{2}} \end{aligned} $$
(36)

The power of the desired subcarrier k=d is evaluated by

$$ \mathbb{E}\left\lbrace\mathbf{u}^{H}_{d}\mathbf{u}_{d}\right\rbrace \approx \frac{1}{M}J^{'2}_{0}(0) = \frac{1}{M} $$
(37)

The power of the interfering subcarriers k≠d is evaluated by

$${} \begin{aligned} \sum_{k=0,k\neq d}^{N_{s}-1}\mathbb{E}\left\lbrace\mathbf{u}^{H}_{k}\mathbf{u}_{k}\right\rbrace&=M\sum_{k=0}^{N_{s}-1}\mathbb{E}\left\lbrace u_{k}u^{\ast}_{k}\right\rbrace-\mathbb{E}\left\lbrace\mathbf{u}^{H}_{d}\mathbf{u}_{d}\right\rbrace\\&=\sum_{i=-N_{s}/2+1}^{N_{s}/2}\frac{1}{M}\frac{\sin^{2}\left(\frac{i\pi}{M}\right)}{\left(\frac{i\pi}{M}\right)^{2}} -\frac{1}{M}, N_{s} \succ \infty\\ &\succ\int^{\infty}_{-\infty}\frac{1}{M}\frac{\sin^{2}\left(\frac{i\pi}{M}\right)}{\left(\frac{i\pi}{M}\right)^{2}}di-\frac{1}{M}\\ &=1-\frac{1}{M} \end{aligned} $$
(38)

where the integration of the sinc squared function is computed by

$$ \int^{\infty}_{-\infty}\frac{1}{M}\frac{\sin^{2}\left(\frac{i\pi}{M}\right)}{\left(\frac{i\pi}{M}\right)^{2}}di =\frac{M}{\pi}\int^{\infty}_{-\infty}\frac{1}{M}\frac{\sin^{2}\left(\frac{i\pi}{M}\right)}{\left(\frac{i\pi}{M}\right)^{2}}d\frac{i\pi}{M} =1 $$
(39)

Hence, with very large number of subcarriers and segments, the interference is approximately bounded by the number of segments M. This is because the time variations can be omitted by the large M.

4.1.2 The upper bound of the SIR for slowly time-varying channels

According to (37) and (38), the SIR can be evaluated by

$$ \gamma_{d}(M) \approx \frac{1}{M\left(1-\frac{1}{M}\right)}=\frac{1}{M-1} $$
(40)

4.2 Case II: equalized signal to interference ratio analysis for multi-segmental OFDM signals

In the previous subsection, we have discussed the pre-equalized SIR without the equalization. For the equalized SIR, we can use a simple form to compute it. According to (11) [27, 28], the SIR of the equalized signals is upper bounded by

$$ \gamma'_{d}(M)\approx \frac{\mathbb{E}^{2}\left\lbrace \mathbf{w}_{d}^{\star H}(\mathbf{f}_{d}+\mathbf{g}_{d})\right\rbrace}{\sum_{k=0,k\neq d}^{N_{s}-1}\text{var}\left\lbrace\mathbf{w}_{d}^{\star H}(\mathbf{f}_{k} +\mathbf{g}_{k})\right\rbrace+ \frac{\sigma^{2}_{v}}{M}} $$
(41)

Because it is not trivial to evaluate \(\text {var}\left \lbrace \sum _{k=0,k\neq d}^{N_{s}-1}\mathbf {w}_{d}^{\star H} (\mathbf {f}_{k} +\mathbf {g}_{k})\vphantom {\sum _{k=0,k\neq d}^{N_{s}-1}}\right \rbrace \), in which the terms are correlated. Let us define f k =H k ε k−d and g k =Φ k (0)ν k−d +Φ k (1)ν k−d′. It can be seen that the entry of g k =[g k (1),…,g k (M)]T is obtained by \(g_{k}(m) = \frac {1}{N_{s}}\int ^{\frac {mN_{s}}{M}}_{\frac {(m-1)N_{s}}{M}}(H_{k}(n)-H_{k}(m)) e^{j 2\pi i \Delta f n}dn, i=k-d\), and we assume a scaled matched filter \(\mathbf {w}^{\ast H}_{d} = M\mathbf {f}^{H}_{d}\) is employed for simplicity. The power of the desired subcarrier approximately equals 1, because the power of signals is normalized, i.e., \(P_{S}=\mathbb {E}^{2}\left \lbrace \mathbf {w}_{d}^{\star H}(\mathbf {f}_{d}+\mathbf {g}_{d})\right \rbrace \approx 1\). We split the interference term into two parts: \(\text {var}\left \lbrace \mathbf {w}^{\star H}_{d}\mathbf {f}_{k} \right \rbrace +\text {var}\left \lbrace \mathbf {w}^{\star H}_{d}\mathbf {g}_{k} \right \rbrace \). Note that these two terms are uncorrelated, the proof of which is given in Appendix B. Additionally, \(\mathbb {E}\left \lbrace \mathbf {w}_{d}^{\star H}\mathbf {f}_{k}\right \rbrace =\mathbb {E}\left \lbrace \mathbf {w}_{d}^{\star H}\mathbf {g}_{k}\right \rbrace = 0\), the proofs of which are similar to the previous one. Hence, the first term of the interference is given as

$${} \begin{aligned} \text{var}\left\lbrace \mathbf{w}_{d}^{\star H}\mathbf{f}_{k} \right\rbrace&= \text{var}\left\lbrace\sum_{m=1}^{M} w^{\ast}_{d}(m)f_{k}(m) \right\rbrace\\ &=\sum_{m_{1}=1}^{M}\text{var}\left\lbrace w^{\ast}_{d}(m_{1})f_{k}(m_{1}) \right\rbrace \\ &\quad+\sum_{m_{1}\neq m_{2}}\text{cov}\left\lbrace w^{\ast}_{d}(m_{1})f_{k}(m_{1}),w^{\ast}_{d}(m_{2})f_{k}(m_{2}) \right\rbrace \\ \end{aligned} $$
(42)

We have proved that the vectors \(\mathbf {w}^{\star H}_{d}\), f k , and g k are uncorrelated. Hence, we can conjecture the entries in these two vector are independent in the sense that a simpler form of (42) can be obtained as

$$ \begin{aligned} \text{var}\left\lbrace \mathbf{w}_{d}^{\star H}\mathbf{f}_{k} \right\rbrace &=\sum_{m_{1}=1}^{M}\text{var}\left\lbrace w^{\ast}_{d}(m_{1}) \right\rbrace\text{var}\left\lbrace f_{k}(m_{1}) \right\rbrace \\ &\quad +\sum_{m_{1}\neq m_{2}}\text{cov}\left\lbrace w^{\ast}_{d}(m_{1}),w_{d}(m_{2}) \right\rbrace\\ &\qquad \text{cov}\left\lbrace f^{\ast}_{k}(m_{1}),f_{k}(m_{2}) \right\rbrace \end{aligned} $$
(43)

where \(\text {var}\left \lbrace w^{\ast }_{d}(m_{1}) \right \rbrace =1\), \(\text {var}\left \lbrace f_{k}(m_{1}) \right \rbrace =\frac {1}{M^{2}}\text {sinc}^{2}\left (\frac {i\pi }{M}\right)\), \(\text {cov}\left \lbrace w^{\ast }_{d}(m_{1}),w_{d}(m_{2}) \right \rbrace =J_{0}\left (2\pi f_{d}(m_{1}-m_{2})\frac {N_{s}}{M}\right)\), and \(\text {cov} \left \lbrace f^{\ast }_{k}(m_{1}),f_{k}(m_{2}) \right \rbrace =\frac {1}{M^{2}}\text {sinc}^{2}\left (\frac {i\pi }{M}\right)J_{0}\left (2\pi f_{d}(m_{1}-m_{2})\frac {N_{s}}{M}\right)\). If the midpoint CFRs between two different segments are uncorrelated and the segment number M is very small, the final expression of the first term of the interference will be given by

$$ \begin{aligned} \sum_{k=0,k\neq d}^{N_{s}-1}\text{var}\left\lbrace \mathbf{w}_{d}^{\star H}\mathbf{f}_{k} \right\rbrace &= \sum_{k=0,k\neq d}^{N_{s}-1} \left(\frac{1}{M}\text{sinc}^{2}\left(\frac{i\pi }{M}\right)\sum_{m_{1}\neq m_{2}}\left(1+J_{0}\left(2\pi F_{d}\frac{N_{s}}{M}(m_{1}-m_{2})\right)\right)\right)\\ &\geq \sum_{k=0,k\neq d}^{N_{s}-1}\frac{M-1}{M}\text{sinc}^{2}\left(\frac{i\pi }{M}\right)\succ \text{sinc}^{2}(i\pi) ~\text{for}~M \succ 1 \end{aligned} $$
(44)

The above equation is simple and can be numerically computed. The second interference term can be evaluated by

$${} \begin{aligned} \text{var}\left\lbrace \mathbf{w}_{d}^{\star H}\mathbf{g}_{k} \right\rbrace &=\sum_{m_{1}=1}^{M}\text{var}\left\lbrace w^{\ast}_{d}(m_{1}) \right\rbrace\text{var}\left\lbrace g_{k}(m_{1}) \right\rbrace \\ &\quad+\sum_{m_{1}\neq m_{2}}\text{cov}\left\lbrace w^{\ast}_{d}(m_{1}),w_{d}(m_{2}) \right\rbrace \\& \qquad \text{cov}\left\lbrace g^{\ast}_{k}(m_{1}),g_{k}(m_{2}) \right\rbrace \end{aligned} $$
(45)

where \(\text {var}\left \lbrace w^{\ast }_{d}(m_{1}) \right \rbrace =1\) and \(\text {cov}\left \lbrace w^{\ast }_{d}(m_{1}),w_{d}(m_{2}) \right \rbrace = J_{0}\left (2\pi F_{d}\frac {N_{s}}{M}(m_{2}-m_{1})\right)\). But the second interference term caused by the time variations will involve a generalized hypergeometric function, and the variance and covariance of g k (m) is unlikely to be expressed in explicit forms, e.g.,

$${} \begin{aligned} \text{var}\left\lbrace g_{k}(m_{1}) \right\rbrace &= \mathbb{E}\left\lbrace\! \frac{1}{N^{2}_{s}}\int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}} \int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}} (H_{k}(n_{1})-H_{k}(m_{1}))(H_{k}(n_{2})\right. \\&\left.\quad-H_{k}(m_{1}))^{\ast} e^{j2\pi i\left(\frac{(n_{1}-n_{2})}{M}\right)} dn_{1}dn_{2}\vphantom{\int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}}}\right\rbrace \end{aligned} $$
(46)

and

$${} \begin{aligned} \text{cov}\left\lbrace g_{k}(m_{1})g_{k}(m_{2}) \right\rbrace&= \mathbb{E}\left\lbrace \frac{1}{N^{2}_{s}}e^{j2\pi\frac{(m_{1}-m_{2})}{M}}\int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}} \int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}} (H_{k}(n_{1})\right.\\ &\quad\left. -H_{k}(m_{1}))(H_{k}(n_{2})\right.\\&\quad\left.-H_{k}(m_{2}))^{\ast} e^{j2\pi i\left(\frac{(n_{1}-n_{2})}{M}\right)} dn_{1}dn_{2}\vphantom{\int^{\frac{N_{s}}{2M}}_{\frac{-N_{s}}{2M}}}\right\rbrace \end{aligned} $$
(47)

With the uncorrelated assumption made above, Eq. (47) approaches 0. Additionally, the midpoint CFRs H k (m 11) and H k (m 12) within \(\left [0,\frac {N_{s}}{2M}\right ]\) and \(\left [-\frac {N_{s}}{2M},0\right ]\) are used to approximate the above integrals. Defining \(A_{1}=\int ^{\frac {N_{s}}{2M}}_{0}e^{j2\pi i \Delta f n}\), \(A_{2}=\int ^{0}_{-\frac {N_{s}}{2M}}e^{j2\pi i \Delta f n }e^{j2\pi i \Delta f n }\), Eq. (46) is simplified as

$${} \begin{aligned} \text{var}\left\lbrace g_{k}(m_{1}) \right\rbrace &= \left((H_{k}(m_{11})-H_{k}(m_{1}))A_{1}+(H_{k}(m_{12})-H_{k}(m_{1}))A_{2}\right)\\ &\;\;\cdot\left((H_{k}(m_{11})-H_{k}(m_{1}))A_{1}+(H_{k}(m_{12})-H_{k}(m_{1}))A_{2}\right)^{\ast}\\ &\approx \frac{1}{M^{2}}\text{sinc}^{2}\left(\frac{i\pi}{M}\right) \left(1-J^{2}_{0}\left(2\pi F_{d}\frac{N_{s}}{4M}\right)\right) \end{aligned} $$
(48)

The second interference term can be approximated as follows

$$ \sum_{k=0,k\neq d}^{N_{s}-1}\text{var}\left\lbrace \mathbf{w}_{d}^{\star H}\mathbf{g}_{k} \right\rbrace \approx 1-J^{2}_{0}\left(2\pi F_{d}\frac{N_{s}}{4M}\right) $$
(49)

Thus, the equalized SIR can be represented in an explicit form as

$${} \gamma'_{d}(M)\approx\frac{1}{\sum_{k=0,k\neq d}^{N_{s}-1}\text{sinc}^{2}(i\pi)+\left(1-J^{2}_{0}\left(2\pi F_{d}\frac{N_{s}}{4M}\right)\right)+\frac{\sigma^{2}_{v}}{M}} $$
(50)

4.3 Discussion on the pre-equalized and equalized SIR

4.3.1 Case I

From (35), it is found that the power of subcarriers mainly comes from the first term \(J^{'2}_{0}\left (\frac {i\pi }{M}\right)\), which is obtained by the multi-segment operations and decays in the square of the sinc function manner across subcarriers. Additionally, the remaining terms except the first one corresponding to the time variations will become small with the large M, but these terms are not considered in [8]. In other words, the equalizer with a small M will be interfered with by the remaining terms. For a small M, it would be better to employ ICI cancellation schemes for high normalized Doppler frequency scenarios. The simulated and theoretical pre-equalized SIR curves with the increasing M in (24) and (40) have been shown in Fig. 3, the curves of which roughly agree with each other as expected in the low normalized Doppler frequency regime. Hence, the theoretical curve can be considered as an upper bound of the pre-equalized SIR. However, when the segment number M grows, the pre-equalized SIR will drop with increasing M. This is because the power of interfering subcarriers will decay slowly, and the interference term is non-zero across the subcarriers with a large M as shown in Fig. 2. But these terms that are relatively fixed can be effectively mitigated by the equalizer as in Fig. 4.

Fig. 3
figure 3

The pre-equalized SIR of multi-segment OFDM signals with exponential power delay profile and different normalized Doppler frequencies, N s =512, L=3

Full size image
Fig. 4
figure 4

The power comparison of subcarriers between the midpoint model and piecewise linear model with M=16, d=511, N s =1024, and F d T s =0.005

Full size image

4.3.2 Case II

The theoretical equalized SIR performance in (50) is a function of the segment number M and the normalized Doppler frequency F d N s . It is improved with the increasing M and will converge at low normalized Doppler frequency regime. In Fig. 5, the theoretical curves approximately agree with the simulated ones at high SNR values, i.e., 25 dB. Although the second interference term is replaced by the midpoint model to avoid the complicated integration of multiple Bessel functions, the derived curves still seem valid for a wide range of normalized Doppler frequencies, which are of interest. Additionally, the theoretical results in [21] can be considered as an upper bound of the equalized SIR at low normalized Doppler frequencies and a lower bound at high normalized Doppler frequencies.

Fig. 5
figure 5

The simulated equalized SIR and theoretical equalized SIR with M=2,4,8,16,32, N s =512, and SNR =25 dB. The dashed line denotes the simulated results, and the solid line denotes the theoretical results

Full size image

5 Simulation results

In this section, we have presented the simulation results of the proposed equalization method with the piecewise linear model. We assume practical simulation parameters as follows: the carrier frequency f c =1800 MHz, the subcarrier spacing Δ f=976.5 Hz with 512 subcarriers, and the OFDM symbol duration T is about 1 ms. The binary phase shift keying (BPSK) is employed to investigate the bit error rate (BER) performance. The channel coefficients are generated by Jakes’ model, and the exponential power delay profile (0,−4.3429,−8.6859 dB) is employed. Additionally, the channel coefficients between different paths are independent identically distributed (i.i.d) with the same maximum normalized Doppler frequency F d T s . The power of the multipath channels is normalized to unit.

5.1 BER performance against normalized doppler frequencies of MMSE with PLM and conventional partial FFT

In Fig. 6, the BER performance of the proposed method against normalized Doppler frequencies at 30 dB SNR is shown. Its performance is improved with the increasing M compared to the conventional partial FFT. In the low regime, the proposed method performs almost the same as the conventional partial FFT, and the performance gain gradually reduces due to too fast time variations of the channels. Additionally, the proposed method can obtain larger gain with a relatively small M, because the time variations of channels in each segment become more significant. In other words, the proposed method approximates the time variations with the piecewise linear model better than assuming the channels remain constant. Thus, the equalizer can further suppress the interference. However, with the increasing normalized Doppler frequencies, the channels in each segment are varying too fast in the sense that the approximations by the PLM and the midpoint model become invalid, and their performance converge at high normalized Doppler frequencies.

Fig. 6
figure 6

BER performance against normalized Doppler frequencies, N s =512, SNR =30 dB

Full size image

5.2 BER performance against SNR of MMSE with PLM, conventional partial FFT, and banded MMSE equalizer

The BER performance against signal to noise ratio (SNR) is plotted in Fig. 7. The normalized Doppler frequency is set to F d T s =0.005. The main objective of OFDM systems over rapidly time-varying channels is to combat the interference induced by the time variations, which has a very negative impact on the overall performance of the systems. The BER performance of the banded equalizer in [4] and the proposed method is shown. Note that there is an error floor at high SNR regime. This is because some residual interference cannot be removed by the equalizers. Furthermore, the CIR channel matrix of the banded equalizer is truncated to a squared matrix, the size of which must equal to the size of FFT. In this case, some channel coefficients except these of the first several paths will be omitted to keep the same size as that of FFT. It will introduce some additional errors. Technically, this issue can be partially addressed by inserting zeros between two consecutive OFDM symbols at the expense of spectral efficiency.

Fig. 7
figure 7

BER performance against SNR, N s =512, F d T s =0.005

Full size image

5.3 BER performance against normalized Doppler frequencies of MMSE with PLM, conventional partial FFT, and banded MMSE equalizer

In Fig. 8, we also present the BER performance against normalized Doppler frequencies of the banded MMSE equalizer. It has poorer performance at low normalized Doppler frequencies. As discussed above, the truncation of the channel matrix omitted some channel coefficients. At the low regime, the power of the desired subcarrier does not spread across the subcarrier. Thus, the performance is even poorer than that at a little higher normalized Doppler frequencies. When the normalized Doppler frequency is getting larger, its performance degrades accordingly.

Fig. 8
figure 8

BER performance against normalized Doppler frequencies, N s =512, SNR =30 dB

Full size image

5.4 BER performance against normalized Doppler frequencies of MMSE with PLM and modified MMSE equalizer with ICI cancellation

The BER performance of the modified MMSE equalizer with ICI cancellation (\(\vert \mathcal {R}\vert =1,3\)) has almost the same behaviours as in Fig. 9. Hence, we choose \(\vert \mathcal {R}\vert =1\) to demonstrate the performance in Fig. 9. Its performance is almost identical to the conventional partial FFT with different M at high normalized Doppler frequencies. In the low regime, it even has better performance with almost the same complexity as MMSE-based equalizers given above.

Fig. 9
figure 9

BER performance against normalized Doppler frequencies, N s =512, SNR =30 dB

Full size image

6 Conclusions

In this paper, we have investigated the multi-segmental OFDM signal equalizer with PLM, which can improve the BER performance with negligible complexity increases compared to the partial FFT method. We have also proposed the modified version of the equalizer, which can significantly save the computational efforts. Additionally, the theoretical pre-equalized and equalized SIR performance have been given in closed-form mathematical expressions with the aid of the simple numerical evaluation. In the future, the proposed method could be extended to the MIMO applications to suppress the ICI and inter-antenna interference simultaneously.

7 Appendix A: derivation of the piecewise linear model

From (8), the PLM for the multi-segmental signals has been obtained, and the expanded form can be divided into the following three equations:

$$ \begin{aligned} \frac{1}{N_{s}}&\sum^{\frac{mN_{s}}{M}}_{n=\frac{(m-1)N_{s}}{M}}e^{j2\pi f_{k-d}n}\\ =\frac{1}{N_{s}}&\int_{\frac{(m-1)N_{s}}{M}}^{\frac{mN_{s}}{M}}e^{j2\pi i \Delta f n} dn \end{aligned} $$
(51)
$$ \begin{aligned} \frac{\alpha_{k}(m_{0})}{N_{s}}&\sum^{\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}}_{n=\frac{(m-1)N_{s}}{M}} \left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi f_{k-d}n} \\ =\frac{\alpha_{k}(m_{0})}{N_{s}}&\int_{\frac{(m-1)N_{s}}{M}}^{\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}}\left(\!n-\frac{(2m-1)N_{s}}{2M}\!\right)e^{j2\pi i \Delta f n} dn\\ \end{aligned} $$
(52)
$$ \begin{aligned} \frac{\alpha_{k}(m_{1})}{N_{s}}&\sum^{\frac{mN_{s}}{M}}_{n=\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}} \left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi f_{k-d}n}\\ =\frac{\alpha_{k}(m_{0})}{N_{s}}&\int^{\frac{mN_{s}}{M}}_{\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}}\left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi i \Delta f n} dn \end{aligned} $$
(53)

The derivation of the first equation has been given in [8], and the second and third equations have the similar format except the upper and lower limit of the integration. For the simplicity, we only give the exact derivation of the second one and the third one can be obtained accordingly. Hence, the integration of Eq. (52) can be computed as

$$ \begin{aligned} &\frac{\alpha_{k}(m_{0})}{N_{s}}\int^{\frac{mN_{s}}{M}}_{\frac{(m-1)N_{s}}{M}+\frac{N_{s}}{2M}}\left(n-\frac{(2m-1)N_{s}}{2M}\right)e^{j2\pi i \Delta f n}\\& dn=\frac{\alpha_{k}(m_{0})}{N_{s}}e^{j2\pi i \frac{4m-3}{4M}}\int^{\frac{N_{s}}{4M}}_{-\frac{N_{s}}{4M}} n e^{j2\pi i \Delta f n} dn \end{aligned} $$
(54)

The first term of the right hand side of (54) can be rewritten as

$$ \begin{aligned} &\frac{\alpha_{k}(m_{0})}{N_{s}}e^{j2\pi i \frac{4m-3}{4M}}\int^{\frac{N_{s}}{4M}}_{-\frac{N_{s}}{4M}} n e^{j2\pi i \Delta f n}dn =\alpha_{k}(m_{0})e^{j2 i\pi \frac{4m-3}{4M}} \\ &\cdot \frac{-jN_{s}\left(i\pi\cos\left(\frac{i\pi}{2M}\right)-2M\sin\left(\frac{i\pi}{2M}\right)\right)}{4i^{2}\pi^{2}M}\\ \end{aligned} $$
(55)

Defining \(x=\frac {i\pi }{2M}\), the terms in (55) can be simplified as

$${} \begin{aligned} \frac{\left(i\pi\cos\left(\frac{i\pi}{2M}\right)-2M\sin\left(\frac{i\pi}{2M}\right)\right)}{4i^{2}\pi^{2}M} &=\frac{1}{8M^{2}}\left(\!\frac{1}{x}\cos(x)-\frac{1}{x^{2}}\sin(x)\!\right)\\ &=-\frac{1}{8M^{2}}J'_{1}(x), i>0\\ &=\frac{1}{8M^{2}}J'_{1}(x), i<0 \end{aligned} $$
(56)

and

$$ \text{sinc}\left(\frac{i\pi}{2M}\right) =J'_{0}\left(\frac{i\pi}{2M}\right) $$
(57)

where the quantities \(J^{\prime }_{n}(x) = \sqrt {\frac {\pi }{2x}}J_{n+\frac {1}{2}}(x)\) and J n (x) denote the spherical Bessel function of the first kind and Bessel function of the first kind, respectively. For i=0, i.e., x=0, \(J^{\prime }_{0}(x)=1\), \(J^{\prime }_{1}(x)=0\). The second term of the right hand side of (54) can be derived as (51).

7.1 Appendix B: proof of uncorrelated terms between \(\mathbf {w}^{\star H}_{d}\mathbf {f}_{k}\) and \(\mathbf {w}^{\star H}_{d}\mathbf {g}_{k}\)

The expected value \(\mathbb {E}\left \{ \mathbf {w}^{\star H}_{d}\mathbf {f}_{k}\mathbf {w}^{\star H}_{d}\mathbf {g}_{k} \right \}\) in a canonical form is given as

$${} \begin{aligned} \mathbb{E}\left\lbrace \mathbf{w}^{\star H}_{d}\mathbf{f}_{k}\mathbf{w}^{\star H}_{d}\mathbf{g}_{k} \right\rbrace=\sum_{m_{1}=1}^{M}\sum_{m_{2}=1}^{M}\mathbb{E}\left\lbrace \frac{1}{M^{2}} f_{k}(m_{1})H_{d}^{\ast}(m_{1})H_{d}^{\ast}(m_{2})g_{k}(m_{2}) \right\rbrace \end{aligned} $$
(58)

If the moderate segment number is chosen, the above equation can be represented as

$${} \begin{aligned} &\sum_{m_{1}=1}^{M}\sum_{m_{2}=1}^{M}\mathbb{E}\left\lbrace \frac{1}{M^{2}} f_{k}(m_{1})H_{d}^{\ast}(m_{1})H_{d}^{\ast}(m_{2})g_{k}(m_{2}) \right\rbrace\\ &\approx \frac{1}{M^{2}}\sum_{m_{1}=1}^{M}\sum_{m_{2}=1}^{M}\mathbb{E}\left\lbrace f_{k}(m_{1})H^{\ast}_{d}(m_{1}) \right\rbrace\mathbb{E}\left\lbrace H^{\ast}_{d}(m_{2})g_{k}(m_{2})\right\rbrace \end{aligned} $$
(59)

where

$$ \mathbb{E}\lbrace f_{k}(m_{1})H^{\ast}_{d}(m_{1}) \rbrace =\text{sinc}\left(\frac{i\pi}{M}\right)e^{\frac{j2\pi i(2m_{1}-1)}{2M}} $$
(60)

Substituting (60) into (58), the equation becomes

$${} \begin{aligned} &\frac{1}{M^{2}}\sum_{m_{1}=1}^{M}\sum_{m_{2}=1}^{M}\mathbb{E}\left\lbrace f_{k}(m_{1})H^{\ast}_{d}(m_{1}) \right\rbrace\mathbb{E}\left\lbrace H^{\ast}_{d}(m_{2})g_{k}(m_{2}) \right\rbrace\\ &=\text{sinc}\left(\frac{i \pi}{M}\right)\sum_{m_{2}=1}^{M} \mathbb{E}\left\lbrace H^{\ast}_{d}(m_{2})g_{k}(m_{2}) \right\rbrace \sum_{m_{1}=1}^{M}e^{\frac{j2\pi i(2m_{1}-1)}{2M}}=0 \end{aligned} $$
(61)

where

$$ \sum_{m_{1}=1}^{M}e^{\frac{j2\pi i(2m_{1}-1)}{2M}} = 0 $$
(62)