1 Introduction

Massive multiple input multiple output antenna array is crucial for the fifth generation wireless communication [1]. No matter in cognitive radio networks, ad hoc networks, or radar networks [2–5], antenna play an important role to ensure data transmission and high Quality of Services (QoS) under certain communication requirements [6–9]. The design of antenna arrays is well known to be a hard nonlinear programming problem [10]. Recently, many researchers attempt to create efficient and effective optimization algorithms to solve the design of antenna arrays. Stochastic algorithms are popularly used because traditional optimization methods are not suitable due to the unavailable of gradient information [11–13]. Stochastic algorithms also show good performance for such design problems [14, 15].

Stochastic algorithms consist of two classes: evolutionary algorithms (EAs) and swarm intelligence (SI) algorithms. Informally, EAs contain genetic algorithm (GA) [16], evolutionary strategies [17], and differential evolution [18]. These algorithms simulate the evolution of genetic process of livings. They usually contain both mutation and crossover operators. SI algorithms contain particle swarm optimization (PSO) [19], artificial bee colony (ABC) [20], neighborhood search optimization [21], etc. SI algorithms emulate the social behaviors of swarms or particles. They usually do not contain crossover operator. Although EAs and SI are created based on different nature, their positive combinations are able to result effective algorithms [22]. In the past, GA, PSO, and ABC have been used in antenna designs [15, 23, 24]. Recently, covariance matrix adaptation evolutionary strategy [25] and differential evolution [26] are applied to synthesize antenna array patterns.

A large number of iterations is needed for standard PSO algorithm to obtain a satisfactory solution [27]. This is not acceptable for users as antenna simulation often takes a long time. In this paper, standard PSO is modified by adding a crossover operator and a parameter adaptation method. The idea is reasonable as memetic with crossover operator can enlarge and promote algorithm’s search; also parameter control is an effective way to make the algorithm adapt to different design problems and saves the fine-tuning efforts of users. The new algorithm is named as adaptive memetic particle swarm optimization (AMPSO), which is applied to tackle antenna design. Numerical experiment is conducted studying the effect of adding crossover and parameter adaptation. The results are discussed based on different metrics and compared with other algorithms.

In the following, Section 2 introduces the antenna array design considered in this paper. Section 3 gives standard PSO and the proposed AMPSO algorithm. Section 4 presents numerical simulation with discussions. Section 5 concludes the paper.

2 Sparse antenna array and related works

Sparse antenna array design can be classified to two categories. One refers to that array elements can be placed anywhere between the aperture of antenna array. The other is that thinning the distance to grids and positions in grids are equally spaced. In the first case, elements can be arbitrarily placed, hence the positions of elements are continuous variables. In the second case, elements could be placed on grids, hence its search space is discrete and finite. However, when the number of array elements increases up to tens or hundreds, search space of such combinatorial optimization problem exponentially increases, which brings huge trouble for conventional optimization algorithms.

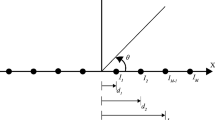
Given a sparse linear antenna array, as shown in Fig. 1, the number of array elements is N (labels above z axis), the space between grids is d, and the number of grid positions along z axis is M (labels below z axis). Hence, the aperture of this linear antenna array is (M−1)d. To keep the same aperture, two array elements have to be placed on the first and the last positions of grids. In this model, the number of variables is N−2 and there are candidate M−2 positions to be placed. Suppose all array elements have no order or priorities, they have the same incentive amplitude and phase distribution. Thus, the total number of combinations of elements is:

$$ C^{(N-2)}_{(M-2)}=\frac{(M-2)!}{(N-2)!(M-N)!}~. $$
(1)
Fig. 1
figure 1

Flow chart of sparse linear antenna array

Full size image

The thinned linear antenna array can be modeled as a minimization problem, whose objective is to minimize peak sidelobe level (PSLL) and maximize main lobe peak level. In this way, interference among elements can be greatly avoided, and the data transmission can be realized in high array gain. The far field pattern is expressed as:

$$ E(\mathbf{u}) = \sum\limits_{i=1}^{M}{\delta_{i} I_{i} e^{j\phi_{i}}e^{jk\mathbf{u}x_{i}}elpat(i)}~, $$
(2)

where δ i denotes whether the ith grid is placed an element (1 for yes and 0 for no); u= cosθ− cosθ 0, I i is the excitation amplitude of element i and ϕ i is the phase position of element i; x i denotes the element position, its distance from the first element is (i−1)d; θ 0 is the direction of main beam, and θ is the sweeping direction of linear antenna array; elpat(i) is the direction pattern of element i. Suppose all elements have the same excitation amplitude and the same phase, then (6) is simplified to:

$$ E(\mathbf{u}) = \sum\limits_{i=1}^{M}{\delta_{i} e^{jk\mathbf{u}x_{i}}}~. $$
(3)

Thus, the optimization model of this type array is:

$$ \begin{array} {ll} \text{min} & f = -\frac{|E(\mathbf{u})|}{|MP|}\\ s.t. & 1 \leq |\mathbf{u}| \leq \frac{\lambda C_{0}}{Nd} \\ & \delta_{i} \in \{0,1\}, i=1,2,\ldots,M\\ \end{array}~, $$
(4)

where MP is mainlobe peak level, C 0 is a correction parameter as the first zero point may shift in nonuniform array. The constraint in (4) is to constrain the value of u so that mainlobe field is removed in computing E(u).

Previously, many researches have reported in literature. Wang et al. considered nonuniform antenna array design for millimeter wave situations [28]. Zhao et al. studied resource allocation problem in MIMO systems such as time allocation [29] and power allocation [30].

3 Optimization algorithms

This section depicts standard PSO and the proposed AMPSO algorithm.

3.1 Standard particle swarm optimization algorithm

The main procedures of standard PSO is expressed in Fig. 2. It can be seen that the main loop of PSO is the updating of velocities and positions of particles. The number of particles is denoted as Np, which also means the size of population. As in initial population step, PSO starts by a set of randomly created particles in given search space. Usually, the evaluation of particles involves the interaction with problem. In this paper, the problem is nonuniform antenna design, which should be preset ahead of executing algorithm. Then, the main generation of standard PSO is executed. Compared with other swarm intelligence approaches, like ABC, dragonfly algorithm and biogeography-based optimization, the procedures of PSO is more concise, though it contains more algorithmic parameters than others.

Fig. 2
figure 2

Flow chart of standard particle swarm optimization algorithm

Full size image

Let D denote problem dimension, updating velocity and position of particle i is realized by the following equation:

$$ \begin{aligned} v_{ij}(t+1) = wv_{ij}(t) + c_{1} r_{1} (p_{ij}-x_{ij}(t)) + c_{2} r_{1} (p_{gj}-x_{ij}(t))~, \end{aligned} $$
(5)
$$ x_{ij}(t+1) = x_{ij}(t) + v_{ij}(t+1)~, $$
(6)

where subscript j∈[1,D] refers to the jth dimension; t refers to the tth generation; r 1 and r 2 are random numbers between 0 and 1. p i and p g are respectively personal best and global best positions that particle i walked through. In this equation, w, c 1, and c 2 are three algorithmic parameters of PSO. Their setting for good performance of algorithm depends on the properties of practical problem. In other words, they are sensitive to problem types.

Recently, many researches have been published about parameter control of PSO. Inertia weight was adapted in a stability-based manner, which could improve the performance of PSO [31]. Khan et al. improved PSO by a random mutation mechanism and a dynamic inertia weight adaptive method, which could facilitate algorithm convergence [32]. Jin et al. improved PSO through enlarging explorative ability of PSO to design a permanent magnet synchronous machine [33].

3.2 Adaptive memetic PSO algorithm

As designated by no free lunch theory [34], the performance of an optimization algorithm could be improved by incorporating prior knowledge or properly hybrid with other search operators or optimization algorithms. This section will present a hybrid algorithm, as mentioned in introduction, the modification contains two parts. The first one is parameter control of PSO algorithm. The second is hybrid with crossover operator.

The main procedures of the proposed algorithm is given in Fig. 3. In this figure, crossover operator step and parameter updating step are highlighted in bold. It is well known that there are many crossover methods reported in literature. Commonly used operators are uniform crossover, binomial crossover, exponential crossover, arithmetic crossover. In this paper, arithmetic crossover is used as its solid theoretic basis. Note that nonuniform antenna problem in this paper is thinned as a binary optimization problem, hence arithmetic crossover is discretized to 0 if the value is less than 0.5; otherwise set to 1.

Fig. 3
figure 3

Flow chart of adaptive memetic particle swarm optimization algorithm

Full size image

The updating of parameters is based on the following thought. In the first stage, algorithm should focus on exploring search space and probe all candidate possible field. In the last stage, algorithm should focus on exploiting the fields with possible global optima found by the algorithm. Clearly, an intermediate stage should exist during the evolutionary process of algorithm, which may cost longer search time than the first and last stages. This is because the locating of global optima is crucial, and locating or trapping in local optimum is not wanted. In this paper, the parameters w, c 1, and c 2 are computed by:

$$ w(t+1) = w^{\text{max}} - (w^{\text{max}} - w^{\text{min}}) \times \frac{1}{1+\exp(6-12t)}~, $$
(7)
$$ c1(t+1) = c1^{\text{max}} - (c1^{\text{max}} - c1^{\text{min}}) \times \frac{1}{1+\exp(12t-6)}~, $$
(8)
$$ c2(t+1) = c2^{\text{max}} - (c2^{\text{max}} - c2^{\text{min}}) \times \frac{1}{1+\exp(12t-6)}~, $$
(9)

where w min and w max are the maximum and minimum value of parameter w; similarly, the minimum and maximum value of c1 and c2 are c1min, c1max and c2min, c2max.

The adaptation of w is shown in Fig. 4; the adaptation of c1 and c2 is given in Fig. 5. w max is 0.9 and w min is 0.4. In literature, a linear decrease of w from w max to w min is used. While the adaptation of w in this paper is alike sigmoid function. As to c1 and c2, both are adapted by the same equation.

Fig. 4
figure 4

Parameter adaptation for w

Full size image
Fig. 5
figure 5

Parameter adaptation for c1 and c2

Full size image

The PSO algorithm combined with crossover operator and parameter adaptation is abbreviated as AMPSO. Compared with standard PSO, the AMPSO algorithm needs more operations to perform two additional steps. For arithmetic crossover, the computing of velocity requires 2D addition and 2D multiplication operations; the computing of position also requires 2D addition and 2D multiplication operations. Thus, in each generation, AMPSO needs 8D computer operations than standard PSO.

4 Numerical experiment

The AMPSO algorithm deals with nonuniform antenna array design problem in this section. The numerical results are also reported and discussed.

4.1 Experimental setting

Electromagnetic phenomena of antenna array systems can be described using Maxwell’s electromagnetic field equations, thus numerical methods of electromagnetic field computation, such as finite element method (FEM), method of moments, Monte Carlo method, and finite volume method, are in a better position for engineers to appreciate and analyze the performance antenna array systems. FEM is used in this paper to simulate antenna array system.

Simulation configuration is described as follows. Nonuniform antenna array design are thinned and then used to study how AMPSO performs in handling binary optimization design problems. The number of elements is 25 (N=25), and the number of grids is 101 (D=M=101). The interval between elements is 0.5λ and the aperture is 50λ.

Standard PSO and the proposed AMPSO are applied to tackle the above design example. In addition, since two methods are used to improve PSO, it is necessary to identify if both could shed positive effect on PSO algorithm. PSO memetic with arithmetic crossover is denoted as MPSO. The configurations of the test algorithms are shown in Table 1. The AMPSO algorithm contains less parameters than PSO. As D is very large, Np is set to 100 based on our empirical experience.

Table 1 Configuration of the PSO, MPSO, and AMPSO algorithms
Full size table

As to termination condition, the maximum number of function evaluations (MFE) is set to 5e4 for all algorithms, i.e., MFE=50,000. Each algorithm is independently run 25 times to gain an average performance. The simulation is implemented in Matlab, and executed on a personal computer with 4-core 3.4 GHz CPU and 4 GB of memory. This could provide a fair comparison environment for the test algorithms.

4.2 Simulation results

The optimal objective function values attained by each algorithm is shown in Table 2. Over 25 independent runs, min denotes the minimum values; similarly, med, max and mean are respectively the median, maximum and mean values; std denotes standard deviation of values. Table 2 contains the five metrics of results found by all algorithms. It is observed from Table 2 that MPSO outperforms PSO in terms of min, med, max, and mean; while the std of results of MPSO is slightly greater than that of PSO. This means that memetic with crossover may cause large variance and increase unstable factor of PSO algorithm; however, the results becomes more stable with parameter adaptive method. Compared with PSO, AMPSO attains better results in all five metrics. Moreover, AMPSO also outperforms MPSO in all five metrics. This means that both crossover operator and parameter adaptation are useful for improve the performance of PSO. Both methods can have positive effect on the algorithm.

Table 2 Optimal f values found by the test algorithms for antenna design
Full size table

The optimal result for thinning nonuniform antenna array by the AMPSO algorithm is shown in Fig. 6. This figure gives the far field pattern plot of Azimuth angle in degree versus PSLL in dB. It can be seen that the difference between mainlobe and sidelobe is more than 11 dB, which shows a high gain and satisfies the requirements of such design. In addition, sidelobe near 80° and 100° are depressed below to 20 dB. This is useful for reducing signal interference between different array elements.

Fig. 6
figure 6

The optimal result for thinning nonuniform antenna array using AMPSO

Full size image

Figure 7 presents the convergence graphs of the best results for the PSO, MPSO, and AMPSO algorithms. It shows the best run of each algorithm over 25 repeated trials. As the curves after 10,000 function evaluations (FEs) are flat, hence, the x axes are shown in log scale. For solving real world design applications, this means that less budget should be set by users. After 1000 FEs, the gap between algorithms becomes larger, which means that the proposed method improves the performance of PSO. Moreover, both the addition of crossover operator and parameter adaptation enhance the algorithm’s performance. Equipped with both methods, the algorithm attains the best solution. Thus, the proposed method explores more than standard PSO and MPSO, and finally locates better solution.

Fig. 7
figure 7

Convergence graphs of the best results for PSO, MPSO, and AMPSO algorithms

Full size image

5 Conclusions

This paper proposes to add crossover operator and parameter adaptation to standard PSO algorithm for tackling the design of nonuniform antenna array. The design of antenna array is thinned to a finite candidate slots. The increase of slot numbers brings enormous difficulties to optimization algorithms. Hence, it is necessary to study more efficient algorithms for such design problems. This paper takes arithmetic crossover and uses rounding method to discretized real values to binary values. Moreover, a novel parameter adaptation method is proposed. Different from traditional linear decrease of parameter values, parameters are adapted alike to sigmoid function. In this way, sensitive parameters are adapted and could be applied to a good many of problem types. Simulated on an example with D=101, the proposed AMPSO algorithm presents good performance in both convergence process and solution quality. Moreover, both the use of crossover and parameter adaptation are shown to be able to positively affect the algorithm.

In antenna array model (4), far field pattern is considered, which is the main metric in evaluating the performance of antenna. The larger the difference between main lobe beam and sidelobe beam, the higher the transmission efficiency is. However, the bandwidth of main lobe beam is not included in this model. Large bandwidth antenna is more reliable in receiving signals in complex terrain and severe weather. This issue will be studied in the future.