Abstract
In-band full duplex has emerged as a solution for high data rate and low access delay for 5G wireless networks after its feasibility has been demonstrated. However, the impact of the in-band full duplex on the system-level performance of multi-cell wireless networks has not been investigated thoroughly. In this paper, we conduct an extensive simulation study to investigate the performance of in-band full duplex for indoor 5G small cell wireless networks. Particularly, we compare the in-band full duplex with static and dynamic time division duplexing schemes which require much less hardware complexity. We examine the effects of beamforming and interference cancellation under various traffic demands and asymmetry situations in the performance comparison. Our objective is to identify under which condition and with which technology support the in-band full duplex becomes advantageous over the simpler duplexing schemes. Numerical results indicate that for highly utilized wireless networks, in-band full duplex should be combined with interference cancellation and beamforming in order to achieve a performance gain over traditional duplexing schemes. Only then in-band full duplex is considered to be advantageous at any number of active mobile stations in the network and any downlink to uplink traffic proportion. Our results also suggest that in order to achieve a performance gain with the in-band full duplex in both links, the transmit power of the access points and the mobile stations should be comparable.
Similar content being viewed by others
1 Introduction
In order to meet the future society’s crave for high data rate and capacity requirements, the next generation of wireless networks, namely 5G, must support one thousand times higher mobile data volume per area and ten to hundred times higher data rate per user than today [1, 2]. Such challenging requirements necessitate the scarce resources to be utilized more efficiently. In-band full duplex (IBFD) is a promising technology that provides an insight into tackling this challenge [3].
It used to be a fundamental belief that radio units cannot transmit and receive concurrently at the same time and frequency resources due to the self-interference (SI) [4], i.e., the duplexing of transmission and reception must be done by either frequency division duplex (FDD) or time division duplex (TDD). Both FDD and TDD have the disadvantage of wasting time and frequency resources [5]. However, recent advances in signal processing have made it possible to reduce the effect of SI, allowing IBFD wireless communications [6, 7]. The authors of [6] demonstrated that it is possible to reduce the SI using analog and digital interference cancellation techniques by more than 78 dB with antenna separations of 20 and 40 cm. In [7], a 110 dB of SI cancellation was achieved in a dense indoor office environment with 80 MHz bandwidth. The analog cancellation circuit in [7] has the dimensions of (10cm × 10cm). Both [6] and [7] suggest that it would be difficult to implement the IBFD in user equipments due to the limited device sizes, whereas it is not a limiting factor for access points (APs).
The IBFD can bring benefits to the wireless systems in various angles. For example, the IBFD can provide a better way to detect collisions in contention-based access protocols [8]. Also, in [9], it is reported that IBFD can improve the secrecy of relay networks significantly. In this study, we focus on the improvement of user data rate in a capacity-demanding indoor environment. In an ideal situation, a wireless system that operates in IBFD only requires half the frequency and time resources required to operate in FDD and TDD or double the data rate with the same amount of resources. In practice, however, IBFD might not lead to the performance improvement because it induces higher interference compared to its half duplex alternatives. It can be particularly the case for a network of high utilization. Thus, system-level performance of full duplex is of profound interest for the design of 5G wireless networks.
Several investigations have been conducted on the performance of IBFD-enabled systems. In [10], the performance of IBFD in a dense small cell network was evaluated and compared against the conventional half duplex transmission. It is argued in [10] that IBFD provides 30–40% mean throughput gain over the half duplex for indoor scenarios. The 100% throughput gain is only noticed when the cells are isolated by extremely high wall loss figures. In [11], it was demonstrated that IBFD cannot double the throughput of half duplex transmission with ALOHA medium access control (MAC) protocol. Even with the perfect SI cancellation, the actual throughput gain ranges from 0–33% for the path loss exponent range [2, 4]. The authors of [11] arrived to the conclusion that there is a strong need for a MAC protocol for IBFD wireless networks that intelligently switches between IBFD and half duplex based on different network configurations. However, both APs and mobile stations (MSs) are assumed to have IBFD capabilities in [10] and [11]. As we discussed earlier, it is far from being a realistic assumption considering the size limitation of the handheld devices. In [12], a hybrid scheduler was proposed that shifts between the IBFD and half duplex based on the best available circumstances. For a scenario where only APs are IBFD capable with 85 dB SI cancellation capability, the throughput was improved by 69% in DL and 81% in UL. But the work in [12] is limited to a single-cell scenario. The authors of [13] studied a multi-cell scenario where only APs are IBFD capable with intelligent scheduler, power allocation, and selection of MSs that maximize the throughput. However, the major focus of [13] lies in the energy efficiency, and the conclusion is that the degradation in energy efficiency due to IBFD operation at the APs can be resolved by operating MSs in IBFD as well.
In this paper, we conduct an extensive simulation study to investigate the performance of in-band full duplex for indoor 5G small cell wireless networks. Our work differs from the previous studies in the following aspects. First, we make a direct performance comparison of IBFD and dynamic TDD (D-TDD). The D-TDD, which is another candidate duplexing scheme for future wireless systems, is known to outperform the traditional static TDD (S-TDD) by adapting to the instantaneous traffic asymmetry between the downlink (DL) and the uplink (UL) [14–16]. Since the D-TDD does not need to handle the SI, the hardware requirement for the D-TDD will be much simpler than that for the IBFD. Therefore, we believe that the implementation of IBFD only makes sense when a considerable performance gain over the D-TDD is expected. Second, we examine the effects of transmitter/receiver techniques, namely beamforming and interference cancellation, on the different duplexing schemes. The major concern of IBFD is the increase in the interference, and thus, it is necessary to investigate the performance of IBFD with and without the advanced interference mitigation techniques. Third, our investigation considers various traffic demands and asymmetry levels as well as different power settings of APs and MSs. We also examine the performances of DL and UL separately because the IBFD is known to enhance the performance of one of the links at the expense of the other, making the total network throughput a non-intuitive performance metric. In summary, our objective is to identify the operating condition of IBFD, i.e., under which parameters and with which technology support the IBFD becomes advantageous over the simpler duplexing schemes. We do not propose a new technique or algorithm in this paper. Rather, we aim at providing insights into the design principles of the 5G wireless systems, particularly on the desirable capabilities in the device level.
We consider an indoor office environment because it is where the data rate requirements can be extremely high [17]. Coordination between APs may be burdensome to the backhaul due to the high data rate demand. Thus, we focus on device-level techniques, i.e., beamforming and interference cancellation, that can be implemented by individual APs and MSs. APs are assumed to use a fixed transmit power. Frequency band of 70 GHz is assumed due to the availability of obtaining a large contiguous spectrum, e.g., 1 GHz bandwidth. Then, a statistical propagation model proposed by [18] is used to model the prorogation loss between the nodes in the system. Most of simulation experiments are conducted with the assumption that the APs are IBFD capable with SI cancellation of 110 dB, while the MSs are half duplex. The effect of SI capability is also examined. In addition, APs can employ beamforming for the transmission and reception depending on the simulation experiments, but MSs are always assumed to be non-beamforming capable. A full buffer traffic model is assumed where the MSs always have data to transmit or receive.
The remainder of this paper is constructed as follows: Section 2 includes an overview of the fundamentals of the duplexing schemes that are considered in this paper; in Section 3, we introduce the system models; in Section 4, we explain the simulation algorithms followed in this paper together with the simulation parameters; the numerical results are presented in Section 5; and in Section 6, we present our conclusions together with the proposed future work.
2 Overview of duplexing schemes
This section provides an overview of duplexing schemes considered in this study, namely S-TDD, D-TDD, and IBFD. We explain our assumptions about how each duplexing scheme operates and highlight the potential interference problems.
2.1 Static time division duplexing
In S-TDD, transmission and reception of data occur at the same frequency band, through allocating distinct time slots for UL and DL. Additionally, the transmission bandwidth of each link is fixed depending on the average traffic load [14, 19].
Consider a simple setup consisting of two APs as in Fig. 1. Each AP is having two MSs within its coverage area; one of the MSs is requesting a DL, while the other MS is requesting an UL. In S-TDD, there will be a DL time slot where only DL MSs are served as in Fig. 1 and an UL time slot where only UL MSs are served as in Fig. 2. This way, S-TDD will always avoid the interference between DL and UL as shown in Figs. 1 and 2.
2.2 Dynamic time division duplexing
In D-TDD, the radio nodes can transmit and receive data on the same frequency band, through allocating distinct time slots for UL and DL just like S-TDD. Conversely, with D-TDD, the DL and the UL bandwidths vary according to the instantaneous traffic load. D-TDD enables efficient and flexible asymmetric services, which improves the spectral efficiency of wireless networks [14, 16]. Nevertheless, D-TDD induces interference between DL and UL as shown in Figs. 3 and 4.
2.3 In-band full duplex
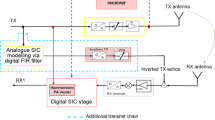
With IBFD, radio nodes transmit and receive on the same frequency and time resources, allowing more MS allocations. Operating in IBFD causes severe interference in the network, composed of inter-cell interference, intra-cell interference, as well as SI as shown in Figs. 5 and 6. If we can reduce the level of interference in IBFD, we could achieve a performance gain over D-TDD and S-TDD.
3 System models
3.1 Environmental model
In this paper, we utilize the indoor office simulation environment shown in Fig. 7 [17]. This simulation environment represents a futuristic scenarios where the nature of office work requires Internet services with high data rates at low latencies. Moreover, this simulation environment has a realistic environmental model geometry, including cubicle offices and tables, adding more credibility to the results obtained in this study [20].
The indoor office simulation environment [17]
Heights and materials of the objects in the simulation environment are given in Table 1.
3.2 Propagation model
In order to satisfy the data rate and latency requirements expected in the future, it is necessary to deploy 5G wireless networks at frequencies in the mmWave bands. The mmWave bands are known to have wide bandwidths; also the very short wavelengths of the mmWave bands allow the implementation of beamforming, with a huge number of antenna elements. In this paper, we will utilize a 70 GHz frequency of operation, at a bandwidth of 1 GHz as suggested in [17]. Furthermore, the propagation models presented in [18] will be exploited to model the propagation channel at the mmWave bands [17].
Accordingly, we will utilize the close-in (CI) free space reference distance path loss model for the case of line-of-sight (LOS) propagation [18]. The CI path loss model is given by
where n los refers to the path loss exponent for LOS transmission, d is the separation distance between the transmitter and the receiver in meters, f c is the frequency of operation in hertz which has to belong to the (0.5–100 GHz) range of frequencies, \(X_{\sigma _{\text {los}}}\) is a zero-mean Gaussian random variable with standard deviation σ los in decibels representing the LOS shadow fading, and P L FS(f c ,1 m) is the free space path loss at 1 m and frequency f c which can be calculated as
with c being the speed of light.
On the other hand, the non-line-of-sight (NLOS) propagation path loss will be modeled with the close-in free space reference distance model with frequency-dependent path loss exponent (CIF) [18]. The CIF path loss model can be expressed as
where n nlos represents the path loss exponent for NLOS propagation, b is an optimization parameter that models the frequency dependency of the path loss exponent, f 0 is a fixed reference frequency, and \(X_{\sigma _{\text {nlos}}}\) is a zero-mean Gaussian random variable with standard deviation σ nlos in decibels representing the NLOS shadow fading [18].
Table 2 summarizes the parameters of the CI and the CIF models, for an indoor office environment as suggested in [18]; the same parameters will be utilized in our simulations.
In our simulations, the propagation between APs is always assumed to be LOS, as the APs are installed at a height of 2.85 m and the cubicles have a height of 1.5 m. On the other hand, the MS to MS and the MS to AP paths can be either LOS or NLOS depending on the locations of the transmitter and the receiver. Furthermore, we assume that the propagation occurs over a Rayleigh fading channel.
3.3 Interference mitigation techniques
3.3.1 Maximal ratio transmit and receive beamforming
When APs have multiple transmit and receive antennas, a multi-stream transmission and reception can be used to combat fading, increase spectral efficiency, and reduce interference. In this paper, we will employ the maximal ratio transmit and receive beamforming technique with 256 antenna elements at the APs side only.
Maximal ratio transmit and receive beamforming utilizes precoding and postcoding to weight information streams, which in return, maximize the desired signal power and keep the interference signals at the same level [21, 22].
3.3.2 Interference cancellation
As some of the received interfering signals may be strong enough to decode, successive interference cancellation allows receivers to decode packets that arrive concurrently. The strongest signal can be decoded and subtracted from the collision, allowing the decoder to recognize weaker interfering signals and decoding them as well. The procedure can be repeated iteratively, as long as the collided signals have different strengths [23, 24].
A simplified successive interference cancellation technique will be implemented in this paper, where we will use the assumption that both APs and MSs can cancel the strongest interferer. Henceforth, we will be referring to this technique as interference cancellation.
3.4 Signal-to-interference-plus-noise ratio model
Given that AP J is serving MS j in DL, MS j will be receiving interference from all APs in DL (A d ) except AP J and all MSs in UL (m u ). Then, the instantaneous signal-to-interference-plus-noise ratio (SINR) of MS j in DL can be formulated as
with \(I_{j}^{d}\) indicating the total interference that MS j is experiencing in DL given by
where P A and P m are the APs’ and the MSs’ transmit powers; \(G_{A_{d},j}\) and \(G_{m_{u},j}\) are the link gains from AP A d and MS m u to MS j; \(\sigma ^{2}_{m}\) being the total noise power at the MSs; \(G_{A_{d},j}\) and \(G_{m_{u},j}\) are the equivalent channel gains from AP A d and MS m u to MS j; and ω value depends on the duplexing scheme according to Table 3.
For maximal ratio transmit beamforming, the equivalent channel gains are given by
with M being the number of antenna elements at the APs, while
Γ(M,1) refers to the gamma distribution with α=M and β=1, and exp(1) refers to the exponential distribution with λ=1. For the case without beamforming, all the equivalent channel gains become exponentially distributed [22, 25].
Let us represent \(I_{j}^{d}\) by a sum of interference terms, i.e.:
where \(i_{n}^{d}\) is an interference term resulting from interferer n∈{1,…,N}, which is either an active DL AP or an active UL MS, and N is the total number of interferers. Then, for the case of interference cancellation, \(I_{j}^{d}\) can be expressed as
In a similar manner, the instantaneous UL SINR at AP J can be calculated as
with \(\sigma ^{2}_{A}\) being the total noise power at the APs and \(I_{j}^{u}\) denoting the total interference at AP J formulated as
while
Without beamforming applied, all the equivalent channel gains become exponentially distributed with λ=1. Here, we can represent \(I_{j}^{u}\) by a sum of interference terms:
where \(i_{n}^{u}\) is an interference term resulting from interferer n∈{1,…,N}. Then, for the case of interference cancellation, \(I_{j}^{u}\) can be expressed as
The value of ρ depends on the duplexing scheme under study according to Table 3, and ζ is the SI cancellation capability factor which ranges from 0 to 1, with 0 indicating perfect SI cancellation.
3.5 Performance metrics
In this paper, we will utilize the following performance metrics:
-
The average mobile station downlink experienced rate, denoted as R d, and referred to as MS DL throughput.
-
The average mobile station uplink experienced rate, denoted as R u, and referred to as MS UL throughput.
-
The average mobile station sum experienced rate, denoted as R, and referred to as MS sum throughput.
These metrics are calculated in the following procedure. Firstly, the instantaneous DL and UL rates of MS j can be calculated according to the modified Shannon capacity formula as in Eq. (16) [26]. The modified Shannon formula takes into account the bandwidth efficiency (η w ), the SINR efficiency (η γ ), and the maximum spectral efficiency (ε max) which is directly related to the modulation and coding scheme utilized by the system and sets a limit to the maximum instantaneous rate that can be achieved by a MS.
In Eq. (16), γ(t) refers to the instantaneous SINR whether it was in DL or UL. γ min is the minimum SINR required for a successful transmission, γ max is the maximum SINR that can be detected, W is the total transmission bandwidth, and S is the overhead scaling [26].
Secondly, we evaluate the average MS experienced rates over T time slots and L MS position realizations. With m being the total number of MSs in the system, m d the subset of MSs scheduled in DL, and m u the subset of MSs scheduled in UL, the average MS experienced DL rate can be formulated as
the average MS experienced UL rate can be calculated as
and the average MS experienced sum rate is expressed as
Henceforth, we will refer to R d, R u, and R as the MS DL throughput, the MS UL throughput, and the MS sum throughput, respectively.
4 System simulations
4.1 Simulation algorithm
We employ the Monte Carlo snapshot-based computer simulations implemented in MATLAB. The general simulation algorithm is briefly described in Algorithm 1.

In every simulation run, we have L MS positioning realizations; for every positioning realization, we have T time slot budget. MSs are distributed randomly, but they can only exist on grids 0.5 m spaced in the x-y plane. The height of the MSs is fixed to 0.75 m. MSs are associated to the closest AP.
A MS demands an UL with probability ψ u and a DL with probability (1−ψ u ). For instance, if we have a total of 20 active MSs, with ψ u =0.1, this means that on average, in every time slot, there will be 2 UL MSs and 18 DL MSs. A full buffer traffic model is assumed, where the MSs always have data to transmit or receive [27]. The instantaneous S-TDD system transmission mode (i_s t a t e) is decided in an alternating manner, such that the system alternates DL and UL in every instance, each AP decides the MS to serve if there is any, and the selection is performed with equal probability among all the MSs with a traffic demand similar to the system’s transmission mode.
For simplicity, we will consider a blind D-TDD scheme where each cell allocates resources in a completely uncoordinated manner whenever there is a need for transmission [14]. The selection in D-TDD is performed such that each AP selects one MS out of all the MSs within its coverage area. The MS is selected with equal probability regardless of its demand.
An IBFD AP selects two MSs within its coverage area to serve. The selected MSs have dissimilar link demand. In each link, the MSs are selected with equal probability among the MSs with a similar link demand. Furthermore, in this paper, we assume an SI cancellation capability of 110 dB at the APs, which is the amount of SI cancellation achieved in [7]. We will not use the same frequency band the researchers in [7] used, but we assume that in the future, such SI cancellation capability, will be possible in the mmWave bands.
4.2 Simulation parameters
Table 4 summarizes the parameters utilized in the numerical simulations. The values of T and L were selected to be 500 each, so we cover enough points inside the simulation environment with all possible selections of MSs. The values of P A and P m were selected to be comparable so that we prevent one of the links to cause massive interference to the other link while the APs operate in D-TDD and IBFD.
5 Numerical results
5.1 Impact of interference mitigation techniques with variable traffic demand
In this section, we will present the numerical results for the MS DL and UL throughput at variable number of active MSs with different combinations of interference mitigation techniques employed.
5.1.1 Downlink
Figure 8 shows the MS DL throughput (R d) at variable number of active MSs (m) for the experiment without interference cancellation or beamforming. We can see that, as the network starts to get lightly utilized, the MS DL throughput attained with D-TDD and IBFD starts to become comparable to that achieved with S-TDD. Interference cancellation will lead D-TDD and IBFD to have higher MS DL throughputs when the network is lightly utilized; nevertheless, D-TDD and IBFD still have similar performance to S-TDD when the network is highly utilized as demonstrated in Fig. 9.
Beamforming adds a substantial DL performance gain to all the duplexing schemes as can be seen in Fig. 10. In this experiment, IBFD is achieving a higher MS DL throughput compared to S-TDD and D-TDD, with the gap in the performance between D-TDD and IBFD increasing with the number of active MSs. In the fourth experiment (i.e., beamforming and interference cancellation being applied), a very little performance gain is noticed with S-TDD and D-TDD compared to the third experiment; IBFD, nevertheless, experienced a substantial performance gain, especially at high number of active MSs as demonstrated in Fig. 11. With 20 MSs in the network, IBFD is amounting to a total of 79% MS DL throughput gain, while D-TDD settles for 13% MS DL throughput gain with the reference being the MS DL throughput achieved with S-TDD in the same experiment and at the same number of active MSs.
Figure 12 shows the MS DL throughput in the third experiment, for 20 active MSs, with variable number of antenna elements. The figure indicates that there is a room for performance enhancement by increasing the number of antenna elements while keeping a practical size of the antenna. Figure 12 also reflects that we need at least eight antenna elements to reach for a positive DL throughput gain for IBFD with respect to S-TDD and D-TDD in the same experiment.
In DL, a special attention needs to be paid to IBFD because it suffers from interference within a cell, i.e., intra-cell interference as illustrated in Fig. 5. Impact of the intra-cell interference is examined in Fig. 13 where the cumulative distribution function (CDF) of DL intra- and inter-cell interference is depicted. The figure shows that the intra-cell interference can be more serious than the inter-cell interference for the worst case users in the absence of IC. Thus, an interference-aware scheduling algorithm would be strongly required for this case. On the other hand, IC effectively reduces the intra-cell interference, making the inter-cell interference the major interference source. It indicates that network-level coordination would be a good supplement of IC.
5.1.2 Uplink
We can notice from Fig. 14 that without beamforming and interference cancellation, the moment the network becomes lightly utilized, IBFD and D-TDD start to have a worse UL performance in comparison to S-TDD. Indeed, this is due to the interference originating from the DL APs as they have a LOS path to the UL APs, besides, the APs’ transmit power is higher than that of MSs. Interference cancellation here adds fairly good amount of UL performance enhancement to D-TDD and IBFD for very low number of active MSs as we can see in Fig. 15, still the performance of IBFD and D-TDD is worse than that of S-TDD at average and high number of active MSs. IBFD, D-TDD, and S-TDD will have comparable performance when the number of active MSs is high as beamforming is activated; this is shown in Fig. 16. With beamforming and interference cancellation, IBFD is superior to both S-TDD and D-TDD at every number of active MSs as we can notice in Fig. 17. IBFD in the fourth experiment at m=20 is obtaining a MS UL throughput gain of 59%, and D-TDD is amounting to a 29% of MS UL throughput gain with respect to the MS UL throughput obtained with S-TDD at the same number of active MSs and experiment.
Figure 18 shows the MS UL throughput with variable number of antenna elements in the third experiment at 20 active MSs. It is clear from the figure that M should be at least 128 for IBFD to start having a similar performance to S-TDD in UL. On the other hand, with 1024 antenna elements, an IBFD MS UL throughput gain of 43% was accomplished, compared to throughput gain of 17% at 256 antenna elements.
If we compare the results obtained in the DL to the results obtained in the UL, we can notice that higher performance gains for IBFD and D-TDD are achieved in the DL; one reason for that is the higher transmitted power of the APs which can cause high interference at the UL APs. Also, the deployment scenario in this study includes no obstacles between the APs, which leads to the fact that an AP to AP path is always LOS, while a MS to AP path can be either LOS or NLOS. Thus, UL is vulnerable to severe AP-to-AP interference. It causes IBFD and D-TDD to have lower performance gains in the UL compared to the DL.
Thus far, we have assumed the self-interference cancellation capability of 110 dB. However, it is obvious that the performance of IBFD in UL depends heavily on the self-interference cancellation capability of the receiver. Figure 19 shows the MS UL throughput with variable self-interference cancellation capabilities with the beamforming-enabled APs for 20 active MSs. From the figure, we can see that IBFD has a performance gain in UL over S-TDD and D-TDD when the self-interference cancellation capability is higher than 80 dB and the capability of 90 dB or higher is required to fully benefit from the IBFD. We will stick to the assumption of 110 dB in the subsequent experiments.
5.2 Impact of interference mitigation techniques with asymmetric traffic demand
Now, we will be looking into the performance of the duplexing schemes with beamforming and interference cancellation under asymmetric traffic demand for 20 active MSs. As shown in Fig. 20, S-TDD will have a poor performance when the traffic demand is highly asymmetric, as then plenty of the time slots will be wasted without any allocations. The amount of unused time slots will decline as the demand becomes more symmetric.
D-TDD behaves excellently under extreme asymmetric traffic demand situations. D-TDD will never waste a time slot as long as there is a MS to serve; thus, when the traffic demand is asymmetric, D-TDD doubles the spectral efficiency of highly utilized S-TDD wireless networks. Conversely, as the demand starts to become symmetric, additional interference will be generated between DL and UL leading to a slight decrease in the achieved MS sum throughput. D-TDD has higher MS sum throughput compared to S-TDD at every DL to UL traffic demand proportion anyway.
IBFD will reduce to a D-TDD system when the traffic is highly asymmetric. The more the demand is symmetric the more MSs are served. Thus, IBFD overcomes S-TDD at every DL to UL traffic proportion. Besides, the gap in the performance between D-TDD and IBFD turns out to be bigger as the demand becomes symmetric.
5.3 Impact of access points’ transmit powers
Now, we will show the significance of choosing comparable APs’ and MSs’ transmit powers. We will only show the results for the experiment with beamforming and interference cancellation applied for 20 active MSs. The MSs’ transmit power is fixed at 25 dBm while we vary the APs’ transmit power from 25 to 50 dBm.
As we can see from Figs. 21 and 22, no change occurs on the performance for S-TDD in either links, regardless of the APs’ transmit power, as S-TDD avoids DL to UL interference. In Fig. 21, we can see that for IBFD and D-TDD, a higher transmit power for the APs is directly translated into higher achievable MS DL throughput. IBFD suffers more than D-TDD in the UL, as depicted in Fig. 22. For IBFD, increasing the APs’ transmit power by 25 dBm will increase the MS DL throughput by 18%, while it will downgrade the UL throughput by 80%.
It is interesting to observe that the aggregated DL and UL throughput decreases as the power of the APs’ goes higher. For the UL, a higher APs’ transmitted power means a higher interference at the UL APs, leading to a worse performance. This effect is particularly severe in our simulation environment where no obstacles exist between the APs. On the DL, however, a higher APs’ transmitted power means a higher DL SINR, which does not contribute much to the rate in high SINR regime. Furthermore, according to the modified Shannon formula we are using in this paper, there is a threshold for the SINR (γ max), after which there is no increase in the achieved rate as described in Section 3.5.
6 Conclusions
In this paper, we investigated the performance of IBFD in comparison to D-TDD for 5G wireless networks. Our objective was to identify when the IBFD becomes advantageous over the D-TDD, particularly under which traffic condition and with which support of interference mitigation techniques. For this, we performed an extensive simulation study in an indoor office environment with high user throughput requirements. We considered beamforming and interference cancellation for the interference mitigation techniques and examined the DL and UL user throughputs of IBFD and D-TDD under various traffic demands and asymmetry conditions.
Numerical result shows that the implementation of IBFD is only beneficial if it is combined with the beamforming. The interference cancellation also provides additional performance gain for the IBFD. With the support of these techniques, IBFD is observed to have a superior performance to the D-TDD regardless of the DL to UL traffic proportion in the network or the number of active MSs. This conclusion is only valid when the transmission power of APs is comparable to that of MSs. Thus, the advanced transmitter/receiver techniques and the careful selection of transmission power are identified as the key factors to make IBFD beneficial.
It is important to mention that we focused on the device-level techniques which do not require any network-level interference coordination. The rationale is to reduce the burden of the backhaul to the indoor small cells. However, such device-level techniques may induce heavy signal processing load and device complexity to the APs and MSs. Furthermore, the device-level techniques do not eliminate the adverse impact of the interference completely. As a complement, network-level techniques ranging from MAC and power control to coordinated multi-point transmission and reception (CoMP) could be employed. Then, an interesting future work lies in striking a balance between the device-level and network-level techniques. Each combination of the techniques will exhibit a certain performance at the cost of device complexity and backhaul requirement. Examining the cost and benefit of the combinations will provide insights into the desired features of the 5G devices and network.
Another direction of the further study is the generalization of this work. This study is limited to an indoor office environment where the user throughput requirements are high and similar transmit power can be allocated to APs and MSs. The performance of IBFD in various environments, such as outdoor urban streets, should be further investigated. Mathematical modeling of the IBFD networks with the beamforming and the interference cancellation also remains as a future work.
References
METIS, deliverable D8.4 METIS final project report (2015). https://www.metis2020.com/wp-content/uploads/deliverables/METIS_D8.4_v1.pdf. Accessed 18 June 2016.
NGMN Alliance, NGMN 5G white paper (2015). https://www.ngmn.org/fileadmin/ngmn/content/downloads/Technical/2015/NGMN_5G_White_Paper_V1_0.pdf. Accessed 29 June 2016.
J Kao, et al., in the 2015 Seventh International Conference on Ubiquitous and Future Networks. Radio resource allocation for D2D-assisted full-duplex cellular networks (IEEESapporo, 2015).
A Goldsmith, Wireless Communications (Cambridge University Press, New York, 2005).
H Haas, Interference analysis of and dynamic channel assignment algorithms in, TD–CDMA/TDD systems. Ph.D. dissertation, Department of Electronics and Electrical Engineering (The University of Edinburgh, Edinburgh, 2000).
M Duarte, et al., in the conference Record of the Forty Fourth Asilomar conference on Signals, Systems and Computers (ASILOMAR). Full-duplex wireless communications using off-the-shelf radios: feasibility and first results (Pacific GroveCalifornia, 2010).
D Bharadia, et al., in the ACM SIGCOMM 2013 conference on SIGCOMM. Full duplex radios (ACMNew York, 2013).
J Choi, et al., in the 16th Annual International Conference on Mobile Computing and Networking (Mobicom 2010). Achieving single channel, full duplex wireless communication (ACMCalifornia, 2010).
G Chen, Y Gong, P Xiao, JA Chambers, Physical layer network security in the full-duplex relay system. IEEE Trans. Informa. Forensics Secur. 10(3), 574–583 (2015).
NH Mahmood, et al., in the Vehicular Technology Conference (VTC Spring), 2015 IEEE 81st. On the potential of full duplex communication in 5G small cell networks (GlasgowScotland, 2015).
Z Tong, M Haenggi, Throughput analysis for full-duplex wireless networks with imperfect self-interference cancellation. IEEE Trans. Commun. 63(11), 4490–4500 (2015).
S Goyal, et al., in the 2014 IEEE International Conference on Communications (ICC). Improving small cell capacity with common-carrier full duplex radios (IEEESydney, 2014).
S Goyal, P Liu, S Panwar, RA DiFazio, R Yang, E Bala, Full duplex cellular systems: will doubling interference prevent doubling capacity?IEEE Commun. Mag. 56(6), 121–127 (2015).
H Celik, et al., in the Vehicular Technology Conference (VTC Spring). On the feasibility of blind dynamic TDD in ultra-dense wireless networks (GlasgowScotland, 2015).
M Dingel, et al., in the 2014 IEEE International Conference on Communications Workshops (ICC). Dynamic TDD transmissions in homogeneous small cell networks (IEEESydney, 2014).
M Dingel, et al., in the 2014 IEEE International Conference on Communications Workshops (ICC). Small cell dynamic TDD transmissions in heterogeneous networks (IEEESydney, 2014).
METIS-II, deliverable D2.1 performance evaluation framework (2016). https://metis-ii.5g-ppp.eu/wp-content/uploads/deliverables/METIS-II_D2.1_v1.0.pdf. Accessed 18 June 2016.
3rd workshop on mobile communications in higher frequency bands (MCHFB), 5G channel model for bands up to 100 GHz (2016). http://www.5gworkshops.com/5GCM.html. Accessed 18 June 2016.
AS Tanenbaum, DJ Wetherall, Computer networks, 5th edn. (Prentice Hall, Pearson Education, Inc. Upper Saddle River, 2011).
METIS-I, deliverable D6.1 simulation guidelines (2013). https://www.metis2020.com/wp-content/uploads/deliverables/METIS_D6.1_v1.pdf. Accessed 18 June 2016.
AM Hunter, JG Andrews, S Weber, Transmission capacity of ad hoc networks with spatial diversity. IEEE Trans. Wireless Commun. 7(12), 5058–5071 (2008).
C Li, J Zhang, KB Letaief, Throughput and energy efficiency analysis of small cell networks with multi-antenna base stations. IEEE Trans. Wireless Commun. 13(5), 1536–1276 (2014).
O Goussevskaia, et al., in the 2012 21st International Conference on Computer Communications and Networks (ICCCN). Scheduling wireless links with successive interference cancellation (IEEEMunich, 2012).
C Psomas, I Krikidis, Successive interference cancellation in bipolar ad hoc networks with swipt. IEEE Wireless Commun. Lett. PP(99), 1 (2016).
D Tse, P Viswanath, Fundamentals of Wireless Communications (Cambridge University Press, New York, 2004).
Ö Bulakci, S Redana, B Raaf, J Hämäläinen, Impact of power control optimization on the system performance of relay based lte-advanced heterogeneous networks. J. Commun. Netw. 13(4), 345–359 (2011).
P Ameigeiras, Y Wang, J Navarro-Ortiz, PE Mogensen, JM Lopez-Soler, in EURASIP Journal on Wireless Communications and Networking. Traffic models impact on OFDMA scheduling design (Springer, 2012), p. 61. doi:10.1186/1687-1499-2012-61.
Acknowledgements
Part of this work has been performed in the framework of the H2020 project METIS-II co-funded by the European Union. The views expressed are those of the authors and do not necessarily represent the project. The consortium is not liable for any use that may be made of any of the information contained therein.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Al-Saadeh, O., Sung, K.W. A performance comparison of in-band full duplex and dynamic TDD for 5G indoor wireless networks. J Wireless Com Network 2017, 50 (2017). https://doi.org/10.1186/s13638-017-0833-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-017-0833-3