Abstract
RFID applications such as monitoring an object for a long time need to identify tags repeatedly within the scope of the reader. Re-identification process can be improved using the information obtained from the previous tag identification process. Couple-resolution blocking (CRB) protocol utilizes the blocking technique that prevents staying tags from being collided by newly arriving tags. Staying tags can be efficiently re-identified by utilizing the retained information. After staying tags are separately all identified, arriving tags are identified. In this paper, we argue that CRB may work more poorly than other protocols which do not consider the repeated tag identification, such as query tree (QT) and collision tree (CT) protocol, when only few tags stay. To tackle the problem, we propose an adaptive CRB (ACRB) protocol. In ACRB, the reader estimates the tag staying ratio during the re-identification process for staying tags. If the estimated ratio is lower than a certain threshold, the blocking technique is immediately abandoned. Instead, staying tags and arriving tags are identified together without considering the retained information. In addition, we propose to improve CRB further using CT protocol, instead of QT protocol. Through computer simulation, we show that ACRB improves the identification efficiency of CRB, especially when the tag staying ratio is low.
Similar content being viewed by others
1 Introduction
A radio frequency identification (RFID) system consists of a reader and multiple tags. The reader broadcasts the query messages and identifies the tags based on the reply messages from the tags. Since the tags typically reply over the shared wireless medium and multiple tags can reply simultaneously to the reader, tag collision may occur at the reader. To resolve this collision problem and to successfully identify all the tags in RFID systems, many tag anti-collision protocols have been proposed. Generally, the anti-collision protocols are categorized into two classes: aloha-based and tree-based protocols. In aloha-based protocols such as dynamic framed-slotted ALOHA (DFSA) [1] and enhanced DFSA (EDFSA) [2], each tag defers for some random time before replying. On the other hand, tree-based protocols continuously split the set of tags into two subsets each time a collision occurs. For the splitting, the binary tree (BT) protocol [3] uses a random number while the query tree (QT) protocol [4] uses tag IDs. Collision tree (CT) protocol [5] enhances QT by using the Manchester code which is used to detect the collided bit [1].
In many RFID applications, the RFID reader may repeatedly identify staying tags, which stay in the reader’s communication range, for object tracking, locating, and monitoring. For that purpose, many protocols have been proposed. The basic idea for all those protocols is to retain the information obtained from the previous tag identification process, called the last frame. Myung et al. [6–8] proposed two protocols, the adaptive query splitting protocol (AQS) and the adaptive binary splitting protocol (ABS). Using the retained information, AQS and ABS can avoid collisions among staying tags. YC Lai et al. [9, 10] proposed a blocking technique which prevents staying tags from being collided by newly arriving tags in this frame. Using the blocking technique, the single resolution blocking ABS (SRB) and the pair resolution blocking ABS (PRB) were proposed based on ABS. The other blocking protocol, the couple-resolution blocking (CRB) [11], were proposed based on AQS which requires less system requirements compared to ABS. Preventing the collision between staying tags and arriving tags, the couple-resolution technique is allowed. Tags are coupled by a query that includes two tags’ ID prefixes. If both tags stay, they simultaneously transmit their IDs and those responses will collide. The reader, however, can recognize two tags from the collision since none of arriving tags is involved in this collision. Recently, the hybrid blocking algorithm (HBA) [12] were proposed to alleviate the overlapping staying tag problem between multiple neighboring readers in dense RFID systems.
In this paper, we notice that CRB may work poorly when most tags have left and only few tags stay. The time for re-identifying the staying tags in CRB depends on the number of tags identified in the last frame, not the actual number of tags in the current frame. Therefore, all queries transmitted for identifying staying tags in the first phase can be a waste when there are no staying tags. Our objective is to improve the performance of CRB when the tag staying ratio is low.
The remainder of the paper is organized as follows. In Section 2, we provide the problem statement and review the CRB protocol. Section 3 provides our motivation for the paper. We propose adaptive CRB (ACRB) protocol in Section 4. In Section 5, the results obtained from the computer simulations are given. Then, we conclude with a discussion of our results.
2 Backgrounds
2.1 Problem statement
In many RFID applications, the reader may repeatedly identify tags in its communication range. In the case, tags can be more efficiently identified using the information obtained from the last frame. Let set S l be the RFID tags identified in the last frame. Let set S c be the RFID tags which should be identified in the current frame. Our problem is to construct set S c with the knowledge of set S l.
We define two important types of tags: staying tags and arriving tags. A tag a s is called the staying tag in the current frame if a s ∈ S C ∩ S L. A tag a a is called the arriving tag in the current frame if a a ∈ S C − S L. Let N represent the number of tags identified in the last frame; N = n(S L) where n(S) means the number of elements of the set S. Let N s and N a represent the number of staying tags and arriving tags, respectively; N s = n(S C ∩ S L) and N a = n(S C − S L). Let tag staying ratio, R s, and tag arriving ratio, R a, be the ratio of the number of staying tags and the ratio of the number of arriving tags, to the number of identified tags in the last frame, respectively; R s = N s /N and R a = N a /N.
Our objective is to minimize the time for constructing set S c, in terms of slot. A slot is the duration that a reader transmits a query to tags, and then the queried tags respond to the reader. For simplicity, we assume that all the slots have the same duration.
2.2 CRB protocol
Our proposed protocol, ACRB, is based on the CRB protocol [11]. Thus, we first briefly introduce CRB protocol in this section. The CRB protocol adopts the blocking technique, which prevents staying tags from being collided by arriving tags. For that purpose, each identification frame is divided into two phases. In the first phase, only staying tags are involved. After staying tags are all identified, arriving tags are identified in the second phase. Note that each tag itself is able to determine whether it is a staying tag or an arriving tag using the reader’s ID and the frame number. Staying tags involve only in the first phase, not in the second phase.
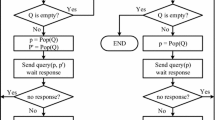
By preventing the collision between staying tags and arriving tags, the couple-resolution technique is allowed in the first phase. In the first phase, CRB checks whether tags identified in the last frame still stay. Figure 1 shows the flow diagram of the CRB protocol. CRB reader has a queue, Q, which is constructed by the QueryConstruction function in the beginning of the first phase. QueryConstruction function finds the readable queries in this frame using all recognized tags’ IDs stored in the last frame. A query in the first phase includes two tags’ ID prefixes. If both of the queried tags simultaneously transmit their IDs and those responses will collide. The key idea of CRB protocol is that the reader, however, can recognize two tags from the collision since none of arriving (unknown) tags is involved in this collision due to the blocking technique.
According to the received response, CRB reader can obtain information as follows:
-
1)
No tag response: both of the queried tags have left.
-
2)
One tag response: one tag stays and the other has left. The responded tag is identified.
-
3)
Collision: both of the queried tags stay. The two queried tags are identified.
After staying tags are all identified, arriving tags are identified in the second phase. In the second phase, CRB operates as QT [4] except that it prepares initial prefixes in advance using QueryInsertion function. The CRB reader estimates the number of arriving tags and then generates a complete binary tree which owns the same number of leaf nodes. The prefixes of the leaf nodes are used to identify arriving tags in the second phase.
Table 1 shows an example of the identifying process using CRB protocol. Suppose four tags whose IDs being 0000, 0010, 1001, and 1100 have been identified in the the ith frame, f i . We are interested in the identification process in the next frame, f i+1. Table 1 shows the identification process in f i+1 where tag 1100 has left and two tags 0101 and 1111 have newly arrived. Hence, S L = {0000, 0010, 1001, 1100} and S C = {0000, 0010, 0101, 1001, 1111}.
In the first phase, the reader checks whether tags in S L stay. At the first slot, the query includes two ID prefixes, 000 and 001, to identify a pair of tags. Since both tags stay, the responses from tags are collided, and then the reader assures that two tags, 0000 and 0001, stay. The second query includes two ID prefixes, 10 and 11. Since tag 1100 has left, the reader receives only a response from tag 1001. Once all tags in S L are checked, the reader transits into the second phase. In the second phase, QT is employed and begins with prepared prefixes. We assume that the number of arriving tags is correctly estimated as 2 and thus the reader prepares two prefixes, 0 and 1, in advance. The arriving tags 0101 and 1111 are identified at the third and fourth slots, respectively. Finally, the reader correctly detects all tags in S C.
3 Motivation
We argue that CRB may work more poorly than QT. CRB checks all tags identified in the last frame whether they still stay in the current frame. The checking process for staying tags is efficient because two tags are identified with just one query. However, note that the length of the checking process for staying tags depends on the number of tags identified in the last frame, not the actual number of tags in the current frame. It means that all queries transmitted for identifying staying tags in the first phase become a waste when there are no staying tags. The number of slots in the first phase is always ⌊(N + 1)/2⌋ because one query contains two tags’ ID prefixes, where N represents the number of tags identified in the last frame. Thus, the number of total slots required to identify all tags in S C with CRB protocol is as follows:
To make the equation simple, Eq. (1) ignores three command slots: the first-phase command, the second-phase command, and the command terminating the frame. They are considered in the Section 5.
On the other hand, QT does not utilize any retained information in the last frame. The performance depends on the actual number of tags in the current frame. Thus, the number of total slots required to identify all tags in S C with QT protocol is as follows:
From Eqs. (1) and (2), it is clear that if the number of staying tags, N s, is very small, then CRB protocol needs more slots than QT protocol. From this intuition, we aim to design an adaptive CRB protocol, which adapts well to the tag staying ratio.
It is well known that T QT(N) ≈ 2.9N − 1 [4]. And when N is sufficiently large, ⌊(N + 1)/2⌋ = N/2. Then, we can obtain the condition that CRB needs more slots than QT,
The condition can be expressed in terms of the tag staying ratio, and we thus have
Figure 2 shows the performance of CRB and QT protocol according to the tag staying ratio. In order to focus on the performance of the first phase, we assume that there are no arriving tags. We can observe that the number of slots required by CRB protocol is not affected by the tag staying ratio. On the other hand, QT requires a linearly proportional number of slots to the tag staying ratio. Note that QT protocol shows better performance than CRB when the tag staying ratio is below than 0.17. It matches well with the analysis result.
In this paper, we propose to transit into the second phase immediately when the tag staying ratio is lower than a certain threshold. The tag staying ratio can be estimated during the re-identification process for staying tags.
4 Adaptive couple-resolution blocking protocol
Here, we propose our new adaptive couple-resolution blocking protocol, ACRB, which is based on the CRB protocol. The ACRB is different from the CRB in two ways. First, a fast transition algorithm is adopted. ACRB transits from the first phase into the second phase immediately when the couple-resolution for the staying tags is not advantageous.
In addition to the fast transition, ACRB uses CT protocol, rather than QT protocol, in the second phase. By adopting CT protocol, the performance of ACRB to identify arriving tags can be improved. Besides, it is noteworthy that the range where the fast transition is advantageous is also widened.
4.1 Fast transition algorithm
We propose to transit into the second phase immediately when the tag staying ratio is significantly low. ACRB reader estimates the tag staying ratio in the first phase. If the estimated ratio is lower than a certain threshold, the blocking technique is immediately abandoned. Instead of re-identifying staying tags separately using the couple-resolution technique, staying tags and arriving tags are identified together without considering the retained information.
The problem is to decide whether the tag staying ratio is sufficiently low and it is more advantageous to transit into the second phase. We assume that staying tags are independently determined by Bernoulli trials. The probability is constant in this frame, and it is same with the tag staying ratio, R s = N s/N. Let X denote the number of staying tags in the sample of size n. X can be viewed as a binomial random variable with parameters (n, R s), that is,
Our objective is to make the correct decision of whether R s > =p 0 (null hypothesis denoted by H 0) or R s < p 0 (alternative hypothesis denoted by H 1). Note that p 0 is a tag staying ratio threshold to determine whether the fast transition is more advantageous, or not; p 0 = 0.17 when QT protocol is used in the second phase, from Eq. (3).
It is clear that we wish to reject H 0 when X is small. We can reject H 0 at the α level of significance when
where k* is the largest value of k for which \( {\displaystyle {\sum}_{i=0}^kP\left(X=i\Big|{R}_{\mathrm{s}}={p}_0\right)}\le \alpha \) [13]. That is,
In testing H 0 versus H 1, there are two types of errors that can be made: H 0 can be falsely accepted (miss detection) or H 0 can be falsely rejected (false alarm). Note that the fast transition is triggered only when H 0 is rejected. Miss detection does not have to be worried because the consequence is to keep operating CRB algorithm. On the other hand, false alarm should be carefully considered. The fast transition may increase the identification time in that case.
In fact, X is a hypergeometric random variable because n sampled tags are randomly chosen “without replacements” out of N tags, of which N s(=NR s) tags are staying tags and the others are leaving tags. Unfortunately, it is difficult to calculate the probability of hypergeometric distribution when Np 0 is not an integer. We use the binomial distribution since it is known that a hypergeometric distribution can be approximated to a binomial distribution if N is large compared to n [13]. Figure 3 compares k* obtained from both distributions. We observe that two curves match well when the sample size is small. The effect of the fast transition gets more significant as the decision is made with a sample of smaller size. Also, note that k* values obtained from binomial distribution are smaller than from hypergeometric distribution. It reduces the probability of false alarm.
4.2 Procedure of fast transition
To implement the fast transition algorithm, we conduct the hypothesis test during the identification process in the first phase. Table 2 represents the operations of the ACRB reader. The identification procedure of ACRB is divided into two phases like CRB. In the first phase, only staying tags are identified (lines 3–26), whereas in the second phase, arriving tags as well as the unidentified staying tags are identified (lines 27–41). The lines different from CRB protocol are marked with comment.
ACRB reader counts the number of staying tags, n s, out of n queried tags. It is clear n is updated when queries are transmitted (lines 9 and 12). n s can be updated according to the tags’ responses (lines 17 and 20). When tag responses are received at the reader, n s is updated as follows:
-
1)
Collision: n s = n s + 2.
-
2)
One tag response: n s = n s + 1.
Next, we should calculate k* according to Eq. (5) (line 22). The time complexity for the calculation is bounded by O(n) since k should be less than or equal to n. The calculation does not need many iterations because small value is used for the significance level, α.
From k* and n s, we can determine whether the fast transition is advantageous or not. If n s ≤ k* (line 23), the fast transition is triggered and as a result the second phase immediately begins.
The QueryConstruction function prepares the prefixes for the first phase using all the recognized tag IDs in the last frame (line 1). The QueryInsertion function generates a complete binary tree which has the amount of leaf nodes being the estimated number of arriving tags (line 28). Since both functions are exactly same with those of the CRB protocol, the details are omitted in this paper.
4.3 ACRB using collision tree protocol and fast transition
In addition to fast transition, we propose to improve CRB protocol further using CT protocol [5, 14] in the second phase, rather than the QT protocol. CT protocol is similar to QT protocol, but CT reader can identify the bit where the collision occurred using Manchester coding. Using this property, CT increases the length of the prefix in the query up to the first collided bit, not just one bit as in QT. The lines different from QT are marked with comment in Table 2 (lines 34 and 35). It is well known that CT reduces the number of total slots about 30% compared to QT; T CT(N) = 2N − 1 (N > 0) and T CT(0) = 1 [5, 14].
It is noteworthy that the range where the fast transition is advantageous increases by using CT. The number of total slots required to identify all tags in S C with CT protocol is as follows:
On the other hand, Eq. (1) should be changed when CT protocol is adopted instead of QT. The number of total slots required to identify all tags in S C with CRB protocol is as follows:
From Eqs. (6) and (7), we can obtain the condition that CRB needs more slots than CT,
Note that the critical value for fast transition, p 0, gets increased from 0.17 to 0.25, using CT instead of QT. If we could find another protocol that improves CT, then the range where the fast transition is advantageous would increase.
4.4 ACRB tag algorithm
The CRB protocol uses the blocking technique, which prevents staying tags from being collided by arriving tags. For that purpose, staying tags are involved only in the first phase and do not respond in the second phase.
However, when the proposed fast transition is triggered, some staying tags may not be identified in the first phase. Thus, unidentified staying tags must be given another chance to be identified. So the tag algorithm of CRB should be a little modified to allow unidentified staying tags to participate in the second phase. Table 3 represents tag’s operation of ACRB. When a query message is received, a tag checks the variable isResponsible, as shown in line 13. In the first phase, only staying tags become responsible. After receiving the second-phase command, arriving tags become responsible.
One line is added for ACRB protocol (line 15). It makes staying tags which did not have a chance to respond in the first phase keep active even in the second phase.
5 Performance evaluation
We evaluate the performance of the proposed ACRB protocol and compare with the original CRB. We focus on the number of total slots required to identify all tags in the (i + 1)th frame, f i+1, assuming that N tags have been identified in the previous frame f i . Our objective is to reduce the number of total slots because it signifies the identification delay in recognizing all of the tags.
The simulation setup is as follows. There are one reader and multiple tags in the simulation area. Each tag has a 96-bit ID, which is uniquely and randomly chosen from a uniform distribution. We run the simulation for each case 1000 times and use their average results. We make the same assumption with [11] that CRB and ACRB can correctly estimate the number of arriving tags, in order to compare two protocols fairly.
5.1 Impact of tag staying ratio
First, we investigate the impact of the tag staying ratio, R s. Figure 4 shows the performance of CRB, CRB with fast transition, and ACRB in terms of the number of total slots in f i+1. CRB with fast transition uses the fast transition in the first phase, and ACRB uses CT instead of QT in the second phase as well as the fast transition. We set N to 500 and vary R s from 0 to 1. The significance level, α, is set to 0.01. We assume that there are no arriving tags to focus on the performance of the first phase.
We observe that the number of total slots with CRB protocol is not affected by the tag staying ratio while CRB with fast transition show better performance when the tag staying ratio is low. ACRB improves the performance of CRB with fast transition further. It is noteworthy that the range where the fast transition is advantageous increases compared with CRB with fast transition. It matches well with the simulation result that the critical value for fast transition, p 0, increases from 0.17 to 0.25, using CT instead of QT.
Note that the simulation results match well with the theoretical approach. Including three command slots, the number of total slots in CRB matches with Eq. (7) where N = 500, N a = 0. When R s = 0.1, we check the simulation results. On the average, the fast transition is triggered after 12 tags are identified during 63.5 slots in the first phase when CRB with fast transition is used. The unidentified 38 tags are identified by QT during 111.5 slots in the second phase. It matches well with the analysis of QT protocol. With ACRB, the fast transition is triggered after 4 tags are identified during 22 slots in the first phase on the average. It is because the critical value for fast transition of ACRB is larger than that of CRB with fast transition. The unidentified 46 tags are identified by CT during 91 slots in the second phase. It matches well with the analysis of CT protocol.
Figure 5 shows the CDF of the number of total slots in all 1000 simulation runs for ACRB when R s is 0.1, 0.2, 0.3, and 0.4. More detail statistics are given in Table 4. When R s is 0.4, it is observed that the fast transition is not activated. It means that ACRB acts as CRB in all 1000 runs. CRB always requires 254 slots; one slot for the first-phase command, 250 slots for queries in the first phase, one slot for the second-phase command, one slot for query in the second phase, and one slot for the command terminating the frame. When R s is 0.1 or 0.2, the fast transition is activated in all 1000 runs and the maximum number of total slots is less than 254 as a result. When R s is 0.3, the maximum number of total slots is 317, larger than 254 though the average value 254.47 is similar, that is, a negative consequence of the false alarm in eight runs. As R s increases, the probability of false alarm gets reduced. However, the negative consequence of false alarm gets greater. When R s is 0.35, the maximum number of total slots is 362, much larger than 254.
5.2 Impact of significance level
The proposed fast transition algorithm has an operational parameter: α. It determines the significance level for the decision of fast transition. Selecting α involves a trade-off between decision time and the probability of the false alarm. Figure 6 shows the impact of α. We can observe that the proposed ACRB transits more quickly and needs less number of total slots with larger α, when the tag staying ratio is less than 0.25.
However, more slots may be required when the tag staying ratio is larger than 0.25 due to the false alarm. The probability of the false alarm is presented in Fig. 7. It is clear that the probability of the false alarm gets higher as the tag staying ratio approaches 0.25 and the significance level, α, increases. In this paper, we set α to 0.01, by default.
5.3 Impact of tag arriving ratio
So far, we have assumed that there are no arriving tags to focus on the first phase. The performance of the second phase highly depends on the number of the arriving tags. We consider the impact of the tag arriving ratio on the performance.
Figure 8 shows the impact of the tag arriving ratio, R a. We consider R a = 0, 0.5, and 1. That is, the number of the arriving tags are 0, 250, and 500, respectively. ACRB shows better performance than the original CRB for all tag arriving ratios.
Note that ACRB requires less slots than the CRB even when the tag staying ratio is greater than 0.25 if the tag arrival ratio is greater than 0. It results from the operation in the second phase. ACRB employs CT instead of QT in the second phase. Therefore, ACRB can identify arriving tags more efficiently than CRB.
5.4 Number of bits sent by a reader
Overhead on the reader is compared with CRB in terms of the number of bits sent by a reader, as in [11]. More number of bits sent by a reader means that more overhead to the reader, and it also causes longer transmission time of signals and longer identification.
Figure 9 shows the number of bits sent by a reader assuming that the lengths of the reader’s ID, the frame numbers, commands are 8 bits. We observe that ACRB shows better performance than the original CRB. It is because the fast transition alleviates the problem that queries for leaving tags are wasted in the first phase.
More detailed data is given in Table 5 to summarize the comparison of CRB with the proposed ACRB. We observe that ACRB does not show worse performance than CRB for any R a and R s. That is, the number of total slots in ACRB is less than CRB. In addition, the number of bits sent by a reader in ACRB is less than CRB. When R s is less than 0.3, ACRB shows better performance than CRB. It is because the fast transition is triggered in the range. Also, the enhancement gets greater as R aincreases. ACRB uses CT instead of QT, and the effect becomes greater as the number of tags to be identified in the second phase increases.
5.5 Impact of the number of tags
The identification performance highly depends on the number of tags. It is trivial that more slots are required as the number of tags increases. We consider N = 100 (Fig. 10) and 1000 (Fig. 11). Both figures show similar patterns, and ACRB improves the original CRB in all cases.
6 Conclusions
Blocking technique which separates staying tags and arriving tags is not helpful when the staying tag ratio is small. We showed that CRB protocol which uses the blocking technique may work more poorly than other protocols such as QT and CT. They do not utilize the retained information from the last frame and do not distinguish staying tags and arriving tags. In this paper, we proposed ACRB protocol which uses fast transition algorithm. The ACRB reader estimates the tag staying ratio while re-identifying staying tags. If the estimated tag staying ratio is lower than a certain threshold, it immediately transits into the second phase. Also, we proposed to use CT instead of QT in the second phase. Through various simulations, we showed that the proposed ACRB protocol improves the performance of CRB protocol, especially when the tag staying ratio is low.
References
K Finkenzeller, RFID handbook: fundamentals and applications in contactless smart cards and identification, (John Wiley & Sons, Chichester, 2003), pp. 206–219
S Lee, S Joo, C Lee, An enhanced dynamic framed slotted ALOHA algorithm for RFID tag identification, in International Conference on Mobile and Ubiquitous Systems: Networking and Services (IEEE, San Diego, 2005), pp. 166–172
D R Hush, C Wood, Analysis of tree algorithms for RFID arbitration, in IEEE International Symposium on Information Theory (IEEE, Cambridge, MA, 1998), pp. 107–107
C Law, K Lee, K Siu, Efficient memoryless protocol for tag identification. In ACM DIAL-M 2000 (ACM, Boston, 2000), pp. 75–84
X Jia, Q Feng, C Ma, An efficient anti-collision protocol for RFID tag identification. IEEE Commun. Lett. 14(11), 1014–1016 (2010)
J Myung, W Lee, TK Shih, An adaptive memoryless protocol for RFID tag collision arbitration. IEEE T. Multimedia 8(5), 1096–1101 (2006)
J Myung, W Lee, J Srivastava, Adaptive binary splitting for efficient RFID tag anti-collision. IEEE Commun. Lett. 10(3), 144–146 (2006)
J Myung, W Lee, J Srivastava, TK Shih, Tag-splitting: adaptive collision arbitration protocols for RFID tag identification. IEEE T. Parall. Distr. Syst. 18(6), 763–775 (2007)
YC Lai, CC Lin, A pair-resolution blocking algorithm on adaptive binary splitting for RFID tag identification. IEEE Commun. Lett. 12(6), 432–434 (2008)
YC Lai, CC Lin, Two blocking algorithms on adaptive binary splitting: single and pair resolutions for RFID tag identification. IEEE/ACM Trans. Network. 17(3), 962–975 (2009)
YC Lai, CC Lin, Two couple-resolution blocking protocols on adaptive query splitting for RFID tag identification. IEEE Trans. Mob. Comput. 11(10), 1450–1463 (2012)
Y Hu, I Chang, J Li, Hybrid blocking algorithm for identification of overlapping staying tags between multiple neighboring readers in RFID systems. IEEE Sens. Journ. 15(7), 4076–4085 (2015)
S Ross, Probability and statistics for engineers and scientists, 4th edn. (Elsevier Academic Press, Burlington, 2009), pp. 158, 325–326
X Jia, Q Feng, L Yu, Stability analysis of an efficient anti-collision protocol for RFID tag identification. IEEE Trans. Commun. 60(8), 2285–2294 (2012)
Acknowledgements
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2011-0023856) and by the National Research Foundation of Korea (NRF) Grant funded by the Korean Government (MSIP) (No. 2016R1A5A1012966).
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Choi, S., Choi, Hi. Adaptive couple-resolution blocking protocol for repeated tag identification in RFID systems. J Wireless Com Network 2016, 279 (2016). https://doi.org/10.1186/s13638-016-0775-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13638-016-0775-1