Energy efficiency and sum rate tradeoffs for massive MIMO systems with underlaid device-to-device communications

Serveh Shalmashi; Emil Björnson; Marios Kountouris; Ki Won Sung; Mérouane Debbah

doi:10.1186/s13638-016-0678-1

EURASIP Journal on Wireless Communications and Networking

December 2016, 2016:175 | Cite as

Energy efficiency and sum rate tradeoffs for massive MIMO systems with underlaid device-to-device communications

Authors
Authors and affiliations

Serveh Shalmashi
Emil Björnson
Marios Kountouris
Ki Won Sung
Mérouane Debbah

Open Access

Research

First Online: 29 July 2016

1.5k Downloads
4 Citations

Abstract

In this paper, we investigate the coexistence of two technologies that have been put forward for the fifth generation (5G) of cellular networks, namely, network-assisted device-to-device (D2D) communications and massive MIMO (multiple-input multiple-output). Potential benefits of both technologies are known individually, but the tradeoffs resulting from their coexistence have not been adequately addressed. To this end, we assume that D2D users reuse the downlink resources of cellular networks in an underlay fashion. In addition, multiple antennas at the BS are used in order to obtain precoding gains and simultaneously support multiple cellular users using multiuser or massive MIMO technique. Two metrics are considered, namely the average sum rate (ASR) and energy efficiency (EE). We derive tractable and directly computable expressions and study the tradeoffs between the ASR and EE as functions of the number of BS antennas, the number of cellular users and the density of D2D users within a given coverage area. Our results show that both the ASR and EE behave differently in scenarios with low and high density of D2D users, and that coexistence of underlay D2D communications and massive MIMO is mainly beneficial in low densities of D2D users.

Keywords

D2D communications Massive MIMO Coexistence Energy efficiency Stochastic geometry

1 Introduction

The research on future mobile broadband networks, referred to as the fifth generation (5G), has started in the past few years. In particular, stringent key performance indicators (KPIs) and tight requirements have been introduced in order to handle higher mobile data volumes, reduce latency, increase the number of connected devices and at the same time increase the energy efficiency (EE) [1, 2]. The current network and infrastructure cannot cope with 5G requirements—fundamental changes are needed to handle future heterogeneous deployments as well as new trends in user behavior such as high quality video streaming and future applications such as e-Health and virtual reality. 5G technology is supposed to evolve existing networks and at the same time integrate new dedicated solutions to meet the KPIs [2]. The new key concepts for 5G include massive MIMO (multiple-input multiple-output), ultra dense networks (UDN), device-to-device (D2D) communications, and huge number of connected devices, known as machine-type communications (MTC). The potential gains and properties of these different solutions have been studied individually, but the realistic gains when they coexist and share network resources are not very clear so far. In this paper, we study the coexistence of two of these key concepts, namely massive MIMO and D2D communication.

Massive MIMO is a type of multiuser MIMO (MU-MIMO) technology where the base station (BS) uses an array with hundreds of active antennas to serve tens of users on the same time/frequency resources by coherent transmission processing [3, 4]. Massive MIMO techniques are particularly known to be very spectral-efficient, in the sense of delivering high sum rates for a given amount of spectrum [5]. This comes at the price of deploying more transceiver hardware, but the solution is still likely to improve the energy efficiency of networks [6, 7]. On the other hand, in a D2D communication, user devices can communicate directly with each other and the user plane data is not sent through the BS [8]. D2D communication is considered for close proximity applications which have the potential to achieve high data rates with little amount of transmission energy, if interference is well-managed. In addition, D2D communications can be used to decrease the load of the core network. D2D users either have their own dedicated time/frequency resources (overlay approach), which in turn leads to elimination of the cross-tier interference between the two types of users (i.e., cellular and D2D users), or they transmit simultaneously with cellular users in the same resource (underlay approach). In the 3rd Generation Partnership Project (3GPP) standardization’s document [9], the underlay case for D2D communications is recommended in the uplink direction, while at the same time, downlink reuse in the time devision duplexing (TDD) scenario is considered for future study. Even though the majority of studies in this area have focused on the uplink, authors in [10] and [11] show the importance of downlink reuse in single-antenna settings. In [10], machine-type communication is enabled via D2D communication where fixed rate zero-outage downlink transmission is achieved, and the work in [11] shows that lower outage probability can be achieved in the downlink compared to the uplink over consecutive time slots in a multi-cell environment.

We consider two network performance metrics in this work: The average sum rate (ASR) in bit/s and the EE which is defined as the number of bits transmitted per Joule of energy consumed by the transmitted signals and the transceiver hardware. It is well-known that these metrics depend on the network infrastructure, radio interface, and underlying system assumptions [7, 12, 13]. The motivation behind our work is to study how the additional degrees of freedom resulting from the high number of antennas in the BS can affect the ASR and EE of a multi-tier network where a D2D tier is bypassing the BS, and how a system with massive MIMO is affected by adding a D2D tier. We focus on the downlink since greater part of the payload data and network energy consumption are ascociated to the downlink [12]. We assume that each D2D pair is transmitting simultaneously with the BS in an underlay fashion. In addition, we assume that the communication mode of each user (i.e., D2D or cellular mode) has already been decided by higher layers. We compare the energy efficiency (EE) and average sum rate (ASR) gains that massive MIMO [6] has been claimed to provide with similar EE and ASR gains that D2D communications can provide.

1.1 Related work

The relation between the number of BS antennas, ASR and EE in cellular networks has been studied in [6, 7, 14, 15] among others. The tradeoff between ASR and EE was described in [6] for massive MIMO systems with negligible circuit power consumption. This work was continued in [14] where radiated power and circuit power were considered. In [7], joint downlink and uplink design of a cellular network was studied in order to maximize EE for a given coverage area. The maximal EE was achieved by having a hundred BS antennas and serving tens of users in parallel, which matches well with the massive MIMO concept. Furthermore, the study [15] considered a downlink scenario in which a cellular network has been overlaid by small cells. It was shown that by increasing the number of BS antennas, the array gain allows for decreasing the radiated signal energy while maintaining the same ASR. However, the energy consumed by the transceiver chains increases. Maximizing the EE is thus a complicated problem where several counteracting factors need to be balanced. This stands in contrast to the maximization of the ASR, which is relatively straightforward since the sum capacity is the fundamental upper bound for the ASR.

There are a few works in the D2D communication literature where the base stations have multiple antennas [16, 17, 18, 19, 20]. In [16], uplink MU-MIMO with one D2D pair was considered. Cellular user equipments (CUEs) were scheduled if they were not in the interference-limited zone of the D2D user. The study [17] compared different multi-antenna transmission schemes. In [18, 19], two power control schemes were proposed for a multi-cell MIMO network. In [20], the ergodic capacity for a scenario with only one CUE and one D2D user is derived and cases of high and low SNR as well as high number of antennas in the downlink have been studied.

The more relevant works to our setup are [21, 22]. The former investigates the mode selection problem in the uplink of a network with potentially many antennas at the BS. The impact of the number of antennas on the quality-of-service (QoS) and transmit power was studied when users need to decide their mode of operation (i.e., D2D or cellular). The study [22] only employs extra antennas in the network to protect the CUEs from interference of D2D users in the uplink.

There are other related works in the context of massive MIMO and D2D communications which study different angles, such as [23] which uses D2D to enable local CSI exchanges in a frequency devision duplexing (FDD) massive MIMO system and [24] which exploits D2D communications to create virtual MIMO in order to avoid huge feedback overhead for CSI acquisition in downlink of a massive MIMO FDD system. Another study [25] considers the problem of BS precoder design and power allocation in multicasting massive MIMO with underlaid D2D communications. The ASR in D2D communications is mostly studied in the context of interference and radio resource management [26, 27]. There are a few works that consider EE in D2D communications, but only for single-antenna BSs, e.g., [28, 29], and [30], where the first one proposed a coalition formation method, the second one designed a resource allocation scheme, and the third one aimed at prolonging the battery life of user devices.

The spatial degrees of freedom offered by having multiple antennas at BSs are very useful in the design of future mobile networks, because spatial precoding enables dense multiplexing of users while keeping the inter-user interference under control. In particular, the performance for cell edge users, which have almost equal signal-to-noise ratios (SNRs) to several BSs, can be greatly improved since only the desired signals are amplified by the transmit precoding [31, 32, 33]. In order to model the random number of users and random user positions, we use mathematical tools from stochastic geometry [34] which are powerful in analytically quantifying certain metrics in closed-form. Some work in the literature of D2D communications in single-antenna systems that exploits these tools can be found in [35, 36, 37, 38, 39, 40]. There are certain studies in the context of MU-MIMO for single tier network in stochastic geometry considering equal or smaller than number of antennas and users like [41, 42]. In this paper, our analysis holds for any number of antennas, but the simulations investigate mostly “massive MIMO regimes” with many more antennas than users.

1.2 Contributions

Our main contributions in this paper can be summarized as follows:

A tractable model for underlaid D2D communication in massive MIMO systems: we model a two-tier network with two different user types. The first-tier users, i.e., CUEs, are served in the downlink by a BS using massive multiuser MIMO precoding to cancel interference. The second-tier users, i.e., D2D users, exploit their close proximity and transmit simultaneously with the downlink cellular transmissions bypassing the BS. The number of D2D transmitters and their locations are modeled according to a homogeneous Poisson point process (PPP) while a fixed number of CUEs are randomly distributed in the network.
Tractable and directly computable expressions: we derive tightly approximated expressions for the coverage probability of D2D users and CUEs. These expressions are directly used to compute our main performance metrics, namely, the ASR and EE. We verify the tightness of these approximations by Monte Carlo simulations. Furthermore, we provide analytical insights on the behavior of these metrics for both CUEs and D2D users.

To the best of our knowledge, the energy efficiency analysis for underlay D2D communications in a network with large number of BS antennas has not been carried out before.
Performance analysis: based on extensive simulations, we characterize the typical relation between the ASR and EE metrics in terms of the number of BS antennas, the number of CUEs, and the D2D user density for a given coverage area and study the incurred tradeoffs in two different scenarios. The modeling and comparative study is an important contribution of the paper.

2 System model

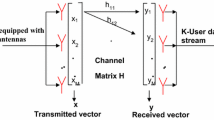
We consider a single-cell scenario where the BS is located in the center of the cell and its coverage area is a disc of radius R. The BS serves U _c single-antenna CUEs which are uniformly distributed in the coverage area. These are simultaneously served in the downlink using an array of T _c antennas located at the BS. It is assumed that 1≤U _c≤T _c so that the precoding can be used to control the interference caused among the CUEs [43].

In addition to the CUEs, there are other single-antenna users that bypass the BS and communicate pairwise with each other using a D2D communication mode. The locations of the D2D transmitters (D2D Tx) are modeled by a homogeneous PPP Φ with density λ _d in $\mathbb {R}^{2}$.¹ This means that the average number of D2D Tx per unit area is λ _d and these users are uniformly distributed in that area. The D2D receiver (D2D Rx) is randomly located in an isotropic direction with a fixed distance away from its corresponding D2D Tx—a model that is similar to the one considered in [36]. We assume that the tier allocation is not the result of radio resource allocation, but given externally by, for instance user applications. Then, the PPP assumption can be well-motivated by the random, uncoordinated and unpredictable mobile user locations and it is not a priori known which users initiate the D2D communications. Furthermore, PPP is the maximum entropy point process and it can be seen as the worst case performance. The system setup is illustrated in Fig. 1. Note that adding successive interference cancellation or using any other interference cancellation technique such as zero-forcing with multiple antennas in the D2D Rx and the cellular UEs as indicated, e.g., in [10, 22, 44], may change the conclusions, but at the same time would increase the complexity and scalability of the problem.

Fig. 1
System model where a multi-antenna BS communicates in the downlink with multiple CUEs, while multiple user pairs communicate in D2D mode. The CUEs are distributed uniformly in the coverage area and the D2D users are distributed according to a PPP. The D2D users that are outside the coverage area are only considered as interferers

Let R _k,j denote the distance between the j-th D2D Tx to the k-th D2D Rx.

The performance analysis for D2D users is carried out for a typical D2D user, which is denoted by the index 0. The typical D2D user is an arbitrary D2D user located in the cell and its corresponding receiver is positioned in the origin. The results for a typical user show the statistical average performance of the network [34]. Therefore, for any performance metric derivation, the D2D users inside the cell are considered and the ones outside the cell are only taken into account as sources of interference. Note that we neglect potential interference from other BSs and leave the multi-cell case for future work. This is because a cellular user or a D2D receiver at the cell edge will see much more interference from D2D transmitters than from the BS in a neighboring cell, simply because the D2Ds are much closer (e.g., at the other side of the cell edge) leading to potentially huge proximity gains.

We assume equal power allocation for both CUEs and D2D users. Let P _c denote the total transmit power of the BS, then the transmit power per CUE is $\frac {P_{c}}{U_{c}}$. The transmit power of the D2D Tx is denoted by P _d.

Let $\mathbf {h}_{j} \in \mathbb {C}^{T_{c} \times 1}$ be the normalized channel response between the BS and the j-th CUE, for j∈{0,…,U _c−1}. These channels are modeled as Rayleigh fading such that $\mathbf {h}_{j} \sim \mathcal {CN}(\mathbf {0},\mathbf {I})$, where $\mathcal {CN}(\cdot,\cdot)$ denotes a circularly symmetric complex Gaussian distribution. Perfect instantaneous channel state information (CSI) is assumed in this work for analytic tractability, but imperfect CSI is a relevant extension [45]. Linear downlink precoding is considered at the BS based on the zero-forcing (ZF) scheme that cancels the interference between the CUEs [43]. The precoding matrix is denoted by $\mathbf {V}=[\mathbf {v}_{0}, \dots, \mathbf {v}_{Uc-1}]\in \mathbb {C}^{T_{c} \times U_{c}}$ in which each column v _j is the normalized transmit precoding vector assigned to the CUE j. Let $\mathbf {f}_{0,\text {BS}} \in \mathbb {C}^{T_{c} \times 1}$ be the channel response from the BS to D2D Rx and let it be Rayleigh fading as $\mathbf {f}_{0,\text {BS}} \sim \mathcal {CN}(\mathbf {0},\mathbf {I})$. Moreover, let $r_{j} \in \mathbb {C}$ and $\mathbf {s} \in \mathbb {C}^{U_{c} \times 1}$ denote the transmitted data signals intended for a D2D Rx and the CUEs, respectively. Since each user requests different data, the transmitted signals can be modeled as zero-mean and uncorrelated with $\mathbb {E}\left [|r_{j}|^{2}\right ]=P_{d}$ and $\mathbb {E}\left [||\mathbf {s}||^{2}\right ]=P_{c}$. The fading channel response between the j-th D2D Tx and the k-th D2D Rx is denoted by $g_{k,j} \in \mathbb {C}$ where $g_{k,j} \sim \mathcal {CN}(0,1)$. Moreover, R _0,BS denotes the random distance between the typical D2D Rx and the BS. The pathloss is modeled as $\phantom {\dot {i}\!}A_{i} d^{-\alpha _{i}}$ with i∈{c,d}, where index c indicates the pathloss between a user and the BS and index d gives the pathloss between any two users. A _i and α _i are the pathloss coefficient and exponent, respectively, where we assume α _i>2. The received signal at the typical D2D Rx is

$$\begin{array}{*{20}l} y_{d,0} &= \sqrt{A_{d}} R_{0,0}^{-\alpha_{d}/2} g_{0,0} r_{0} +\underbrace{\sqrt{A_{c}} R_{0,\text{BS}}^{-\alpha_{c}/2} \mathbf{f}_{0,\text{BS}}^{\,H} \mathbf{V} \mathbf{s} }_{\textrm{Interference from the BS}} \\ &\quad + \underbrace{\sqrt{A_{d}} \sum_{j\neq 0} R_{0,j}^{-\alpha_{d}/2} g_{0,j} r_{j}}_{\textrm{Interference from other D2D users}} + \, \eta_{d}, \end{array} $$

(1)

where η _d is zero-mean additive white Gaussian noise with power $N_{0} = \tilde {N}_{0} B_{w}$, $\tilde {N}_{0}$ is the power spectral density of the white Gaussian noise, and B _w is the channel bandwidth. For given channel realizations, the signal-to-interference-plus-noise ratio (SINR) at the typical D2D Rx is

$$\begin{array}{*{20}l} \text{SINR}_{d} = \frac{P_{d} R_{0,0}^{-\alpha_{d}}|g_{0,0}|^{2}}{I_{\text{BS},0} + I_{d,0} + \frac{N_{0}}{A_{d}}}, \end{array} $$

(2)

in which both the numerator and the denominator have been normalized by A _d. I _BS,0 is the received interference power from the BS and I _d,0 is the received interference power from other D2D users that transmit simultaneously which are defined as

$$\begin{array}{*{20}l} I_{\text{BS},0} &\triangleq \frac{\zeta R_{0,\text{BS}}^{-\alpha_{c}}}{A_{d}}\|\mathbf{f}_{0,\text{BS}}^{\,H} \mathbf{V}\|^{2}, \end{array} $$

(3)

$$\begin{array}{*{20}l} I_{d,0} &\triangleq \sum_{j\neq 0} P_{d} R_{0,j}^{-\alpha_{d}} |g_{0,j}|^{2}, \end{array} $$

(4)

where

$$ \zeta \triangleq A_{c} \frac{P_{c}}{U_{c}}. $$

(5)

Let D _0,k and $e_{0,k}\in \mathbb {C}$ with $e_{0,k}\sim \mathcal {CN}(0,1)$ be the distance and fading channel response between a typical CUE and the k-th D2D Tx, respectively, and let D _0,BS denote the distance between a typical CUE and the BS. Then, the received signal at the typical CUE is

$$\begin{array}{*{20}l} y_{c,0} &= \sqrt{A_{c}} D_{0,\text{BS}}^{-\alpha_{c}/2} \mathbf{h}_{0}^{H} \mathbf{V} \mathbf{s} + \underbrace{\sqrt{A_{d}} \sum_{j} D_{0,j}^{-\alpha_{d}/2} e_{0,j} r_{j}}_{\textrm{Interference from all D2D users}} + \eta_{c}, \end{array} $$

(6)

where η _c is zero-mean additive white Gaussian noise with power N ₀. Then, the corresponding SINR for the typical CUE is

$$\begin{array}{*{20}l} \text{SINR}_{c} = \frac{|\mathbf{h}_{0}^{H} \mathbf{v}_{0}|^{2}}{\frac{A_{d} }{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d} }\right)}, \end{array} $$

(7)

where

$$ I_{d,c} \triangleq \sum_{j} P_{d} D_{0,j}^{-\alpha_{d}} |e_{0,j}|^{2} $$

(8)

is the received interference power from all D2D users (normalized by A _d).

3 Performance analysis

In this section, we first introduce the performance metrics that are considered in this paper. Then, we proceed to derive the coverage probability for both CUEs and D2D users which are needed to compute these metrics.

3.1 Performance metrics

In this paper, two main performance metrics for the network are considered: the average sum rate (ASR) and energy efficiency (EE). The metrics used here are aligned to requirements that are demanded in 5G [1, 46, 47]. We investigate this scenario in order to get an understanding of how such coexistence would perform. Another important fact is that to the best of our knowledge no one has compared the EE and ASR performance of D2D communication in a massive MIMO system. Both of these technologies are known to bring high ASR and are likely to be more energy-efficient. However, there is no work in literature showing the impact of high number of antennas and cellular users along with the density of D2D users in such a setting.

The ASR is obtained from total rates of both D2D users and CUEs as

$$ \text{ASR}= U_{c} \bar{R}_{c} + \pi R^{2} \lambda_{d} \bar{R}_{d}, $$

(9)

where π R ² λ _d is the average number of D2D users in the cell and $\bar {R}_{t}$ with t∈{c,d} denotes the average rates of the CUEs and D2D users, respectively. $\bar {R}_{t}$ for both cellular and D2D users is computed as the successful transmission rate by

$$ \bar{R}_{t} = \underset{\beta_{t} \geq 0}{\text{sup}}~B_{w} \log_{2}(1 + \beta_{t}) \mathrm{P}^{t}_{\text{cov}} (\beta_{t}). $$

(10)

This ASR metric is referred to as the transmission capacity [45, 48] which guarantees the highest spatial reuse under a maximum outage constraint. In (10),

$$ \mathrm{P}^{t}_{\text{cov}} (\beta_{t}) = \text{Pr}\left\{\text{SINR}_{t} \geq \beta_{t} \right\} $$

(11)

is the coverage probability when the received SINR is higher than a specified threshold β _t needed for successful reception. Note that SINR_t contains random channel fading and random user locations. Finding the supremum guarantees the best constant rate for the D2D users and the CUEs. If we know the coverage probability ($\mathrm {P}^{t}_{\text {cov}} (\beta _{t})$), (10) can easily be computed by using line search for each user type independently. Moreover, (10) is easily achievable in practice since the modulation and coding is performed without requiring that every transmitter knows the interference characteristics at its receiver.

Energy efficiency is defined as the benefit-cost ratio between the ASR and the total consumed power:

$$ \text{EE} = \frac{\text{ASR}}{\text{Total power}}. $$

(12)

For the total power consumption, we consider a detailed model described in [7]:

$$ \begin{aligned} \text{Total power}&=\frac{1}{\eta} \left(P_{c} +\lambda_{d} \pi R^{2} P_{d}\right) + C_{0} + T_{c} C_{1} \\ & \quad + \left(U_{c} + 2 \lambda_{d} \pi R^{2}\right)C_{2}, \end{aligned} $$

(13)

where P _c+λ _d π R ² P _d is the total transmission power averaged over the number of D2D users, η is the amplifier efficiency (0<η≤1), C ₀ is the load independent power consumption at the BS, C ₁ is the power consumption per BS antenna, C ₂ is the power consumption per user device, and U _c+2λ _d π R ² is the average number of active users.

In order to calculate the ASR and EE, we need to derive the coverage probability for both cellular and D2D users. The analytic derivation of these expressions is one of the main contributions of this paper.

3.2 Coverage probability of D2D users

We first derive the expression for the coverage probability of D2D users.

Proposition 1

The approximate coverage probability for a typical D2D user is given by

$$\begin{array}{*{20}l} \mathrm{P}^{d}_{\text{cov}}(\beta_{d}) &\approx \frac{(\kappa\beta_{d})^{2/\alpha_{c}}}{R^{2}}\left(y^{U_{c} + \frac{2}{\alpha_{c}}-1} (1-y)^{- \frac{2}{\alpha_{c}}} \right.\notag \\ &\;\quad \left. - \! \left(\!U_{c} \,+\, \frac{2}{\alpha_{c}}\,-\,1\right) \mathcal{B}\left(\! y; U_{c} + \frac{2}{\alpha_{c}}-1, 1-\frac{2}{\alpha_{c}}\right) \right) \notag \\ &\;\quad \cdot \exp\left(- \frac{\pi \lambda_{d} R_{0,0}^{2}}{{\text{sinc}}\left(\frac{2}{\alpha_{d}}\right)} \beta_{d}^{2/\alpha_{d}}\right) \exp\left(\frac{-\beta_{d}} {\bar{\gamma}_{d}}\right), \end{array} $$

(14)

where $\kappa \triangleq \frac {\zeta }{P_{d} A_{d} R_{0,0}^{-\alpha _{d}}}$ with ζ defined in (5), $y \triangleq \frac {1}{\kappa \beta _{d} R^{-\alpha _{c}} + 1}$, $\text {sinc}(x) = \frac {\sin (\pi x)}{\pi x}$, $\bar {\gamma }_{d} = \frac {A_{d} R_{0,0}^{-\alpha _{d}}P_{d}}{N_{0}}$ is the average D2D SNR, and $\mathcal {B}(x;a,b)$ is the incomplete Beta function.

Proof

The proof is given in Appendix 1: Proof of Proposition 1. □

The coverage probability expression in Proposition 1 allows us to compute the average data rate of a typical D2D user in (10). The approximation in this proposition is due to neglecting the spatial interference correlation resulting from the fact that multiple interfering streams are coming from the same location (more details can be found in Appendix 1: Proof of Proposition 1). We note that (14) is actually a tight approximation and its tightness is evaluated in Section 4. From the expression in (14), we make several observations as listed below.

Remark 1

In the high-SNR regime for the D2D users where $\bar {\gamma }_{d} \gg \beta _{d}$, the last term in (14) converges to one, i.e., $\exp \left (- \frac {\beta _{d}} {\bar {\gamma }_{d}}\right) \to 1$, and we have

$$ {\begin{aligned} \mathrm{P}^{d}_{{\text{cov}}}(\beta_{d}) &= \frac{(\kappa\beta_{d})^{2/\alpha_{c}}}{R^{2}}\left(y^{U_{c} + \frac{2}{\alpha_{c}}-1} (1-y)^{- \frac{2}{\alpha_{c}}} - \left(U_{c} + \frac{2}{\alpha_{c}}-1\right) \right. \\ &\;\quad \cdot \left. \mathcal{B}\left(y; U_{c} + \frac{2}{\alpha_{c}}-1, 1-\frac{2}{\alpha_{c}}\right) \right) \exp\left(- \frac{\pi \lambda_{d} R_{0,0}^{2}}{{\text{sinc}}\left(\frac{2}{\alpha_{d}}\right)} \beta_{d}^{2/\alpha_{d}}\right). \end{aligned}} $$

(15)

This can also be referred to as the interference-limited regime.

Remark 2

The coverage probability of a typical D2D user is a decreasing function of the D2D density λ _d. Because higher λ _d results in more interference among D2D users. In particular, it can be seen that $\mathrm {P}^{d}_{ {\text {cov}}}$ in (14) is a function of λ _d through exp(−C λ _d) with $C\triangleq \frac {\pi R_{0,0}^{2} \beta _{d}^{2/\alpha _{d}}}{{\text {sinc}}\left (\frac {2}{\alpha _{d}}\right)} > 0$. Thus, if λ _d→∞, $\mathrm {P}^{d}_{{\text {cov}}} \to 0$. Recall that in our model, the D2D Rx is associated to the D2D Tx which is located at a fixed distance away. However, if we had assumed that the D2D Rx’s association to a D2D Tx is based on, for example, the shortest distance or the maximum SINR, then the $\mathrm {P}^{d}_{{\text {cov}}}$ would have been unaffected by the D2D density (in the high-interference regime). Similar observation can be found in [ 49 , 50 ].

Now, considering the number of BS antennas or the number of CUEs as variables, we have the following behavior of the D2D coverage probability.

Remark 3

$\mathrm {P}^{d}_{{\text {cov}}}$ is not affected by the number of BS antennas T _c. The BS antennas are used to cancel out the interference among CUEs and they do not have any impact on D2D users’ performance as long as the number of CUEs U _c is constant and does not vary with the number of BS antennas T _c. The coverage probability of a typical D2D user $\mathrm {P}^{d}_{{\text {cov}}}$ is a decreasing function of U _c. However, increasing the number of CUEs have a small effect on D2D users’ performance. This is due to the fact that the resulting interference from the BS to D2D users does not change significantly by increasing the number of CUEs as the transmit power of the BS is the same irrespective of the number of users and the precoding is independent of the D2D channels. Thus, a change of U _c will only change the distribution of the interference but not its average.

Next, we comment on how changes in the transmit powers of the BS and D2D Tx as well as the distance between D2D user pairs affect the coverage probability of D2D users.

Remark 4

$\mathrm {P}^{d}_{{\text {cov}}}$ is a decreasing function of the ratio between the transmit power of the BS and of the D2D users, i.e., $\frac {P_{c}}{P_{d}}$, which is part of the first term in (14) and corresponds to the interference from the BS. For instance, if we fix P _c and decrease P _d, the coverage probability for D2D users decreases as the interference from the BS would be the dominating factor. At the same time, if we decrease P _c, it would improve the coverage of D2D users.

Remark 5

$\mathrm {P}^{d}_{{{\text {cov}}}}$ is a decreasing function of the distance between D2D Tx-Rx pairs R _0,0 and the cell radius R. Increasing the cell radius with the same D2D user density reduces the effect of the interference from the BS. Also by decreasing the distance between D2D Tx-Rx pairs, it is evident that a better performance for D2D users can be obtained.

Using Proposition 1, the following corollary provides the optimal D2D user density that maximizes the D2D ASR, i.e., $\pi R^{2} \lambda _{d} \bar {R}_{d}$, where $\bar {R}_{d}$ is given in (10). The optimal density is also evident in our numerical results in Section 4.

Corollary 1

For a given SINR threshold β _d, the optimal density of D2D users $\lambda _{d}^{*}$ that maximizes the D2D ASR is

$$\begin{array}{*{20}l} \lambda_{d}^{*}(\beta_{d}) = \frac{{\text{sinc}}\left(\frac{2}{\alpha_{d}}\right)}{\pi R_{0,0}^{2}}\beta_{d}^{-2/\alpha_{d}}. \end{array} $$

(16)

Proof

Given the SINR threshold β _d and using (9)–(10), the D2D ASR is

$$ \pi R^{2} \lambda_{d} B_{w}\log_{2} (1+\beta_{d}) \mathrm{P}^{d}_{\text{cov}}(\beta_{d}), $$

(17)

where $\mathrm {P}^{d}_{\text {cov}}(\beta _{d})$ is given in (14) and depends on λ _d through an exponential function. Taking the second derivative of (17) with respect to λ _d, we observe that for $\lambda _{d} < 2 \frac {\text {sinc}\left (\frac {2}{\alpha _{d}}\right)}{\pi R_{0,0}^{2}}\beta _{d}^{-2/\alpha _{d}}$, the function is concave. Therefore, setting the first derivative of (17) with respect to λ _d to zero yields the optimal D2D user density $\lambda _{d}^{*}(\beta _{d})$ given in (16) that maximizes the D2D ASR. □

3.3 Coverage probability of cellular users

Next, we compute the coverage probability for CUEs.

Proposition 2

The coverage probability for a typical cellular user is given by

$$ {\begin{aligned} \mathrm{P}^{c}_{{\text{cov}}}(\beta_{c})\! &=\! \mathbb{E}_{D_{0,\text{BS}}}\!\left[\! e^{-\frac{N_{0}}{A_{d}}s} \sum_{k=0}^{T_{c} - U_{c}} \frac{s^{k}}{k!} \sum_{i=0}^{k} {k \choose i}\! \left(\frac{N_{0}}{A_{d} }\right)^{k-i}\!(-1)^{i} \;\Upsilon(\lambda_{d},s,i)\right], \end{aligned}} $$

(18)

with

$$ {\begin{aligned} \Upsilon(\lambda_{d},s,i) &= \exp\left(-C_{d} \lambda_{d} s^{2/\alpha_{d}} \right) \\ &\;\quad \cdot \sum_{(j_{1},\ldots,j_{i})\in\mathcal{J}}\! i! \prod_{\ell=1}^{i}\frac{1}{j_{\ell}!(\ell!)^{j_{\ell}}}\!\left(\!-C_{d} \lambda_{d} s^{\frac{2}{\alpha_{d}}-\ell}\prod_{q=0}^{\ell-1}\left(\frac{2}{\alpha_{d}}-q\right)\!\right)^{j_{\ell}}, \end{aligned}} $$

(19)

where $s\triangleq \frac {A_{d}}{\zeta } D_{0, {\text {BS}}}^{\alpha _{c}}\beta _{c}$ with ζ defined in (5), $C_{d} \triangleq \frac {\pi P_{d}^{2/\alpha _{d}}}{{\text {sinc}}\left (\frac {2}{\alpha _{d}}\right)}$, and

$$\mathcal{J}\triangleq \left\{(j_{1},\ldots,j_{i}): j_{\ell} \in \mathbb{Z}_{\geq 0}, \; \sum_{\ell=1}^{i} \ell j_{\ell} = i \right\}. $$

Proof

The proof is given in Appendix Appendix 2: Proof of Proposition 2. □

This proposition gives an expression for the coverage probability of CUEs in which there is only one random variable left. The expectation in (18) with respect to D _0,BS is intractable to derive analytically but can be computed numerically. The analytical results of Proposition 1 and Proposition 2 have been verified by Monte Carlo simulations in Section 4. A main benefit of the analytic expressions (as compared to pure Monte Carlo simulations with respect to all sources of randomness) is that they can be computed much more efficiently, which basically is a prerequisite for the multi-variable system analysis carried out in Section 4.

Next, we present some observations from the result in Proposition 2 as follows.

Remark 6

In the interference-limited regime where I _d,c≫N ₀, the coverage probability in (18) for a typical cellular user is simplified to

$$\begin{array}{*{20}l} \mathrm{P}^{c}_{{\text{cov}}}(\beta_{c}) &= \mathbb{E}_{D_{0,{\text{BS}}}}\left[\sum_{k=0}^{T_{c} - U_{c}} \frac{(-s)^{k}}{k!}\Upsilon(\lambda_{d},s,k)\right]. \end{array} $$

(20)

The result obtained in Remark 6 has a lower computational complexity compared to the expression in Proposition 2 and at the same time it is a tight approximation for Proposition 2. This can be observed from the denominator of the (7) where the term $\frac {N_{0}}{A_{d} }\approx 0$.

Remark 7

The coverage probability of a typical CUE $\mathrm {P}^{c}_{\text {cov}}(\beta _{c})$ is a decreasing function of the D2D user density λ _d. From Proposition 2, only Υ(λ _d,s,i) is a function of λ _d which is composed of an exponential term in λ _d multiplied by a polynomial term in λ _d. Thus, if λ _d→∞, the exponential term which has a negative growth dominates the polynomial term and $\mathrm {P}^{c}_{{\text {cov}}}(\beta _{c}) \to 0$.

We proceed to analyze the behavior of Proposition 2 by considering a number of special cases. The impact of these special cases is also corroborated in our numerical results in Section 4.

Corollary 2

If T _c=U _c, which is a classical MU-MIMO scenario as indicated in [ 51 ], the coverage probability for a typical cellular user is given by

$$\begin{array}{*{20}l} \mathrm{P}^{c}_{{\text{cov}}}(\beta_{c}) &= \mathbb{E}_{D_{0,{\text{BS}}}}\left[\exp\left(-\frac{N_{0}}{A_{d}}s - C_{d} \lambda_{d} s^{2/\alpha_{d}}\right)\right], \end{array} $$

(21)

where $s = \frac {A_{d}}{\zeta } D_{0,{\text {BS}}}^{\alpha _{c}} \beta _{c}$ and $C_{d}=\frac {\pi P_{d}^{2/\alpha _{d}}}{{\text {sinc}}\left (\frac {2}{\alpha _{d}}\right)}$.

Proof

(21) follows directly from (18) by setting T _c−U _c=0. □

Corollary 2 applies for any case of MU-MIMO and massive MIMO is a form of MU-MIMO [52,53]. The important distinction is that MU-MIMO has traditionally been considered for the case of equal number of antennas and users, while massive MIMO employs a large number of antennas compared to the number of users [52 , 53]. As a rule-of-thumb, T _c>50 and T _c/U _c>2 are required to exploit the favorable propagation of massive MIMO [52]. Next, we consider the case where massive number of antennas are deployed in the BS.

Corollary 3

If (T _c−U _c)→∞, the coverage probability for a typical cellular user tends to one, that is,

$$\begin{array}{*{20}l} {\lim}_{(T_{c} - U_{c}) \to \infty}~\mathrm{P}^{c}_{{\text{cov}}}(\beta_{c}) = 1. \end{array} $$

(22)

Proof

Let m=T _c−U _c. Substituting SINR_c from (7) into (11), we have

$${ \begin{aligned} {\lim}_{m \to \infty}~\mathrm{P}^{c}_{\text{cov}}(\beta_{c}) &= {\lim}_{m \to \infty}~\text{Pr}\left\{ |\mathbf{h}_{0}^{H} \mathbf{v}_{0}|^{2} \geq \frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d}}\right)\beta_{c} \right\} \\[-3pt] &\overset{(a)}= {\lim}_{m \to \infty}~\mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\left[e^{-\frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d}}\right)\beta_{c}} \right.\\[-3pt] &\;\quad\cdot \left.\sum_{k=0}^{m} \frac{1}{k!}\left(\frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d}}\right)\beta_{c}\right)^{k}\right] \\[-3pt] &\overset{(b)}= {\lim}_{m \to \infty}~\mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\left[e^{-z} \sum_{k=0}^{m} \frac{z^{k}}{k!}\right] \\[-3pt] &\overset{(c)}= \mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\left[{\lim}_{m \to \infty} e^{-z} \sum_{k=0}^{m} \frac{z^{k}}{k!}\right] \\[-3pt] &\overset{(d)}= \mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\left[e^{-z} e^{z} \right] = 1, \end{aligned}} $$

where (a) follows from the CCDF of $|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2}$ with $2|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2} \sim {\chi ^{2}_{2}}$ given D _0,BS and I _d,c (refer to Appendix 5 for more details). Step (b) follows from setting $z = \frac {A_{d}}{\zeta } D_{0,\text {BS}}^{\alpha _{c}}\left (I_{d,c} + \frac {N_{0}}{A_{d}}\right)\beta _{c}$. Step (c) is obtained from the dominated convergence theorem which allows for an interchange of limit and expectation and step (d) is due to the fact that $\sum _{k=0}^{\infty } \frac {z^{k}}{k!} = e^{z}$. □

Corollary 3 gives an indication that the desired signal can be amplified by adding more antennas. However, note that even if the power gain becomes much stronger than the D2D interference, it will, in practice, eventually become limited by pilot contamination, hardware distortion, and/or finite modulation sizes.

In the results so far, we have discussed the case where there exist some D2D users as underlay to the cellular network, that is, λ _d≠0, However, it is interesting to see what can be achieved without D2D users.

Corollary 4

If λ _d=0, the coverage probability for a typical cellular user is given by

$$ {\begin{aligned} \mathrm{P}^{c}_{{\text{cov}}}\left(\beta_{c}\right) &= \frac{2}{\alpha_{c} R^{2}}\Gamma\left(\frac{2}{\alpha_{c}}\right)\left(\frac{N_{0}}{\zeta} \beta_{c} \right)^{-2/\alpha_{c}} \sum_{k=0}^{T_{c}-U_{c}}{\frac{2}{\alpha_{c}}+k-1 \choose k}, \end{aligned}} $$

(23)

where Γ(·)is the Gamma function and ζ is defined in (5).

Proof

Substituting SINR_c from (7) into (11) and setting λ _d=0, we have

$$ {\begin{aligned} \mathrm{P}^{c}_{\text{cov}}(\beta_{c}) &= \text{Pr}\left\{ |\mathbf{h}_{0}^{H} \mathbf{v}_{0}|^{2} \geq \frac{D_{0,\text{BS}}^{\alpha_{c}}}{\zeta} N_{0} \beta_{c} \right\}\\[-3pt] &\overset{(a)}= \mathbb{E}_{z}\left[\sum_{k=0}^{T_{c}-U_{c}}\frac{l^{k}}{k!}z^{k} e^{-lz} \right]\\[-3pt] &\overset{(b)}=\frac{2}{\alpha_{c} R^{2}}\Gamma\left(\frac{2}{\alpha_{c}}\right) \sum_{k=0}^{T_{c}-U_{c}}\frac{(-l)^{k}}{k!} ~\frac{\mathrm{d}^{k}}{{\mathrm{d}l}^{k}} ~l^{-2/\alpha_{c}}, \end{aligned}} $$

(24)

where (a) follows from the CCDF of $|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2}$ with $2|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2} \sim {\chi ^{2}_{2}}$ given D _0,BS and setting $l= \frac {N_{0}}{\zeta } \beta _{c}$ and $z = D_{0,\text {BS}}^{\alpha _{c}}$ with PDF $f(z)=\frac {2}{\alpha _{c}R^{2}}z^{\frac {2}{\alpha _{c}}-1}$. Step (b) follows from taking the expectation with respect to z which is similar to the expression in (35) with the Laplace transform $ \mathcal {L}_{z}(l) = \frac {2}{\alpha _{c} R^{2}}\Gamma \left (\frac {2}{\alpha _{c}}\right)l^{-2/\alpha _{c}}$. Simplifying the k-th derivative to $\frac {\mathrm {d}^{k}}{\mathrm {d}l^{k}} ~l^{-2/\alpha _{c}} = (-1)^{k} l^{-\frac {2}{\alpha _{c}}-k} \prod _{i=0}^{k-1}\left (\frac {2}{\alpha _{c}}+i\right)$ and using the identity $\frac {1}{k!}\prod _{i=0}^{k-1}\left (\frac {2}{\alpha _{c}}+i\right) = {\frac {2}{\alpha _{c}}+k-1 \choose k}$, (23) follows. □

The closed-form results in Corollary 4 for λ _d=0 depends only on noise rather than interference and perhaps can result in higher ASR for CUEs. The ASR for λ _d>0 also depend on noise but its impact is much smaller. However, we note that this result is obtained for a single-cell scenario. Thus, comparing Proposition 2 and Corollary 4 and evaluating the potential performance gain/loss due to introducing D2D communications would make more sense in a multi-cell scenario.

Using the results from Proposition 1 and Proposition 2, we proceed to evaluate the network performance in terms of the ASR and EE from (9) and (12), respectively.

4 Numerical results

In this section, we assess the performance of the setup in Fig. 1 in terms of ASR and EE using numerical evaluations. As we pointed out in Section 3, many parameters affect these performance metrics. Initially, we consider the EE and the ASR as functions of three key parameters, namely, the number of BS antennas T _c, the density of D2D users λ _d, and the number of cellular users U _c. We show the individual effect of these system parameters on the two performance metrics while other parameters such as BS transmit power P _c, D2D transmit power P _d, and distance between D2D Tx-Rx pair R _0,0 are fixed. Later on, we also comment on the choice of these fixed parameters. The system and simulation parameters are given in Table 1. The path loss model parameters for our simulations are adapted from the model presented in [54].

Table 1

System and simulation parameters

Description	Parameter	Value
D2D TX power	P _d	6 dBm
BS TX power	P _c	30 dBm
Cell radius	R	500 m
Bandwidth	B _w	20 MHz
Thermal noise power	N ₀	−101 dBm
Noise figure in UE	F	5 dB
Carrier frequency	f _c	2 GHz
D2D pair distance	R _0,0	35 m
Pathloss exponent between devices	α _d	3
Pathloss exponent between BS–device	α _c	3.67
Pathloss coefficient between devices	A _d	38.84 dB
Pathloss coefficient between BS–device	A _c	30.55 dB
Amplifier efficiency	η	0.3
Load-independent power in BS	C ₀	5 W
Power per BS antenna	C ₁	0.5 W
Power per UE handset	C ₂	0.1 W
Monte Carlo runs	MC	5000

Before we proceed to the performance evaluation, we verify the analytical results of Proposition 1 and Proposition 2 by Monte Carlo simulations. The locations of the D2D Txs are generated in an area with radius 10R according to the PPP as opposed to our analytical assumption that they are located in the whole $\mathbb {R}^{2}$ region. As depicted in Fig. 2, simulation results closely follow the analytical derivations and the finite-region approximation in the simulation has a negligible impact on the results. The small gap in Fig. 2 a is due to the spatial interference correlation resulting from the fact that multiple interfering streams are coming from the same location, hence, the Chi-squared distribution in (28) is an approximation. This is a quite standard approximation in analyzing MIMO systems [41].

Fig. 2
Coverage probability as a function of β _t, t∈{d,c}: analysis versus Monte Carlo simulations for a D2D users with λ _d=10⁻⁵ and b CUEs with λ _d=10⁻⁵ and T _c∈{4,70}. The number of CUEs is U _c=4

We consider two scenarios corresponding to the number of CUEs U _c in our evaluations. First, we assume that U _c is chosen as a function of the number of BS antennas T _c. Then, we move on to the case where we fix the number of CUEs and study the tradeoffs among other parameters. Both scenarios are relevant in the design of massive MIMO systems. In order to speed up the numerical computations, based on the insight obtained in Remark 6, we neglected the terms that are very small.

4.1 Number of CUEs as a function of the number of BS antennas

In this scenario, we assume that there is a fixed ratio between the number of CUEs U _c and the number of BS antennas T _c. We assume this ratio to be $\frac {T_{c}}{U_{c}}=5$. Simply put, to serve one additional user, we add five more antennas at the BS since the main gains from massive MIMO come from multiplexing of many users rather than only having many antennas.

Figure 3 shows the ASR as a function of the density of D2D users λ _d and the number of CUEs U _c, which is scaled by T _c. It is observed that increasing U _c, or equivalently T _c, never decreases the ASR, and usually leads to an increase in ASR. In contrast, there is an optimal value of λ _d as derived in Corollary 1 which results in the maximum ASR for all values of U _c and appears approximately at λ _d=10⁻⁴. However, there is a difference in the shape of the ASR between the lower and higher values of U _c. In order to clarify this effect, we plot the ASR versus λ _d in a 2-D plot with U _c∈{1,14} equivalent to T _c∈{5,70} in Fig. 4 a.

Fig. 3
ASR [Mbit/s] as a function of the number of CUEs U _c and the D2D user density λ _d for a fixed ratio $\frac {T_{c}}{U_{c}}= 5$

As seen in Fig. 4 a, for U _c=1 user and T _c=5 antennas, the rate contributed from the CUEs to the sum rate is low as there is only one CUE. This rate is in a comparable level as the contribution of D2D users sum rate to the total ASR. Adding D2D users to the network (i.e., increasing λ _d), which may cause interference, will nevertheless leads to an increase in the ASR. This increase in the ASR continues until reaching a certain density that gives the maximum ASR. By further increasing λ _d, the interference between D2D users reduces their coverage probability as previously observed in Remark 2. This limits the per link data rate and even a high number of D2D users cannot compensate for the D2D rate loss. At the same time, increasing λ _d tremendously affects the CUEs sum rate (cf. Remark 7). Consequently, as λ _d increases, the ASR decreases.

By increasing the number of CUEs and BS antennas to U _c=14 users and T _c=70 antennas, respectively, in Fig. 4 a, the average rates of the CUEs become higher than the case with U _c=1 user and T _c=5 antennas as expected from Corollary 3 and the multiplexing gain from having many CUEs. However, by introducing a small number of D2D users, there is a substantial probability that the interference from the D2D users reduces the CUEs’ rates per link as observed in Remark 7. The reduction in these rates are not compensated in the ASR by the contribution of the D2D users’ rates. Note that, as we stated in Remark 3, when U _c is scaled with T _c, it impacts the D2D coverage probability, but the decrease in the performance of D2D users is not significant. Furthermore, if we keep increasing λ _d, even though the rate per link decreases for both CUEs and D2D users, there is a local minima after which the aggregate D2D rate over all D2D users becomes higher and the ASR increases again. The second turning point follows from the same reasoning as for the case of U _c=1 user and T _c=5 antennas, i.e., in higher D2D densities, the interference from D2D users are the limiting factor for the ASR. This effect can also be observed in Fig. 4 b where the ASR performance is depicted versus different number of CUEs (and BS antennas) for two D2D densities. At the lower density, the ASR is linearly increasing with U _c (and T _c), however, in the interference-limited regime (higher λ _d), increasing the number of CUEs and BS antennas do not impact the network ASR performance.

The reasoning in Fig. 4 a, b can be well understood from Fig. 5 which explains the tradeoff between the ASR of CUEs and D2D users in the network. In the scenario in which we have T _c=70 antennas and U _c=14 users, the cellular network contributes more to the total ASR for the low D2D density regime (e.g., λ _d=10⁻⁶) due to high number of CUEs and BS antennas. In this region, the ASR gains from massive MIMO is large. By increasing λ _d, the gain from massive MIMO vanishes as the interference added by the D2D users dominates and degrades the performance that was achieved by interference cancellation between CUEs. Therefore, with medium D2D user density, if there is a fixed rate constraint for CUEs, the network can still benefit (from the ASR perspective) from underlay D2D communications. However, in the high D2D density regime (e.g., λ _d=10⁻⁴), the cellular ASR is too small and it is better that the cellular and D2D tiers use the overlay approach for communication instead of the underlay approach.

In Fig. 6, we show the network performance in terms of the EE as a function of the parameters λ _d and U _c with $\frac {T_{c}}{U_{c}}= 5$. It is observed that the EE is a decreasing function of U _c and T _c. In contrast, there is a maximum point in the EE based on different values of λ _d. To study this result further, similar to the ASR, we first plot the EE versus λ _d for U _c∈{1,14} and T _c∈{4,70} in Fig. 7 a. We can see that the pattern for both low and high number of BS antennas are similar to Fig. 4 a. The higher EE is achieved with U _c=1 user and T _c=5 antennas as opposed to U _c=14 users and T _c=70 antennas. This is because the extra circuit power of the cellular tier with U _c=14 users and T _c=70 antennas does not bring any substantial ASR improvement over the case with U _c=1 user and T _c=5 antennas.

Fig. 7
EE [Mbit/Joule]: a as a function of the D2D user density λ _d for a fixed ratio $\frac {T_{c}}{U_{c}}= 5$ with the number of CUEs U _c∈{1,14}; b as a function of the number of CUEs U _c with the D2D user density λ _d∈{10⁻⁶,10⁻⁴} for a fixed ratio $\frac {T_{c}}{U_{c}}= 5$

Furthermore, if we plot the EE versus U _c, we see a different behavior for low and high D2D densities. Figure 7 b illustrates that in the low D2D density regime (λ _d=10⁻⁶), even though the ASR increases linearly, the EE almost stays the same as the number of CUEs, and correspondingly the number of BS antennas, increases. From (13), we can observe that for a fixed λ _d, only the circuit power is changed by increasing U _c and T _c. At the same time, the circuit power dominates the total power consumption and increases almost linearly leading to an (almost) constant EE. The network performance in terms of the EE is poor with high density of D2D users (λ _d=10⁻⁴). This is due to the fact that the sum rate contributed by the CUEs is already degraded by the interference from high number of D2D users, and additionally, increasing U _c (and accordingly T _c) increases the circuit power without any gain in the total ASR. Consequently, the EE decreases. Thus, massive MIMO is only beneficial in terms of EE if the D2D user density is small, as the resulting ASR gain compensates the significant increase in the circuit power consumption due to higher number of U _c and T _c. On the other hand, for high D2D user density, the EE performance degrades with higher number of U _c and T _c since massive MIMO gains cannot compensate the higher circuit power consumption. Therefore, in the latter case dedicated resources or underlaying with fewer BS antennas could be more beneficial.

4.2 Fixed number of CUEs

In this section, we evaluate the system performance when the number of CUEs is fixed with U _c=4 users. The general trend of the network performance is the same as the case with $\frac {T_{c}}{U_{c}} =5$ in the previous section. However, there are some differences which are highlighted in Fig. 8 a, b for the ASR and EE, respectively. As it is shown in Fig. 8 a, in the low D2D user density regime (i.e., λ _d=10⁻⁶) the ASR is increasing in T _c, however, with a lower slope as compared to the case of $\frac {T_{c}}{U_{c}} =5$. By increasing the number of BS antennas for the fixed number of CUEs, better performance per user can be achieved, however in this case, as the number of CUEs is not high, the ASR increases with a small slope. For high D2D user density (i.e., λ _d=10⁻⁴), the ASR is almost flat.

Fig. 8
a ASR [Mbit/s] and b EE [Mbit/Joule] as a function of the number of BS antennas T _c for U _c=4 users and λ _d∈{10⁻⁶,10⁻⁴}

Figure 8 b illustrates that when the D2D user density is low, the EE benefits from adding extra BS antennas until the sum of the circuit power consumption of all antennas dominates the performance and leads to a gradual decrease in the EE. As the figure implies, there exists an optimal number of BS antennas which is relatively small since the main massive MIMO gains come from multiplexing rather than just having many antennas. However, in a high density D2D scenario, which is an interference-limited scenario, the EE decreases monotonically with T _c. Increasing the number of BS antennas in this region cannot improve the ASR significantly, as shown in Fig. 8 a; at the same time, the circuit power consumption increases as a result of the higher number of BS antennas, which in turn leads to decreasing network EE.

The conclusion is that the D2D user density has a very high impact on a network that employs the massive MIMO technology. In the downlink, these two technologies can only coexist at low D2D user densities and careful interference coordination. The number of CUEs should be a function of the number of BS antennas in order to benefit from massive MIMO in terms of the ASR and EE. Otherwise, at high D2D user densities, D2D communication should use the overlay approach rather than the underlay, that is, dedicated time/frequency resources should be allocated to the D2D tier. As discussed earlier, adding successive interference cancellation or using any other interference cancellation technique may change the conclusions but at the same time it would increase the complexity and scalability of the problem.

4.3 The effect of other system parameters

So far, we have discussed the results based on constant transmit power P _c, D2D transmit power P _d, and distance between D2D Tx-Rx pairs R _0,0 given in Table 1. Now we comment on the choice of these parameters and study their effects on the system performance. From Proposition 1, Proposition 2, and Remark 4, it is evident that the coverage probability for both D2D and cellular tiers, and consequently the network ASR and EE, depend on the ratio of P _d and P _c. Therefore, we fix P _c and vary P _d.

Figure 9 a shows the ASR as function of λ _d under two different power levels, i.e., P _d=6 dBm and P _d=13 dBm in a scenario where the number of CUEs U _c is scaled by T _c. We see that higher P _d degrades the ASR at higher number of CUEs (and BS antennas) when the D2D user density is low, but has negligible impact at lower number of CUEs. The reason is that increasing P _d, on the one hand, boosts the D2D user rates, and on the other hand, causes more interference to CUEs that deteriorates their rates. Consequently, at low D2D user densities and high number of CUEs and BS antennas where the cellular sum rate is the main contributor to the total ASR, the interference caused by higher D2D transmit power is the dominant factor leading to lower total ASR. However, as λ _d increases, the contribution of the D2D sum rate to the total ASR increases, and thus with higher P _d, the increase in the D2D sum rates compensates the decrease in CUEs sum rate and the difference in terms of the total ASR between the different power levels vanishes. When the number of CUEs is small, i.e., U _c=1 user and T _c=5 antennas, the CUE and D2D users have almost the same contributions to the ASR and increasing P _d has negligible impact on the performance.

Fig. 9
a ASR [Mbit/s] and b EE [Mbit/Joule] as a function of the D2D user density λ _d for different D2D transmit power and a fixed ratio $\frac {T_{c}}{U_{c}}= 5$ with the number of CUEs U _c∈{1,14}

Figure 9 b depicts the EE as a function of λ _d under the same two levels of D2D transmit power. It is observed that lower P _d is more beneficial in terms of the EE in both cases of U _c=1 user and U _c=14 users. This is particularly visible in higher density of D2D users (e.g., λ _d=3×10⁻⁵) with U _c=1 user and T _c=5 antennas when the interference is the limiting factor. With U _c=14 users and T _c=70 antennas, the CUEs have higher impact on the ASR, and as a consequence, the system benefits from lower transmit power of D2D users in terms of the EE. Therefore, we have chosen P _d=6 dBm in the previous performance evaluation, as it has a better impact on the ASR as well as EE, especially in higher number of BS antennas.

Another important parameter that impacts the ASR is the distance between D2D Tx-Rx pairs, i.e., R _0,0. The effect of this parameter is only on the coverage probability of D2D users as seen in Proposition 1 and Proposition 2. Figure 10 illustrates the cellular ASR versus the D2D ASR for different values of λ _d and R _0,0. The figure verifies that by decreasing R _0,0 only the ASR of D2D tier increases and as Remark 5 implies increasing R _0,0 decreases the coverage probability of D2D users leading to lower ASR and EE. Since D2D communication is mostly meant for close proximity applications, we have chosen R _0,0=35 m in our performance study. Moreover, by decreasing the distance between D2D users, more D2D users can coexist simultaneously. This is observed in Fig. 10 that with R _0,0=35 m the maximum ASR (of the D2D tier as well as the network) is achieved at the D2D density λ _d=10⁻⁴ while with R _0,0=50 m, it is achieved at the D2D density λ _d=3.98×10⁻⁵.

Fig. 10
Cellular ASR vs. D2D ASR [Mbit/s] for different distances between D2D Tx and D2D Rx with U _c=4 users and T _c=70 antennas. The curves are obtained by varying the value of λ _d from 10⁻⁶ to 10⁻²

5 Conclusions

We studied the coexistence of two key 5G concepts: device-to-device (D2D) communication and massive MIMO. We considered two performance metrics, namely, the average sum rate in bit/s and the energy efficiency in bit/Joule. We considered a setup with uniformly distributed cellular users in the cell, while the D2D transmitters are distributed according to a Poisson point process. We derived tractable expressions for the coverage probabilities of both cellular and D2D users which led to computation of the average sum rate and energy efficiency. We then studied the tradeoff between the number of base station antennas, the number of cellular users, and the density of D2D users for a given coverage area in the downlink. Our results showed that both the average sum rate and energy efficiency behave differently in scenarios with low and high density of D2D users. Underlay D2D communications and massive MIMO can only coexist in low densities of D2D users with careful interference coordination, because the massive MIMO gains vanish when the interference from the D2D tier becomes extremely large. The number of cellular users should scale with the number of BS antennas in order to benefit from massive MIMO in terms of the average sum rate and energy efficiency. If there is a high density of D2D users, the D2D communication should use the overlay approach rather than the underlay or the network should only allow a subset of the D2D transmissions to be active at a time.

6 Endnote

¹ The assumption that the D2D Tx are distributed in the whole $\mathbb {R}^{2}$ plane removes any concern about the boundary effects and makes the model more mathematically tractable. The boundary effects are local effects in which users at the network boundary experience less interference than the ones closer to the center, because they have fewer neighbors.

7 Appendix 1: Proof of Proposition 1

The proof follows by substituting the definition of SINR_d from (2) into (11) where we obtain

$$ {\begin{aligned} \mathrm{P}^{d}_{\text{cov}}(\beta_{d}) &= \text{Pr}\left\{\text{SINR}_{d} \geq \beta_{d} \right\} \\ &= \text{Pr} \left\{ P_{d} R_{0,0}^{-\alpha_{d}} |g_{0,0}|^{2} \geq \beta_{d} \left(I_{\text{BS},0} + I_{d,0} + \frac{N_{0}}{A_{d} }\right) \right\} \\ &= \text{Pr} \left\{ |g_{0,0}|^{2} \geq \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} \left(I_{\text{BS},0} + I_{d,0} + \frac{N_{0}}{A_{d} }\right) \right\} \\ &\overset{(a)}= \mathbb{E}_{I_{\text{BS},0}, I_{d,0}} \left[\exp\left(- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} \left(I_{\text{BS},0} + I_{d,0} + \frac{N_{0}}{A_{d} }\right)\right)\right] \\ &\overset{(b)}= \mathbb{E}_{I_{\text{BS},0}}\left[\!\exp\left(\!- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} I_{\text{BS},0}\!\right)\!\right] \mathbb{E}_{I_{d,0}}\!\left[\!\exp\left(\!- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} I_{d,0}\right)\right]\! \cdot \exp\!\left(\!-\frac{\beta_{d} }{\bar{\gamma}_{d}}\right)\\ &\overset{(c)}= \mathcal{L}_{I_{\text{BS},0}}\left(\frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}}\right)\mathcal{L}_{I_{d,0}}\left(\frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}}\right) \exp\left(-\frac{\beta_{d}}{\bar{\gamma}_{d}}\right). \end{aligned}} $$

(25)

Step (a) comes from the fact that |g _0,0|²∼ exp(1) and (b) follows since the noise and interference terms are mutually independent. In step (c), the Laplace transform defined as $\mathcal {L}_{x}(s) = \mathbb {E}_{x}\left [e^{- sx}\right ]$ is identified.

The first Laplace transform in (25) is with respect to I _BS,0 in (3) which is a function of two random variables, namely $\|\mathbf {f}_{0,\text {BS}}^{H} \mathbf {V}\|^{2}$ and R _0,BS. This Laplace transform is calculated as

$$ {\begin{aligned} \mathcal{L}_{I_{\text{BS},0}}&\left(\frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}}\right) = \mathbb{E}_{I_{\text{BS},0}} \left[\exp\left(- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} I_{\text{BS},0}\right)\right]\\ &= \mathbb{E}_{R_{0,\text{BS}}} \left[\mathbb{E}_{\|\mathbf{f}_{0,\text{BS}}^{H} \mathbf{V}\|^{2}}\left[\exp\left(- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} \frac{\zeta R_{0,\text{BS}}^{-\alpha_{c}}}{A_{d}}\|\mathbf{f}_{0,\text{BS}}^{H} \mathbf{V}\|^{2} \right) \left| R_{0,\text{BS}} \right. \right]\right] \\ &=\mathbb{E}_{R_{0,\text{BS}}} \left[ \mathcal{L}_{\|\mathbf{f}_{0,\text{BS}}^{H} \mathbf{V}\|^{2}}\left(\frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} \frac{\zeta R_{0,\text{BS}}^{-\alpha_{c}}}{A_{d}}\right)\right] \\ &\overset{(a)}= \mathbb{E}_{R_{0,\text{BS}}} \left[\frac{1}{(\kappa \beta_{d} R_{0,\text{BS}}^{-\alpha_{c}} + 1)^{U_{c}}}\right] \\ &\overset{(b)}= {\int_{0}^{R}} \frac{2r}{R^{2}(\kappa \beta_{d} r^{-\alpha_{c}}+1)^{U_{c}}} \mathrm{d}r\\ &\overset{(c)}= \frac{2(\kappa\beta_{d})^{2/\alpha_{c}}}{\alpha_{c} R^{2}}{\int_{0}^{y}} \frac{t^{U_{c}+\frac{2}{\alpha_{c}}-1}}{(1-t)^{\frac{2}{\alpha_{c}}+1}}\mathrm{d}t \\ &\overset{(d)}= \frac{(\kappa\beta_{d})^{2/\alpha_{c}}}{R^{2}}\left(y^{U_{c} + \frac{2}{\alpha_{c}}-1} (1-y)^{- \frac{2}{\alpha_{c}}}- \left(U_{c} + \frac{2}{\alpha_{c}}-1\right) \right. \\ &\;\quad \cdot \left. \mathcal{B}\left(y; U_{c} + \frac{2}{\alpha_{c}}-1, 1-\frac{2}{\alpha_{c}}\right) \right) \end{aligned}} $$

(26)

for α _c>2, where (a) follows by introducing the notation

$$ \kappa = \frac{\zeta}{P_{d} A_{d} R_{0,0}^{-\alpha_{d}}} $$

(27)

and from the Laplace transform of the probability density function (PDF) of $\|\mathbf {f}_{0,\text {BS}}^{\,H} \mathbf {V}\|^{2}$ which, by neglecting the spatial correlation, is tightly approximated by a Chi-squared distribution as $2\|\mathbf {f}_{0,\text {BS}}^{\,H} \mathbf {V}\|^{2} \sim \chi ^{2}_{2U_{c}}$ [41]. Note that

$$\begin{array}{*{20}l} \left\|\mathbf{f}_{0,\text{BS}}^{\,H} \mathbf{V}\right\|^{2} &= \left\|\mathbf{f}_{0,\text{BS}}^{\,H} [\mathbf{v}_{0},\ldots,\mathbf{v}_{{U_{c}}-1}]\right\|^{2} \\ &=\sum_{i=0}^{U_{c}-1} |\mathbf{f}_{0,\text{BS}}^{\,H}\mathbf{v}_{i}|^{2}, \end{array} $$

(28)

where $\mathbf {f}_{0,\text {BS}}^{\,H}\mathbf {v}_{i}$, i={0,…,U _c−1}, are zero-mean circular symmetric complex Gaussian random variables with unit variance. Therefore, $\sum _{i=0}^{U_{c}-1} |\mathbf {f}_{0,\text {BS}}^{\,H}\mathbf {v}_{i}|^{2}$ is the summation of U _c i.i.d. exponential random variables which has an Erlang(U _c,1) distribution. Equivalently, the sum scaled down by $\frac {\sigma ^{2}}{2}$ (i.e., multiplied by $\frac {2}{\sigma ^{2}}$) has a (standard) Chi-squared distribution with 2U _c degrees of freedom. Hence, the PDF of $\|\mathbf {f}_{0,\text {BS}}^{\,H} \mathbf {V}\|^{2}$ is

$$ f_{\|\mathbf{f}_{0,\text{BS}}^{\,H} \mathbf{V}\|^{2}} (x) = \frac{x^{Uc-1}e^{-x}}{(U_{c}-1)!}. $$

(29)

From Laplace transform theory we know that $\mathcal {L}\left [t^{n} e^{-\alpha t}\right ] = \frac {n!}{(s+\alpha)^{n+1}}$ and with some simplifications, we obtain the result in step (a). Step (b) in (26) follows from the PDF of R _0,BS which is

$$ f_{R_{0,\text{BS}}}(r) = \left\{\begin{array}{ll} \frac{2r}{R^{2}}, & \text{if}\,\, 0\leq r \leq R,\\ 0, & \text{otherwise}, \end{array} \right. $$

(30)

as the typical D2D Rx is uniformly distributed over the cell area and the BS is located in the cell center. Step (c) in (26) is obtained by the change of variable $\frac {1}{\kappa \beta _{d} r^{-\alpha _{c}} + 1}\rightarrow t$ which leads to the integral boundary $y \triangleq \frac {1}{\kappa \beta _{d} R^{-\alpha _{c}} + 1} $. Finally, (d) follows by integration by part where $\mathcal {B}(x;a,b)$ is the incomplete Beta function defined as

$$ \mathcal{B}(x;a,b) = {\int_{0}^{x}} t^{\,a-1} (1-t)^{b-1} \mathrm{d}t, $$

(31)

for a,b>0.

Next, we proceed to calculate the second Laplace transform in (25). This transform is with respect to I _d,0 in (4) which is a function of two random variables, that is |g _0,j|² and R _0,j. Therefore, we have

$$ {\begin{aligned} \mathcal{L}_{I_{d,0}} \left(\frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}}\right) &= \mathbb{E}_{I_{d,0}}\left[\exp\left(- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} I_{d,0}\right)\right]\\ &= \mathbb{E}_{R_{0,j},|g_{0,j}|^{2}} \left[\exp\left(- \frac{\beta_{d}}{P_{d}R_{0,0}^{-\alpha_{d}}} \sum_{j\neq 0} P_{d} R_{0,j}^{-\alpha_{d}} |g_{0,j}|^{2}\right)\right] \\ &= \mathbb{E}_{R_{0,j}} \left[\prod_{j} \mathbb{E}_{|g_{0,j}|^{2}}\left[\exp\left(-\frac{\beta_{d}}{R_{0,0}^{-\alpha_{d}}} R_{0,j}^{-\alpha_{d}} |g_{0,j}|^{2}\right)\right]\right]\\ &\overset{(a)}= \! \exp\left(\! \!-2 \pi \lambda_{d} \int_{0}^{\infty}\! \!\left(1-\mathbb{E}_{G}\left[\exp\!\left(\!-\frac{\beta_{d}}{R_{0,0}^{-\alpha_{d}}} r^{-\alpha_{d}} G\!\right)\!\right]\right)r\,\mathrm{d}r \right) \\ &\overset{(b)}=\exp\left(-2 \pi \lambda_{d} \int_{0}^{\infty} \frac{r}{\frac{R_{0,0}^{\alpha_{d}}}{\beta_{d}} r^{\alpha_{d}}+1}\mathrm{d}r \right)\\ &\overset{(c)}= \exp\left(-\frac{\pi \lambda_{d}}{\text{sinc}(\frac{2}{\alpha_{d}})}\left(\frac{\beta_{d}}{R_{0,0}^{-\alpha_{d}}}\right)^{2/\alpha_{d}}\right), \end{aligned}} $$

(32)

where (a) is based on the probability generating functional (PGFL) [48], and (b) follows from the fact that G∼ exp(1) and $\mathcal {L}\left [e^{-t}\right ] = \frac {1}{s+1}$. Step (c) follows by solving the integral in step (b) and using $\text {sinc}(x) = \frac {\sin (\pi x)}{\pi x}$.

Substituting (26) and (32) in (25) concludes the proof of Proposition 1. □

8 Appendix 2: Proof of Proposition 2

Substituting SINR_c from (7) into (11), we get

$$ {\begin{aligned} &\mathrm{P}^{c}_{\text{cov}}(\beta_{c}) = \text{Pr}\left\{ |\mathbf{h}_{0}^{H} \mathbf{v}_{0}|^{2} \geq \frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d} }\right)\beta_{c} \right\}\\ &\quad\overset{(a)}= \mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\!\!\left[\!\!e^{-\frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\left(I_{d,c} + \frac{N_{0}}{A_{d}}\right)\beta_{c}} \sum_{k=0}^{T_{c} - U_{c}} \!\!\frac{1}{k!}\!\left(\!\frac{A_{d}}{\zeta} D_{0,\text{BS}}^{\alpha_{c}}\!\!\left(\!I_{d,c}\! +\! \frac{N_{0}}{A_{d}}\!\right)\!\beta_{c}\!\right)^{k}\!\right]\\ &\quad\overset{(b)}= \mathbb{E}_{D_{0,\text{BS}}, I_{d,c}}\left[e^{-\frac{N_{0}}{A_{d}}s} \sum_{k=0}^{T_{c} - U_{c}} \frac{s^{k}}{k!} \sum_{i=0}^{k} {k \choose i} \left(\frac{N_{0}}{A_{d} }\right)^{k-i} I_{d,c}^{i} e^{-s I_{d,c}} \right]\\ &\quad\overset{(c)}= \mathbb{E}_{D_{0,\text{BS}}}\left[e^{-\frac{N_{0}}{A_{d}}s} \sum_{k=0}^{T_{c} - U_{c}} \frac{s^{k}}{k!} \sum_{i=0}^{k} {k \choose i} \left(\frac{N_{0}}{A_{d} }\right)^{k-i} \mathbb{E}_{I_{d,c}}\left[I_{d,c}^{i} e^{-s I_{d,c}} \right] \right]\\ &\quad\overset{(d)}= \mathbb{E}_{D_{0,\text{BS}}}\left[e^{-\frac{N_{0}}{A_{d}}s} \sum_{k=0}^{T_{c} - U_{c}} \frac{s^{k}}{k!} \sum_{i=0}^{k} {k \choose i} \left(\frac{N_{0}}{A_{d} }\right)^{k-i} (-1)^{i}\frac{\mathrm{d}^{i}}{{\mathrm{d}s}^{i}}\mathcal{L}_{I_{d,c}}(s)\right], \end{aligned}} $$

(33)

where (a) follows from the CCDF of $|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2}$ with $2|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2} \sim \chi ^{2}_{2(T_{c}-U_{c}+1)}$ given D _0,BS and I _d,c. Since the BS employs ZF with perfect CSI under Rayleigh fading channel to cancel out the interference while boosting the desired signal power, (U _c−1) degrees of freedom is used to null the interference created from other cellular users, hence array gain is reduced to T _c−U _c+1. The distribution of the desired signal power $|\mathbf {h}_{0}^{H} \mathbf {v}_{0}|^{2}$, as mentioned above, follows from the projection of a random vector v ₀ into an independent (T _c−U _c+1)-dimensional space of the channel. A detailed proof can be found in [41 , 42] and references therein.

In step (b) of (33), we use binomial expansion as

$$\begin{array}{*{20}l} \left(I_{d,c} + \frac{N_{0}}{A_{d}}\right)^{k} &= \sum_{i=0}^{k} {k \choose i} \left(\frac{N_{0}}{A_{d}}\right)^{k-i} I_{d,c}^{i}, \end{array} $$

(34)

and (c) follows by taking the expectation with respect to the interference I _d,c. Step (d) follows from

$$\begin{array}{*{20}l} \mathbb{E}_{I_{d,c}}\left[I_{d,c}^{i} e^{-s I_{d,c}} \right] = (-1)^{i} \frac{\mathrm{d}^{i}}{{\mathrm{d}s}^{i}} \mathcal{L}_{I_{d,c}}(s), \end{array} $$

(35)

where $\mathcal {L}_{I_{d,c}}(s)$ is obtained using similar steps as in the derivation of $\mathcal {L}_{I_{d,0}}$ in (32):

$$\begin{array}{*{20}l} \mathcal{L}_{I_{d,c}}(s) = \exp\left(-\frac{\pi \lambda_{d} P_{d}^{2/\alpha_{d}}}{\text{sinc}\left(\frac{2}{\alpha_{d}}\right)} s^{2/\alpha_{d}}\right). \end{array} $$

(36)

Substituting (36) in (33) and using the Faà di Bruno’s formula for the i-th derivative of a composite function f(g(s)) with f(s)=e ^s and $g(s) = - \frac {\pi \lambda _{d} P_{d}^{2/\alpha _{d}}}{\text {sinc}\left (\frac {2}{\alpha _{d}}\right)} s^{2/\alpha _{d}}$, Proposition 2 follows. □

Notes

References

1.
A Osseiran, F Boccardi, V Braun, K Kusume, P Marsch, M Maternia, O Questeh, M Schellmann, H Schotten, H Taoka, H Tulberg, MA Uusitalo, B Timus, M Fallgren, Scenarios for 5G mobile and wireless communications: the vision of the METIS project. IEEE Commun. Mag.52(5), 26–35 (2014).CrossRefGoogle Scholar
2.
E Björnson, E Jorswieck, M Debbah, B Ottersten, Multi-objective signal processing optimization: The way to balance conflicting metrics in 5G systems. IEEE Signal Process. Mag.31(6), 14–23 (2014).CrossRefGoogle Scholar
3.
TL Marzetta, Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wireless Commun.9(11), 3590–3600 (2010).CrossRefGoogle Scholar
4.
F Rusek, D Persson, LK Buon, EG Larsson, TL Marzetta, O Edfors, F Tufvesson, Scaling up MIMO: opportunities and challenges with very large arrays. IEEE Signal Process. Mag.30(1), 40–60 (2013).CrossRefGoogle Scholar
5.
E Björnson, EG Larsson, M Debbah, Massive MIMO for maximal spectral efficiency: how many users and pilots should be allocated?IEEE Trans. Wireless Commun.15(2), 1293–1308 (2016).CrossRefGoogle Scholar
6.
HQ Ngo, EG Larsson, TL Marzetta, Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun.61(4), 1436–1449 (2013).CrossRefGoogle Scholar
7.
E Björnson, L Sanguinetti, J Hoydis, M Debbah, Optimal design of energy-efficient multi-user MIMO systems: is massive MIMO the answer?IEEE Trans. Wireless Commun.14(6), 3059–3075 (2015).CrossRefGoogle Scholar
8.
K Doppler, M Rinne, C Wijting, CB Ribeiro, K Hugl, Device-to-device communication as an underlay to LTE-advanced networks. IEEE Commun. Mag.47(12), 42–49 (2009).CrossRefGoogle Scholar
9.
3rd Generation Partnership Project, study on LTE device to device proximity services; Radio aspects, 3GPP TR 36.843 (2014).Google Scholar
10.
NK Pratas, P Popovski, Zero-outage cellular downlink with fixed-rate D2D underlay. IEEE Trans. Wireless Commun.14(7), 3533–3543 (2015).CrossRefGoogle Scholar
11.
JF Schmidt, MK Atiq, U Schilcher, C Bettstetter, in Proc. IEEE Int. Symp. on Personal, Indoor, Mobile Radio Commun. (PIMRC). Underlay device-to-device communications in LTE-A: uplink or downlink (Hong Kong, 2015).Google Scholar
12.
S Tombaz, A Vastberg, J Zander, Energy- and cost-efficient ultra-high-capacity wireless access. IEEE Wireless Commun.18(5), 18–24 (2011).CrossRefGoogle Scholar
13.
G Auer, V Giannini, C Desset, I Godor, P Skillermark, M Olsson, MA Imran, D Sabella, MJ Gonzalez, O Blume, A Fehske, How much energy is needed to run a wireless network?IEEE Wireless Commun.18(5), 40–49 (2011).CrossRefGoogle Scholar
14.
H Yang, TL Marzetta, in Proc. IEEE Online Conference on Green Commun. (OnlineGreenCom). Total energy efficiency of cellular large scale antenna system multiple access mobile networks (Piscataway, NJ, 2013).Google Scholar
15.
E Björnson, M Kountouris, M Debbah, in Proc. IEEE Int. Conf. on Telecommun. (ICT). Massive MIMO and small cells: improving energy efficiency by optimal soft-cell coordination (Casablanca, Morocco, 2013).Google Scholar
16.
H Min, J Lee, S Park, D Hong, Capacity enhancement using an interference limited area for device-to-device uplink underlaying cellular networks. IEEE Trans. Wireless Commun.10(12), 3995–4000 (2011).CrossRefGoogle Scholar
17.
W Yu, L Liang, SJ H. Zhang, JCF Li, M Lei, in Proc. IEEE Global Telecommun. Conf. (GLOBECOM). Performance enhanced transmission in device-to-device communications: beamforming or interference cancellation? (Anaheim, CA, 2012).Google Scholar
18.
N Reider, G Fodor, A distributed power control and mode selection algorithm for D2D communications. EURASIP J. on Wireless Commun. Netw. 2012(1), 1–25 (2012).CrossRefGoogle Scholar
19.
MGDS Rêgo, TF Maciel, HDHM Barros, FRP Cavalcanti, G Fodor, in Proc. Int. Symp. of Wireless Commun. Syst. (ISWCS). Performance analysis of power control for device-to-device communication in cellular MIMO systems (Paris, 2012).Google Scholar
20.
Y Ni, S Jin, W Xu, M Matthaiou, S Shaoand, H Zhu, in Proc. IEEE Int. Conf. on Commun. Workshops. Beamforming and interference cancellation schemes for D2D communications (London, UK, 2015).Google Scholar
21.
S Shalmashi, E Björnson, SB Slimane, M Debbah, in Proc. IEEE Wireless Commun. Network. Conf. (WCNC). Closed-form optimality characterization of network-assisted device-to-device communications (Istanbul, Turkey, 2014).Google Scholar
22.
X Lin, RW Heath Jr, JG Andrews, The interplay between massive MIMO and underlaid D2D networking. IEEE Trans. Wireless Commun.14(6), 3337–3351 (2015).CrossRefGoogle Scholar
23.
H Yin, L Cottatellucci, D Gesbert, in Proc. IEEE Asilomar Conf. Signals, Systems, and Computers. Enabling massive MIMO systems in the FDD mode thanks to D2D communications (Pacific Grove, CA, 2014).Google Scholar
24.
SAM Ghanem, L Cottatellucci, D2D cooperation to avoid instantaneous feedback in nonreciprocal massive MIMO systems. IEEE COMSOC MMTC Electronics. Lett.10(1), 39–42 (2015). Special issue on Novel approaches and technologies for 5G.Google Scholar
25.
BS Amin, YR Ramadan, AS Ibrahim, MH Ismail, in Proc. IEEE Wireless Commun. Network. Conf. (WCNC). Power allocation for device-to-device communication underlaying massive MIMO multicasting networks (New Orleans, LA, 2015).Google Scholar
26.
S Shalmashi, G Miao, SB Slimane, in Proc. IEEE Int. Symp. on Personal, Indoor, Mobile Radio Commun. (PIMRC). Interference management for multiple device-to-device communications underlaying cellular networks (London, UK, 2013).Google Scholar
27.
M Zulhasnine, S Changcheng, A Srinivasan, in Proc. IEEE Int. Conf. on Wireless and Mobile Computing, Networking, and Commun. (WiMob). Efficient resource allocation for device-to-device communication underlaying LTE network (Niagara Falls, ON, Canada, 2010).Google Scholar
28.
E Yaacoub, O Kubbar, in Proc. IEEE Global Telecommun. Conf. Workshops. Energy-efficient device-to-device communications in LTE public safety networks (Anaheim, CA, 2012).Google Scholar
29.
S Mumtaz, KMS Huq, A Radwan, J Rodriguez, RL Aguiar, in Proc. IEEE Int. Conf. on Commun. (ICC). Energy efficient interference-aware resource allocation in LTE-D2D communication (Sydney, Australia, 2014).Google Scholar
30.
F Wang, C Xu, L Song, Q Zhao, X Wang, Z Han, in Proc. IEEE Int. Conf. on Commun. (ICC). Energy-aware resource allocation for device-to-device underlay communication (Budapest, Hungary, 2013).Google Scholar
31.
R Baldemair, E Dahlman, G Fodor, G Mildh, S Parkvall, Y Selen, H Tullberg, K Balachandran, Evolving wireless communications: addressing the challenges and expectations of the future. IEEE Veh. Technol. Mag.8(1), 24–30 (2013).CrossRefGoogle Scholar
32.
Bjo, Ë,rnson, E Jorswieck, Optimal resource allocation in coordinated multi-cell systems. Foundations Trends Commun. Inform. Theory. 9(2–3), 113–381 (2013).CrossRefzbMATHGoogle Scholar
33.
D Gesbert, M Kountouris, RW Heath, CB Chae, T Salzer, Shifting the MIMO paradigm. IEEE Signal Process. Mag.24(5), 36–46 (2007).CrossRefGoogle Scholar
34.
M Haenggi, Stochastic Geometry for Wireless Networks (Cambridge University Press, Cambridge, UK, 2013).zbMATHGoogle Scholar
35.
X Lin, J Andrews, A Ghosh, Spectrum sharing for device-to-device communication in cellular networks. IEEE Trans. Wireless Commun.13(12), 6727–6740 (2014).CrossRefGoogle Scholar
36.
N Lee, X Lin, JG Andrews, RW Heath Jr, Power control for D2D underlaid cellular networks: modeling, algorithms and analysis. IEEE J. Sel. Areas Commun.33(1), 1–13 (2015).CrossRefGoogle Scholar
37.
MC Erturk, S Mukherjee, H Ishii, H Arslan, Distributions of transmit power and SINR in device-to-device networks. IEEE Commun. Lett.17(2), 273–276 (2013).CrossRefGoogle Scholar
38.
H ElSawy, E Hossain, MS Alouini, Analytical modeling of mode selection and power control for underlay D2D communication in cellular networks. IEEE Trans. Wireless Commun.62(11), 4147–4161 (2014).CrossRefGoogle Scholar
39.
Z Chen, M Kountouris, in Proc. IEEE Int. Conf. on Commun. Workshops. Guard zone based D2D underlaid cellular networks with two-tier dependence (London, UK, 2015).Google Scholar
40.
G George, RK Mungara, A Lozano, An analytical framework for device-to-device communication in cellular networks. IEEE Trans. Wireless Commun.14(11), 6297–6310 (2015).CrossRefGoogle Scholar
41.
HS Dhillon, M Kountouris, JG Andrews, Downlink MIMO HetNets: Modelling, ordering results and performance analysis. IEEE Trans. Wireless Commun.12(10), 5208–5222 (2013).CrossRefGoogle Scholar
42.
V Chandrasekhar, M Kountouris, JG Andrews, Coverage in multi-antenna two-tier networks. IEEE Trans. Wireless Commun.8(10), 5314–5327 (2009).CrossRefGoogle Scholar
43.
E Björnson, M Bengtsson, B Ottersten, Optimal multiuser transmit beamforming: a difficult problem with a simple solution structure [lecture notes]. IEEE Signal Process. Mag.31(4), 142–148 (2014).CrossRefGoogle Scholar
44.
H Shokri-Ghadikolaei, C Fischione, P Popovski, M Zorzi, Design aspects of short range millimeter wave networks: a MAC layer perspective. IEEE Network. 30(3), 88–96 (2016).CrossRefGoogle Scholar
45.
M Kountouris, JG Andrews, Downlink SDMA with limited feedback in interference-limited wireless networks. IEEE Trans. Wireless Commun.11(8), 2730–2741 (2012).Google Scholar
46.
JG Andrews, S Buzzi, W Choi, SV Hanly, A Lozano, ACK Soong, JC Zhang, What will 5G be?IEEE J. Sel. Areas Commun.32(6), 1065–1082 (2014).CrossRefGoogle Scholar
47.
P Popovski, V Braun, H-P Mayer, P Fertl, et al, ICT-317669-METIS/D1.1 scenarios, requirements and KPIs for 5G mobile and wireless system. Technical report (2013). http://www.metis2020.com/. Accessed 30 Apr 2013.
48.
S Weber, JG Andrews, Transmission capacity of wireless networks. Foundations Trends Netw. 5(2–3), 109–281 (2012).zbMATHGoogle Scholar
49.
J Han-Shin, JS Young, X Ping, JG Andrews, Heterogeneous cellular networks with flexible cell association: a comprehensive downlink SINR analysis. IEEE Trans. Wireless Commun.11(10), 3484–3495 (2012).CrossRefGoogle Scholar
50.
JG Andrews, F Baccelli, RK Ganti, A tractable approach to coverage and rate in cellular networks. IEEE Trans. Commun.59(11), 3122–3134 (2011).CrossRefGoogle Scholar
51.
N Jindal, MIMO broadcast channels with finite-rate feedback. IEEE Trans. Inf. Theory. 52(11), 5045–5060 (2006).MathSciNetCrossRefzbMATHGoogle Scholar
52.
E Björnson, EG Larsson, TL Marzetta, Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 54(2), 114–123 (2016).CrossRefGoogle Scholar
53.
EG Larsson, F Tufvesson, O Edfors, TL Marzetta, Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 52(2), 186–195 (2014).CrossRefGoogle Scholar
54.
H Xing, S Hakola, in Proc. IEEE Int. Symp. on Personal, Indoor, Mobile Radio Commun. (PIMRC). The investigation of power control schemes for a device-to-device communication integrated into OFDMA cellular system (Istanbul, Turkey, 2010), pp. 1775–1780.Google Scholar
55.
S Shalmashi, E Björnson, M Kountouris, KW Sung, M Debbah, in Proc. IEEE Int. Conf. on Commun. Workshops. Energy efficiency and sum rate when massive MIMO meets device-to-device communication (London, UK, 2015).Google Scholar

Copyright information

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

Serveh Shalmashi
- 1
Email authorView author's OrcID profile
Emil Björnson
- 2
Marios Kountouris
- 3
Ki Won Sung
- 1
Mérouane Debbah
- 3

1.Department of Communication SystemsKTH Royal Institute of TechnologyStockholmSweden
2.Department of Electrical Engineering (ISY)Linköping UniversityLinköpingSweden
3.Mathematical and Algorithmic Sciences LabFrance Research Center, Huawei Technologies Co. Ltd.ParisFrance

Energy efficiency and sum rate tradeoffs for massive MIMO systems with underlaid device-to-device communications

Abstract

Keywords

1 Introduction

1.1 Related work

1.2 Contributions

2 System model

3 Performance analysis

3.1 Performance metrics

3.2 Coverage probability of D2D users

Proposition 1

Proof

Remark 1

Remark 2

Remark 3

Remark 4

Remark 5

Corollary 1

Proof

3.3 Coverage probability of cellular users

Proposition 2

Proof

Remark 6

Remark 7

Corollary 2

Proof

Corollary 3

Proof

Corollary 4

Proof

4 Numerical results

4.1 Number of CUEs as a function of the number of BS antennas

4.2 Fixed number of CUEs

4.3 The effect of other system parameters

5 Conclusions

6 Endnote

7 Appendix 1: Proof of Proposition 1

8 Appendix 2: Proof of Proposition 2

Notes

References

Copyright information

Authors and Affiliations

Personalised recommendations