1 Introduction

Fifth generation (5G) networks will face new challenges that will require a higher level of flexibility from the physical layer (PHY). 3D and 4k video will push the throughput and spectral efficiency. Tactile Internet [1] will demand latencies at least one order of magnitude smaller than what fourth generation (4G) can achieve. Machine type communication (MTC) [2] will require loose synchronization, low power consumption and a massive number of connections. Wireless Regional Area Network (WRAN) [3] needs to cover wide areas to provide Internet access in low populated regions. The future mobile networks must have a flexible PHY to address several different scenarios.

Generalized Frequency Division Multiplexing (GFDM) [4] is a recent waveform that can be engineered to address various use cases. GFDM arranges the data symbols in a time-frequency grid, consisting of M subsymbols and K subcarriers, and applies a circular prototype filter for each subcarrier. GFDM can be easily configured to cover other waveforms, such as Orthogonal Frequency Division Multiplexing (OFDM) [5] and Single Carrier Frequency Domain Multiple Access (SC-FDMA) [6] as corner cases. The subcarrier filtering can reduce the out-of-band (OOB) emissions, control peak to average power ratio (PAPR) and allows dynamic spectrum allocation. GFDM, with its block-based structure, can reuse several solutions developed for OFDM, for instance, the concept of a cyclic prefix (CP) to avoid inter-frame interference. Hence, frequency-domain equalization can be efficiently employed to combat the effects of multipath channels prior to the demodulation process. With these features, GFDM can address the requirements of 5G networks.

The main disadvantage of a flexible waveform is the complexity required for its implementation. Reducing the GFDM complexity is essential to bring its flexibility to 5G networks. The understanding of GFDM as a filtered multicarrier scheme leads to a modem implementation based on time-domain circular convolution for each subcarrier, performed in the frequency domain [4]. This paper follows the well-known polyphase implementation of filter bank modulation [5–7] and applies it to GFDM.

As one main contribution, the investigation in this paper reveals that the Poisson summation formula [8] can be utilized in the demodulation process, considering a per-subsymbol circular convolution and decimation in the frequency domain. This operation can be performed as an element-wise multiplication with subsequent simple M-fold accumulation in the time domain. This simple re-orientation of the data symbol processing allows for a considerable reduction in complexity, which makes GFDM applicable in a wide range of scenarios.

This paper also contributes to reformulate the modulation and demodulation as matrix-vector operations based on M (K)-point discrete Fourier transforms (DFTs). As an outcome, it becomes evident that DFT can actually be considered as a precoding operation. Moreover, they can be replaced by other transformations as well. This observation facilitates arbitrary precoding of the GFDM data, which adds a new level of flexibility to the system, which will be exemplified by the use of three different transforms: (i) Walsh-Hadamard transform (WHT) [9]; (ii) constant amplitude zero auto-correlation (CAZAC) [10] and; (iii) discrete Hartley transform (DHT) [11].

It is worth mentioning that the proposed low complexity signal processing complements the work in [4] because the requirement for block alignment is loosened. It can be usable for supporting pipeline inner receiver implementations, particularly when building synchronization and channel estimation circuits for embedded training sequences [12, 13]. It can also be beneficial to develop future non-linear and recursive detection algorithms.

The remainder of this paper is organized as follows: Section 2 describes the classical approach for GFDM modulation and demodulation and introduce reformulated expressions for a less complex implementation. Section 3 presents the matrix notation to describe the modulation and demodulation processes. Section 4 introduces precoding to the GFDM communication chain. Section 5 shows the complexity analysis of the precoded schemes. Section 6 brings three examples of precoding using different unitary transforms and Section 7 concludes the paper.

2 Classical GFDM description and low-complexity reformulation

Consider a wireless communication system that transmits data in a block-based structure that consists of K subcarriers and M subsymbols. Let N=K M be the total number of data symbols in the block and d k,m , \(k=0, \dots, K-1\), \(m=0, \dots, M-1\), denote the complex valued data symbol that is transmitted on the kth subcarrier and mth subsymbol. The classical description of GFDM signal generation [14] is given by

$$ x[\!n] = \sum_{k=0}^{K-1}\left(g[\!n] \exp\left(j2\pi \frac{k}{K}n\right)\right)\circledast d_{k}[\!n] $$
(1)

with

$$ d_{k}[\!n] = \sum_{m=0}^{M-1}d_{k,m}\delta[n-mK], $$
(2)

where \(n=0,\dots,N-1\), \(\circledast \) describes circular convolution carried out with period N and g[ n] denotes the impulse response of the transmit prototype filter.

The subcarrier filtering does not guarantee orthogonality between subcarriers, unless specific prototype filters are used, such as the Dirichlet pulse [15]. Offset Quadrature Amplitude Modulation (OQAM) mapping can also be employed to achieve real-orthogonality [16] and avoid self-interference. In a more general case, the demodulator needs to deal with self-interference. Matched filter (MF) can be combined with successive interference cancellation (SIC) [17] or, alternatively, the self-interference can be mitigated with zero-forcing (ZF) or minimum mean square error (MMSE) filters, for which a simple design based on the Zak transform is available [18].

Using the N-point DFT \(\mathcal {F}_{N}\), (1) can be carried out as

$$ \begin{aligned} x[\!n] =\mathcal{F}_{N}^{-1} \sum_{k=0}^{K-1}\left\{ \underbrace{\mathcal{F}_{N}\left\{g[\!n]\exp\left(j2\pi \frac{k}{K}n\right)\right\}}_{G[\left<f-kM\right>_{N}]} \underbrace{\mathcal{F}_{N}\{d_{k}[\!n]\}}_{\mathcal{F}_{M}\left\{d_{k,(\cdot)}\right\}|_{f}}\right\}, \end{aligned} $$
(3)

where \(\left <\bullet \right >_{N}\) denotes the remainder modulo N and \(G[f]=\mathcal {F}_{N}\{g[\!n]\}\). Due to periodicity of \(\mathcal {F}_{M}\) with period M and \(f=0,\dots,MK-1\), \(\mathcal {F}_{M}\{d_{k,(\cdot)}\}\) is concatenated K times. This leads to the low-complexity modulator implementation described in [4]. Now, expressing the convolution in (1) explicitly, the transmission equation can be reformulated as [6]

$$ {{}\begin{aligned} x[\!n] = \sum_{m=0}^{M-1}g\left[\left<n-mK\right>_{N}\right]\underbrace{\sum_{k=0}^{K-1}d_{k,m}\exp\left(j2\pi \frac{k}{K}n\right)}_{K\mathcal{F}^{-1}_{K}\left\{d_{(\cdot),m}\right\}|_{n}}. \end{aligned}} $$
(4)

The sequence obtained from the Inverse Discrete Fourier Transform (IDFT) is concatenated M times in time-domain due to \(n=0,\dots,MK-1\). Such multiplication in the time-domain expresses the convolution of the subcarrier filter with the data in the frequency domain for each subsymbol.

Assuming a flat and noiseless channel, the convolution of the received signal y[ n]=x[ n] with a demodulation filter γ[ n], is given by

$$ {{}\begin{aligned} \hat{\!\!\!d}_{k,m}=\left(\gamma^{*}\left[\left<-n\right>_{N}\right]\circledast y[\!n]\exp\left(-j2\pi \frac{k}{K}n\right)\right)|_{n=mK}. \end{aligned}} $$
(5)

With the help of DFT, (5) can be rewritten as

$$ \begin{aligned} \hat{\!\!\!d}_{k,m}=&\mathcal{F}^{-1}_{N}\left\{ \underbrace{\mathcal{F}_{N}\left\{\gamma^{*}\left[\left<-n\right>_{N}\right]\right\}}_{\Gamma^{*}\left[f\right]}\right.\\ &\left.\left.\underbrace{\mathcal{F}_{N}\left\{y[\!n]\exp\left(-j2\pi \frac{k}{K}n\right)\right\}}_{Y\left[\left< f+kM\right>_{N}\right]} \right\}\right|_{mK}, \end{aligned} $$
(6)

where \(\mathcal {F}_{N}\left \{\gamma [\!n]\right \}=\Gamma [f]\) and \(\mathcal {F}_{N}\left \{y[\!n]\right \}=Y[f]\). For example, this leads to the low-complexity demodulator implementation described in [4] for the MF γ[ n]=g[ n], which was later extended to more general filter types in [18]. Now, directly expressing the convolution and sampling in (5) leads to the time-domain multiplication

$$ {{}\begin{aligned} \hat{d}_{k,m}&=\sum_{n=0}^{N-1}\gamma^{*}\left[\left<n-mK\right>_{N}\right]y[\!n]\exp\left(-j2\pi \frac{kM}{KM}n\right)\\ &= \mathcal{F}_{N}\left\{\gamma^{*}\left[\left<n-mK\right>_{N}\right]y[\!n]\right\}|_{kM}, \end{aligned}} $$
(7)

where the N-point DFT is only evaluated at every Mth sample. According to the Poisson summation formula [8], this can be reduced to a \(\frac {N}{M}=K\) point DFT

$$\begin{array}{*{20}l} \mathcal{F}_{N}\{u[\!n]\}|_{kM}&=\mathcal{F}_{\frac{N}{M}}\left.\left\{\sum_{m=0}^{M-1}u\left[\left<n-mK\right>_{N}\right]\right\}\right|_{k}. \end{array} $$
(8)

Equation 7 describes a sampled short-time Fourier transform (STFT). This is clear since the GFDM demodulator is actually performing a Gabor transform [18], which can be understood as a sampled STFT. For this reason, (7) does not allow to employ different prototype filters per subcarrier. This constraint is circumvented by performing equalization before demodulation or the presented scheme can be used to initially access the channel state information by demodulation of training data. Also, the proposed scheme facilitates the implementation of odd number of subsymbols [18] avoiding the use of M-point DFT and IDFT required in [4].

Notice that (7) holds when MF, ZF or MMSE filters are used. ZF or MMSE filters can deliver good symbol error rate (SER) performance, while MF needs SIC to remove the SER floor caused by the self-interference. Hence, (7) shall be used to implement ZF and MMSE demodulators, while MF can be considered when the transmit filters are orthogonal or OQAM is employed.

3 GFDM matrix model

Arranging the data symbols d k,m in a two-dimensional structure leads to the data matrix

$$ \mathbf{D}=\left(\mathbf{d}^{\text{c}}_{0} \,\, \mathbf{d}^{\text{c}}_{1} \,\, \cdots \,\, \mathbf{d}^{\text{c}}_{M-1}\right),=\left(\begin{array}{c} \mathbf{d}^{\text{r}}_{0}\\ \mathbf{d}^{\text{r}}_{1}\\ \vdots\\ \mathbf{d}^{\text{r}}_{K-1} \end{array}\right), $$
(9)

where \(\mathbf {d}^{\text {c}}_{m} = \left (d_{0,m} \,\,\, d_{1,m} \,\,\, \dots \,\,\, d_{K-1,m}\right)^{\mathrm {T}}\) denotes the data symbols transmitted in the mth subsymbol.

According to the GFDM description in Section 2, the rows and columns correspond to the time and frequency resources in Fig. 1, respectively. Hence, the kth row of D represents the data symbols transmitted in the kth subcarrier, \(\mathbf {d}^{\text {r}}_{k} = \left (d_{k,0} \,\,\, d_{k,1} \,\,\, \dots \,\,\, d_{k,M-1} \right)\). The time-domain circular convolution of the modulation process can be expressed in the frequency domain as [4]

$$ \mathbf{x} = \frac{1}{N}\mathbf{W}_{N}^{\mathrm{H}} \sum \limits_{k=0}^{K-1} \mathbf{P}^{(k)} \mathbf{G} \mathbf{R}^{(K,M)} \mathbf{W}_{M} {\mathbf{d}^{\text{r}}_{k}}^{\mathrm{T}}. $$
(10)
Fig. 1
figure 1

Overview of block structure and terminology

Full size image

For each subcarrier, the data vector is taken to the frequency domain by the M-point DFT matrix W M . The corresponding time domain up sampling operation is realized in the frequency domain by duplicating the transformed data symbols vectors K times, using the repetition matrix \(\mathbf {R}^{(K,M)} = \mathbf {1}_{K,1}\otimes \mathbf {I}_{M}\), where I M is an M size identity matrix, 1 i,j is a i×j matrix of ones and ⊗ is the Kronecker product. Each subcarrier is then filtered with G=diag(W N g), where diag(∙) returns a matrix that contains the argument vector on its diagonal and zeros otherwise and g is the vector containing the transmit filter impulse response. An up-conversion of the kth subcarrier to its respective subcarrier frequency is performed by the shift matrix

$$ \mathbf{P}^{(k)}=\mathbf{\Psi}\left(\mathbf{p}^{(k)}\right)\otimes\mathbf{I}_{M}, $$
(11)

where Ψ(∙) returns the circulant matrix based on the input vector and p (k) is a column vector where the kth element is 1 and all others are zeros. The K subcarriers are summed and transformed back to the time domain with \(\mathbf {W}_{N}^{H}\) to compose the GFDM signal. On the demodulator side, the recovered data symbols for the kth subcarrier are given by

$$ \hat{\mathbf{d}}_{k}^{\text{r}}= \mathbf{W}_{\!\!M\,\,}^{\mathrm{H}} \left(\mathbf{R}^{(K,M)}\right)^{\mathrm{T}} \boldsymbol{\Gamma} \left(\mathbf{P}^{(k)} \right)^{\mathrm{T}} \mathbf{W}_{N} \mathbf{y}, $$
(12)

where y is the equalized vector at the input of the demodulator, Γ=diag(W N γ) with γ being the demodulation filter impulse response, e.g., MF, ZF, or MMSE filters.

The modulation and demodulation processes can be simplified just by changing the processing order of the data symbols, as derived in (4). In this new matrix model, the GFDM vector is given by

$$ \mathbf{x} = \sum\limits_{m=0}^{M-1} \mathbf{P}^{(m)} \text{diag}(\boldsymbol{g}) \mathbf{R}^{(M,K)} \mathbf{W}_{K}^{\text{H}} \mathbf{d}^{\text{c}}_{m}. $$
(13)

Observe that (13) is similar to a polyphase filter structure, but with the difference that cyclic time-shifts are used here and frequency domain convolution is performed in time domain as element-wise vector multiplication. With this approach, the first step is to obtain a time domain version of \( \mathbf {d}^{\text {c}}_{m} \) by multiplying it with an inverse DFT (IDFT) matrix \(\mathbf {W}_{K}^{\mathrm {H}}\). M times upsampling in frequency domain is performed in time by duplicating the transformed data symbols with a repetition matrix R (M,K). Each subsymbol is then pulse-shaped with g. P (m) shifts the mth subsymbol to its respective position in time. The GFDM signal is obtained by summing all the pulse-shaped subsymbols, with no need of the N-IDFT domain conversion in (10).

The demodulation operations are also simplified by using the circular-convolution in frequency domain, leading to

$$ \hat{\mathbf{d}}^{\text{c}}_{m} = {\mathbf{W}_{K}}\left(\mathbf{R}^{(M,K)}\right)^{\mathrm{T}} \text{diag}(\boldsymbol{\gamma}) \left(\mathbf{P}^{(m)} \right)^{\mathrm{T}} \mathbf{y}. $$
(14)

While the new approach describing GFDM modulation and demodulation as convolution in the frequency domain reduces the implementation complexity; in the next section, this principle will be expanded to a more general structure, where domain conversions will be understood as a precoding process.

4 DFT-based precoding for GFDM

Equations (13) and (14) bring a new interpretation of the GFDM chain that further increases the flexibility of this waveform. Let the transmit vector from (13) be redefined as

$$ \mathbf{x} = \sum\limits_{m=0}^{M-1} \mathbf{P}^{(m)} \text{diag}(\boldsymbol{g}) \mathbf{R}^{(M,K)} \boldsymbol{\delta}_{m}, $$
(15)

where

$$ \boldsymbol{\delta}_{m}=\mathbf{T}\mathbf{d}^{\text{c}}_{m} $$
(16)

is the information coefficient vector to be transmitted and T is a transformation matrix. For classical GFDM, where a time-frequency grid is used to transmit the information, \(\mathbf {T}=\mathbf {W}_{K}^{H}\). However, (16) can be seen as precoding the information vector by a generic matrix T. Different matrices can be used to achieve different requirements. Hence, by transmitting precoded data, GFDM can be even more flexible to address requirements of future wireless networks.

On the receiver side, the recovered coefficients are given by

$$ \hat{\boldsymbol{\delta}}_{m} = \left(\mathbf{R}^{(M,K)}\right)^{\mathrm{T}} \text{diag}(\boldsymbol{\gamma}) \left(\mathbf{P}^{(m)} \right)^{\mathrm{T}} \mathbf{y}. $$
(17)

The estimated data symbols are obtained by reverting the precoding operation on (17), leading to

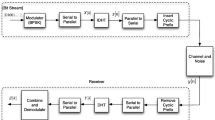
$$ \hat{\mathbf{d}}^{\text{c}}_{m}=\mathbf{S}\hat{\boldsymbol{\delta}}_{m}. $$
(18)

where S removes precoding. For conventional GFDM, S=W K . A block diagram that describes the proposed GFDM modem is presented in Fig. 2. The demodulation part can be implemented to run continuously, which can be used for tracking specific properties of the estimated information coefficient vector \(\hat {\boldsymbol {\delta }}_{m}\) containing training data.

Fig. 2
figure 2

Block diagram of low-complexity modulator and demodulator with precoding

Full size image

The precoding concept can be enlarged to embrace any transform taking into account the two dimensions of the GFDM data block D, which is defined as a time-frequency grid spanning over several subcarriers and subsymbols, as depicted in Fig. 1. Hence, in the default configuration, the columns of the matrix contain data defined in the frequency domain, while the rows have data in the time domain. The precoded data block Δ can be generalized to

$$ \underset{K \times M}{\boldsymbol{\Delta}{\vphantom{\mathbf{T}_{\text{c}}}}} = \underset{K \times K}{\mathbf{T}_{\text{c}}} \cdot \underset{K \times M}{\mathbf{D}{\vphantom{\mathbf{T}_{\text{c}}}}} \cdot \underset{M \times M}{\mathbf{T}_{\text{r}}}, $$
(19)

where D is now a data block defined in an arbitrary domain, T c is a K by K precoding matrix applied to the columns and T r is a M by M precoding matrix applied to the rows of D. For instance, choosing T c and T r to be Fourier matrices yields four domains for the GFDM data block,as given in Table 1, where the frequency-time (FT) domain corresponds to standard GFDM.

Table 1 Precoding in time (T) and frequency (F) domains
Full size table

The choice of the data domain has impact on the robustness of the system regarding time- and frequency- selective fading. The concept is not limited to DFT and, in general, any meaningful transform can be applied to the rows and columns, as exemplified in Section 5.

Taking the concept one step further, (19) can be formulated as

$$ \operatorname{vec}\!\left(\boldsymbol{\Delta}\right) = \operatorname{vec}\!\left(\mathbf{T}_{\text{c}} \mathbf{D} \mathbf{T}_{\text{r}}\right). $$
(20)

With the help of the Kronecker product, the right part of (20) can be expressed as

$$ \operatorname{vec}\!\left(\mathbf{T}_{\text{c}} \mathbf{D} \mathbf{T}_{\text{r}}\right) = \left(\mathbf{T}_{\text{r}}^{\mathrm{T}} \otimes \mathbf{T}_{\text{c}} \right) \operatorname{vec}\!\left(\mathbf{D}\right). $$
(21)

The resulting matrix

$$ \mathbf{\mathcal{T}} = \left(\mathbf{T}_{\text{r}}^{\mathrm{T}} \otimes \mathbf{T}_{\text{c}} \right) $$
(22)

can be seen as an even more general way of precoding that is not restricted to subcarriers or subsymbols but allows arbitrary coupling between any elements of d= vec(D). The precoding is then applied leading to \(\boldsymbol {\delta } = \mathbf {\mathcal {T}} \mathbf {d}\).

5 Out of band, PAPR and complexity analysis

The special precoding examples presented in Section 4 can have specific applications. The FT mode allows for use of null subsymbols and subcarriers to support non-continuous bands, achieving a low OOB radiation as shown in Fig. 3. The time-time (TT) case leads GFDM to become a single-carrier system occupying the whole system bandwidth. This precoding is especially beneficial for power-limited systems that cannot afford complex signal processing. Another beneficial aspect of the TT precoding is the low PAPR, as can be observed in Fig. 3. In contrast, frequency-frequency precoding (FF) results in a DFT-precoded GFDM system, with a spectrum similar to OFDM. In FF mode, data is defined directly in the frequency domain, according to (3). In this case, one data symbol occupies no more than two frequency bins, assuming a bandlimited transmit filter, such as raised cosine. This property simplifies equalization, as only ICI remains, but on the other hand reduces frequency diversity in channels with strong frequency selectivity. Finally, time-frequency precoding (TF) also corresponds to the single carrier, but with symbols spread in time, creating potential for exploiting time diversity.

Fig. 3
figure 3

OOB, PAPR and complexity analysis for precoded GFDM. FT/FF: M=16, M on=15, K=128, K on=75, TT/TF: K=1, M=1200, OFDM: N=2048, N on=1200

Full size image

The complexity of the precoding operation of the GFDM transceiver based on DFT algorithms are evaluated in Table 1. The number of complex valued multiplications, a costly operation in implementations, is the chosen criterion for the analysis. The comparison is carried out under the assumption that N=K M complex data symbols are transmitted. As the baseline for the comparison in Fig. 3, MN multiplications from (17) are added to the precoding operations and the OFDM algorithm requires naturally the complexity of a DFT operation, with \(N\log _{2}(N)\) multiplications. For purposes of comparison, Table 2 also shows an example assuming a scenario equivalent to Long-Term evolution (LTE) with 20 MHz bandwidth [19]. On the receiver side, the GFDM signal is demodulated with a ZF filter [17], which is a worst-case scenario, since the benefits from a sparse frequency response cannot be harvested.

Table 2 Number of multiplications of DFT models. Modulation and demodulation complexity are the same with this criterion
Full size table

The GFDM modulator and demodulator proposed in [4] require the complexity of the M-point DFT algorithm with additional K times complex multiplications over repeated chunks of M complex samples, resulting from a DFT operation. Even when the frequency response of the demodulation filter is assumed to be sparse, e.g., when roll-off is small and a ZF filter span L can be smaller than the total number of subcarriers, the modem scheme presented in this paper is less complex than the solution proposed in [4]. Another obstacle for the implementation in [4] is that it is based M-point DFT operations and M is optimally chosen to be odd as shown in [18]. Hence, DFT of odd length would need to be implemented which cannot be achieved by radix-2 FFT algorithms.

Recently, an alternative formulation for low-complexity implementation of GFDM modulators and demodulators was shown in [20]. The presented algorithm relies on a block-diagonalization of the transmitter and receiver matrix by using a block-DFT matrix, which can be easily implemented by means of the FFT. The achieved complexity statistics in [20] are comparable to the ones presented in the present paper. However, [20] relies on a specific structure of the transmitter and receiver filters, such that the diagonalization can be employed. Fortunately, at the receiver, this structure is obeyed for MF, ZF and MMSE receiver filters. However, the solution is not general in the sense that any filter at the receiver can be employed with the algorithm in [20]. For example, different filters might be employed when the channel noise is correlated, polluted by interference or not all subcarriers are allocated. In contrast, the algorithm presented in this paper does not rely on any structure of the receiver filter and hence equally works with any time-domain function γ[ n] in (5). This is achieved by smartly rearranging the terms in (5) without making any assumptions on γ[ n].

6 Expanding GFDM features with unitary transform precoding

Several different unitary transforms can be associated with GFDM to achieve specific goals. Three examples based on WHT, CAZAC, and DHT will be explored in the following.

6.1 WHT-GFDM

WHT can be combined with GFDM [9] to increase the system robustness against frequency-selective channels. In this case, the WHT is applied to the data symbols on each subsymbol \(\mathbf {d}^{\text {c}}_{m}\), leading to

$$ \boldsymbol{\delta}_{m} = \frac{1}{\sqrt{K}}\mathbf{W}_{K}^{\text{H}}\boldsymbol{\Omega}_{K}\mathbf{d}^{\text{c}}_{m}, $$
(23)

where

$$ \boldsymbol{\Omega}_{K} = \left(\begin{array}{c c} \boldsymbol{\Omega}_{K/2} & \boldsymbol{\Omega}_{K/2}\\ \boldsymbol{\Omega}_{K/2} & -\boldsymbol{\Omega}_{K/2}\end{array}\right) $$
(24)

with Ω 1=(1) is the Walsh-Hadamard matrix. Notice that, in this case,

$$ \mathbf{T}= \frac{1}{\sqrt{K}}\mathbf{W}_{K}^{\text{H}}\boldsymbol{\Omega}_{K} $$
(25)

and (15) can be used to generate the WHT-GFDM symbol.

On the receiver side, (17) can be used to obtain the recovered coefficients and the reverse precoding matrix

$$ \mathbf{S}=\frac{1}{\sqrt{K}}\boldsymbol{\Omega}_{K}\mathbf{W}_{K} $$
(26)

is used to obtain the received data vectors, i.e.,

$$ \hat{\mathbf{d}}^{\text{c}}_{m}=\mathbf{S}\hat{\boldsymbol{\delta}}_{m}=\frac{1}{\sqrt{K}}\boldsymbol{\Omega}_{K}\mathbf{W}_{K}\hat{\boldsymbol{\delta}}_{m}. $$
(27)

6.2 CAZAC-GFDM

The CAZAC transform is a unitary transform where the coefficients of its matrix are given by [21]

$$ \left[\mathbf{C}_{K}\right]_{i,l} =\frac{1}{\sqrt{K}} \exp\left(j\pi(i+lK)^{2}\right), $$
(28)

with \(i=0,\,1,\,\dots,\,K-1\), \( l=0,\,1,\,\dots,\,K-1\) and \(\mathbf {C}_{K}^{\text {H}}\mathbf {C}_{K}=\mathbf {I}_{K}\).

Like the WHT, the CAZAC matrix can be used to precode the data symbols in the GFDM system. In this case, the coefficient vector transmitted by the CAZAC-GFDM system is given by [10]

$$ \boldsymbol{\delta}_{m} = \mathbf{W}_{K}^{\text{H}}\mathbf{C}_{K}\mathbf{d}^{\text{c}}_{m}. $$
(29)

Therefore, the precoding matrix for the CAZAC-GFDM is given by

$$ \mathbf{T} = \mathbf{W}_{K}^{\text{H}}\mathbf{C}_{K} $$
(30)

and the inverse precoding matrix is

$$ \mathbf{S}=\mathbf{C}_{K}^{\text{H}}\mathbf{W}_{K}. $$
(31)

The recovered data symbols are given by

$$ \hat{\mathbf{d}}^{\text{c}}_{m}=\mathbf{S}\hat{\boldsymbol{\delta}}_{m}= \mathbf{C}_{K}^{\text{H}}\mathbf{W}_{K} \hat{\boldsymbol{\delta}}_{m}. $$
(32)

6.3 DHT-GFDM

The discrete Hartley transform (DHT) is a linear unitary transform with matrix coefficients given by [11]

$$ \left[\boldsymbol{\Theta}_{K}\right]_{i,j}= \frac{1}{\sqrt{K}}\left(\cos\left(\frac{2\pi ij}{K}\right)+\sin\left(\frac{2\pi ij}{K}\right)\right). $$
(33)

Notice that \(\boldsymbol {\Theta }_{K}^{\text {T}}\boldsymbol {\Theta }_{K}=\mathbf {I}_{K}\).

DHT can be combined with GFDM, leading to the following precoding coefficients

$$ \boldsymbol{\delta}_{m} = \mathbf{W}_{K}^{\text{H}}\boldsymbol{\Theta}_{K}\mathbf{d}^{\text{c}}_{m}. $$
(34)

The precoding and inverse precoding matrices are given by

$$ \begin{aligned} \mathbf{T}&=\mathbf{W}_{K}^{\text{H}}\boldsymbol{\Theta}_{K}\\ \mathbf{S}&=\boldsymbol{\Theta}_{K}^{\text{T}}\mathbf{W}_{K}, \end{aligned} $$
(35)

respectively. Therefore, the recovered data symbols can be written as

$$ \hat{\mathbf{d}}^{\text{c}}_{m}=\mathbf{S}\hat{\boldsymbol{\delta}}_{m}= \boldsymbol{\Theta}_{K}^{\text{T}}\mathbf{W}_{K} \hat{\boldsymbol{\delta}}_{m}. $$
(36)

6.4 Precoding performance analysis

The main advantage of the precoding schemes presented in this section is that each subcarrier carries a linear combination of all data symbols from a given subsymbol. This procedure spreads the information over all subcarriers, allowing the receiver to exploit frequency diversity. Since the columns and rows of the precoding matrices are orthogonal to each other, the data symbols can be recovered on the receiver side without self-interference introduced by the precoding operation. Therefore, the precoding GFDM schemes experience a performance gain over conventional GFDM in frequency-selective channels, as can be seen in Fig. 4. The parameters used for simulation are presented in Table 3.

Fig. 4
figure 4

Symbol error rate of GFDM with and without precoding over the frequency selective channel presented in Table 3

Full size image
Table 3 Simulations parameters
Full size table

The theoretical symbol error rate for GFDM is given by [17]

$$ \begin{aligned} p=&2\left(\frac{\kappa-1}{\kappa K}\right)\sum_{l=0}^{K-1}\text{erfc}\left({\sqrt{\gamma_{l}}}\right)-\\ &\frac{1}{K}\left(\frac{\kappa-1}{\kappa}\right)^{2}\sum_{l=0}^{K-1}\text{erfc}^{2}\left(\sqrt{\gamma_{l}}\right), \end{aligned} $$
(37)

where κ 2=2μ, μ is the number of bits per symbol and

$$ \gamma_{l}=\frac{3R_{T}}{2(2^{\mu}-1)}\cdot \frac{E_{s}}{\xi_{l}N_{0}}. $$
(38)

E s is the average energy per symbol of the quadrature amplitude modulation (QAM) constellation, R T is the throughput efficiency reduction due to CP, N 0 is the noise spectral density and ξ l is the noise enhancement factor per subcarrier, which is given by

$$ \xi_{l}=\frac{1}{MK}\sum_{k=0}^{MK-1}\left|\frac{G[-k]}{H[\!k]}\right|^{2}, $$
(39)

with H[ k] and G[ k] being the channel frequency response and the prototype filter frequency response, respectively.

Equation (37) can also be used to estimate the symbol error rate for precoding GFDM using unitary transform [9] but, in this case,

$$ \gamma_{l}=\frac{3|H_{\text{eq}}|^{2}R_{T}}{2(2^{\mu}-1)}\cdot \frac{E_{s}}{\xi_{l}N_{0}}, $$
(40)

where

$$ H_{\text{eq}} = \left(\frac{1}{MK}\sum_{k=0}^{MK-1}\frac{1}{\left|H[\!k]\right|^{2}}\right)^{-\frac{1}{2}}, $$
(41)

and ξ l must be redefined as

$$ \xi_{l}=\sum_{i=0}^{MK-1}\left|\left[\mathbf{A}(\mathbf{I}_{M}\otimes\mathbf{T})\right]^{-1}_{l,i}\right|^{2}. $$
(42)

Another benefit that is obtained by precoding the data symbols before the GFDM modulation is the PAPR reduction, as can be seen in the complementary cumulative density function (CCDF) curves shown in Fig. 5. Since the subcarriers carry a weighted average of all data symbols from a given subsymbol, the probability of achieving high amplitude peaks is reduced, leading to a small PAPR when compared with conventional GFDM. Here, the employed precoding matrix affects the achieved PAPR. The best PAPR reduction is achieved by the CAZAC transform, followed by DHT and WHT, respectively. The explanation for this behavior lies on the aperiodic autocorrelation function [10] of the coefficients δ m . CAZAC transforms lead to coefficients with smaller aperiodic autocorrelation sidelobes. This property leads to a lower PAPR for the CAZAC-GFDM.

Fig. 5
figure 5

CCDF of the GFDM PAPR with and without precoding

Full size image

7 Conclusions

This paper introduces a GFDM modulator and demodulator based on a low-complexity multiplication in the time domain. The new matrix model allows to consider the coefficients transmitted by the subcarriers as the precoding of the data symbols. This approach broadens the GFDM flexibility, allowing to use different transforms to achieve different goals. Precoding can be used to improve the system SER performance over frequency-selective channels and to reduce the PAPR. The three unitary transforms considered in this paper presented the same SER performance. The CAZAC-GFDM achieved the lowest PAPR among the considered transforms. The computational complexity of the new GFDM modulator and demodulator have been compared with the solution proposed in [4], showing that the modem solution proposed in this paper can reduce the number of complex valued multiplications, even when sparse filters in the frequency domain are employed.