1 Introduction

As a common communication scenario, two-way relaying realizes information exchange between two nodes simultaneously. Recently, the two-way relay network (TWRN) has attracted many attentions from both academic and industrial communities [1-5], due to its bandwidth efficiency and potential applications to cellular networks and peer-to-peer networks. Generally, the data transmission in TWRN can take place in either three or two phases. For the three-phase TWRN, network coding (NC) is the most popular relaying protocol [6]. In NC, two source nodes S 1 and S 2 transmit to the relay R separately over the first two phases. After decoding the received signals, the relay R performs bit-level exclusive OR (XOR) operations and then broadcasts the XOR-coded bits to the two source nodes in the third phase.

It shows that the two-phase TWRN protocol can achieve a maximum throughput gain of one half over the three-phase TWRN. Therefore, various protocols for two-phase TWRN have been proposed in the literatures. Two way amplify-and-forward (AF) relaying was proposed in [7,8], where a relay directly amplifies and forwards the sum of received signals. Physical-layer network coding (PLNC) was proposed in [9,10], where self-information at source nodes is eliminated by XOR operations. In [11], the denoise-and-forward (DNF) protocol was proposed, where the relays apply a denoising function to map the receive signal into another quantized symbol that can be used by each source node to uniquely decode the symbol transmitted from the other end. The AF relaying protocol has less complexity than that of PLNC and DNF at the relay since no decoding operation is required at the relay node. The AF relaying protocol requires perfect channel state information (CSI) at the two source nodes to remove the self-interference. Most of the existing works assume that both the sources and the relay have perfect CSI knowledge of all links. In a practical system, these CSIs need to be estimated at the receiver. It is more difficult to estimate the CSIs in two-way relay networks than that in conventional point-to-point communication systems. To mitigate the difficulties involved in estimating the CSI in TWRN, non-coherent or differential transmission schemes have been proposed for TWRN [12-14]. In [13], the AF and decode-and-forward (DF) TWRN protocols using differential modulation were proposed. It shows that these schemes suffer from more than 3 dB performance loss compared with their coherent counterparts. In [14], Guan and Liu analyzed performance of TWRN with DNF relaying protocol using differential binary phase-shift-keying (DBPSK) modulation over fading channel. It is shown that the achievable diversity order of the proposed scheme is about half of the number of relays. The two-phase TWRN with non-coherent receiver not only achieve high spectral efficiency but also reduce the overhead of estimation of channel. Thus, it is a good option of information exchange for low cost wireless network, such as wireless sensor networks (WSNs).

The lifetime of the network is an important performance indicator in energy-constrained wireless networks, such as WSNs, since sensors are usually equipped with limited energy supplies. Harvesting energy from the environment is a promising approach to prolong the lifetime of the energy-constrained wireless networks. The basic idea of simultaneous wireless information and power transfer (SWIPT) was first proposed in [15,16], and a general receiver architecture was then developed in [17]. Then, the SWIPT was extended to various communication scenarios such as the cellular system [18], the broadcasting system [19,20] with a single energy receiver and a single information receiver when they are separately located or co-located, the cooperative relay system [21-25], the two-way relaying system [26], and the interference channel [27-29]. For broadcasting system, [19] investigated the R-E trade-off for a transmitter transferring energy and information to two separated/co-located information-decoding and energy harvesting receivers. And [20] optimized the beamforming designs of general broadcasting system where there are multiple separated/co-located information-decoding and energy harvesting receivers. For a DF cooperative network, [21] derives the outage probability of time switching relay receiver. In [22], the authors studied the outage probability and network capacity of end-to-end one-way relay system with a battery-free relay. For multiple source-destination pairs communication system aided by a relay, [23] studied the relays’ strategies to distribute the harvested energy among the multiple users and their impact on the system performance. For multiple-input multiple-output relay channels, [24] proposed a low complexity dynamic antenna switching between information decoding and energy harvesting based on the principles of the generalized selection combiner. In [25], the authors studied the relay selection problem in AF relay network with QoS and harvested energy constraints. In [26], the trade-off end-to-end outage probability and power splitting coefficient are studied in a two-way AF relay system where two source nodes exchange data via an energy harvesting relay. In [28] and [29], the authors investigated joint wireless information and energy transfer in the two-user/multiple-user MIMO interference channel, in which each receiver either information decoding or energy harvesting.

As is mentioned above, almost of the aforementioned SWIPT protocols assume that the transmitted signal satisfies Gaussian distribution and do not consider the modulation scheme. To the best of the authors’ knowledge, simultaneous wireless information and power transfer in the two-phase TWRN with differential modulation has not been addressed so far. Here, we study a two-phase TWRN using differential BPSK modulation, where a battery-free relay node harvests energy from the received RF signal and uses the harvested energy to exchange the two source nodes’ information. The main contributions of this paper are summarized as follows:

  1. 1)

    Based on the power splitting (PS) and time switching (TS) receiver architectures at relay node, we propose the PS-based relaying (PSR) and the TS-based relaying (TSR) protocols to enable wireless information transferring and energy harvesting at the battery-free relay in a DNF-TWRN.

  2. 2)

    For PSR and TSR protocols, we deduce the maximum likelihood (ML) decoding algorithm at relay and source nodes. Then, we derive the end-to-end error performance and normalized throughput of the two proposed protocols. These derived expressions provide practical design insights into the effect of various parameters on the system performance. By maximizing end-to-end throughput of system, we can optimize the power on two source nodes, power splitting coefficient, time switching factor, and other system parameters.

  3. 3)

    Differing from convention two-way relaying network, the numerical results show that locating the relay node closer to the source nodes yields larger throughput for both the TSR and the PSR protocols. By comparing PSR and TSR protocols, the numerical results also show that the throughput performance of the PSR protocol is superior to the TSR protocol.

The rest of this paper is organized as follows. The next section presents system model of energy harvesting TWRN with a battery-free relay. In section ‘Performance analysis’, end-to-end BER expressions and throughput are derived. Numerical simulations and discussions are presented in ‘Numerical results’ section. ‘Conclusions’ section concludes the paper.

2 System model

Here, we consider two relaying protocols for separate information decoding and energy harvesting at a battery-free relay node, namely, i) PS-based relaying PSR protocol and ii) TS-based relaying TSR protocol [22]. In PSR protocol, the relay uses a faction of the received power from two source nodes for energy harvesting and the remaining power for information decoding. In TSR protocol, the relay use a fraction of time for energy harvesting and the remaining time for information decoding.

2.1 PSR protocol

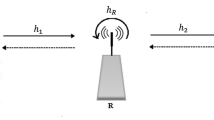
There are two sources S 1 and S 2 that want to exchange information with the help of a relay R in a TWRN. The key parameters of PSR protocol and receiver of relay are illustrated in Figure 1. At the begin of multiple access (MA) phase, S i (i=1,2) generates a sequence of uncoded BPSK symbols b i (n)∈{−1,+1} of length L (n=1,2,…,L). Then, these raw symbols are re-encoded through differential modulation, i.e., x i (n)=x i (n−1)×b i (n) for n=1,2,…,L with x i (0)=1 as the reference symbol. Two sources then simultaneously send the whole differential modulated block to the relay during MA phase. At the end of MA phase, the nth (n=0,1,2,…,L) symbol received at the relay is

$$ {{y}_{r}}(n)=\sqrt{{{P_{1}}}}{{h}_{1,r}}{{x}_{1}}(n)+\sqrt{{{P}_{2}}}{{h}_{2,r}}{{x}_{2}}(n)+w_{a,r}^{MA}(n) $$
((1))
Figure 1
figure 1

Power splitting protocol.(a) The parameters of the PSR protocol for energy harvesting and information decoding at the relay in TWRN. (b) The block diagram of receiver at relay.

Full size image

where P i =α i P is power of the ith (i=1,2) source, P is total power, α i is power ratio of the ith source. Assume that the channel gain is \(\sigma _{i,r}^{2}=1/d_{i,r}^{\mu }\), where d i,r is distance between source node to relay, μ is the path loss exponent. Thus, \({{h}_{i,r}}\sim \mathcal {CN}\left (0,\sigma _{i,r}^{2} \right)\) is the independent channel coefficient from the ith (i=1,2) source to the relay during MA phase. It is also assumed that the channels remain unchanged within one block of length (L+1). \(w_{a,r}^{MA}(n)\sim \mathcal {CN}\left (0,{\sigma _{a}^{2}} \right)\) is the independent additive white Gaussian noise (AWGN) due to receive antenna at the relay within the nth (n=0,1,…,L) symbol interval during MA phase.

We assume that relay knows channel gain \(\sigma _{i,r}^{2}\) but does not know channel coefficient h i,r . The basic idea of energy harvesting relaying is that an energy constrained relay recharges its battery by using the energy from its observations. For power splitting [17], let ρ denote the power splitting coefficient for the relay, i.e., ρ is the fraction of observations used for energy harvesting. Thus, at the end of the MA phase, the relay’s information receiver is based on the following observation

$$ \begin{aligned} {{\tilde{y}}_{r}}(n)&=\sqrt{1\,-\,{{\rho}}}\left(\sqrt{{P}_{1}}{{h}_{1,r}}{{x}_{1}}(n) \,+\,\sqrt{{P}_{2}}{{h}_{2,r}}{{x}_{2}}(n)+w_{a,r}^{MA}(n)\right)\\ &\quad+w_{c,r}^{MA}(n) \end{aligned} $$
((2))

where \(w_{c,r}^{MA}\sim \mathcal {CN}\left (0,{\sigma _{c}^{2}} \right)\) is the sampled AWGN due to RF band to base-band signal conversion. The harvested energy in the first (L+1) symbols is

$$ E_{h}=(L+1)\eta {{\rho }}\left({{\alpha }_{1}}P\sigma_{1,r}^{2}+{{\alpha }_{2}}P\sigma_{2,r}^{2} + {\sigma_{a}^{2}}\right) $$
((3))

where 0<η≤1 is the energy conversion efficiency which depends on the rectification process and the energy harvesting circuit. And power per symbol in the BC phase is

$$ P_{r}=E_{h}/(L+1)=\eta {{\rho }}\left({{\alpha }_{1}}P\sigma_{1,r}^{2}+{{\alpha }_{2}}P\sigma_{2,r}^{2} + {\sigma_{a}^{2}}\right) $$
((4))

To facilitate demonstrations, we define a sequence of auxiliary symbols b(n)=b 1(n)×b 2(n)∈{−1,+1} to indicate whether the two raw BPSK symbols have the same signs or not. With DNF [11,14], the relay just maps the nth received symbol to a BPSK symbol \(\hat {b}_{r}\) which is used by each source to uniquely decode the symbol transmitted from the other end. Here, it can be regarded as an estimate of the auxiliary symbol b(n). As no CSI is available, we use the single-symbol ML decoder in [14], i.e.,

$$ \hat{b}_{r}(n)={\text{sign}}\Big(\ln\big({\text{lrf}}({{{\boldsymbol{\tilde{y}}}}_{r}}(n)\big|b(n))\big)\Big) $$
((5))

where \({{\boldsymbol {\tilde {y}}}_{r}}(n)={{\left [ {{{\tilde {y}}}_{r}}(n),{{{\tilde {y}}}_{r}}(n-1) \right ]}^{T}}\), \({\text {lrf}}\big ({{\boldsymbol {\tilde {y}}}_{r}}(n)|b(n)\big)\) is the likelihood ratio function (LRF) of \({{\boldsymbol {\tilde {y}}}_{r}}(n)\) conditional on b(n),

$$ {\text{lrf}}({{\boldsymbol{\tilde{y}}}_{r}}(n)|b(n))=\frac{g\left({{{\boldsymbol{\tilde{y}}}}_{r}}(n),{{\mathbf{\Sigma }}_{1,r}} \right)+g\left({{{\boldsymbol{\tilde{y}}}}_{r}}(n),{{\mathbf{\Sigma }}_{2,r}} \right)}{g\left({{{\boldsymbol{\tilde{y}}}}_{r}}(n),{{\mathbf{\Sigma }}_{3,r}} \right)+g\left({{{\boldsymbol{\tilde{y}}}}_{r}}(n),{{\mathbf{\Sigma }}_{4,r}} \right)} $$
((6))

where g(y,Σ) is the probability density function (PDF) of \(\mathbf {y}\sim \mathcal {CN}(0,\mathbf {\Sigma })\) is given by

$$ g\left(\mathbf{y},\mathbf{\Sigma } \right)=\frac{1}{{{\pi }^{2}}\left| \mathbf{\Sigma } \right|}\exp \left(-{{\mathbf{y}}^{H}}\mathbf{\Sigma y} \right) $$
((7))

Denote the channel signal-to-noise ratio (SNR), i.e., \({{\gamma }_{i,r}}=\frac {\left (1-{{\rho }} \right){{\alpha }_{i}}P\sigma _{i,r}^{2}}{\left (1-{{\rho }} \right){\sigma _{a}^{2}}+{\sigma _{c}^{2}}}\) is from the ith (i=1,2) source to relay, and

$$I_{2}=\left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right], \hat{I}_{2}=\left[\begin{array}{cc} 0 & 1\\ 1 & 0\\ \end{array}\right]$$

are two constant matrix.

In the terms of reference [14], the conditional covariance matrices are given by

$$ \fontsize{8}{12}{\left\{\!\!\! \begin{array}{l} \mathbf{\Sigma }_{{{b}_{1}}(n)=1,{{b}_{2}}(n)=1}^{r}\triangleq{{\mathbf{\Sigma }}_{1,r}}={\sigma_{r}^{2}}\left({{\gamma }_{1,r}}+{{\gamma }_{2,r}}+1 \right){{I}_{2}}+{\sigma_{r}^{2}}\left({{\gamma }_{1,r}}+{{\gamma }_{2,r}} \right)\hat{I}_{2}\\ \mathbf{\Sigma}_{{{b}_{1}}(n)=-1,{{b}_{2}}(n)=-1}^{r}\triangleq {{\mathbf{\Sigma}}_{2,r}}={\sigma_{r}^{2}}\left({{\gamma}_{1,r}}+{{\gamma}_{2,r}}+1\right){{I}_{2}}-{\sigma_{r}^{2}}\left({{\gamma}_{1,r}} \,+\,{{\gamma}_{2,r}}\right)\hat{I}_{2}\\ \mathbf{\Sigma}_{{{b}_{1}}(n)=1,{{b}_{2}}(n)=-1}^{r}\triangleq {{\mathbf{\Sigma}}_{3,r}}={\sigma_{r}^{2}}\left({{\gamma}_{1,r}}+{{\gamma}_{2,r}}+1\right){{I}_{2}}+{\sigma_{r}^{2}} \left({{\gamma}_{1,r}}-{{\gamma}_{2,r}}\right)\hat{I}_{2}\\ \mathbf{\Sigma}_{{{b}_{1}}(n)=-1,{{b}_{2}}(n)=1}^{r}\triangleq {{\mathbf{\Sigma}}_{4,r}} ={\sigma_{r}^{2}}\left({{\gamma}_{1,r}}+{{\gamma}_{2,r}}+1\right){{I}_{2}}+{\sigma_{r}^{2}}\left({{\gamma}_{2,r}} -{{\gamma}_{2,r}}\right)\hat{I}_{2} \end{array}\right.} $$
((8))

where \({\sigma _{r}^{2}}=\left (1-{{\rho }} \right){\sigma _{a}^{2}}+{\sigma _{c}^{2}}\), it is the equivalent noise variance of information decoding at relay. After decoding, the relay re-encode \(\hat {b}_{r}(n)\) into \({{t}_{r}}(n)={{t}_{r}}(n-1)\times \hat {b}_{r}(n)\) for n=1,2,…,L based on reference symbol t r (0)=1. The relay then uses harvested energy in the MA phase for transmitting information in the broadcasting (BC) phase. Without considering the energy consumed by signal processing, from Equation 3, the harvested energy per symbol duration is P r , this is energy constraint of the relay in the BC phase. Thus, at the end of BC phase, the ith (i=1,2) source will receive from the relay,

$$ {{r}_{i}}(n)=\sqrt{{{P}_{r}}}{{h}_{r,i}}{{t}_{r}}(n)+w_{i}^{BC}(n), \begin{array}{ll} \\ \end{array} n=0, 1, 2, \dots, L $$
((9))

where P r is power per symbol given by Equation 4, \({h_{r,i}}\sim \mathcal {CN}\left (0,\sigma _{r,i}^{2}\right)\) is the independent channel coefficient from the relay to the ith (i=1,2) source.

During BC phase, we assume h i,r and h r,i (i=1,2) are independent but have the same variance, which is determined by the distance between two terminals. \(w_{i}^{BC}(n)\sim \mathcal {CN}\left (0,\sigma _{a}^{2}+{\sigma _{c}^{2}}\right)\) includes the antenna and conversion AWGNs at the ith (i=1,2) source within the nth (n=0,1,2,…,L) symbol interval in the BC phase.

We again use the single-symbol ML decoder in BC phase, the received signal of the ith source is

$$ \hat{b}_{{{s}_{i}}}(n)= {\text{sign}}\Big({\ln\big({\text{lrf}}({{r}_{i}}(n)|b(n))\big)}\Big) $$
((10))

where \({{\mathbf {r}}_{i}}(n)={{\left [ {{r}_{i}}(n),{{r}_{i}}(n-1) \right ]}^{T}}, \mathbf {{r}}_{i}(n){{|}_{b_{r}(n)}}\sim \mathcal {CN} \left (0,\mathbf {\Sigma }_{b_{r}(n),{{s}_{i}}}^{k}\right)\), conditional covariance matrices are given by

$$ \left\{\!\!\! \begin{array} {l}\mathbf{\Sigma }_{{{b}_{r}}(n)\,=\,1,{{s}_{i}}}^{r}\triangleq\mathbf{\Sigma }_{1,{{s}_{i}}}^{r}=\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}} \right)\left({{\gamma }_{r,i}}\,+\,1 \right){{I}_{2}}\,+\,\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}} \right){{\gamma }_{r,i}}\hat{I}_{2}\\ \mathbf{\Sigma}_{{{b}_{r}}(n)=-1,{{s}_{i}}}^{r}\!\triangleq\!\mathbf{\Sigma}_{2,{{s}_{i}}}^{r}\,=\,\left({\sigma_{a}^{2}} \,+\,{\sigma_{c}^{2}}\right)\!\left({{\gamma}_{r,i}}\,+\,1\right){{I}_{2}}\,-\,\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}}\right){{\gamma}_{r,i}}\hat{I}_{2} \end{array}\right. $$
((11))

where \({{\gamma }_{r,i}}=\frac {\eta {{\rho }}P\left ({{\alpha }_{1}}\sigma _{1,r}^{2}+{{\alpha }_{2}}\sigma _{2,r}^{2} +{\sigma _{a}^{2}}\right)\sigma _{r,i}^{2}}{{\sigma _{a}^{2}}+{\sigma _{c}^{2}}}\). The two kinds of conditional decoding error at the relay are assumed as follow,

$$ \begin{aligned} {{{P}_{M,r}}}&=\Pr (\hat{b}_{r}(n)=-1|b(n)=+1)\\ &=\Pr\Big(\ln({\text{lrf}}({{{\boldsymbol{\tilde{y}}}}_{r}}(n)|b(n))\le 0|b(n)=+1\Big),\\ \end{aligned} $$
((12))

and

$$ \begin{aligned} {{{P}_{F,r}}}&=\Pr(\hat{b}_{r}(n)=+1|b(n)=-1)\\ &=\Pr\Big(\ln({\text{lrf}}({{{\boldsymbol{\tilde{y}}}}_{r}}(n)|b(n))>0|b(n)=-1\Big)\\ \end{aligned} $$
((13))

Thus, the LRF ln(lrf(r i (n)|b(n))) is

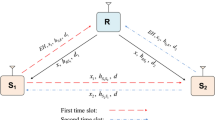
$$ \begin{aligned} &\ln \left({\text{lrf}}({{\mathbf{r}}_{i}}(n)|b(n)) \right)\\ &\,\,\,\,=\ln \left[ \frac{g\left({{\mathbf{r}}_{i}}(n),\mathbf{\Sigma }_{1,{{s}_{i}}}^{r} \right)\left(1-{{P}_{M,r}} \right)+g\left({{\mathbf{r}}_{i}}(n),\mathbf{\Sigma }_{2,{{s}_{i}}}^{r} \right){{P}_{M,r}}}{g\left({{\mathbf{r}}_{i}}(n),\mathbf{\Sigma }_{1,{{s}_{i}}}^{r} \right){{P}_{F,r}}+g\left({{\mathbf{r}}_{i}}(n),\mathbf{\Sigma }_{2,{{s}_{i}}}^{r} \right)\left(1-{{P}_{F,r}} \right)} \right] \end{aligned} $$
((14))

2.2 TSR Protocol

TSR protocol is shown in Figure 2. We assume that data rate of direction transmission is \(\hat {R}\). In PSR, the data rate is always \(\hat {R}\). However, in TSR, data rate of two-way system is dependent on the time splitting factor α. In total symbol duration 2(L+1), we also assume that the total power constraint is same as PSR protocol in 2(L+1) symbols, i.e., (L+1)P. Therefore, the power per symbol in energy harvesting and MA phase is

$$ {P}'=\frac{(L+1)P}{(2\alpha +1-\alpha)(L+1)}=\frac{P}{\alpha +1} $$
((15))
Figure 2
figure 2

Time switching protocol.(a) The parameters of the TSR protocol for energy harvesting and information decoding at the relay in TWRN. (b) The block diagram of receiver at relay.

Full size image

At the end of MA phase, the nth (n=2α(L+1),2α(L+1)+1,…,(α+1)(L+1)) symbol received at the relay is

$$ {{y}_{r}}(n)=\sqrt{{{P}_{1}}}{{h}_{1,r}}{{x}_{1}}(n)+\sqrt{{{P}_{2}}}{{h}_{2,r}}{{x}_{2}}(n)+w_{a,r}^{MA}(n)+w_{c,r}^{MA}(n) $$
((16))

where \({{P}_{i}}={{\alpha }_{i}}{P}'=\frac {{{\alpha }_{i}}P}{1+\alpha }~(i=1, 2)\). Denote the channel SNR, i.e., \({{\gamma }_{i,r}}=\frac {{{\alpha }_{i}}P\sigma _{i,r}^{2}}{\left (1+\alpha \right)\left ({\sigma _{a}^{2}}+{\sigma _{c}^{2}} \right)}\) is from the i th (i=1,2) source to the relay. The LRF of y r (n) conditional on b(n) is the same as Equation 6 with the same conditional covariance matrices of PSR (see Equation 8) with \({\sigma _{r}^{2}}= {\sigma _{a}^{2}}+{\sigma _{c}^{2}}\).

The harvested energy in the first 2α(L+1) is

$$ E{{H}_{r}}=\eta 2\alpha (L+1){P}'\left({{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2}+{\sigma_{a}^{2}}\right) $$
((17))

while the power per symbol in the BC phase is

$$ \begin{aligned} {{P}_{r}}&=\frac{E{{H}_{r}}}{(1-\alpha)(L+1)}\\ &=\frac{2\eta \alpha (L+1){P}'\left({{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2}+{\sigma_{a}^{2}}\right)}{(1-\alpha)(L+1)} \\ & =\frac{2\eta \alpha P\left({{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2}+{\sigma_{a}^{2}}\right)}{1-{{\alpha }^{2}}} \end{aligned} $$
((18))

Therefore, at the end of BC phase, the ith (i=1,2) source receives the signal from the relay is

$$ \begin{aligned} {{r}_{i}}(n)&=\sqrt{{{P}_{r}}}{{h}_{r,i}}{{t}_{r}}(n)+w_{i}^{BC}(n),~n=0, 1, 2,..., (1-\alpha)L \end{aligned} $$
((19))

Similar to the BC phase of PSR protocol, \({\mathbf {r}_{i}}(n){{|}_{b_{r}(n)}}\sim \mathcal {CN}\left (0,\mathbf {\Sigma }_{\hat {b}_{r}(n),{{s}_{i}}}^{r}\right)\) with the conditional covariance matrix

$$ \left\{\!\!\! \begin{array} {l} \mathbf{\Sigma }_{{{b}_{r}}(n)=1,{{s}_{i}}}^{r}\!\triangleq\!\! \mathbf{\Sigma }_{1,{{s}_{i}}}^{r}\,=\,\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}} \right)\left({{\gamma }_{r,i}}\,+\,1 \right){{I}_{2}}\,+\,\left({\sigma_{a}^{2}}+{\sigma_{c}^{2}} \right){{\gamma }_{r,i}}\hat{I}_{2}\\ \mathbf{\Sigma}_{{{b}_{r}}(n)=-1,{{s}_{i}}}^{r}\!\triangleq\!\mathbf{\Sigma}_{2,{{s}_{i}}}^{r} \,=\,\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}}\right)\!\left({{\gamma}_{r,i}}\,+\,1\right){{I}_{2}} \,-\,\left({\sigma_{a}^{2}}\,+\,{\sigma_{c}^{2}}\right)\!{{\gamma}_{r,i}}\hat{I}_{2} \end{array}\right. $$
((20))

where \({{\gamma }_{r,i}}=\frac {2\eta \alpha P({{\alpha }_{1}}\sigma _{1,r}^{2}+{{\alpha }_{2}}\sigma _{2,r}^{2}+{\sigma _{a}^{2}})\sigma _{i,r}^{2}}{\left (1-{{\alpha }^{2}} \right)\left ({\sigma _{a}^{2}}+{\sigma _{c}^{2}} \right)}\).

3 Performance analysis

Utilizing Equation 12 and 13, the relay decoding error can be evaluated as

$$ {{P}_{e,{{r}}}}=\Pr \left({{{\hat{b}}}_{{{r}}}}(n)\ne b(n) \right)=\frac{1}{2}\left({{P}_{M,{{r}}}}+{{P}_{F,{{r}}}} \right) $$
((21))

The two kinds of conditional decoding error of in Equation 12 and 13 are given by[14]

$$\begin{aligned} {{{P}_{M,r}}}&=h\left({{\mu }_{1,r}},{{\mu }_{2,r}},{{a}_{r}},{{b}_{r}},\gamma_{th}^{r}\right),\\ {{{P}_{F,r}}}&=1-h\left({{\mu }_{3,r}},{{\mu }_{4,r}},{{a}_{r}},{{b}_{r}},\gamma_{th}^{r}\right), \end{aligned} $$

and

$$\begin{aligned} h({{t}_{1}},{{t}_{2}},a,b,\gamma)&=\frac{4ab{{t}_{1}}{{t}_{2}}}{{{a}^{2}}{{\left({{t}_{1}}-{{t}_{2}} \right)}^{2}}-{{b}^{2}}{{\left({{t}_{1}}+{{t}_{2}} \right)}^{2}}}\\ &\quad\times\exp \left(-\frac{{{t}_{1}}+{{t}_{2}}}{2a}\ln \gamma \right), \end{aligned} $$
$$\begin{aligned} {{a}_{r}}&=-\frac{4{{\gamma }_{1,r}}{{\gamma }_{2,r}}\left({{\gamma }_{1,r}}+{{\gamma }_{2,r}}+1 \right)}{{{N}_{0}}\left(2{{\gamma }_{1,r}}+2{{\gamma }_{2,r}}+1 \right)\left(2{{\gamma }_{1,r}}+1 \right)\left(2{{\gamma }_{2,r}}+1 \right)},\\ &{{b}_{r}}\,=\,\frac{4{{\gamma }_{1,r}}{{\gamma }_{2,r}}\!\left({{\gamma }_{1,r}}\,+\,{{\gamma }_{2,r}} \right)\,+\,2\!\min\! \left({{\gamma }_{1,r}},{{\gamma }_{2,r}} \right)\!\!\left(2{{\gamma }_{1,r}}\,+\,2{{\gamma }_{2,r}}\,+\,1 \right)}{{{N}_{0}}\left(2{{\gamma }_{1,r}}\,+\,2{{\gamma }_{2,r}}\,+\,1 \right)\!\!\left(2{{\gamma }_{1,r}}\,+\,1 \right)\!\!\left(2{{\gamma }_{2,r}}\,+\,1 \right)},\\ \end{aligned} $$
$$\gamma_{th}^{r}=\frac{\left(2{{\gamma }_{1,r}}+2{{\gamma }_{2,r}}+1 \right)}{\left(2{{\gamma }_{1,r}}+1 \right)\left(2{{\gamma }_{2,r}}+1 \right)}, $$
$${{\mu }_{1,r}}=\frac{1}{{{N}_{0}}\left(2{{\gamma }_{1,r}}+2{{\gamma }_{2,r}}+1 \right)}, $$
$${{\mu }_{2,r}}=\frac{1}{{{N}_{0}}}, $$
$${{\mu }_{3,r}}=\frac{1}{{{N}_{0}}\left(2{{\gamma }_{1,r}}+1 \right)}, $$
$${{\mu }_{4,r}}=\frac{1}{{{N}_{0}}\left(2{{\gamma }_{2,r}}+1 \right)}. $$

In the BC phase, the two kinds of conditional decoding errors between the relay and the ith source are non-coherent DBPSK decoder [30], they are given by

$$ \begin{aligned} P_{D,{{S}_{i}}}^{r}&=\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=1|{{{\hat{b}}}_{{{r}}}}(n)=-1 \right) \\ & =\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=-1|{{{\hat{b}}}_{{{r}}}}(n)=1 \right) \\ & \approx\frac{2}{2\left({{{{\gamma }}}_{r,i}}+1 \right)} \\ \end{aligned} $$
((22))

Similar to Equation 12 and 13, the two kinds of conditional decoding error at the ith source are given as,

$$ \begin{aligned} P_{M,{{S}_{i}}}^{r}&=\Pr \left({{{\hat{b}}}_{{{S}_{i}}}}(n)=-1|b(n)=1 \right) \\ & =\sum\limits_{{{{\hat{b}}}_{{{r}}}}(n)\in \left\{ -1,1 \right\}}{\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=-1|{{{\hat{b}}}_{{{r}}}}(n),b(n)=1 \right)}\\ &\quad\times\Pr \left({{{\hat{b}}}_{{{r}}}}(n)|b(n)=1 \right) \\ & =\sum\limits_{{{{\hat{b}}}_{{{r}}}}(n)\in \left\{ -1,1 \right\}}{\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=-1|{{{\hat{b}}}_{{{r}}}}(n) \right)}\\ &\quad\times\Pr \left({{{\hat{b}}}_{{{r}}}}(n)|b(n)=1 \right) \\ & =P_{D,{{S}_{i}}}^{r}\left(1-{{P}_{M,{{r}}}} \right)+\left(1-P_{D,{{S}_{i}}}^{r} \right){{P}_{M,{{r}}}}\\ \end{aligned} $$
((23))
$$ \begin{aligned} P_{F,{{S}_{i}}}^{r}&=\Pr \left({{{\hat{b}}}_{{{S}_{i}}}}(n)=1|b(n)=-1 \right) \\ & =\sum\limits_{{{{\hat{b}}}_{{{r}}}}(n)\in \left\{ -1,1 \right\}}{\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=1|{{{\hat{b}}}_{{{r}}}}(n),b(n)=-1 \right)}\\ &\quad\times\Pr \left({{{\hat{b}}}_{{{r}}}}(n)|b(n)=-1 \right) \\ & =\sum\limits_{{{{\hat{b}}}_{{{r}}}}(n)\in \left\{ -1,1 \right\}}{\Pr \left({{{\hat{b}}}_{{{r}},{{S}_{i}}}}(n)=1|{{{\hat{b}}}_{{{r}}}}(n) \right)}\\ &\quad\times\Pr \left({{{\hat{b}}}_{{{r}}}}(n)|b(n)=-1 \right) \\ & =P_{D,{{S}_{i}}}^{r}\left(1-{{P}_{F,{{r}}}} \right)+\left(1-P_{D,{{S}_{i}}}^{r} \right){{P}_{F,{{r}}}}\\ \end{aligned} $$
((24))

Therefore, the end-to-end error probability of the ith source node is

$$ \begin{aligned} P_{e,{{S}_{i}}}&=\Pr \left({{{\hat{b}}}_{{{S}_{i}}}}(n)\ne b(n) \right)\\ & =\frac{1}{2}\left(P_{M,{{S}_{i}}}^{r}+P_{F,{{S}_{i}}}^{r} \right) \\ & =\frac{1}{2}\!\left[ P_{D,{{S}_{i}}}^{r}\!\left(1\,-\,{{P}_{M,{{r}}}} \right)\,+\,\left(\! 1\,-\,P_{D,{{S}_{i}}}^{r} \right){{P}_{M,{{r}}}}\,+\,P_{D,{{S}_{i}}}^{r}\left(1\,-\,{{P}_{F,{{r}}}} \right)\right.\\ &\quad+\left.\left(1-P_{D,{{S}_{i}}}^{r} \right){{P}_{F,{{r}}}} \right] \\ & =P_{D,{{S}_{i}}}^{r}\left(1-\frac{{{P}_{M,{{r}}}}+{{P}_{F,{{r}}}}}{2} \right)+\left(1-P_{D,{{S}_{i}}}^{r} \right)\frac{{{P}_{M,{{r}}}}+{{P}_{F,{{r}}}}}{2} \\ & =P_{D,{{S}_{i}}}^{r}\left(1-{{P}_{e,{{r}}}} \right)+\left(1-P_{D,{{S}_{i}}}^{r} \right){{P}_{e,{{r}}}} \end{aligned} $$
((25))

According to [14], the average BER of two sources can be approximated at high SNRs as

$$ \begin{aligned} {P}_{e}\approx \frac{1}{2}\left({{P}_{M,{{r}}}}+{{P}_{F,{{r}}}}+P_{D,{{S}_{1}}}^{r}+P_{D,{{S}_{2}}}^{r} \right) \end{aligned} $$
((26))

where

$$ \left\{ \begin{array} {l} {{P}_{M,{{r}}}}\approx \frac{{{c}_{M,{{r}}}}}{{\bar{\gamma }}},{{c}_{M,{{r}}}}=\frac{1}{2\min \left({{\alpha }_{1}}\sigma_{1,r}^{2},{{\alpha }_{2}}\sigma_{2,r}^{2} \right)} \\ {{P}_{F,{{r}}}}\approx \frac{{{d}_{F,{{r}}}}}{{\bar{\gamma }}}\ln \frac{{\bar{\gamma }}}{{{d}_{F,{{r}}}}},{{d}_{F,{{r}}}}=\frac{{{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2}}{2{{\alpha }_{1}}{{\alpha }_{2}}\sigma_{1,r}^{2}\sigma_{2,r}^{2}} \\ P_{D,{{S}_{i}}}^{r}\approx \frac{1}{2\eta \rho \left({{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2} +{\sigma_{a}^{2}}\right)\sigma_{i,r}^{2}\gamma } \quad \text{for } \quad \text{PSR} \\ P_{D,{{S}_{i}}}^{r}\approx \frac{1-{{\alpha }^{2}}}{4\eta \alpha \left({{\alpha }_{1}}\sigma_{1,r}^{2}+{{\alpha }_{2}}\sigma_{2,r}^{2} +{\sigma_{a}^{2}}\right)\sigma_{i,r}^{2}\gamma }\quad \text{for } \quad \text{TSR} \end{array}\right. $$
((27))

and

$$ \left\{ \begin{array}{l} \bar{\gamma }=\left(1-\rho \right)\gamma \quad \text{for } \quad \text{PSR} \\ \bar{\gamma }=\frac{\gamma }{(1+\alpha)} \quad \text{for } \quad \text{TSR} \end{array}\right. $$
((28))

where \(\gamma =\frac {P}{{\sigma _{a}^{2}}+{\sigma _{c}^{2}}}\) is system SNR. Substituting Equation 27 and 28 into Equation 26, we can get the BER expression of \(P_{e}^{\text {PSR}}\) and \(P_{e}^{\text {TSR}}\) for the PSR and TSR protocol, respectively. We ignore the overhead of reference symbol in the differential modulation. Thus, the end-to-end normalized throughput are defined respectively as follow,

$$ \begin{aligned} & {T}_{\text{PSR}}=\left(1-H\left(P_{e}^{\text{PSR}}\right) \right),\\ & {T}_{\text{TSR}}=(1-\alpha)\left(1-H\left(P_{e}^{\text{TSR}}\right) \right). \end{aligned} $$
((29))

respectively, where \(P_{e}^{\text {PSR}}\) and \(P_{e}^{\text {TSR}}\) are the end-to-end average error probability of the PSR and TSR protocol, respectively. The binary entropy function H(x) is given by

$$ H(x)=-x{{\log }_{2}}(x)-(1-x){{\log }_{2}}(1-x) $$
((30))

Therefore, through above expressions of throughput and BER, we are about to investigate that the power allocation (α 1 and α 2) among the two sources, the energy harvesting factor (ρ or α) at the relay and other system parameters impact on the performance. In the next section, some numerical results will be illustrated based on these analyzed formulas.

4 Numerical results

In this section, we use the derived analytical results to provide insights into the various design choices. The optimal value of normalized throughput for given distance between source and relay, optimal value of power splitting ratio ρ in the PSR protocol and optimal value of time switching factor α in the TSR protocol are investigated for different values of the noise variances, the two source to relay distances, \(d_{S_{1}R}\) and \(d_{S_{2}R}\) and energy harvesting efficiency, respectively. Unless otherwise stated, we set the energy harvesting efficiency, η=0.5, total source transmission power, P=0.1 mw, distance between two source nodes, \(d=d_{S_{1}R}+d_{S_{2}R}\) and path loss exponent μ=2.5.

Figure 3 shows the BER with respect to ρ,0≤ρ≤1 for PSR protocol and α,0≤α≤1 for TSR protocol. The analytical results for the BER as shown in Equation 26 and 27 are examined and verified through simulations for both the PSR and the TSR protocols. The antenna noise variance, \({\sigma _{a}^{2}}\), and conversion noise variance, \({\sigma _{c}^{2}}\), is set to −90 and −80 dBm, respectively. The two source nodes have the same power, i.e., α 1=α 2=0.5, and \(d_{S_{1}R}=d_{S_{2}R}=7\) m. It can be observed from Figure 3 that the analytical and the simulation results match well for all possible values of ρ and α for both the PSR and the TSR protocols. Figure 3 also demonstrates that the PSR has a power splitting coefficient to get minimum BER, but the TSR has not a energy harvesting time ratio to get minimum BER. The reason is that there is more energy harvesting time during MA phase, there is higher transmitted power of relay during the BC phase.

Figure 3
figure 3

BER versus PSR coefficient ρ (TSR coefficient α). P=0.1 mw, \({\sigma _{c}^{2}}=-80\) dBm, \({\sigma _{a}^{2}}=-90\) dBm, \(d_{S_{1}R}=d_{S_{2}R}=7\) m, μ=2.5, α 1=α 2=0.5, and η=0.5.

Full size image

In order to further observe the effect of power splitting coefficient ρ and energy harvesting time ratio α on the two protocols, Figure 4 shows the normalized throughput of two protocols, which is got by Equation 28. Figure 4 demonstrates that both PSR and TSR has the value of ρ and α to get maximum normalized throughput. We also can see that the maximum throughput of PSR protocol is higher than that of the TSR protocol. The throughput of TSR increases as α increases from 0 to maximum point, then starts decreasing quickly as α increases to 1. On the contrary, the throughput of PSR protocol change slowly with ρ. This is because there is only 1−α time for information transmission in the TSR protocol, but all time is used for information transmission in the PSR protocol. Therefore, the TSR protocol achieves better BER performance, shown as in Figure 3, but it has lower throughput.

Figure 4
figure 4

Throughput versus PSR coefficient ρ (TSR coefficient α). P=0.1 mw, \({\sigma _{c}^{2}}=-80\) dBm, \({\sigma _{a}^{2}}=-90\) dBm, \(d_{S_{1}R}=d_{S_{2}R}=7\) m, μ=2.5, α 1=α 2=0.5, and η=0.5.

Full size image

The optimal values in Figures 5, 6, 7, 8, and 9 are obtained through exhaustive search based on the expressions in the ‘Performance analysis’ section. Here, we set the step of parameters ρ,α and α 1 is 0.01. Figure 5 shows the optimal throughput for the PSR and the TSR protocols for different values of the source node S 1 to relay distance, \(d_{S_{1}R}\). The source node S 2 to destination distance, \(d_{S_{2}R}\) is set to \(d_{S_{2}R} = d - d_{S_{1}R}\) where d=14 m and the noise variances are kept fixed, i.e., \({\sigma _{a}^{2}} = -90\) dBm and \({\sigma _{c}^{2}} = -80\) dBm. It can be observed from figure 5 that for both the TSR and the PSR protocols, the optimal throughput decreases as \(d_{S_{1}R}\) increases until \(d_{S_{1}R}=7\) m, which is the half of distance between source node S 1 and S 2. From \(d_{S_{1}R}=7\) m, as increasing of \(d_{S_{1}R}\), the throughput of two protocols are both increasing. It is important to note that, as illustrated in Figure 5, the worst relay location of the two energy harvesting protocols is at the middle of two source nodes.

Figure 5
figure 5

Distance source node S 1 to relay, \(d_{S_{1}R}\), versus optimal throughput for PSR and TSR protocol. P=0.1 mw, \({\sigma _{c}^{2}}=-80\) dBm, \({\sigma _{a}^{2}}=-90\) dBm, μ=2.5, and η=0.5.

Full size image
Figure 6
figure 6

Distance source node S 1 to relay, \(d_{S_{1}R}\), versus optimal PSR coefficient ρ (TSR coefficient α). P=0.1 mw, \({\sigma _{c}^{2}}=-80\) dBm, \({\sigma _{a}^{2}}=-90\) dBm, μ=2.5, and η=0.5.

Full size image
Figure 7
figure 7

Distance source node S 1 to relay, \(d_{S_{1}R}\), versus optimal power coefficient of source node S 1. P=0.1 mw, \({\sigma _{c}^{2}}=-80\) dBm, \({\sigma _{c}^{2}}=-90\) dBm, μ=2.5, and η=0.5.

Full size image
Figure 8
figure 8

Optimal values of ρ for the PSR protocol for different values of antenna noise variance.\({\sigma _{a}^{2}}\) and \({\sigma _{c}^{2}}=-80\) dBm (fixed). Other parameters: P=0.1 mw, η=0.5, and μ=2.5.

Full size image
Figure 9
figure 9

Optimal values of α for the TSR protocols for different values of conversion noise variance.\({\sigma _{c}^{2}}\) and \({\sigma _{a}^{2}}=-80\) dBm (fixed). Other parameters: P=0.1 mw, η=0.5, and μ=2.5.

Full size image

Figure 6 shows the optimal values of ρ and α for the TSR and the PSR protocols, respectively, for different values of the source node S 1 to relay distance, \(d_{S_{1}R}\). Figure 6 states that both optimal power splitting coefficient ρ and time switching factor α are even symmetry with \(d_{S_{1}R}\). The value of ρ and α both reach to maximum when relay is at the middle of two source nodes. It is shown that relay need more harvested energy to forward data when relay is at middle of two source nodes. Figure 6 also illustrates small α for all distance area. This is because the parameter α imposes two sides effect on throughput. On the one hand, throughput is increased with more harvested energy (lower end-to-end BER), on the other hand, throughput is decreased quickly with increasing of α.

Figure 7 shows the optimal value of power allocation coefficient α 1 of source node S 1 of two protocols for different values of the source node S 1 to relay distance. The figure demonstrates that optimal α 1 is odd symmetry with distance \(d_{S_{1}R}\) for both PSR and TSR protocols.

Figures 8 and 9 show the optimal values of ρ and α for the PSR and the TSR protocols, respectively, for different values of antenna noise variance \({\sigma _{a}^{2}}\) and different values of conversion noise variance \({\sigma _{c}^{2}}\). Figure 8 illustrates that the optimal value of ρ increases by increasing \({\sigma _{a}^{2}}\) and ρ decrease by increasing \({\sigma _{c}^{2}}\). The reason is that for PSR protocol, the antenna noise w a,r (n) affects both the signal \(\sqrt {\rho }y_{r}(n)\) used energy harvesting and the signal \(\sqrt {(1-\rho)}y_{r}(n)\) used information decoding in MA phase, while the conversion noise w c,r (n) only affects the signal \(\sqrt {(1-\rho)}y_{r}(n)\) used information decoding. In the BC phase, two noises impose same effects on the receiver. Thus, the trend for the optimal value of ρ is different when curves are plotted with respect to the noise variances \({\sigma _{a}^{2}}\) or \({\sigma _{c}^{2}}\). However, it shows in Figure 9 that the optimal value of α has the same trends by increasing \({\sigma _{a}^{2}}\) or \({\sigma _{c}^{2}}\). This is because for the TSR protocol, the antenna noise w a,r (n) and the conversion noise w c,r (n) affect the received signal in the same way.

Figures 10 and 11 show the maximum throughput for the TSR and the PSR protocols, respectively, for different values of antenna noise variance, \({\sigma _{a}^{2}}\) or conversion noise variance \({\sigma _{c}^{2}}\). It can be observed from Figures 10 and 11 that the analytical results are agreement to the simulations for both the PSR and the TSR protocols with different geometry scenarios. Figures 10 and 11 also show that the antenna noise and conversion noise have almost similar effects on the two relaying protocols in different geometrical scenario.

Figure 10
figure 10

Optimal throughput for the PSR protocol for different values of antenna noise variance.\({\sigma _{a}^{2}}\) and \({\sigma _{c}^{2}}=-80\) dBm (fixed). Other parameters: P=0.1 mw, η=0.5, and m u=2.5. The real lines represent analytical results, and markers represent simulations.

Full size image
Figure 11
figure 11

Optimal throughput for the TSR protocol for different values of conversion noise variance.\({\sigma _{c}^{2}}\) and \({\sigma _{a}^{2}}=-80\) dBm (fixed). Other parameters: P=0.1 mw, η=0.5, and m u=2.5. The real lines represent analytical results, and markers represent simulations.

Full size image

Finally, the optimal throughput for the PSR and the TSR protocols for different values of energy harvesting efficiency, η, are shown in Figure 12. It illustrates that the PSR protocol outperforms the TSR protocol for all the values of η in various geometry of the nodes. It also can be observed that the throughput of the two protocols is not sensitive the changing of η when η is large enough.

Figure 12
figure 12

Energy conversion efficiency versus optimal throughput. P=0.1 mw, \({\sigma _{c}^{2}}={\sigma _{c}^{2}}=-80\) dBm, and μ=2.5.

Full size image

5 Conclusions

In this paper, we have investigated two SWIPT protocols, called by PSR and TSR, in TWRN with non-coherent DBPSK modulation, where a battery-free relay node harvests energy from the received RF signal and uses that harvested energy to exchange information between the two source nodes via the relay. We have developed ML decoder of this TWRN and analyzed BER expressions of the two proposed protocols. Based on end-to-end BER and normalized throughput expressions of the TWRN, we have investigated the effect of power allocation on sources, time switching factor, power splitting coefficient, noise power, and other system parameters on the performance. Future work may focus on relay selection and schedule for extended energy harvesting TWRN with multiple battery-free relays network.