1 Introduction

Over the past few years, ultra-wideband (UWB) has been promised as an efficient technology for future wireless short-range high data rate communication [1]. It has received great attention in both academia and industry for applications in wireless communications since 2002 when the Federal Communications Commission (FCC) of the USA reserved the frequency band between 3.1 and 10.6 GHz for indoor UWB applications. This decision has led to the introduction of Institute of Electrical and Electronic Engineering (IEEE) 802.15 high rate alternative physical layer (PHY) Task Group 3a for wireless personal area networks (WPAN). And ever since then, various researches on UWB systems have been conducted all over the world for the final high-speed WPAN standard. One of them, the multiband orthogonal frequency division multiplexing (MB-OFDM)-based UWB system has been proposed, by the Multiband OFDM Alliance (MBOA), for European Computer Manufacturers Association (ECMA)-368 standard to provide low power and high data rate transmission [2-4].

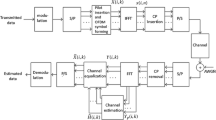
A collection of problems including channel measurements and modeling, channel estimation, and synchronization have been widely studied by researchers [5-10]. Clearly, all the performance improvement and capacity increase are based on accurate channel state information. Therefore, the most important component of MB-OFDM UWB system, represented by the block diagram of Figure 1, is that blue highlighted channel estimation and equalization component.

Figure 1
figure 1

The structure of a multiband OFDM UWB. OFDM UWB, orthogonal frequency division multiplexing ultra-wideband.

Full size image

In the UWB literature, the channel estimation has mostly been studied for its effect on error rate performance and computational complexity [8-18]. For example, a minimum mean square error (MMSE) estimator has been proposed by Beek et al., and they have shown that it gives a performance gain over least square (LS) estimator [8]. Moreover, Li et al. have proposed a low-complexity channel estimator developed by first averaging the over-lap-added (OLA) received preamble symbols within the same band and then applying time-domain least squares method followed by the discrete Fourier transform [9]. Also, a low-sampling-rate scheme, based on multiple observations generated by transmitting multiple pulses, for ultra-wideband channel estimation has been proposed in [12]. Furthermore, authors in [18] propose preamble-based improved channel estimation in the presence of both multiple-access interference (MAI) and narrowband interference (NBI). The afore-mentioned estimators are applied for strictly linear systems.

Outside the UWB literature, there has been growing interest to widely linear (WL) processing which takes into account both the original values of the signal data as well as their conjugates. For example, Chevalier et al. have presented the widely linear mean square estimation with complex data [19,20]. They have shown that widely linear systems outperform significantly the strictly linear one. Also, Sterle has compared linear and widely linear MMSE transceivers for multiple input multiple output (MIMO) channels [21]. The results have shown that the widely linear MMSE transceiver provides considerable mean square error (MSE) and signal error rate (SER) gains over the linear one. Similarly, Cheng and Haardt have investigated the use of widely linear processing for MIMO systems employing filter bank multi-carrier/offset quadrature amplitude modulation (FBMC/OQAM) [22]. Moreover, the WL processing has been considered to channel estimation firstly in [23] for multi-carrier code division multiple access (MC-CDMA) systems and it has been shown via simulations that the asymptotic bias and the MSE are significantly reduced when WL processing is employed. Furthermore, the WL processing has been investigated to suppress inter-/intra-symbol interference, multiuser interference, and narrowband interference in a high data rate direct sequence ultra-wideband (DS-UWB) system [24]. The WL processing has shown that it outperforms the linear one. However, it has been shown that the WL processing presented a high computational cost [24-26].

Many studies (see, e.g., [24,27-38]) have shown that significant complexity reduction can be achieved by rank reduction techniques. Among these techniques, the eigenvalue decomposition (EVD) and its related singular value decomposition (SVD) techniques have had growing interest. For example, a reduced-rank maximum likelihood estimation (RRMLE) has been derived in [27] for the ML estimation of the regression matrix in terms of the data covariances and their Eigen elements. Also, Scharf and Van Veen have proposed low-rank detectors for gaussian random vectors, and they have shown that rank reduction can be performed with no loss in performance [28]. Novel reduced-rank scheme based on joint iterative optimization of adaptive filters with a low-complexity implementation using normalized least mean square (NLMS) algorithms has been proposed in [29]. The simulation results of the proposed scheme for CDMA interference suppression show a performance significantly better than existing schemes and close to the optimal full-rank MMSE. Moreover, Marzook et al. have proposed a novel channel estimation technique based on SVD technique for time division code division multiple access (TD-SCDMA) [30]. The results have shown that the proposed technique improves the performance of the TD-SCDMA system with low-rank processing and low computation complexity. Furthermore, channel estimation techniques based on SVD for reduced-rank MIMO systems have been proposed in [36]. It has been shown that the SVD-based estimation largely improves the system performance. In all these studies, it has been proved that the rank reduction techniques, especially SVD technique, give a best tradeoff between performance and complexity.

The aim of the paper is twofold. Firstly, based on complex-to-real transformation, we propose a real-valued WLMMSE channel estimator algorithm. Secondly, and based on SVD technique, we propose to reduce the rank of the obtained real-valued WLMMSE channel estimator.

The rest of the paper is organized as follows. MB-OFDM UWB system model describes the system model. The structure of the proposed low-rank real-valued widely linear minimum mean square error (Lr-RWLMMSE) channel estimator is presented in channel estimation. Computational complexity evaluation is dedicated to the computational complexity evaluation of the conventional and proposed schemes. Performance evaluations provide the performance evaluations. Finally, some concluding comments are given in ‘Conclusions’.

2 MB-OFDM UWB system model

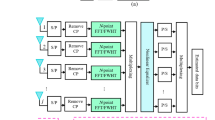
Multiband OFDM (MB-OFDM) is the main solution considered for high rate UWB transmission. Firstly, it was proposed by A. Batra et al. from Texas Instruments for the IEEE 802.15.3a task group [3]. Secondly, it was introduced by the MBOA consortium as their global UWB standard [4]. According to this standard, the available spectrum (3.1 − 10.6 GHz) is divided into 14 sub-bands. Each sub-band of 528 MHz offers 480 Mbit/s. In order to introduce multiple accessing capabilities and to exploit the inherent frequency diversity, each OFDM symbol obtained from a 128-point inverse fast Fourier transform (IFFT), is transmitted on a different sub-band as dictated by a time-frequency code (TFC), shown in Figure 2, that leads to band hopping [4]. The architectures of the transmitter and the receiver of a MB-OFDM UWB system, based on the specifications of ECMA-368 standard, are shown in Figure 1. The modified blocks are those highlighted. These blocks are mainly the rhombic-dual carrier modulation (DCM) mapping at the transmitter and the rhombic-DCM demapping at the receiver proposed by Hajjaj et al. (unpublished work) for MB-OFDM UWB systems. In addition, low-rank real-valued WLMMSE channel estimation and equalization is applied. All MB-OFDM UWB system parameters are detailed in Table 1.

Figure 2
figure 2

Time-frequency coding for the MB-OFDM system using the first three bands with a TFC of {1, 2, 3, 1, 2, 3} [ 39 ]. OFDM, orthogonal frequency division multiplexing.

Full size image
Table 1 MB-OFDM UWB system parameters
Full size table

At the baseband transmitter, the bits from information sources are first scrambled into a pseudo random sequence. The resulting scrambled sequence is then encoded using convolutional encoder of rate R = 1/3 and constraint length K = 7, interleaved via bit interleaver and converted into the l th OFDM symbol of N D = 100 tones. The N D energy-carrying tones are modulated using rhombic-DCM. Then, a total of N P = 12 pilot tones, N G = 10 guard tones and 6 null tones are inserted into the OFDM symbol. An IFFT is used to transform the block of N IFFT (N IFFT = N D + N P + N G + 6 nulls) tones into time-domain. The duration for the OFDM symbol is T IFFT = 242.42 ns. Then, a zero padding sequence of length N ZP = 32 and duration T ZP = 60.61 ns is added to the resulting time-domain OFDM symbol, to eliminate the intersymbol interference (ISI) caused by the multipath propagation, and a guard interval of length 5 and duration T GI = 9.47 ns is added to the end of the OFDM symbol, to ensure the frequency hopping. Thus, each transmitted OFDM symbol has a duration T S = T IFFT + T ZP + T GI = 312.5 ns and includes N S = N IFFT + N ZP + 5 = 165 subcarriers.

The useful discrete-time OFDM signal model is defined by:

$$ x\left(l,n\right)=\frac{1}{\sqrt{N_{\mathrm{IFFT}}}}\left[{\displaystyle \sum_{k=0}^{N_D-1}D\left(l,k\right){e}^{\frac{j2\pi {q}_D(k)n}{N_{\mathrm{IFFT}}}}+{\displaystyle \sum_{k=0}^{N_P-1}P\left(l,k\right){e}^{\frac{j2\pi {q}_P(k)n}{N_{\mathrm{IFFT}}}}}+{\displaystyle \sum_{k=0}^{N_G-1}G\left(l,k\right){e}^{\frac{j2\pi {q}_G(k)n}{N_{\mathrm{IFFT}}}}}}\right] $$
(1)

where n = 0,…, N IFFT −1, D, P and G are the k th data, pilot, and guard subcarriers of the l th OFDM symbol, respectively, and the functions q D , q P , and q G define a mapping functions for data, pilot, and guard subcarriers, respectively.

The baseband of the receiver, in general, consists of similar blocks of the baseband in the transmitter but in the reverse order [2].

The RF-transmitted signal is obtained by converting the baseband signal into continuous-time waveforms via a digital-to-analog converter (DAC) and then up-converting it to the appropriate center frequency, as:

$$ {s}_{RF}(t)=\mathrm{R}\mathrm{e}\left\{{\displaystyle \sum_{l=0}^{N_{sym}-1}x\left(t-l{T}_S\right){e}^{j2\pi {f}_c\left(q(l)\right)t}}\right\} $$
(2)

where Re(⋅) represents the real part of the signal, Nsym is the number of symbols, f c (m) is the center frequency for the m th frequency band, q(l) is a function that maps the l th symbol to the appropriate frequency band, and x(t) is the complex baseband signal representation for the l th symbol. x(t) must satisfy the following property: x(t) = 0 for t ∉[0, TS].

The radiated signal S RF (t) is transmitted over the UWB channel proposed for the IEEE 802.15.3a standard [40]. The impulse response of the multipath UWB channel model is described as:

$$ {h}_i(t)={\chi}_i{\displaystyle \sum_{l=0}^L\sum_{k=0}^K{\alpha}_{k,l}^i\delta}\left(t-{T}_l^i-{\tau}_{k,l}^i\right) $$
(3)

where \( \left\{{\alpha}_{k,l}^i\right\} \) and \( \left\{{\tau}_{k,l}^i\right\} \) are the gain and the delay of the k th multipath component relative to the l th cluster arrival time \( \left({T}_l^i\right) \), respectively, {χ i } is the log-normal shadowing of the i th channel realization.

The IEEE 802.15.3a task group also defined four different configurations (CM1, CM2, CM3, and CM4) identified by the propagation scenarios line of sight (LOS) and non-line of sight (NLOS), and the distance between the transmitting and receiving antennas. The main characteristics of the UWB channel models are listed in Table 2.

Table 2 UWB channel models characteristics
Full size table

The discrete-time UWB channel is modeled as a N h -tap finite-impulse-response (FIR) filter whose channel frequency response (CFR) of the l th OFDM symbol on its corresponding sub-band is given by:

$$ H(l)={\left[H\left(l,0\right),\kern0.5em H\left(l,1\right),\dots, H\left(l,{N}_{\mathrm{IFFT}}-1\right)\right]}^T $$
(4)

where (⋅)T denotes the transposition operation.

At the receiver side, the received signal r RF (t), which is the sum of the output of the channel and additive white Gaussian noise (AWGN) w(t), is first filtered via bandpass filter and down-converted to baseband, and then the zero padding is removed using OLA method [41]. Then, the unitary fast Fourier transform (FFT) is applied to transform the discrete combined signal into frequency domain as:

$$ Y(1)=X(l)H(l)+W(l) $$
(5)

where X(l) = diag{X(l, 0), X(l, 1), …, X(l, N IFFT − 1)} represents the transmitted data, Y(l) = [Y(l, 0), Y(l, 1), …, Y(l, N IFFT − 1)]T denotes the received data, and \( W(l)={\left[\begin{array}{cccc}\hfill W\left(l,0\right),\hfill & \hfill W\left(l,1\right),\hfill & \hfill \dots, \hfill & \hfill W\left(l,{N}_{IFFT}-1\right)\hfill \end{array}\right]}^T \) indicates the additive noise component, of the l th OFDM symbol.

For the sake of simplicity, we refer, in this paper, to Y(l), X(l), H(l), and W(l) as Y, X, H, and W, respectively.

Wiener filter (WF) based on LMMSE criterion, employing the second-order statistics of the channel conditions, is considered for channel estimation [8]. However, since the proposed MB-OFDM UWB system is dealing with non-circular signals, it requires widely linear processing to take into account all the second-order statistics of the channel conditions and the received signal. Therefore, the received signal, in the frequency domain, is augmented with its conjugate as:

$$ \begin{array}{l}\underset{\bar{\mkern6mu}}{Y}=\left[\begin{array}{c}\hfill Y\hfill \\ {}\hfill Y*\hfill \end{array}\right]=\left[\begin{array}{c}\hfill XH\hfill \\ {}\hfill X*H*\hfill \end{array}\right]+\left[\begin{array}{c}\hfill W\hfill \\ {}\hfill W*\hfill \end{array}\right]\\ {}\kern1em =\left[\begin{array}{cc}\hfill X\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill X*\hfill \end{array}\right]\left[\begin{array}{c}\hfill H\hfill \\ {}\hfill H*\hfill \end{array}\right]+\left[\begin{array}{c}\hfill W\hfill \\ {}\hfill W*\hfill \end{array}\right]\\ {}\kern1em =\underset{\bar{\mkern6mu}}{X}\underset{\bar{\mkern6mu}}{H}+\underset{\bar{\mkern6mu}}{W}\end{array} $$
(6)

3 Channel estimation

The MB-OFDM UWB systems employ frame-based transmission. As shown in Figure 3, each MB-OFDM UWB frame, which is referred to PPDU (PLCP protocol data unit), is composed of three components: the PLCP (Physical Layer Convergence Protocol) preamble, the PLCP header, and the PSDU (PLCP service data unit) [3]. The PLCP preamble consists of three distinct portions: packet synchronization sequence, frame synchronization sequence, and the channel estimation sequence. The latter portion is used to estimate the channel frequency response. The channel estimation sequence is followed by the PLCP Header which contains the data rate, the data length, the transport mode, the preamble type, and the MAC Header. The last component of the PPDU is the PSDU, which contains the actual information data (coming from higher layers).

Figure 3
figure 3

PLCP protocol data unit (PPDU) structure.

Full size image

We focus in this section on channel estimation for MB-OFDM UWB systems. There are two main methods: the first is based on the channel estimation sequence (CES) of the PLCP preamble and the second is based on pilot signals insertion into each OFDM symbol. Here, even assuming that the UWB channel is invariant over the transmission period of an OFDM frame, the channel estimation can be performed using the channel training sequence.

In the end of the MB-OFDM UWB system model, we have shown the relation between the augmented output \( \underset{\bar{\mkern6mu}}{Y} \) and the augmented transmitted symbol \( \underset{\bar{\mkern6mu}}{X} \) as:

$$ \underset{\bar{\mkern6mu}}{Y}=\underset{\bar{\mkern6mu}}{X}\underset{\bar{\mkern6mu}}{H}+\underset{\bar{\mkern6mu}}{W} $$
(7)

This relation can be equally written for the N (N = 112) CSES data subcarriers of a single training OFDM symbol as:

$$ \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}=\overset{\smile }{\underset{\bar{\mkern6mu}}{X}}\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}+\overset{\smile }{\underset{\bar{\mkern6mu}}{W}} $$
(8)

where \( \overset{\smile }{\underset{\bar{\mkern6mu}}{X}} \) is 2 N × 2 N diagonal matrix with diagonal entries the N nonzero transmitted data augmented with its conjugate, \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}},\overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) and \( \overset{\smile }{\underset{\bar{\mkern6mu}}{W}} \) are 2 N × 1 related sub-blocks of \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}},\overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) and \( \underset{\bar{\mkern6mu}}{W} \), respectively.

3.1 Augmented LS estimator

Let \( \widehat{\underset{\bar{\mkern6mu}}{H}} \) be the estimate of \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \). The expression of augmented LS estimation is:

$$ {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{LS}={\overset{\smile }{\underset{\bar{\mkern6mu}}{X}}}^{-1}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} $$
(9)

which minimizes \( \left(\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}-\overset{\smile }{\underset{\bar{\mkern6mu}}{X}}\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\right)H\left(\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}-\overset{\smile }{\underset{\bar{\mkern6mu}}{X}}\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\right) \)

3.2 WLMMSE estimator

We denote the widely linear estimator of the augmented transfer function of channel \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) by:

$$ {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}}=\overset{\smile }{A}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} $$
(10)

Based on the orthogonality principle for linear estimation \( E\left[\left({\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}}-\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\right){\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^H\right]=0 \) [42], the optimal Ă is given by:

$$ \overset{\smile }{A}=E\left[\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^H\right]{\left(E\left[\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^H\right]\right)}^{-1}={C}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}{C}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^{-1} $$
(11)

Hence, the WLMMSE estimator of \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) can be written as:

$$ {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}}={C}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}{C}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^{-1}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} $$
(12)

where the augmented auto-covariance matrix of \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} \) is given by:

$$ {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{Y}\overset{\smile }{Y}}=\left[\begin{array}{cc}\hfill \overset{\smile }{X}{C}_{\overset{\smile }{H}\overset{\smile }{H}}{\overset{\smile }{X}}^{*}+{\sigma}_{\overset{\smile }{W}}^2\hfill & \hfill \overset{\smile }{X}{\tilde{C}}_{\overset{\smile }{H}\overset{\smile }{H}}\overset{\smile }{X}\hfill \\ {}\hfill {\overset{\smile }{X}}^{*}{\tilde{C}}_{\overset{\smile }{H}\overset{\smile }{H}}^{*}{\overset{\smile }{X}}^{*}\hfill & \hfill {\overset{\smile }{X}}^{*}{C}_{\overset{\smile }{H}\overset{\smile }{H}}^{*}\overset{\smile }{X}+{\sigma}_{\overset{\smile }{W}}^2\hfill \end{array}\right] $$
(13)

and the augmented cross-covariance matrix is defined as:

$$ {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{H}\overset{\smile }{Y}}=\left[\begin{array}{cc}\hfill {C}_{\overset{\smile }{H}\overset{\smile }{H}}{\overset{\smile }{X}}^{*}\hfill & \hfill {\tilde{C}}_{\overset{\smile }{H}\overset{\smile }{H}}\overset{\smile }{X}\hfill \\ {}\hfill {\tilde{C}}_{\overset{\smile }{H}\overset{\smile }{H}}^{*}{\overset{\smile }{X}}^{*}\hfill & \hfill {C}_{\overset{\smile }{H}\overset{\smile }{H}}^{*}\overset{\smile }{X}\hfill \end{array}\right] $$
(14)

In strictly linear case, the LMMSE estimator is given by:

$$ \begin{array}{l}{\widehat{H}}_{\mathrm{LMMSE}}={C}_{\overset{\smile }{H}\overset{\smile }{Y}}{C}_{\overset{\smile }{Y}\overset{\smile }{Y}}^{-1}\overset{\smile }{Y}\\ {}\kern3em ={C}_{\overset{\smile }{H}\overset{\smile }{H}}{\left({C}_{\overset{\smile }{H}\overset{\smile }{H}}+{\sigma}_{\overset{\smile }{W}}^2{\left(\overset{\smile }{X}{\overset{\smile }{X}}^{*}\right)}^{-1}\right)}^{-1}{\widehat{H}}_{LS}\end{array} $$
(15)

3.3 Low-rank real-valued WLMMSE estimator

We denote by H R , X R , W R , and Y R the real composite representation of \( \overset{\smile }{H},\overset{\smile }{X},\overset{\smile }{W} \), and \( \overset{\smile }{Y} \), respectively:

$$ {H}_R=\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right] $$
(16)

where H r and H i are the real and imaginary vectors of \( \overset{\smile }{H} \)

$$ {X}_R=\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right] $$
(17)

where X r and X i are the real and imaginary matrices of \( \overset{\smile }{X} \)

$$ {W}_R=\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right] $$
(18)

where W r and W i are the real and imaginary vectors of \( \overset{\smile }{W} \)

$$ {Y}_R=\left[\begin{array}{c}\hfill {Y}_r\hfill \\ {}\hfill {Y}_i\hfill \end{array}\right] $$
(19)

where Y r and Y i are the real and imaginary vectors of \( \overset{\smile }{Y} \).

From (16) and (17):

$$ \overset{\smile }{X}\overset{\smile }{H}={X}_r{H}_r-{X}_i{H}_i+j\left({X}_r{H}_i+{X}_i{H}_r\right) $$
(20)

Then,

$$ \begin{array}{l}{Y}_R=\left[\begin{array}{c}\hfill {Y}_r\hfill \\ {}\hfill {Y}_i\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {X}_r{H}_r-{X}_i{H}_i\hfill \\ {}\hfill {X}_r{H}_i+{X}_i{H}_r\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]\\ {}\kern1em =\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]\end{array} $$
(21)

The linear-to-complex transformation gives the following relations

  • The relation between the augmented vector \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} \) and the real vector Y R can be described by: \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}=T{Y}_R \) where \( T=\left[\begin{array}{cc}\hfill I\hfill & \hfill jI\hfill \\ {}\hfill I\hfill & \hfill -jI\hfill \end{array}\right] \) is unitary up to a factor of 2: TT H = T H T = 2I, and I is the identity matrix.

  • The relation between the augmented vector \( \overset{\smile }{\underset{\bar{\mkern6mu}}{W}} \) and the real vector W R can be described by \( \overset{\smile }{\underset{\bar{\mkern6mu}}{W}}=T{W}_R \).

  • The relation between the augmented vector \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) and the real vector H R can be described by \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}}=T{H}_R \).

We assume that \( \overset{\smile }{H} \) and \( \overset{\smile }{W} \) are uncorrelated as in all stochastic filtering applications, i.e., \( \overset{\smile }{H}{\overset{\smile }{W}}^H=\overset{\smile }{W}{\overset{\smile }{H}}^H=0 \).

Then, the augmented auto-covariance matrix of \( \overset{\smile }{Y} \) can be expressed as:

$$ \begin{array}{l}{\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}=E\left[\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^H\right]\\ {}\kern1em =E\left[\left(T{Y}_R\right){\left(T{Y}_R\right)}^H\right]\\ {}\kern1em =E\left[T{Y}_R{Y}_R^H{T}^H\right]\\ {}\kern1em =TE\left[{Y}_R{Y}_R^H\right]{T}^H\\ {}\kern1.5em =T{R}_{Y_R{Y}_R}{T}^H\kern1em \end{array} $$
(22)

where \( {R}_{Y_R{Y}_R} \) is the auto-correlation matrix of Y R .

$$ \begin{array}{l}{R}_{Y_R{Y}_R}=E\left[\left(\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]\right){\left(\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]\right)}^H\right]\\ {}\kern2em =E\left(\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H\right)+E\left(\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)+\\ {}\kern3em E\left(\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)+E\left(\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H\right)\\ {}\kern2em =\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\underset{R_{H_R{H}_R}}{\underbrace{E\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H\right)}}{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H+E\left(\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)+\\ {}\kern3em \left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\underset{0}{\underbrace{E\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)}}+\underset{0}{\underbrace{E\left(\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H\right)}}{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H\end{array} $$
(23)
$$ \begin{array}{l}E\left(\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)=E\left(\left({T}^{-1}\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}\right){\left({T}^{-1}\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}\right)}^H\right)\\ {}\kern6em =E\left({T}^{-1}\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^H\right)\\ {}\kern6em ={T}^{-1}E\left(\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^H\right){\left({T}^H\right)}^{-1}\\ {}\kern6em ={T}^{-1}{\sigma}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^2{\left({T}^H\right)}^{-1}\\ {}\kern6em ={\sigma}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^2{\left(T{T}^H\right)}^{-1}\\ {}\kern6em =2{\sigma}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^2I\end{array} $$
(24)

Then,

$$ {R}_{Y_R{Y}_R}={X}_R{R}_{H_R{H}_R}{X}_R^H+2{\sigma}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{W}}}^2I $$
(25)

where \( {R}_{H_R{H}_R} \) is the auto-correlation matrix of H R .

The augmented cross-covariance matrix can be determined as:

$$ \begin{array}{l}{\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}=E\left[\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}}^H\right]\\ {}\kern2em =E\left[\left(T{H}_R\right){\left(T{Y}_R\right)}^H\right]\\ {}\kern2em =E\left[T{H}_R{Y}_R^H{T}^H\right]\\ {}\kern2em =TE\left[{H}_R{Y}_R^H\right]{T}^H\\ {}\kern2em =T{R}_{H_R{Y}_R}{T}^H\end{array} $$
(26)

where

$$ \begin{array}{l}{R}_{H_R{Y}_R}=E\left[\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]\right){\left(\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]\right)}^H\right]\\ {}\kern2em =E\left[\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H\right)\right]+\underset{0}{\underbrace{E\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {W}_r\hfill \\ {}\hfill {W}_i\hfill \end{array}\right]}^H\right)}}\\ {}\kern2em =\underset{R_{H_R{H}_R}}{\underbrace{E\left(\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]{\left[\begin{array}{c}\hfill {H}_r\hfill \\ {}\hfill {H}_i\hfill \end{array}\right]}^H\right)}}{\left[\begin{array}{cc}\hfill {X}_r\hfill & \hfill -{X}_i\hfill \\ {}\hfill {X}_i\hfill & \hfill {X}_r\hfill \end{array}\right]}^H\\ {}\kern2em ={R}_{H_R{H}_R}{X}_R^H\end{array} $$
(27)

By inserting the expression of \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{H}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}},{\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}\overset{\smile }{\underset{\bar{\mkern6mu}}{Y}}} \), and \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} \) into (12), the resulting real-valued WLMMSE (RWLMMSE) estimator of \( \underset{\bar{\mkern6mu}}{H} \) is denoted by:

$$ \begin{array}{l}{\underset{\bar{\mkern6mu}}{\widehat{H}}}_{\mathrm{RWLMMSE}}=\left(T{R}_{H_R{Y}_R}{T}^H\right){\left(T{R}_{Y_R{Y}_R}{T}^H\right)}^{-1}\left(T{Y}_R\right)\\ {}\kern4em =T{R}_{H_R{Y}_R}{T}^H{\left({T}^H\right)}^{-1}{R}_{Y_R{Y}_R}^{-1}{T}^{-1}T{Y}_R\\ {}\kern4em =T{R}_{H_R{Y}_R}{R}_{Y_R{Y}_R}^{-1}{Y}_R\\ {}\kern4em =T{R}_{H_R{H}_R}{X}_R^H{\left({X}_R{R}_{H_R{H}_R}{X}_R^H+2{\sigma}_{\underset{\bar{\mkern6mu}}{W}}^2I\right)}^{-1}{Y}_R\end{array} $$
(28)

The LS estimator of \( \overset{\smile }{\underset{\bar{\mkern6mu}}{H}} \) is:

$$ {\underset{\bar{\mkern6mu}}{\widehat{H}}}_{LS}={\underset{\bar{\mkern6mu}}{\overset{\smile }{X}}}^{-1}\underset{\bar{\mkern6mu}}{\overset{\smile }{Y}}\iff \underset{\bar{\mkern6mu}}{\overset{\smile }{Y}}=\underset{\bar{\mkern6mu}}{\overset{\smile }{X}}{\underset{\bar{\mkern6mu}}{\widehat{H}}}_{LS}\iff {Y}_R={X}_R{\widehat{H}}_{L{S}_R} $$
(29)

where \( {H}_{L{S}_R}=\left(\begin{array}{c}\hfill {H}_{L{S}_r}\hfill \\ {}\hfill {H}_{L{S}_i}\hfill \end{array}\right) \), and \( {H}_{L{S}_r} \) and \( {H}_{L{S}_i} \) are the real and imaginary vectors of \( {\overset{\smile }{H}}_{LS} \).

Then,

$$ \begin{array}{l}{\underset{\bar{\mkern6mu}}{\widehat{H}}}_{\mathrm{RWLMMSE}}=T{R}_{H_R{H}_R}{X}_R^H{\left({X}_R{R}_{H_R{H}_R}{X}_R^H+2{\sigma}_{\underset{\bar{\mkern6mu}}{W}}^2I\right)}^{-1}{X}_R{\widehat{H}}_{L{S}_R}\\ {}\kern4em =T{R}_{H_R{H}_R}{X}_R^H{X}_R{\left({X}_R{R}_{H_R{H}_R}{X}_R^H+2{\sigma}_{\underset{\bar{\mkern6mu}}{W}}^2I\right)}^{-1}{\widehat{H}}_{L{S}_R}\\ {}\kern4em =T{R}_{H_R{H}_R}{\left({R}_{H_R{H}_R}+2{\sigma}_{\underset{\bar{\mkern6mu}}{W}}^2{\left({X}_R{X}_R^H\right)}^{-1}\right)}^{-1}{\widehat{H}}_{L{S}_R}\\ {}\kern4em =T{R}_{H_R{H}_R}{\left({R}_{H_R{H}_R}+\xi I\right)}^{-1}{\widehat{H}}_{L{S}_R}\end{array} $$
(30)

where

$$ \xi ={\scriptscriptstyle \frac{2{\sigma}_{W_R}^2}{\sigma_{X_R}^2}} $$
(31)

To further reduce the computational complexity, we adopt the low-rank approximation technique based on SVD [35]. The SVD of \( {R}_{H_R{H}_R} \) is denoted by \( {R}_{H_R{H}_R}=U\varLambda {U}^H \), where U is a matrix with orthonormal columns u0, u1, . . ., u2N-1 and Λ is a diagonal matrix, containing the singular values λ 0 ≥ λ 1 ≥ … ≥ λ 2N − 1 ≥ 0 on its diagonal. Since some singular values of the matrix Λ are negligible, by selecting r significant singular values, we can obtain optimal rank r channel estimator.

The proposed rank r channel estimator is given by:

$$ {\underset{\bar{\mkern6mu}}{\widehat{H}}}_{Lr-\mathrm{RWLMMSE}}=TU\left(\begin{array}{cc}\hfill {\varDelta}_r\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right){U}^H{\widehat{H}}_{L{S}_R} $$
(32)

where Δ r is a diagonal matrix containing the values:

$$ {\delta}_k=\frac{\lambda_k}{\lambda_k+\xi },k=0,1,\dots, r-1 $$
(33)

4 Computational complexity evaluation

In this section, we analyze the performance of our proposed estimator in terms of computational complexity. It is shown that the multiplication of two N × N complex matrixes requires 3 N 3 + 2 N 2 real additions and 4 N 3 real multiplications [43].

  • ➢ The calculation of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}} \) requires:

    • 12 N 3 + 8 N 2 real additions and 12 N 3 real multiplications to calculate \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{H}\overset{\smile }{Y}} \),

    • 24 N 3 + 20 N 2 real additions and 24 N 3 real multiplications to calculate \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{Y}\overset{\smile }{Y}} \),

    • 8 N 3 operations to calculate the inverse of \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{Y}\overset{\smile }{Y}} \),

    • 48 N 3 + 8 N 2 operations to calculate the product of \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{H}\overset{\smile }{Y}} \) by \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{Y}\overset{\smile }{Y}}^{-1} \),

    • and 64 N 2 operations to calculate the product of \( {\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{H}\overset{\smile }{Y}}{\underset{\bar{\mkern6mu}}{C}}_{\overset{\smile }{Y}\overset{\smile }{Y}}^{-1} \) by \( \overset{\smile }{\underset{\bar{\mkern6mu}}{Y}} \).

Then, the computational complexity of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}} \) is given by:

$$ \begin{array}{l}O\left({\underset{\bar{\mkern6mu}}{\widehat{H}}}_{\mathrm{WLMMSE}}\right)=12{N}^3+8{N}^2+12{N}^3+24{N}^3+20{N}^2+24{N}^3+8{N}^2+48{N}^3+8{N}^2+64{N}^2\\ {}\kern5em =120{N}^3+108{N}^2\end{array} $$
(34)

  • ➢ The calculation of Ĥ LMMSE requires:

    • 3 N 3 + 2 N 2 real additions and 3 N 3 real multiplications to calculate \( {C}_{\overset{\smile }{H}\overset{\smile }{Y}} \),

    • 6 N 3 + 5 N 2 real additions and 6 N 3 real multiplications to calculate \( {C}_{\overset{\smile }{Y}\overset{\smile }{Y}} \),

    • N 3 operations to calculate the inverse of \( {C}_{\overset{\smile }{Y}\overset{\smile }{Y}} \),

    • 6 N 3 + 3 N 2 operations to calculate the product of \( {C}_{\overset{\smile }{H}\overset{\smile }{Y}} \) by \( {C}_{\overset{\smile }{Y}\overset{\smile }{Y}}^{-1} \),

    • and 8 N 2 operations to calculate the product of \( {C}_{\overset{\smile }{H}\overset{\smile }{Y}}{C}_{\overset{\smile }{Y}\overset{\smile }{Y}}^{-1} \) by \( \overset{\smile }{Y} \).

Then, the computational complexity of Ĥ LMMSE is given by:

$$ \begin{array}{l}O\left({\widehat{H}}_{\mathrm{LMMSE}}\right)=3{N}^3+2{N}^2+3{N}^3+6{N}^3+5{N}^2+6{N}^3+{N}^3+6{N}^3+3{N}^2+8{N}^2\\ {}\kern4.5em =25{N}^3+18{N}^2\end{array} $$
(35)

Therefore, the computational complexity of WLMMSE estimator requires about five times more operations than the LMMSE estimator.

  • ➢ The calculation of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{RWLMMSE}} \) requires:

    • 8 N 3 operations to calculate the product of T by \( {R}_{H_R{H}_R} \),

    • 4 N 2 operations to calculate the addition of \( {R}_{H_R{H}_R} \) and ξI,

    • 8 N 3 operations to calculate the inverse of \( \left({R}_{H_R{H}_R}+\xi I\right) \),

    • 8 N 3 operations to calculate the product of \( T{R}_{H_R{H}_R} \) by \( {\left({R}_{H_R{H}_R}+\xi I\right)}^{-1} \),

    • and 4 N 2 operations to calculate the product of \( T{R}_{H_R{H}_R}{\left({R}_{H_R{H}_R}+\xi I\right)}^{-1} \) by \( {\widehat{H}}_{L{S}_R} \).

Then, the computational complexity of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{RWLMMSE}} \) is given by:

$$ \begin{array}{l}O\left({\underset{\bar{\mkern6mu}}{\widehat{H}}}_{\mathrm{RWLMMSE}}\right)=8{N}^3+4{N}^2+8{N}^3+8{N}^3+4{N}^2\\ {}\kern5em =24{N}^3+8{N}^2\end{array} $$
(36)

  • ➢ The calculation of \( {\underset{\bar{\mkern6mu}}{\widehat{H}}}_{Lr-\mathrm{RWLMMSE}} \) requires:

    • 4N 2 r + 2Nr operations to calculate \( U\left(\begin{array}{cc}\hfill {\varDelta}_r\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right){U}^H \),

    • 8 N 3 operations to calculate the product of T by \( U\left(\begin{array}{cc}\hfill {\varDelta}_r\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right){U}^H \),

    • and 4 N 2 operations to calculate the product of \( TU\left(\begin{array}{cc}\hfill {\varDelta}_r\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill \end{array}\right){U}^H \) by \( {\widehat{H}}_{L{S}_R} \).

Then, the computational complexity of \( {\underset{\bar{\mkern6mu}}{\widehat{H}}}_{Lr-\mathrm{RWLMMSE}} \) is given by:

$$ O\left({\widehat{\underset{\bar{\mkern6mu}}{H}}}_{Lr\mathit{\hbox{-}}\mathrm{RWLMMSE}}\right)=8{N}^3+4{N}^2r+4{N}^2+2Nr $$
(37)

Thus, the computational complexity of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{RWLMMSE}} \) requires a total of 24 N 3 + 8 N 2 operations, which is about 5 times less than that of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{WLMMSE}} \) and slightly less than that of Ĥ LMMSE. Consequently, the real-valued WLMMSE channel estimator reduces the computational complexity by 80% and accomplishes a computational complexity comparable with that of LMMSE channel estimator. Furthermore, by applying the low-rank Wiener filter technique, the complexity of \( {\widehat{\underset{\bar{\mkern6mu}}{H}}}_{\mathrm{Lr}\hbox{-} \mathrm{RWLMMSE}} \) is significantly reduced mainly for small values of r.

5 Performance evaluations

In this section, we compare the bit error rate (BER) of the proposed low-rank RWLMMSE channel estimator with that of WLMMSE channel estimator. The MB-OFDM UWB system parameters are summarized in Table 1. In our simulations, we adopt the CM1 and CM2 UWB channel models of the standard IEEE 802.15.3a.

In Figures 4 and 5, the BER performance of the proposed channel estimator for MB-OFDM UWB system for various values of rank r are evaluated in terms of signal-to-noise ratio (SNR) in CM1 and CM2, respectively. The used modulation is the rhombic-DCM with a rhombic deformation coefficient ε = 0.5. In these figures, the legends WLMMSE, Lr-RWLMMSE (r = 16), Lr-RWLMMSE (r = 32), and Lr-RWLMMSE (r = 64) present the estimators based on WLMMSE, Lr-RWLMMSE with rank r = 16, Lr-RWLMMSE with rank r = 32, and Lr-RWLMMSE with rank r = 64, respectively. In both figures, it is observed that the performance of the Lr-RWLMMSE estimator is comparable with that of WLMMSE at low SNR and slightly under the WLMMSE estimator’s performance at high SNR. For Lr-RWLMMSE estimator, the performance degrades slightly as the rank r decreases. This is due to the loss of channel information when the rank of the channel correlation matrix is reduced. These results are further proved by the Figures 6 and 7 which give the performance of the WLMMSE and Lr-RWLMMSE with rank r = 32 for different values of rhombic deformation coefficient.

Figure 4
figure 4

BER vs. SNR for WLMMSE and Lr-RWLMMSE estimators over CM1 channel model. BER, bit error rate; WLMMSE, widely linear minimum mean square error; Lr-RWLMMSE, low-rank real-valued widely linear minimum mean square error.

Full size image
Figure 5
figure 5

BER vs. SNR for WLMMSE and Lr-RWLMMSE estimators over CM2 channel model. BER, bit error rate; WLMMSE, widely linear minimum mean square error; Lr-RWLMMSE, low-rank real-valued widely linear minimum mean square error.

Full size image
Figure 6
figure 6

BER vs. SNR of WLMMSE and Lr-RWLMMSE estimators for \( \boldsymbol{\upvarepsilon} \mathbf{\in}\left\{\begin{array}{ccc}\hfill \mathbf{0.3},\hfill & \hfill \mathbf{0.5},\hfill & \hfill \mathbf{0.7}\hfill \end{array}\right\} \) over CM1 channel model. BER, bit error rate; WLMMSE, widely linear minimum mean square error; Lr-RWLMMSE, low-rank real-valued widely linear minimum mean square error.

Full size image
Figure 7
figure 7

BER vs. SNR of WLMMSE and Lr-RWLMMSE estimators for \( \boldsymbol{\upvarepsilon} \mathbf{\in}\left\{\begin{array}{ccc}\hfill \mathbf{0.3},\hfill & \hfill \mathbf{0.5},\hfill & \hfill \mathbf{0.7}\hfill \end{array}\right\} \) over CM2 channel model. BER, bit error rate; WLMMSE, widely linear minimum mean square error; Lr-RWLMMSE, low-rank real-valued widely linear minimum mean square error.

Full size image

6 Conclusions

In this paper, we have presented a low-complexity channel estimator for MB-OFDM UWB system. We have investigated the WLMMSE channel estimator algorithm, and we have proceeded with real-valued algorithm followed by low-rank approximation of such channel estimator algorithm. The proposed low-rank real-valued WLMMSE channel estimator algorithm has reduced the computational complexity while maintaining the performance improvement of the WLMMSE one. As a consequence, the proposed Lr-RWLMMSE channel estimator algorithm has provided not only BER performance improvement but also lower computation cost.