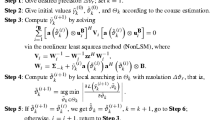1 Introduction

Acoustic direction-of-arrival (DOA) estimation is a key technology in audio signal processing where it enables source localization for humanoid robots [1, 2], drones [3, 4], teleconferencing [5, 6], and hearing aids [7]. The goal of acoustic DOA estimation is to obtain the bearing angle of acoustic waves generated by sound sources using a microphone array. According to the Rayleigh criterion [8], the resolution of traditional DOA estimation approaches (e.g., the classical beamforming (CBF)Footnote 1 based approach and the steered-response power phase transform (SRP-PHAT) method [9]) is limited by the array aperture. Therefore, for some applications like humanoid robots and drones with a small platform size, the traditional approaches suffer in scenarios with multiple sources simultaneously present. Although methods such as the minimum variance distortionless response (MVDR) [8, 10], multiple signal classification (MUSIC) [11], and estimation of signal parameters via the rotational invariance technique (ESPRIT) [12] can offer a high-resolution performance, they are sensitive to calibration errors and errors in the assumed or estimated signal statistics [13, 14]. The robustness of the MVDR and MUSIC methods have been studied in the presence of array errors [15–17]. However, these studies rely on asymptotic properties, i.e., high signal-to-noise ratio (SNR) scenarios and large numbers of snapshots. Thus, these studies do not apply when only a small number of snapshots is available.

Sparse signal recovery-based DOA estimation methods have enjoyed much success in recent decades by exploiting the sparsity of sources in the spatial domain [18, 19]. These approaches are attractive because (1) they offer robustness against noise and limitations in data quality [18], (2) they have a good performance with a small number of snapshots [20], (3) they offer a higher resolution performance than MVDR and MUSIC methods [21, 22], and (4) they have the capability to resolve coherent sources [23]. In [18], the source localization problem was first formulated as an over-complete basis representation problem. To estimate the source amplitudes, an l1-norm based singular value decomposition (SVD) method was proposed. In [24], a complex least absolute shrinkage and selection operator (cLASSO) method was proposed for DOA estimation. In [25], a re-weighted regularized sparse recovery method was proposed for DOA estimation with unknown mutual coupling. All these methods are based on convex optimization theory, that is, the signals are recovered by solving a regularized optimization problem. They have a good performance with a properly chosen regularization factor, but the regularization factor needs to be determined empirically [26].

Because of its self-regularization nature and its ability to quantify uncertainty, the sparse Bayesian learning (SBL)-based methods have attracted a lot of attention in sparse signal recovery and compressed sensing. The SBL principle was originally proposed in [27] for obtaining sparse solutions to regression and classification tasks. The SBL algorithm was applied to the compressed sensing in [28], and an SBL-based Bayesian compressed sensing method using Laplace priors was proposed in [29]. More recently, a scalable mean-field SBL was proposed in [30]. In [31], an SBL-based DOA estimation method with predefined grids was proposed. In that paper, the DOA estimation is formulated as a sparse signal recovery and compressed sensing problem. To obtain refined estimates of the DOA, an off-grid DOA estimation method was proposed in [32]. In [21], a multi-snapshot SBL (MSBL) method was proposed for the multi-snapshot DOA estimation problem. The method was further applied to sound source localization and speech enhancement in [22]. To reduce the computational complexity of the wide-band approach, a computationally efficient DOA estimation method was proposed in [33] based on a sparse Bayesian framework. Additionally, some of our previous works are related to this paper. In [34], we proposed an SBL method with compressed data for sound source localization. The results show that the SBL method offers an excellent estimation accuracy for sound source localization even with low data quality. In [35], we proposed an SBL-based acoustic reflector localization method, which models the acoustic reflector localization problem as a sparse signal recovery problem. It shows that the SBL-based method offers a more robust performance for basis mismatch compared to the state-of-the-art methods. However, a common drawback of these approaches is that the traditional SBL-based approaches are computationally complex due to the matrix inversion operation required for updating the covariance matrix of the source signals.

Computationally efficient SBL algorithms have also been proposed in various applications. For example, in [36], a basis adding/deleting scheme based on the marginal distribution was proposed. In [37], an inverse free SBL method was proposed by relaxing the evidence lower bound. In [38], a space alternating variational estimation (SAVE) algorithm was proposed to push the variational Bayesian inference (VBI) based SBL to a scalar level. The experimental results show that the SAVE approach has a faster convergence and a lower minimum mean square error (MMSE) performance than other fast SBL algorithms.

Based on this, we propose a space alternating SBL-based acoustic DOA estimation method for high-resolution estimation in this paper. A hierarchical Bayesian framework with group sparse priors is built to model multiple measurement vector (multi-snapshot) signals. As direct calculation of the posterior distribution is not possible, variational Bayesian inference is applied to infer all hidden variables in the proposed model. Furthermore, we extend the SAVE method [38] to the multiple measurement vector (MMV) case to reduce the computational complexity of the algorithm. The proposed algorithm can be applied to each frequency bin independently. To jointly utilize the recovered signals from all frequency bins, a complex Gaussian mixture model (CGMM) based expectation–maximization (EM) algorithm is proposed. We refer to the proposed method as the SAVE-MSBL-EM method.

The rest of this paper is organized as follows: In Section 2, we pose the narrow-band acoustic DOA estimation problem as a sparse signal recovery problem with an over-complete dictionary. Moreover, under the assumption that the DOAs of all sources do not change in a frame, a hierarchical Bayesian framework is built by exploiting the group sparsity of the MMV source signals. In Section 3, the SAVE-MSBL algorithm is proposed to infer all the hidden variables in the hierarchical Bayesian model for one frequency bin. Then, the CGMM-based EM algorithm is formulated to deal with the wide-band acoustic DOA estimation. In Section 4, we evaluate the performance of the proposed algorithm using both synthetic data and real data. Finally, we provide our conclusions in Section 5.

Note that vectors and matrices are represented using bold lowercase and uppercase letters, respectively. The superscripts (·)T and (·)H denote the transpose and conjugate transpose operator, respectively. Moreover, L×L identity matrix is denoted as IL. The lp norm and Frobenius norm are represented using ∥·∥p and ∥·∥F, respectively.

2 Signal model

2.1 Problem formulation

The problem considered in this paper can be stated as follows. We consider the scenario that P sound sources exist in the far-field of an arbitrary microphone array with M microphones which are used to record the signals. The center point of the microphone array is denoted as O. All the microphones are assumed to be omnidirectional and synchronized. As it is shown in [18, 22, 33], the DOA estimation problem can be formulated as a sparse signal recovery problem using an over-complete dictionary with basis vectors containing the DOA information. Let θ=[θ1,θ2,⋯,θK]T denote a set of candidate DOAs, where K denotes the total number of candidate DOAs. The signal model for the fth (1≤f≤F) frequency bin of one frame can be expressed as

$$ \boldsymbol{X}_{f}=\boldsymbol{A}_{f}\boldsymbol{S}_{f}+\boldsymbol{N}_{f}, $$
(1)

where

$$\begin{array}{*{20}l} \boldsymbol{X}_{f}&=\left[\boldsymbol{x}_{f,1},\boldsymbol{x}_{f,2},\cdots,\boldsymbol{x}_{f,L}\right],\\ \boldsymbol{x}_{f,l}&=\left[x_{f,l,1},x_{f,l,2},\cdots,x_{f,l,M}\right]^{\mathrm{T}},\\ \boldsymbol{A}_{f}&=\left[\boldsymbol{a}_{f,1},\boldsymbol{a}_{f,2},\cdots,\boldsymbol{a}_{f,K}\right],\\ \boldsymbol{a}_{f,k}&=\left[1,e^{-j\omega_{f}\tau_{k2}},\cdots,e^{-j\omega_{f}\tau_{kM}}\right]^{\mathrm{T}},\\ \boldsymbol{S}_{f}&=\left[\boldsymbol{s}_{f,1},\boldsymbol{s}_{f,2},\cdots,\boldsymbol{s}_{f,K}\right]^{\mathrm{T}},\\ \boldsymbol{s}_{f,k}&=\left[s_{f,k,1},s_{f,k,2},\cdots,s_{f,k,L}\right]^{\mathrm{T}}, \end{array} $$

F is the total number of frequency bins, Xf\(\in \mathbb {C}^{M\times L}\) is a collection of signal snapshots in the frequency-domain with xf,l,m being the signal at the fth frequency bin, lth snapshot, and mth microphone. We refer to the matrix Xf as one frame and xf,l\(\in \mathbb {C}^{M}\) as one snapshot, l∈[1,2,⋯,L] is the index of the snapshotsFootnote 2. The matrix Af\(\in \mathbb {C}^{M\times N}\) is the dictionary for the fth frequency bin with the basis vector af,k\(\in \mathbb {C}^{M}\) representing the array response for the direction θk,ωf is the fth angular frequency, and τkm is the relative time delay of source k between microphone m and the array center point O. Moreover, Sf\(\in \mathbb {C}^{K\times L}\) is a collection of the source signals with sf,k being the kth row. The noise matrix Nf\(\in \mathbb {C}^{M\times L}\) is defined similarly to Sf. Assuming that several sound sources are active in one frame, let θs (θs⊂θ) denote the true DOA set and ks(ks⊂[1,2,⋯,K]) denote the true index set. Based on the above definition and the signal model in (1), Sf is an all-zero matrix except for the elements of the rows within the ground truth index set ks. An example is given in Fig. 1, which uses a uniform linear array (ULA). In this example, the target space is sampled uniformly with an interval of 10∘. Two sources are located at −30∘ and 40∘, respectively. Thus, when the two sources are active simultaneously, only the elements in the two rows of Sf corresponding to the bearing angles −30∘ and 40∘ are non-zero.

Fig. 1
figure 1

The candidate DOAs in the target space. The red circles denote the microphones. The blue circles denote the positions of the sound sources

Full size image

Based on (1), to obtain the DOA estimator, we can first recover the source signal, Sf, given the MMV, Xf, and the predefined dictionary, Af, using MMV sparse signal recovery methods, and then find the row index set of the non-zero elements, which indicates the acoustic DOAs. We assume that the sound sources are static or move slowly such that the direction of the sound sources do not change within the snapshots in a frame. We further assume that the number of active sound sources P is very small compared to the number of candidate DOAs K, i.e., P≪K. As a result, the sound source signal, Sf, is a signal matrix with group sparsity and the algorithms for sparse signal recovery can be applied [18, 19]. In this paper, we propose a space alternating MSBL method to improve the estimation performance by exploiting the group sparsity of Sf.

2.2 Probabilistic models

The SBL method is a widely used sparse signal reconstruction method. It is a probabilistic parameter estimation approach based on a hierarchical Bayesian framework. It learns the sparse signal from the over-complete observation model, resulting in a robust maximum likelihood estimation method [27, 39]. Like other Bayesian algorithms, SBL estimates model parameters by maximizing the posterior with a sparse prior. However, instead of adding a specialized model prior, SBL encourages sparsity by using a hierarchical framework that controls the scaling of Gaussian priors through updating individual parameters of each model [27, 40].

2.2.1 Sparse signal model

Following the SBL method proposed in [27], a hierarchical Bayesian framework is used to model the signal matrix, Sf. For the sake of brevity, we omit the dependency of random variables on the subscript, f, where appropriate. First, we assume that the candidate sources are independent to each other. Then, a multivariate complex Gaussian distribution is used to describe the kth candidate source signal sk with zero mean and a covariance matrix \(\lambda _{k}^{-1}\mathbf {I}_{L}\), i.e.,

$$ p(\boldsymbol{S}|\boldsymbol{\lambda})=\prod\limits_{k=1}^{K}\mathcal{CN}\left({\boldsymbol{s}}_{k}|\boldsymbol{0},\lambda_{k}^{-1}\mathbf{I}_{L}\right), $$
(2)

where λ=[λ1,λ2,⋯,λK]T is the hyper-parameter vector, λk is the hyper-parameter related to the amplitude of the kth candidate source signal sk, e.g., the amplitude of sk is 0 when λk→∞. Moreover, IL is the L×L identity matrix, \(\mathcal {CN}(\cdot)\) denotes the complex Gaussian distribution and λk is the precision of sk. Note that, for each candidate DOA (e.g., the kth DOA), an individual precision λk is used, but the precision λk is set to the same for the signal in different snapshots, thereby encouraging group sparsity [41].

The motivation is that the DOAs of the sound sources, as well as the set of active sources, are assumed to not change within a frame. For different candidate DOAs, different precisions are used to encourage the sparsity (see [18, 19] for further details).

In the second layer of the hierarchy, we assume that the precision variables are independent and follow gamma distributions, i.e.,

$$ p(\boldsymbol{\lambda}|\boldsymbol{\gamma})=\prod\limits_{k=1}^{K}\mathcal{G}\left(\lambda_{k}|1,\gamma_{k}\right), $$
(3)

where \(\mathcal {G}(a,b)\) denotes the gamma distribution with the shape parameter a and the rate parameter b. There are two reasons for this particular choice of prior distribution: (1) the gamma distribution is a conjugate prior for the variable λk in the complex Gaussian distribution, leading to a tractable posterior, and (2) the marginal distribution \(\int p(\boldsymbol {S}|\boldsymbol {\lambda }) p(\boldsymbol {\lambda }|\boldsymbol {\gamma }) d\boldsymbol {\lambda }\) is a Student’s t distribution encouraging sparsity [27].

To facilitate the inference of γ, we further assume that the variables in γ=[γ1,⋯,γk,⋯,γK]T follow i.i.d. gamma distributions, i.e.,

$$ p(\boldsymbol{\gamma})=\prod\limits_{k=1}^{K}\mathcal{G}(\gamma_{k}|a,b), $$
(4)

where a and b are model parameters that will be treated as hyper-parameters.

2.2.2 Likelihood function and noise model

Under the assumption of circular symmetric complex Gaussian noises, the likelihood function can be written as

$$ p(\boldsymbol{X}|\boldsymbol{S},\rho)=\prod\limits_{l=1}^{L}\mathcal{CN}\left(\boldsymbol{x}_{l}|\boldsymbol{A}\boldsymbol{s}_{l},\rho^{-1}\mathbf{I}_{M}\right), $$
(5)

where ρ denotes the noise precision.

For tractability, we assume that ρ follows a gamma distribution as follows

$$ p(\rho)=\mathcal{G}(\rho|c,d), $$
(6)

where c and d are modeling parameters.

The hierarchical Bayesian model is built using (2), (3), (4), (5) and (6), and the graphical model is shown in Fig. 2.

Fig. 2
figure 2

Probabilistic graphical model

Full size image

3 Bayesian inference using space alternating variational estimation

3.1 Variational Bayesian inference

Let Θ={S,λ,γ,ρ} denote the set of hidden variables. Based on the graphical model shown in Fig. 2, the joint pdf can be written as

$$\begin{array}{*{20}l} p(\boldsymbol{X},\boldsymbol{\Theta})=&p(\boldsymbol{X}|\boldsymbol{S},\rho)p(\boldsymbol{S}|\boldsymbol{\lambda})p(\boldsymbol{\lambda}|\boldsymbol{\gamma})p(\boldsymbol{\gamma})p(\rho). \end{array} $$
(7)

A closed-form expression of the full posterior p(Θ|X) requires computation of the marginal pdf (X), which is intractable. In this paper, VBI is therefore applied to obtain an approximation of true posterior using a factorized distribution [42, 43]

$$ q(\boldsymbol{\Theta})=q(\rho)\left(\prod_{k=1}^{K}q({\boldsymbol{s}}_{k})q({\lambda}_{k})q({\gamma}_{k})\right), $$
(8)

where q(Θ) is an approximation of the full posterior p(Θ|X). For notational simplicity, the dependency of the approximated posterior on the observed signal X is omitted. Note that, instead of pursuing the full posterior q(S) of the source signals, a factorial form of the posterior \(\prod _{k=1}^{K}q({\boldsymbol {s}}_{k})\) is used to reduce the computational complexity. This is an extension to the SAVE proposed in the single measurement vector (SMV) scenario [38]. When L=1, the proposed approximation model (8) reduces to the model in SAVE. We also assume that the approximate posteriors have the same functional forms as the priors for all the hidden variables. For example, both the prior p(sk|λk) and posterior q(sk) are complex Gaussian. The VBI approach minimizes the Kullback–Leibler (KL) divergence between p(Θ|X) and q(Θ) by maximizing the following variational objective:

$$ \mathcal{L}=\mathrm{E}_{q(\boldsymbol{\Theta})}\left[\ln p(\boldsymbol{X},\boldsymbol{\Theta})\right]-\mathrm{E}_{q(\boldsymbol{\Theta})}\left[\ln q(\boldsymbol{\Theta})\right], $$

where Eq[·] denotes the expectation operator over the distribution q, i.e., \(\mathrm {E}_{q(x)}[p(x)]=\int q(x)p(x)\mathrm {d}x\).

Since the prior and likelihood of all nodes of the model shown in Fig. 2 fall within the conjugate exponential family, the VBI can be written as [42, 43]

$$ \ln q(\boldsymbol{\Theta}_{i})=\mathrm{E}_{q(\boldsymbol{\Theta}_{\bar{i}})}\left[\ln p(\boldsymbol{S},\boldsymbol{\Theta})\right]+\mathrm{C}, $$
(9)

where C is a constant and Θi denotes one of the variables in the factorized distribution (8), such as sk. The notation \(\boldsymbol {\Theta }_{\bar {i}}\) denotes the hidden variable set Θ excluding Θi.

3.2 The logarithm of the joint distribution

As shown in (9), the logarithmic form of the joint distribution is required for VBI. Substituting (2), (3), (4), (5), and (6) into (7), we have

$$\begin{array}{*{20}l} &\ln p(\boldsymbol{X},\boldsymbol{\Theta})= ML\ln\rho-\rho\|\boldsymbol{X}-\boldsymbol{A}\boldsymbol{S}\|_{F}^{2}+\\ &L\sum\limits_{k=1}^{K}\ln \lambda_{k}- \sum\limits_{k=1}^{K}\lambda_{k}{\boldsymbol{s}}_{k}{\boldsymbol{s}}_{k}^{\mathrm{H}}+\sum\limits_{k=1}^{K}\ln \gamma_{k}-\\ &\sum\limits_{k=1}^{K}\gamma_{k}\lambda_{k}+(a-1)\sum\limits_{k=1}^{K}\ln\gamma_{k}-\\ &b\sum\limits_{k=1}^{K}\gamma_{k}+(c-1)\ln\rho-d\rho+\mathrm{C}, \end{array} $$
(10)

where ∥·∥F denotes the Frobenius norm. Next, we present the approximate posterior by substituting (10) into (9).

3.2.1 Update of s k

The approximate posterior of sk can be written as Footnote 3

$$\begin{array}{*{20}l} \!\!\!\!\!\!\! \!\! \ln q({{\boldsymbol{s}}_{k}})=&-\text{tr}\left[{\boldsymbol{s}}_{k}^{\mathrm{H}}\left(\left<\rho\right>\boldsymbol{a}_{k}^{\mathrm{H}}\boldsymbol{a}_{k}+\left<\lambda_{k}\right>\right){\boldsymbol{s}}_{k}-\right.\\ &\left.\left<\rho\right>{\boldsymbol{s}}_{k}^{\mathrm{*}}\boldsymbol{a}_{k}^{\mathrm{H}}\left(\boldsymbol{X}-\boldsymbol{A}_{{\bar{k}}}\left<\boldsymbol{S}_{\bar{k}}\right>\right)-\right.\\ &\left.\left<\rho\right>\left(\boldsymbol{X}-\boldsymbol{A}_{{\bar{k}}}\left<\boldsymbol{S}_{\bar{k}}\right>\right)^{\mathrm{H}}\boldsymbol{a}_{k}{\boldsymbol{s}}_{k}^{\mathrm{T}}\right]+\mathrm{C}, \end{array} $$
(11)

where

$$\begin{array}{*{20}l} \left<\boldsymbol{S}_{\bar{k}}\right>=&\mathrm{E}_{q(\boldsymbol{S}_{\bar{k}})}\left[\boldsymbol{S}_{\bar{k}}\right] \\ =&\left[\boldsymbol{\mu}_{1},\cdots,\boldsymbol{\mu}_{k-1},\boldsymbol{\mu}_{k+1}\cdots,\boldsymbol{\mu}_{K}\right]^{T},\\ \left<\rho\right>=&\mathrm{E}_{q(\rho)}[\rho],\; \left<\lambda_{k}\right>=\mathrm{E}_{q(\lambda_{k})}[\lambda_{k}], \end{array} $$

and <·> is the shorthand of the expectation operator Eq[·]. Moreover, tr[·] denotes the trace operator, ak denotes the kth column of \(\boldsymbol {A}, \boldsymbol {A}_{{\bar {k}}}\) is the matrix A with the kth column ak being removed, and \(\boldsymbol {S}_{\bar {k}}\) is the matrix S with the kth row \({\boldsymbol {s}}_{k}^{\mathrm {T}}\) being removed. From (11), it can be shown that \(q({\boldsymbol {s}}_{k})=\mathcal {CN}\left ({\boldsymbol {s}}_{k}|\boldsymbol {\mu }_{k},\sigma ^{2}_{k}\mathbf {I}\right)\), where

$$\begin{array}{*{20}l} \!\!\!\!\!\!\! \!\! \sigma^{2}_{k}=&\left(M\left<\rho\right>+\left<\lambda_{k}\right>\right)^{-1}, \end{array} $$
(12)
$$\begin{array}{*{20}l} \!\!\!\!\!\!\! \!\! \boldsymbol{\mu}_{k}=&\sigma^{2}_{k}\left<\rho\right>\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\left<\boldsymbol{S}_{\bar{k}}\right>\right)^{\mathrm{T}}\boldsymbol{a}_{k}^{\mathrm{*}}, \end{array} $$
(13)

where the property \(\boldsymbol {a}_{k}^{\mathrm {H}}\boldsymbol {a}_{k}=M\) is used. Note that the mean {μk} is updated based on the space alternating approach [38, 44], where the newest estimates are always used.

3.2.2 Update of λ,γ and ρ

The approximate posteriors for λ,γ and ρ can be derived in a similar way as sk, and we only give the results here.

Update q(λk): \(q(\lambda _{k})=\mathcal {G}({\alpha _{\lambda _{k}}},\beta _{\lambda _{k}})\), where

$$\begin{array}{*{20}l} \alpha_{\lambda_{k}}&=1+L,\; \beta_{\lambda_{k}} = \boldsymbol{\mu}_{k}^{H} \boldsymbol{\mu}_{k}+L\sigma_{k}^{2}+\left<\gamma_{k}\right>, \\ \left<\lambda_{k}\right>&=\frac{\alpha_{\lambda_{k}}}{\beta_{\lambda_{k}}}. \end{array} $$
(14)

Update q(γk): \(q(\lambda _{k})=\mathcal {G}\left ({\alpha _{\gamma _{k}}},\beta _{\gamma _{k}}\right)\), where

$$\begin{array}{*{20}l} \alpha_{\gamma_{k}}=1+a, \ \beta_{\gamma_{k}}= \left<\lambda_{k}\right>+b, \ \left<\gamma_{k}\right>=\frac{\alpha_{\gamma_{k}}}{\beta_{\gamma_{k}}}. \end{array} $$
(15)

Update q(ρ): \(q(\rho)=\mathcal {G}({\alpha _{\rho }},\beta _{\rho })\), where

$$\begin{array}{*{20}l} \alpha_{\rho}&=ML+c,\\ \beta_{\rho}&= \|\boldsymbol{X}-\mathbf{A}\left<\boldsymbol{S}\right>\|_{F}^{2}+L\text{tr}\left[\boldsymbol{\Sigma}\boldsymbol{A}^{\mathrm{H}}\boldsymbol{A}\right]+d, \\ &= \|\boldsymbol{X}-\mathbf{A}\left<\boldsymbol{S}\right>\|_{F}^{2}+ML\sum_{k=1}^{K} \sigma_{k}^{2}+d, \\ \left<\rho\right>&=\frac{\alpha_{\rho}}{\beta_{\rho}}, \end{array} $$
(16)

where \(\boldsymbol {\Sigma }=\text {diag}[\sigma ^{2}_{1},\cdots,\sigma ^{2}_{2},\cdots,\sigma ^{2}_{K}]\) and diag[·] denotes a diagonal matrix.

We refer to the proposed algorithm as SAVE-MSBL. By using the space alternating approach, the computationally complex matrix inversion operation of the traditional MSBL [19] can be avoided. Moreover, instead of using the above formulas directly, we can further reduce the computational complexity by introducing a temporary matrix \(\widehat {\boldsymbol {X}}\), which can be seen as an approximation of X. By removing or adding the terms \(\boldsymbol {a}_{k}{\boldsymbol {\mu }}_{k}^{T}\), the two terms \(\boldsymbol {A}_{\bar {k}}\left <\boldsymbol {S}_{\bar {k}}\right >\) and A<S> in (13) and (16) can be updated using \(\boldsymbol {a}_{k}{\boldsymbol {\mu }}_{k}^{T}\), resulting in a computationally efficient implementation. The pseudocode for the proposed method is shown Algorithm 1. Note that the proposed SAVE-MSBL algorithm can be applied to each frequency bin independently.

3.3 CGMM-based acoustic DOA estimator

Up to this point, the posteriors of the source signals (i.e., {q(sf,k)}) from all the frequency bins are obtained independently. The source signals sf,k can be estimated using the MMSE estimator, i.e.,

$$\begin{array}{*{20}l} \widehat{\boldsymbol{s}}_{f,k}=\boldsymbol{\mu}_{f,k}, \end{array} $$
(17)

where \(\widehat {\boldsymbol {s}}_{f,k}\) denotes the estimate of the source signal. In this section, we propose an acoustic DOA estimator, jointly utilizing the estimated source signals from all the frequency bins, based on the CGMM model. By fitting the observations and estimates of the source signals to the CGMM model, the weighting parameters can be obtained using the EM algorithm. The weighting parameter of each mixture component in the CGMM can be seen as the probability that there is an active acoustic source at the corresponding candidate location. With a known number of sources, the DOA estimates for all the sources can be obtained using peak-picking on the weighting parameters.

Inspired by the Gaussian mixture model [45, 46] and the probabilistic steered-response power (SRP) model [47, 48], we assume that xf,l follows a CGMM distribution with estimated source signals sf,k, i.e.,

$$ p(\boldsymbol{x}_{f,l};\boldsymbol{w})=\sum\limits_{k=1}^{K} w_{k} \mathcal{CN}\left(\boldsymbol{x}_{f,l}|\boldsymbol{a}_{f,k}\mu_{f,k,l},\eta\right), $$

where η is an empirically chosen small value, and wk≥0 is the weighting parameter for the kth complex Gaussian component with the constraint \(\sum _{k=1}^{K} w_{k}=1\). Then, the distribution of the observation set for all frequency bins can be expressed as

$$ p(\boldsymbol{Y};\boldsymbol{w})=\prod\limits_{f=1}^{F} \sum\limits_{k=1}^{K} w_{k}\left[\prod\limits_{l=1}^{L} \mathcal{CN}\left(\boldsymbol{x}_{f,l}|\boldsymbol{a}_{k,f}\mu_{f,k,l},\eta\right)\right], $$
(18)

where \(\boldsymbol {Y}=\{\boldsymbol {X}_{f}\}_{f=1}^{F}\) is the observation set for all frequency bins. Once (18) is maximized, each weight wk represents the probability of an acoustic source being active in the direction θk. However, it is intractable to maximize the function in (18) due to its high dimensionality. Therefore, an EM procedure is applied to deal with this maximization problem. Following [42], we introduce a set of hidden variables \(\boldsymbol {z}=\{\boldsymbol {r}_{f}\}_{f=1}^{F}\). The rf contains binary random variables with only one particular element rf,k being 1 while the others are all zeros. The variable rf,k can be seen as an indicator associated with the acoustic source from the direction θk at the fth frequency bin. Assuming p(rf,k=1)=wk, we can write the joint distribution as follows:

$$ p(\boldsymbol{z};\boldsymbol{w})=\prod\limits_{f=1}^{F}\prod\limits_{k=1}^{K} w_{k}^{r_{f,k}}. $$
(19)

The conditional distribution of the observation set Y given z is

$$ p(\boldsymbol{Y}|\boldsymbol{z})=\prod\limits_{f=1}^{F}\prod\limits_{k=1}^{K} \left[\prod\limits_{l=1}^{L}\mathcal{CN}(\boldsymbol{x}_{f,l}|\boldsymbol{a}_{k,f}\mu_{f,k,l},\eta)\right]^{r_{f,k}}. $$
(20)

Then, the joint distribution can be derived from (19) and (20) using Bayes’ rule, i.e.,

$$\begin{array}{*{20}l} &p(\boldsymbol{Y},\boldsymbol{z};\boldsymbol{w})=p(\boldsymbol{Y}|\boldsymbol{z})p(\boldsymbol{z};\boldsymbol{w})\\ &=\prod\limits_{f=1}^{F}\prod\limits_{k=1}^{K}\left[w_{k}\prod\limits_{l=1}^{L}\mathcal{CN}(\boldsymbol{x}_{f,l}|\boldsymbol{a}_{k,f}\mu_{f,k,l},\eta)\right]^{r_{f,k}}. \end{array} $$
(21)

3.3.1 E-step

In the E-step, we use the current parameter \(\hat {\boldsymbol {w}}^{\text {old}}\) to update the posterior mean of the hidden variable denoted as \(\mathrm {E}[r_{f,k}|\boldsymbol {Y};\hat {\boldsymbol {w}}^{\text {old}}]\). From (21), the E-step can be written as

$$\begin{array}{*{20}l} &Q(\boldsymbol{w};\hat{\boldsymbol{w}}^{\text{old}})=\mathrm{E}[r_{f,k}|\boldsymbol{Y};\hat{\boldsymbol{w}}^{\text{old}}]\\ &=\sum\limits_{f=1}^{F}\sum\limits_{k=1}^{K}\mathrm{E}\left[r_{f,k}|\boldsymbol{Y};\hat{\boldsymbol{w}}^{\text{old}}\right]\left[\ln \hat{w}_{k}^{\text{old}}+\phi_{f,k,l}\right], \end{array} $$
(22)

where

$$\begin{array}{*{20}l} \phi_{f,k,l}&=\sum\limits_{l=1}^{L}\left[\ln\mathcal{CN}(\boldsymbol{x}_{f,l}|\boldsymbol{a}_{k,f}\mu_{f,k,l},\eta)\right]\\ &=\sum\limits_{l=1}^{L}\left\{-M\ln\eta-\frac{1}{\eta}\left[\|\boldsymbol{x}_{f,l}-\boldsymbol{a}_{k,f}\mu_{f,k,l}\|^{2}\right\}\right., \end{array} $$

where μf,k,l is obtained using Algorithm 1.

Therefore, the expected value \(\mathrm {E}[r_{f,k}|\boldsymbol {Y};\hat {\boldsymbol {w}}^{\text {old}}]\) is given by [42, 49]

$$ \mathrm{E}\left[r_{f,k}|\boldsymbol{Y};\hat{\boldsymbol{w}}^{\text{old}}\right]=\frac{\hat{w}_{k}^{\text{old}}{\exp{\left(\phi_{f,k,l}\right)}}}{{\sum_{\tilde{k}=1}^{K}\hat{w}_{\tilde{k}=1}^{\text{old}}\exp{\left(\phi_{f,\tilde{k},l}\right)}}}=\left< r_{f,k}\right>. $$
(23)

3.3.2 M-step

In the M-step, the required parameter w is updated through a constrained maximization of (22), i.e.,

$$\begin{array}{*{20}l} \hat{\boldsymbol{w}}^{\text{new}}=&\arg \max\limits_{\boldsymbol{w}} Q\left(\boldsymbol{w};\boldsymbol{w}^{\text{old}}\right) \\ &s.t. \sum\limits_{k=1}^{K} w_{k}=1; 0< w_{k}<1. \end{array} $$
(24)

Therefore, the M-step can be stated as

$$ \hat{w}_{k}^{\text{new}}=\frac{\sum_{f=1}^{F}\left< r_{f,k}\right>}{\sum_{f=1}^{F}\sum_{\tilde{k}=1}^{K}\left< r_{f,\tilde{k}}\right>}=\frac{1}{F}\sum_{f=1}^{F}\left< r_{f,k}\right>. $$
(25)

Given an initial value for the parameter w, the EM algorithm iterates between the E-step in (23) and the M-step in (25) until convergence. The EM algorithm is summarized in Algorithm 2.

4 Results and discussion

In this section, we first investigate the computational complexity of the proposed SAVE-MSBL-EM method. Then, we test the performance of our proposed SAVE-MSBL-EM algorithm using both synthetic data and real data from the LOCATA datasetFootnote 4. The performance of the different methods are tested in three different scenarios. In the first scenario, we test the recovery accuracy and the resolution performance using narrow-band sources and a ULA. In the second part, we consider a complicated scenario with closely spaced sources in a virtual room. Last, the proposed method is tested using real data.

4.1 Computational complexity analysis

We first analyze the computational complexity of the proposed SAVE-MSBL algorithm by counting the number of mathematical multiplication/division operations in each iteration. As can be seen from Algorithm 1, in each “for” loop, the complexity of the proposed algorithm mainly depends on the update of the temporary matrix \(\bar {\boldsymbol {X}}\) and μk, which is \(\mathcal {O}(ML)\). The computational complexity of updating <ρ> is \(\mathcal {O}(ML)\). Therefore, the computational complexity of the proposed algorithm for each iteration is \(\mathcal {O}(KML)\). If we consider the variational Bayesian inference without the space alternating approach, the computational complexity is \(\mathcal {O}(M^{3}L^{3})\). Thus, the space alternating approach leads to a significant reduction on the computational complexity. Moreover, the computational complexity of MSBL proposed in [19] is \(\mathcal {O}(KM^{2})\). Therefore, the proposed method is faster than the MSBL method when L<M. Since the SVD approach can be utilized for data reduction [18], the condition L<M is met in most cases. For the EM algorithm, the computational complexity is \(\mathcal {O}(KML)\) for one frequency bin. Thus, the computational complexity of the proposed SAVE-MSBL-EM method is \(\mathcal {O}(KML)\) for each frequency bin.

We further measure the computational complexity using the “cputime” function provided by MATLAB. The computer is equipped with an i7-8700 processor. The clock rate is 3.19 GHz. The operation system is Windows 10. The software is MATLAB 2019a. We test the computational complexity for one frequency bin. The number of iterations is fixed to 100, the number of candidate DOAs is set to 41, the number of microphones is set to 15, the number of snapshots is set to 10, and the number of Monte-Carlo experiments is set to 1000. For a single frequency bin, the time consumption of the proposed SAVE-MSBL-EM method and the MSBL proposed in [19] are 0.08 and 0.25 s, respectively, i.e., the proposed method is faster than the MSBL method by a factor of ∼3. Note that, in practice, the time consumption for the acoustic DOA estimation algorithm is proportional to the number of frequency bins.

4.2 Experimental results

The methods used for comparison in this section are summarized as following: CBF refers to classical beamforming based method which is widely used in practice; SRP-PHAT is another widely used method for sound source localization especially in reverberant environments [9]; and MVDR is a method offering high-resolution performance [10]. Note that the implementation of the MVDR method is based on the observed signal statistics. Moreover, MSBL refers to the multiple snapshots SBL method for narrowband signals proposed in [19]. MSBL-EM is an acoustic DOA estimator which combines the MSBL algorithm and proposed EM algorithm. Furthermore, SAVE-MSBL is the proposed method for narrow-band signals and SAVE-MSBL-EM is the proposed method for acoustic DOA estimation. For the MSBL method, the threshold for stopping the iteration errmax is set to 1e−10. For the proposed SAVE-MSBL-EM method, the modeling parameters a, b, c, and d are all set to 1e−3, the parameter η is set to 0.1, the threshold for the SAVE-MSBL algorithm errmax is set to 1e−10, and the threshold for the EM algorithm err0 is set to 1e−3.

4.2.1 Recovery performance analysis using a ULA

In this section, we test the recovery performance of the proposed SAVE-MSBL algorithm using four acoustic sources comprising pure sinusoidal signals. Two assumptions are made in this simulation: (1) all the acoustic sources are located in the far-field of the microphone array and (2) the power of all the acoustic sources are equal. The frequencies of all the sources are set to 1 kHz. For each source, the initial phase is generated randomly. Assume that a ULA with 15 omni-directional microphones is used to receive the signals. The distance between adjacent microphones is set to 0.05 m in this simulation. The microphone array data are generated by assigning different time delays according to the true bearing angles of the sources. White Gaussian noise is added to the clean array data and the SNR is set to 10 dB. The sampling frequency is set to 16 kHz. The time-domain data are converted to the frequency-domain using the short-time Fourier transform (STFT). The temporal length of the snapshot is set to 1024. The length of the increment for the snapshots is set to 256, i.e., the overlap is 75%. The length of the FFT is set to 2048. The number of snapshots is set to 10. As the frequencies of all sources are 1 kHz, only the frequency bin whose center frequency is 1kHz is used for the estimation. We define the fan-shaped horizontal plane in the range from −60∘ to 60∘ as the target space (see Fig. 1). The target space is uniformly separated with a grid interval of 3∘, i.e., the number of grid points is 41 and the array response matrix (dictionary) is pre-computed according to these grid points. Moreover, the bearing angles of four pure sinusoidal sources are −33∘,−27∘,−12∘, and −3∘, respectively. Figure 3 shows the estimation results of the CBF, MVDR, SRP-PHAT, and SAVE-MSBL methods.

Fig. 3
figure 3

The resolution performance for different methods

Full size image

It can be seen that the CBF and SRP-PHAT methods fail to separate the two sources located at −33∘ and −27∘, but the MVDR and proposed SAVE-MSBL methods still work in this case.

We now proceed to test the performance of the proposed method with respect to the number of snapshots. The number of Monte-Carlo runs is 1000. The recovery accuracy is measured by the root-mean-square-error (RMSE), defined as

$$ e_{rec}=\left(\sqrt{\frac{1}{N_{MC}L}\sum\limits_{i=1}^{N_{MC}}\frac{\|\hat{\boldsymbol{S}}-\boldsymbol{S}\|_{F}^{2}}{\|\boldsymbol{S}\|_{F}^{2}}}\right), $$
(26)

where \(\hat {\boldsymbol {S}}\) is the recovered signal, S is the true signal, ∥·∥F denotes the Frobenius norm, L is the number of snapshots, and NMC is the number of Monte-Carlo experiments. We compare the proposed method with the CBF method in [6] and one of the widely used MSBL algorithms proposed in [19]. The results of the RMSEs of the recovered signals are illustrated in Fig. 4. It can be seen that the recovery performance of all the methods improve dramatically as the number of snapshots increases in the range from 1 to 3. Moreover, the simulation result shows that the proposed SAVE-MSBL method achieves better recovery accuracy compared with the CBF and MSBL methods.

Fig. 4
figure 4

Recovery accuracy with different numbers of snapshots

Full size image

4.2.2 Simulation with virtual room

In this part, we test the resolution performance of the proposed method with respect to different intervals of bearing angles between two sources. The synthetic array data are generated using the “signal-generator”Footnote 5 with a virtual room. Note that the “signal-generator” is designed for the moving source scenario. The room setup is summarized in Table 1.

Table 1 Parameter setup
Full size table

In this virtual room, a uniform circular array (UCA) with 32 omni-directional microphones is used to record the signals. The center position of the UCA is (5,3.5,3) m. The radius of the UCA is set to 0.25 m. Two acoustic sources are used. Both of them play uninterrupted harmonic signals. The fundamental frequencies of the two sources are 300 Hz and 350 Hz, respectively. The spectrograms of the two sound sources are shown in Fig. 5.

Fig. 5
figure 5

The spectrograms of the two sources. a The spectrogram of source 1. b The spectrogram of source 2

Full size image

We assume the sound sources are moving on a horizontal plane where the microphone array is located in. The horizontal plane is separated into 73 grid points from 0∘ to 360∘ with an angle interval 5∘, where 0∘ is in the positive direction of the x-axis and 90∘ is in the positive direction of the y-axis. For simulation 1, the trajectories of the two sources are illustrated in Fig. 6. The first source moves along the negative direction of y-axis while the second source moves along the negative direction of x-axis. The original positions of the first and second sound sources are (3.5,5,3) m and (6,5.5,3) m. The end positions are (3.5,3,3) m and (4,5.5,3) m, respectively. The true DOA trajectories of the two sources with respect to the microphone array are shown in Fig. 7(a).

Fig. 6
figure 6

Illustration of the first virtual room setup with two moving sources for the simulation 1

Full size image
Fig. 7
figure 7

Estimation results for the first virtual room setup. For the CBF, MVDR,and SRP-PHAT methods, the estimation results are shown using the spatial spectrum of all frames. For the proposed SAVE-MSBL-EM method, the estimation results are shown using the weights w of all frames. a The trajectories of two source. b Estimation result of CBF method in free field. c Estimation result of CBF method in low reverberation. d Estimation result of SRP-PHAT method in free field. e Estimation result of SRP-PHAT method in low reverberation. f Estimation result of MVDR method in free field. g Estimation result of MVDR method in low reverberation. h Estimation result of the proposed SAVE-MSBL-EM method in free field. i Estimation result of the proposed SAVE-MSBL-EM method in low reverberation

Full size image

According to the simulation setup, the time-domain array signals can be generated using the “signal-generator.” Then, the received array signals are first segmented into a batch of snapshots with 87.5% overlap. By applying the fast Fourier transform (FFT) on each snapshot, the time-domain array signals are converted to the frequency-domain array data. Then, the frequency-domain array data is segmented into several frames with L consecutive snapshots grouped as one frame. In the first and second simulations, L is set to 15. The effect of L is discussed in the last part of this subsection. Note that the SVD approach is used for data reduction in this paper. After applying acoustic DOA estimation methods for each frame, we find the peaks for each frame and label these peaks according to the ground truth DOAs of the two sources. The error range is set to 15∘, i.e., if the minimum error between the estimated angle and all ground truth angles is larger than 15∘, we label the peak as a false estimate. In this paper, we use the black and red circles to denote estimates of the first source and the second source, respectively. Moreover, we use magenta triangles to denote false estimates.

To quantitatively show the difference of the resolution performance between the proposed SAVE-MSBL-EM method and other methods, the RMSE, the false alarm (FA) rate, and the miss-detected (MD) rate are used to measure the recovery performance. The RMSE is defined as

$$ e=\sqrt{\frac{1}{N_{c}}\sum_{i=1}^{N_{c}}\left|\tilde{\theta}_{i}-\theta_{i}\right|^{2}}, $$
(27)

where Nc is the total number of correct estimates, \(\tilde {\theta }_{i}\) is the ith correct estimate, and θi is the ith true bearing angle. Following [50], the FA rate is defined as the percent of sources that are falsely estimated out of the total number of sources and the MD rate is defined as the percent of sources that are miss-detected out of the total number of sources, i.e.,

$$ FA = \frac{N_{F}}{N_{T}}\times 100\%,\;\; MD = \frac{N_{M1}+N_{M2}}{2N_{T}}\times 100\%, $$

where NF is the number of sources with false estimation, NT is the total number of sources for all frames, and NM1 and NM2 are the miss-detected number of the first source and the second source, respectively. Note that two continuous harmonic sound signals are used in this simulation. Thus, two active sources exist in each frame.

We consider two reverberation conditions for all the methods: the free-field (no reverberation) and low-reverberation conditions (RT60 = 0.25 s). For the CBF, MVDR, and SRP-PHAT methods, the estimation results are shown using the spatial spectrums of all frames. For the proposed SAVE-MSBL-EM method, the estimation results are shown using the weight, w, of all frames. For comparison, all the data are normalized frame by frame and displayed using color maps.

In simulation 1, the estimation results of the CBF method in free-field and low-reverberation environments are shown in Figs. 7b and c, respectively. The estimation results of the different methods in both the free field and low reverberation conditions are shown in Fig. 7b–i. The RMSE, FA, and MD are shown in Table 2. Note that “FF” refers to the free-field condition and “RB” refers to the reverberation environment. It can be seen that all the methods perform well under the free-field condition. In the presence of reverberation, the good accuracy performance of the CBF, SRP-PHAT, and proposed SAVE-MSBL-EM method are retained but the MVDR method degrades considerably.

Table 2 Performance of all the methods for simulation 1
Full size table

To further verify the performance of the proposed SAVE-MSBL-EM method in terms of resolution, another scenario is considered. In this case, all of the setup remains the same except the trajectories of the two sources. We refer to this simulation as simulation 2. The original position of the first source is (2.5,5.5,3) m while the second is (7.5,5.5,3) m. The end positions are (4,7,3) m and (6,7,3) m, respectively. Figure 8 shows the trajectories of the two sources in the virtual room.

Fig. 8
figure 8

Illustration of the second virtual room setup with two moving sources for the simulation 2

Full size image

The true bearing angles of the two sources with respect to the microphone array are illustrated in Fig. 9a. The estimation results of the CBF, SRP-PHAT, MVDR, and SAVE-MSBL-EM methods in the free-field environment are shown in Figs. 9b, d, f, and h, respectively, while the results for the low reverberation condition are shown in Figs. 9c, e, g, and i, respectively. The RMSE, FA, and MD are summarized in Table 3.

Fig. 9
figure 9

Estimation results for the second virtual room setup. For the CBF, MVDR and SRP-PHAT methods, the estimation results are shown using the spatial spectrum of all frames. For the proposed SAVE-MSBL-EM method, the estimation results are shown using the weights w of all frames. a The trajectories of two source. b Estimation result of CBF method in free field. c Estimation result of CBF method in low reverberation. d Estimation result of SRP-PHAT method in free field. e Estimation result of SRP-PHAT method in low reverberation. f Estimation result of MVDR method in free field. g Estimation result of MVDR method in low reverberation. h Estimation result of the proposed method in free field. i Estimation result of the proposed method in low reverberation

Full size image
Table 3 Performance of all the methods for simulation 2
Full size table

From Figs. 9b, c, d, e, f, and g, it can be seen that the performance of the CBF, SRP-PHAT and MVDR methods degrade dramatically as two sound sources move closer. However, the proposed SAVE-MSBL-EM method retains an accurate estimation performance for the acoustic DOA estimation. In this case, the proposed SAVE-MSBL-EM method offers higher resolution performance than other methods.

We then test the performance of the proposed method and MVDR method using static sources and the results are shown in Fig. 10.

Fig. 10
figure 10

Simulation results. a False alarm rate in low-reverberation environment. b Miss-detected rate in low-reverberation environment

Full size image

The microphone array signals are generated using the “rir-generator”Footnote 6. The distance between the sound sources and the microphone array center is set to 3 m. We tested the FA rate with different bearing intervals between the two sound sources in the low reverberation condition (RT60 = 0.25 s). Figure 10(a) depicts the FA rates of the MVDR method and the proposed algorithm.

It can be seen that the proposed SAVE-MSBL-EM algorithm has a lower FA rate in the interval range from 15∘ to 40∘. Figure 10(b) shows he MD rates of two algorithms. Compared with the MVDR method, the proposed method has a lower MD rate in the range from 15∘ to 40∘. From Figs. 7, 9 and 10, we can thus conclude that the proposed SAVE-MSBL-EM method provides a better resolution performance than the CBF, SRP-PHAT, and MVDR methods in both free-field and low-reverberation conditions.

To test the effect of the frame (window) length L on the localization performance, we conduct a simulation for different number of snapshots L. The simulation setup is the same as that of simulation 2, that is, the trajectories of the two sources and the true bearing angles of the two sources with respect to the microphone array are shown in Figs. 8 and 9a, respectively. The simulation is conducted in the reverberation environment (RT60 = 0.25 s). The results are illustrated in Fig. 11. The RMSE, FA, and MD are shown in Table 4.

Fig. 11
figure 11

The performance of the proposed method versus different number of snapshots L in a frame. a L=1. b L=5. c L=10. d L=15

Full size image
Table 4 Performance of the proposed method versus L
Full size table

It can be seen that the proposed method works for all snapshot numbers. However, the localization performance degrades if the number of snapshots is small, e.g., the FA and MD in Figs. 11a and b are higher than the FA and MD in Figs. 11c and d.

4.2.3 Real data experiments

The LOCATA dataset provides a series of microphone array data recorded in the Computing Laboratory of the Department of Computer Science of Humboldt University Berlin [51]. The room size is 7.1×9.8×3 m, with the reverberation time RT60 = 0.55 s. In this paper, we use the “benchmark2” microphone array data in task #6 to test the high-resolution performance of the proposed method. The number of microphones of the ‘’benchmark2” array is 12. Two speakers are moving and continuously speaking with short pauses. The spectrograms of the two sources recorded with one microphone are illustrated in Fig. 12.

Fig. 12
figure 12

The spectrograms of the two sources. a The spectrogram of source 1. b The spectrogram of source 2

Full size image

In this experiment, we just consider the azimuth angle estimation with the elevation angle fixed at 90∘. The target plane is uniformly separated into 73 grid points from −180∘ to 180∘ with a uniform interval of 5∘. The true positions and sound source signals of two sources are provided by the LOCATA dataset. We applied a voice activity detector [52] to these source signals to obtain ground-truth voice activity information of the two sound sources. Figure 13a shows the true trajectories of the two sources. We also applied the voice activity detector to the microphone array signals to obtain the voice activity information of each frame. Similar to the simulation part, we find two peaks for each voice active frame and label these peaks according to the true source position. Note that a threshold δ is set to judge the existence of peaks, i.e, if the amplitude of peaks is less than δ, this estimated peak is considered as an invalid estimate. The black circles and red circles denote the true DOAs of the first and second sources, respectively. The magenta triangles denote the false estimates.

Fig. 13
figure 13

Estimation results for the real data. For the CBF, MVDR and SRP-PHAT methods, the estimation results are shown using the spatial spectrum of all frames. For the MSBL-EM and proposed SAVE-MSBL-EM method, the estimation results are shown using the weights w of all frames. All the data are normalized frame by frame. a The truth trajectory of two source. b The results of CBF based method. c The results of MVDR based method. d The results of SRP-PHAT method. e The results of MSBL-based method. f The results of the proposed method

Full size image

The estimation results of the CBF, MVDR, SRP-PHAT, and MSBL-EM methods are shown in Figs. 13b, c, d, and e, respectively. Moreover, the estimation results of the proposed SAVE-MSBL-EM method is shown in Fig. 13f. From Figs. 13b–d, it can be seen that the two sources can hardly be separated in the time range from 6 to 10 s using the CBF, SRP-PHAT, and MVDR methods. However, the proposed SAVE-MSBL-EM method can separate two sources successfully, indicating a higher resolution than the CBF, SRP-PHAT, and MVDR methods (see Fig. 13f). Comparing Fig. 13e and f, it can be seen that the proposed SAVE-MSBL-EM method achieves better recovery performance than MSBL-EM method in the time range from 8 to 10 s. To evaluate the performance of all the methods, the MD rate versus FA rate is computed by varying the peak selection threshold (see Fig. 14). For all the curves in Fig. 14, the closer to the left-bottom the better. It can be seen that the proposed SAVE-MSBL-EM method achieves better performance than state-of-the-art methods.

Fig. 14
figure 14

The MD rate versus FA rate by varying the peak selection threshold

Full size image

We further report the estimation result for a fixed peak selection threshold δ=−40 dB (see Table 5). It can be seen that the proposed SAVE-MSBL-EM method outperforms other methods especially for the FA rate and RMSE. The reason is that the proposed method successfully resolves the two sources while the others are failing in the range from 6 to 10 s. The results indicate that the proposed SAVE-MSBL-EM method provides a higher resolution performance than state-of-the-art methods also in real conditions where all assumptions of the proposed method might not hold.

Table 5 Results for the real data
Full size table

5 Conclusion

In this paper, we propose a space alternating MSBL method for acoustic DOA estimation that offers a high-resolution performance. First, we build a group sparse prior based hierarchical Bayesian framework for the MMV signal model by exploiting the group sparsity of candidate source amplitude matrix. Then, the computational efficient SAVE-MSBL algorithm is proposed to infer all hidden variables in the Bayesian model. Moreover, an EM algorithm is proposed to deal with the acoustic DOA estimation problem. In the experimental parts, the performance of the proposed method is investigated using both synthetic and real data. The results show that the proposed method has lower RMSE and FA rate than state-of-the-art methods in both free-field and low-reverberation conditions. As a result, the proposed method can be applied to some applications (e.g., humanoid robots and drones) to improve the resolution performance for acoustic DOA estimation.

6 Appendix A: Derivation of (11)

According to Eq. 9 and Eq. 10, the signal sk can be updated using the space alternating approach as follows:

$$\begin{aligned} \ln q({\boldsymbol{s}_{k}})&=\mathrm{E}_{q(\boldsymbol{\Theta}/{\boldsymbol{s}}_{k})}\left[p(\boldsymbol{X},\boldsymbol{\Theta})\right]\\ &=\mathrm{E}_{q(\boldsymbol{\Theta}/{\boldsymbol{s}}_{k})}\left[-\rho\|{\boldsymbol{X}}-{\boldsymbol{A}}{\boldsymbol{S}}\|_{F}^{2}-\sum\limits_{k=1}^{K}\lambda_{k}{\boldsymbol{s}}_{k}^{\mathrm{H}}{\boldsymbol{s}_{k}}\right]\\ &=-\mathrm{E}_{q(\boldsymbol{\Theta}/{\boldsymbol{s}}_{k})}\left[\text{tr}\left[\rho\left(\boldsymbol{X}-\boldsymbol{A}\boldsymbol{S}\right)^{\mathrm{H}}\right.\right.\\ &\quad\left.\left.\times\left(\boldsymbol{X}-\boldsymbol{A}\boldsymbol{S}\right)+\lambda_{k}{\boldsymbol{s}}_{k}^{\mathrm{H}}{\boldsymbol{s}}_{k}\right]\right]+\mathrm{C}\\ &=-\mathrm{E}_{q(\boldsymbol{\Theta}/{\boldsymbol{s}}_{k})}\left[\text{tr}\left[\rho\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\boldsymbol{S}_{\bar{k}}-\boldsymbol{a}_{k}{\boldsymbol{s}}_{k}^{\mathrm{T}}\right)^{\mathrm{H}}\right.\right.\\ &\quad\times\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\boldsymbol{S}_{\bar{k}}-\boldsymbol{a}_{k}{\boldsymbol{s}}_{k}^{\mathrm{T}}\left)+\lambda_{k}{\boldsymbol{s}}_{k}^{\mathrm{H}}{\boldsymbol{s}}_{k}\right]\right]+\mathrm{C}\\ &=-\mathrm{E}_{q(\boldsymbol{\Theta}/{\boldsymbol{s}}_{k})}\left[\text{tr}\left[{\boldsymbol{s}}_{k}^{\mathrm{H}}\left(\rho\boldsymbol{a}_{k}^{\mathrm{H}}\boldsymbol{a}_{k}+\lambda_{k}\right){\boldsymbol{s}}_{k}-\rho{\boldsymbol{s}}_{k}^{*}\boldsymbol{a}_{k}^{\mathrm{H}}\right.\right.\\ &\left.\left.\quad\times\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\boldsymbol{S}_{\bar{k}}\right)-\rho\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\boldsymbol{S}_{\bar{k}}\right)^{\mathrm{H}}\boldsymbol{a}_{k}{\boldsymbol{s}}_{k}^{\mathrm{T}}\right]\right]+\mathrm{C}\\ &=-\text{tr}\left[{\boldsymbol{s}}_{k}^{\mathrm{H}}\left(\left<\rho\right>\boldsymbol{a}_{k}^{\mathrm{H}}\boldsymbol{a}_{k}+\left<\lambda_{k}\right>\right){\boldsymbol{s}}_{k}+\left<\rho\right>{\boldsymbol{s}}_{k}^{\mathrm{*}}\boldsymbol{a}_{k}^{\mathrm{H}}\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\left<\boldsymbol{S}_{\bar{k}}\right>\right)\right.\\ &\left.\quad-\left<\rho\right>\left(\boldsymbol{X}-\boldsymbol{A}_{\bar{k}}\times\left<\boldsymbol{S}_{\bar{k}}\right>\right)^{\mathrm{H}}\boldsymbol{a}_{k}{\boldsymbol{s}}_{k}^{\mathrm{T}}\right]+\mathrm{C}, \end{aligned} $$

where Θ/sk denotes the set of variables with sk removed, C denotes a constant. Note that AS can be rewritten as \(\boldsymbol {A}_{{\bar {k}}}\boldsymbol {S}_{\bar {k}}+\boldsymbol {a}_{k}{\boldsymbol {s}}_{k}^{\mathrm {T}}\).