Abstract
In speech enhancement, noise power spectral density (PSD) estimation plays a key role in determining appropriate de-nosing gains. In this paper, we propose a robust noise PSD estimator for binaural speech enhancement in time-varying noise environments. First, it is shown that the noise PSD can be numerically obtained using an eigenvalue of the input covariance matrix. A simplified estimator is then derived through an approximation process, so that the noise PSD is expressed as a combination of the second eigenvalue of the input covariance matrix, the noise coherence, and the interaural phase difference (IPD) of the input signal. Later, to enhance the accuracy of the noise PSD estimate in time-varying noise environments, an eigenvalue compensation scheme is presented, in which two eigenvalues obtained in noise-dominant regions are combined using a weighting parameter based on the speech presence probability (SPP). Compared with the previous prediction filter-based approach, the proposed method requires neither causality delays nor explicit estimation of the prediction errors. Finally, the proposed noise PSD estimator is applied to a binaural speech enhancement system, and its performance is evaluated through computer simulations. The simulation results show that the proposed noise PSD estimator yields accurate noise PSD regardless of the direction of the target speech signal. Therefore, slightly better performance in quality and intelligibility can be obtained than that with conventional algorithms.
Similar content being viewed by others
1 Introduction
The purpose of speech enhancement is to improve the quality and intelligibility of speech signals by suppressing daily environmental noise while allowing a minimal level of speech distortion. The Wiener filter and statistic model-based estimators [1] are well-known examples of the speech enhancement algorithm. Since the de-noising gains of the speech enhancement algorithm are fundamentally determined by the noise power spectral density (PSD), it is important to obtain an accurate noise PSD estimate. Therefore, extensive research has been conducted on noise PSD estimations using a single-microphone system [2,3,4,5]; however, they often exhibit limited performances in situations with non-stationary noise or a low signal-to-noise (SNR) ratio [6].
To overcome the limitations of single-channel systems, various multi-channel techniques have been developed, including the minimum variance distortionless response (MVDR) [7] and the multi-channel Wiener filter (MWF) with constraints [8,9,10,11,12]. The MVDR is a widely used spatial filter in multi-channel systems that minimizes output power under the constraint that the desired signal is not affected [7]. On the other hand, the MWF provides an optimal solution for broadband noise reduction from a minimum mean square error (MMSE) perspective. Speech-distortion-weighted MWF (SDW-MWF) has been introduced to control speech distortion and noise reduction [8]. Algorithms such as SDW-MWF and MVDR preserve speech binaural cues, but distort noise binaural cues [10]. Therefore, extensions for preserving the binaural cues of directional sources using additional cost functions or linear constraints have been proposed [10, 11]. As a result, another extension to preserve interaural coherence (IC) has been proposed [12] as part of a study of spatially isotropic noise, the spatial characteristic of which is represented by IC.
Although MWF-based extension algorithms can achieve significant noise reduction, there is always a trade-off between noise reduction and cue preservation regarding directional sources and background noise. One way to overcome the problem of binaural cue preservation is to apply a real-valued equal gain to both sides, rather than applying a complex-valued filter. This method diminishes noise reduction performance by acting as a single-channel noise reduction method, but preserves all binaural cues [13]. MWF performance critically depends on the statistical estimates of desired and undesired signal components. The Voice Activity Detector (VAD) is a general method for estimating noise or speech statistics, where the noise statistic can be updated during a noise-only time-frequency (TF) bin index. However, this method has the drawback that when the noise is time-varying and non-stationary, more sophisticated techniques are required to estimate signal statistics.
Many studies on binaural or multi-channel speech enhancement [14,15,16,17,18] based on real-valued gain function have shown that superior speech quality can be obtained by utilizing spatial information for both target speech and noise. Coherence-based binaural noise reduction was proposed in [14] and proven effective in terms of tracking the PSD of the diffuse noise. However, the effectiveness was validated using only the target speech source located in front of the listener. Other studies [15, 17] have proposed a prediction filter-based binaural noise PSD estimator where the diffuse noise PSD was obtained by solving a second-order equation formulated using a channel prediction model. Theoretically, this method should enable the device to obtain a true noise PSD when the target is situated at any location within a given distance of the listener. However, this approach requires a delay between channel signals to ensure the causality condition for the prediction filter, and the prediction error needs to be explicitly calculated. These factors directly affect the PSD estimator performance [16, 19].
Recently, neural network-based speech enhancement algorithms have been investigated [20, 21]. These algorithms are typically divided into two processes. In the learning process, features are extracted from a large training data set to learn the model and apply speech enhancement gains based on that model in the speech enhancement part. Although extensive research has been conducted on speech enhancement using neural networks, it is difficult to apply portable applications because of its high complexity.
In this paper, a new noise PSD estimator for a binaural speech enhancement system that can be operated in a fast time-varying diffuse noise field is presented. First, it is established that noise PSD can be estimated from the eigenvalues of the input covariance matrix without dependence on the target speech direction. Then, a method of approximating the obtained noise PSD is presented. The result is that the smaller eigenvalue is combined with the noise correlation function and the binaural phase difference.
The auto- and cross-PSDs of the input binaural signal are often estimated using a first-order recursive averaging filter [22]. In a rapidly changing noise environment, averaging with a short time constant is required to quickly reflect the signal statistics of the signal PSDs. However, the use of short time constants leads to bias in PSD estimates, which in turn degrades the overall performance of the speech enhancement system. In this paper, a method of compensating for the bias is proposed that uses the statistical characteristic of eigenvalues with a minor increase of the computational cost. The proposed algorithm can be adopted widely in speech-related applications, such as hearing aids and mobile phones.
The remainder of this paper is organized as follows. Section 2 presents a description of the general two-channel speech enhancement algorithm. A new noise PSD estimator based on the eigenvalue of the input covariance matrix is presented in Section 3. In Section 4, a compensation method to improve the performance of the noise estimator in a practical environment is discussed. Section 5 presents the simulation results, in which the performance of the proposed algorithm is compared with the results achieved using the conventional techniques. Finally, Section 6 concludes this paper.
2 Configuration of the speech enhancement algorithm for binaural systems
In this section, we begin with a mathematical modeling of noisy input signals in noisy environments. Following that, the configuration of a binaural speech enhancement system that can be applied to the proposed noise PSD estimator is briefly described.
2.1 Input signal model
The binaural noisy input signals, x i (t), corrupted by additive noise in the temporal domain can be written as
where s(t) is the speech signal and n i (t), i = L, R are the environmental noises received by the left and right channel microphones, respectively, at time index t. h i (t) represents the acoustic impulse response from the speech source to the i-th channel microphone and ⊗ denotes the convolution operation. After applying the short-time Fourier transforms (STFTs), (1) can be rewritten in the frequency domain as
where k and l are the frequency and frame indices, respectively. In this paper, the noise, N i (k, l), is assumed as a diffuse noise which is a non-directional signal with equal power and random phase [23, 24]. Under the assumption that the speech and noises are uncorrelated, the auto- and cross-PSD of the noisy input signals are obtained as
where ∗ denotes the complex conjugate, Φ S (k, l) and Φ N (k, l), respectively, are the speech and noise auto-PSDs, i.e., Φ S (k, l) = E[|S(k, l)|2] and Φ N (k, l) = E[|N L (k, l)|2] ≈ E[|N R (k, l)|2]. Lastly, \( {\varPhi}_N^{ij}\left(k,l\right)=E\left[{N}_i\left(k,l\right){N}_j^{\ast}\left(k,l\right)\right] \) is the cross-PSD between the left and right channel noises.
In practice, the PSDs of the noisy input signals are obtained using a first-order recursive averaging filter [22, 25, 26],
where α ∈ [0, 1] is the smoothing factor that controls the trade-off relationship between the fast capturing of the time-varying statistics of the signals and the low-variance estimation of the spectrum.
2.2 Binaural speech enhancement system
Figure 1 presents a block diagram of the general binaural speech enhancement system consisting of two microphones at the left and right ear positions of the listener. First, the noisy input signals are picked up by the left and right channel microphones and are transformed into frequency-domain signals via STFT. After estimating the noise, the de-noising gain, G i (k, l), is determined based on the estimated noise and input PSDs. The enhanced speech signal, \( {\widehat{S}}_i\left(k,l\right) \), is then obtained as
Various investigations have been performed on the noise reduction gain in single-channel [1, 27] and multi-channel speech enhancement systems [7,8,9,10,11,12, 28]. For binaural applications, a system that is capable of generating binaural outputs and preserving binaural cues such as the interaural level difference (ILD) and interaural time difference (ITD) is preferred [29]. These binaural cues are crucial for spatial awareness and also important for speech intelligibility [30, 31]. To obtain the enhanced binaural output with interaural cue preservation, a real-valued equal gain is often applied to both left and right channels. For example, if the left and right channel spectra gains are computed using the Wiener filter approach, the equal gain is determined as [32]
where \( {\xi}_i\left(k,l\right)={\varPhi}_S^i\left(k,l\right)/{\varPhi}_N\left(k,l\right) \) is an a priori SNR that can be estimated using the decision-directed method [1]. Instead of (7), more sophisticated multi-channel techniques such as a multi-channel Wiener filter with various constraints [8,9,10,11,12] and generalized sidelobe canceller (GSC)-based method [33, 34] can be used. Although such techniques have demonstrated great potential in reducing both stationary and non-stationary noises, combining spectral and spatial filtering, there is always a trade-off between noise reduction performance and interaural cue preservation for interfering sources and the background noise [13]. Therefore, in this paper, real-valued gain (7) is applied to preserve the perceptual impression of the acoustic scene. In any case, the accuracy of the estimated noise PSD has a direct impact on the performance of the speech enhancement system. Therefore, in this paper, we propose a robust noise PSD estimation algorithm for the binaural speech signal.
3 The proposed noise PSD estimator
In this section, we introduce the proposed noise PSD estimator based on eigenvalue of input covariance matrix. After that, approximation of the proposed estimator based on interaural binaural cues is presented.
3.1 Noise PSD estimation based on eigenvalues
Under the assumption that the noises are uncorrelated, the cross-correlation between the left and right channel noises becomes zero for most frequencies; however, diffuse noises in practical environments have significant correlation, especially at low frequencies [35]. Several coherence models for diffuse noise field have been proposed [36,37,38]. It is well-known that spatial coherence between two omnidirectional microphones in a spherically isotropic field can be modeled as real-valued analytic sinc function. In subsequent studies, several coherence models for binaural noise field considering the shadowing effect of the head have been proposed [22, 37, 38]. In this paper, we use the sinc function Γ N = sinc(2πfd LR /c), where d LR and c are the distance between the left and right microphones and the speed of sound, respectively, to model the coherence in the diffuse noise field. This was chosen because it is a simple and effective method and applied for many binaural speech enhancement techniques [15, 18, 39]. In addition, the head shadowing effect can be approximated simply by adjusting the distance between the microphones [17]. Using the coherence model, the cross-correlation between the left and right channel diffuse noise of a binaural system can be expressed as \( {\Phi}_N^{LR}={\Gamma}_N{\Phi}_N \) [17]. Then, the 2 × 2 covariance matrix of the binaural input signal in (2) becomes
where we omitted the frequency and frame indices for the sake of simplicity. Furthermore, the eigenvalues of the covariance matrix in (9) can be computed by solving a characteristic equation:
The above characteristic equation can be rewritten using the signal and noise PSDs as
where \( \mathfrak{R}\left\{\bullet \right\} \) denotes real part. Using the fact that auto- and cross-PSD of target speech can be expressed by \( {\varPhi}_S{H}_i{H}_j^{\ast }={\varPhi}_X^{ij}-{\varPhi}_N \), (11) can be rearranged for the noise PSD Φ N :
Now, by solving (12), the noise PSD is obtained as
It should be noted that both the first and second eigenvalues of the input covariance matrix satisfy the above equation.
The estimator in (13) can be compared with the previous channel prediction-based noise PSD estimator in [17], where the noise PSD was obtained by solving a quadratic equation formed using the signals of the channel prediction filter. By substituting (3) and (4) into (13), it is straightforward to show that the estimator in (13) and the one in [17] are equivalent. The details are provided in the Appendix. Thus, the two estimators are expected to achieve numerically identical noise PSD under an ideal condition. On the other hand, another noise PSD estimator using the prediction filter was proposed in [15]. That method in [15] estimates the binaural noise PSD using the target-blocking signal based on the interaural transfer function (ITF) information obtained through the two-channel prediction filter.
However, there are two major differences when the implementation is considered. First, the algorithm in [17] requires an appropriate delay between channel signals to satisfy the causality of the system. It was shown in [40] that inappropriate delays could degrade the performance of the algorithm. Second, the prediction error and ITF need to be calculated explicitly. Therefore, inaccuracies occurring in the process of calculating the prediction error can lead to a bias of the estimated noise PSD. To reduce this bias, [13] proposed a method of calculating those variables using a time-domain adaptive prediction error filter (PEF). However, the performance of the adaptive PEF depends on the filter order, the input SNR, and the delay between the input signals. On the other hand, the proposed algorithm obtains the noise PSD estimate directly from the auto- and cross-PSD of the binaural input signal. Therefore, it can be less sensitive to the bias error of the estimated variables, compared with the method in [13]. In the next section, we first present a method of simplifying the estimator in (13), and later, a method of reducing the bias error will be addressed.
3.2 Approximation of the eigenvalue-based noise PSD estimator
From the characteristic equation in (11), the two eigenvalues of the covariance matrix are calculated as
where
In our previous study [16], Eq. (15) was approximated as ∆ ≈ ((|H L |2 + |H R |2)Φ S + 2Φ N Γ N )2 based on assumptions that ILDs and ITDs are negligible. As a result, the second eigenvalue was simplified to λ2 = Φ N (1 − Γ N ), from which the noise PSD was obtained as \( {\widehat{\Phi}}_N\approx {\uplambda}_2/\left(1-{\Gamma}_N\right) \). However, ITD at low frequencies normally shows a dependency on the direction of the sound source [29], and therefore affects the directional perception of the sound source. In addition, the noise coherence is particularly high at low frequencies; this can amplify the bias caused by an erroneous approximation at low frequencies. Thus, ignoring ITD causes significant errors in the noise PSD estimates, especially when the speech is located anywhere but in front of the listener. In this paper, we present a simple but accurate approximation of (15), which is effective for not only all target directions but also all frequency bands.
Creating a new term, \( 4\left({\left|{H}_L\right|}^2+{\left|{H}_R\right|}^2\right){\Phi}_S{\Phi}_N{\Gamma}_N\cos \left(\angle {\Phi}_S^{LR}\right) \), and using the fact that \( 4{\Gamma}_N^2{\Phi}_N^2=4{\Gamma}_N^2{\Phi}_N^2\left({\cos}^2\left(\angle {\Phi}_S^{LR}\right)+{\sin}^2\left(\angle {\Phi}_S^{LR}\right)\right) \), we can rewrite (15) as
where ∠x denotes the angle in radians of the function x. Now, ∆ is composed of three terms including a perfect square. Because the low-frequency ILDs are known to be insignificant [41], it can be generally assumed that |H L | ≈ |H R | at low frequencies. At high frequencies, on the other hand, the noise coherence Γ N becomes insignificant. Thus, it is possible to ignore the term A in (16). The third term B consists of two functions; \( {\sin}^2\left(\angle {\varPhi}_S^{LR}\right) \) and \( {\varGamma}_N^2 \). The \( {\sin}^2\left(\angle {\varPhi}_S^{LR}\right) \) function will have small values at low frequencies, regardless of the location of the speech source, due to the relatively long wavelength compared with the microphone distance. However, at high frequencies, it monotonically increases according to the angle of the speech source until the relative phase difference reaches 90∘. However, because the noise coherence Γ N will be small at high frequencies, the multiplicative combination of \( {\sin}^2\left(\angle {\varPhi}_S^{LR}\right) \) and Γ N will be still insignificant, compared with the perfect square term.
Based on these observations, we approximate (16) as
By substituting (17) to (14), the second eigenvalue can be expressed as
In practice, the IPD of the target speech, \( \angle {\Phi}_S^{LR} \), is not available. Thus, in this paper, we use the IPD estimate obtained from the noisy input instead of \( \angle {\Phi}_S^{LR} \). Several studies have been conducted on the cross phase of input and clear speech in noisy environments. Although \( \angle {\Phi}_S^{LR} \) and \( \angle {\Phi}_X^{LR} \) are different, the \( \cos \left(\angle {\Phi}_S^{LR}\right) \) value used in Eq. (18) is combined with the noise coherence, approaches zero at high frequencies, and has a meaningful value only at low frequencies. Experimental results show that using \( \angle {\Phi}_X^{LR} \) instead of \( \angle {\Phi}_S^{LR} \) has a negligible effect on the final result. Finally, we estimate the noise PSD using (18) as
where \( \angle {\varPhi}_X^{LR} \) denotes the IPD estimate obtained from the noisy input signal. The practical noise coherence shows as lower than one due to the head influence [17, 38, 42]. Thus, by setting the upper bound of the noise coherence as less than one, the divide-by-zero problem can be avoided. Unlike the complicated noise PSD equation in (13), the above equation can estimate the noise PSD with only the second eigenvalue and IPD obtained from the noisy input signals. Thus, the accuracy of the noise PSD estimate in (19) is affected by the accuracy of the second eigenvalue and IPD of the target speech. The second eigenvalue in the numerator represents the power of the uncorrelated components contained in the two microphone signals, and thus, it is independent of the presence and direction of the target speech. Since the IPD in the denominator is combined with the noise coherence, the direction of the target speech is considered only at low frequencies below 500 Hz. The error caused by the approximation will be measured in computer simulations.
4 Compensation for underestimation of noise PSD
When the auto- and cross-PSDs of the input signal are estimated using the first-order recursion algorithm in (5), the smoothing factor, α, has to cope with two contradictory constraints: capturing the time-varying statistics of the signal component and reducing the estimator variance [22, 26, 43]. When the noise statistics are fast time varying, capturing of the instantaneous statistics of the signals is necessary. To this end, a short-term averaging needs to be conducted. However, the short-term averaging can result in bias error of the estimated PSD [16, 25]. In this section, we propose a method of compensating the bias using the speech presence probability.
4.1 Bias compensation for eigenvalue
In the absence of speech, the two eigenvalues of the input covariance matrix in (9) are expected to be identical. However, the fluctuation of auto- and cross-PSD estimates causes the first eigenvalue to be larger and the second eigenvalue to be smaller than the actual values, while it is still satisfied that the sum of diagonal elements of the covariance matrix, i.e., the sum of left and right channel noise PSDs, is identical to the sum of eigenvalues. Thus, in the absence of speech, it is possible to obtain a more accurate eigenvalue by averaging the two eigenvalues as given by
where β n is a weighting parameter. On the other hand, during the presence of speech, only the second eigenvalue reflects the noise power. Thus, the eigenvalue averaging in (20) can be applied only during the speech absence period.
To this end, we propose a soft-decision approach similar as in [44] in which the weighting parameter is determined based on the SPP:
where \( {\beta}_n^{\hbox{'}} \) is a minimum bound of the weighting parameter and p is an estimate of SPP. When a frequency band is with high SPP (p ≈ 1), β n ≈ 1, and λ c ≈ λ 2. Thus, during the presence of speech, only the second eigenvalue is reflected in the noise PSD estimate. When the frequency band is with low SPP (p ≈ 0), β n becomes \( {\beta}_n^{\hbox{'}} \), and the two eigenvalue are combined with the minimum bound, \( {\beta}_n^{\hbox{'}} \). Accordingly, the bias compensation for eigenvalue in (20) is mainly applied only to frequency bands with low SPP, i.e., noise-dominant frequency bands. Using (17), the maximum eigenvalue can be approximated as \( {\uplambda}_1=\left({\left|{H}_L\right|}^2+{\left|{H}_R\right|}^2\right){\varPhi}_S+{\Phi}_N\left(1+{\varGamma}_N\mathit{\cos}\left(\angle {\varPhi}_S^{LR}\right)\right) \). Thus, the averaged eigenvalue using (20) can be expressed as \( {\uplambda}_{\mathrm{c}}={\Phi}_N\left(1+{\varGamma}_N\mathit{\cos}\left(\angle {\varPhi}_S^{LR}\right)-2\beta {\varGamma}_N\mathit{\cos}\left(\angle {\varPhi}_S^{LR}\right)\right)+\left(1-\beta \right)\left({\left|{H}_L\right|}^2+{\left|{H}_R\right|}^2\right){\varPhi}_S \), which results in a new noise PSD estimator:
In a speech dominant region, i.e., β n ≈ 1, the second term in the numerator goes to zero. On the other hand, in a speech absence region, i.e., β n ≈ 0, we have Φ S ≈ 0. Therefore, the second term in the numerator can be ignored. Based on these observations, the new noise PSD estimator based on the averaged eigenvalue can be re-expressed as
The minimum bound of the weighting parameter, \( {\beta}_n^{\hbox{'}} \), is experimentally determined as the one providing the lowest logarithmic error (LogErr) between the true and estimated noise PSD. A more detailed procedure can be found in the experimental evaluation. Also, the bands or regions with low SPPs still need to be identified, so in the next subsection, we propose a method of estimating SPP using eigenvalue ratios.
4.2 Estimation of the speech presence probability
The eigenvalue compensation method introduced in the previous subsection requires an SPP estimator in order to obtain p. Energy ratio-based approaches [27, 44,45,46,47] have been widely used to determine the speech activity region. Under the assumption that the left and right channel diffuse noise are uncorrelated, (14) is reduced to \( {\uplambda}_1=\left({\left|{H}_L\right|}^2+{\left|{H}_R\right|}^2\right){\Phi}_S+{\Phi}_N={\widehat{\Phi}}_S+{\Phi}_N \) and λ 2 = Φ N . Then, a priori SNR can be calculated as \( \xi ={\widehat{\Phi}}_S/{\Phi}_N={\lambda}_1/{\lambda}_2-1 \), which indicates that the eigenvalue ratio λ 1/λ 2 can be used as an alternative to the energy ratio. Thus, in this paper, the energy ratio-based SPP in [3] is modified using the eigenvalue ratio.
First, using the eigenvalue ratio, a local likelihood of speech is calculated as
where
The eigenvalues of adjacent 2k 1 bands are averaged prior to the likelihood calculation to reduce random fluctuation. The threshold, T L , can be empirically determined using a method similar to that in [3]. In order to improve the robustness of performance, an additional frame likelihood of speech is measured as
where
Similar to the methods in [48, 49], the threshold, T F (l), is updated using a convex combination:
where 0 ≤ β com ≤ 1 is a weighting factor and B S + N (l) and B N (l) denote buffers corresponding to noisy and noise-only cases, respectively, in which the log ratios of L consecutive frames, 10log10 ρ F (m), l − L + 1 ≤ m ≤ l, are stored. Now, the threshold, T F (l), is adaptively adjusted according to the convex combination between the minimum of the elements of B S + N (l) and the maximum of the elements of B N (l). Finally, the SPP is estimated as
where p' (k, l) = P L (k, l) · P F (l) and 0 ≤ α SPP ≤ 1 is a smoothing parameter. It is important to mention that the proposed SPP estimator in (29) re-uses the eigenvalues computed using (10).
4.3 The proposed noise PSD estimator with SPP-based eigenvalue compensation
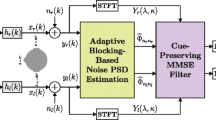
A block diagram of the proposed noise PSD estimator is depicted in Fig. 2. First, the auto- and cross-PSD are estimated using a first-order recursive averaging filter, as in (5). Two eigenvalues are computed using the estimated PSDs as in (10), and the energy compensation in (20) is selectively applied to the noise-dominant regions. Finally, the PSD of the noise is obtained using (23). A new binaural speech enhancement system can be developed by replacing the noise PSD estimation block in Fig. 1 with the proposed noise PSD estimator in Fig. 2.
5 Computer simulations
In this section, the performance of the proposed noise PSD estimator is evaluated through computer simulations in a binaural speech enhancement situation and compared with those of the previous methods. All speech sentences used in the computer simulations were taken from the TIMIT database [50] and convolved with binaural room impulse responses (BRIRs) from the Oldenburg database [51] to simulate target directions. Binaural noises taken from the ETSI database [52] and Oldenburg database were added to the target speech at various SNRs. The left and right channel input signals were decomposed into 32 ms subframes with 50% overlap at a sampling rate of 16 kHz. The length of the subframe was determined to satisfy the rank-1 property [53].
5.1 Bias analysis of the approximated noise PSD estimator
First, we measured the total error caused by the approximation in (19). To this end, the logarithmic error (LogErr) [5] between the noise PSDs obtained using the ideal estimator, \( {\Phi}_N^o\left(k,l\right) \) in (13), and its approximated version in (19) were calculated:
In the simulation of 5.1 and 5.2, the 20 sentences from the TIMIT database were convolved with BRIRs from the Oldenburg database measured in an office environment to generate the target speech signal. Results were obtained using various noise types at 0 dB (Fig. 3a, b) and 5 dB (Fig. 3c, d) SNRs. At low frequencies below 1 kHz (Fig. 3a, c), the maximum LogErr was less than 0.3 dB, which is lower than the just-noticeable level difference [54]. At high frequencies from 1 to 8 kHz (Fig. 3b, d) where the noise coherence is relatively insignificant, the maximum LogErr was 0.03 dB, which is much lower than that found at low frequencies. The results in Fig. 3 show that the effect of approximation was fairly independent of the noise type and target direction.
We also measured the cosine difference between the clean and noisy cross-PSD phase, \( \cos \left(\angle {\Phi}_X^{LR}\right) \), and the \( \cos \left(\angle {\Phi}_S^{LR}\right) \) results are depicted in Fig. 4a, b. In addition, the corresponding scaling differences between \( 1/\left(1-{\Gamma}_N\cos \left(\angle {\Phi}_X^{LR}\right)\right) \) and \( 1/\left(1-{\Gamma}_N\cos \left(\angle {\Phi}_S^{LR}\right)\right) \) are shown in Fig. 4c, d. The results at the low frequencies, below 1 kHz, are presented in (a) and (c), while the results above 1 kHz are presented in (b) and (d). Figure 4 shows that even at the low frequencies the difference between the noisy and clean speech phases had a negligible effect on the scaling factor. Consequently, in terms of accuracy and robustness, the estimator in (19) with the noisy cross-PSD phase can be considered a very good approximation of the ideal estimator in (13).
5.2 Effectiveness of the eigenvalue compensation method
First, to implement the eigenvalue compensation scheme, the minimum bound of the weighting parameter, \( {\beta}_n^{\hbox{'}} \), needs to be determined. To this end, we measured the LogErr under the speech absence hypothesis (p = 0) by changing \( {\beta}_n^{\hbox{'}} \). The noise PSD was obtained using (23) with the energy-compensated eigenvalue, λ c . The results for nine different noise types are displayed in Fig. 5, where it can be observed that the minimum LogErr was obtained at around \( 0.2<{\beta}_n^{\hbox{'}}<0.4 \), regardless of the noise type. Thus, we set \( {\beta}_n^{\prime }=0.35 \) for all following simulations employing the eigenvalue compensation scheme.
Next, the overall effect of the eigenvalue compensation was assessed. The eigenvalue compensation was proposed to alleviate the bias problem caused by short-term averaging. Thus, the accuracy of the estimated noise PSD was measured in terms of LogErr by changing the smoothing factor, α, of the first-order recursion algorithm in (5). For this simulation, 20 speech sentences taken from the TIMIT database and mensa noise from the ETSI database [52] at 0 dB SNR were used as input. For the LogErr calculation, the auto PSD of the left channel noise was considered the true noise PSD. The results are shown in Fig. 6. It can be observed that the noise PSDs obtained using (19), blue lines with circle and square markers, were significantly biased, particularly when the averaging was conducted over short terms with small α. High variation of the input PSDs resulted in high LogErr. The results obtained using (13) are represented by black lines with diamonds and triangle markers and are almost identical to those obtained with (19). However, the LogErr was noticeably reduced by using the proposed eigenvalue compensation scheme as indicated by the red asterisk and diamond markers. The results in Fig. 6 clearly confirm the benefits of the proposed eigenvalue compensation scheme. The parameter choice α will be discussed in Section 5.3.
To utilize the benefits of the eigenvalue compensation scheme, it is important to have a correct SPP parameter, p. Thus, the SPP estimator in (29) was evaluated and compared with the conventional energy-based SPP in [3]. All test parameters were set as described in [3]. We used β com = 0.1 for the convex combination, and the size of the buffers, B S + N (l) and B N (l), was set to 15. The β SPP in (27) and α SPP in (29) were fixed to 0.65 and 0.3, respectively. We used k 1 = 1, T L = 6 for under 5500 Hz, and T L = 8 for over 5500 Hz.
Figure 7a shows the spectrogram of the noisy input signal. In this simulation, target speeches were convolved with a cafeteria BRIR and cafeteria ambient noise was added to them at 0 and 5 dB. The reference SPP was obtained from a clean speech signal using the method in [48] Eqs. (1) and (7) and depicted in Fig. 7b. The SPP results of the conventional and proposed SPP estimators are plotted in Fig. 7c, d, respectively. It is evident from the results in Fig. 7b–d that the SPP masker from the proposed method is closer to the reference masker than the conventional method and performs well even in the 0 dB SNR condition.
5.3 Noise estimation evaluation
The proposed noise PSD estimator in Fig. 2 was evaluated in comparison to the previous methods including the single-channel SPP-based noise PSD estimator (SC-SPP) [5], the improved dual-channel noise PSD estimator (ImNPSD) [17], the dual-channel noise PSD estimator (DC-NPSD) [6], and the bias-corrected blocking method of the interaural transfer function (BB-ITF) [15]. The proposed noise PSD estimator in (23) is referred to as “Prop” in all plots. To make the comparison consistent, the smoothing factor for the estimation of auto-and cross-PSDs was fixed at α = 0.65 in all tested algorithms. As mentioned in Section 4, long-term smoothing can reduce the estimator variance, but at the same time, short-term smoothing is required to capture the fast time-varying statistics of the signals. Thus, as a compromise between these two contradictory requirements, we experimentally chose a smoothing factor that can balance the tracking performance and LogErr. BB-ITF was implemented using the fast least-mean square (FLMS) algorithm [55] based on a 256-tap prediction error filter. The forgetting factor for signal power smoothing was set to 0.9, and the step size for updating the weight was 0.1. We also used a causality delay of 32 samples to account for the largest possible ITD of the binaural system. The same error signal, i.e., (4a) in [15] was utilized to implement ImNPSD.
First, snapshots of the estimated noise PSDs are compared in Fig. 8, where cafeteria noise from the Oldenburg database was added to the speech signal at 0 dB SNR. Cafeteria BRIRs were also used to simulate speech sources in different directions. For visualization purposes, the results obtained using DC-NPSD, ImNPSD, and BB-ITF were shifted vertically. Figure 8a shows the estimation results in the speech absence region. The proposed algorithm achieves the most accurate noise PSD among the compared algorithms. Figure 8b, c shows the results in speech presence regions when the speech source was located at 0° and − 90° to the left of the listener, respectively. For ImNPSD and BB-ITF, noticeable overestimation was observed in the 1–3 kHz frequency band due to the bias of the channel prediction filter. On the other hand, the proposed algorithm maintained a reasonable accuracy regardless of target direction. However, DC-NPSD produced high overestimation errors at high frequencies, because it is based on the assumption that the levels of target speech at both channels are equal.
To numerically evaluate the accuracy of the noise PSD estimate, an averaged logarithmic error (LogErr) was measured. The over- and underestimation of LogErrs were measured separately and combined as suggested in [5]. In this simulation, 20 speech signals, the nine different noises listed in Fig. 3, and cafeteria noises from the Oldenburg database were used. Figure 9a, b shows the averaged LogErr at different SNR conditions for a speech source located at 0∘ and − 90° azimuth, respectively. The experimental results show that the proposed algorithm always obtained the lowest LogErr among the compared algorithms in all tested conditions. BB-ITF achieved the second-best performance. For ImNPSD and BB-ITF, the causality delay was determined to achieve the best performance, resulting in a 32-sample delay. For the target speech at − 90°, all binaural algorithms underwent slight performance degradation. However, the proposed algorithm still maintained the best performance even though there was no consideration of signal delay. Additionally, the single-channel algorithm (SC-SPP) showed a comparable performance to the binaural algorithms for the target speech at − 90°. However, this was not concerned with the preservation of the binaural cues such as ILD and ITD.
To assess the tracking performance, noisy speech containing a sudden increase and decrease of the noise power level was implemented in the noise PSD estimators. The test conditions were the same as in Fig. 8b. The noise power was increased by approximately 15 dB during 1.5–2.5 s and then decreased to the original level. Figure 10 shows the power curves of the noise PSD estimates. The power curves were obtained by summing the estimated noise PSD over the entire frequency band. It can be seen that the SC-SPP could not effectively track the noise power, while the channel prediction-based approach (BB-ITF) and the proposed algorithm reflected the sudden variation of noise power in their PSD estimates. However, BB-ITF exhibited slightly higher estimation error than the proposed algorithm.
5.4 Speech enhancement performance
The binaural speech enhancement system in Fig. 1 was implemented by using the proposed noise PSD estimator (Fig. 2) and conventional noise PSD estimators, and their respective performances were evaluated in terms of the quality and intelligibility of the enhanced speech. To this end, we measured the frequency-weighted SNR improvement (∆fwSNR) [56], short-time objective intelligibility improvement (∆STOI) [57], and perceptual evaluation of speech quality improvement (∆PESQ). All objective parameters were expressed as a difference of the correspondent measures in the output and the input of the system. Since fwSNR [56] was optimized at a 8-kHz sampling rate, the signals were down-sampled to 8 kHz before the measurement. Other objective measures including ∆STOI and ∆PESQ were obtained at a 16-kHz sampling rate.
The 10 different noises were added to the speech signals in each of − 5 ~ 5 dB SNR conditions respectively. The Wiener filter gain of Eq. (8) was calculated using the estimated noise PSDs with the minimum bound 0.1, and a decision-directed approach was utilized to compute the a priori SNR. Then, estimated gains were applied to the input speech spectrum to obtain enhanced output speech. The measurements were independently conducted for each noisy type and averaged over different noise types. The input SNR was computed over all frames, including speech-active and speech-inactive periods. Figure 11a shows the ∆fwSNR results for the left channel with a frontal target speech source. The proposed noise PSD estimator achieved the best improvement among the tested systems. This was mainly due to the superior accuracy of the proposed noise PSD estimator at low frequencies, where the noise power was concentrated. Results with a speech source at − 90° are presented in (b). It was also found that the proposed algorithm obtained the best performance. Again, all algorithms achieved lower performance than the case with a target at 0°. DC-NPSD worsened ∆fwSNR due to the mismatched assumption.
To assess the intelligibility and quality, STOI and PESQ improvements were calculated. The results are shown in Figs. 12 and 13, respectively. Only the left channel results are shown here, but similar results were obtained in the right channel. For the non-frontal target, DC-NPSD degraded both PESQ and STOI. SC-SPP improved PESQ but noticeably degraded STOI. Only BB-ITF and the proposed algorithm improved both PESQ and STOI. In addition, the proposed algorithm showed better STOI and PESQ improvement than BB-ITF. Therefore, it can be concluded that the proposed noise PSD estimator achieved the best quality and intelligibility performance among the tested algorithms.
6 Conclusions
A robust noise PSD estimator for a binaural speech enhancement system was presented. The proposed algorithm obtained the noise PSD based on the second eigenvalue of the covariance matrix of the binaural input signal. To improve the accuracy of the noise PSD estimate, the eigenvalues in noise-dominant periods were averaged using SPP, which resulted in a reduction of bias error. The proposed algorithm robustly estimated the noise PSD for targets located in all directions around the listener in fast time-varying noise environments. The proposed algorithm is theoretically equivalent to the conventional channel prediction-based algorithm. However, since it does not require a causality delay and explicit estimation of the prediction errors, it is less computationally demanding and has less chance of being affected by the estimation bias due to fast smoothing. The experimental results confirmed that the proposed algorithm could achieve higher performance than the conventional algorithms regardless of the target direction, input SNR, and noise types. The objective parameters also confirmed that the proposed algorithm could obtain slightly better speech quality and intelligibility performance than the conventional techniques.
References
Ephraim, Y, & Malah, D. (1984). Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator. IEEE Trans. Acoust., Speech and Signal Process, 32(6), 1109–1121.
Martin, R. (2001). Noise power spectral density estimation based on optimal smoothing and minimum statistics. IEEE Trans. Speech and Audio Process., 9(5), 504–512.
Rangachari, S, & Loizou, PC. (2006). A noise-estimation algorithm for highly non-stationary environments. Speech Comm., 48(2), 220–231.
Fan, N, Rosca, J, Balan, R (2007). Speech noise estimation using enhanced minima controlled recursive averaging. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE.
Gerkmann, T, & Hendriks, RC. (2012). Unbiased MMSE-based noise power estimation with low complexity and low tracking delay. IEEE Trans. Audio, Speech, and Lang. Process, 20(4), 1383–1393.
Nelke, CM, Beaugeant, C, Vary, P (2013). Dual microphone noise PSD estimation for mobile phones in hands-free position exploiting the coherence and speech presence probability. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP).
Souden, M, Benesty, J, Affes, S. (2010). A study of the LCMV and MVDR noise reduction filters. IEEE Trans. Signal Process., 58(9), 4925–4935.
Doclo, S, et al. (2007). Frequency-domain criterion for the speech distortion weighted multichannel wiener filter for robust noise reduction. Speech Comm., 49(7), 636–656.
Spriet, A, Moonen, M, Wouters, J. (2004). Spatially pre-processed speech distortion weighted multi-channel Wiener filtering for noise reduction. Signal Process., 84(12), 2367–2387.
Cornelis, B, et al. (2010). Theoretical analysis of binaural multimicrophone noise reduction techniques. IEEE Trans. on Audio, Speech, and Lang. Process, 18(2), 342–355.
Marquardt, D, et al. (2015). Theoretical analysis of linearly constrained multi-channel Wiener filtering algorithms for combined noise reduction and binaural cue preservation in binaural hearing aids. IEEE/ACM Trans. on Audio, Speech, and Lang. Process, 23(12), 2384–2397.
Marquardt, D, Hohmann, V, Doclo, S. (2015). Interaural coherence preservation in multi-channel wiener filtering-based noise reduction for binaural hearing aids. IEEE/ACM Trans. on Audio, Speech and Lang. Process, 23(12), 2162–2176.
Thiemann, J, et al. (2016). Speech enhancement for multimicrophone binaural hearing aids aiming to preserve the spatial auditory scene. EURASIP J. on Advances in Signal Process, 2016(1), 12.
Jeub, M, et al. (2011). Robust dual-channel noise power spectral density estimation. In Proceedings of the European Signal Processing Conference (EUSIPCO), Barcelona, Spain.
Azarpour, M, Enzner, G, Martin, R (2014). Binaural noise PSD estimation for binaural speech enhancement. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE.
Ji, Y, et al. (2013). Robust noise PSD estimation for binaural hearing aids in time-varying diffuse noise field. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE.
Kamkar-Parsi, AH, & Bouchard, M. (2009). Improved noise power spectrum density estimation for binaural hearing aids operating in a diffuse noise field environment. IEEE Trans. on Audio, Speech, and Lang. Process, 17(4), 521–533.
Braun, S, & Habets, EA. (2015). A multichannel diffuse power estimator for dereverberation in the presence of multiple sources. EURASIP J. on Audio, Speech, and Music Process, 2015(1), 1–14.
Azarpour, M, Enzner, G, Martin, R (2013). Adaptive binaural noise reduction based on matched-filter equalization and post-filtering. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP) IEEE.
Xu, Y, et al. (2014). An experimental study on speech enhancement based on deep neural networks. IEEE Signal processing letters, 21(1), 65–68.
Xu, Y, et al. (2015). A regression approach to speech enhancement based on deep neural networks. IEEE/ACM Trans. on Audio, Speech and Lang. Process, 23(1), 7–19.
Laska, BN, Bolic, M, Goubran, RA (2010). Coherence-assisted Wiener filter binaural speech enhancement. In Instrumentation and Measurement Technology Conference (I2MTC), 2010 IEEE IEEE.
McCowan, IA, & Bourlard, H (2002). Microphone array post-filter for diffuse noise field. In Proceedings of the international conference on acoustics, speech, and signal processing (ICASSP) IEEE.
Abutalebi, HR, et al. (2004). A hybrid subband adaptive system for speech enhancement in diffuse noise fields. Signal Processing Letters, IEEE, 11(1), 44–47.
Merimaa, J, Goodwin, MM, Jot, J-M (2007). Correlation-based ambience extraction from stereo recordings. In Audio Engineering Society Convention 123 Audio Engineering Society.
Guérin, A, Le Bouquin-Jeannés, R, Faucon, G. (2003). A two-sensor noise reduction system: applications for hands-free car kit. EURASIP J. on Applied Signal Process., 2003, 1125–1134.
Cohen, I. (2002). Optimal speech enhancement under signal presence uncertainty using log-spectral amplitude estimator. Signal Processing Letters, IEEE, 9(4), 113–116.
Griffiths, LJ, & Jim, CW. (1982). An alternative approach to linearly constrained adaptive beamforming. IEEE Trans. on Antennas and Propagation, 30(1), 27–34.
Li, J, et al. (2011). Two-stage binaural speech enhancement with Wiener filter for high-quality speech communication. Speech Comm., 53(5), 677–689.
Blauert, J. Spatial hearing: The psychophysics of human sound localization (MIT press, Cambridge, 1997)
Doclo, S, et al. (2015). Multichannel signal enhancement algorithms for assisted listening devices: exploiting spatial diversity using multiple microphones. Signal Processing Magazine, IEEE, 32(2), 18–30.
Loizou, PC. Speech enhancement: Theory and practice (CRC press, Boca Raton, 2013)
Krueger, A, Warsitz, E, Haeb-Umbach, R. (2011). Speech enhancement with a GSC-like structure employing eigenvector-based transfer function ratios estimation. IEEE Trans. on Audio, Speech, and Lang. Process, 19(1), 206–219.
Roman, N, Srinivasan, S, Wang, D. (2006). Binaural segregation in multisource reverberant environments. The Journal of the Acoustical Society of America, 120(6), 4040–4051.
Dorbecker, M, & Ernst, S (1996). Combination of two-channel spectral subtraction and adaptive Wiener post-filtering for noise reduction and dereverberation. In Proceedings of the European Signal Processing Conference (EUSIPCO) Citeseer.
Cook, RK, et al. (1955). Measurement of correlation coefficients in reverberant sound fields. The J. of the Acoustical Society of America, 27(6), 1072–1077.
Lindevald, I, & Benade, A. (1986). Two-ear correlation in the statistical sound fields of rooms. The J. of the Acoustical Society of America, 80(2), 661–664.
Jeub, M, Dorbecker, M, Vary, P. (2011). A semi-analytical model for the binaural coherence of noise fields. Signal Processing Letters, IEEE, 18(3), 197–200.
McCowan, IA, & Bourlard, H. (2003). Microphone array post-filter based on noise field coherence. IEEE Trans. Speech and Audio Process., 11(6), 709–716.
Azarpour, M, Enzner, G, Martin, R (2012). Distortionless-response vs. matched-filter-array processing for adaptive binaural noise reduction. In Acoustic Signal Enhancement; Proceedings of IWAENC 2012; International Workshop on VDE.
Algazi, VR, Avendano, C, Duda, RO. (2001). Elevation localization and head-related transfer function analysis at low frequencies. The J. of the Acoustical Society of America, 109(3), 1110–1122.
Lefkimmiatis, S, & Maragos, P. (2007). A generalized estimation approach for linear and nonlinear microphone array post-filters. Speech Comm., 49(7), 657–666.
Rahmani, M, Akbari, A, Ayad, B. (2009). An iterative noise cross-PSD estimation for two-microphone speech enhancement. Appl. Acoust., 70(3), 514–521.
Cohen, I, & Berdugo, B. (2002). Noise estimation by minima controlled recursive averaging for robust speech enhancement. Signal Processing Letters, IEEE, 9(1), 12–15.
Soleimani, S, & Ahadi, S (2008). Voice activity detection based on combination of multiple features using linear/kernel discriminant analyses. In Information and communication technologies: From theory to applications, 2008. ICTTA 2008. 3rd International Conference on IEEE.
Evangelopoulos, G, & Maragos, P (2005). Speech event detection using multiband modulation energy. In INTERSPEECH.
Davis, A, Nordholm, S, Togneri, R. (2006). Statistical voice activity detection using low-variance spectrum estimation and an adaptive threshold. IEEE Trans. on Audio, Speech, and Lang. Process, 14(2), 412–424.
Ghosh, PK, Tsiartas, A, Narayanan, S. (2011). Robust voice activity detection using long-term signal variability. IEEE Trans. on Audio, Speech, and Lang. Process., 19(3), 600–613.
Ma, Y, & Nishihara, A. (2013). Efficient voice activity detection algorithm using long-term spectral flatness measure. EURASIP J. on Audio, Speech, and Music Process, 2013(1), 1–18.
Zue, V, Seneff, S, Glass, J. (1990). Speech database development at MIT: TIMIT and beyond. Speech Comm., 9(4), 351–356.
Kayser, H, et al. (2009). Database of multichannel in-ear and behind-the-ear head-related and binaural room impulse responses. EURASIP J. on Advances in Signal Process., 2009, 6.
ETSI, EG, and 202396-1, Speech multimedia transmission quality (STQ); speech quality performance in the presence of background noise; part 1: background noise simulation technique, and background noise database. 2009.
Kim, G, & Cho, NI. (2008). Frequency domain multi-channel noise reduction based on the spatial subspace decomposition and noise eigenvalue modification. Speech Comm., 50(5), 382–391.
Moore, BC. An introduction to the psychology of hearing (Brill, Leiden, 2012)
Haykin, SS (2008). Adaptive filter theory. India: Pearson Education.
Hu, Y, & Loizou, PC. (2008). Evaluation of objective quality measures for speech enhancement. IEEE Trans. on Audio, Speech, and Lang. Process, 16(1), 229–238.
Taal, CH, et al. (2011). An algorithm for intelligibility prediction of time-frequency weighted noisy speech. IEEE Trans. on Audio, Speech, and Lang. Process, 19(7), 2125–2136.
Author information
Authors and Affiliations
Contributions
The main contribution of this article is the introduction of simple and robust noise PSD estimator for binaural speech enhancement systems. The proposed algorithm computes the time-varying diffuse noise PSD based on eigenvalue of input covariance matrix. Therefore, it can be seen that the noise PSD in the current frame can be calculated regardless of the presence or absence or speech or the direction of the speech. In addition, an eigenvalue compensation method is applied to improve the accuracy of the estimator based on speech presence probability. As a result, the proposed algorithm showed better results than previous algorithms in terms of accuracy, quality, and intelligibility. It also does not require a causality delay. All authors discussed the final results. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The noise PSD estimator in (13) can be compared with the conventional estimator in [17]. According to Eq. (53) in [17], the noise PSD in a diffuse noise field environment is estimated as
In the above equation, the real-valued noise coherence Γ N [39] was considered to compensate for the underestimation problem at low frequencies. Comparing (31) with (13), it can be noticed that only the last term inside root, \( {\Phi}_E^C{\Phi}_X^{RR} \), is different. However, it can be proven that the both equations are equivalent.
According to Eq. (52) in [17], the error PSD in (31) can be described as
where \( {H}_W={\varPhi}_X^{LR}/{\varPhi}_X^{RR} \) is the transfer function of the channel prediction filter. Thus, substituting (32) into (31), the last term inside root can be rewritten as
On the other hand, the eigenvalue can be computed from (10) as
Now, substituting (34) into (13) results in
Therefore, the noise PSD estimator in (13) and the previous method in [17] are equivalent.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ji, Y., Baek, Y. & Park, Yc. Robust noise power spectral density estimation for binaural speech enhancement in time-varying diffuse noise field. J AUDIO SPEECH MUSIC PROC. 2017, 25 (2017). https://doi.org/10.1186/s13636-017-0122-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13636-017-0122-4