1 Introduction

The seismic signals obtained in the field are often superimposed with a variety of interference-related signals during processing. These data are not suitable to be directly used for geological interpretation, and the interference-related signals need to be suppressed to extract useful information from the seismic signals. Noise filtering is an important step in preprocessing seismic data as well as for conducting follow-up work, such as interpreting the data and extracting the attributes of the seismic signals.

The Fourier transform is among the most important methods used to filter the fundamental frequency domain to compare the variations between the constructive signals and the interfering signals in the frequency band. However, denoising based on the Fourier transform cannot satisfy the relevant requirements when the frequency band of noise overlaps with that of the seismic signals.

As a common mathematical tool used for signal analysis, the wavelet transform can localize time–frequency signals at multiple resolutions [1]. It compensates for the shortcomings of the Fourier transform, which can analyze signals only in the frequency domain during processing. The wavelet transform has a wider range of applications in signal decomposition [2,3,4], function analysis [5], sparse signal representing [6]. Compression, denoising, and research on wavelet analysis has yielded fruitful results [7,8,9,10,11]. Fu et al.[12] proposed a denoising method based on the quadratic wavelet transform. However, this method can deal only with the first layer of the high-frequency wavelet coefficients of the signal. Li et al. [13] used wavelet entropy to obtain the variance in the noise contained in signals at different scales, and used correlations between the data to preserve the wavelet coefficients of useful signals. However, this method cannot determine the empirical conditions for retaining useful signals. Liu et al. [14, 15] combined the wavelet threshold with empirical mode decomposition to achieve a satisfactory denoising effect.

Crucial to wavelet threshold-based denoising algorithms for seismic signals is the determination of the threshold. Many researchers have resorted to transcendental analyses of noise-related signals to obtain their statistical properties and estimate the threshold, but this method is highly speculative.

Jansen et al. [16] proposed a function to determine the threshold based on generalized cross-validation. It can be combined with intelligent optimization algorithms to identify the optimal threshold without any prior information on the wavelet coefficients of noisy signals, and is more suitable for use than other methods to this end.

The fruit fly optimization algorithm (FOA) has the advantages of a small number of parameters of adjustment and ease of implementation [17,18,19,20]. However, it has shortcomings similar to those of other optimization algorithms, including susceptibility to the local optimum and a low speed of convergence. In this article, we propose an improved Kent chaos-based fruit fly optimization algorithm, which optimizes the generalized cross-validation (GCV) as the threshold function, to develop an optimal method for denoising seismic signals. The optimization enables the algorithm to converge quickly to the global optimal solution. This, combined with a soft threshold function, yields satisfactory results in terms of denoising seismic signals.

2 Wavelet Threshold-based Denoising Algorithm

2.1 Basic steps of Wavelet Threshold Method

The method of thresholding proposed by Donoho [21] is commonly used in denoising algorithms because of its good performance and ease of implementation. This method consists of the following three steps:

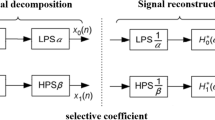
1) Select a suitable wavelet basis for the multilevel wavelet decomposition of noisy signals. This yields the high-frequency and low-frequency wavelet coefficients of the noisy signals at various scales. Let \(x(n)\) be the original noisy seismic signal. Its wavelet decomposition can be expressed as follows:

$$\begin{array}{*{20}l} {a\left( {j,k} \right) = \sum\limits_{n} {a_{{\left( {j - 1,n} \right)}} } \times h\left[ {2k - n} \right]} \hfill \\ {d\left( {j,k} \right) = \sum\limits_{n} {a_{{\left( {j - 1,n} \right)}} } \times {\text{g}}\left[ {2k - n} \right]} \hfill \\ \end{array}$$
(1)

where \(h(n)\) is a low-pass filter, \(g(n)\) is a high-pass filter, \(j\) is the level of decomposition of the signal, \(a(j,k)\) and \(d(j,k)\) represent the low-frequency and high-frequency wavelet coefficients at the \(jth\) scale, respectively, and \(k = 0,1,2 \cdots ,n\) are discrete sampling points.

2) The high-frequency wavelet coefficients obtained by decomposition are thresholded to eliminate the wavelet coefficients of the noisy signals while retaining those of the useful signals. Two types of thresholding functions are commonly used, hard and soft threshold functions, as shown in Eqs. (2) and (3), respectively:

$$W\left[ {d\left( {j,k} \right)} \right] = \left\{ {\begin{array}{*{20}c} {d\left( {j,k} \right)} & {\left( {\left| {d\left( {j,k} \right)} \right| \ge \lambda } \right)} \\ 0 & {\left( {\left| {d\left( {j,k} \right)} \right| < \lambda } \right)} \\ \end{array} } \right.$$
(2)
$$W[d(j,k)] = \left\{ {\begin{array}{ll} {{\text{sgn}} \left[ {d\left( {j,k} \right)\;} \right] \cdot\left( {\left| {d\left( {j,k} \right)\;\;} \right| - \lambda } \right)} & {\left( {\left| {d\left( {j,k} \right)} \right| \ge \lambda } \right)} \\ 0 & {\left( {\left| {d\left( {j,k} \right)} \right| < \lambda } \right)} \\ \end{array} } \right.$$
(3)

where \(W\left[ {d\left( {j,k} \right)} \right]\) is the approximation of the wavelet coefficient of the useful signal after thresholding, \({\text{sgn}} []\) is a symbol function, and \(\lambda\) is the threshold.

3) After thresholding, we perform an inverse wavelet transform on the wavelet coefficients \(W\left[ {d\left( {j,k} \right)} \right]\). We then reconstruct the denoised signal and obtain the model of the inverse wavelet transform as follows:

$$a(j - 1,n) = \sum\limits_{n} {a(j,n)h(k - 2n) + \sum\limits_{n} {W[d(j,k)]g(k - 2n)} }$$
(4)

2.2 GCV Threshold Function

Researchers have proposed a variety of methods of threshold selection [22, 23]. However, many of them require either estimating the signal-to-noise ratio (SNR) or analyzing the statistical properties of the signals, and their results are highly speculative. The GCV optimal threshold function is based on the asymptotic optimal solution that minimizes the mean-squared error. It avoids the problem of variance in noise to help estimate the statistical features of noisy signals. The optimal threshold required by the wavelet threshold-based method can then be obtained without prior information.

The theoretical model of the GVC function is as follows:

$$GCV(\lambda ) = \frac{{\frac{1}{N}\left\| {\vec{d} - \vec{W}_{d} } \right\|^{2} }}{{\frac{{N_{0}^{2} }}{{N^{2} }}}}$$
(5)

where \(N\) is the total number of wavelet coefficients, \(N_{0}\) is the number of wavelet coefficients set to zero after thresholding, \(\overrightarrow {d}\) represents the high-frequency wavelet coefficient of the noisy signal, and \(\overrightarrow {{W_{d} }}\) is the high-frequency wavelet coefficient that is retained after applying the threshold.

According to Eq. (4), the wavelet threshold can be progressively optimized by continuously finding an appropriate value for it that yields the smallest possible value of \(\lambda\). Therefore, the task of finding an appropriate threshold can be considered to be an optimization problem that can be solved by using an optimization algorithm to find the optimal threshold \(\lambda_{0}\).

3 Proposed Method

3.1 Standard Fruit Fly Optimization Algorithm

The FOA is a particle swarm optimization algorithm based on observations and analyses of the foraging behavior of fruit flies. Its basic steps [24] are as follows:

Step 1 Set the initial parameters. Let \(N_{p}\) be the size of the fruit fly population, \(Maxgen\) be the maximum number of iterations of the algorithm, and \(X\_a\) and \({\text{Y}}\_a\) represent the initial position of the fruit fly population.

Step 2 Obtain the random directions of the fruit flies as follows:

$$\left\{ \begin{gathered} x_{i} = X\_a + Rand() \hfill \\ y_{i} = Y\_a + Rand() \hfill \\ \end{gathered} \right.$$
(6)

where \(Rand()\) is a random number in the interval [0,1], \(i = 1,2, \cdots N_{p}\).

Step 3 The location of the food (the optimal solution in this case) is unknown at the beginning of the search. We thus estimate \(d_{i}\), which is the distance between each fruit fly and the origin. \(S_{i}\), which is the smell concentration value, is then calculated as follows:

$$\left\{ \begin{gathered} d_{i} = (x_{{_{i} }}^{2} + y_{i}^{2} )^{1/2} \hfill \\ S_{i} = 1/d_{i} \hfill \\ \end{gathered} \right.$$
(7)

Step 4 By using \(S_{i}\) in the smell concentration function, we have:

$$Smell_{i} = f\left( {S_{i} } \right)$$
(8)

Step 5 The best position of the individual fruit fly, \(x_{i}\) and \(y_{i}\), is obtained through comparison to identify the best smell concentration. Other fruit flies in the population should fly to this location as follows:

$$\left[ {bestSmell\;\;bestIndex} \right] = \max \left( {Smell_{i} } \right)$$
(9)
$$Smellbest = bestSmell$$
(10)
$$\begin{array}{*{20}c} {X\_a_{0} = X\left( {bestIndex} \right)} \\ {Y\_a_{0} = Y\left( {bestIndex} \right)} \\ \end{array}$$
(11)

where Smellbest is the best smell concentration in the current iteration, bestIndex is the label of the best individual fruit fly in the population in this iteration, and X_a0 and Y_a0 represent its position.

Step 6 If the best value of the smell concentration in the current iteration is larger than that in the previous one, it is set as the global best position of the individual fruit fly, and is otherwise kept constant.

Step 7 Repeat the above steps until the maximum number of iterations or the maximum value of smell concentration is reached.

3.2 Improved Kent Chaotic search algorithm

All individuals in the fruit fly population have access to only their optimal individual smell concentrations during iterative optimization. If the optimal individual is at the local optimal location, the speed of convergence and precision of the algorithm decrease rapidly, and it may converge prematurely. Therefore, we introduce chaotic search to the FOA to take advantage of the characteristics [25, 26] of chaotic sequences, including their ergodicity and randomness. In each iteration, the optimal individual is searched for to avoid the local optimum and obtain the global optimal solution.

We optimize the individual fruit flies after each iteration by using Kent mapping to generate an optimized chaotic sequence that improves the capability of the algorithm for global search. We obtain the Kent maps as follows:

$$Z_{k + 1} = \left\{ {\begin{array}{*{20}c} {{{z_{k} } \mathord{\left/ {\vphantom {{z_{k} } \alpha }} \right. \kern-0pt} \alpha }} & {0 \le z_{k} \le \alpha } \\ {{{\left( {1 - z_{k} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - z_{k} } \right)} {\left( {1 - \alpha } \right)}}} \right. \kern-0pt} {\left( {1 - \alpha } \right)}}} & {\alpha \le z_{k} \le 1} \\ \end{array} } \right.$$
(12)

where Zk is a chaotic variable in the interval (0, 1), and \(\alpha \in \left[ {0,1} \right]\) is the control parameter of the chaotic sequence.

Performing N iterations of Eq. (13) yields a chaotic sequence of length n. When \(\alpha = 0.4\), the probability density function of the Kent mapping is uniformly distributed. Therefore, we set \(\alpha = 0.4\).

Having obtained the chaotic sequence, we assume that the optimal position of the individual fruit fly after one iteration is represented by \(X^{ * }\) and \(Y^{ * }\). When loading the chaotic sequence into the original solution space, the chaos-based optimal search yields the new position of the individual fruit fly as follows:

$$\begin{array}{*{20}l} {X\left( j \right) = X^{ * } + v_{x} \cdot z\left( j \right)} \hfill \\ {Y\left( j \right) = Y^{ * } + v_{y} \cdot z\left( j \right)} \hfill \\ \end{array}$$
(13)

where \(v_{x}\) and \(v_{y}\) are the coefficients of adjustment to the position of the fruit fly, and \(Z\left( j \right)\) is the chaotic variable of the sequence of fruit flies, \(j = 1,2, \cdots N\).

We also introduce two adjustment coefficients, \(v_{x}\) and \(v_{{\text{y}}}\), as correction factors for the chaotic sequence. To enable the individual fruit fly to more quickly jump out of the local optimum, a large coefficient of adjustment is needed early in the iterations to prompt the population to search over a larger area and speed-up convergence. As the iterations progress, the range of area searched by the individual fruit flies should be gradually reduced to obtain an accurate solution. We thus determine the inverse relationship between the range of search and the number of iterations as follows:

$$V_{x} = R\left( a \right) \times \frac{1}{2m} \times X^{ * }$$
(14)
$$V_{y} = R\left( a \right) \times \frac{1}{2m} \times Y^{ * }$$
(15)

where \(m\) is the current number of iterations and \(R\left( a \right)\) is the radius of chaotic search.

We set the radius of the search to half of the absolute maximum value of the high-frequency wavelet coefficient at each scale:

$$R\left( a \right) = \frac{{\left| {d\left( {j,k} \right)} \right|_{\max } }}{2}$$
(16)

where \(d\left( {j,k} \right)\) is the high-frequency wavelet coefficient at the \(jth\) scale.

3.3 Steps of the Algorithm

The main steps of the proposed Kent chaotic mapping-based wavelet thresholding algorithm inspired by fruit fly optimization are as follows:

Step 1 Select a suitable wavelet basis, and decompose the wavelets of the noisy seismic signal at scale \(J\) to obtain the high-frequency and low-frequency wavelet coefficients.

Step 2 Initialize the size of the fruit fly population, the maximum number of iterations Maxgen, the original position of the individual fruit fly \(X\_a\), \(Y\_a\), and the number of iterations of chaotic search \(N\).

Step 3 Set the GCV threshold function as the function of smell concentration. Obtain the current best smell concentration and the optimal position of the individual fruit fly through steps 2–5 of the standard fruit fly optimization algorithm.

Step 4 Perform a chaotic search for the optimal position of the individual fruit flies according to Eqs. (12)–(16). Following this, obtain the optimal smell concentration and the optimal individual fruit fly in the chaotic search sequence according to steps 3–5 of the standard fruit fly optimization algorithm, and update the original values.

Step 5 Determine whether the termination condition is met. If so, output the optimal threshold, and otherwise return to step 2.

Step 6 Combine the optimal threshold in step 5 with the soft threshold to denoise the high-frequency wavelet coefficients. Reconstruct the final wavelet coefficients and obtain the signal after denoising.

4 Experiments and results

4.1 Processing synthetic seismic records

To analyze the effect of the proposed algorithm in terms of denoising seismic signals, we constructed two Ricker wavelets at a sampling rate of 1 ms and main frequencies of 30 and 45 Hz. We synthesized them into a seismic record with 50 gathers and 512 sampling points, as shown in Fig. 1a. Random noise with an SNR of − 1 dB was added to the seismic records, as shown in Fig. 1b.

Fig. 1
figure 1

a Using two Ricker wavelets, with frequencies of 30 Hz and 45 Hz, and a sampling rate of 1 ms to construct a seismic record with 50 gathers and 512 samples. b The seismic record obtained by adding random noise with an SNR of −1 dB

Full size image

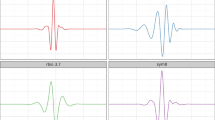
We compared the capabilities of denoising of the Daubechies, Symlet, and Coiflet wavelets in our experiments. All of them are commonly used for denoising, and the results are shown in Fig. 2. All three types of wavelets improved the SNR of the seismic signals. The Daubechies wavelet and the Symlet wavelet yielded the best effects at orders 4 and 3, respectively, while the Coiflet wavelet delivered poor results.

Fig. 2
figure 2

Comparison of the denoising performance of different wavelets

Full size image

Because the phase values obtained by denoising based on the Daubechies wavelet were very close to the those of seismic signals over a long period, we chose the Daubechies wavelet of order 4 (db4) as the wavelet basis, and decomposed four layers while balancing computational complexity with signal smoothness.

We compared the proposed method with classical wavelet threshold-based denoising algorithms. The algorithms and their parameters are as follows:

  1. 1.

    Donoho universal threshold method. The threshold was \(Thr = \sigma \sqrt {2\ln \left( N \right)}\). The variance in the noise, \(\sigma\), was calculated as the median of the first layer of the high-frequency wavelet coefficients divided by 0.6745.

  2. 2.

    SureShrink thresholding method [27].

  3. 3.

    Standard fruit fly optimization-based method of wavelet thresholding. We set the population of fruit flies to 20 and the maximum number of iterations to 50.

It is clear from the results of denoising obtained by the Donoho universal and SureShrink thresholding methods, shown in Fig. 3, which the main and side lobes of each seismic signal were distorted, and the in-phase axis was not clear. A large number of burrs were observed in the smooth waveform of the seismic record.

Fig. 3
figure 3

The results of denoising of the Donoho universal threshold method (a) and SureShrink threshold method (b)

Full size image

Figure 4 shows the results of denoising of the standard fruit fly optimization algorithm and the proposed method. The standard fruit fly optimization algorithm reduced the degree of signal distortion such that the synthetic signals and their phase axis became clearer. However, glitches and jitters were still notable in the stationary waveform of the entire seismic record. The proposed method yielded signals containing mild distortion, the smooth main, and side lobes of which were nearly free of burrs and jitter. The signals were also in phase on the same axis. In general, the proposed method had a much better denoising effect than the other methods considered here.

Fig. 4
figure 4

The results of denoising when using the standard fruit fly optimization algorithm (a) and the proposed method (b)

Full size image

Figure 5a shows the local enlargement in the single-channel seismic signals mixed with − 1 dB of noise after they had been denoised by each of the above algorithms. The 18th channel of the signals was randomly selected as the observed signal, and a comparison of the amplitudes of its spectra obtained by the different methods is shown in Fig. 5b. It is clear that the proposed method was able to eliminate random noise from the seismic signals, and could process both high-frequency and low-frequency noisy signals.

Fig. 5
figure 5

a Local enlargement of the ideal signal, noisy signal, and denoised signals obtained by the Donoho threshold, standard FOA, and the proposed method. b The corresponding amplitudes of the spectra of the ideal signal, noisy signal, and signals denoised by all methods

Full size image

To further verify the effectiveness of the proposed method, we analyzed its denoising effect by using the quantization method. We added three types of noise, with intensities of − 5, − 1, and 4 dB, respectively, and different SNRs, to the synthetic seismograms. We compared the proposed method with the three methods mentioned above in terms of denoising the synthetic record, and calculated the SNRs and mean-squared error (MSE) of the signals obtained after denoising. The SNR and MSE were calculated as follows [28]:

$$SNR = 10\log_{10} \frac{{\sum\limits_{n - 1}^{N} {f^{2} \left( n \right)} }}{{\sum\limits_{n - 1}^{N} {\left| {f\left( n \right) - \mathop f\limits^{ \wedge } \left( n \right)} \right|^{2} } }}$$
(17)
$$MSE = \frac{1}{N}\sum\limits_{n - 1}^{N} {\left( {f\left( n \right) - \mathop f\limits^{ \wedge } \left( n \right)} \right)}^{2}$$
(18)

where \(f\left( n \right)\) is the original noisy seismic signal, \(\mathop f\limits^{ \wedge } \left( n \right)\) is the signal obtained after denoising, and \(N\) is the total number of signals. The SNR and MSE of the denoised signals obtained by different methods are shown in Table 1, and the best results are given in bold. The SNR and MSE of signals obtained by the proposed method were clearly better than those of the other algorithms under different noise-related conditions.

Table 1 SNR and MSE of denoised seismic signals obtained by different methods
Full size table

4.2 Effect of signal denoising

We also conducted comparative experiments on empirically acquired seismic records of explosives detonated in a test field. The sampling rate was 1 ms and the number of channels was 115, as shown in Fig. 6a. The seismic record contained a large amount of random noise. The noise had a significant influence on the signals in channels 35, 89, 110, and 112, and this significantly affected seismic data processing.

Fig. 6
figure 6

Measured seismic record (a) of an explosive source in a test field. Results of denoising obtained by using the standard fruit fly optimization algorithm (b) and the SureShrink threshold method. c Results of denoising obtained by the Donoho threshold method (d) and the proposed method (e)

Full size image

The results of denoising of the SureShrink and Donoho threshold methods are shown in Fig. 6c, d, respectively. It is evident that they were able to remove some random noise given a prior estimate of the signal. However, severe random noise persisted in channels 35, 89, 110, and 112 of the measured data after denoising, which means that these two methods delivered unsatisfactory performance. The results of denoising of the standard fruit fly optimization algorithm and the proposed method are shown in Fig. 6b, e, respectively. Their denoising effects were much better than those of the SureShrink and Donoho threshold methods, and they were able to remove strong noise from the signals. Moreover, the proposed method was better able to eliminate noise from the background than the standard fruit fly optimization algorithm.

We can conclude from the above that the denoising effect of the proposed method was superior to that of the other methods. The phase axis obtained by it was clearer, and it was able to retain useful information in the seismic data.

5 Conclusions

The conventional method of wavelet thresholding requires analyzing prior information on the signal and a statistical model to determine the threshold. In this article, we proposed a wavelet threshold-based method of denoising seismic signals based on improved chaotic fruit fly optimization. The conclusions are as follows:

  1. (1)

    We analyzed variations in the solution space during optimization to propose a chaotic adjustment factor to optimize the chaotic sequence.

  2. (2)

    We introduced improved the chaotic Kent map to the fruit fly optimization algorithm, optimized the positions of individual fruit flies in each iteration, and improved the algorithm such that it searched over a larger space and obtained a more accurate solution to minimize the negative effect of the local optimum.

  3. (3)

    Using the GCV threshold function to select the optimal wavelet threshold helped avoid the difficult task of obtaining prior information on the signal when selecting the threshold. The SNR of the proposed method was considerably superior to that of classical wavelet threshold-based algorithms, and it was able to retain more useful information in the seismic signals.