1 Introduction

Time-delay and Doppler estimation holds a pivotal role across various engineering domains, encompassing navigation, radar, reflectometry, sonar, and communication fields, to name a few [1,2,3,4,5,6,7,8,9], where it serves as the initial step in the receiver’s operational sequence [5, 8, 9]. When designing and evaluating estimation techniques for these applications, it becomes imperative to grasp the attainable performance’s ultimate benchmark in terms of Mean Squared Error (MSE). This valuable information can be provided by the Cramér–Rao bound (CRB) [10], the most widely used lower bound on MSE, renowned for its ease of calculation in various scenarios (see [4, §8.4] and [11, Part III]). Furthermore, the CRB effectively approximates the MSE of the Maximum Likelihood Estimator (MLE) in the asymptotic region of operation, particularly in cases involving large sample sizes or high Signal-to-Noise Ratios (SNRs) under the Gaussian conditional signal model (CSM) [12, 13]. Consequently, multiple CRB expressions have emerged over recent decades for the time-delay and Doppler estimation problem. These expressions encompass a spectrum of signal types, ranging from finite narrow-band signals [2, 14,15,16,17,18,19,20,21,22] to finite wide-band signals [14, 17, 20, 23,24,25,26], and even infinite bandwidth signals [27]. All these previous investigations consider that the wave transmission process introduces an unknown phase element, due to the assumption of incomplete knowledge regarding the propagation medium, the characteristics of transmitter and/or receiver antennas (including the phase center and hyper-frequency electronics), and/or the radio-frequency equipment. The studies reviewed tend to combine the phase term with the amplitude component, treating the resulting complex parameter as one entity. As a result, subsequent derivations rely on this unified parameter without clarifying the impact of the different sources it comprises. This tendency may be the reason why there appears to be a gap in existing literature addressing scenarios in which part of this unknown phase elements can be estimated and rectified, which would give way to more detailed estimation performance formulations. Indeed, nowadays, there are applications in which the unknown phase component introduced by the wave transmission process can be calibrated [3] at a predefined pace, ensuring its stationarity from calibration to calibration. This is evident in some scenarios such as navigation with static emitters and a moving receiver, commonly referred to as anchors and tags in robotics, where the primary task is to navigate among predetermined waypoints. One practical example is found in warehouse robots used in logistics [28]. Among various types of robots offering varying functionality, those employed in automated storage and retrieval systems (AS/RS) are specifically designed to automate the inventory process. They accomplish this by retrieving goods for shipment or use and returning items to their designated storage locations. At each of these well-known storage locations, the receiver remains static. Consequently, its position and velocity are known, allowing it to estimate the phase components associated with the transmission process [3]. These components are then compensated for as the receiver progresses towards the next predetermined waypoint. Building upon these considerations, this article begins by introducing the signal model in Sect. 2 as a specific instance of the Gaussian CSM. The latter accommodates the description of a wideband band-limited signal considering the influence of the Doppler effect. Given this general scenario, a novel MLE (different from the commonly used [24]) is presented in Sect. 3. Then, a closed-form expression of the associated CRB is derived in Sect. 4, based on the Slepian-Bangs formula [10] and the band-limited signal assumption. In Sect. 5, the relationship between the CRB and the ambiguity function, known for the standard CSM [2, §10] [5, §3.9.4], is extended to the considered signal model. Then, such results are particularized for two simplified scenarios in Sect. 6. The first one considers the narrowband signal model, i.e. the Doppler effect does not have an impact on the baseband signal samples. Next, the second one considers that the Doppler effect is known and perfectly compensated, which constitutes a case of monoparametric (time-delay) estimation problem. The obtained CRB and MLE equations are validated through Monte Carlo simulations in Sect. 7, where the MLE’s MSE convergence to the CRB is shown under specific SNR conditions, known as ”SNR Threshold”. These outcomes enable the assessment on how each signal component (carrier-phase and base-band signal) impacts the achievable MSE for time-delay and Doppler estimation as a function of the SNR. This analysis reveals five regions of operation of the MLE, in contrast to the widely known three regions of operation [29,30,31,32]. Finally, the paper’s main findings and contributions are summarized in Sect. 8.

2 General signal model

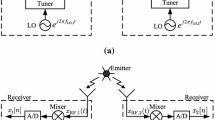
The signal model utilized in this manuscript is based on the well-known CSM [12, 13], and it is formulated according to previous contributions in the same topic [24,25,26, 32, 33]. The latter is assumed to be the result of a direct transmission of a band-limited signal a(t) modulated by a carrier waveform with frequency \(\mathrm {F_c}\) across the line of sight (LoS) between a transmitter T and a receiver R. The band-limited signal a(t) with bandwidth B can be expressed as

$$\begin{aligned} a(t)=\sum _{n=N_{1}^{\prime }}^{N_{2}^{\prime }}a \bigg (\frac{n}{B} \bigg ) \textrm{sinc}\bigg (\pi B \bigg (t-\frac{n}{B}\bigg )\bigg ), \end{aligned}$$
(1)

and the Fourier Transform (FT) to the frequency domain f is given by

$$\begin{aligned} A(f)=\frac{1}{B}\sum _{n=N_{1}^{\prime }}^{N_{2}^{\prime }}a\bigg (\frac{n}{B} \bigg )e^{-j2\pi n\frac{f}{B}},\quad -\frac{B}{2}\le f\le \frac{B}{2}, \end{aligned}$$
(2)

with \(N_{1}^{\prime },N_{2}^{\prime }\in {\mathbb {Z}}\), and B is the length of the support of A(f). The radial distance between T and R is defined as

$$\begin{aligned} D_{TR}(t) = \Vert P_T(t) - P_R(t) \Vert , \end{aligned}$$
(3)

with \(P_T(t)\) the transmitter position and \(P_R(t)\) the receiver position. Note that \(D_{TR}(t)\) changes over time depending on relative velocity. Then, the distance used in the ranging operation can be redefined as \(D_{TR}(t;{\varvec{\eta }}) = c \tau (t;\varvec{\eta })\), with c the speed of light, and \(\tau (t;\varvec{\eta })\) the time-delay depending on time and on the parameters characterizing the radial distance between T and R. For navigation, radar and sonar systems, the radial distance is usually approximated to the first order, as

$$\begin{aligned} D_{TR}(t;\varvec{\eta })=c\tau (t;\varvec{\eta })\approx d+vt,\quad \tau (t; \varvec{\eta })\approx \tau +bt,\quad \tau =\frac{d}{c},~b=\frac{v}{c},~ \varvec{\eta }=\left( \begin{array}{c} \tau \\ b \end{array} \right) . \end{aligned}$$
(4)

Note that \(\tau\) is the time-delay due to the propagation path and \((1-b)\) is the dilatation induced by the Doppler effect. Using (4), the complex analytic signal at the output of the receiver’s antenna can be expressed as [25]

$$\begin{aligned} x_{R}(t)=\alpha a^{\prime }(t;\varvec{\eta })e^{jw_{c}t}+n_{A}(t), \end{aligned}$$
(5)
$$\begin{aligned} a^{\prime }(t;\varvec{\eta })=a(t;\varvec{\eta })e^{-j\phi (t;\varvec{\eta } )},\quad a(t;\varvec{\eta })=a((1-b)(t-\tau )), \end{aligned}$$
(6)

with \(w_c = 2\pi \mathrm {F_c}\), \(\phi (t;\varvec{\eta }) = \psi + \varphi (t;\varvec{\eta })\), \(\alpha \in \mathbb {R^+}\) the signal’s amplitude, and \(n_A(t) \in {\mathbb {R}}\) a zero-mean additive white Gaussian noise (AWGN). Parameter \(\psi\) represents the phase component stemming from the transmitter and/or receiver antenna characteristics (including center of phase and hyper-frequency electronics) and/or the radio-frequency electronics. Parameter \(\varphi (t;\varvec{\eta })\) is the phase component associated the propagation path which depends on \(\tau\) and b (4). As discussed in the introduction, this study considers applications in which the unknown phase component introduced by the wave transmission process can be calibrated [3] at a predefined pace, ensuring its stationarity from calibration to calibration. In other words, it is assumed that \(\psi\) is known and compensated for during the observation interval, resulting in \(\phi (t;\varvec{\eta }) = \varphi (t;\varvec{\eta })\). Subsequently, the received signal at the output of the Hilbert filter can be expressed as,

$$\begin{aligned} x(t)=\alpha a^{\prime }\left( t;\varvec{\eta }\right) +n(t),\quad a^{\prime }\left( t;\varvec{\eta }\right) =a(t;\varvec{\eta })e^{-jw_{c}(\tau +b(t-\tau ))}, \end{aligned}$$
(7)

with n(t) a complex centered circular Gaussian noise with unknown variance \(\sigma _n^2\). Note that other contributions [17, 20, 23,24,25,26, 30, 31] assume that \(\psi\) is unknown yielding the following standard signal model at the output of the Hilbert filter,

$$\begin{aligned} x(t)=\left( \alpha e^{j(\psi -w_{c}\tau )}\right) a(t;\varvec{\eta } )e^{-jw_{c}b(t-\tau )}+n(t), \end{aligned}$$
(8)

where one cannot differentiate \(\psi\) from \(w_c\tau\), leading to an unknown complex amplitude term \(\alpha ' = \alpha e^{j(\psi -w_c\tau )}\in {\mathbb {C}}\). The acquisition of \(N' = N_2' - N_1' + 1\) samples from (7) is considered, where \((N_1' \ll N_1, \, N_2' \gg N_2)\) and

$$\begin{aligned} \mathrm {T_s}=1/\mathrm {F_s}, \quad {\mathrm {F_s}\ge \textrm{B}}, \end{aligned}$$
(9)

which yields the following observation vector

$$\begin{aligned} {\textbf{x}}=\alpha \mathbf {a^{\prime }(\varvec{\eta })}+{\textbf{n}},~{\textbf{x}} =\left( \begin{array}{c} x(N_{1}^{\prime }\mathrm {T_s}) \\ \vdots \\ x(N_{2}^{\prime }\mathrm {T_s}) \end{array} \right) ,~{\textbf{n}}=\left( \begin{array}{c} n(N_{1}^{\prime }\mathrm {T_s}) \\ \vdots \\ n(N_{2}^{\prime }\mathrm {T_s}) \end{array} \right) , \end{aligned}$$
(10)
$$\begin{aligned} {\textbf{a}}^{\prime }(\varvec{\eta })=\left( \begin{array}{c} a\left( (N_{1}^{\prime }\mathrm {T_s}-\tau )(1-b)\right) e^{-jw_{c}(\tau +b(N_{1}^{\prime }\mathrm {T_s}-\tau ))} \\ \vdots \\ a\left( (N_{2}^{\prime }\mathrm {T_s}-\tau )(1-b)\right) e^{-jw_{c}(\tau +b(N_{2}^{\prime }\mathrm {T_s}-\tau ))} \end{array} \right) , \end{aligned}$$
(11)

where \({\textbf{n}} \sim \mathcal{C}\mathcal{N}(0, \sigma _n^2 {\textbf{I}}_{N'})\). The set of unknown parameters to be estimated are \(\varvec{\epsilon }^{\textrm{T}} = (\sigma _n^2, \alpha , \varvec{\eta }^{\textrm{T}})\), where \(\alpha\) is a real positive valued scalar variable as opposed to the state-of-the-art case.

3 Maximum likelihood estimator

Given the Gaussian nature of the likelihood distribution, the MLE of \(\varvec{\eta }\) is obtained through the following well-known mean-squared error minimization

$$\begin{aligned} \left\| {\textbf{x}}-{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) \alpha \right\| ^{2}&=\left\| \underline{{\textbf{x}}}-\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) \alpha \right\| ^{2} \nonumber \\&=\left\| \Pi _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) }\left( \underline{{\textbf{x}}}-\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) \alpha \right) \right\| ^{2}+\left\| \Pi _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\left( \underline{{\textbf{x}}}-\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) \alpha \right) \right\| ^{2} \nonumber \\&=\left\| \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) \left( {\widehat{\alpha }}_{u}\left( \varvec{\eta }\right) -\alpha \right) \right\| ^{2}+\left\| \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\underline{{\textbf{x}}}\right\| ^{2}, \end{aligned}$$
(12)

where \(\underline{{\textbf{a}}}^{\prime }(\varvec{\eta })=[\textrm{Re}\{{\textbf{a}}^{\prime }(\varvec{\eta })\},\textrm{Im} \{{\textbf{a}}^{\prime }(\varvec{\eta })\}]^{\textrm{T}}\) and \(\underline{{\textbf{x}}}=[\textrm{Re}\{{\textbf{x}}\},\textrm{Im} \{{\textbf{x}})\}]^{\textrm{T}}\). Moreover, \(\varvec{\Pi }_{\textbf{A}} = {\textbf{A}}({\textbf{A}}^{\textrm{H}} {\textbf{A}})^{-1}{\textbf{A}}^{\textrm{H}}\) and \(\varvec{\Pi }_{{\textbf{A}}}^{\bot } = {\textbf{I}} - \varvec{\Pi }_{{\textbf{A}}}\) are orthogonal projectors over S and \(S^{\bot }\), respectively, where \(S = \text {span}({\textbf{A}})\), with \({\textbf{A}}\) being a matrix, represents the linear span of the set of its column vectors. Furthermore,

$$\begin{aligned} {\hat{\alpha }}_{u}\left( \varvec{\eta } \right) =\frac{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{T}}\underline{{\textbf{x}}}}{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{T}}\underline{{\textbf{a}}}^{\prime }\left( \tau \right) }=\frac{\textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}\right\} }{{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) }, \end{aligned}$$

denotes the unconstrained estimator of \(\alpha\) [34], when the condition \(\alpha > 0\) is not applicable. Minimizing the cost function in (12) results in

$$\begin{aligned} \left( \begin{array}{c} \widehat{\varvec{\eta }} \\ {\widehat{\alpha }} \end{array} \right) =\arg \underset{\varvec{\eta },\alpha \ge 0}{\min }\left\{ \left( {\hat{\alpha }}_{u}\left( \varvec{\eta } \right) -\alpha \right) ^{2}\left\| \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) \right\| ^{2} +\left\| \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) }^{\bot }\underline{{\textbf{x}}}\right\| ^{2}\right\} . \end{aligned}$$
(13)

Since \(\left\| \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) }^{\bot }\underline{{\textbf{x}}}\right\| ^{2}=\left\| \underline{{\textbf{x}}}\right\| ^{2}-\left\| \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) }\underline{{\textbf{x}}}\right\| ^{2}\), (13) leads to

$$\begin{aligned} \left( \begin{array}{c} \widehat{\varvec{\eta }} \\ {\widehat{\alpha }} \end{array} \right) =\arg \underset{\varvec{\eta },\alpha \ge 0}{\min }\left\{ \left\| {\textbf{x}}\right\| ^{2}+\left( \alpha -{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) \right) ^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| ^{2} -\textrm{Re}\left\{ \left( \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) }{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| }\right) ^{\textrm{H}}{\textbf{x}}\right\} ^{2} \right\} . \end{aligned}$$
(14)

Given that \(\frac{d(\alpha - {\hat{\alpha }}_{u}(\varvec{\eta }))^{2}}{d\alpha } = 2(\alpha - {\hat{\alpha }}_{u}(\varvec{\eta }))\), the following conditions apply for any given \(\varvec{\eta }\):

$$\begin{aligned} \bullet ~\text {if }{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) > 0 \text { then } \left\{ \begin{array}{l} \underset{\alpha \ge 0}{\min }\left\{ \left( \alpha -{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) \right) ^{2}\right\} =0 \\ {\widehat{\alpha }}\left( \varvec{\eta } \right) ={\hat{\alpha }}_{u}\left( \varvec{\eta } \right) \qquad ~ \end{array} \right. \end{aligned}$$

and \(({\widehat{\alpha }}\left( \varvec{\eta } \right) -{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) )^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| ^{2}=0\).

$$\begin{aligned} \bullet ~\text {if }{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) \le 0\text { then }\left\{ \begin{array}{l} \underset{\alpha \ge 0}{\min }\left\{ \left( \alpha -{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) \right) ^{2}\right\} ={\hat{\alpha }}_{u}^{2}\left( \varvec{\eta } \right) \\ {\widehat{\alpha }}\left( \varvec{\eta } \right) =0\qquad ~ \end{array} \right. \end{aligned}$$

and \(({\widehat{\alpha }}\left( \varvec{\eta } \right) -{\hat{\alpha }}_{u}\left( \varvec{\eta } \right) )^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| ^{2}=\textrm{Re}\left\{ \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}} {\textbf{x}}}{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| }\right\} ^{2}\).

Thus, for any given \(\varvec{\eta }\), the minimization of (14) with respect to \(\alpha\) results in

$$\begin{aligned} \underset{\alpha \ge 0}{\min }\left\{ \left\| {\textbf{x}}-{\textbf{a}} ^{\prime }\left( \varvec{\eta } \right) \alpha \right\| ^{2}\right\} = \left\| {\textbf{x}}\right\| ^{2}-\textrm{Re}\left\{ \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}}{\left\| {\textbf{a}} ^{\prime }\left( \varvec{\eta } \right) \right\| }\right\} ^{2} 1_{\{{{\textbf{x}}|\textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}\right\} > 0\}}}, \end{aligned}$$
(15)

where \(1_{\mathcal {D}}\) denotes the indicator function of subset \(\mathcal {D}\) of \({\mathbb {R}}^{N'}\), and the solution of (14) with respect to \(\left( \varvec{\eta },\alpha \ge 0\right)\) is then given by

$$\begin{aligned} \widehat{\varvec{\eta }}=\arg \underset{\left\{ \varvec{\eta }|\textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}\right\} >0\right\} }{\min }\left\{ \left\| {\textbf{x}}\right\| ^{2}-\textrm{Re}\left\{ \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}}{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| }\right\} ^{2}\right\} , \end{aligned}$$
(16a)

or equivalently

$$\begin{aligned} \widehat{\varvec{\eta }}=\arg \underset{\left\{ \varvec{\eta } | \textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}\right\} >0\right\} }{\max }\left\{ \textrm{Re}\left\{ \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta } \right) ^{\textrm{H}}{\textbf{x}}}{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| } \right\} ^{2}\right\} . \end{aligned}$$
(16b)

4 Cramér–Rao bound (CRB)

Let us denote \(\varvec{\epsilon }^{0}=\left( \left( \sigma _{n}^{2}\right) ^{0},\alpha ^{0},\varvec{\eta }^{0}\right) ^{\textrm{T}}\) the true value of \(\varvec{\epsilon }\). As shown in [35], in case of a parameter constraint, the CRB is unchanged at a regular point, i.e. where no equality constraint is active. Thus for \(\alpha >0\), the CRB is obtained from the inversion of the standard Fisher Information Matrix (FIM),

$$\begin{aligned} \textbf{CRB}_{\varvec{\epsilon }|\varvec{\epsilon }}\left( \varvec{\epsilon } ^{0}\right) ={\textbf{F}}\left( \varvec{\epsilon }^{0}\right) ^{-1}. \end{aligned}$$
(17)

Given the Gaussian nature of the signal model under study, the FIM is derived from the Slepian-Bangs formula [10] where \(\underline{{\textbf{x}}}\sim \mathcal {N}\left( {\textbf{m}}_{\underline{{\textbf{x}}}}\left( \mathbf { \epsilon }\right) ,{\textbf{C}}_{\underline{{\textbf{x}}}}\left( \mathbf { \epsilon }\right) \right)\),

$$\begin{aligned} \left( {\textbf{F}}\left( \varvec{\epsilon }\right) \right) _{k,l}=\frac{ \partial {\textbf{m}}_{\underline{{\textbf{x}}}}\left( \varvec{\epsilon }\right) }{\partial \epsilon _{k}}^{\textrm{T}}{\textbf{C}}_{\underline{{\textbf{x}}}}^{-1}\left( \varvec{\epsilon }\right) \frac{\partial {\textbf{m}}_{\underline{{\textbf{x}}} }\left( \varvec{\epsilon }\right) }{\partial \epsilon _{l}} +\frac{1}{2}tr\left( {\textbf{C}}_{\underline{{\textbf{x}}}}^{-1}\left( \mathbf { \epsilon }\right) \frac{\partial {\textbf{C}}_{\underline{{\textbf{x}}}}\left( \varvec{\epsilon }\right) }{\partial \epsilon _{k}}{\textbf{C}}_{\underline{ {\textbf{x}}}}^{-1}\left( \varvec{\epsilon }\right) \frac{\partial {\textbf{C}}_{ \underline{{\textbf{x}}}}\left( \varvec{\epsilon }\right) }{\partial \epsilon _{l}}\right) . \end{aligned}$$
(18)

The present study focuses on the derivation of \(\textbf{CRB}_{\varvec{{\eta } }|\varvec{\epsilon }}\left( \varvec{\epsilon }\right) = {{\textbf {F}}}^{-1}_{\varvec{\eta }|\varvec{\epsilon }}(\varvec{\epsilon })\), which for the CSM is given by [10]

$$\begin{aligned} {\textbf{F}}_{\varvec{\eta }|\varvec{\epsilon }}(\varvec{\epsilon })=\frac{ 2\alpha ^{2}}{\sigma _{n}^{2}}\varvec{\Phi }(\varvec{\eta }),~\varvec{\Phi }( \varvec{\eta })=\left( \frac{\partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }{\partial \varvec{\eta }^{\textrm{T}}}\right) ^{\textrm{T}}\varvec{\Pi } _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot } \frac{\partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }{\partial \varvec{\eta }^{\textrm{T}}},~\frac{\partial \underline{{\textbf{a}}} ^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}=\left[ \begin{array}{c} \textrm{Re}\left\{ \frac{\partial {\textbf{a}}^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} \\ \textrm{Im} \left\{ \frac{\partial {\textbf{a}}^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} \end{array} \right] . \end{aligned}$$
(19)

The term \(\varvec{\Phi }(\varvec{\eta })\) from (19) can be also expressed as a function of \({\textbf{a}}^{\prime }(\varvec{\eta })\) to provide a closed-form expression under the assumption of band-limited signals. Since

$$\begin{aligned} \varvec{\Phi }(\varvec{\eta })=\bigg (\frac{\partial \underline{{\textbf{a}}} ^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\bigg )^{\textrm{T}}\frac{ \partial \underline{{\textbf{a}}}^{\prime }(\varvec{\eta })}{\partial \mathbf { \eta }^{\textrm{T}}}-\frac{1}{\underline{{\textbf{a}}}^{\prime }(\varvec{\eta })^{\textrm{T}} \underline{{\textbf{a}}}^{\prime }(\varvec{\eta })}\bigg (\underline{{\textbf{a}}} ^{\prime }(\varvec{\eta })^{\textrm{T}}\frac{\partial \underline{{\textbf{a}}}^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\bigg )^{\textrm{T}}\bigg (\underline{ {\textbf{a}}}^{\prime }(\varvec{\eta })^{\textrm{T}}\frac{\partial \underline{{\textbf{a}} }^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\bigg ), \end{aligned}$$
(20)

by considering the following relationships,

$$\begin{aligned} \bigg ( \frac{\partial \underline{{\textbf{a}}}^{\prime }\left( {{\varvec{\eta }}} \right) }{\partial \varvec{\eta }^{\textrm{T}} }\bigg )^{\textrm{T}} \frac{\partial \underline{{\textbf{a}}}^{\prime }\left( {{\varvec{\eta }}} \right) }{\partial \varvec{\eta }^{\textrm{T}} }&= \textrm{Re}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} ^{\textrm{T}} \textrm{Re}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} + \textrm{Im}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} ^{\textrm{T}} \textrm{Im}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} \nonumber \\&= \textrm{Re}\left\{ \bigg (\frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}} \bigg ) ^{\textrm{H}}\frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} , \cdot \end{aligned}$$
(21a)
$$\begin{aligned} \underline{{\textbf{a}}}^{\prime }(\varvec{\eta })^{\textrm{T}} \frac{\partial \underline{{\textbf{a}}}^{\prime }\left( {{\varvec{\eta }}} \right) }{\partial \varvec{\eta }^{\textrm{T}} }&= \textrm{Re}\left\{ {\textbf{a}}^{\prime }(\varvec{\eta })\right\} ^{\textrm{T}} \textrm{Re}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} + \textrm{Im}\left\{ {\textbf{a}}^{\prime }(\varvec{\eta }) \right\} ^{\textrm{T}} \textrm{Im}\left\{ \frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} \nonumber \\&= \textrm{Re}\left\{ {\textbf{a}}^{\prime }(\varvec{\eta })^{\textrm{H}}\frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} . \end{aligned}$$
(21b)

Then, (20) can be rewritten as

$$\begin{aligned} \varvec{\Phi }(\varvec{\eta })=\textrm{Re}\left\{ \bigg (\frac{\partial {\textbf{a}} ^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\bigg )^{\textrm{H}}\frac{ \partial {\textbf{a}}^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}} \right\} -\frac{1}{\Vert {\textbf{a}}^{\prime }(\varvec{\eta })\Vert ^{2}}\Re \left\{ {\textbf{a}}^{\prime }(\varvec{\eta })^{\textrm{H}}\frac{\partial {\textbf{a}} ^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} ^{\textrm{T}}\Re \left\{ {\textbf{a}}^{\prime }(\varvec{\eta })^{\textrm{H}}\frac{\partial {\textbf{a}} ^{\prime }(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}\right\} . \end{aligned}$$
(22)

Given the derivative of \(a^{\prime }(t;\varvec{\eta })\) with respect to \(\varvec{\eta }\),

$$\begin{aligned} \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial \varvec{\eta }} =\left( \begin{array}{c} \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial \tau } \\ \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial b} \end{array} \right) =-\left( \begin{array}{c} (1-b)\frac{\partial a(t;\varvec{\eta })}{\partial t}+jw_{c}(1-b)a(t;\mathbf { \eta }) \\ (t-\tau )\frac{\partial a(t;\varvec{\eta })}{\partial t}+jw_{c}(t-\tau )a(t; \varvec{\eta }) \end{array} \right) e^{-j\varphi (t;\varvec{\eta })}, \end{aligned}$$

that is,

$$\begin{aligned} \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial \varvec{\eta }}=- {\textbf{Q}}{\textbf{v}}(t;\varvec{\eta })e^{-j\varphi (t;\varvec{\eta })}, \end{aligned}$$
(23a)
$$\begin{aligned} {\textbf{Q}}= \begin{bmatrix} jw_{c}(1-b) &{} 0 &{} (1-b) &{} ~0 \\ 0 &{} jw_{c} &{} 0 &{} ~1 \end{bmatrix},\quad {\textbf{v}}(t;\varvec{\eta })= \begin{bmatrix} a(t;\varvec{\eta }) \\ (t-\tau )a(t;\varvec{\eta }) \\ \frac{\partial a(t;\varvec{\eta })}{\partial t} \\ (t-\tau )\frac{\partial a(t;\varvec{\eta })}{\partial t} \end{bmatrix}. \end{aligned}$$
(23b)

A convenient matrix version of (22) is obtained applying (23) as follows,

$$\begin{aligned} \bigg (\frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}} \bigg ) ^{\textrm{H}}\frac{\partial {\textbf{a}}'(\varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}} = {\textbf{Q}} \bigg (\sum ^{N2'}_{n=N_1'} {\textbf{v}}(n\mathrm {T_s};\varvec{\eta }) \, {\textbf{v}}^{\textrm{H}}(n\mathrm {T_s};\varvec{\eta }) \bigg ){\textbf{Q}}^{\textrm{H}} = {\textbf{Q}} {\textbf{W}}{\textbf{Q}}^{\textrm{H}}, \end{aligned}$$
(24a)
$$\begin{aligned} {\textbf{a}}^{\prime }(\varvec{\eta })^{\textrm{H}}\frac{\partial {\textbf{a}}^{\prime }( \varvec{\eta })}{\partial \varvec{\eta }^{\textrm{T}}}=-\bigg (\sum _{n=N_{1}^{\prime }}^{N2^{\prime }}{\textbf{v}}(n\mathrm {T_s};\varvec{\eta })a^{*}(n\mathrm {T_s};\mathbf { \eta })\bigg )^{\textrm{T}}{\textbf{Q}}^{\textrm{T}}=-\left( {\textbf{Q}}{\textbf{w}}\right) ^{\textrm{T}}, \end{aligned}$$
(24b)
$$\begin{aligned} \Vert {\textbf{a}}(\varvec{\eta })\Vert ^2 = \sum _{n = N_1'}^{N_2'} \vert a(n\mathrm {T_s};\varvec{\eta }) \vert ^2, \end{aligned}$$
(24c)

where \({{\textbf {W}}}\) and \({{\textbf {w}}}\) are obtained after applying the Nyquist-shannon theorem as in [24], so that the resulting terms are expressed in the continuous-time domain, giving way to the following closed-form expressions:

$$\begin{aligned} \lim _{(N_1', N_2') \rightarrow (-\infty , \infty )} T_s \sum ^{N2'}_{n=N_1'} {\textbf{v}}(n\mathrm {T_s};\varvec{\eta }) \, {\textbf{v}}^{\textrm{H}}(n\mathrm {T_s};\varvec{\eta }) = \mathrm {F_s}\int _{-\infty }^{\infty } {\textbf{v}}(t) \, {\textbf{v}}^{\textrm{H}}(t) \, dt = \mathrm {F_s} {\textbf{W}} , \end{aligned}$$
(25a)
$$\begin{aligned} \lim _{(N_1', N_2') \rightarrow (-\infty , \infty )} T_s \sum ^{N2'}_{n=N_1'}{\textbf{v}}(n\mathrm {T_s};\varvec{\eta }) a^*(n\mathrm {T_s};\varvec{\eta }) = \mathrm {F_s}\int _{-\infty }^{\infty } {\textbf{v}}(t) a^*(t)\, dt = \mathrm {F_s} {\textbf{w}}. \end{aligned}$$
(25b)

Under the previously introduced matrix notation, the terms \({{\textbf {W}}}\) and \({{\textbf {w}}}\) are given by

$$\begin{aligned} {\textbf{W}} = \begin{bmatrix} w_1 &{} w^*_2 &{} w^*_3 &{} w_4^*\\ w_2 &{} W_{2,2} &{} w_4^* &{} W^*_{4,2}\\ w_3 &{} w_4 &{} W_{3,3} &{} W^*_{4,3}\\ w_4 &{} W_{4,2} &{} W_{4,3} &{} W_{4,4} \end{bmatrix}, \quad {\textbf{w}} = \begin{bmatrix} w_1\\ w_2\\ w_3\\ w_4 \end{bmatrix}. \end{aligned}$$
(26)

Each of the elements of (26) have been derived in previous contributions, for instance [32], and are

$$\begin{aligned}&w_{1} = \frac{1}{\mathrm {F_s}}{\textbf{a}}^{\textrm{H}}{\textbf{a}}, \quad w_{2} = \frac{1}{\mathrm {F_s}^2}\frac{{\textbf{a}}^{\textrm{H}}\textbf{D a}}{(1-b)^2}, \quad w_{3} =\frac{{\textbf{a}}^{\textrm{H}}\varvec{\Lambda } {\textbf{a}}}{(1-b)}, \quad w_4 = \mathrm {F_s}\frac{{\textbf{a}}^{\textrm{H}}{\textbf{D}}^{\textrm{H}}\varvec{\Lambda }{\textbf{a}}}{(1-b)^2},\\&W_{2,2} = \frac{1}{\mathrm {F_s}^3}{\textbf{a}}^{\textrm{H}}{\textbf{D}}^2{\textbf{a}}, \quad W_{4,2} = \frac{1}{\mathrm {F_s}}\frac{\left( {\textbf{a}}^{\textrm{H}} {{\textbf {D}}}\varvec{\Lambda }{{\textbf {D}}}{\textbf{a}}^{\textrm{H}} - {\textbf{a}}^{\textrm{H}}{{\textbf {D}}}{\textbf{a}}\right) }{(1-b)^3}, \quad W_{3,3} = \mathrm {F_s}\frac{{\textbf{a}}^{\textrm{H}}\textbf{Va}}{(1-b)}, \\&W_{4,3} = {\textbf{a}}^{\textrm{H}}\varvec{\Lambda }{\textbf{a}} + {\textbf{a}}^{\textrm{H}}{{\textbf {V}}}{{\textbf {D}}}{\textbf{a}}, \quad W_{4,4} = \frac{1}{\mathrm {F_s}}\left( {\textbf{a}}^{\textrm{H}}{\textbf{a}} + {\textbf{a}}^{\textrm{H}} {{\textbf {D}}}{{\textbf {V}}}{{\textbf {D}}}{\textbf{a}} - 2\textrm{Re}\left\{ {\textbf{a}}^{\textrm{H}}\varvec{\Lambda } {{\textbf {D}}}{\textbf{a}}\right\} \right) , \end{aligned}$$
(27)

where \({\textbf{D}} = \text {diag}\left( N_1',\ldots ,N_2'\right)\) and

$$\begin{aligned}&\left( \varvec{\Lambda } \right) _{n,n^{\prime }}=\left| \begin{array}{l} n^{\prime }\ne n:\frac{\left( -1\right) ^{\left| n-n^{\prime }\right| }}{n-n^{\prime }}\\ n^{\prime }=n:0 \end{array} \right. , \end{aligned}$$
(28)
$$\begin{aligned}&\left( {\textbf{V}}\right) _{n,n^{\prime }}=\left| \begin{array}{l} n^{\prime }\ne n:\left( -1\right) ^{\left| n-n^{\prime }\right| } \frac{2}{\left( n-n^{\prime }\right) ^{2}} \\ n^{\prime }=n:\frac{\pi ^{2}}{3} \end{array} \right. . \end{aligned}$$
(29)

Thanks to (24a) and (24b), (22) can be expressed in a more compact form. This is,

$$\begin{aligned} \varvec{\Phi }(\varvec{\eta }) = \mathrm {F_s} \textrm{Re}\bigg \{ {\textbf{Q}} {\textbf{W}} {\textbf{Q}}^{\textrm{H}} \bigg \} - \frac{\mathrm {F_s}}{w_1} \textrm{Re}\bigg \{{\textbf{Q}}{\textbf{w}} \bigg \} \textrm{Re}\bigg \{{\textbf{Q}}{\textbf{w}} \bigg \}^{\textrm{H}} = \mathrm {F_s} \begin{bmatrix} \Phi _{1,1} &{} \Phi _{1,2}\\ \Phi _{2,1} &{} \Phi _{2,2} \end{bmatrix}, \end{aligned}$$
(30)

with

$$\begin{aligned} \begin{aligned} \Phi _{1,1}&= (1-b)^2 \bigg (\textrm{Re}\{ W_{3,3}\} + w_c^2w_1 + 2w_c \textrm{Im}\{ w_3\} - \frac{\textrm{Re}\{ w_3\}^2 }{w_1}\bigg ),{} & {} \\ \Phi _{1,2}&= (1-b) \bigg (w_c^2\textrm{Re}\{ w_2\} + 2 w_c\textrm{Im}\{ w_4\} +\textrm{Re}\{ W_{4,3}\} + w_c\frac{ \textrm{Re}\{ w_3\} \textrm{Im}\{ w_2^*\} }{w_1} - \frac{ \textrm{Re}\{ w_3 w_4^*\} }{w_1}\bigg ),\\ \Phi _{2,1}&= \Phi _{1,2}, \\ \Phi _{2,2}&= w_c^2\textrm{Re}\{W_{2,2}\} + w_c^2\frac{\textrm{Im}\{w_2\}^2}{w_1} - 2w_c\textrm{Im}\{W_{4,2}\} + \textrm{Re}\{W_{4,4}\} \\&+ 2w_c\frac{\textrm{Re}\{ w_4\} \textrm{Im}\{ w_2\}}{w_1} - \frac{\textrm{Re}\{w_4\}^2}{w_1}. \end{aligned} \end{aligned}$$
(31)

Finally, the CRB for the time-delay and Doppler estimation is obtained as,

$$\begin{aligned} \varvec{\text {CRB}}_{\varvec{{\eta }}|\varvec{\epsilon }}\left( \mathbf { \epsilon }\right) ={\textbf{F}}_{\varvec{\eta }|\varvec{\epsilon }}^{-1}( \varvec{\epsilon })=\frac{\sigma _{n}^{2}}{2\mathrm {F_s}\alpha ^{2}} \begin{bmatrix} \Phi _{1,1} &{} \Phi _{1,2} \\ \Phi _{2,1} &{} \Phi _{2,2} \end{bmatrix} ^{-1}= \begin{bmatrix} \textrm{CRB}_{\tau |\varvec{\epsilon }} &{} \textrm{CRB}_{b,\tau |\varvec{\epsilon }} \\ \textrm{CRB}_{\tau ,b|\varvec{\epsilon }} &{} \textrm{CRB}_{b|\varvec{\epsilon }} \end{bmatrix}. \end{aligned}$$
(32)

The result obtained in (32) can be compared to the one in [24, Eq.(25)], which provides the asymptotic estimation performance of the time-delay and Doppler for the signal model introduced in (8). Note that the main difference is the addition of extra terms dependent on \(w_c\), which become, in most applications, the predominant terms due to the order of magnitude of \(w_c\). Whenever these terms are predominant, the CRB behaves as a parametric function purely dependent on the signal to noise ratio and on the carrier frequency.

5 Ambiguity function

Since (16b)

$$\begin{aligned} \widehat{\varvec{\eta }}=\arg \underset{\left\{ \varvec{\eta }|\textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta }\right) ^{\textrm{H}}{\textbf{x}}\left( \varvec{\epsilon }^{0}\right) \right\} >0\right\} }{\max }\left\{ \left\| \Pi _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) } \underline{{\textbf{x}}}\left( \varvec{\epsilon }^{0}\right) \right\| ^{2}\right\} , \end{aligned}$$

the ambiguïty function can be defined as the score function without noise, that isFootnote 1

$$\begin{aligned} \Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right)= & {} \left\| \Pi _{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) \alpha ^{0}\right\| ^{2} \end{aligned}$$
(33a)
$$\begin{aligned}= & {} \left( \alpha ^{0}\right) ^{2}\frac{\left( \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) ^{\textrm{T}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) \right) ^{2}}{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) ^{\textrm{T}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }=\left( \alpha ^{0}\right) ^{2}\frac{\textrm{Re}\left\{ {\textbf{a}}^{\prime }\left( \varvec{\eta }\right) ^{\textrm{H}}{\textbf{a}}^{\prime }\left( \varvec{\eta }^{0}\right) \right\} ^{2}}{\textrm{Re}\left\{ {\textbf{a}} ^{\prime }\left( \varvec{\eta }\right) ^{\textrm{H}}{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) \right\} } \nonumber \\ \Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right)= & {} \left( \alpha ^{0}\right) ^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } ^{0}\right) \right\| ^{2}\textrm{Re}\left\{ \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) ^{\textrm{H}}{\textbf{a}}^{\prime }\left( \varvec{\eta } ^{0}\right) }{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta }\right) \right\| \left\| {\textbf{a}}^{\prime }\left( \varvec{\eta }^{0}\right) \right\| }\right\} ^{2}. \end{aligned}$$
(33b)

Firstly, since according to (33a) \(\Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right) =\left( \alpha ^{0}\right) ^{2} \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T} }\Pi _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) } \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right)\), its first derivative can be expressed as

$$\begin{aligned}&\left\{ \begin{array}{l} \frac{\partial \Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right) }{ \partial \eta _{p}}=\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T}}\frac{\partial \Pi _{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }}{\partial \eta _{p}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) , \\ \frac{\partial \Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right) }{ \partial \eta _{p}}=-\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T}}\frac{\partial \varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{ \partial \eta _{p}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) , \end{array} \right. \end{aligned}$$
(34a)

and its second derivative as

$$\begin{aligned}&\left\{ \begin{array}{l} \frac{\partial ^{2}\Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right) }{ \partial \eta _{p}\partial \eta _{p^{\prime }}}=\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T}} \frac{\partial ^{2}\Pi _{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }}{\partial \eta _{p}\partial \eta _{p^{\prime }}}\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) , \\ \frac{\partial ^{2}\Xi \left( \varvec{\eta };\varvec{\eta }^{0}\right) }{ \partial \eta _{p}\partial \eta _{p^{\prime }}}=-\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T}} \frac{\partial ^{2}\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}\partial \eta _{p^{\prime }}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) . \end{array} \right. \end{aligned}$$
(34b)

Secondly, considering the properties of the projector \(\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\),

$$\begin{aligned} \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }={\textbf{I}}-\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) },\quad \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }={\textbf{0}}=\varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) },\quad \mathbf { \Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }=\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } \right) }^{\bot }\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }, \end{aligned}$$
(35)

the derivative terms in (34) can be recast as

$$\begin{aligned}&\frac{\partial \varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{ \partial \eta _{p}}=\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\frac{\partial \varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}}+\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}}\varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }, \end{aligned}$$
(36a)
$$\begin{aligned}&\frac{\partial ^{2}\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p^{\prime }}\partial \eta _{p}} =\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p^{\prime }}}\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}}+\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\frac{\partial ^{2}\varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{ \partial \eta _{p^{\prime }}\partial \eta _{p}}+\frac{\partial ^{2}\mathbf { \Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot } }{\partial \eta _{p^{\prime }}\partial \eta _{p}}\varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }+\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}}\frac{\partial \varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p^{\prime }}}. \end{aligned}$$
(36b)

Therefore, after substituting expression (36b) in (34b), one obtains

$$\begin{aligned}&\frac{\partial ^{2}\Xi \left( \varvec{\eta }^{0};\varvec{\eta }^{0}\right) }{ \partial \eta _{p}\partial \eta _{p^{\prime }}}=-\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{ \textrm{T}}\frac{\partial ^{2}\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p}\partial \eta _{p^{\prime }}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) \nonumber \\&=-\left( \alpha ^{0}\right) ^{2}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T}}\left( \begin{array}{c} \frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \mathbf { \eta }^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}}\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }}{\partial \eta _{p}}+\frac{\partial \varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{ \partial \eta _{p}}\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}}+ \\ \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }\frac{\partial ^{2}\varvec{\Pi }_{\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}\partial \eta _{p}}+\frac{\partial ^{2}\varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{ \partial \eta _{p^{\prime }}\partial \eta _{p}}\varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot } \end{array} \right) \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) . \end{aligned}$$
(37)

Note that since

$$\begin{aligned} \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) =\left( \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) ^{T} \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\right) ^{T}={\textbf{0}}, \end{aligned}$$

expression (37) reduces to

$$\begin{aligned} \frac{\partial ^{2}\Xi \left( \varvec{\eta }^{0};\varvec{\eta }^{0}\right) }{ \partial \eta _{p}\partial \eta _{p^{\prime }}}=-\left( \alpha ^{0}\right) ^{2}\left( \begin{array}{l} \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T} }\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}}\frac{ \partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }}{\partial \eta _{p}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) + \\ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) ^{\textrm{T} }\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p}}\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}}\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) \end{array} \right) \\ =.-2\left( \alpha ^{0}\right) ^{2}\left( \frac{\partial \varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{ \partial \eta _{p}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) \right) ^{\textrm{T}}\frac{\partial \varvec{\Pi }_{\underline{ {\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }^{\bot }}{\partial \eta _{p^{\prime }}}\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) . \end{aligned}$$

Moreover as

$$\begin{aligned} \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) = {\textbf{0}}~\Rightarrow ~\frac{\partial \varvec{\Pi }_{\underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }\right) }^{\bot }}{\partial \eta _{p}} \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) +\varvec{\Pi }_{ \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }^{\bot }\frac{ \partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }\right) }{ \partial \eta _{p}}={\textbf{0}}, \end{aligned}$$

(37) is reformulated as

$$\begin{aligned} \frac{\partial ^{2}\Xi \left( \varvec{\eta }^{0};\varvec{\eta }^{0}\right) }{ \partial \eta _{p}\partial \eta _{p^{\prime }}}=-2\left( \alpha ^{0}\right) ^{2}\left( -\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \mathbf { \eta }^{0}\right) }^{\bot }\frac{\partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }{\partial \eta _{p}}\right) ^{\textrm{T} }\left( -\varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }\frac{\partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }{\partial \eta _{p^{\prime }}}\right) \nonumber \\ =-2\left( \alpha ^{0}\right) ^{2}\frac{\partial \underline{{\textbf{a}}} ^{\prime }\left( \varvec{\eta }^{0}\right) }{\partial \eta _{p}}^{\textrm{T}} \varvec{\Pi }_{\underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta } ^{0}\right) }^{\bot }\frac{\partial \underline{{\textbf{a}}}^{\prime }\left( \varvec{\eta }^{0}\right) }{\partial \eta _{p^{\prime }}}=-2\left( \alpha ^{0}\right) ^{2}{\textbf{e}}_{p}^{\textrm{T}}\varvec{\Phi }\left( \varvec{\eta }^{0}\right) {\textbf{e}}_{p^{\prime }}. \end{aligned}$$

Finally,

$$\begin{aligned} \Xi \left( \varvec{\eta }^{0}+d\varvec{\eta };\varvec{\eta }^{0}\right)&\simeq \Xi \left( \varvec{\eta }^{0};\varvec{\eta }^{0}\right) +\frac{1}{2}d \varvec{\eta }^{\textrm{T}}\left. \frac{\partial ^{2}\Xi \left( \varvec{\eta }; \varvec{\eta }^{0}\right) }{\partial \varvec{\eta }\partial \varvec{\eta } ^{\textrm{T}}}\right| _{\varvec{\eta }^{0}}d\varvec{\eta } \end{aligned}$$
(38a)
$$\begin{aligned}&\simeq \left( \alpha ^{0}\right) ^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta }^{0}\right) \right\| ^{2}\left( 1-d\varvec{\eta }^{\textrm{T}}\left( \frac{\varvec{\Phi }\left( \varvec{\eta }^{0}\right) }{\left\| {\textbf{a}} ^{\prime }\left( \varvec{\eta }^{0}\right) \right\| ^{2}}\right) d\mathbf { \eta }\right) , \end{aligned}$$
(38b)

and

$$\begin{aligned} \textbf{CRB}_{\varvec{\eta }\mid \varvec{\epsilon }}\left( \varvec{ \epsilon }^{0}\right) ={\textbf{F}}_{\varvec{\eta }\mid \varvec{\epsilon } }^{-1}\left( \varvec{\epsilon }^{0}\right) ,\quad {\textbf{F}}_{\mathbf { \eta }\mid \varvec{\epsilon }}\left( \varvec{\epsilon }^{0}\right) = \frac{2\left( \alpha ^{0}\right) ^{2}}{\left( \sigma _{n}^{2}\right) ^{0}} \varvec{\Phi }\left( \varvec{\eta }^{0}\right) =\frac{-1}{\left( \sigma _{n}^{2}\right) ^{0}}\left. \frac{\partial ^{2}\Xi \left( \varvec{\eta }; \varvec{\eta }^{0}\right) }{\partial \varvec{\eta }\partial \varvec{\eta } ^{\textrm{T}}}\right| _{\varvec{\eta }^{0}}, \end{aligned}$$
(38c)

which generalizes the known result for the standard CSM (8) [2, §10] [5, §3.9.4].

6 A simplified signal model: the narrowband signal model

This contribution finds it valuable to explore simpler observation models, such as the narrowband model, which assumes that the baseband signal remains unaffected by the Doppler effect. Therefore, the model presented in (7), can be simplified as follows

$$\begin{aligned} x(t)=\alpha a^{\prime }(t;\varvec{\eta })+n(t),\quad a^{\prime }(t;\mathbf { \eta })=a(t-\tau )e^{-jw_{c}(\tau +b(t-\tau ))}, \end{aligned}$$
(39)

the discrete vector \({\textbf{a}}^{\prime }(\varvec{\eta })\) defined in (10) simply becoming

$$\begin{aligned} {\textbf{a}}^{\prime }(\varvec{\eta })=\left( \begin{array}{c} a\left( N_{1}^{\prime }\mathrm {T_s}-\tau \right) e^{-jw_{c}(\tau +b(N_{1}^{\prime }\mathrm {T_s}-\tau ))} \\ \vdots \\ a\left( N_{2}^{\prime }\mathrm {T_s}-\tau \right) e^{-jw_{c}(\tau +b(N_{2}^{\prime }\mathrm {T_s}-\tau ))} \end{array} \right) , \end{aligned}$$
(40)

which does not change the MLE expression (16b). However, it is required to update the CRB expression for this particular signal model, since now

$$\begin{aligned} \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial \varvec{\eta }}= \begin{pmatrix} \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial \tau } \\ \frac{\partial a^{\prime }(t;\varvec{\eta })}{\partial b} \end{pmatrix} =- \begin{pmatrix} \frac{\partial a(t-\tau )}{\partial t}+jw_{c}(1-b)a(t-\tau ) \\ jw_{c}(t-\tau )a(t-\tau ) \end{pmatrix} e^{-j\varphi (t;\varvec{\eta })}. \end{aligned}$$

As noted above, \(\partial a^{\prime }(t;\varvec{\eta })/\partial \mathbf { \eta }\) can be expressed using matrix notation (23) where \({\textbf{Q}}\) and \({\textbf{v}}\) terms are given by

$$\begin{aligned} {\textbf{Q}}= \begin{bmatrix} jw_{c}(1-b) &{} 0 &{} 1 \\ 0 &{} jw_{c} &{} 0 \end{bmatrix},\quad {\textbf{v}}(t;\varvec{\eta })=\left[ \begin{array}{c} a(t-\tau ) \\ (t-\tau )a(t-\tau ) \\ \frac{\partial a(t-\tau )}{\partial t} \end{array} \right] . \end{aligned}$$
(41)

Following the same procedure as in Sect. 4, \({\textbf{W}}\) and \({\textbf{w}}\) are redefined as

$$\begin{aligned} {\textbf{W}}= \begin{bmatrix} w_{1} &{} w_{2}^{*} &{} w_{3}^{*} \\ w_{2} &{} W_{2,2} &{} w_{4}^{*} \\ w_{3} &{} w_{4} &{} W_{3,3} \end{bmatrix},\quad {\textbf{w}}= \begin{bmatrix} w_{1} \\ w_{2} \\ w_{3} \end{bmatrix}, \end{aligned}$$
(42)

were each of the elements were already introduced in (27). Again, \(\varvec{\Phi }(\varvec{\eta })\) is

$$\begin{aligned} \varvec{\Phi }(\varvec{\eta }) = \mathrm {F_s} \begin{bmatrix} \Phi _{1,1} &{} \Phi _{1,2} \\ \Phi _{2,1} &{} \Phi _{2,2} \end{bmatrix}, \end{aligned}$$
(43)

with

$$\begin{aligned} \begin{aligned} \Phi _{1,1}&= W_{3,3} + \textrm{Re}\left\{ w_1\right\} (1-b)^2 \, w_c^2 - \frac{\textrm{Re}\left\{ w_3\right\} ^2}{w_1} + \textrm{Im}\left\{ w_3\right\} (1-b) 2w_c,{} & {} \\ \Phi _{1,2}&= \textrm{Re}\left\{ w_2\right\} (1-b) w_c^2 - \frac{\textrm{Re}\left\{ w_3\right\} \textrm{Im}\left\{ w_2\right\} }{w_1} w_c - \textrm{Im}\left\{ w_{4}^*\right\} w_c,\\ \Phi _{2,1}&= \Phi _{1,2}, \\ \Phi _{2,2}&= W_{2,2} w_c^2- \frac{\textrm{Im}\left\{ w_2\right\} ^2}{w_1} w_c^2. \end{aligned} \end{aligned}$$
(44)

The latter terms can be compared with other studies, which provide the asymptotic estimation performance of the time-delay and Doppler estimation considering a narrowband signal and a complex signal amplitude, for instance in [30]. Again, as it could be observed for the case of the wideband signal model, extra terms can be found in the FIM which are dependent on the carrier frequency \(w_{c}\). These are denoted as \(\Delta \Phi _{1,1}\) for the first diagonal term and \(\Delta \Phi _{1,2}\) for the non-diagonal term.

$$\begin{aligned} \begin{aligned} \Delta \Phi _{1,1}&= \textrm{Re}\{w_1\}(1-b)^2w_c^2 + \textrm{Im}\{w_3\} (1-b)w_c, \\ \Delta \Phi _{1,2}&= \Delta \Phi _{2,1} = \textrm{Re}\{w_2\}(1-b)w_c^2. \end{aligned} \end{aligned}$$
(45)

As previously mentioned, in most applications, those terms are going to be predominant due to the order of magnitude of \(w_{c}\).

6.1 Narrowband signal model with known and compensated Doppler effect

In the event that the Doppler effect is known and thus compensated, the only remaining variable of interest for the estimation performance assessment is \(\tau\). In such case, (7) can be simplified to

$$\begin{aligned} x(t)=\alpha a^{\prime }(t;\tau )e^{-jw_{c}\tau }+n(t),\quad a^{\prime }(t;\tau )=a(t-\tau )e^{-jw_{c}\tau }, \end{aligned}$$
(46)

the discrete vector \({\textbf{a}}^{\prime }(\varvec{\eta })\) defined in (10) simply becoming

$$\begin{aligned} {\textbf{a}}^{\prime }(\varvec{\eta })\triangleq {\textbf{a}}^{\prime }(\tau )=\left( \begin{array}{c} a\left( N_{1}^{\prime }\mathrm {T_s}-\tau \right) \\ \vdots \\ a\left( N_{2}^{\prime }\mathrm {T_s}-\tau \right) \end{array} \right) e^{-jw_{c}\tau }={\textbf{a}}(\tau )e^{-jw_{c}\tau }. \end{aligned}$$
(47)

Note that for the signal model defined in (46), the MLE’s expression is particularized for \(\varvec{\eta }\triangleq \tau\), and (16b) yields

$$\begin{aligned} {\widehat{\tau }}=\arg \underset{\left\{ \tau |\textrm{Re}\left\{ e^{jw_{c}\tau }\left( {\textbf{a}}\left( \tau \right) ^{\textrm{H}}{\textbf{x}}\right) \right\} >0\right\} }{\max }\left\{ \textrm{Re}\left\{ e^{jw_{c}\tau }\frac{{\textbf{a}}\left( \tau \right) ^{\textrm{H}}{\textbf{x}}}{\left\| {\textbf{a}}\left( \tau \right) \right\| }\right\} ^{2}\right\} . \end{aligned}$$
(48)

In order to compute the CRB for this particular signal model, it suffices to update the derivative of \(a^{\prime }(t;\varvec{\eta })\) with respect to \(\varvec{\eta }\), which reduces to

$$\begin{aligned} \frac{\partial a^{\prime }(\tau )}{\partial \tau }=-\left( \frac{\partial a(t-\tau )}{\partial t}+jw_{c}a(t-\tau )\right) e^{jw_{c}\tau }=-{\textbf{q}} {\textbf{v}}(t;\tau )e^{-jw_{c}\tau }, \end{aligned}$$

with \({\textbf{q}}= \begin{bmatrix} jw_{c}&~1 \end{bmatrix}\) and \({\textbf{v}}(t;\tau )= \begin{bmatrix} a(t-\tau ) \\ \frac{\partial a(t-\tau )}{\partial t} \end{bmatrix}\), yielding

$$\begin{aligned} \varvec{\Phi }(\varvec{\eta })\triangleq \varvec{\Phi }(\tau )=\mathrm {F_s}\left( w_{2}-\frac{\textrm{Re}\left\{ w_{3}\right\} ^{2}}{w_{1}}+w_{c}^{2}w_{1}+2w_{c}\textrm{Im} \left\{ w_{3}\right\} \right) . \end{aligned}$$
(49)

Last, the ambiguity function (33b) becomes

$$\begin{aligned} \Xi (\tau ^{0}+d\tau ;\tau ^{0})=\left( \alpha ^{0}\right) ^{2}\left\| {\textbf{a}}(\tau ^{0})\right\| ^{2}\times \textrm{Re}\left\{ \frac{{\textbf{a}} (\tau ^{0}+d\tau )^{\textrm{H}}{\textbf{a}}(\tau ^{0})}{\left\| {\textbf{a}}(\tau ^{0}+d\tau )\right\| \left\| {\textbf{a}}(\tau ^{0})\right\| } e^{jw_{c}d\tau }\right\} ^{2}, \end{aligned}$$

and its relationship with the CRB reads

$$\begin{aligned} \textrm{CRB}_{\tau \mid \varvec{\epsilon }}\left( \varvec{\epsilon } ^{0}\right) =\frac{1}{F_{\tau \mid \varvec{\epsilon }}\left( \varvec{ \epsilon }^{0}\right) },\quad F_{\tau \mid \varvec{\epsilon }}\left( \varvec{\epsilon }^{0}\right) =\frac{2\left( \alpha ^{0}\right) ^{2}}{ \left( \sigma _{n}^{2}\right) ^{0}}\Phi (\tau )=\frac{-1}{\left( \sigma _{n}^{2}\right) ^{0}}\left. \frac{\partial ^{2}\Xi \left( \tau ;\tau ^{0}\right) }{\partial ^{2}\tau }\right| _{\tau ^{0}}. \end{aligned}$$
(50)

Moreover, at the vicinity of \(\tau ^{0}\), since \(\frac{{\textbf{a}}\left( \tau ^{0}+d\tau \right) ^{\textrm{H}}{\textbf{a}}\left( \tau ^{0}\right) }{\left\| {\textbf{a}}\left( \tau ^{0}+d\tau \right) \right\| \left\| {\textbf{a}}\left( \tau ^{0}\right) \right\| }\in {\mathbb {R}}\), then

$$\begin{aligned} \Xi \left( \tau ^{0}+d\tau ;\tau ^{0}\right) \simeq \Xi _{a}\left( \tau ^{0}+d\tau ;\tau ^{0}\right) \cos \left( w_{c}d\tau \right) ^{2},~\Xi _{a}\left( \tau ;\tau ^{0}\right) =\left( \alpha ^{0}\right) ^{2} \textrm{Re}\left( \frac{{\textbf{a}}\left( \tau \right) ^{\textrm{H}}{\textbf{a}}\left( \tau ^{0}\right) }{ \left\| {\textbf{a}}\left( \tau \right) \right\| }\right) ^{2}, \end{aligned}$$
(51)

where \(\Xi _{a}\left( \tau ;\tau ^{0}\right)\) is the ambiguity function of the baseband signal \(a\left( t\right)\) for the CSM (7), and for the standard CSM (8) if \(a\left( t\right)\) is real valued [24]. Expression (51) is essential to predict (and understand) the behaviour of \({\widehat{\tau }}\) (48) with respect to the SNR.

7 Validation of CRB and MLE expressions

The simulations outlined in this section aimed to achieve three main objectives. Firstly, the primary goal was to validate the accurate derivation of the CRB and MLE expressions. This is demonstrated by showing that the MSE of the MLE gradually approaches its minimum value, as defined by the CRB, with increasing SNR. This lower bound acts as a benchmark, providing valuable insights into the optimal estimation performance of the time delay (\(\tau\)) for all the signal models presented and the Doppler effect (b) for Sect. 2 and 6. To contextualize this assessment, an additional CRB simulation was included based on the narrow-band signal model in [30], following the approach pointed out in (8). Secondly, the simulations aimed at illustrating the expected performance degradation due to the addition of the Doppler unknown in Sect. 6 compared to the model outlined in Sect. 6.1. Thirdly, due to the dependency of all signal models on \(\mathrm {F_c}\), and also on \(\mathrm {F_s}\) for Sect. 2 and Sect. 6, the simulations sought to analyze their impact on estimation performance exploring several values for such parameters.

To achieve these objectives, a testing setup was designed employing a GPS L1 C/A signal [37], which is composed by a periodic Gold CDMA sequence of 1023 chip modulated by a Binary Phase Shift Keying (BPSK) at frequency \(\mathrm {F_c}\). An integration time of 1ms   set, together with a Doppler effect of 500 Hz. The SNR at the output of the MLE (16b) (also known as the matched filter [10]) for the true parameter \(\varvec{\eta }^{0}\) can be determined as

$$\begin{aligned} \text {SNR}_{out}=\left. \frac{\textrm{Re}\left\{ \left( \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) }{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta } \right) \right\| }\right) ^{\textrm{H}}\left( \alpha ^{0}{\textbf{a}}^{\prime }\left( \varvec{\eta }^{0}\right) \right) \right\} ^{2}}{\textrm{E}\left[ \textrm{Re}\left\{ \left( \frac{{\textbf{a}}^{\prime }\left( \varvec{\eta }\right) }{\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta }\right) \right\| }\right) ^{\textrm{H}} {\textbf{n}}\right\} ^{2}\right] }\right| _{\varvec{\eta }=\varvec{\eta } ^{0}}=\frac{\left( \alpha ^{0}\right) ^{2}\left\| {\textbf{a}}^{\prime }\left( \varvec{\eta }^{0}\right) \right\| ^{2}}{\frac{\left( \sigma _{n}^{0}\right) ^{2}}{2}}=\frac{2\left\| {\textbf{a}}\right\| ^{2}}{ \left( \sigma _{n}^{0}\right) ^{2}}\left( \alpha ^{0}\right) ^{2}. \end{aligned}$$
(52)

Note that the FIM can be expressed as \({\textbf{F}}_{\varvec{\eta }|\varvec{\epsilon }}(\varvec{\epsilon })= \frac{\text {SNR}_{out}}{{\textbf{a}}^{\textrm{H}}{\textbf{a}}} \, \varvec{\Phi }(\varvec{\eta })\). To verify the MLE and CRB expression, a set of simulations were conducted comprising 1000 Monte-Carlo runs for different values of \(\mathrm {F_c}\) and \(\mathrm {F_s}\), with \(\mathrm {F_s}\) being defined as multiples of the baseband signal bandwidth.

To enhance clarity, the nomenclature used to denote the various derivations presented in the succeeding sections is introduced next. The MLE (16b) and CRB (32) for the general signal model discussed in Sect. 2 are denoted as \(\textrm{MLE}_{\tau | \varvec{\eta }}\) and \(\textrm{CRB}_{\tau | \varvec{\eta }}\) for (\(\tau\)) parameter, and \(\textrm{MLE}_{b | \varvec{\eta }}\) and \(\textrm{CRB}_{b | \varvec{\eta }}\) for (b) parameter. In the case of the narrowband context of Sect. 6, the corresponding CRB matches \(\textrm{CRB}_{\tau | \varvec{\eta }}\) from the wideband model. The main reason is that for the selected simulation scenario (commonly used in the GNSS community), the Doppler effect does not affect the baseband signal samples and therefore the wideband model converges to the narrowband model. Then, for the signal model in Sect. 6.1 the designation used is \(\textrm{MLE}_\tau\) and \(\textrm{CRB}_{\tau }\). The MLE and CRB from [30] are denoted \(\textrm{MLE}^m_{\tau \vert \varvec{\eta }}\) and \(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), and are also simulated for comparison purposes since they characterize the standard CSM (8). As a brief reminder, it is important to note that in the present work, the signal model used does not incorporate the carrier-phase component into the parameter \(\alpha\). This contrasts with the approach taken in references [30, 32], as the primary objective in this case is to investigate how the carrier-phase component influences the overall performance.

By shifting focus to the results presented in Figs. 1, 2, 3, 4, 5, 6, 7 and 8, significant insights are identified. Figure 1 shows the \(\textrm{MLE}_{\tau | \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\) for \(\mathrm {F_s} = [1,2,5]\) and \(\mathrm {F_c} = 1575.42 \, \textrm{MHz}\). A foremost observation is that the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) converges asymptotically to \(\textrm{CRB}_{\tau | \varvec{\eta }}\) for any given \(\mathrm {F_s}\) value, thus validating the theoretical framework presented in Sect. 4 for the time-delay parameter. Moreover, two interesting points can be drawn. On the one side, increasing \(\mathrm {F_s}\) decreases the SNR threshold, i.e. the \(\textrm{SNR}_{\textrm{out}}\) level required for the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) convergence to the \(\textrm{CRB}_{\tau | \varvec{\eta }}\). On the other side, in the region before the SNR threshold, there is a \(\textrm{SNR}_{\textrm{out}}\) below which the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) behaves as the classical unconstrained MLE, since it converges to \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\).

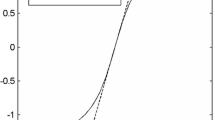
Figure 2, illustrates the ambiguity function derived in Sect. 5, which facilitates the interpretation of the MLE and CRB behaviour, and whose relationship to the simplified scenario of the general signal model was described in Sect. 6.1. Note in (51), that the term \(\cos (2\pi \mathrm {F_c} (\tau - \tau )\)) exhibits characteristics resembling a Dirac comb sampling the ambiguity function \(\Xi _a(\tau , \tau _0)\) of the baseband signal a(t) (51). Figure 2 shows how this sampling process results in the generation of an ambiguity function \(\Xi (\tau , \tau _0)\) displaying multiple local maxima within the main lobe of \(\Xi _a(\tau , \tau _0)\). Consequently, given the high SNR condition, the MLE score function in (12) converges towards a sampled version of \(\Xi _a(\tau , \tau _0)\). The MLE parameter \(\tau _0\) remains in proximity to the maximum maximorum of \(\Xi (\tau , \tau _0)\), specifically close to \(\tau _0\), exhibiting a variance associated with the curvature of \(\Xi (\tau , \tau _0)\) in the vicinity of \(\tau _0\), denoted as \(\textrm{CRB}_{\tau |\epsilon }\) when \(\epsilon = \epsilon _0\).

Figure 3 shows the \(\textrm{MLE}_{\tau }\), \(\textrm{MLE}_{\tau | \varvec{\eta }}\) as well as the error levels defined by \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and \(\textrm{CRB}_{\tau }\). Notably, \(\textrm{CRB}_{\tau }\) consistently exhibits lower MSE levels than \(\textrm{CRB}_{\tau | \varvec{\eta }}\). This discrepancy confirms the negative effect on the estimation performance due to the uncertainty introduced by the unknown Doppler effect term (b) in (44), which was assumed to be known and compensated for in (49). The MSE difference between \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and \(\textrm{CRB}_{\tau }\) remains approximately \(6 \, \textrm{dB}\) across all SNR values. It is observed as well that \(\textrm{MLE}_{\tau }\) converges to the associated \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\) before reaching lower MSE levels. The difference in performance can be justified by the fact that the Doppler and time-delay estimation are no longer decoupled. A well-known result in the state of the art is that for any instance of the CSM based on a real valued basedband signal, the estimation performance between the Doppler and time-delay components are decoupled, i.e. the FIM for time-delay and Doppler is diagonal [30, 32]. However, the FIM obtained in (32) is not diagonal, indicating that the different parameters are involved in one another’s FIM, which degrades the resulting estimation performance.

Figures 4, 5 and 6 delve into the impact of the carrier frequency \(\mathrm {F_c}\) on the obtained results, due to the dependency of the discussed MLE and CRB on such parameter (32). In addition, they include \(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\) for comparison with the standard CSM (8). Such figures highlight the following relationship: lower values of \(\mathrm {F_c}\) degrade the time-delay estimation performance while allowing an earlier convergence of the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) to the \(\textrm{CRB}_{\tau | \varvec{\eta }}\). This can be clearly seen, for instance in Fig. 4, where it is observed that, for \(\mathrm {F_s}= 1\), the higher the value selected for \(\mathrm {F_c}\), the smaller the MSE error defined by the CRB. This reduction in the resulting MSE seems to come at the cost of shifting the convergence point to higher values of SNR. This pattern is also observed in Figs. 5 and 6. A numeric comparison supporting this discussion is provided in Tables 1 and 2. Table 1 shows that \(\textrm{CRB}_{\tau | \varvec{\eta }}\) is shifted farther down from \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\) towards lower MSE levels as the value selected for \(\mathrm {F_c}\) increases. The opposite happens when \(\mathrm {F_s}\) is increased. In contrast, Table 2 shows that the same adjustments in \(\mathrm {F_c}\) and \(\mathrm {F_s}\) that lower the MSE levels of \(\textrm{CRB}_{\tau | \varvec{\eta }}\), yield an increase in the \(\textrm{SNR}_{\textrm{out}}\) required for \(\textrm{MLE}_{\tau | \varvec{\eta }}\) to attain \(\textrm{CRB}_{\tau | \varvec{\eta }}\). Figures 4, 5 and 6 together with Tables 1 and 2 prove that the impact of modifying \(\mathrm {F_c}\) and \(\mathrm {F_s}\) have an inverse effect on the lowest MSE attained by the \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and the \(\textrm{SNR}_{\textrm{out}}\) required by the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) to attain \(\textrm{CRB}_{\tau | \varvec{\eta }}\). In addition, such observed impact suggests that \(\mathrm {F_c}\) and \(\mathrm {F_s}\) could constitute system design variables to be modified to attain specific performance metrics for practical applications.

Table 1 This table collects the improvement in the MSE [dB] of \(\textrm{CRB}_{\tau | \varvec{\eta }}\) with respect to \(\textrm{CRB}^m_{\tau | \varvec{\eta }}\), for multiples of \(\mathrm {F_s}\) (9), and \(\mathrm {F_c}\) in MHz
Full size table
Table 2 Similarly to Table 1, this table shows the \(\textrm{SNR}_{\textrm{out}}\) for which \(\textrm{MLE}_{\tau | \varvec{\eta }}\) converges to the different \(\textrm{CRB}_{\tau | \varvec{\eta }}\)
Full size table

Figure 7, shows the convergence of \(\textrm{MLE}_{b| \varvec{\tau }}\) for different values of \(\mathrm {F_c}\) to the associated \(\textrm{CRB}_{b | \varvec{\eta }}\). These results validate the derivations from Sect. 4 for the case of the Doppler-frequency parameter.

Figure 8 leverages a larger SNR range to show five distinct operational regions denoting the behavior of the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) for \(\mathrm {F_c}=1540 \, \textrm{MHz}\) and \(\mathrm {F_s}=1\). The first region corresponds to SNR values too low to provide discernible trends in the behavior of \(\textrm{MLE}_{\tau | \varvec{\eta }}\). The second region shows the SNR range where \(\textrm{MLE}_{\tau | \varvec{\eta }}\) starts to converge towards the \(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\). Once this convergence occurs, the \(\textrm{MLE}_{\tau | \varvec{\eta }}\) remains in a third region where its MSE aligns with \(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\). Subsequently, the MSE decreases again in the fourth region, aiming to reach the level defined by \(\textrm{CRB}_{\tau | \varvec{\eta }}\). The second convergence, marking the fifth region, showcases consistent MSE levels for subsequent SNR levels.

Fig. 1
figure 1

\(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \eta }\) and \(\textrm{MLE}_\tau\) for \(\mathrm {F_c} = 1540\) MHz, and \({\textrm{F}}_{\textrm{s}} = [1, 2, 5 ]\)

Full size image
Fig. 2
figure 2

Normalized ambiguity function (51)

Full size image
Fig. 3
figure 3

\(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \varvec{\eta }}\) \(\textrm{CRB}_{\tau }\) and \(\textrm{MLE}_{\tau }\) for Fs = 1

Full size image
Fig. 4
figure 4

\(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \eta }\), \(\textrm{CRB}_{\tau }\) and \(\textrm{MLE}_\tau\) for \(\mathrm {F_s} = 1\) and \(\mathrm {F_c} ( \textrm{MHz}) = [1540, 770, 385 ]\)

Full size image
Fig. 5
figure 5

\(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \eta }\) and \(\textrm{CRB}_{\tau | \varvec{\eta }}\) for \(\mathrm {F_s} = 2\) and \(\mathrm {F_c} ( \textrm{MHz}) = [1540, 770, 385 ]\)

Full size image
Fig. 6
figure 6

\(\textrm{CRB}^m_{\tau \vert \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and \(\textrm{MLE}_{\tau | \varvec{\eta }}\) for \(\mathrm {F_s}=5\) and \(\mathrm {F_c} ( \textrm{MHz}) = [1540, 770, 385 ]\)

Full size image
Fig. 7
figure 7

\(\textrm{CRB}_{b | \varvec{\eta }}\) and \(\textrm{MLE}_{b | \varvec{\eta }}\) for \(\mathrm {F_s} = 1\) and \(\mathrm {F_c} ( \textrm{MHz}) = [1540, 770, 385 ]\)

Full size image
Fig. 8
figure 8

\(\textrm{CRB}^m_{\tau | \varvec{\eta }}\), \(\textrm{CRB}_{\tau | \varvec{\eta }}\) and the five regions of operation of \(\textrm{MLE}_{\tau | \varvec{\eta }}\), for \(\mathrm {F_s}=1\) and \(\mathrm {F_c}=1540 \, \textrm{MHz}\)

Full size image

8 Conclusions

This study evaluated the estimation performance of a signal model that can significantly improve the accuracy of applications requiring higher levels of precision. For example, consider a receiver moving through a predefined set of way-points that can periodically measure specific terms of the received signal’s carrier phase at each way-point. This information can then be used to enhance the accuracy of time delay and Doppler estimation, as shown in this manuscript. This performance assessment was conducted parting from the signal model presented in Sect. 2. Then, two novel expressions for the associated MLE and CRB were derived in Sects. 3 and 4, respectively. Both contributions are key to not only understand the behavior of time-delay and Doppler estimators, but also to provide and idea of the optimal performance. The ambiguity function was provided in Sect. 5, which is also useful for characterizing the performance of time delay and Doppler estimators. In the conducted simulations, several critical insights were revealed, shaping the understanding of the estimation process. The first notable observation involved the validation of derived CRB and MLE expressions. This validation was substantiated by the convergence of MLE’s MSE to the CRB, affirming the accuracy of these expressions and establishing a robust foundation for subsequent analyses. A significant finding emerged regarding the impact of Doppler effect compensation on time-delay estimation accuracy within the general signal model. The absence of compensation led to a discernible decline in accuracy due to the observed coupling between time-delay and Doppler on the CRB. Furthermore, the balance between carrier frequency \(\mathrm {F_c}\) and sampling frequency \(\mathrm {F_s}\) played a pivotal role in influencing the convergence behavior of MLE to the CRB. Higher values of \(\mathrm {F_s}\) led to earlier convergence. Such convergence could be shifted to even lower SNR values by reducing the value selected for \(\mathrm {F_c}\); however, that worsened the MSE level attained by the CRB. This observation highlighted that the relationship between these frequencies can be crucial for optimizing estimation performance during system design stages in practical applications. A comprehensive analysis of the ambiguity function concerning \(\mathrm {F_c}\) and \(\mathrm {F_s}\) unveiled intricate trade-offs. Higher \(\mathrm {F_s}\) yielded a narrower baseband ambiguity function, enhancing accuracy in time-delay estimation. Conversely, raising \(\mathrm {F_c}\) narrowed the lobes in the carrier ambiguity function, decreasing the achievable MSE, however at the cost of requiring more energy to remain in the main lobe. Unlike previous studies that identified three regions of operation for the MLE, the present work highlighted five distinct regions. From a broader perspective, the specific CSM considered here is representative of a class of nonlinear problems in which the likelihood function displays numerous ambiguities that are closely spaced. Thus, the present work suggests the presence of five distinct regions for the MLE within this class. Last but not least, from a practical perspective, this study equips us with the necessary tools to evaluate the advantages of compensating for transmission phase when conducting delay and Doppler estimation.