1 Introduction

The space-air-ground integrated IoT is the integration network of interconnected devices, sensors and systems that can communicate and share data seamlessly across different dimensions, including space, air and ground [1, 2]. Relying on the long-endurance advantage of aerial platforms, drones, balloons and other air-based infrastructure, aerial network provides low-cost and wide-area coverage capability for 5 G and beyond (B5G/6 G) [3,4,5] with the massive deployment of high-performance computing devices in aerial platforms and the widespread application of air-to-ground communication (ATG) for B5G/6 G network and non-terrestrial networking (NTN) technology, and gradually forms informative and intelligent air-ground integrated ubiquitous network system [6, 7]. Constructing an cloud-edge collaborative computing model of air-ground integrated networks, orchestrating and controlling computing-storage-communication-perception resources to provide ubiquitous real-time service support for explosive growth of emerging services, such as holographic communication, extended reality, haptics, telemedicine and health monitoring.

However, with the booming development of B5G/6 G and the continuous influx of various emerging services, the heterogeneous ground terminals with limited capacity are finding it tough to meet the demand for high reliability and ultra-low latency services. The imbalance in the spatial and temporal distribution of computing, storage, communication and other system resources leads to inefficient task scheduling in the ground network, which makes it cumbersome to adapt accurately to varying task requirements [8]. In addition, the computational decision is subject to multiple constraints such as device computational capacity, available communication resources and channel selection, making it difficult to satisfy both latency and power requirements simultaneously [9].

To solve the above problems, the scholars in the field proposed to use aerial network-assisted communication-computation to alleviate the pressure of ground terminals [10, 11]. Heuristic and group intelligence methods achieve group offloading optimization by randomly or strategically changing individual behaviours, which have slow convergence speeds and are prone to falling into local optima [12]. Machine learning- and deep learning-based methods rely on a large amount of data for training and autonomous learning to obtain optimal offloading decisions [9, 13, 14]. These methods require the design of complex network models with high algorithmic complexity [15, 16]. Game-based methods [17, 18] simulate the offloading process by analysing the resource competition between devices to solve the optimal offloading decision. Its complexity is closely related to the amount of tasks.

Aiming at the problem of cloud-edge collaborative computing of air-ground integrated networks, this paper proposes a distributed computing offloading and resource allocation (DCORA) optimization scheme based on distributed gaming. The main contributions of this paper are as follows.

  1. 1.

    We construct an cloud-edge collaborative computing model. With the goal of minimizing task processing latency and energy consumption, an offloading decision objective function (ODOF) is constructed. The ODOF is proved to be a mixed inferior nonlinear programming problem (MINLP), it is hard to solve because of its nonlinear and non-convex nature. ODOF is converted to be a full potential game, and the Nash equilibrium solution exists.

  2. 2.

    The resource allocation subproblem is proven to be a convex optimization problem under specified available resources and task states. The resource allocation problem is converted into an unconstrained problem using Lagrange number multipliers. A Karush–Kuhn–Tucker (KKT) condition-based computational resource allocation (KCRA) algorithm is proposed to solve it. On this basis, DCORA algorithm is proposed to minimize the offloading cost by jointly optimizing the offloading mode selection, channel selection and offloading object selection.

  3. 3.

    Numerous simulation results show that DCORA has a fast convergence speed and can effectively reduce the task offloading delay and energy consumption. DCORA obtains minimum offload costs with changes in the number of channels, bandwidth, amount of task data and number of tasks. Compared with the traditional schemes, the convergence performance of DCORA is reduced by about 50%, the convergence time is shortened by about 13.3% and the average task processing delay is reduced by 10%.

The rest of the paper is organized as follows: In Sect. 2, related work is presented. In Sect. 3, the cloud-edge collaborative computing model and the objective problem are presented. In Sect. 4, the KCRA algorithm and the DCORA algorithm are described in detail. Finally, we conduct simulation experiments and results analysis in Sect. 5, and conclusions are drawn in Sect. 6.

2 Related work

This subsection provides an introduction to mainstream computational offloading algorithm research efforts, including heuristic and swarm intelligence methods, machine learning (ML) and deep learning (DL) approaches and game-based strategies.

Swarm intelligence algorithms are stochastic algorithms inspired by biological or physical phenomena, where individuals continuously modify their actions to achieve collective optimization of the population. These algorithms have been widely used to address multi-objective optimization problems, such as computation offloading and resource allocation. Lv et al. [19] proposed an approach based on heuristic algorithms to predict the impact of offloading decisions. Ali et al. [20] introduced an optimization model based on discrete non-dominated sorting genetic algorithm to handle discrete multi-objective task scheduling problems. Dai et al. [21] proposed an optimization method based on particle swarm optimization by splitting tasks for offloading. Dong et al. [22] combined particle swarm optimization and quantum particle swarm optimization to propose a computation offloading task strategy and validated its effectiveness. Yuan et al. [23] established a fine-grained task offloading model, proposing a task prediction algorithm based on the long short-term memory neural network model and an online offloading algorithm based on particle swarm optimization. When the number of offloading tasks is small, swarm intelligence algorithms exhibit higher complexity. However, with a larger number of tasks, swarm intelligence algorithm often encounters challenges such as prolonged convergence time and being trapped in local optima.

Computation offloading methods based on ML or DL, with neural networks at their core, rely on extensive data for training and autonomous learning, can address various complex environments. Yang et al. [24] devised a collaborative offloading and resource allocation scheme based on energy prediction, optimizing transmission power, computing resource allocation and task offloading ratios. Liu et al. [25] proposed a distributed optimization problem for offloading parameters and designed strategies for task offloading and energy conservation response. Gao et al. [26] presented a multi-tier fog computing system that predicts offloading and resource allocation, reducing average power consumption. Dai et al. [27, 28] employed Lyapunov optimization to transform stochastic problems into deterministic ones for each time slot, using an asynchronous behaviour critic algorithm to find the optimal offloading strategy. Liu et al. [29] constructed a mathematical optimization model for power consumption and time overhead, proposing intelligent task offloading solutions, enhancing system network performance through decision tree algorithms and double-depth algorithms. Qu et al. [30] combined multiple parallel deep neural networks with Q-learning to derive optimal offloading strategies from dynamic environments. However, methods based on ML or DL currently face challenges such as slow learning speed, weak adaptability to new environments and reliance on prior data for training.

Yu et al. [31] proposed a mixed-strategy Nash equilibrium (NE) based on virtual game theory, decomposing the offloading decision problem of the entire system into a hierarchical game problem. Xu et al. [32] designed a fuzzy task offloading and resource allocation scheme based on Takagi–Sugeno fuzzy neural networks and game theory to minimize user task processing latency. Wang et al. [33] introduced a resource allocation incentive mechanism based on Stackelberg game and devised an optimization strategy using the alternating direction method of multipliers. Pham et al. [34] utilized precise potential game theory to design a low-complexity distributed offloading scheme and determined the optimal offloading ratio and resource allocation using the subgradient method. Luo et al. [35] proposed a distributed offloading decision algorithm based on game theory models, achieving Nash equilibrium through self-learning to minimize offloading latency and cost. Huang et al. [36] addressed the latency optimization offloading problem using non-cooperative game theory and provided a solution. Teymoori et al. [37] described the offloading decision process as a stochastic game model to minimize mutual interference during channel access, solving for Nash equilibrium based on multi-agent reinforcement learning. Mensah et al. [38] combined device-to-device (D2D) communication with vehicular networks, formulating the task offloading and resource allocation problem as a mixed-strategy game and solving for Nash equilibrium. Yang et al. [39] regarded the computation offloading process as a competitive game to minimize the cost of executing a single task, proposing a lightweight algorithm to solve for Nash equilibrium. Fan et al. [40] presented an offloading scheme based on non-cooperative game theory to alleviate node load, balance task delays and demonstrated the existence of Nash equilibrium using variational inequalities and regularization techniques. Pham et al. [41], based on coalition game theory, studied a low-complexity algorithm that guarantees convergence, compared it with three baseline schemes and verified its effectiveness.

Compared to methods based on swarm intelligence, ML or DL, game-based approaches are more suitable for distributed computing due to their lower complexity and faster convergence. Therefore, this paper proposes a distributed game-based computation offloading optimization method to address the problem more efficiently.

3 System model

3.1 Cloud-edge collaborative computing model

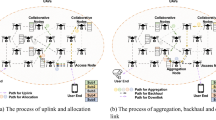
The air-ground integrated IoT network model is shown in Fig. 1, and it includes a ground network, a low-altitude network and a high-altitude network. The ground network consists of emergency communication vehicles, IoT devices, base stations, intelligent robots and other devices. The low-altitude part of the network consists of UAV swarms and fixed-wing UAV. The fixed-wing UAV with the strongest computational capacity is called distributed computing node (DCN). Since small UAVs have limited computing and communication capabilities, the fixed-wing UAV is provided to support the UAV swarm. The high-altitude network consists of floating airships with deployed mobile edge computing (MEC).

The cloud consists of floating airships with deployed mobile edge computing (MEC), and edge consists of UAVs and fixed-wing UAV. The UAV swarms in the low-altitude network will assist the ground equipment with computing tasks. The UAVs are divided into two disjoint sets based on their current operational status. UAVs with computing tasks are referred to as active devices, denoted by set \({\mathcal {N}}=\left\{ 1,2,\ldots ,N\right\}\). UAVs without computing tasks are referred to as auxiliary devices, denoted by set \({\mathcal {H}}=\left\{ 1,2,\ldots ,H\right\}\). The DCN establishes a D2D link and jointly computes with the devices in \({\mathcal {H}}\). It will help the UAV terminal to generate offload decisions and perform mission computation. If the UAV is not connected to the DCN, and the UAV is within the communication range of the aerial platform. The aerial platform in the high-altitude segment will take over some of the computing tasks from the UAV according to the offload strategy. The available bandwidth B is divided into \(K_{d+e}\) mutually orthogonal subcarriers, including \(K_d\) for D2D communication and \(K_e\) for cellular communication, which can be represented as follows: \({\mathcal {K}}=\left\{ 1,2,\ldots ,K_d,K_{d+1},\ldots ,K_{d+e}\right\}\).

Fig. 1
figure 1

The cloud-edge collaborative computing model

Full size image

The state information of computing task \(n\in {\mathcal {N}}\) can be described by set \(\Lambda _n=\left\{ s_n,c_n\right\}\). \(s_n\) is the data size of the task and measured in bits. \(c_n\) is the required computing resource to compute one bit of the task and measured in CPU cycles per bit. We use a binary offloading policy for offloading tasks that are offloaded completely without task segmentation. The offloading mode variate \(x_{n,m}\) represents whether the task n is offloaded to the destination m, where \(x_{n,m}\in \left\{ 0,1\right\}\), \(m\in {\mathcal {H}}\cup \left\{ 0\right\}\) represents the offloading destination of the device n, 0 is the edge server identity. In the three different offloading modes, the practical significance of \(x_{n,m}\) is expressed as follows:

  1. 1.

    When \(x_{n,m}=1,m=n\), it means that task n executes locally.

  2. 2.

    When \(x_{n,m}=1,m\in {\mathcal {N}}\), it means that the task n is offloaded to DCNs for execution via the D2D link.

  3. 3.

    When \(x_{n,m}=1,m=0\), it means that the task n is offloaded to MEC for execution via the cellular link.

3.2 Delay and energy model

(1) Local computing model When the task n is executed locally, the task does not require transmission, so the offloading cost only includes the computation delay \(t^{loc,cmp}_n\) and energy consumption \(e^{loc,cmp}_n\).

$$\begin{aligned} t^{loc,cmp}_n=\frac{s_nc_n}{f_n} \end{aligned}$$
(1)
$$\begin{aligned} e^{loc,cmp}_n=\kappa _nc_nf_n^2 \end{aligned}$$
(2)

Where \(f_n\) is the number of CPU cycles per second of terminal n, which represents its computing power. \(\kappa _n\) denotes the effective switching capacity of terminal n, and its value is a constant term. In order to prolong the usage time of the terminal device and consider the energy consumption and delay during the task completion process, we sets the local offloading cost function is \(v_n^{loc}\).

$$\begin{aligned} v_n^{loc}=\beta _tt_n^{loc,cmp}+\beta _ee_n^{loc,cmp} \end{aligned}$$
(3)

Where \(\beta _t,\beta _e\in [0,1]\) and \(\beta _t+\beta _e=1\) are weight constants. \(\beta _t\) denotes the weight of delay in the completion of task, and \(\beta _e\) denotes weight of the energy consumption of device.

(2) D2D offloading When task n is offloaded to DCNs via D2D link, the uplink transmission rate \(r_{n,h}\) can be found in Eq. 4.

$$\begin{aligned} r_{n,h}={\bar{B}}log_2\left(1+\frac{x_{n,h}w_{n,h}^kp_nh_{n,h}^k}{N_0+\sum _{i=1}^Nx_{i,h}w_{i,h}^kp_ih_{i,h}^k}\right) \end{aligned}$$
(4)

Where \({\bar{B}}=B/k_{d+e}\) is the sub-carrier bandwidth. \(k\in \left\{ 1,2,\ldots ,K_d\right\}\) represents the exclusive channel of D2D communication mode. A value of 1 for the binary variable \(w_{n,h}^k=\left\{ 0,1\right\}\) means that the channel k is selected when the task n is offloaded to the destination h, and \(h\in {\mathcal {H}}\). \(p_n\) denotes the transmission power of the device. \(h_{n,h}^k\) represents the channel gain during D2D transmission, the value is related to the transmission distance and the maximum D2D transmission distance is \(d_{max}\). \(N_0\) is the noise power within each sub-channel. For efficient use of spectrum resource, devices in the same transmission mode can be allowed to be reused in the sub-channels during communication, \(\sum _{i=1}^Nx_{i,h}w_{i,h}^kp_ih_{i,h}^k\) denotes interference between D2D links due to spectral reuse.

Therefore, the computation delay \(t_n^{d2d,cmp}\) in D2D offloading mode can be found in Eq. 5.

$$\begin{aligned} t^{d2d,cmp}_n=\frac{s_nc_n}{f_{n,h}} \end{aligned}$$
(5)

Where \(f_{n,h}\) represents the computing resource that can be allocated when the task n is offloaded to the DCN m. The delay and energy consumption during transmission can be expressed as \(t_n^{d2d,trans}\) and \(e_n^{d2d,trans}\), respectively.

$$\begin{aligned} t_n^{d2d,trans}=\frac{s_n}{r_{n,h}} \end{aligned}$$
(6)
$$\begin{aligned} e_n^{d2d,trans}=p_nt_n^{d2d,trans} \end{aligned}$$
(7)

Considering that the offloading result response signal data size is much less than the task data size, the result backhaul delay is ignored. Therefore, the D2D offloading cost function \(v_n^{d2d}\) is defined as the weighted sum of computing delay, transmission delay and transmission energy consumption.

$$\begin{aligned} v_n^{d2d}=\beta _t(t_n^{d2d,cmp}+t_n^{d2d,trans})+\beta _ee_n^{d2d,trans} \end{aligned}$$
(8)

(3) Edge offloading When task n is offloaded to MEC via cellular link, the uplink transmission rate \(r_{n,0}\) can be defined as Eq. 9.

$$\begin{aligned} r_{n,0}={\bar{B}}log_2\left(1+\frac{x_{n,0}w_{n,0}^kp_nh_{n,0}^k}{N_0+\sum _{i=1}^Nx_{i,0}w_{i,0}^kp_ih_{i,0}^k}\right) \end{aligned}$$
(9)

Where \(k\in \left\{ k_{d+1},\ldots ,K_{d+e}\right\}\) represents the exclusive channel of cellular communication mode. The binary variable \(w_{n,0}^k=\left\{ 0,1\right\}\) value of 1 indicates that the channel k is selected when the task n is offloaded to MEC. \(h_{i,0}^k\) represents the channel gain during cellular transmission. Devices in the same transmission mode are also allowed to be reused to sub-channels during communication, \(\sum _{i=1}^Nx_{i,0}w_{i,0}^kp_ih_{i,0}^k\) represents interference due to spectral reuse between cellular links.

From the previous discussion, the task computation delay \(t_n^{mec,cmp}\) can be found in Eq. 10.

$$\begin{aligned} t^{mec,cmp}_n=\frac{s_nc_n}{f_{n,0}} \end{aligned}$$
(10)

Where \(f_{n,0}\) represents the computing resource allocated when the task n is offloaded to MEC. The delay of the task transmission process and energy consumption can be expressed as \(t_n^{mec,trans}\) and \(e_n^{mec,trans}\), respectively.

$$\begin{aligned} t_n^{mec,trans}=\frac{s_n}{r_{n,0}} \end{aligned}$$
(11)
$$\begin{aligned} e_n^{mec,trans}=p_nt_n^{mec,trans} \end{aligned}$$
(12)

In summary, the MEC offloading cost function can be expressed as \(v_n^{mec}\).

$$\begin{aligned} v_n^{mec}=\beta _t(t_n^{mec,cmp}+t_n^{mec,trans})+\beta _ee_n^{mec,trans} \end{aligned}$$
(13)

(4) Problem formulation Compared with the edge computing model, D2D offloading can ensure shorter communication delay to reduce the upstream network transmission pressure. On the other hand, an edge server can provide a significant amount of computational resources. The aim of our work is to realize the target problem joint optimization and minimize the global task offloading cost through the offloading mode, offloading destination selection, channel selection and computing resource allocation. The current moment task n cost function and global target optimization function \(\textbf{P1}\) can be found in Eqs. 14 and 15, respectively.

$$\begin{aligned} v_n=x_{n,0}v_n^{mec}+x_{n,h}v_n^{d2d}+x_{n,n}v_n^{loc} \end{aligned}$$
(14)
$$\begin{aligned} \mathbf {P1:}&\min _{a_n}\sum _{n=1}^Nv_n \nonumber \\ s.t. \quad&C1:x_{n,m}\in \left\{ 0,1\right\} \nonumber \\&C2: x_{n,0}+x_{n,h}+x_{n,n}=1 \nonumber \\&C3: 0\le f_{n,0} \le f_{0} \\&C4: 0\le f_{n,h}\le f_h \nonumber \\&C5: 0\le \sum _{n=1}^Nx_{n,0}f_0=f_0 \nonumber \\&C6: 0\le \sum _{n=1}^Nx_{n,h}f_h=f_h \nonumber \\&C7: \beta _t,\beta _e\in [0,1], \beta _t+\beta _e=1 \nonumber \end{aligned}$$
(15)

Where \(a_n=\left\{ x_{n,m},w_{n,m}^k,f_{n,0},f_{n,h}\right\}\) is the set of variables to be optimized. C1 states that the offload mode decision is a binary value and each task must and can choose only one offload mode. C2 and C3 indicate that the computational resources allocated to the tasks when offloading to the MEC and DCN must be within the maximum constraint. C4 and C5 indicate that all tasks offloaded to the MEC and DCN together occupy the entire computational resources. C6 specifies the range of value for the weights of the cost function.

(5) Game theory analysis The objective optimization problem can be described as a multi-knapsack problem. The multi-knapsack problem refers to the task of skillfully selecting a subset of items from a finite set, each with specific weights or profits, and efficiently placing them into a limited capacity knapsack. The objective is to maximize or minimize the total weight or total profit of the items loaded into the knapsack [42]. Specifically, limited computing tasks n are equivalent to items, the offloading destination m is the backpack, total profit is the weighted sum of delay and energy consumption. The target problem is the reasonable decision action \(a_n=\left\{ x_{n,m},w_{n,m}^k,f_{n,0},f_{n,h}\right\}\) to minimize the total profit of the backpack. The multi-knapsack problem has been widely shown to be an NP-hard problem [43]. Since the decision variables \(\left\{ x_{n,m},w_{n,m}^k\right\}\) are discrete variables, \(\left\{ f_{n,0},f_{n,h}\right\}\) are continuous values in a finite interval, and the objective function has its nonlinear properties. Thus, the problem \(\textbf{P1}\) is a mixed integer nonlinear programming (MINLP). In order to solve this problem, a distributed computation offloading and resource allocation scheme is formulated.

Game theory is a mathematical method for analysing decision problems. When there is a competition for a certain resource among multiple participants, the decisions between participants often influence each other. Game theory studies the decision process of participants through the influence relationship [36].

During the game process, all devices share global resource and state information. The goal of the decision is to continuously minimize the offloading cost function, in order to obtain the optimal offloading experience. The game can be expressed as follows: \(G=<\mathcal {N,{\mathcal {A}},{\mathcal {U}}}>\). \({\mathcal {N}}\) is a set of players as well as a set of tasks. \({\mathcal {A}}=\left\{ d_n|n\in {\mathcal {N}} \right\}\) is the set of actions that the player n can select. \(d_n=\left\{ x_{n,m},w_{n,m}^k\right\}\) represents the action decision made by player n regarding the selection of the offloading destination and channel. \({\mathcal {U}}=\left\{ u_n(d_n,d_{-n})|n\in {\mathcal {N}}\right\}\) represents the player’s utility function value under the current action. The utility function is set to Eq. 16, each player takes action targeting lowering the cost of global offloading.

$$\begin{aligned} u_n(d_n,{d_{-n}})=v_n(d_n,{d_{-n}})+\sum _{i\ne n}[v_i(d_i,d_{-i})-v_i(d_i,d_{-i\setminus n})] \end{aligned}$$
(16)

Where \(d_{-n}\) is the vector of the other player’s current actions. \(v_i(d_i,d_{-i\setminus n})\) represents the utility function value of player i when player n gives up switching action. \(\sum _{i\ne n}[v_i(d_i,d_{-i})-v_i(d_i,d_{-i\setminus n})\) illustrates the sum of the value of the other player utility function that changes when the player n switches its action. Each player takes action \(d_n^*\) based on the action combination \(d_{-n}^*\) chosen by the other players. Game G reaches a Nash equilibrium when Eq. 17 is satisfied [33].

$$\begin{aligned} u_n(d_n^*,d_{-n}^*)\le u_n(d_n,d_{-n}^*) \qquad \forall n\in {\mathcal {N}}, \forall d_n\in {\mathcal {A}} \end{aligned}$$
(17)

Where \({d}_{-{\varvec{n}}}^*=\left( d_1^*, \ldots , d_{n-1}^*, d_{n+1}^*, \ldots , d_N^*\right)\). Each player has already chosen their optimal action. Furthermore, it is important to note that no player will alter their decision. Specifically, any player who chooses an action other than \(d_n^*\) will not be able to achieve a lower utility value.As a result, the current set of actions represents the global optimum.

Definition

If a game has a potential function \(P_n(d_n,d_{-n})\) such that Eq. 18 holds for all \(\forall n\in {\mathcal {N}}, \forall d_n\in {\mathcal {A}}\), then the game is referred to as a completely potential game [34].

$$\begin{aligned} u_n(\bar{d_n},d_{-n})-u_n(d_n,d_{-n})=P_n(\bar{d_n},d_{-n})-P_n(d_n,d_{-n}) \end{aligned}$$
(18)

Completely potential games are a specific type of game. What sets them apart from ordinary games is that when a player unilaterally changes their own action, the potential function accurately reflects changes in the player’s utility function.

Proof

\(G=<\mathcal {N,{\mathcal {A}},{\mathcal {U}}}>\) is a completely potential game.

$$\begin{aligned} u_n(\overline{d_n},&d_{-n})-u_n(d_n,d_{-n}) \nonumber \\&=v_n(\overline{d_n},d_{-n})+\sum _{i\ne n}[v_i(d_i,\overline{d_{-i}})-v_i(d_i,\overline{d_{-i\setminus n}})] \nonumber \\&\qquad - v_n(d_n,d_{-n})+\big \{\sum _{i\ne n}[v_i(d_i,d_{-i})-v_i(d_i,d_{-i\setminus n})] \big \} \nonumber \\&=v_n(\overline{d_n},d_{-n})-v_n(d_n,d_{-n})+\sum _{i\ne n}[v_i(d_i,\overline{d_{-i}}) \nonumber \\&\qquad -v_i(d_i,d_{-i})]-\sum _{i\ne n}[v_i(d_i,\overline{d_{-i\setminus n}})-v_i(d_i,d_{-i\setminus n})] \nonumber \\&=v_n(\overline{d_n},d_{-n})-v_n(d_n,d_{-n}) \nonumber \\&\qquad +\sum _{i\ne n}[v_i(d_i,\overline{d_{-i}})-v_i(d_i,d_{-i})] \nonumber \\&=\sum _{i=1}^N[v_i(\overline{d_i},d_{-i})-v_i(d_i,d_{-i})] \nonumber \\&=\sum _{i=1}^Nv_i(\overline{d_i},d_{-i})-\sum _{i=1}^Nv_i(d_i,d_{-i}) \nonumber \\&=P_n(\overline{d_n},d_{-n})-P_n(d_n,d_{-n}) \end{aligned}$$
(19)

The player’s switch action from \(d_n\) to \(\bar{d_n}\) will cause a change in the utility value of other players. But when the player n gives up switching decision and other users maintain their decision, the other players’ function utility value remains the same \(v_{i}(d_{i},\overline{d_{-i{\setminus } n}})=v_i(d_i,d_{-i{\setminus } n})\). Consequently, during each iteration, there is always a potential function \(P_n(d_n,d{-n})=\sum _{i=1}^Nv_i(d_i,d_{-i})\) regardless of how the player’s n action changes.

Theorem 1

All potential games with finite action spaces must have a Nash equilibrium.

It is easy to verify that action space \({\mathcal {A}}=\left\{ d_n|n\in {\mathcal {N}} \right\}\) is finitely closed set. In conclusion, the game \(G=<\mathcal {N,{\mathcal {A}},{\mathcal {U}}}>\) is a completely potential game whose Nash equilibrium is always exist.

4 Distributed computation offloading and resource allocation scheme

4.1 Computing resource allocation problem analysis

In the context of computational offloading, UAVs, MEC and DCNs serve as auxiliary nodes. When computational resources are allocated to MEC, assuming that the set of I tasks unloaded to MEC for calculation is \(I_0\), and the channel selection is fixed. The computing resource assigned to each computation task can be defined as \(\left\{ f_i|i\in I_0 \right\}\). Therefore, the subproblem function associated to computing resource allocation in problem \(\textbf{P1}\) can be converted to \(\textbf{P2}\).

$$\begin{aligned} \mathbf {P2:} \min _{f_i}&F(f_i)=\min _{f_i}\sum _{i\in I_0}\frac{s_ic_i}{f_i} \nonumber \\ s.t. \quad&C1:0\le f_i\le f_0 \nonumber \\&C2: \sum _{i\in I_0}f_i=f_0 \end{aligned}$$
(20)

Theorem 2

\(F(f_i)\) is a strictly convex function.

The Hessian matrix of the target problem \(\textbf{P2}\) can be calculated by Eq. 21.

$$\begin{aligned} \textrm{H}=\left[ \begin{array}{ccc} \frac{\partial ^2 \mathrm {~F}\left( \textrm{f}_1\right) }{\partial \left( \textrm{f}_1\right) ^2} &{} \cdots &{} \frac{\partial ^2 \mathrm {~F}\left( \textrm{f}_1\right) }{\partial \left( \textrm{f}_1\right) \partial \left( \textrm{f}_{\textrm{I}}\right) } \\ \vdots &{} \ddots &{} \vdots \\ \frac{\partial ^2 \mathrm {~F}\left( \textrm{f}_{\textrm{I}}\right) }{\partial \left( \textrm{f}_{\textrm{I}}\right) \partial \left( \textrm{f}_1\right) } &{} \cdots &{} \frac{\partial ^2 \mathrm {~F}\left( \textrm{f}_{\textrm{I}}\right) }{\partial \left( \textrm{f}_{\textrm{I}}\right) ^2} \end{array}\right] \end{aligned}$$
(21)

The second-order derivatives and mixed partial derivatives of \(F(f_i)\) are given as follows:

$$\begin{aligned} \frac{\partial ^2 F(f_i)}{\partial (f_i)^2}=\frac{2s_ic_i}{f_i^3} \qquad \forall i\in I_0 \end{aligned}$$
(22)
$$\begin{aligned} \frac{\partial ^2 F(f_i)}{\partial (f_i)\partial (f_j)}=0 \qquad \forall i\in I_0,i\ne j \end{aligned}$$
(23)

Thus, the eigenvalues of the Hessian matrix H are all greater than zero, which means that the Hessian matrix of the target problem \(\textbf{P2}\) is positive definite. Moreover, the \(\textbf{P2}\) is a strictly convex function. KKT conditions can transform the optimization problem of equality and inequality mixed constraints into an unconstrained problem, which is a necessary and sufficient condition to judge that a certain point of convex programming is an extreme point. Consequently, \(\textbf{P2}\) can be solved by the Lagrange multiplier method with the KKT condition. The Lagrangian is constructed as described in Eq. 24.

$$\begin{aligned} F(f_1,\ldots&,f_I,\lambda ,\mu _1,\ldots ,\mu _I) \nonumber \\&=\sum _{i\in I_0}\frac{s_ic_i}{f_i}+\lambda (\sum _{i\in I_0}f_i-f_0)+\sum _{i\in I_0}\mu _i(f_i-f_0) \end{aligned}$$
(24)

Where \(\lambda\) and \(\mu _1,\ldots ,\mu _I\) are non-negative Lagrange multiplier whose value changes with the iteration. The KKT condition can be calculated as follows:

$$\begin{aligned} -\frac{s_ic_i}{f_i^{2} }+\lambda +\mu _i=0 \end{aligned}$$
(25a)
$$\begin{aligned} \sum _{i\in I_0}f_i-f_0=0 \end{aligned}$$
(25b)
$$\begin{aligned} \mu _i(f_i-f_0)=0 \end{aligned}$$
(25c)

During each iteration, the Lagrange multipliers can be updated according to a specific step-size formula to gradually approach the optimal solution. The Lagrange multiplier must greater than zero and cannot be zero when used as a denominator. Therefore, when the multipliers take negative values, we update them to an infinitesimal value \(\varepsilon _1\). The update formula is as follows:

$$\begin{aligned} \lambda (t+1)&= \max \{\varepsilon _1, \lambda (t) + \delta _1(t)\sum _{i\in I_0}(f_i-f_0)\}\end{aligned}$$
(26a)
$$\begin{aligned} \mu _i(t+1)&= \max \{\varepsilon _1, \mu _i(t) + \delta _1(t)(f_i-f_0)\} \end{aligned}$$
(26b)

The resource allocated for each computation task can be expressed as follows: \(\left\{ f_i|i\in I_h \right\}\). The KKT conditions and the update formula for the Lagrange multipliers are as follows:

$$\begin{aligned} -\frac{s_ic_i}{f_i^{2}}+\lambda +\mu _i=0 \end{aligned}$$
(27a)
$$\begin{aligned} \sum _{i\in I_h}f_i-f_h=0 \end{aligned}$$
(27b)
$$\begin{aligned} \mu _i(f_i-f_h)=0 \end{aligned}$$
(27c)
$$\begin{aligned} \lambda (t+1)&= \max \big \{\varepsilon _1, \lambda (t) + \delta _2(t)\sum _{i\in I_h}(f_i-f_h)\big \}\end{aligned}$$
(28a)
$$\begin{aligned} \mu _i(t+1)&= \max \big \{\varepsilon _1, \mu _i(t) + \delta _2(t)(f_i-f_h)\big \} \end{aligned}$$
(28b)

We propose a KKT-based resource allocation algorithm as shown in Algorithm 1 to solve the target problem \(\textbf{P2}\). Initially, the parameters are initialized, and then, the resource allocation decisions are computed based on the Lagrange multipliers. During the iterative process, we update the Lagrange multiplier values for the next iteration according to the step size. This process continues until the gap between the computed resources and node computing capacity is less than an infinitesimal value \(\varepsilon _2\).

Algorithm 1
figure a

KCRA algorithm.

Full size image

4.2 DCORA algorithm

The computation offloading based on distributed game algorithm is used to solve problem \(\textbf{P1}\). Specifically, we utilize the finite improvement property of games to progressively eliminate dominated strategies, seeking a global optimum that satisfies Nash equilibrium. The UAV and MEC engage in collaborative decision-making through multiple rounds of information sharing. This information exchange encompasses task status, global channel conditions and computational resource status. The information exchange process for each round of iteration in this algorithm is detailed below.

  1. (1)

    The UAV transmits the task status information and initial offloading decisions to the MEC as pilot signals.

  2. (2)

    MEC collects all task status information, decision information and resource status information as a feedback signal. Then, MEC broadcasts it to all UAV to support decision update.

  3. (3)

    The UAV receives the feedback information and decides whether to update the current decision according to Algorithm 2 and strive for renewal opportunities. To avoid redundant and ineffective computations, each device will exclude the decision made in the previous iteration from its available action space in each round of iteration.

  4. (4)

    MEC collects update applications. To avoid local optimum, MEC randomly selects one device from the updated device set for decision update. And it broadcasts information as described in (2).

Repeat the above steps until no device applies for update, the specific algorithm is shown below.

Algorithm 2
figure b

DCORA algorithm.

Full size image

During the running of our distributed offloading algorithm, each device parallel runs the algorithm 7–20 lines. The calculation complexity of the two cycles within the devices is \(O(a*b)\). Where a is the length of available destination decision set, which value is \(1+H\). Moreover, b is the length of available channel set, which value is \(K_{d+e}-1\). Obviously, the computation complexity of DCORA is of \(O(n^2)\). If the centralized decision-making is adopted, all devices offload the task information to the MEC. It makes the iterative decision, the corresponding computation complexity is \(O(a*b*n)\), which is of \(O(n^3)\).

5 Simulation and result analysis

5.1 Parameter setting

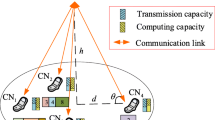
Consider a cellular network covering a range of \(200\times 200\) meters with \(N=20\) computation tasks and \(H=8\) MEC nodes. Each UAV can cover an area with a radius of 50m by D2D communication. Figure 2 illustrates a schematic diagram of the network topology. The channel number of cellular link and D2D link is \(K_d=3\) and \(K_e=4\), respectively. The total channel bandwidth is 35 MHz. Meanwhile, the channel gain is \(128.1+37.6log_{10}d_{n,m}\) and \(148.1+40log_{10}d_{n,m}\), respectively. Where \(d_{n,m}\) represents the distance between the UAV and the offloading destination. And the channel noise is \(N_0=10^{-10}\) mw. The task data size follows randomly distributed within [0.2, 2] Mbits. Furthermore, the calculation required number follows randomly distributed within [1500, 2000] cycle/bit. Table 1 lists the specific parameter [44,45,46].

Fig. 2
figure 2

Network topology simulation diagram

Full size image
Table 1 Parameter setting
Full size table

5.2 Simulation and result analysis

The proposed scheme is discussed in comparison with the following four offloading schemes:

  1. (1)

    Full local computing scheme.

  2. (2)

    Full edge offloading scheme. In this case, all tasks will be offloaded to the edge server. The scheme includes channel allocation and the computing resource allocation process based on KCRA algorithm.

  3. (3)

    Full random offloading scheme. In this scenario, the devices randomly select the offloading destination and channel, moreover allocate computing resource according to KCRA algorithm.

  4. (4)

    DMCTO scheme [42]. In this scheme, the tasks offloaded to the DCN will be allocated computational resources evenly. We take the average of multiple runs as the final result.

Figure 3a illustrates the impact of the number of iterations on the global offloading cost. As the number of iterations increases, the global cost for different task quantities shows a decreasing trend and converges to a stable value. The stable value corresponds to the Nash equilibrium solution, which is the optimal offloading decision. It can be observed that as the number of tasks N increases, the global offloading cost also increases. The reason is that as the number of terminal devices increases, more tasks need to be computed, resulting in higher total computation time and energy consumption. Therefore, the cost of offloading increases with the number of devices. Figure 3b depicts how the number of devices affects the number of iteration times. It can be seen that as the number of tasks increases, the iteration times for task convergence also increase. The reason for this is that the greater the number of devices, the greater the number of feasible solutions. This means that DCORA needs to perform more iterations to find the optimal or suboptimal solution from a large number of feasible solutions. In summary, as the number of iterations increases, the DCORA algorithm gradually reduces the global cost and slows down the convergence speed. Compared to the DMCTO algorithm, the convergence performance has improved by approximately 50\(\%\), and the convergence time has been reduced by approximately 13.3\(\%\).

Fig. 3
figure 3

a Relationship between iteration times and offloading cost with different tasks in DCORA and b relationship between the number of devices and iteration times in DCORA

Full size image

Figure 4 illustrates the impact of weights on average delay and energy consumption. With \(\beta\) increases, the average delay gradually reduced, while the average energy consumption gradually increases. As \(\beta\) varies from 0 to 1, the DCORA algorithm exhibits significantly lower average delay compared to the DMCTO algorithm. Thus, there is little difference in average energy consumption compared to the DMCTO algorithm. In summary, compared to the DMCTO algorithm, DCORA demonstrates superior performance in optimizing task processing delay. The reason for this phenomenon is that DCORA can achieve perfect matching between task volume and computing resources. However, when using DMCTO for task computing, there will be mismatch between task volume and computing resources, resulting in an increase in calculation delay. Since the total amount of computational tasks is the same, the energy consumption of DMCTO and DCORA is basically the same.

Fig. 4
figure 4

The average processing delay and energy consumption change under different weights

Full size image

Figure 5 represents the impact of data size on offloading cost. The change of data size will directly affect the change of delay and energy consumption. In order to highlight the impact of data size on offloading cost, we set the data volume for each computing task to be the same, with data sizes increasing from 1 Mbits to 4 Mbits. And the computing resource required for each task \(c_n\) is randomly distributed within the range set in Table 1. It can been seen that the DCORA scheme has the lowest offloading cost than other offloading schemes. This is because as the data volume increases, it allows UAV to choose appropriate strategies for data processing, effectively reducing task processing and energy consumption. With the increase in data volume, the advantages of the DCORA algorithm become more pronounced. Under high data volume scenarios, the feasibility and superiority of the DCORA algorithm can be demonstrated.

Fig. 5
figure 5

Offloading cost under different data size and offloading mode

Full size image

Figure 6 reflects the impact of the number of offloading tasks on offloading cost. As the number of tasks to be offloaded increases, both computational and transmission pressures also increase. Therefore, we compared the global offloading costs under different offloading modes as the number of tasks varied from 5 to 30. It can be observed that the global offloading cost increases with the number of tasks increasing. And the DCORA algorithm having the smallest increase. The DCORA algorithm gradually pulls ahead as the number of tasks increases compared to other offloading schemes. This is because, in a fixed number of channels, an increase in the number of tasks leads to a decrease in transmission rates for devices. Simultaneously, the increasing number of computational tasks results in increased task processing delays and energy consumption. Additionally, when the number of tasks exceeds 25, all-edge offloading costs exceed the random decision mechanism. Due to the increase in the number of tasks, MEC computational resources cannot support all tasks. Random decision offloads some tasks to DCNs, alleviating the computational pressure on MEC. In summary, DCNs can effectively share the computational load of MEC, and the DCORA algorithm can minimize offloading costs by efficiently allocating communication and computational resources.

Fig. 6
figure 6

Offloading cost under different number of tasks and offloading mode

Full size image

Figure 7a and b depicts the impact of available channel count on offloading cost. The number of available channels and bandwidth is important component elements of communication resource. The change of channel resource will affect the transmission interference and then affect the transmission rate and delay. Figure 7a shows the variation trend of offloading cost under different numbers of channels, with the sub-channel bandwidth is fixed at 5 MHz. With the increase in the number of channels available to the devices, except for the local computing scheme, the offloading cost of other schemes shows a downward trend. This is because when selecting the offloading scheme, the option with the least co-channel interference was chosen, reducing task transmission delay and energy consumption. Figure 7b shows the variation trend with the total channel bandwidth fixed. The offloading cost slightly increases under various offloading mechanisms. Although the number of channels increases, prudent channel decisions lead to reduced co-channel interference. The DCORA algorithm consistently maintains the lowest offloading cost under varying channel conditions, demonstrating the effectiveness of the approach.

Fig. 7
figure 7

a The offloading cost when sub-channels bandwidth is fixed and the number of channels varies, and b the offloading cost of changing the number of channels when the total channel bandwidth is fixed

Full size image

6 Conclusion

Aiming at the cloud-edge collaborative computing problem of air-ground integrated networks, we constructed an cloud-edge collaborative computing model. And we propose a computational offloading and resource allocation optimization scheme based on distributed game to minimize the offloading cost. Extensive simulation results show that the offloading cost increases when the number of tasks and the amount of data increase, and the changes of weight parameters and channel states affect the processing delay and energy consumption of the tasks. The DCORA scheme performs well in terms of convergence performance and convergence speed. The proposed scheme is able to significantly reduce the average task processing delay and always keep the minimum offloading cost compared the traditional schemes.