Abstract
FBMC is a pivotal system in 5G, serving as a cornerstone for efficient use of available bandwidth while simultaneously meeting stringent requirements for high spectral efficiency. Notably, FBMC harnesses the power of multicarrier modulation (MC), a good alternative to orthogonal frequency division multiplexing (OFDM) technology that supports fourth-generation (4G) systems. The wireless communications field is full of challenges, the most important of which are channel estimation and interference cancellation, both of which deserve comprehensive study to increase the efficiency of data transmission. In this paper, our investigation takes a deliberate step towards the convergence of two prominent modulation models: OFDM and FBMC. We specifically contrast these modulation techniques with the intricate field of joint channel estimation and interference cancellation (JCEIC). In this research study, we take advantage of recurrent neural networks' (RNNs') efficiency as a vehicular channel to perform precise channel estimation and recovery of uncorrupted transmitted signals, thereby lowering the bit error rate (BER). Our channel estimation for a dual selective channel is based on the thoughtful placement of pilots scattered over the temporal and frequency dimensions, and is further improved by the interference cancellation method of low complexity that was selected. Our JCEIC proposal aims to integrate RNNs carefully, using the output sequences of JCEIC algorithms as useful inputs to this neural architecture. By clearly demonstrating a decrease in BER as compared to traditional approaches, it is evident that the performance of the novel approach is near to that of a perfect channel. Additionally, a comparison of the performance of FBMC and OFDM systems at various signal-to-noise ratios reveals a clear performance divide that favors the former in terms of system efficiency. The BER is restricted by FBMC to a commendable threshold of less than 0.1 at a modest 5 dB, continuing the higher trend started by its improved RNN-based channel estimate. The accuracy of channel estimation is clearly improved by this paradigm shift, and the computing complexity typical of 5G networks is also clearly reduced.
Similar content being viewed by others
1 Introduction
Future wireless systems should be able to handle a wide range of potential use cases, including low latency transmissions, machine-to-machine interactions, and high data rates. Due to its poor spectrum behavior, traditional OFDM is unable to assign the available time–frequency resources in a flexible manner needed for this. Due to its substantially improved spectrum qualities, FBMC becomes an effective substitute for OFDM for such a wide range of applications. Channel estimation and interference cancellation are important steps to recover the original signals with low BER at Low SNR.
Within the architectural framework of the imminent wireless communication paradigm known as the 5G technology, a ubiquitous transmission mechanism emerges in the form of FBMC. This mechanism assumes a role of paramount significance, particularly given the pressing demand within the 5G context to achieve a momentous 1000-fold enhancement in data transmission rates. Underpinning FBMC's modulation scheme is the MC technique, a versatile modality that facilitates the realization of FBMC's communication objectives.
MC modulation, in essence, entails the utilization of a waveform composed of multiple carriers, closely spaced within a given block, to convey information. These carrier blocks congregate in a structure known as a filter bank, representing a pivotal architectural element of the FBMC system. It is noteworthy that current research endeavors in the domain of mobile communication systems have orchestrated a pivot towards the exploration of exceedingly flexible 5G networks, thereby deviating from the paradigms characterizing third and fourth-generation counterparts [1].
Against the backdrop of 5G's exacting requisites, MC modulation emerges as a formidable enabler, poised to play a pivotal role in addressing the multifarious demands of this next-generation milieu. In this context, it is salient to draw a parallel to OFDM, a representative modulation technology of the preceding fourth generation. OFDM, a precursor to MC, introduces a cyclic prefix (CP) as a guard interval, effectively mitigating both intersymbol interference (ISI) and delay within wireless channels. Despite these merits, the OFDM methodology does bear certain limitations that detract from its efficacy in the realm of 5G challenges. Chief among these is its propensity to constrain Bandwidth (BW) efficiency, a constraint exacerbated by its susceptibility to elevated side-lobes, thus engendering a surge in spectral expansion [2].
In this scholarly discourse, we navigate the intricate terrain of modulation methodologies, casting a spotlight on the symbiotic relationship between FBMC and MC within the burgeoning 5G landscape. As we unravel the intricate tapestry of these modulation paradigms, the nuanced contours of their respective strengths and limitations become increasingly apparent, thereby paving the way for an enlightened trajectory towards the realization of seamless and efficient wireless communication in the 5G era.
The emergence of the Internet of Things (IoT) landscape has engendered a profound paradigm shift, imposing stringent imperatives of synchronization and coordination that entail the conveyance of substantial control information. Moreover, the diverse spectrum of IoT applications underscores the requisites for both low-latency and asynchronous transmissions. This shifting landscape is mirrored in the exponential proliferation of connected devices, a corollary of which is the commensurate escalation in data volumes managed by the network. Consequently, the evolution from 5G networks to the realm beyond demands an unprecedented degree of versatility and adaptability to accommodate this burgeoning complexity [3].
The nascent phase of 5G's deployment witnessed a judicious recourse to an OFDM variant, chiefly motivated by the desire for compatibility with extant 4G infrastructures. However, as we extrapolate to the vistas of forthcoming communication networks, the imperatives of asynchronous and uncoordinated transmissions necessitate the amelioration of synchronization and orthogonality constraints intrinsic to OFDM waveforms. In this endeavor, alternative waveforms, such as FBMC, emerge as promising contenders, poised to alleviate the limitations associated with OFDM. Notably, FBMC, characterized by its intricate prototype filter, affords superior frequency localization compared to the rectangular pulse filters ubiquitous in OFDM. The expulsion of the cyclic prefix bolsters FBMC's prowess in terms of spectrum efficiency, a domain where it outshines OFDM [4]. This enhancement is embodied in the FBMC scheme harnessing Offset Quadrature Amplitude Modulation (OQAM), a technique that bestows orthogonality upon sub-carriers through the judicious alternation of quadrature and in-phase samples, enriched by a half-symbol period shift. The real-domain manifestation of FBMC-OQAM unveils orthogonality with the intrinsic interference within the imaginary signal component [5].
Eminently significant within this communicative milieu is the pivotal role of channel estimation and interference cancellation, each exerting their influence towards the eventual recovery of transmitted signals. Traditional paradigms, such as the Minimum Mean Squared Error (MMSE) scheme, have surfaced for channel estimation, albeit marred by elevated BER, particularly in conditions of diminished SNRs [6]. To mitigate these limitations, we undertake a novel approach that amalgamates channel estimation and interference cancellation within the aegis of RNNs, a technique endowed with the capacity to revolutionize the landscape of signal recovery. The genesis of our proposed RNN is rooted in the MMSE channel estimation method's outputs, synergistically accompanied by a low-complexity interference cancellation framework. The ultimate ambition underlying this architectural marriage is to realize a paradigm wherein high BER performance is achieved across divergent SNR profiles. This pioneering effort thus ensues to fathom the uncharted domain of synergistic RNN-empowered channel estimation and interference cancellation for both OFDM and FBMC systems, entailing the confluence of methodological sophistication and computational parsimony.
The present scholarly endeavor furnishes a compendium of notable contributions, the crux of which is outlined herewith:
-
1.
Thorough Examination of OFDM and FBMC Systems: A comprehensive appraisal of both OFDM and FBMC systems stands as a cornerstone, elucidating the virtues and limitations intrinsic to each. Notably, a meticulous dissection is undertaken to expound upon how FBMC systematically mitigates the deficiencies endemic to the OFDM paradigm, thereby illuminating its potential as a viable alternative.
-
2.
Scrutiny of Conventional Methods for Channel Estimation and Interference Cancellation: The inquiry extends to encompass an exhaustive survey of conventional methodologies germane to channel estimation and interference cancellation. This critical survey establishes a foundational understanding of existing paradigms, paving the way for the subsequent strides in methodology augmentation.
-
3.
Channel Response Estimation via MMSE Technique: A pivotal facet of this scholarly odyssey resides in the precise estimation of channel responses. This task is deftly executed through the application of the MMSE method, representing an intellectual conduit to unravel the intricacies of channel characteristics.
-
4.
RNN-Enabled Channel Response Prediction: The narrative proceeds to unfold an innovative orchestration, wherein previously estimated channel responses are harnessed as input to a RNN. This pioneering initiative propels the prediction of current channel responses, thereby culminating in a paradigmatic convergence of traditional methodology and cutting-edge neural network architecture.
-
5.
Empirical Validation of Optimized RNN Structure: Empirical validation serves as the crucible within which the trained and optimized RNN structure is subjected to rigorous testing. This validation unfolds against the backdrop of previously ascertained channel responses, thereby furnishing an empirical rubric to gauge the efficacy of the proposed augmentation.
-
6.
RNN Empowerment for Enhanced Performance: The zenith of this academic expedition culminates in the strategic application of the RNN paradigm, harnessed to elevate the performance thresholds of systems tethered to joint channel estimation and interference cancellation. The efficacy of this augmentation is rigorously assessed across both OFDM and FBMC systems, unfurling a vista of augmented efficiency and efficacy.
In summation, the multifaceted contributions proffered by this study engender a panorama of erudition, showcasing a symphony of inquiry, innovation, and validation, all orchestrated towards the overarching objective of amplifying the capacities of joint channel estimation and interference cancellation in the context of OFDM and FBMC systems.
The ensuing sections of this paper are meticulously organized to facilitate a coherent exposition of the research contributions. The structure unfolds as follows. A comprehensive overview of the relevant academic landscape is encapsulated within Sect. 2. The summative essence of prior research endeavors serves as a foundational framework upon which our own investigative journey is meticulously built. Section 3 assumes the mantle of elucidating the underpinning system model. This pivotal segment serves as a fulcrum, affording an intricate portrayal of the modus operandi, with a specific focus on doubly selective channel estimation and the attendant intricacies of interference cancellation. The methodological prowess of RNNs takes center stage in Sect. 4. Herein, we expound upon the innovative channel estimation mechanism, meticulously detailing the seamless integration of RNNs to realize a paradigm shift in channel estimation efficacy. The empirical crucible of Sect. 5 resonates with the embodiment of our investigative endeavors, manifesting as a substantive discussion that spans an array of simulation results. In the crucible of empirical validation, our propositions stand illuminated against the backdrop of concrete evidence. The denouement of our scholarly journey unfolds within Sect. 6, wherein a comprehensive synthesis of our contributions coalesces. This section encapsulates the culmination of our research expedition, epitomizing the insights garnered and the potential trajectories that lie ahead. In the subsequent sections, we embark upon a meticulous voyage that traverses the realms of theoretical discourse, empirical validation, and methodological innovation. Each segment stands as a pivotal cornerstone, collectively culminating in a scholarly edifice that both enriches the academic milieu and propels the discourse within the realm of joint channel estimation and interference cancellation to new horizons.
2 Related works
The discourse on channel estimation within the context of FBMC-OQAM systems is enriched through the advent of a novel scattered pilot method, an innovation substantiated in [7]. This method derives its essence from the strategic utilization of a sparse assemblage of auxiliary pilot symbols, judiciously harnessed to curtail the encroachment of imaginary interference upon each scattered pilot. Augmenting this paradigmatic leap, a nuanced symphony of transmitter-side power multiplexing and receiver-side successive interference cancellation, as articulated in [4], engenders a transformative stratagem. This intricate orchestration culminates in an efficacious methodology, characterized by the meticulous reduction of intrinsic interference sans the inadvertent omission of data symbols. This principled augmentation inexorably ushers forth heightened spectral efficiency, eclipsing the benchmarks set by antecedent methodologies. To illuminate the conceptual underpinnings, [4] conveys a predictive methodology tailored for doubly-selective channels, wherein temporal and frequency correlations are harnessed to empower the scatter pilot constellation.
In consonance with this trajectory, the treatise set forth in [5] proffers a paradigmatically versatile iteration of interference cancellation, germane to a spectrum encompassing linear modulation techniques, inclusive of OFDM and FBMC. A further augmentation to channel estimation is proffered in [6], wherein an innovative preamble structure takes center stage. This symmetrical prelude, meticulously architected, seamlessly dovetails the consideration of interference weights, orchestrating a symmetrical schema that ingeniously quells the invasive influence of interference.
The mettle of multicarrier communication methodologies is notably underpinned in the scholarship evidenced by [6, 8], constituting a resounding endorsement of the efficacy of such techniques in the pursuit of high-data-rate transmission paradigms. Encompassing the realm of FBMC-QAM systems, the exploration of iterative interference cancellation (IIC) assumes prominence. The tenets of [3] manifest in an IIC receiver architecture, a nexus wherein received signals are diligently bifurcated into odd and even numbered subcarrier components. A meticulously devised iterative process, underpinned by demodulated even subcarrier symbols, orchestrates the progressive attenuation of interference impact, embodying a testament to the dynamic symbiosis between modulation, interference mitigation, and signal fidelity.
A corpus of contemporary scholarship unveils a mosaic of innovative strategies aimed at enhancing the efficacy of channel estimation within diverse communication paradigms. One noteworthy avenue traverses the terrain of frequency-selective channels, where the challenge emerges from the non-fixed and non-a priori nature of the frequency selectivity (FS). Pioneering research [9] harnesses a k-nearest neighbor-based machine learning technique to discern the FS and judiciously determine the optimal window length of Fractional Fourier Transform (FDA). Through panoply of extensive simulations, the proposed channel estimation (CE) scheme stands vindicated, underscored by a rigorous theoretical comparison of Mean Squared Error (MSE). Impressively, adaptive CE techniques manifest their prowess, resonating with the semblance of lower CE-MSE and superior bit error rates, all orchestrated sans the need for anterior knowledge of frequency selectivity [9].
The intricacies intrinsic to FBMC/OQAM signals, augmented by the challenges arising from their non-orthogonal disposition in the imaginary realm, engender a vexing conundrum within the ambit of Multiple-Input Multiple-Output (MIMO) technology deployment. Herein, a redoubtable solution emerges in the form of a pioneering deep neural network (DNN)-based methodology [10], intricately tailored to quell the formidable interference inculcated within the FBMC/OQAM milieu, thereby creating a fertile terrain conducive to the fruitful deployment of MIMO technology.
In parallel, the OFDM/OQAM domain confronts a distinct set of predicaments, emblematic of inter-symbol and inter-carrier interference inherent to dispersive channels. The scholarly discourse [11] presents an innovative channel estimation approach juxtaposed with a judicious pilot structure for the OFDM/OQAM paradigm. The crux of this methodology rests upon judiciously predetermined pilot positions, facilitating the robust reconstruction of transmitted symbols, which subsequently empowers the computation and elimination of interference stemming from received signals.
The scholarly tapestry unfurls with the advent of DeepSIC [12], an iterative soft interference cancellation (SIC) technique, emblematic of a data-driven approach buttressed by deep learning principles. DeepSIC, characterized by its capacity to glean insights from a diminutive training dataset bereft of linear channel or predetermined parameter prerequisites, outshines its model-based counterparts, particularly when confronted with the enigma of Channel State Information (CSI) ambiguity.
Delving further, [13] embarks on an ambitious expedition wherein an ensemble of diverse deep neural networks is harnessed to augment interference cancellation performance within the realm of non-orthogonal signals. The discerning findings from simulations underscore the profound efficacy of meticulously engineered neural networks, substantiating their capacity to markedly attenuate interference in signals characterized by Subcarrier Index Modulation Enhanced Frequency Division Multiplexing (SEFDM). This empirical nexus unveils a profound interplay between signal waveforms and neural architectures, often necessitating comprehensive neural interconnections for optimal performance.
Collectively, these pioneering endeavors stand as a testament to the scholarly acumen dedicated towards the elucidation of formidable challenges pervading the spectrum of communication systems, illuminated by innovative methodologies underscored by the tenets of machine learning and deep neural networks.
Embedded within the continuum of innovative strategies for channel estimation, a multipronged approach emerges, encompassing facets of demodulation, interference mitigation, and neural network architectures. This confluence of methodologies unfolds as follows:
Enhanced demodulation strategy The purview of the proposed Interference Cancellation (IC) strategy embraces the augmentation of the demodulation process, engendering a substantial reduction in the error floor that besets the demodulated symbols integral to interference component calculations. Noteworthy is the empirical validation, wherein simulation data underscores the remarkable efficacy of the prescribed channel estimation approach. Evidently, its superiority is distinctly pronounced when the specter of Inter-Symbol Interference (ISI) looms large, synergistically coupled with a SNR surpassing the threshold of 15 dB. An augmentation, wherein the technique harmonizes with a Space–Time Block Code (STBC), culminates in a superlative Symbol Error Ratio (SER), a pivotal metric encapsulating the system's performance [14].
Deep learning augmentation in LTE-A channel estimation [15] A distinctive fusion of deep learning and channel estimation manifests in [15], wherein an elaborate algorithm strives to refine the LTE-A uplink channel estimation algorithmic architecture. Through the dexterous development of SC-FDMA databases founded upon diverse channel propagation models, the training and testing paradigms are meticulously tailored. The apparatus of choice is an Artificial Neural Network, diligently engendered to fathom the labyrinthine terrain of SC-FDMA link channel estimation. The iterative evolution of the neural network, encapsulated within dynamic alterations of weight and bias parameters, culminates in a calibrated neural construct, thereafter effectively operationalized within the receiver.
Signal-interference nexus through neural networks [13] Embarks on a voyage wherein the catalytic potential of deep neural networks is harnessed to eviscerate the specter of interference within the ambit of non-orthogonal signals. Empirical insights gleaned through simulations corroborate the profound efficacy of meticulously designed neural networks, particularly in attenuating the invasive interference enveloping signals characterized by SEFDM. The profound link between signal waveforms and neural network architectures emerges as a salient outcome, guiding the assertion that a maximal interconnection of neurons within each stratum is indispensable for optimal functionality.
FreqTimeNet and AttenFreqTimeNet for OFDM channel estimation enhancement [16] Charts a trajectory of advancement through the conceptualization of a frequency-time division network (FreqTimeNet) calibrated to augment DL-based OFDM channel estimation. The underpinning architectural hypothesis predicates orthogonal concomitance between time and frequency domains, thereby nurturing parallel processing of input information. The ensuing innovation, christened as AttenFreqTimeNet, incorporates an attention mechanism alongside SNR awareness, further enriching the efficacy of the FreqTimeNet framework. Rigorous evaluation against the backdrop of 3GPP channel models elucidates the MSE dynamics across diverse operational scenarios, illuminating the manifold potentials of these structures.
Spatial-frequency and temporal CNNs in channel estimation [17] Unfurls a profound augmentation within the domain of channel estimation, anchored upon the synergy between spatial, frequency, and temporal correlations. A Deep Convolutional Neural Network (CNN) serves as the vanguard, culminating in the spatial-frequency CNN (SF-CNN), an instrumentality that robustly incorporates neighboring subcarriers to enhance channel matrix feed. This augmentation is harmoniously complemented by a spatial-frequency-temporal CNN (SFT-CNN), a construct that harnesses temporal correlation to fortify accuracy. Furthermore, the conceptualization of the spatial pilot-reduced CNN (SPR-CNN) ushers forth a memory-driven channel estimation paradigm, orchestrating channel organization and estimation within successive coherence intervals.
In summation, this eclectic assortment of methodologies reverberates with the symphony of innovation, underscoring the profundity of inquiry and ingenuity that underpin contemporary research in channel estimation paradigms. These multifaceted endeavors not only enrich the theoretical landscape but also offer tangible empirical insights, fostering the continual advancement of communication systems.
In the annals of contemporary research, a spectrum of pioneering contributions endeavors to reshape the contours of channel estimation, permeating various communication paradigms with the transformative potential of DL methodologies. These seminal contributions, elucidated below, collectively converge to usher forth a new epoch within the landscape of channel estimation and enhancement:
DL-infused channel estimation network ChanEstNet [18] In the seminal work expounded in [18], a DL-based channel estimation network, ChanEstNet, takes center stage, ingeniously marrying the potency of deep CNNs and RNNs. Within this architectural symphony, RNNs embark upon channel estimation, while CNNs, acting as virtuoso feature extractors, orchestrate the distillation of channel response feature vectors. An offline regime of substantial high-speed channel data bestows upon the learning network the profound insights requisite to discern the intricate tapestry of non-stationary channels, navigate through the labyrinthine terrains of fast time-varying dynamics, and ultimately bolster the real-time adaptability essential for heightened performance within high-speed environments.
DL-CE for FBMC systems [19] Building upon the foundational edifice of DL, [19] ushers forth innovative DL-based channel estimation and equalization technique (DL-CE) tailored explicitly for FBMC systems. The crux of this architectural marvel resides in the erudite edifice of a DNN model, which progressively assimilates the constellation demapping technique and CSI. This alchemical amalgamation, a testament to the potency ofDL, engenders implicit equalization of malformed frequency-domain sequences, effectuating the direct derivation of binary bits within the DL-CE framework.
Theoretical underpinnings of DL in SIMO systems [20] Embarks upon a foundational expedition, elucidating the theoretical bedrock underlying DL-based channel estimation, with a specific focus on single-input multiple-output (SIMO) systems. Within this scholarly realm, the spotlight cascades upon the rectified linear unit (ReLU) activation function, emblematic of a theoretical nexus that renders DNNs akin to piecewise linear functions. This theoretical tenet unlocks the capacity for DL estimators to achieve global approximation across an expansive spectrum of functions, artfully harnessing piecewise linearity to navigate multifaceted landscapes. Moreover, the theoretical architecture discerns asymptotically-linked echoes of MMSE estimation, spanning a gamut of scenarios without necessitating anterior knowledge of channel statistics.
DL-driven symbol detection in communication systems [21] Unfolds a discourse that seamlessly weaves DL prowess into the fabric of symbol detection, meticulously tailored for scenarios where receivers grapple with the dearth of CSI. This strategic alignment culminates in a DL-based detector (DLD), a computational marvel that, sans extraneous operations, adeptly unveils symbols for all users. This revelation, orchestrated through the analysis of received data signals and pilot responses, underscores the potency of DL in decoding the intricate language of communication signals. A panoply of Monte Carlo simulations takes center stage, heralding the empirical appraisal of DLD performance vis-à-vis benchmark counterparts.
Augmented capacity through pilot-symbol-aided channel estimation [22] The seminal treatise espoused in [22] adroitly navigates the realm of imaginary interference cancellation, seamlessly harmonizing the tenets of channel estimation with pilot symbols. Through a judicious matrix formulation, this pioneering endeavor imbues auxiliary pilot symbols with communal attributes, fostering an augmentation of peak-to-average power ratio and practical capacity. This strategic augmentation, meticulously calibrated through the prism of linear precoding, crystallizes into a transformative scheme, poised to unravel the elusive potential of interference cancellation and engender a dynamic augmentation of system capacity.
Joint detection-channel estimation in OFDM systems [23] Two ML-based structures for joint detection-channel estimation in OFDM systems are presented and thoroughly defined. In order to improve data detection performance, two machine learning (ML) architectures—Deep Neural Network (DNN) and Extreme Learning Machine (ELM)—were developed and put up against the conventional matched filter (MF)detector with MMSE and LS channel estimators [23].
Digital self-interference (SI)cancellation in a single RF chain [24] The digital self-interference (SI)cancellation in a single RF chain massive MIMO full-duplex (FD) OFDM system with phase noise is examined in this study. A weighted linear SI channel estimator is constructed to reduce the residual SI power in each OFDM symbol in order to account for the phase noise, which causes SI channel estimate error and subsequently degrades the SI cancellation performance. Analysis is done on the suggested method's ability to cancel out digital SI, which is measured as the difference between the SI power before and after the cancellation [24].
Minimize interference by giving up data symbol [4] Low spectrum leakage, lax synchronization demands, and good spectral efficiency are all major benefits of FBMC as a viable choice for OFDM. While most approaches minimize interference by giving up data symbols, the loss of orthogonality in FBMC results in intrinsic interference, which has a non-negligible negative impact on spectral efficiency. By utilizing power multiplexing in the transmitter and a successive interference cancellation scheme in the receiver, in comparison to earlier techniques, completely eliminates intrinsic interference without sacrificing any data symbols [4].
Double threshold (DT) channel estimation method [25] The double threshold (DT) channel estimation method based on adaptive frame statistics (AFS) is thus suggested in this study. In order to detect the channel structure, the method first adaptively calculates the number of statistical frames based on the temporal correlation of the received signals. Next, it examines the distribution properties of the multipath sampling points and noise sampling points during subsequent frames. The separation between multipath and noise sampling sites is then further expanded using a multi-frame averaging method [25].
Channel estimation is done using DL [26] In this study, pilot-based channel estimation in OFDM is done using DL approaches. Due to noise amplification during the estimation process, intercarrier interference, a lack of primary channel data, and poor performance with few pilots, conventional channel estimators in pilot-symbol-aided OFDM systems perform worse, especially in low SNR regions, despite having lower complexity and requiring implicit channel statistics knowledge. The use of DL with peephole long short-term memory (peephole LSTM) is a novel approach for channel estimation. After offline training with generated datasets, the proposed peephole LSTM-based channel state estimator is deployed online to track channel parameters, enabling reliable recovery of transmitted data [26].
RLS-based channel estimation approach [27] This work suggests an RLS-based channel estimation approach to lower bit error rates and enhance anti-interference performance. The final estimation data is modified using the RLS channel estimation method to produce the current estimation data. To acquire all estimated data, the forgetting factor and recursive formula are used to adjust the data in real-time once the initial data is estimated by LS. The outcomes demonstrate the RLS channel estimating algorithm's ability to decrease computation, increase channel estimation accuracy, and suppress noise interference. The accuracy of the channel estimation will improve with more iterations, hence lowering the bit error rate [27].
From the previous literature review, the channel estimation and the interference cancellation are important steps in the receiving process. We cannot recover the original signal without the true prediction of the channel and remove the interfere signals from the received signal. The previous methods that used for this challenge take more time and have a computational complexity, because it uses two different methods to do this. The performance of the previous method was low at low SNR. Exploiting RNNs to perform this task is solving these problems jointly.
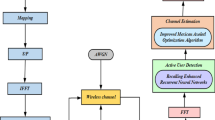
Resonating harmoniously with this symphony of innovation, our present endeavor unfurls a novel chapter in the narrative of channel estimation and interference cancellation. Within this scholarly discourse, we proffer a Joint Channel Estimation and Interference Cancellation (JCEIC) framework, meticulously calibrated to weave the tapestry of OFDM and FBMC systems. Anchored within the realm of doubly-selective channels, predicated upon the frequency and time correlation of scattered pilots, our endeavor is imbued with the finesse of low-complexity interference cancellation. A paradigmatic innovation unfurls through the architectural integration of RNNs, standing sentinel over the strategic confluence of channel estimation and interference mitigation. Figure 1 artfully encapsulates this innovative system, an emblematic representation of our scholarly pursuit that aspires to redefine the horizons of channel estimation and interference cancellation.
3 System model
OFDM uses a rule that allows several messages to be broadcast simultaneously over a single radio channel. Each modulation station in FDM uses a different set of frequencies. Every frequency signal has enough space between them so that they don't overlap with each other or with other frequencies in the spectrum. Each frequency transmission is individually filtered by a bandpass filter to obtain the opposite complete signal, excluding the signal that the base station needs to consider for the receiver. The initial signal is reversed to receive the acknowledged signal [28]. Multicarrier modulation, or OFDM, sends a small amount of bits over each channel while using two carrier signals with the same frequency. However, all of the sub-channels in the case of OFDM are reserved for a single records source.
A group of synthesis and analysis filters in FBMC are built with sufficient spectrum selectivity and bandwidth efficiency in mind. Although it is possible to build each filter separately, it is more effective to construct a single prototype low-pass filter and modulate it to a number of predetermined center frequencies in order to produce the synthesis and analysis filters. The filters are typically even- or odd-stacked, extremely spectrally selective to reduce crosstalk with neighboring subcarriers, and consistently spaced [29].
In the multi-carrier systems, \(\mathrm{k}\) is the time position, \(\mathrm{l}\) is the subcarrier position, and the transmitted symbols \({x}_{\mathrm{l},\mathrm{k}}\) is modulated by the base pulses \({g}_{l,k}(t)\), so that the transmitted signal \(s\left(t\right)\) is in the time domain [5]:
with
basis pulse \({g}_{l,k}\left(t\right)\) is a shifted version frequency and time of prototype filter \({p}_{\mathrm{TX}}(t)\). The receiver uses different prototype filters, so the received base pulse \({\mathrm{q}}_{\mathrm{l},\mathrm{k}}\left(\mathrm{t}\right)\) is expressed in the following form.can be expressed as,
In CP-OFDM \({\mathrm{p}}_{\mathrm{RX}}(\mathrm{t}\)) a slightly shorter rectangular pulse and \({p}_{\mathrm{TX}}(t\)) is a rectangular pulse, and the basis pulses are orthogonal, that is,\(\langle {g}_{{l}_{1},{k}_{1}}\left(t\right),{q}_{{l}_{2},{k}_{2}}\left(t\right)\rangle ={\delta }_{\left({l}_{1}-{l}_{2}\right),\left(k-{k}_{2}\right)}\) and the time–frequency spacing is \(TF = 1 + {T}_{\mathrm{CP}}F.\) In FBMC, based on a Hermite prototype filter for example,\(p\left(t\right)={p}_{\mathrm{TX}}\left(t\right)={p}_{\mathrm{RX}}(t)\) is a smoother function, and complex for time-frequency spacing of TF = 2. The time–frequency spacing is minimized to TF = 0.5 in FBMC, to enhance the spectral efficiency, only real-valued data symbols \({x}_{l,k}\epsilon {\mathbb{R}}\) are transmitted. Orthogonally, and it holds in the real domain, \(\mathfrak{R}\left\{\langle {g}_{{l}_{1},{k}_{1}}\left(t\right),{q}_{{l}_{2},{k}_{2}}\left(t\right)\rangle \right\}={\delta }_{\left({l}_{1}-{l}_{2}\right),\left(k-{k}_{2}\right)}\).
A discrete time system model will be considered, simplifying the analytical description, and the transmitted base pulses sampled with rate \({f}_{\mathrm{s}}=\frac{1}{\Delta t}={\mathrm{FN}}_{\mathrm{FFT}}\) and all samples are stacked in a large vector \({\mathrm{g}}_{\mathrm{l},\mathrm{k}}\left(\mathrm{t}\right)\upepsilon {\mathbb{C}}^{\mathrm{N}\times 1}\). And all basis pulse vectors are stacked in matrix \(\mathrm{G}=\left[{\mathrm{g}}_{\mathrm{0,0}}\dots {\mathrm{g}}_{\mathrm{L}-1,\mathrm{K}-1}\right]\upepsilon {\mathbb{C}}^{\mathrm{N}\times \mathrm{LK}}\). The samples of the receive basis pulse are stacked in matrix \(\mathrm{Q}=\left[{\mathrm{q}}_{\mathrm{0,0}}\dots {\mathrm{q}}_{\mathrm{L}-1,\mathrm{K}-1}\right]\upepsilon {\mathbb{C}}^{\mathrm{N}\times \mathrm{LK}}\). Only the true orthogonally condition is valid, that is, \(\mathfrak{R}\left\{{\mathrm{Q}}^{\mathrm{H}}\mathrm{G}\right\}={\mathrm{I}}_{\mathrm{LK}}\). The transmission across a doubly-selective channel is defined as \(\mathrm{y}\) by the following connection [5],
where vector \(\mathrm{x}=\left[{\mathrm{x}}_{\mathrm{0,0}}\dots {\mathrm{x}}_{\mathrm{L}-1,\mathrm{K}-1}\right]\upepsilon {\mathbb{C}}^{\mathrm{LK}\times 1}\) illustrates the transmitted data symbols.\(\mathrm{y}={\mathbb{C}}^{\mathrm{LK}\times 1}\) are the symbols that received, and \(\mathrm{D\epsilon }{\mathbb{C}}^{\mathrm{LK}\times \mathrm{LK}}\) the transmission matrix, defined as,
where \(n\sim \mathcal{C}\mathcal{N}({\mathrm{P}}_{\mathrm{n}}{\mathrm{Q}}^{\mathrm{H}}\mathrm{Q})\) is the Gaussian noise.
4 Channel estimation
We take into account the pilot symbol-aided channel estimate, which is a total of \(\left|\mathcal{P}\right|\) symbols \({\mathrm{x}}_{\mathcal{P}}\upepsilon {\mathrm{C}}^{\left|\mathcal{P}\right|\times 1},\) the pilots that are identified firstly at the receiver. For the one-tap channel, Least Squares (LS) estimation is allowed at the pilot positions \({\widehat{\mathrm{h}}}_{\mathrm{p}}^{\mathrm{LS}}\upepsilon {\mathrm{C}}^{\left|\mathrm{p}\right|\times 1}\), depending on,
Simple LS estimate of the one-tap channel is not possible due to the imaginary interference in FBMC. Preprocessing must be done further. In particular, we use precoding by, where \(\widetilde{\mathrm{x}}\) defined by,
where the data symbols are \(\widetilde{\mathrm{x}}\) and at the pilot positions,\(\mathrm{C}\) neglects the imaginary interference, that is,
Data spreading approach or auxiliary symbol method may be represented by cancellation matrix \(\mathrm{C}\), it should be noted. For the latter, at the receiver, extra despreading is needed [5].
-
Doubly selective channel estimation
Numerous articles attempt to estimate the channel impulse response \(\widehat{\mathbf{H}}\), in the situation of a doubly-selective channel. The active subcarriers number in real systems is less than the size of the Fast Fourier Transform (FFT)\(L<{N}_{FFT}\). This suggests that, at the zero subcarriers, it is impossible to estimate the channel transfer function accurately, precluding an accurate impulse response assessment. To the channel transfer function, one can only get a pseudo impulse response by performing an inverse Fourier transform of the active subcarriers \(L\) active subcarriers, implicitly presuming a rectangular filter. Even though the genuine impulse response could be time-limited, the pseudo impulse response delay taps are not. For estimate techniques at the edge subcarriers that depend on the presumption that the lateness taps are time-limited, this is brought on by the cutout of the channel transfer function. The complexity of computation is another factor. Even if the impulse response can be precisely estimated, assessing the matrix multiplication in (5) is still necessary, which adds a significant, computing overhead. By directly predicting the transmission matrix \(\widehat{\mathbf{D}}\), all of these limitations can be avoided. Due to the fact that the one-tap channel is typically approximated using interpolation, this is happening to some extent already in practical systems. By one-tap channel coefficients, the diagonal elements of \(\widehat{\mathbf{D}}\) are represented [5].
The time-variant transfer function is interpolated by an approximation of the whole time-variant transfer function is produced. A strong link between frequency and time makes this possible. As previously indicated, without using the channel transfer function's diversion, it is more effective computationally to directly estimate \(\widehat{\mathbf{D}}\) which preserves the underlying correlation. At rowposition \(\overline{{l }_{1}{k}_{1}}={l}_{1}+L{k}_{1}\) and column position \(\overline{{l }_{2}{k}_{2}}={l}_{2}+L{k}_{2}\), one element of the transmission matrix \(\widehat{\mathbf{D}}\) can be estimated by:
where a weighting vector can be represented by \({\widetilde{\mathrm{w}}}_{{l}_{1,}{k}_{1},{l}_{2,}{k}_{2}}^{H}\epsilon {\mathbb{C}}^{\left|p\right|\times 1}\) and at the pilot positions,\(\epsilon {\mathbb{C}}^{\left|p\right|\times 1}\) is the LS channel estimates. The weighting vector significantly influences the accuracy of channel estimate. We take into account a weighting vector for MMSE, which is the better \({\widehat{h}}_{p}^{LS}\) channel estimate technique feasible in terms of MSE. We use the theorem of the orthogonal projection.
The weighting vector for MMSE in (9) can be derived by the following equation, which says that the estimator's error must be orthogonal to the estimator.
With correlation matrix of the LS channel is defined by \({\mathbf{R}}_{{\widehat{h}}_{p}^{LS}}^{-1}={\mathbb{E}}\left\{{\widehat{h}}_{p}^{LS}{({\widehat{h}}_{p}^{LS})}^{H}\right\}\epsilon {\mathbb{C}}^{\left|p\right|\times \left|p\right|}\) that estimates at the pilot positions and \({r}_{{\widehat{h}}_{p}^{LS},\left[\mathbf{D}\right]\frac{}{{l}_{1}{k}_{1}}\frac{}{{l}_{2}{k}_{2}}}\) the correlation vector between one element of transmission matrix \(D\) and the LS channel estimates at the pilot positions. The largest difficulty is locating the necessary correlation matrices. The ithandjth LS channel estimates are, respectively,\({R}_{{\widehat{h}}_{{p}_{i}}^{LS},{\widehat{h}}_{{p}_{j}}^{LS}}={\mathbb{E}}\left\{{\widehat{h}}_{{p}_{i}}^{LS}{({\widehat{h}}_{{p}_{j}}^{LS})}^{H}\right\}\epsilon {\mathbb{C}}^{1\times 1}\).The interference is uncorrelated, as well as the noise, assuming \(i\ne j\), so that \({R}_{{\widehat{h}}_{{p}_{i}}^{LS},{\widehat{h}}_{{p}_{j}}^{LS}}={R}_{h{p}_{i.}h{p}_{j}}\). By utilizing the Kronecker product, \(h{p}_{i}={q}_{{p}_{i}}^{\mathrm{H}}\mathbf{H}{g}_{{p}_{i}}=\left({g}_{{P}_{i}}^{T}\otimes q\right)vec\left\{H\right\},\) at the pilot positions, the correlation between the LS channel estimates at the pilot positions, when \(i\ne j\), according to,
At the pilot positions, we must take interference \({g}_{{p}_{i}\otimes }^{T}{q}_{{p}_{i}}^{H}\) into consideration for the power since it causes:
The overall correlation matrix is \({\mathbf{R}}_{{\widehat{h}}_{{p}_{i}}^{LS}}\), Eqs. (12) and (13) are used and based on the correlation matrix of the channel,\({\mathbf{R}}_{vec\left\{H\right\}}={\mathbb{E}}\left\{vec\left\{\mathbf{H}\right\}vec{\left\{\mathbf{H}\right\}}^{\mathrm{H}}\right\}\). Since the time-variant impulse response correlation \({\mathbb{E}}\left\{{h}_{conv.}\left[{n}_{1},{m}_{1}\right]{h}_{conv.}^{*}\left[{n}_{2},{m}_{2}\right]\right\}\) is considered to be known, the elements of this correlation matrix are simple to calculate. Due to the vectorized nature, only the mapping of this connection to the appropriate place in \({\mathbf{R}}_{vec\left\{H\right\}}\) poses certain difficulties. At the ith pilot position, the correlation between the channel estimation LS and one transmission matrix \({\varvec{D}}\) element can be determined similarly as in (12) by,
In (11) to calculate the MMSE weighting vector, with (12)-(13) we have all the necessary tools, that is \({r}_{{\widehat{h}}_{p}^{LS},\left[\mathbf{D}\right]\frac{}{{l}_{1}{k}_{1}}\frac{}{{l}_{2}{k}_{2}}}\epsilon {\mathbb{C}}^{\left|p\right|\times 1}\). The fact that the correlation matrices are imperfectly known in real-world systems may lead one to believe that channel estimate method is impractical. The true correlation matrices are difficult to find, in most cases, a rough estimate may be found and is sufficient [5].
-
Interference cancellation
We discuss a low-complexity interference cancellation strategy for channel equalization in addition to the difficulty of doubly-selective channel estimation. Because interference taints the LS channel estimates at the pilot points, for the channel estimation process, interference cancellation is also crucial. The accuracy of the channel estimation can be increased by canceling this interference. The ith iteration step is indicated by the superscript (.)(i) in the following description of how interference cancellation technique and iterative channel estimation operates. MMSE channel estimation of the transmission matrix \({\widehat{\mathbf{D}}}^{(0)}\). One-tap equalization and quantization, \({\widehat{x}}_{l,k}^{(0)}=\mathcal{Q}\left\{{y}_{l,k}^{(0)}/{\widehat{h}}_{l,k}^{(0)}\right\}\) with \({\widehat{h}}^{(0)}=diag\left\{{\widehat{\mathbf{D}}}^{(0)}\right\}\). Interference cancellation,\({y}^{i+1}=y-{\widehat{(\mathbf{D}}}^{\left(i\right)}-dig\left\{diag\left\{{\widehat{\mathbf{D}}}^{(i)}\right\}\right\}{\widehat{x}}^{(i)}\) enhanced estimation of the transmission matrix \({\widehat{D}}^{(i+1)}\), enhances one-tap equalization and quantization, and is enabled by decreased interference at the pilot positions \({\widehat{x}}_{l,k}^{(i+1)}=\mathcal{Q}\left\{{y}_{l,k}^{(i+1)}/{\widehat{h}}_{l,k}^{(i+1)}\right\}\) [5].
Due to nonlinearities that make the analytical computation difficult, the underlying correlation at the pilot points does not account for interference cancellation as in (13). Therefore, we utilize a little mismatched MMSE calculation to get around this issue.
5 Proposed JCEIC based on RNN
In this section, we embark upon an exploration of a well-established channel estimation methodology, one that stands as a vanguard for the integration of DL frameworks in the relentless pursuit of minimizing channel estimate errors. Rooted in a meticulous confluence of theoretical and practical foundations, this methodology endeavors to surmount the limitations attendant to Least Squares (LS) and Linear Minimum Mean Square Error (LMMSE) estimations, engendering a Channel Estimation based on RNN that accentuates the potency of MMSE between channel estimates. Table 1 shows the main differences between CNNs and RNNs.
The proposed architecture of the RNN stands resplendent as a testament to its structural sophistication, akin to an architectural marvel adorned with meticulously organized strata. As depicted in Fig. 2, this RNN edifice encompasses a triad of pivotal layers: the input layer, the hidden layer, and the output layer. Albeit the intrinsic potential for numerous hidden layers within an RNN, our conceptual schema adroitly navigates this design space. The architecture optimally balances complexity and functionality, embedding within its hidden layers an assembly of neurons meticulously calibrated to harmonize with the unique demands posed by both OFDM and FBMC systems.
Central to this architectural symphony, neurons manifest as the quint essential computational entities, diligently orchestrated to execute an intricate array of computations. These computations, as delineated in [17], transcend the realm of mere algorithmic operation, encapsulating the nuanced essence of information processing, transformation, and optimization within the OFDM and FBMC system context.
In the ensuing discourse, we embark upon an odyssey that seamlessly blends theoretical prowess and empirical validation, diligently navigating the realms of computation, modulation, and channel estimation. This research endeavor, a fusion of theory and application, endeavors to unravel the enigma of channel estimation errors, harmoniously weaving the tapestry of DL and neural architectures into the very fabric of channel estimation enhancement. As illustrated through Fig. 2, the architectural expanse of the RNN emerges as a testament to this meticulous pursuit, poised to recalibrate the trajectories of channel estimation and minimize errors within OFDM and FBMC systems.
where the number of inputs is M to this neuron for which \({{\varvec{w}}}_{{\varvec{i}}}\) is the ith weight corresponding to the ith input;\({{\varvec{x}}}_{{\varvec{i}}}\) is the ith input\(({\varvec{i}}\boldsymbol{ }=\boldsymbol{ }1,\boldsymbol{ }.\boldsymbol{ }.\boldsymbol{ }.\boldsymbol{ },\boldsymbol{ }{\varvec{M}})\); \({\varvec{o}}\) is the output of this neuron, and \({\varvec{b}}\) is a bias. In (14), the activation function f(.) is employed to describe the data's nonlinearity. In the proposed framework, the tanh function serves as the activation function in the proposed architecture, which is defined as:
By LS estimation as input, given the channel estimates provided. The Channel estimation based on RNN learns the actual channel information in order to reduce the MMSE. The training process for a realization of the input is specifically defined as
where \({\varvec{n}}\) denotes the nth realization; \({\varvec{R}}{\varvec{e}}\{\cdot \}\) and \({\varvec{I}}{\varvec{m}}\left\{\cdot \right\}\) are the real part and imaginary part of a complex number. The output of the neural network is,
where at the nth realization \({\widehat{{\varvec{h}}}}^{{\varvec{n}}}\) is the neural network output. To tackle the complex numbers for the neural network, we separate the channel estimate in (16) and (17) into real part and imaginary parts. The one-by-one mapping is handled by the learning process:
The neural network's output should match the actual channels exactly as required. As an alternative, the goal of channel estimation based on RNN is to, on average, reduce the MMSE between the prediction and real channels; as a result, during training, the loss function that used is specified as,
for training, the number of realizations \({\varvec{N}}\) is used, and the actual channel \({{\varvec{h}}}^{{\varvec{n}}}\left({\varvec{t}}\right)\) is corresponding to \({\widehat{{\varvec{h}}}}^{{\varvec{n}}}\left({\varvec{t}}\right)\).\(\mathcal{B}\) and \(\mathcal{W}\) biases and weights, respectively. By minimizing the loss function (20),the weights and biases are updated from a group of initial values with forward and backward propagation [22].
5.1 Long short-term memory-based channel estimation
The present study introduces a suite of channel estimation methodologies rooted in the application of RNNs. In response to the challenges inherent to channel estimation, a pragmatic avenue emerges through the integration of neural network paradigms, notably the potent framework of Recurrent Neural Networks. The RNN architecture embodies a temporal cognition, wherein the input for the current time step seamlessly transforms into the output of the preceding time step. This intricate dynamic endows the RNN with the remarkable capacity to recollect prior input information, thereby facilitating a coherent assimilation of temporal dependencies. The computational core of the elementary RNN cell assumes a pivotal role, orchestrating a multifaceted spectrum of calculations that engender an integrated operational milieu, thereby steering the channel estimation endeavor towards a judicious fulfillment of its intended objectives.
where \(f(\cdot )\) is the activation function; at the time step \(t, {x}_{t}\) and \({Y}_{t}\) are the input and the output at the time step \(t\) and\(t-1\), \(;{h}_{t}\) and \({h}_{t-1}\) are the hidden states respectively;\({b}_{ih}, {b}_{hh}\), and \({b}_{ho}\) are the corresponding biases and\({W}_{ih},{W}_{hh}\), and \({W}_{ho}\) are the weights for the input layer to the hidden layer, the hidden layer to the next hidden layer, and the hidden layer to the output layer, respectively [28].
The fundamental Simple RNN cell, while conceptually elegant, harbors intrinsic limitations that warrant careful consideration. One notable limitation resides in its incapacity to harness future data points for decision-making, despite the temporal interplay between the channel's past, present, and future states at a given time step 't'. To address this temporal asymmetry and propel the network towards heightened performance, a contextual deployment of the network is imperative. Secondly, the succinct RNN structure falters in capturing long-term dependencies intrinsic to complex data patterns. In response, the integration of Long Short-Term Memory (LSTM) networks emerges as a judicious panacea. In recognition of these exigencies, the present research advocates the strategic adoption of LSTM networks as an efficacious conduit for channel estimation in the realm of 4G and 5G communication systems [28].
The schematic manifestation of our proposed channel estimation and interference cancellation framework, imbued with the Adam optimizer, finds eloquent expression in Fig. 2. This intricate orchestration, depicted in Fig. 3, commences with a comprehensive training phase, wherein input signals are deftly maneuvered to unfurl the channel response through the prism of the MMSE estimation. These resultant channel responses then assume the mantle of input parameters for the LSTM model, which is meticulously calibrated through an iterative training regimen. The true mettle of this model unfurls during the testing phase, where the estimated channel responses of signals, derived from real-world scenarios, assume the role of inputs for the trained LSTM model. The confluence of these inputs, meticulously shepherded by the intrinsic dynamics of the LSTM structure, culminates in the estimation of the current channel response. This estimation, a manifestation of the interplay between input parameters and loss function minimization, underscores the potency of the LSTM paradigm as a conduit for channel response prediction and interference cancellation.
In summation, the architecture depicted in Figs. 2 and 3 not only embodies the intricate dance between theoretical underpinnings and empirical validation but also epitomizes the paradigmatic shift towards LSTM-driven sophistication in the landscape of channel estimation. As researchers and scholars, our collective endeavor is poised to unravel the latent complexities inherent to communication systems, illuminating hitherto uncharted realms through the fusion of theoretical ingenuity and computational acumen.
6 Simulation results
Within the purview of this scholarly exposition, we delve into an extensive array of simulation results, meticulously navigating the landscapes of OFDM and FBMC systems, each wielding profound significance within the ambit of fourth and fifth-generation networks. The experimental framework envelops a paradigm wherein the Number of Subcarriers is set at 24, accompanied by a robust embrace of 256 Quadrature Amplitude Modulation (QAM) modulation. Central to our analytical voyage is the strategic integration of a RNN, imbued with a tiered architecture comprising five distinctive layers: the sequence input layer, LSTM layer housing 1440 hidden units, a fully connected layer, the SoftMax layer, and the classification output layer.
Within this intricate orchestration, a pivotal cornerstone assumes the form of a diamond-shaped pilot pattern, comprising 32 pilots artfully distributed across the temporal and frequency domains with resourceful precision. This tapestry of pilots spans a temporal domain characterized by LF = 360 kHz and KT = 2 ms, emblematic of a dyadic fusion encompassing two subframes traversing eight resource blocks. In the realm of OFDM, a meticulous calibration of overhead, accounting for pilot symbols and the cyclic prefix (CP), yields an overhead magnitude of \(\frac{{\mathrm{LFT}}_{\mathrm{CP}}\mathrm{K}+\left|\mathcal{P}\right|}{\mathrm{KTLF}} = 11\mathrm{\%}.\)
In the context of FBMC, a judicious recourse to the auxiliary symbol channel estimation methodology is discerned. This strategic choice materializes through the deployment of four auxiliary symbols per pilot, meticulously orchestrated to mitigate interference effects and optimize channel performance. The RNN, a beacon of predictive power, derives its efficacy through an optimization process steered by the Adam optimizer—a potent amalgam of RMSprop and Stochastic Gradient Descent with momentum. The learning rate is calibrated at 0.01 for the RNN, intricately tailored to strike a harmonious balance between convergence and efficiency. The intricate dance of training is orchestrated within a contextual enclave delineated by a batch size of 30, evolving over a maximum of 1000 epochs.
Within this panoramic vista, the network's input channels unfurl as sequences of MMSE channel estimation and interference cancellation, enshrining a complex data milieu. This intricate interplay necessitates a judicious partitioning into real and imaginary components, adeptly calibrated to suit the network's computational requisites. The mantle of training and testing is borne by a robust ensemble of 1000 sequences per SNR for training and 100 sequences per SNR for testing, a corpus engineered to encompass the intricacies of estimated channel interference amidst the symphony of interference cancellation. This monumental training endeavor transcends SNR domains spanning from -10 dB to 40 dB, thus embracing a comprehensive panorama reflective of a diverse spectrum of signal strengths.
Figures 4, 5, 6, 7, 8, 9, 10, 11 present a comprehensive exposition of BER analyses across varying SNRs for diverse scenarios within the domain of OFDM systems. Within this tableau of figures, we embark upon a nuanced journey through distinct scenarios, each shedding light on the intricate interplay between RNN-driven interference cancellation and the backdrop of distinct channel conditions.
Figure 4 unfurls an insightful panorama, wherein interference cancellation through RNN engenders commendable BER performance across diverse SNRs. The intricacies of the "no edge" scenario, as illustrated in Fig. 5, illuminate the prowess of the MMSE methodology, outshining RNN. Figure 6 emerges as a testament to the adeptness of RNN in the context of one-tap equalization, particularly in higher SNR environments. A juxtaposition of one-tap equalization and the "no edge" milieu, as depicted in Fig. 7, accentuates RNN's prowess in mitigating BER. Figure 8 resonates with the resonance of RNN's capabilities within the precincts of perfect CSI and one-tap equalization. Figure 9 sheds light on the dichotomy between RNN and MMSE, with the former asserting its supremacy in the realm of one-tap equalization, devoid of edge conditions. Figure 10 introduces the prism of perfect CSI and interference cancellation, elucidating the BER disparities between RNN and MMSE. In Fig. 11, the interplay of perfect CSI, interference cancellation, and the absence of edge conditions unravels RNN's strength in SNR-constrained environments.
Figures 12, 13, 14, 15, 16, 17, 18 pivot towards the arena of FBMC systems, wherein the symbiotic dance of RNN and MMSE unfolds. Figure 12 paints a picture of MMSE's potency in low SNR domains, while RNN ascends the pedestal at higher SNRs. One-tap equalization coupled with auxiliary symbols, as portrayed in Fig. 13, witnesses RNN's prowess surmounting MMSE. In the realm of auxiliary symbols with one-tap equalization and the "no edge" configuration, as presented in Fig. 14, RNN ushers in near-zero BER at elevated SNRs. Figure 15 unveils the harmony between auxiliary symbols, one-tap equalization, and perfect CSI sans edge conditions, underscoring RNN's ascendancy over MMSE. Figure 16 sketches a scenario wherein code symbols blend with one-tap equalization, signaling RNN's proximity to MMSE in BER. The synergy between code symbols, one-tap equalization, and "no edge" conditions, elucidated in Fig. 17, underscores RNN's supremacy. Figure 18 unveils the zenith of RNN's performance with code symbols, one-tap equalization, and perfect CSI.
From this extensive trajectory of analyses, a cardinal observation emerges—RNN exemplifies a potent catalyst for channel estimation and interference cancellation. Figure 19 interjects with a broader vista, accentuating RNN's efficacy within the echelons of 5G systems, outperforming the traditional OFDM paradigm. Figure 20 accentuates RNN's efficacy across FBMC and OFDM, marking its ascendancy at elevated SNRs. This discourse concludes with an incipient horizon, as RNN's transformative potential extends beyond this realm, poised to permeate diverse transmission systems, encompassing the realms of MIMO and Non-Orthogonal Multiple Access (NOMA). Through these figures, we navigate a rich tapestry of simulation results, unraveling the multifaceted impact of RNN across a spectrum of transmission landscapes. The drawback for RNN is the time that taken for the training process and the huge data needed for training. The advantage of this method is the high accuracy of the testing process which reach to 97% and low loss. Accuracy of the RNN is an evaluation indicators and achieve a high accuracy for both OFDM and FBMC systems. The BER for the recovered signal is affected by the high-precision CSI estimation problem. One of the most serious problems is the high Peak-to-Average Power Ratio (PAPR) of the transmitted OFDM signal since these large peaks introduce a serious degradation in performance. The original OFDM signal, which suffers from a high peak-to-average power ratio (PAPR), is introduced with pilot tones using these estimate methods. The signal frequency offset caused by the time variability of wireless signals during transmission does not affect the accuracy of channel estimation and interference cancellation.
7 Conclusions and future work
In this scholarly pursuit, we present an innovative application of Recurrent Neural Networks (RNN) to the realm of Joint Channel Estimation and Interference Cancellation (JCEIC) within Orthogonal Frequency Division Multiplexing (OFDM) and Filter Bank Multicarrier (FBMC) systems. Our approach entails channel estimation within the intricate domain of doubly-selective channels, harnessing the synergy of scattered pilots' temporal and frequency correlation. Concurrently, a judiciously tailored low-complexity interference cancellation framework complements the channel estimation endeavor. The cornerstone of our JCEIC architecture resides in Long Short-Term Memory (LSTM), a variant of RNN esteemed for its aptitude in temporal modeling.
The essence of our methodology encapsulates the orchestration of channel estimation and interference cancellation. These dynamic processes converge to generate output sequences that unfurl as inputs to the LSTM framework, fostering an insightful interplay between these pivotal components. Empirical validation is realized through an array of simulation results, wherein our proposed technique asserts its mettle, manifesting superior Bit Error Rate (BER) performance relative to antecedent methodologies. Of paramount import is the revelation that Filter Bank Multicarrier (FBMC) systems eclipse their Orthogonal Frequency Division Multiplexing (OFDM) counterparts in terms of performance.
The implications of our findings reverberate across diverse echelons of wireless communication, spanning the realms of Fourth and Fifth Generation (4G and 5G) networks, particularly in the domain of low Signal-to-Noise Ratios (SNRs) and wireless sensor networks. A trajectory of future exploration is delineated, wherein our proposed methodology serves as the nucleus for future endeavors encompassing Non-Orthogonal Multiple Access (NOMA) systems. Moreover, the overarching framework holds the promise of cascading into joint signal detection, channel estimation, and interference cancellation arenas, attesting to its transformative potential.
However, it is imperative to acknowledge the nuanced limitations inherent within our work. First and foremost, the efficacy of our approach may hinge upon the availability of substantial training data, potentially rendering data collection and labeling a resource-intensive endeavor. The intricate architecture of our proposed RNN may exact a computational toll, demanding considerable resources for real-time deployment. The system's interference cancellation efficacy may also be contextually contingent, potentially displaying performance disparities in the face of dynamically unpredictable interference scenarios.
In light of these considerations, our future trajectory unfurls with vigor. We aspire to engineer streamlined and resource-efficient RNN architectures, tailored for real-time operation on power-constrained devices. The pursuit of generalization guides our exploration into adapting our approach to a panorama of communication standards and diverse contextual scenarios. The integration of unsupervised learning methodologies beckons to augment our reliance on labeled data. Rigorous empirical validation in real-world environments and under divergent interference conditions stands as a cardinal waypoint of our future exploration.
Concurrently, the potential of synergistic enhancements beckons, invoking the prospect of amalgamating our approach with other interference mitigation techniques to distill unprecedented heights of performance. Through these collective endeavors, we aspire to lay the groundwork for an augmented paradigm, culminating in a holistic advancement of channel estimation and interference cancellation frameworks within modern wireless communication landscapes.
Limitations of the proposed work may include:
-
Data availability: The approach may require a large amount of training data to accurately estimate the channel and cancel interference. However, collecting and labelling such data can be expensive and time-consuming.
-
Complexity: The proposed RNN architecture may be computationally expensive and require significant resources for real-time implementation.
-
Interference cancellation performance: The interference cancellation performance of the proposed approach may depend on the type and level of interference present in the communication system, and it may not perform optimally in highly dynamic and unpredictable interference environments.
Future work on this work could include:
-
Developing more efficient and lightweight RNN architectures that can be implemented in real-time on low-power devices.
-
Investigating the generalization of the proposed approach to other communication standards and scenarios.
-
Exploring the use of unsupervised learning techniques to reduce the reliance on labelled data.
-
Evaluating the performance of the proposed approach in real-world scenarios and under different interference conditions.
-
Studying the potential benefits of combining the proposed approach with other interference mitigation techniques to further enhance the system's performance.
Availability of data and materials
The authors do not have permission to share data.
Change history
18 December 2023
A Correction to this paper has been published: https://doi.org/10.1186/s13634-023-01090-3
References
J. Srikanth, P. Sreesrinivas, M. Kethavath, Interference Cancellation and Doubly Selective Channel Estimation in FBMC-based OFDM Systems. Turk. J. Comput. Math. Educ. (TURCOMAT) 11(2), 844–853 (2020)
C. Lele, et al., Preamble-based channel estimation techniques for OFDM/OQAM over the powerline, in 2007 IEEE International Symposium on Power Line Communications and Its Applications. (IEEE, 2007).
S. Mahama, et al., Iterative interference cancellation in FBMC-QAM systems, in 2019 IEEE Wireless Communications and Networking Conference (WCNC). (IEEE, 2019).
J. Li et al., Intrinsic interference cancellation scheme for FBMC-OQAM systems based on power multiplexing. Electronics 11(9), 1443 (2022)
R. Nissel, F. Ademaj, M. Rupp, Doubly-selective channel estimation in FBMC-OQAM and OFDM systems, in 2018 IEEE 88th Vehicular Technology Conference (VTC-Fall). (IEEE, 2018).
H. Wang, W. Du, L. Xu, Novel preamble design for channel estimation in FBMC/OQAM systems. KSII Trans. Internet Inf. Syst. (TIIS) 10(8), 3672–3688 (2016)
W. Cui et al., Coded auxiliary pilots for channel estimation in FBMC-OQAM systems. IEEE Trans. Vehic. Technol. 65(5), 2936–2946 (2015)
H. Wang et al., Preamble design with interference cancellation for channel estimation in MIMO-FBMC/OQAM systems. IEEE Access 6, 44072–44081 (2018)
V. Kumar Singh et al., Supervised learning and frequency domain averaging-based adaptive channel estimation scheme for filterbank multicarrier with offset quadrature amplitude modulation. ETRI J. 43(6), 966–977 (2021)
A. Bedoui, M. Et-tolba, A deep neural network-based interference mitigation for MIMO-FBMC/OQAM systems. Front. Commun. Netw. 2, 728982 (2021)
G.B. Cheng et al., Interference cancellation aided channel estimation for OFDM/OQAM system. Sci. China Inf. Sci. 56(12), 1–8 (2013)
N. Shlezinger, Fu. Rong, Y.C. Eldar, DeepSIC: deep soft interference cancellation for multiuser MIMO detection. IEEE Trans. Wireless Commun. 20(2), 1349–1362 (2020)
T. Xu, T. Xu, I. Darwazeh, Deep learning for interference cancellation in non-orthogonal signal based optical communication systems, in 2018 Progress in Electromagnetics Research Symposium (PIERS-Toyama). (IEEE, 2018).
V.-D. Nguyen et al., Channel estimation and interference cancellation for MIMO-OFDM systems. IEICE Trans. Commun. 90(2), 277–290 (2007)
L. Smirani, Contribution of deep learning algorithm to improve channel estimation performance. Open Access Lib. J. 7(3), 1–16 (2020)
A. Yang, et al., Deep Learning Based OFDM Channel Estimation Using Frequency-Time Division and Attention Mechanism, in 2021 IEEE Globecom Workshops (GC Wkshps). (IEEE, 2021).
P. Dong et al., Deep CNN-based channel estimation for mmWave massive MIMO systems. IEEE J. Sel. Top. Signal Process. 13(5), 989–1000 (2019)
Y. Liao, et al., ChanEstNet: A deep learning based channel estimation for high-speed scenarios, in ICC 2019–2019 IEEE international conference on communications (ICC). (IEEE, 2019).
P. Dong, et al., Deep CNN for wideband mmWave massive MIMO channel estimation using frequency correlation, in ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). (IEEE, 2019).
X. Cheng et al., Deep learning-based channel estimation and equalization scheme for FBMC/OQAM systems. IEEE Wirel. Commun. Lett. 8(3), 881–884 (2019)
Q. Hu et al., Deep learning for channel estimation: interpretation, performance, and comparison. IEEE Trans. Wirel. Commun. 20(4), 2398–2412 (2020)
A. Emir et al., Deep learning-based flexible joint channel estimation and signal detection of multi-user OFDM-NOMA. Phys. Commun. 48, 101443 (2021)
W. de Souza Junior, T. Abrao, Machine Learning-based Methods for Joint {Detection-Channel Estimation} in OFDM Systems (2023). arXiv e-prints: arXiv-2304.
M. He, C. Huang, Self-interference cancellation for full-duplex massive MIMO OFDM with single RF chain. IEEE Wirel. Commun. Lett. 9(1), 26–29 (2019)
Song, C., et al. A Double-Threshold Channel Estimation Method Based on Adaptive Frame Statistics (2023).
E. Ali, M. Hassan et al., Deep learning peephole LSTM neural network-based channel state estimators for OFDM 5G and beyond networks. Mathematics 11(15), 3386 (2023)
H.Y. Sun, S.Y. Li, RLS channel estimation combined with channel equalization in oversampled frequency domain for FBMC-QAM systems. J. Phys. Conf. Ser. 2476(1), 1 (2023)
D. Khosla, et al. OFDM modulation technique & its applications: a review, in International Conference on Innovations in Computing (ICIC 2017) (2017).
B.D. Tensubam, S. Singh, A review on FBMC: an efficient multicarrier modulation system. Int. J. Comput. Appl. 98(17), 6–9 (2014)
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: Following publication of the original article, we have been notified that the last three references were not mentioned in the text and should be removed from the reference list.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Al-Makhlasawy, R.M., Khairy, M. & El-Shafai, W. Recurrent neural networks for enhanced joint channel estimation and interference cancellation in FBMC and OFDM systems: unveiling the potential for 5G networks. EURASIP J. Adv. Signal Process. 2023, 120 (2023). https://doi.org/10.1186/s13634-023-01077-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-023-01077-0