Abstract
Increasing the spectrum and time utilization rate is the goal of the next wireless communication networks. This work studies the outage performance of the reconfigurable intelligent surface (RIS)-aided integrated satellite duplex unmanned-aerial-vehicle relay terrestrial networks. Especially, the RIS is installed in the tall building to enhance the communication. To further increase the time utilization rate, the duplex unmanned aerial vehicle is utilized to enhance the time utilization efficiency. However, owing to the practical reasons, the imperfect hardware and co-channel interference are further researched in this paper. Particularly, the accurate expression for the outage probability (OP) is gotten to confirm the effects of RIS parameters, channel parameters and imperfect hardware on the considered network. To gain more insights of the OP at high signal-to-noise ratios, the asymptotic analysis for the OP is derived. Finally, some Monte Carlo simulations are provided to verify the rightness of the theoretical analysis. The simulations indicate that the OP is mainly judged by the satellite transmission link. The results also indicate that although RIS can enhance the system performance, the system performance is not decided by RIS.
Similar content being viewed by others
1 Introduction
Satellite communication (SatCom) is regarded as a wishing method to achieve the goal of the next generation wireless communication networks for its own characters, for instance, wide coverage and high energy utilization efficiency [1,2,3]. However, owing to the some practical reasons, the satellite sometimes cannot communicate with the terrestrial users directly, which needs the help of the terrestrial/aerial networks [4,5,6,7,8,9]. On this foundation, the combination of the SatCom and terrestrial/aerial networks appears, which forms the integrated satellite terrestrial/aerial networks (IST/ANs) [10,11,12]. IST/ANs overcome the shortages of the SatCom and terrestrial/aerial networks. Besides, IST/ANs utilize the advantages of the both networks, which have been regarded as the future issue for the next wireless communication networks [13, 14]. IST/ANs have been considered as the important part in the practical systems, such as Digital Video Broadcasting (DVB) networks and the Space-Ground Integrated Information Network Engineering of China [15, 16].
1.1 Related literatures
The investigation for IST/ANs is regarding as a hot topic these years, it has attract so many interests [17,18,19,20]. In [19], the authors proposed a relay selection algorithm for a representative uplink IST/AN, moreover, the outage probability (OP) was investigated along with the asymptotic analysis. In [20], the threshold was introduced into the terrestrial selection algorithm for the considered IST/AN with several terrestrial relays and several users. In addition, the system complexity was further investigated after the OP analysis. In [21], the max-max terrestrial relay/user scheduling algorithm was proposed to improve the system performance, i.e., reducing the OP. In [22], the secondary networks selection algorithm was utilized to enhance the ergodic capacity (EC) for the IST/ANs in the presence for several terrestrial relays and several users. The authors in [23] gave a user scheduling algorithm for an uplink IST/AN with two channel state information (CSI) scenarios. To enhance the spectrum utilization, cognitive technology is used for the IST/ANs [24,25,26]. Through [17], the secure problem was researched for the IST/ANs with cognitive technology, furthermore, the secrecy OP was studied. The authors in [24] researched the secure beamforming issue for the cognitive IST/ANs by using wireless power. In [25], the authors researched the EC for the non-orthogonal multiple access (NOMA)-assisted IST/ANs by utilizing cognitive technology. In [26], the authors proposed an optimization issue by jointly utilizing the terrestrial beamforming design and the satellite scheduling for the IST/ANs. In [27], the authors investigated the delay optimization problem for the IST/ANs by utilizing the multi-tier computing method.
As announced before, high energy utilization efficiency is one of the target requirements of the next generation networks. To achieve this goal, two-way and duplex relay technique come to our sights [28,29,30,31]. Owing to the fact that in the common networks, the relay or the UAV will take two time slots for the whole communication in only one transmission link, namely, the uplink transmission link or the downlink [32, 33]. In [34], a two-way terrestrial relay was utilized in the IST/ANs to enhance the transmission, besides, the OP was deeply investigated along with the closed-form expressions. In [35], several two-way terrestrial relays were utilized to enhance the communication quality and improve the energy efficiency in the presence of closed-form and asymptotic expressions for the IST/ANs. In [36], several two-way terrestrial relays were used for the IST/ANs with non-ideal hardware, particularly, the secrecy OP (SOP) was further investigated, besides, the secrecy diversity order and secrecy coding gain were also gotten. In [37], the authors proposed the optimization method, whose goal is optimize the full-duplex IST/ANs with NOMA. In [38], the authors researched the secrecy problem for the IST/ANs against eavesdropping and jamming.
Another famous technology that can improve the energy utilization efficiency is the reconfigurable intelligent surface (RIS) technology [39,40,41]. RIS can save the energy by utilizing the man-made electromagnetic surfaces which can be controlled through electronic tools [42]. RIS has been the widely investigated in the terrestrial networks, also consisted of the UAV networks [43]. In [44], the widely used RIS channel was proposed in this paper, which provided a computable probability density function (PDF) for the terrestrial networks. Besides, the OP was deeply investigated along with the closed-form expressions. In [45], the authors researched the OP for the RIS-enabled IST/ANs with the help of a UAV along with the non-ideal hardware. The most importance was that the famous RIS channel model used came from [44]. In [46], the authors explored the rate-splitting multiple access scheme RIS-enabled vehicle networks along with the UAV and interference. Particularly, the average OP was analyzed. In [47], the capacity of the system was maximized for the RIS-UAV networks in the presence of trajectory and phase shift optimization. In [48], RIS was used in the NOMA-assisted networks to enhance the system performance, particularly, they formulated an optimization issue whose goal is to enhance the sum rate. In [49], the secrecy performance was investigated in the RIS-aided communication systems through the help of UAVs. In [50], the SOP was investigated for the IST/ANs with multiple eavesdroppers, particularly, the accurate expressions for the SOP were along derived. In [51], the authors investigated the impact of simultaneously transmitting and reflecting-RIS on the cognitive IST/ANs, furthermore, the authors obtained closed-form expressions of OP for the secondary users.
As mentioned before, the satellite owns wider coverage when compared with the terrestrial nodes, which leads to the fact that several terrestrial relays/UAVs exist in one satellite transmission beam [52,53,54,55]. In addition, to simplify the analysis, relay selection algorithm is always utilized, through the selection algorithm, two famous algorithms are used in the literatures, namely, the opportunistic relay selection algorithm and partial relay selection algorithm [53, 55]. However, the opportunistic selection scheme needs the whole CSI of the whole links. Thus, the partial selection scheme appears, which needs only the CSI of one transmission link not the whole link which reduces the complexity and can get the acceptable performance [20]. Above all, in our work, we use the partial selection algorithm to analyze the system performance.
1.2 Motivations
To its regret, most of the former works focused on the perfect hardware, which is not practical in real systems. In practical scenarios, the hardware often suffers from several kinds of imperfect limitations, for example high power amplifier nonlinearity, phase noise, and the other issues [56,57,58]. In [59], the authors summarized the whole issues and gave a popular imperfect hardware (IH) model which is widely utilized in so many papers. In [60], the authors researched the influence of IH on the SatCom, besides, the detailed investigations of OP was further investigated. In [61], the effect of IH was analyzed on the secrecy IST/ANs along with NOMA along with opportunistic terrestrial relay selection algorithm. In [19], the influence of IH was investigated for the uplink IST/ANs along with several terrestrial relays. In [20], the authors utilized the threshold-based terrestrial scheduling algorithm for the IST/ANs in the presence of IH, particularly, the impact of IH was investigated for the considered system through the system complexity analysis. Furthermore, the investigations for the SOP were obtained. The influence of IH on the two-way terrestrial relay for the IST/ANs has been investigated in [34, 35]. However, to the authors’ best efforts, the investigations for the RIS-assisted IST/ANs in the presence of a full-duplex UAV remain unreported, especially by considering the IH. The above illustrations motivate the major work of this paper.
1.3 Our contributions
Discussed by the above observations, by both considering the IH, RIS and a duplex UAV into our consideration, this paper investigates the performance for the regarded ISAN by utilizing partial UAV selection scheme. Particularly, self-interference and co-channel interference are also analyzed in this paper. The major work of this paper is given in the following
-
By both taking the IH and duplex UAV relay into our consideration, this paper forms an investigated model, namely, the integrated satellite multiple duplex UAV relay terrestrial networks (ISMDURTNs). In this system model, several UAVs are utilized. In addition, decode-and-forward (DF) scheme is used at UAVs to help the satellite transmit the transmission signals.
-
Upon the considered network, we get the accurate analysis for the OP. To reduce the secrecy complexity, partial UAV selection algorithm is applied to balance the complexity and performance. Moreover, the investigations for the OP are gotten, which can guide the engineering work.
-
The analysis for the OP in high signal-to-noise ratio (SNR) regime is also given. Relied on these derivations, the coding gain and diversity order are also gotten. The results show that IH has great impact on the OP. Besides, partial UAV selection algorithm also has a great influence on the OP.
The remaining of our paper is shown as what follow. In Sect. 2, the system model is illustrated along with the signal transmission process. In Sect. 3, the OP is detailed investigated, particularly, the satellite transmission model, the RIS channel model and the accurate analysis for OP is further researched. In Sect. 4, the asymptotic analysis for the OP is gotten along with the coding gain and diversity order. Through Sect. 5, some representative Monte Carlo (MC) simulation results are given to confirm the theoretical analysis. Finally, the whole summary of our work is provided in Sect. 6.
2 System model and signal transmission
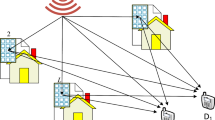
As introduced in Fig. 1, in our work, we investigate an ISMDURTN, which contains a satellite (S), P duplex UAVs (R) and a vehicle user (D). Owing to some practical reasons, the S or UAV cannot transmit the signal to D, directlyFootnote 1. On this foundation, the RIS is installed in a tall building to assist the transmission. Besides, owing to the wide coverage, M interferers are considered to affect the R and D. To balance the system complexity and performance, partial UAV selection algorithm is utilized to gain better system. All the transmission nodes own one antennaFootnote 2. For the whole system, it needs 2 time slots to complete the transmission.
In the 1st time slot, S sends it signal \(s\left( t \right)\) with \(E\left[ {{{\left| {s\left( t \right) } \right| }^2}} \right] = 1\) to R, as R is the duplex relay with two antennas, thus the received signal at R is given as
where \(P_S\) depicts the transmission power for S, \(h_{SR_p}\) depicts the channel issue between S and the pth R which suffers from the shadowed-Rician (SR) fading, \({\eta _S}\left( t \right)\) is the distortion noise cased by the IH [62, 63] that satisfies \(\eta _{S}(t) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,k_{S}^2} \right)\) with \(k_S\) being the IH level [62, 63] at S. \(P_{RR_p}\) depicts the power of the pth R for the self-interference caused by the duplex mode, \(h_{RR_p}\) denotes the channel fading for the self-interference which suffers Rayleigh fading, \({{s_{R{R_p}}}\left( t \right) }\) is the self-interference signal with \(E\left[ {{{\left| {{s_{R{R_p}}}\left( t \right) } \right| }^2}} \right] = 1\), \({\eta _{RR_p}}\left( t \right)\) is the distortion noise cased by the IH that satisfies \(\eta _{RR_p}(t) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,k_{RR_p}^2} \right)\) with \(k_{RR_p}\) denoting the IH level at the pth self-interference R. \(P_{I{r}}\) represents the interference power from the rth I, \(h_{I_rR_p}\) represents the channel shadowing between the rth I and pth R with suffering Rayleigh fading, \({\eta _{I_rR_p}}\left( t \right)\) is the distortion noise cased by the IH that satisfies \(\eta _{{I_rR_p}}(t) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,k_{{I_rR_p}}^2} \right)\) with \(k_{I_rR_p}\) giving as the IH level at the rth I for the \(I_r \rightarrow R_p\) link. \({n_{{R_p}}}\left( t \right)\) represents the additive white Gaussian noise (AWGN) at the pth R with the form as \({n_{{R_p}}}\left( t \right) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,\delta _{R_p}^2} \right)\).
For the 2nd time slot, as announced before, the chosen R re-transmits the received signal \(s\left( t \right)\) to D via the help of the RIS element. At the same time, M interferes affect D by sending the information signal. Finally, the gotten signal at D is seen as
where \(P_{R_p}\) depicts the transmission power for the pth R of the \(R \rightarrow D\) link, N is the number of the RIS elements. \({\varphi _i}\) depicts the phase shift utilized by the ith reflecting factor of the RIS, \(h_{RV_i}\) and \(h_{V_iD}\) are the channel gains with presentations as \({h_{R{V_i}}} = {\chi _i}{e^{ - {\phi _i}}}/\sqrt{{L_{R{V_i}}}}\), \({h_{{V_i}D}} = {\kappa _i}{e^{ - {\theta _i}}}/\sqrt{{L_{{V_i}D}}}\), respectively. \({\chi _i}\) and \({\kappa _i}\) are the Rayleigh random variable with mean \(\sqrt{\pi }/2\) and variance \(\left( {4 - \pi } \right) /4\). \({L_{R{V_i}}} = 10{\log _{10}}\left( {d_{R{V_i}}^\vartheta } \right) + A\) and \({L_{{V_i}D}} = 10{\log _{10}}\left( {d_{{V_i}D}^\vartheta } \right) + A\) denote the path loss, where A denotes as a fixed value which relies on the transmission frequency and transmission environment, \(d_{RV_i}\) and \(d_{V_iD}\) represent the distance of the \(R-RIS\) and \(RIS-D\) links with \(\vartheta\) being the path loss issue. \({{\eta _{{R_p}}}\left( t \right) }\) is the distortion noise cased by the IH that satisfies \(\eta _{R_p}(t) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,k_{R_p}^2} \right)\) with \(k_{R_p}\) being the IH level at the pth transmission R. \(h_{I_rD}\) depicts the channel factor between the rth I and D which suffers from Rayleigh fading, \({{\eta _{{I_rD}}}\left( t \right) }\) represents the distortion noise cased by the IH that satisfies \(\eta _{I_rD}(t) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,k_{I_rD}^2} \right)\) with \(k_{I_rD}\) regarding as the IH level at the rth I for the \(I_r \rightarrow D\) link. \({n_{{D}}}\left( t \right)\) depicts the AWGN at the D which is represented as \({n_{{D}}}\left( t \right) \sim {{\mathcal {C}}{\mathcal {N}}}\left( {0,\delta _{D}^2} \right)\).
From (1), the obtained signal-to-interference-and-noise-plus-distortion ratio (SINDR) is shown as
where \({\lambda _{S{R_p}}} = \frac{{{P_S}{{\left| {{h_{S{R_p}}}} \right| }^2}}}{{\delta _{{R_p}}^2}}\), \({\lambda _{R{R_p}}} = \frac{{{P_{R{R_p}}}{{\left| {{h_{R{R_p}}}} \right| }^2}}}{{\delta _{{R_p}}^2}}\) and \({\lambda _{I{R_p}}} = \sum \limits _{r = 1}^M {\frac{{{P_{{I_r}}}{{\left| {{h_{{I_r}{R_p}}}} \right| }^2}}}{{\delta _{{R_p}}^2}}}\).
Owing to the partial selection scheme, the derived SINDR for the first transmission link is given byFootnote 3
With the help of [45], by letting \({\varphi _i} = {\phi _i} + {\theta _i}\), the maximal output signal for the \(R \rightarrow D\) link is written as
From (2), the signal-to-noise and distortion ratio (SNDR) for the second transmission link is derived as
where \({\lambda _{{R_p}D}} = \frac{{{P_{{R_p}}}{{\left( {\sum \nolimits _{i = 1}^N {{\chi _i}{\kappa _i}} } \right) }^2}}}{{{L_{R{V_i}}}{L_{{V_i}D}}\delta _D^2}}\), \({\lambda _{ID}} = \sum \nolimits _{r = 1}^M {\frac{{{P_{{I_r}}}{{\left| {{h_{{I_r}D}}} \right| }^2}}}{{\delta _D^2}}}\)
As described before, DF forward protocol is utilized at R, thus the total SINDR of the whole network is written as
3 System performance evaluation
During this Section, the detailed investigations for the OP of the considered system will be given. At the very beginning, the illustration of the channel model is given.
3.1 The channel model
3.1.1 The interference link model
In the system model, we have illustrated that there are M interferes interfering the R and D. As the popular assumption, the channel model for \(\lambda _{IR_p}\) and \(\lambda _{ID}\) are considered to suffer from the Rayleigh fading, relied on [20], then the PDF for \(\lambda _Q,Q \in \left\{ {I{R_p},ID} \right\}\) is given by
where \({A_Q} = diag\left( {{{\overline{\lambda }}_{{Q_1}}}, \ldots ,{{\overline{\lambda }}_{{Q_q}}}, \ldots ,{{\overline{\lambda }}_{{Q_M}}}} \right)\), \({\rho \left( {{A_Q}} \right) }\) represents the number of distinct factors of \(A_Q\), \({\overline{\lambda }_{{Q_{\left\langle 1 \right\rangle }}}}> {\overline{\lambda }_{{Q_{\left\langle 2 \right\rangle }}}}> \cdots > {\overline{\lambda }_{{Q_{\left\langle {\rho \left( {{A_Q}} \right) } \right\rangle }}}}\) depicts the ascending order of \({{{\overline{\lambda }}_{{Q_{\left\langle q \right\rangle }}}}}\), \({{\tau _q}\left( {{A_Q}} \right) }\) is the multiplicity of \({{{\overline{\lambda }}_{{Q_{\left\langle q \right\rangle }}}}}\), and \({{\mu _{q,j}}\left( {{A_Q}} \right) }\) denotes the \(\left( {q,j} \right)\)th characteristic factor of \(A_Q\) [20].
By utilizing [34], the channel mode for the self-interference link of the duplex R is given by
where \({\overline{\lambda }}\) denotes the channel gain.
3.1.2 The R \(\rightarrow\) D link model
By utilizing [45], the PDF for \(\lambda _{R_pD}\) can be written as
where \(s = N\pi /4\) and \({\delta ^2} = N\left( {1 - {\pi ^2}/16} \right)\).
Then, by utilizing some calculating steps, the cumulative distribution function (CDF) for \(\lambda _{R_pD}\) has the expression as
where
where \(A = \frac{1}{{2{\delta ^2}\overline{\lambda }_{{R_p}D}^2}}\), \(B = \frac{{ - s}}{{2{\delta ^2}{{\overline{\lambda }}_{{R_p}D}}}}\) and \(C = \frac{{{s^2}}}{{2{\delta ^2}}}\). Besides, \(erf\left( x \right)\) depicts the error function which has been defined in [64]. By [64], \(erf\left( x \right)\) has the following expression as
where \(\left( \cdot \right) !!\) represents the double factorial function [64].
3.1.3 The satellite transmission model
In our work, the geosynchronous Earth orbit (GEO) satelliteFootnote 4 is taken for an example. In addition, the satellite is considered to own several transmission beams. time division multiple access (TDMA) [65] is used for the GEO. \(h_{SR_p}\) can be written as
where \(f_{SR_p}\) depicts the SR issue. \(C_{SR_p}\) is the influence of the antenna pattern and the free space loss (FSL), which has the form as
where c is regarding as the communication speed, f represents the communication frequency. d is the distance between the satellite’s center and the UAV. Besides, \(d_0\approx 35{,}786\;{\text{km}}\), \(G_{SR_p}\) represents the gain of the UAV antenna. \(G_R\) depicts the on-board beam gain of the satellite.
From the similar method of [60], \(G_R\) has the following expression as
where \({\overline{G} _{\max }}\) denotes the maximal value of the beam gain. \(\vartheta\) depicts the angle of the off-boresight. By investigating \(G_{SR_p}\), \(\theta _k\) is assumed as the angle of the transmission. \(\bar{\theta }_k\) is expressed as the 3 dB angle. By considering all of these factors, \(G_{SR_p}\) can be re-written as [18, 60]
where \(G_{max}\) depicts the largest value of the beam gain. Besides, \({u_k} = 2.07123\sin {\theta _k}/\sin {\overline{\theta }_k}\), \(K_3\) and \(K_1\) represents the 1st-kind bessel function of order 3 and order 1, respectively. In order to get the best beam gain, \({\theta _k}\) is set as 0 value, which can results into the fact that \({G_{SR_p}} \approx {G_{\max }}\). Based on these considerations, \({h_{SR_p}} = C_{SR_p}^{\max }{f_{SR_p}}\) can be gotten.
By considering the \(f_{SR_p}\), a widely utilized fading model is provided in [66], which has been the popular assumption for the land mobile satellite (LMS) communication [18]. In [60], \(f_{SR_p}\) has the expression as \({f_{SR_p}} = {\overline{f} _{SR_p}} + {\widetilde{f}_{SR_p}}\), where \({\widetilde{f}_{SR_p}}\) has the consideration as i.i.d Rayleigh fading distribution. In addition, \({\overline{f} _{SR_p}}\) represents the factor of line-of-sight (LoS) component which has the fading as i.i.d Nakagami-m shadowing.
Moreover, the PDF of \({\lambda _{SR_p}} = {\overline{\lambda }_{SR_p}}\left| {C_{SR_p}^{\max }{f_{SR_p}}} \right|\) is derived as
where \({\overline{\lambda }_{SR_p}}\) denotes the average SNR between the satellite and UAV. \({\Delta _{SR_p}} = \frac{{{\beta _{SR_p}} - {\sigma _{SR_p}}}}{{{{\overline{\lambda }}_{SR_p}}}}\), \({\alpha _{SR_p}} = {\left( {\frac{{2{b_{SR_p}}{m_{SR_p}}}}{{2{b_{SR_p}}{m_{SR_p}} + {\Omega _{SR_p}}}}} \right) ^{{m_{SR_p}}}}/2{b_{SR_p}}\), \({\delta _{SR_p}} = \frac{{{\Omega _{SR_p}}}}{{\left( {2{b_{SR_p}}{m_{SR_p}} + {\Omega _{SR_p}}} \right) 2{b_{SR_p}}}}\), \({\beta _{SR_p}} = 1/2{b_{SR_p}}\), where \(m_{SR_p} \ge 0\), \(2b_{SR_p}\) and \({\Omega _{SR_p}}\) are t the channel factors with the definition as the fading severity parameter, the multipath’s component’s power and the LoS element’s average power. From the popular consideration, \(m_{SR_p}\) is regarded as an integer in this paper [22]. When \(m_{SR_p} \rightarrow \infty\), the shadowed-Rician channel will be reduced to the Rician fading. At last, \({\left( \cdot \right) _{{k_1}}}\) represents the Pochhammer symbol [64].
By utilizing (18) and the help of [21], the CDF of \(\lambda _{SR_p}\) has been shown as
3.2 The OP
By utilizing [60], the OP is defined as
With the help of (7), (20) can be re-given as
The accurate expression for OP will be given in Theorem 1.
Theorem 1
The closed-form expression for OP of the considered system is given by
where \({A_1} = \frac{{\left( {1 + k_{R{R_p}}^2} \right) {\gamma _0}}}{{1 - k_S^2{\gamma _0}}}\), \(B = \frac{{\left( {1 + k_{{I_r}{R_p}}^2} \right) {\gamma _0}}}{{1 - k_S^2{\gamma _0}}}\), \(C = \frac{{{\gamma _0}}}{{1 - k_S^2{\gamma _0}}}\), \(E = \frac{{\left( {1 + k_{{I_r}D}^2} \right) {\gamma _0}}}{{\left( {1 - k_{{R_p}D}^2{\gamma _0}} \right) }}/\sqrt{2{\delta ^2}\overline{\lambda }_{{R_p}D}^2}\) and \(F = \left[ {\frac{{{\gamma _0}}}{{1 - k_{{R_p}D}^2{\gamma _0}}} - s} \right] /\sqrt{2{\delta ^2}\overline{\lambda }_{{R_p}D}^2}\).
Proof
The detailed step can be seen in “Appendix 1”. \(\square\)
4 The asymptotic OP
To derive further investigations of the major issues on the OP, the approximate analysis for the OP can be obtained in the following analysis. When \(\bar{\gamma }_{SR_p} \rightarrow \infty\) and \(\bar{\gamma }_{R_pD} \rightarrow \infty\), (19) and (11) has the expression as
where \(o\left( x \right)\) represents the higher order of x.
The asymptotic analysis for OP is given in Theorem 2.
Theorem 2
The asymptotic expression for OP of the considered network is obtained as
Proof
The detailed proof will be given in “Appendix 2”. \(\square\)
5 Numerical results
Some representative MC figures are shown to investigate the correctness of the theoretical results. Channel and system parameters are provided in Table 1 [2] and Table 2 [18], respectively. Besides, \(L_{RV_i} = L_{V_iD} = L = 20\) is assumed. In addition, \(\bar{\lambda }_{SR_p} = \bar{\lambda }_{R_pD} = \bar{\gamma }\), \(k_S = k_{I_rR_p} = k_{R_pD} = k_{I_rD} = k\), \(\delta _{R_p}^2 = \delta _{D}^2 = \delta ^2 = 1\), \(\bar{\lambda }_{I_rR_p} = \bar{\lambda }_{I_rD} = \bar{\gamma }_{I}\), and \(\bar{\gamma }_{RR_p} = \bar{\gamma }_{RR}\). By utilizing the infinite series function, when \(N=2\), 10 terms are acceptable; when \(N=10\), 30 terms are needed to gain the suitable performance.
Figure 2 examines the OP versus \(\bar{\gamma }\) for some shadow fading and IH level with \(\bar{\gamma }_I\) = 5 dB, \(\gamma _0=1\) dB, \(\bar{\gamma }_{RR}=10\) dB, \(M=3\), \(P=3\) and \(N=5\). Firstly, we can find that the simulation results are nearly the same with the theoretical results which verify the rightness of our analysis. Moreover, at high SNRs, the asymptotic results are the tight across the simulation results, which also proves the rightness of our analytical investigations. In addition, it can be found that when the channel is under light fading, the OP will be smaller. At last, if the system suffers light IH, the OP will be smaller, too.
Figure 3 illustrates the OP versus \(\bar{\gamma }\) for some P and IH level with \(\bar{\gamma }_I\) =5 dB, \(\gamma _0=1\) dB, \(\bar{\gamma }_{RR}=10\) dB, \(M=3\) and \(N=5\) in FHS scenario. From Fig. 3, the same insights with the theoretical results, P has a serious impact on the OP, and the diversity order is the function of P. When P is smaller, the OP will be higher.
Figure 4 examines the OP versus \(\bar{\gamma }\) for some N and IH level with \(\bar{\gamma }_I\) = 5 dB, \(\gamma _0=1\) dB, \(\bar{\gamma }_{RR}=10\) dB, \(M=3\) and \(P=1\) in FHS scenario. From Fig. 4, it can be seen that the N has an influence on the OP. When N is smaller, the OP will be higher. However, it is a conclusion that gap between the curves with different N is small for the reason that the satellite transmission link is the major decision of the OP performance. which leads to results of these curves. From Fig. 4, we can see that these curves are relatively closely spaced, which indicate that the RIS transmission link is not the decision link.
Figure 5 introduces the OP versus \(\bar{\gamma }\) for some \(\bar{\gamma }_I\) and IH level with \(\gamma _0=1\) dB, \(\bar{\gamma }_{RR}=10\) dB, \(M=3\), \(N=5\), and \(P=3\) in FHS scenario. From Fig. 5, we could know that when interference’s power become smaller, the OP will be lower. Besides, we can observe that these curves with different \(\bar{\gamma }_I\) are parallel for the reason that the diversity order is the same.
Figure 6 shows the OP versus \(\bar{\gamma }\) for some \(\bar{\gamma }_{RR}\) and IH level with \(\gamma _0=1\) dB, \(\bar{\gamma }_{I}=3\) dB, \(M=3\), \(N=2\), and \(P=3\) in FHS scenario. Moreover, we can find that when \(\bar{\gamma }_{RR}\) is becoming larger, the OP will be larger. In addition, we see that in high SNR regime, these curves has the trend that they have the same OP, which is the inherent character of the NI system.
Figure 7 plots the OP versus \(\bar{\gamma }\) for some \(\gamma _{0}\) and IH level with \(\bar{\gamma }_{RR}=5\) dB, \(\bar{\gamma }_{I}=5\) dB, \(M=3\), \(N=2\), and \(P=3\) in AS scenario. From Fig. 7, it has the scenario that with \(\gamma _0\) becoming larger, the OP will be larger, too. This is because that the outage threshold is getting larger, which indicates that the system needs larger power to keep the transmission.
Figure 8 illustrates the OP versus \(\gamma _{0}\) for some P and IH level with \(\bar{\gamma }=20\) dB, \(\bar{\gamma }_{RR}=5\) dB, \(\bar{\gamma }_{I}=5\) dB, \(M=3\) and \(N=2\) in FHS scenario. Form Fig. 8, it can be found that when \(\bar{\gamma }_0\) is larger than a fixed value, the OP will be always 1, and this fixed values has not influence with the P. When the NI level is lager, this fixed value is smaller. This is the inherent character of the IH system.
6 Conclusion
Through this work, we researched the OP for the RIS-aided ISDURTNs. To gain the balance between the performance and complexity, partial UAV selection scheme was utilized in the considered network. Particularly, the accurate expression for the OP was gotten, which has given an efficient way to verify the impacts of major parameters on the OP. In addition, the asymptotic analysis for the OP was further studied in high SNR regime. From the simulation results, it could be derived that the light channel fading, the larger N, the weaker IH level and the less interference power would lead to a lower OP, which guide the future engineering design.
Availability of data and materials
The raw/processed data required to reproduce the above findings cannot be shared at this time as the data also form part of an ongoing study.
Notes
It is mentioned that, in this paper, the terrestrial nodes are equipped with only one antenna, while the results are also suitable to the case that transmission nodes are equipped with multiple antennas and beamforming (BF) is utilized at each multiple antenna node.
In partial selection scheme, the transmission link with best system performance factor is chosen. In this paper, this system performance factor is the signal-to-interference-and-noise plus distortion ratio (SINDR), thus (4) appears.
Although GEO is taken an example for an example, however the derived results are still fit for the scenario with MEO and LEO satellite.
References
K.Y. Jo, Satellite Communications Network Design and Analysis (Artech House, Norwood, 2011)
K. Guo et al., NOMA-based cognitive satellite terrestrial relay network: secrecy performance under channel estimation errors and hardware impairments. IEEE Internet Things J. 9(18), 17334–17347 (2022)
O. Kodheli, E. Lagunas, N. Maturo, S.K. Sharma, B. Shankar, J.F.M. Montoya, J.C.M. Duncan, D. Spano, S. Chatzinotas, S. Kisseleff, J. Querol, L. Lei, T.X. Vu, G. Goussetis, Satellite communications in the new space era: a survey and future challenges. IEEE Commun. Surv. Tutor. 23(1), 70–109 (2021)
ETSI TS 102 585 V1.1.2, Digital Video Broadcasting (DVB); System specifications for Satellite services to Handheld devices (SH) below 3 GHz (2008)
S. Han et al., Challenges of physical security in a satellite-terrestrial network. IEEE Netw. 36(3), 98–104 (2022)
X. Zhu et al., Creating efficient integrated satellite-terrestrial networks in the 6G era. IEEE Wirel. Commun. 29(4), 154–169 (2022)
S. Zheng et al., Design and analysis of uplink and downlink communications for federated learning. IEEE J. Sel. Areas Commun. 39(7), 2150–2167 (2021)
Y. Guo et al., Distributed machine learning for multiuser mobile edge computing systems. IEEE J. Sel. Top. Signal Process. 16(3), 460–473 (2022)
L. Chen et al., Relay-assisted federated edge learning: performance analysis and system optimization. IEEE Trans. Commun. 71(6), 3387–3401 (2023)
D. Peng et al., Integrating terrestrial and satellite multibeam systems toward 6G: techniques and challenges for interference mitigation. IEEE Wirel. Commun. 29(1), 24–31 (2022)
G. Araniti et al., Toward 6G non-terrestrial network. IEEE Netw. 36(1), 113–120 (2022)
J. Xia et al., Secure cache-aided multi-relay networks in the presence of multiple eavesdroppers. IEEE Trans. Commun. 67(11), 7672–7685 (2019)
G. Geraci et al., Integrating terrestrial and non-terrestrial networks: 3D opportunities and challenges. IEEE Commun. Mag. 61(4), 42–48 (2023)
T. Ma et al., Satellite-terrestrial integrated 6G: an ultra-dense LEO networking management architecture. IEEE Wirel. Commun. early access, p. 1 (2022)
K. Guo et al., Deep reinforcement learning and NOMA-based multi-objective RIS-assisted IS-UAV-TNs: trajectory optimization and beamforming design. IEEE Trans. I. Trans. Syst., ealy access, p. 1–1 (2023)
M. Lin, Q. Huang, T. de Cola, J.-B. Wang, J. Wang, M. Guizani, J.-Y. Wang, Integrated 5G-satellite networks: a perspective on physical layer relibility and security. IEEE Wirel. Commun. 27(6), 152–159 (2020)
K. An, M. Lin, J. Ouyang, W.-P. Zhu, Secure transmission in cognitive satellite terrestrial networks. IEEE J. Sel. Areas in Commun. 34(11), 3025–3037 (2016)
K. Guo, K. An, B. Zhang et al., Physical layer security for multiuser satellite communication systems with threshold-based scheduling scheme. IEEE Trans. Vehi. Technol. 69(5), 5129–5141 (2020)
K. Guo et al., On the performance of the uplink satellite multi-terrestrial relay networks with hardware impairments and interference. IEEE Syst. J. 13(3), 2297–2308 (2019)
K. Guo, M. Lin, B. Zhang, J.-B. Wang, Y. Wu, W.-P. Zhu, J. Cheng, Performance analysis of hybrid satellite-terrestrial cooperative networks with relay selection. IEEE Trans. Veh. Technol. 69(8), 9053–9067 (2020)
P.K. Upadhyay, P.K. Sharma, Max-max user-relay selection scheme in multiuser and multirelay hybrid satellite-terrestrial relay systems. IEEE Commun. Lett. 20(2), 268–271 (2016)
P.K. Sharma, P.K. Upadhyay, D.B. costa, P.S. Bithas, A.G. Kanatas, Performance analysis of overlay spectrum sharing in hybrid satellite-terrestrial systems with secondary network selection. IEEE Trans. Wirel. Commun. 16(10), 6586–6601 (2017)
L. Zhu et al., Efficient user scheduling for uplink hybrid satellite-terrestrial communication. IEEE Trans. Wirel. Commun. 22(3), 1885–1899 (2023)
Z. Lin, M. Lin, W.-P. Zhu, J.-B. Wang, J. Cheng, Robust secure beamforming for wireless powered cognitive satellite-terrestrial networks. IEEE Trans. Cognitive Commun. Network. 7(2), 567–580 (2021)
K. Guo et al., Ergodic capacity of NOMA-based overlay cognitive integrated satellite-UAV-terrestrial networks. Chin. J. Electron. 32(2), 273–282 (2023)
H. Dong et al., Joint beamformer design and user scheduling for integrated terrestrial-satellite neetworks. IEEE Trans. Wirel. Commun., early access, p. 1–1 (2023)
X. Zhu et al., Delay optimization for cooperative multi-tier computing in integrated satellite-terrestrial networks. IEEE J. Sel. Areas Commun. 41(2), 366–380 (2023)
G.Y. Suk et al., Full duplex integrated access and backhaul for 5G NR: analyses and prototype measurements. IEEE Wirel. Commun. 29(4), 40–46 (2022)
G. Pan et al., Full duplex integrated access and backhaul for 5G NR: analyses and prototype measurements. IEEE Wirel. Commun. 28(3), 122–129 (2021)
B. M. ElHalawany et al., Ergodic capacity analysis of NOMA-based Two-way relaying systems, in IEEE 42nd International Conference on Distributed Computing Systems Workshops (ICDCSW), Bologna, Italy (2022), pp. 175–180
C. Gamal et al., Performance of hybrid satellite-UAV NOMA systems, in EEE International Conference on Communications 2022, Seoul, Korea, Republic of, 2022 (2022), pp. 189–194
R. Askar et al., Interference handling challenges toward full duplex evolution in 5G and beyond cellular networks. IEEE Wirel. Commun. 28(1), 51–59 (2021)
X. Hao et al., When full duplex wireless meets non-orthogonal multiple access: Opportunities and challenges. IEEE Wirel. Commun. 26(4), 148–155 (2019)
K. Guo et al., Performance analysis of two-way satellite terrestrial relay networks with hardware impairments. IEEE Wirel. Commun. Lett. 6(4), 430–433 (2017)
K. Guo et al., Performance analysis of two-way satellite multi-terrestrial relay networks with hardware impairments. Sensors 18(5), 1–19 (2018)
K. Guo et al., Integrated satellite multiple two-way telay networks: secrecy performance under multiple eves and vehicles with non-ideal hardware. IEEE Trans. Intell. Veh. 8(2), 1307–1318 (2023)
Q. Ling et al., Jointly optimized beamforming and power allocation for full-duplex cell-free NOMA in space-ground integrated networks. IEEE Trans. Commun. 71(5), 2816–2830 (2023)
C. Liao et al., Secure transmission in satellite-UAV integrated system against eavesdropping and jamming: a two-level stackelberg game model. China Commun. 19(7), 53–66 (2022)
C. Huang, A. Zappone, G.C. Alexandropoulos, M. Debbah, C. Yuen, Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 18(8), 4157–4170 (2019)
B. Di, H. Zhang, L. Song, Y. Li, Z. Han, H.V. Poor, Hybrid beamforming for reconfigurable intelligent surface based multi-user communications: achievable rates with limited discrete phase shifts. IEEE J. Sel. Areas Commun. 38(8), 1809–1822 (2020)
C. Huang, R. Mo, C. Yuen, Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning. IEEE J. Sel. Areas Commun. 38(8), 1839–1850 (2020)
Y. Su, X. Pang, S. Chen, X. Jiang, N. Zhao, F.R. Yu, Spectrum and energy efficiency optimization in IRS-assisted UAV networks. IEEE Trans. Commun. 70(10), 6489–6502 (2022)
Z. Lin et al., Refracting RIS aided hybrid satellite-terrestrial relay networks: joint beamforming design and optimization. IEEE Trans. Aeros. Elect. Syst. 58(4), 3717–3724 (2022)
L. Yang et al., Secrecy performance analysis of RIS-aided wireless communication systems. IEEE Trans. Veh. Technol. 69(10), 12296–12300 (2020)
K. Guo, K. An, On the performance of RIS-assisted integrated satellite-UAV-terrestrial networks with hardware impairemnts and interference. IEEE Wirel. Commun. Lett. 11(1), 131–135 (2022)
A. Bansal et al., RIS selection scheme for UAV-based multi-RIS-aided multiuser downlink network with imperfect and outdated CSI. IEEE Trans. Commun., early access, pp. 1–1 (2023)
H. Zhang et al., Capacity maximization in RIS-UAV networks: a DDQN-based trajectory and phase shift optimization approach. IEEE Trans. Wirel. Commun. 22(4), 2583–2591 (2023)
S.K. Singh et al., NOMA enhanced hybrid RIS-UAV-assisted full-duplex communication system with imperfect SIC and CSI. IEEE Trans. Commun. 70(11), 7609–7627 (2022)
L. Wei et al., Secrecy performance analysis of RIS-aided communication system with reandomly flying eavesdroppers. IEEE Wirel. Commun. Lett. 11(10), 2240–2244 (2022)
F. Zhou, X. Li, M. Alazab, R.H. Jhaveri, K. Guo, Secrecy performance for RIS-based integrated satellite vehicle networks with a UAV relay and MRC eavesdropping. IEEE Trans. Intell. Veh. 8(2), 1676–1685 (2023)
K. Guo et al., STAR-RIS-empowered cognitive non-terrestrial vehicle network with NOMA. IEEE Trans. Intell. Veh. 8(6), 3735–3749 (2023)
K. Guo et al., Performance analysis of two-way multiantenna multi-relay networks with hardware impairments. IEEE Access 5, 15971–15980 (2017)
K. Guo et al., Secrecy performance of satellite wiretap channels with multi-user opportunistic scheduling. IEEE Wirel. Commun. Lett. 7(6), 1054–1057 (2018)
K. Guo et al., On the performance of the uplink satellite multi-terrestrial relay networks with hardware impairments and interference. IEEE Syst. J. 13(3), 2297–2308 (2019)
X. Tang et al., On the performance of two-way multiple relay non-orthogonal multiple access based networks with hardware impairments. IEEE Access 7, 128896–128909 (2019)
X. Li, M. Huang, Y. Liu, V.G. Menon, A. Paul, Z. Ding, I/Q imbalance aware nonlinear wireless-powered relaying of B5G networks: security and reliability analysis. IEEE Trans. Netw. Sci.Eng. 8(4), 2995–3008 (2021)
X. Li, Y. Zheng, M. D. Alshehri, L. Hai, V. Balasubramanian, M. Zeng, Gaofeng Nie, “Cognitive AmBC-NOMA IoV-MTS networks with IQI: Reliability and security analysis.” IEEE Trans. Intelligent Transportation Systems, early access, pp. 1-12, (2021)
X. Li, J. Li, Y. Liu, Z. Ding, A. Nallanathan, Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Trans. Wirel. Commun. 19(1), 680–695 (2020)
E. Bjornson, M. Matthaiou, M. Debbah, A new look at dual-hop relaying: performance limits with hardware impairments. IEEE Trans. Commun. 61(11), 4512–4525 (2013)
K. Guo et al., On the performance of LMS communication with hardware impairments and interference. IEEE Trans. Commun. 67(2), 1490–1505 (2019)
K. Guo, K. An, F. Zhou, T.-A. Tsiftsis, G. Zheng, S. Chatzinotas, On the secrecy performance of NOMA-based integrated satellite multiple-terrestrial relay networks with hardware impairments. IEEE Trans. Veh. Technol. 70(4), 3661–3676 (2021)
N. Maletic, M. Cabarkapa, N. Neskovic, D. Budimir, Hardware impairments impact on fixed-gain AF relaying performance in Nakagami-m fading. Electron. Lett. 52(2), 121–122 (2016)
J. Zhang, L. Dai, X. Zhang, E. Bjornson, Z. Wang, Achievable rate of Rician large-scale MIMO channels with transceiver hardware impairments. IEEE Trans. Veh. Technol. 65(10), 8800–8806 (2016)
I.S. Gradshteyn, I.M. Ryzhik, A. Jeffrey, D. Zwillinger, Table of Integrals, Series and Products, 7th edn. (Elsevier, Amsterdam, 2007)
J. Arnau, D. Christopoulos, S. Chatzinotas, C. Mosquera, B. Ottersten, Performance of the multibeam satellite return link with correlated rain attenuation. IEEE Trans. Wirel. Commun. 13(11), 6286–6299 (2014)
A. Abdi et al., A new simple model for land mobile satellite channels: first-and second-order statistics. IEEE Trans. Wirel. Commun. 2(3), 519–528 (2003)
Acknowledgements
The authors would like to extend their gratitude to the anonymous reviewers for their valuable and constructive comments, which have largely improved and clarified this paper.
Funding
This work is supported in part by the National Natural Science Foundation of China under Grant No. 62001517.
Author information
Authors and Affiliations
Contributions
JS, KG, FZ, XW, and MZ conceived of and designed the experiments. JS and KG performed the experiments. JS, FZ and XW analyzed the data. MZ contributed analysis tools; JS, KG, FZ, XW wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
Proof of Theorem 1
From (21), we can get the first thing is to get the CDF of \(\Pr \left( {{\gamma _{SR}} \le {\gamma _0}} \right)\) and CDF of \(\Pr \left( {{\gamma _{RD}} \le {\gamma _0}} \right)\). In the following, \(\Pr \left( {{\gamma _{SR}} \le {\gamma _0}} \right)\) will be given at first.
By utilizing (4), \(\Pr \left( {{\gamma _{SR}} \le {\gamma _0}} \right)\) will written as
In (26), we should derive the expression for \({\Pr \left( {{\gamma _{S{R_p}}} \le {\gamma _0}} \right) }\), then, with the help of (3), \({\Pr \left( {{\gamma _{S{R_p}}} \le {\gamma _0}} \right) }\) is obtained as
By using [60], when \({\gamma _0} \le \frac{1}{{k_S^2}}\), (27) has the following expression as
Then with the help of (19), (8) and (8), (28) can be re-written as (29), which is shown as
After some simple steps, \(J_1\) can be re-derived as (30), which can be seen as
By using [64, Eq. 3.351.1], \(J_2\) and \(J_3\) can be re-written as
Then, by using \({\left( {1 - x} \right) ^N} = 1 - \sum \nolimits _{i = 1}^N {{N \atopwithdelims ()i}{{\left( { - 1} \right) }^{i + 1}}{x^i}}\), the final expression for \({\Pr \left( {{\gamma _{S{R_p}}} \le {\gamma _0}} \right) }\) will be derived.
At first, the accurate expression for \({F_{{\gamma _{R_pD}}}}\left( {{\gamma _0}} \right)\) is obtained. By recalling (6), \({F_{{\gamma _{R_pD}}}}\left( {{\gamma _0}} \right)\) has the following expression as
When \({\gamma _0} \le 1/k_{R_pD}^2\), with the help of (32) and after some steps, (32) is obtained as
where \(K = \left( {1 + k_{I_rD} ^2} \right) {\gamma _0}/\left( {1 - k_{R_pD}^2{\gamma _0}} \right)\) and \(G = {\gamma _0}/\left( {1 - k_{R_pD}^2{\gamma _0}} \right)\).
Then by substituting (8) and (11) into (33), (33) is re-given by
Next, by some calculation steps, the accurate expression for \({F_{{\gamma _1}}}\left( {{\gamma _0}} \right)\) is obtained as
The proof is completed.
Appendix 2
Proof of Theorem 2
Firstly, it should be known that when \(\bar{\gamma }\rightarrow \infty\), \({P_{out}}\left( {{\gamma _0}} \right)\) has the following approximation as
Then, by replacing (19) and (11) with (23) and (24), with the similar method of Theorem 1, the asymptotic expression for OP will be gotten.
The proof is over.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, J., Guo, K., Zhou, F. et al. Ris-aided integrated satellite duplex UAV relay terrestrial networks with imperfect hardware and co-channel interference. EURASIP J. Adv. Signal Process. 2023, 109 (2023). https://doi.org/10.1186/s13634-023-01067-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-023-01067-2