1 Introduction

Millimeter-wave (mmWave) massive multiple-input multiple-output (MIMO) technology has been has been widely recognized as a promising technology for 5G and beyond wireless communication systems for providing a large bandwidth of (30–300 GHz), high gain, and significant data rate [1,2,3]. However, a large number of antennas and radio-frequency (RF) chains in the mmWave massive MIMO systems inevitably bring very high and even unaffordable hardware complexity and power consumption [4,5,6]. To solve the problems of high hardware complexity, power consumption, and path loss, a lens antenna array for mmWave massive MIMO systems has been proposed [7]. A lens antenna array directs the signals arriving from different directions to different antennas and converts the spatial channel of a mmWave massive MIMO system to a beamspace channel with sparse scattering nature [8,9,10]. This reduces the effective array dimension and the number of associated RF chains by selecting a number of power-focused beams, which can significantly reduce power consumption and hardware complexity [11]. However, a beamspace channel with a relative high dimensional is still required at a base station (BS) to select the power-focused beams. Because the number of antennas is much larger than the number of RF chains, it is problematic for mmWave massive MIMO systems with lens antenna arrays to observe the complete channel state information (CSI) in the baseband directly.

By using the sparse characteristics of the channel response of a lens antenna array, the channel estimation can be regarded as a sparse signal recovery. An expectation–maximization (EM)-based algorithm was proposed in [12]. In [13], a channel estimation method based on the sparse mask detection (SMD), which uses the classic least squares (LS) algorithm to estimate the reduced dimension channel, was proposed. Although this method can effectively reduce the channel dimension of a beamspace, it has a high pilot overhead and requires certain prior knowledge about channel sparsity, which can increase the computational complexity, making this method not suitable for practical applications. An antenna selection and path number estimation algorithm were proposed in [14] to construct a criterion function to infer the actual position of the arrival signal by using the discrete Fourier-transform (DFT) beam difference (DBD). This algorithm has the advantage of not requiring any prior information on a channel. In [15], a parallel scheme for a lens array millimeter-wave full-dimensional (FD) MIMO system was constructed, and a pilot training framework based on compressed sensing (CS) was proposed under the constraint of antenna switching network (ASN). In addition, a dedicated redundant dictionary for an FD lens array was constructed, and the pilot signals were transmitted or received to improve the channel estimation performance. The aforementioned beamspace channel estimation schemes have been designed for narrowband systems, but with growing demands for higher data rates and larger system capacity, the research being conducted on wideband millimeter-wave systems has been increasing rapidly.

The increase in bandwidth and dimension in wideband systems can lead to a beam squint effect that results in a beam direction changes as response to the frequency and beam energy distribution of different path components on different carrier frequencies. Thus, narrowband channel estimation schemes cannot be directly applied to a wideband system. In [16], an explicit wideband channel estimation technique, which can be used in the time or frequency domain and combined time-frequency domain, was proposed. This technique first estimates the support of each of the wideband beamspace channels at certain frequencies individually and then combines them into common support at all frequencies. In [17], the estimated sparse vectors shared a common support set, and an EM-based algorithm was developed to improve the channel estimation accuracy. This algorithm makes full use of channel characteristics and reduces the number of unknown parameters significantly. Further, the wideband beamspace channel estimation problem was regarded as a multiple measurement vector (MMV) problem associated with common support in [18], and a simultaneous orthogonal matching pursuit (SOMP) based scheme was proposed. Although the above-mentioned schemes can improve the channel estimation accuracy of wideband millimeter-wave systems to a certain extent by assuming a common support set, the system performance is limited because of the beam squint effect [19,20,21]. To address this problem, a parameter extraction of the uplink and downlink channel estimation strategy was proposed in [22] using the channel sparsity in the angle and delay domains. However, this method has the drawback of requiring knowledge about the whole channel matrix before training, which results in unacceptably high training overhead. An innovative framework that jointly exploits the channel’s low-rank and angular information was proposed in [23]. This framework not only improves performance in short-beam training lengths but also can work under high-noise conditions. To solve the beam squint effect of the mmWave MIMO system, [24] exploited the shift-invariant block sparsity of the resulting nonstandard channel model to develop a compressive sensing-based channel estimation algorithm. In [25], the block sparsity of massive MIMO channels was exploited, and the channel autocorrelation matrix was calculated by investigating the prior channel information based on the CS theory. A compression-based linear minimum mean square error (CLMMSE) channel estimation algorithm, which solves the convex optimization problem by using the regularized method, also was proposed. In [26], performance bounds on the channel estimation of one-bit mmWave massive MIMO receivers were defined for different types of channel models. The angles of arrival (AoAs) and angles of departure (AoDs) have been continuously distributed in practice. The channel estimation algorithms in [23,24,25,26] assume that the AoAs/AoDs are discrete, which causes the power leakage problem and results in an inevitable loss of channel estimation performance under the beam squint effect. To reduce the beam squint effect caused by a wide bandwidth in practice, a sparse Bayesian learning-based algorithm was proposed in [27]. This algorithm updates channel parameters iteratively to maximize the posterior probability. It is sensitive to the initial value, however, and is prone to fall into a local optimum. In [28], a successive support detection (SSD)-based scheme was proposed to avoid the common support assumption. This scheme follows the classical idea of successive interference cancellation; the support of each path component is jointly estimated at different frequencies to improve the accuracy, and the influence caused by the beam squint effect is removed when estimating the remaining path components. However, the preset value of a fixed-value SSD scheme causes the number of nonzero elements near the strongest element to be retained, which will cause more nonzero elements to be discarded for components with high sparsity, thus affecting the estimation accuracy. The mmWave communications strongly rely on precise directional alignment of the transmitter and receiver beams, and neglecting the beam squint effect can result in severe performance losses. However, the narrowband channel estimation schemes cannot be directly applied to a wideband system. In addition, the existing wideband schemes always adopt the common support assumption, which leads to significant performance losses and can cause high computational complexity. Therefore, it is of great significance to realize high-precision channel estimation at a low pilot cost and low complexity for broadband systems.

In this paper, we propose a beam-band function-based orthogonal matching pursuit (BBOMP) algorithm for beamspace channel estimation to reduce the beam squint effect in a wideband mmWave massive MIMO system. By using the frequency-dependent property of the wideband beamspace channel, the channel estimation problem is formulated as a carrier frequency beam direction estimation problem. Then, we develop a beam-band method to estimate the spatial direction of a beam, in which the support of a path component is uniquely determined by the carrier frequency, where its spatial direction lies according to the frequency-dependence. We also define a beam-band function that is equivalent to a tie to delineate a range containing several adjacent array flow vectors. The proposed method captures the power of a path component through correlation calculations so that the index of the strongest element could be determined, and the spatial direction of the carrier frequency could be obtained. Moreover, to improve the estimation accuracy, the proposed algorithm adaptively determines how many nonzero elements could be retained based on the sparsity of each path component to calculate the support. Theoretical analyses verify that the proposed scheme has a lower pilot overhead than some existing schemes. In addition, the simulation results demonstrate that the proposed BBOMP scheme has better estimation accuracy than the existing schemes, under both in the case of low and high signal-to-noise (SNR) conditions.

The rest of this paper is structured as follows. In Sect. 2, the channel model of a wideband mmWave massive MIMO system using lens antenna arrays is presented. In Sect. 3, the sparse reconstruction problem is formulated, and the proposed BBOMP algorithm is introduced. Simulation results and analysis are given in Sect. 4. Finally, the main conclusions are drawn in Sect. 5.

Notations: The following notations used throughout the paper are as follows: a, \({{\textbf {a}}}\), \({{\textbf {A}}}\) represent the scalar, vector, and matrix, respectively; \({{{\textbf {A}}}^T}\), \({{{\textbf {A}}}^H}\), and \({{{\textbf {A}}}^{ - 1}}\) denote the transpose, conjugate transpose, and inverse of matrix \({{\textbf {A}}}\), respectively; \(\left| {{\textbf {A}}} \right|\) and \(\left\| {{\textbf {A}}} \right\|\) denote absolute value and second-norm, respectively; \({\left\| {{\textbf {A}}} \right\| _F}\)stands for the Frobenius norm of \({{\textbf {A}}}\).

2 Methods

In this paper, we first introduce the research background and related channel estimation methods for mmWave massive MIMO systems in Sect. 1. Compared with narrowband channel estimation algorithms, wideband channel estimation schemes are more in line with the practical requirements of multi-user services in modern communication systems. However, the existing wideband channel estimation algorithms perform channel estimation with relatively low computational complexity, and their estimation accuracy is problematic because they do not take into account the problem that the beam direction changes as the response to the frequency and beam energy distribution of different path components on different carrier frequencies due to the beam squint effect caused by the increase in bandwidth and dimension in wideband systems. Therefore, wideband channel estimation schemes with low complexity and high accuracy become a key solution for mmWave massive MIMO communication systems.

We propose a wideband channel estimation scheme based on compressed sensing for downlink multi-user multi-antenna mmWave massive MIMO systems to address the beam squint effect. To reduce the complexity while ensuring the estimation accuracy, the wideband channel estimation is divided into channel estimation transformation problem and algorithm design. In the transformation of channel estimation, we exploit the special frequency-dependent sparse structure of the wideband beamspace channel to transform the channel estimation problem into a beamspace direction estimation problem. In the algorithm design, we propose an beam-band function-based orthogonal matching pursuit algorithm, which constructs a beam-band function for capturing the power of each path component to estimate the spatial direction. In addition, the effect of beam squint effects is reduced by estimating the support of each path component at different sub-carriers. Moreover, the support is estimated adaptively to further improve the estimation accuracy.

To verify the effectiveness of the proposed algorithm, we have conducted a variety of experiments to obtain the comparison results between the proposed BBOMP scheme and some existing broadband schemes. The comparison results and specific analysis obtained can be found in Sect. 5.

3 System model

3.1 Wideband beamspace channel model

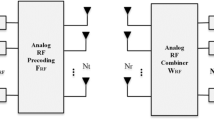
Consider a time-division duplexing (TDD) wideband mmWave massive MIMO system with a BS and K single-antenna users as shown in Fig. 1. The BS employs a lens antenna array with I antennas and \({I_{RF}}\) RF chains. The number of sub-carriers in the orthogonal frequency-division multiplexing (OFDM) scheme is M, and it is assumed that the cyclic prefix (CP) is long enough to handle the maximum multipath delay and maximum propagation delay of electromagnetic waves traveling across the antenna array.

Fig. 1
figure 1

Block diagram of a wideband mmWave massive MIMO-OFDM system with a lens antenna array

Full size image

The widely used Saleh–Valenzuela multipath channel model is used in the frequency domain to characterize the dispersive mmWave MIMO channel [28, 29]. The spatial channel of the k-th user can be expressed as follows: \({{\textbf {H}}} = [{{{\textbf {h}}}_1},{{{\textbf {h}}}_2},\ldots ,{{{\textbf {h}}}_M}]\).

Assume there are \({L_k}\) resolvable paths from the k-th user to a BS; then, the channel at the sub-carrier m \((m = 1,2,\ldots M)\) is given by

$$\begin{aligned} {{{\textbf {h}}}_m} = \sqrt{\frac{I}{{{L_k}}}} \sum \limits _{l = 1}^{{L_k}} {{\beta _l}{{\textbf {a}}}({\phi _{l,m}}){e^{ - j2\pi {\rho _l}{f_m}}}} ,l = 1,2,\ldots {L_k}, \end{aligned}$$
(1)

where \({\beta _l}\) and \({\rho _l}\) are the complex gain and time delay of the l-th path, respectively; \({f_m}\) is the frequency of the sub-carrier m, and it is defined as

$$\begin{aligned} {f_m} = \frac{B}{M}\left( {m - 1 - \frac{{M - 1}}{2}} \right) + {f_c}, \end{aligned}$$
(2)

where \({f_c}\) and B are the carrier frequency and bandwidth, respectively [30]; \({\phi _{l,m}} = \frac{{{f_m}}}{{2{f_c}}}\sin {\theta _l}\) is the spatial direction at a sub-carrier m; \({\theta _l}\) is the physical direction; and \({{\textbf {a}}}({\phi _{l,m}})\) is the array response vector of \({\phi _{l,m}}\). In this paper, a typical uniform linear array (ULA) is used [31], so \({{\textbf {a}}}({\phi _{l,m}})\) can be expressed as follows:

$$\begin{aligned} {{\textbf {a}}}({\phi _{l,m}}) = \frac{1}{{\sqrt{I} }}{e^{ - j2\pi {\phi _{l,m}}\tau }},\tau \in {{\textbf {T}}}, \end{aligned}$$
(3)

where \({{\textbf {T}}} = {[ - \frac{{I - 1}}{2}, - \frac{{I + 1}}{2},\ldots ,\frac{{I - 1}}{2}]^T}\).

Fig. 2
figure 2

Block diagram of a wideband mmWave massive MIMO-OFDM system with a lens antenna array

Full size image

An electromagnetic lens is similar to an optical lens, which can change the propagation direction of electromagnetic rays to realize energy focusing or beam collimation. As shown in Fig. 2, the electromagnetic wave \(\omega\) arriving at the lens passes through the plane lens at a certain incidence angle and is gathered on the feed antenna A located at the focal point of the lens for constructive superposition. By employing a lens antenna array, the spatial channel (2) can be converted into a beamspace. By carefully designing the phase shift profile, electromagnetic rays received at the lens focal curvature can be approximated to the spatial DFT of the electromagnetic rays received at the lens’s aperture [32]. Then, a lens antenna array can be expressed as a DFT matrix \(\textbf{U} \in {\mathbb{C}}^{I \times I}\), which is given by \({{\textbf {U}}} = \left[ {{{\textbf {a}}}({{{\bar{\phi }} }_1}),{{\textbf {a}}}({{{\bar{\phi }} }_2}),\ldots ,{{\textbf {a}}}({{{\bar{\phi }} }_I})} \right]\), where \({{\bar{\phi }} _i} = \frac{1}{I}(i - \frac{{I + 1}}{2})\), \(i = 1,2,\ldots ,I\) is the predefined spatial orientation of the lens antenna array, indicating that I orthogonal directions of the array response vector spanning the entire space are contained in matrix \({{\textbf {U}}}\).

Consequently, the beamspace channel \({{{\textbf {H}}}^B}\) can be expressed as \({{{\textbf {H}}}^B} = {{{\textbf {U}}}^H}{{\textbf {H}}} = [{{\textbf {h}}}_1^b,{{\textbf {h}}}_2^b,\ldots ,{{\textbf {h}}}_M^b]\), and \({{\textbf {h}}}_m^b = {{{\textbf {U}}}^H}{{{\textbf {h}}}_m}\) is defined as follows \({{\textbf {h}}}_m^b = \sqrt{\frac{I}{{{L_k}}}} \sum \limits _{l = 1}^{{L_k}} {{\beta _l}{e^{ - j2\pi {\rho _l}{f_m}}}{{{\textbf {b}}}_{l,m}}}\) where \({{{\textbf {b}}}_{l,m}} = {{{\textbf {U}}}^H}{{\textbf {a}}}({\phi _{l,m}})\) denotes the component of a sub-carrier m on the l-path. Based on the analysis in [33], \({{{\textbf {b}}}_{l,m}}\) can be expressed as

$$\begin{aligned} {{{\textbf {b}}}_{l,m}} = {[f({\phi _{l,m}} - {{\bar{\phi }} _1}),f({\phi _{l,m}} - {{\bar{\phi }} _2}),\ldots ,f({\phi _{l,m}} - {{\bar{\phi }} _I})]^T}, \end{aligned}$$
(4)

where \(f(x) = \frac{{\sin I\pi x}}{{xin\pi x}}\) is the Dirichlet sinc function. When \({\phi _{l,m}}\) is the same as one of the beam directions predefined by a lens antenna array (i.e., one of the directions set \([{{\bar{\phi }} _1},{{\bar{\phi }} _2},\ldots ,{{\bar{\phi }} _I}]\), the power of \({{{\textbf {b}}}_{l,m}}\) will be focused on only one beam. In practice, \({\phi _{l,m}}\) is arbitrary, with a high probability of being different from any of \({{\bar{\phi }} _i}\). Therefore, the path power will be distributed on several predefined beams. According to the property of f(x) that it is larger when x is closer to zero, the indices of the power-focused beams should be adjacent, which means that most of the power of \({{{\textbf {b}}}_{l,m}}\) is concentrated in a small number of elements. In addition, the number of paths \({L_k}\) is small because of the limited scattering capability of a mmWave, so \({{\textbf {h}}}_m^b\) is a sparse vector [34].

4 Wideband beamspace channel estimation

4.1 Proposed BBOMP scheme

Fig. 3
figure 3

Diagram of the frequency-dependent spatial direction beam squint effect in the wideband system

Full size image

Because of the considerable time delay of electromagnetic wave propagation throughout an antenna array, different antennas may receive different time-domain symbols from the same physical path at the same sampling time in communication systems using large-scale antenna arrays. The beam squint effect results in AoA diffusion and broadens the beamwidth of the desired signal in the spatial domain. It is observed from Fig. 3 that the actual spatial AoAs change with the signal frequency \({f_1},{f_2},{f_3}\). Specifically, in OFDM systems, different sub-carriers observe different physical AoAs for the same physical path due to the beam squint effect. Moreover, the effect of beam squint is even magnified as the increase in the number of antennas and bandwidth in mmWave massive MIMO system. When the system is a narrowband system or the number of antennas I is small, we have \(B \ll {f_c}\) and \({f_c} \approx {f_m}\). In this case, \({\phi _{l,m}} = \frac{{1}}{{2}}\sin {\theta _l}\) is frequency-independent. However, when the number of antennas I is large or the system is a wideband system, the approximation of \({f_c} \approx {f_m}\) does not hold, and \({\phi _{l,m}}\) is frequency-dependent. Therefore, the beam power distribution of the l-th path component at different sub-carriers will be different, that is \({{{\textbf {b}}}_{l,{m_1}}} \ne {{{\textbf {b}}}_{l,m2}}\), \({m_1} \ne {m_2}\), which indicates that beam squint introduces more serious influence for wideband systems.

Since the beam squint and the reality that the beamspace channel are the sum of several resolvable path components, the support of beamspace channel is frequency-dependent, which is different from the common support assumptions considered in existing beamspace channel estimation schemes. Therefore, the beam squint effect should be thoroughly considered in channel estimation. Without the loss of generality, a transmission channel is assumed to remain constant within the uplink pilot transmission time slot, and the widely used orthogonal pilot transmission approach is employed to make the estimation of a user’s channel independent of the other channels’ estimations [35]. Finally, an adaptive selection network is used to combine the received pilots [36].

Assume \({x_{m,q}}\) is a pilot symbol of a user at a sub-carrier m; then, the received pilot vector \(\textbf{y}_{m, q} \in {\mathbb{C}}^{I_{R F} \times 1}\) at the BS can be expressed as

$$\begin{aligned} {{{\textbf {y}}}_{m,q}} = {{{\textbf {W}}}_q}({{\textbf {h}}}_m^b{x_{m,q}} + {{{\textbf {n}}}_{m,q}}),m = 1,2,\ldots ,M;q = 1,2,\ldots ,Q, \end{aligned}$$
(5)

where \(\textbf{n}_{m, q} \in {\mathbb{C}}^{I \times 1}\) is the noise vector and \(\textbf{W}_{q} \in {\mathbb{C}}^{I_{R F} \times I}\) is the receiver combining matrix. Further, assume that all users have a pilot frequency transmission instant of Q; then, the measurement vector \(\hat{\textbf{y}}_{m} \in {\mathbb{C}}^{Q I_{R F} \times 1}\) after all Q pilot transmission instants have been finished can be obtained as

$$\begin{aligned} {{\hat{{{\textbf {y}}}}}_m} = {[{{\textbf {y}}}_{m,1}^T,{{\textbf {y}}}_{m,2}^T,\ldots ,{{\textbf {y}}}_{m,Q}^T]^T} = {\hat{{{\textbf {W}}}h}}_m^b + {{\hat{{{\textbf {n}}}}}_m}, \end{aligned}$$
(6)

where \({{\hat{{{\textbf {n}}}}}_m} = {[{{{\textbf {W}}}_1}{{{\textbf {n}}}_{m,1}},\ldots ,{{{\textbf {W}}}_Q}{{{\textbf {n}}}_{m,Q}}]^T}\) is the effective noise vector, and \(\hat{\textbf{W}}=\left[ \textbf{W}_{1}^{T}, \textbf{W}_{2}^{T}, \ldots , \textbf{W}_{Q}^{T}\right] ^{T} \in {\mathbb{C}}^{I_{R F} Q \times I}\) is the collective combining matrix; each column in \({\hat{{{\textbf {W}}}}}\) has low interdependence to ensure a high recovery accuracy in the sparse recovery process using the compressed sensing theory.

Without the loss of generality, it is always assumed that \({x_{m,q}} = 1\) [37]. Then, according to (9), \({{\textbf {h}}}_m^b\) can be recovered using known values of \({{\hat{{{\textbf {y}}}}}_m}\) and \({\hat{{{\textbf {W}}}}}\). Because \({{\textbf {h}}}_m^b\) is a sparse vector, it can be solved by a compressed sensing approach and does not require a large pilot overhead (i.e., \(Q< < \frac{I}{{{I_{RF}}}}\)) [38].

Based on this analysis, when the actual spatial direction of a beam is closest to the predefined spatial direction of a lens antenna array, the beam occupies the largest part of the path power, which also means that index \({i'_{l,m}}\) of the dominant element of \({{{\textbf {b}}}_{l,m}}\) is determined by \({\phi _{l,m}}\), which can be expressed as follows: \({i'_{l,m}} = \arg \mathop{\min }\limits _i \left| {{\phi _{l,m}} - {{{\bar{\phi }} }_i}} \right|\). Furthermore, because the other weaker nonzero elements are distributed around the dominant element, the support \({\sigma _{l,m}}\) of \({{{\textbf {b}}}_{l,m}}\) can be obtained

$$\begin{aligned} {\sigma _{l,m}} = {\Xi _I}({i'_{l,m}} - \Omega ,\ldots ,{i'_{l,m}} + \Omega ), \end{aligned}$$
(7)

where \({\Xi _I}(x) = {\bmod _I}(x - 1) + 1\) ensures that all element in \({\sigma _{l,m}}\) are in nonzero positive integers, and \(\Omega\) is a parameter that defines how many nonzero elements of \({{{\textbf {b}}}_{l,m}}\) can be retained.

When solving the channel estimation problem, traditional algorithms usually consider \(\Omega\) a fixed value; for instance, \(\Omega\) was set to four in [30]. However, this can cause some of the nonzero elements to be discarded for path components with a relatively large sparsity; also, some part of the path power will be lost, and the estimation accuracy will be limited. To address these shortcomings, we propose a solution to adaptively estimate \(\Omega\). Similar to the definition of \({i'_{l,m}}\), the beam with the largest deviation in the spatial direction from the predefined direction of a lens antenna array has the weakest path power. Then, the index of the weakest element of \({{{\textbf {b}}}_{l,m}}\) can be obtained as

$$\begin{aligned} {i''_{l,m}} = \arg \mathop{\max }\limits _i \left| {{\phi _{l,m}} - {{{\bar{\phi }} }_i}} \right| . \end{aligned}$$
(8)

Next, \(\Omega\) can be adaptively adjusted with \({i'_{l,m}}\) and \({i''_{l,m}}\) as \({{\Omega }} = \left| {{{i'}_{l,m}} - {{i''}_{l,m}}} \right| - 1\), where the value of minus one is adopted to reduce the error because the weakest element is almost always suppressed by the noise and can be rounded off.

Based on the definition of \({\phi _{l,m}}\), the spatial direction \({\phi _{l,c}}\) of the l-th path at a carrier frequency \({f_c}\) can be obtained by \({\phi _{l,c}} = \frac{1}{2}\sin {\theta _l}\). Then, \({f_m}\) can be rewritten as

$$\begin{aligned} {f_m} = (\frac{B}{{{f_c}M}}(m - 1 - \frac{{M - 1}}{2}) + 1){f_c} . \end{aligned}$$
(9)

Based on the definition of \({\phi _{l,m}}\) and \({\phi _{l,c}}\), (9) can be re-expressed as

$$\begin{aligned} {\phi _{l,m}} = {\phi _{l,c}}\frac{{{f_m}}}{{{f_c}}} = {\phi _{l,c}}\left[ {\frac{B}{{{f_c}M}}\left( {m - 1 - \frac{{M - 1}}{2}} \right) + 1} \right] . \end{aligned}$$
(10)

where M, \({f_c}\), and B are given system parameters. Because \({\phi _{l,m}}\) is determined by \({\phi _{l,c}}\), it holds that \({\sigma _{l,m}}\) can be determined by \({\phi _{l,c}}\).

To realize the beamspace channel estimation, first, beam-band functions are defined to obtain the support set. By assuming that \({\phi _{l,c}}\) is one of the predefined spatial directions \({{\bar{\phi }} _i}\) of a lens antenna array and defining the path component matrix \({{{\textbf {B}}}_i} = [{{{\textbf {b}}}_{l,1}},{{{\textbf {b}}}_{l,2}},..,{{{\textbf {b}}}_{l,M}}]\), the power of the n-th row of \({{{\textbf {B}}}_i}\) can be calculated as

$$\begin{aligned} \left\| {{{{\textbf {B}}}_i}(n,:)} \right\| _2^2 = \sum \limits _{m = 1}^M {{f^2}({\phi _{l,m}} - {{{\bar{\phi }} }_n})}. \end{aligned}$$
(11)

where \(w = \frac{{2\pi }}{\lambda }d\sin \theta\) represents the corresponding spatial frequency. According to (10), \({{\hat{\phi }} _m} = \frac{{B{\phi _{l,c}}}}{{{f_c}M}}\left( {m - 1 - \frac{{M - 1}}{2}} \right)\); substituting it into (11) yields,

$$\begin{aligned} \left\| {{{{\textbf {B}}}_i}(n,:)} \right\| _2^2 = \sum \limits _{m = 1}^M {{f^2}(\frac{{i - n}}{I} + {{{\hat{\phi }} }_m})}. \end{aligned}$$
(12)

Because \({\phi _{l,c}} = {{\bar{\phi }} _i} = \frac{1}{I}(n - \frac{{I + 1}}{2})\), (12) can be re-expressed as follows:

$$\begin{aligned} \left\| {{\mathbf{B}}_{i} (n,:)} \right\|_{2}^{2} & = \sum\limits_{{m = 1}}^{M} {f^{2} (\phi _{{l,m}} - \bar{\phi }_{n} )} = \sum\limits_{{m = 1}}^{M} {f^{2} (\phi _{{l,c}} + \hat{\phi }_{m} - \bar{\phi }_{n} )} \\ & \quad = \sum\limits_{{m = 1}}^{M} {f^{2} \left[ {\frac{1}{I}\left( {i - \frac{{I + 1}}{2}} \right) - \frac{1}{I}\left( {n - \frac{{I + 1}}{2}} \right) + \hat{\phi }_{m} } \right]} \\ & \quad = \sum\limits_{{m = 1}}^{M} {f^{2} (\frac{{i - n}}{I} + \hat{\phi }_{m} )} \\ \end{aligned}$$
(13)

where \({{\hat{\phi }} _m}\) is small because of the large number of sub-carriers m. Equation (12) can be approximated to the integral form as follows:

$$\begin{aligned} \left\| {{{{\textbf {B}}}_i}(n,:)} \right\| _2^2 = \frac{{M{f_c}}}{{{{{\bar{\phi }} }_i}B}}\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {{f^2}\left( {\frac{{i - n}}{I} + {\hat{\phi }} } \right) d} {\hat{\phi }} . \end{aligned}$$
(14)

In the process of transforming (12) into integral form, the upper and lower limit of the integral is, respectively, expressed as

$$\begin{aligned}{} & {} {{\hat{\phi }} _M} = - \frac{{{f_s}{\phi _{l,c}}}}{{{f_c}}} \cdot \frac{1}{M} \cdot \frac{{M - 1}}{2}\mathop\approx \limits ^\Delta - \frac{{{f_s}{\phi _{l,c}}}}{{2{f_c}}}, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} {{\hat{\phi }} _1} = \frac{{{f_s}{\phi _{l,c}}}}{{{f_c}}} \cdot \frac{1}{M} \cdot \frac{{M - 1}}{2}\mathop\approx \limits ^\Delta \frac{{B{\phi _{l,c}}}}{{2{f_c}}}, \end{aligned}$$
(16)

where \(\Delta\) is valid because the value of M is large, \(\frac{{M - 1}}{M} \approx 1\). In this way, the power of any row in \({{{\textbf {B}}}_i}\), namely the power of any beam, can be obtained.

Because of the beam squint effect, the power of each beam cannot be obtained accurately, which limits the estimation performance. To solve this problem, we propose a beam-band function. Considering the beam squint effect, the beam-band is defined as

$$\begin{aligned} {\Pi _i} = {\Xi _I}(i - \delta ,i - \delta + 1,\ldots ,i + \delta ), \end{aligned}$$
(17)

which denotes the portion centered at the i-th row of \({{{\textbf {B}}}_i}\) from (\(i - \delta\)) to (\(i + \delta\)).

Then, based on (14), we can use \({\Pi _i}\) to clutch part of power of \({{{\textbf {B}}}_i}\),

$$\begin{aligned} \left\| {{{{\textbf {B}}}_i}({\Pi _i},:)} \right\| _F^2 = \frac{{M{f_c}}}{{{{{\bar{\phi }} }_i}B}}\sum \limits _{t = - \delta }^\delta {\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {{f^2}\left( {\frac{t}{I} + {\hat{\phi }} } \right) d{\hat{\phi }} } } ,t \in {\Pi _i}, \end{aligned}$$
(18)

and the total power of \({{{\textbf {B}}}_i}\) is M. Because it holds that \(\sum \limits _{n = 1}^I {{f^2}({\phi _{l,m}} - {{{\bar{\phi }} }_n})} = 1\), the ratio of the power of a beam-band to the total power \(\eta\) can be obtained as

$$\begin{aligned} \eta = \frac{{\left\| {{{{\textbf {B}}}_i}({\Pi _i},:)} \right\| _F^2}}{{\left\| {{{{\textbf {B}}}_i}} \right\| _F^2}} = \frac{{{f_c}}}{{{{{\bar{\phi }} }_i}B}}\sum \limits _{t = - \delta }^\delta {\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {{f^2}\left( {\frac{t}{I} + {\hat{\phi }} } \right) d} {\hat{\phi }} } ,t \in {\Pi _i}. \end{aligned}$$
(19)

In contrast, \(f(x) = \frac{{\sin I\pi x}}{{\sin \pi x}} = \sum \limits _{i \in {{\textbf {T}}}} {{e^{ - j2\pi ix}}}\)[10], so (19) can be rewritten as

$$\begin{aligned} \eta = \frac{{{f_c}}}{{{{{\bar{\phi }} }_i}B}}\int _{i - \delta }^{i + \delta } {\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {{e^{ - j4\pi I(\frac{t}{I} + {\hat{\phi }} )}}dtd} {\hat{\phi }} } ,t \in {\Pi _i}. \end{aligned}$$
(20)

According to (20), when \({\phi _{l,c}}\) is equal to any \({{\bar{\phi }} _i}\), a suitable beam-band function can capture most of the power of \({{{\textbf {B}}}_i}\). The full power of the received signal can be obtained by applying I beam-band functions, and then, the support can be obtained as follows:

$$\begin{aligned} i' = \arg \mathop{\max }\limits _i \frac{{\left\| {{{{\textbf {B}}}_i}({\Pi _i},:)} \right\| _F^2}}{{\left| {{\Pi _i}} \right| }}, \end{aligned}$$
(21)

where \(\left| {{\Pi _i}} \right| = 2\delta + 1\); thus, it follows that \({\phi _{l,c}} = {{\bar{\phi }} _{i'}}\).

In (20), all parameters except for \(\delta\) are predefined, so a suitable beam-band function should be defined so that \(\delta\) is appropriate for a beam. To extract as much power as possible from \({{{\textbf {B}}}_i}\) and handle the interference and noise that \({{{\textbf {B}}}_i}\) may encounter, \({\Pi _i}\) should satisfy the following condition:

$$\begin{aligned} {\Pi '_i} = \arg \mathop{\max }\limits _{{\Pi _i}} \left\| {{{{\textbf {B}}}_i}\left( {{\Pi _i},:} \right) } \right\| _F^2. \end{aligned}$$
(22)

At the same time, to avoid interference, the other beam-band \({\Pi _{i''}}(i'' \ne i')\) should acquire as little power of \({{{\textbf {B}}}_i}\) as possible, which is given as follows:

$$\begin{aligned} {\Pi '_{i''}} = \arg \mathop {\min }\limits _{{\Pi _{i''}}} \left\| {{{{\textbf {B}}}_i}\left( {{\Pi _{i''}},:} \right) } \right\| _F^2. \end{aligned}$$
(23)

Then, to estimate \({\phi _{l,c}}\) correctly, it should satisfy the following condition:

$$\begin{aligned} \left\| {{{{\textbf {B}}}_i}\left( {{\Pi _i},:} \right) } \right\| _F^2 > \mathop {\max }\limits _{i'' \ne i} \left( {\left\| {{{{\textbf {B}}}_i}\left( {{\Pi _{i''}},:} \right) } \right\| _F^2} \right) , \end{aligned}$$
(24)

which means that if the goal is that the beam-band extracts the most power of the current component, \(\delta\) should satisfy the following condition:

$$\begin{aligned} {\delta ^*} = \mathop {\arg \max }\limits _\delta \left[ {\left\| {{{{\textbf {B}}}_i}({\Pi _i},:)} \right\| _F^2 - \mathop {\max }\limits _{i'' \ne i} \left( {\left\| {{{{\textbf {B}}}_{i''}}({\Pi _i},:)} \right\| _F^2} \right) } \right] . \end{aligned}$$
(25)

Because the Dirichlet sinc function has the power-focusing capability, \(\left\| {{{{\textbf {B}}}_{i''}}\left( {{\Pi _i},:} \right) } \right\| _F^2\) may be larger than \(\left\| {{{{\textbf {B}}}_i}\left( {{\Pi _i},:} \right) } \right\| _F^2\) when \(i''\) is close to i; then, \(\mathop {\max }\limits _{i'' \ne i} \left( {\left\| {{{{\textbf {B}}}_{i''}}({\Pi _i},:)} \right\| _F^2} \right)\) can be rewritten as

$$\begin{aligned} \mathop {\max }\limits _{i'' \ne i} \left( {\left\| {{{{\textbf {B}}}_{i''}}({\Pi _i},:)} \right\| _F^2} \right) = \left\| {{{{\textbf {B}}}_{{\Xi _I}(i + 1)}}({\Pi _i},:)} \right\| _F^2, \end{aligned}$$
(26)

where \({\Xi _I}(i + 1)\) is introduced to ensure that \(i''\) belongs to \([1,\ldots ,I]\) and \(i'' \ne i\). When I is large, \({{\bar{\phi }} _{\,{\Xi _I}(i + 1)}}\) can be approximated to \({{\bar{\phi }} _i}\), and (25) can be rewritten as

$$\begin{aligned} {\delta ^*} = \mathop {\arg \max }\limits _\delta \left[ {\frac{{M{f_c}}}{{B{{{\bar{\phi }} }_i}}}\sum \limits _{t = - \delta }^\delta {\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {\left[ {{f^2}\left( {\frac{t}{I} + {\hat{\phi }} } \right) - {f^2}\left( {\frac{{t + 1}}{I} + {\hat{\phi }} } \right) } \right] d{\hat{\phi }} } } } \right] . \end{aligned}$$
(27)

Exchanging the orders of integration and summation in (27) and following the even function property of the Dirichlet function, we have the following:

$$\begin{aligned} {\delta ^*} = \mathop {\arg \max }\limits _\delta \frac{{M{f_c}}}{{B{{{\bar{\phi }} }_i}}}\int _{{{{\hat{\phi }} }_1}}^{{{{\hat{\phi }} }_M}} {\left[ {{f^2}\left( {\frac{\delta }{I} + {\hat{\phi }} } \right) - {f^2}\left( {\frac{{\delta + 1}}{I} + {\hat{\phi }} } \right) } \right] d{\hat{\phi }} }. \end{aligned}$$
(28)

According to the integral properties, \(\delta\) should satisfy the following condition

$$\begin{aligned} \frac{\delta }{I} = {{\hat{\phi }} _M} = \frac{{B{{{\bar{\phi }} }_i}(M - 1)}}{{2{f_c}M}}. \end{aligned}$$
(29)

So, the optimal \(\delta\) can be calculated as

$$\begin{aligned} \delta = \frac{{B{{{\bar{\phi }} }_i}(M - 1)I}}{{2{f_c}M}}. \end{aligned}$$
(30)

The specific steps of the proposed BBOMP scheme for wideband beamspace channel estimation are shown in Algorithm 1. Before the algorithm starts, the residual matrices \({{\textbf {E}}}\) initialized as, \({{\textbf {E}}} = {\hat{{{\textbf {Y}}}}}\) and (6) is rewritten as follows

$$\begin{aligned} {\hat{{{\textbf {Y}}}}} = {\hat{{{\textbf {W}}}}}{{{\textbf {H}}}^b} + {{\textbf {N}}}, \end{aligned}$$
(31)

where \({\hat{{{\textbf {Y}}}}} = [{{\hat{{{\textbf {y}}}}}_1},{{\hat{{{\textbf {y}}}}}_2},\ldots ,{{\hat{{{\textbf {y}}}}}_M}]\), \({{{\textbf {H}}}^b} = [{{\textbf {h}}}_1^b,{{\textbf {h}}}_2^b,\ldots ,{{\textbf {h}}}_M^b]\), and \({{\textbf {N}}} = [{{\hat{{{\textbf {n}}}}}_1},{{\hat{{{\textbf {n}}}}}_2},\ldots ,{{\hat{{{\textbf {n}}}}}_M}]\).

figure a

Compared to the traditional OMP algorithm, the proposed BBOMP algorithm considers noise and beam squint effect. Since without considering noise and beam squint effect, the traditional OMP algorithm estimates the indexes of all elements sequentially in one iteration step, which increases computation complexity and decreases estimation accuracy. In contrary, to reduce the interference of noise, the BBOMP algorithm calculates the supports of the strongest path component at all sub-carriers jointly. Then, the influence is removed when estimating the second strongest path component and the procedure is repeated until all path components have been considered. In addition, to compensate the performance loss caused by the beam squint effect, a beam-band function is derived to process adjacent beams simultaneously. This improves the performance significantly under both high and low SNR conditions. Compared with SSD-based scheme, the proposed BBOMP scheme maintains the nonzero elements of the sparse vector dynamically. According to the deviation of a beam’s direction from the predefined spatial direction of a lens antenna array, the proposed BBOMP scheme can adaptively adjust \({{\Omega }}\) to retain nonzero elements in different path components to improve the estimation accuracy.

4.2 Complexity analysis

As shown in Algorithm 1, the complexity is mainly reflected in Steps 1, 3, 9, 10, and 12, and it is characterized by the number of multiplications. In Step 1, the multiplication of \(\hat{\textbf{W}}^{H} \in {\mathbb{C}}^{I \times I_{R F} Q} \quad\) and \(\quad \textbf{E} \in {\mathbb{C}}^{I_{R F} Q \times M}\) is calculated, so the complexity is \(O({I_{RF}}MQI)\). In Step 3, the power of I \({{{\textbf {R}}}_i}({\Pi _i},:)\) is calculated, which has a complexity of O(IM). In Step 9, matrices \({\hat{{{\textbf {W}}}}}{(:,{\sigma _{l,m}})^H}\) and \({{{\textbf {E}}}_m}\) are multiplied, so the complexity is \(O({I_{RF}}Q\Omega )\). In Step 10, \({\hat{{{\textbf {W}}}}}(:,{\sigma _{l,m}})\) and \({{{\textbf {b}}}_{l,m}}({\sigma _{l,m}})\) are multiplied, and the complexity of this step is \(O({I_{RF}}Q\Omega )\). In Step 12, the supports of all components are merged, so the complexity is \(O({I_{RF}}Q{\left| {\sigma '} \right| ^2})\), which is similar to the complexity in Step 9. Finally, considering the loops in which the individual steps are located, the total complexity of the BBOMP scheme is calculated as \(O(M{I_{RF}}Q\Omega L) + O(M{I_{RF}}Q\Omega {L^2}) + O({I_{RF}}QL)\)

Because the value of \(\Omega\) is much smaller than the number of antennas I, the complexity of the BBOMP scheme is much lower than that of the traditional OMP-based scheme; particularly, it is lower by one order of magnitude I. Note that the SSD-based scheme proposed in [28] has lower complexity than the proposed BBOMP scheme because it removes the path components computed in the previous iteration at the current iteration, so the computational effort decreases with the iteration number. However, the advantage of the proposed BBOMP scheme in solving the support set is that the retention of nonzero elements can be realized dynamically instead of statically, which improves the estimation accuracy. The complexity comparison results of the OMP, SSD, and BBOMP schemes are presented in Table 1.

Table 1 Complexity comparison results of different schemes
Full size table

5 Simulation results and discussion

We conducted several simulations to verify the performance of the proposed BBOMP scheme. The proposed scheme is compared with the conventional OMP, SOMP, SSD, and Oracle LS schemes. In simulations, we assume that locations of the maximum power elements are known in the Oracle LS scheme, so the Oracle LS scheme is used as an optimal performance reference. The normalized mean-squared error (NMSE) is used as a performance evaluation indicator. The simulation parameters are shown in Table 2.

Table 2 System simulation parameters
Full size table
Fig. 4
figure 4

The NMSE performance of different schemes under different SNR values

Full size image

We compare the NMSE performance of the proposed BBOMP scheme with the NMSE performance of some existing broadband schemes under different SNR values. As shown in Fig. 4, the accuracy of the OMP and SOMP schemes is poor, because the common support assumption does not hold in wideband systems due to the beam squint effect. The BBOMP and SSD schemes have higher accuracy than the OMP and SOMP schemes under all SNR values and achieve an NMSE performance close to that of the Oracle LS scheme. The BBOMP and SSD schemes exploit the sparse structure of a wideband beamspace channel and suppress the beam squint effect. The proposed BBOMP, however, has a better performance than the SSD scheme. Because the proposed scheme does not use a fixed \(\Omega\), the support set could be estimated more accurately for some of the components. Finally, note that for all schemes, the elements of the wideband beamspace channel with indices outside the support are regarded as zeros, which make the performance of the schemes converge gradually to a fixed value as the SNR increases.

Fig. 5
figure 5

The NMSE performance of different schemes versus the number of users K. a. SNR=0 dB, b. SNR=15 dB

Full size image

The NMSE performance of different schemes versus the number of users K is presented in Fig. 5, where the SNR is 0 dB and 15 dB. As shown in Fig. 5, when the number of users increases, the performance of the traditional OMP scheme decreases significantly and its performance is not as good as those of the other schemes; thus, this scheme is not suitable for multi-user situations. Because the increase in the number of users indicates an increase in the number of pilots, the estimation error of the common support assumption increases accordingly. In addition, the curves in Fig. 5a and b show a decreasing and smooth trend, which indicates that an estimation error caused by the inter-user interference and hardware loss exists. In contrast, the proposed BBOMP scheme has a relatively stable performance for a different number of users and is more robust to changes in the number of users. In addition, it has a better performance than the currently advanced SSD scheme, proving that the proposed BBOMP scheme could provide a reliable channel estimation performance when the number of users is relatively large.

Fig. 6
figure 6

The NMSE performance of different schemes versus the channel bandwidth B

Full size image

The NMSE performance comparison of the schemes against the bandwidth B is shown in Fig. 6, where SNR is 15 dB. As shown in Fig. 6, when the bandwidth is narrow (e.g., \(B = 1\,{\rm{{ GHz}}}\)), the beam squint effect is not obvious, and the SOMP scheme could achieve satisfactory performance. However, as the bandwidth increases, the performance of the SOMP scheme gradually decreases; at a wide bandwidth, the performance of the SOMP scheme is even worse than that of the OMP scheme. When the bandwidth is large, the support of different sub-carriers for the wideband beamspace channel is more dispersed, and the common support assumption leads to more severe decay in the estimated performance. The proposed BBOMP scheme has better robustness to the bandwidth than the advanced SSD scheme.

Fig. 7
figure 7

The NMSE performance of different schemes versus the number of instants Q. a. SNR=0 dB, b. SNR=15 dB

Full size image

The NMSE performance of different schemes versus the number of pilot transmission instants Q under SNR of 0 dB and 15 dB is shown in Fig. 7. As shown in Fig. 7, the higher the pilot overhead is, the higher the accuracy of channel estimation is. This is because more pilot symbols contain richer information on the channel state. When the pilot overhead is too high, however, the system spectral efficiency is reduced. Compared with the other schemes, the proposed BBOMP scheme has a lower NMSE performance under the same number of pilot overhead and needs fewer pilot symbols to achieve the same estimation accuracy. This result demonstrates that the pilot overhead of the proposed BBOMP scheme is lower and more advantageous than those of the other schemes.

Fig. 8
figure 8

The NMSE performance of all schemes when the number of sub-carriers changes. a. SNR=0 dB, b. SNR=15 dB

Full size image

The NMSE performance comparison results of all schemes when the number of sub-carriers m changes are shown in Fig. 8. In Fig. 8, it can be seen that the performance of each of the schemes remains stable with the increase in the sub-carrier number. As the bandwidth increases, the OFDM system contains more sub-carriers, but they are orthogonal to each other and do not affect each other. Therefore, the increase in the number of sub-carriers has a slight impact on the channel estimation performance. In addition, the proposed BBOMP scheme is robust to the number of sub-carriers, and its performance is better than those of the other schemes. This is in agreement with the bandwidth performance experiment, whose results are presented in Fig. 6, which has proven that the proposed BBOMP scheme is preferable for a broadband system. Moreover, the proposed scheme can also achieve good channel estimation performance in narrowband systems; namely, when the beam spread effect is not obvious or even disappear, the proposed scheme still work normally.

Fig. 9
figure 9

The NMSE performance results of different schemes versus the number of antennas I

Full size image

The performance comparison of different schemes for a different number of base station antennas under SNR of 15 dB is presented in Fig. 9. As shown in Fig. 9, the OMP and SOMP schemes have the worst performance among all schemes. Specifically, the NMSE value of the SOMP scheme increases obviously with the number of base station antennas, indicating that the channel estimation performance of this scheme shows a downward trend. As the number of receiving antennas increases, the interference also increases, and the common support assumption of the SOMP scheme leads to the estimation performance degradation. On the contrary, the performance of the proposed BBOMP scheme remains stable with the number of base station antennas. It is expected that with the rapid development of wireless communication, the number of antennas in future base stations inevitably will increase gradually. According to the results shown in Fig. 9, the proposed BBOMP scheme could have certain application potential in the future.

Fig. 10
figure 10

Achievable sum-rate comparison against SNR for data transmission

Full size image

Figure 10 shows the achievable sum-rate performance comparison for a different downlink SNR. According to Fig. 10, when the uplink SNR is high, for instance, 15 dB, the achievable sum-rate performance of all channel estimation schemes is improved. Obviously, a larger uplink SNR makes the channel estimation more accurate, and the receiver has more accurate information on the channel state, which improves the system’s achievable sum-rate. Furthermore, the BBOMP and SSD schemes achieve a higher achievable sum-rate than the other schemes. The performance of the proposed BBOMP scheme is close to that of the ideal channel when the SNR is high, which further proves the performance advantage of the proposed BBOMP scheme.

Fig. 11
figure 11

Effect of hardware impairment on different schemes

Full size image

Finally, considering the impact of problems such as unstable signal reception caused by system hardware damage on channel estimation, supplementary experiments are carried out in this paper. The simulation parameters are the same as Table 2, but additional error coefficients are added to the system model in the simulation experiment. In existing communication protocols, the hardware damage is commonly defined by the error vector amplitude (EVM). The error vector amplitude at the transmitter is expressed as \({{\mathop {\rm{EVM}}\nolimits } _{T}} = \sqrt{{K_{T}}}\), where the coefficient \({K_{T}} \in \left[ {0\;,1} \right]\) indicates the degree of hardware damage. During the experiment, \({K_{T}}\) is set as 0.98. Figure 11 compares BBOMP with Oracle LS scheme. It can be seen that the hardware damage does have a significant impact on the channel estimation performance, but BBOMP scheme has a similar certain adaptability as Oracle LS scheme to the system error caused by hardware damage.

6 Conclusion

In this paper, we propose a channel estimation scheme for wideband mmWave massive MIMO systems with a lens antenna array to reduce the beam squint effect. The proposed scheme has low complexity but high estimation accuracy. Specifically, the channel estimation problem is formulated as a carrier frequency beam direction estimation problem using frequency-dependent sparse structure of a wideband beamspace channel. We propose a BBOMP channel estimation scheme to obtain the power of different path components by constructing a beam-band function and jointly estimating the support of each path component at different sub-carriers. In this way, the impact of the beam squint effect on the estimation performance is minimized, and the assumption of common support is abandoned, which improves the estimation accuracy. Additionally, an adaptive threshold method is proposed to extract indexes of nonzero dynamically elements when estimating the support to improve the estimation accuracy further. Simulation results show that the proposed scheme has better performance than some existing wideband channel estimation schemes and is robust to bandwidth. Finally, the proposed scheme is also suitable for narrowband systems.