1 Introduction

The joint direction-of-arrival (DOA) and polarization estimation of the polarization sensitive array (PSA) is one of the classical topics in array signal processing and has been widely used in radar, telecommunications, seismology [1]. In most scenarios, these estimation methods are proposed based on the linear array or planar array. Recently, the conformal array has aroused great concern. A conformal array [2, 3] is generally an array amounted with radiating sensors on the curvature surface. The conformal array has many benefits including reduction of aerodynamic drag, wide angle coverage, space saving, reduction of radar cross-section and so on. Complicated surface structure of CPSA will lead to the non-uniformity of element pattern and polarization characteristics, which brings lots of new challenges to parameters estimation. Therefore, the research on parameters estimation of CPSA is relatively significant.

At present, the DOA and polarization estimation methods based on the conformal array or the PSA are mainly according to their similar characteristics with the conventional array signal model and extended from the traditional parameter estimation techniques to conformal and PSA array. As a result, various approaches for cylindrical conformal arrays have been suggested to carry out two-dimensional (2D) DOA estimation, such as multiple signal classification (MUSIC) [4] and signal parameters via rotational invariance technique (ESPRIT) methods [5]. However, due to the direction diversity of the antenna, these conventional methods demand large signal to noise ratio (SNR) and snapshots. In practical electromagnetic environment, the increasingly dense signals and jamming signals, and more mobility targets will cause the received signal to face the problems of low SNR and small snapshots, which would cause the algorithm performance to deteriorate or even fail. In order to solve this problem, by considering the multidimensional structure of the array received data, the tensor technique is utilized to the MUSIC algorithm for cylindrical conformal array to improve the estimation performance [6, 7] proposed a 2D DOA estimation method by using the nested array on the cylindrical conformal arrays, which shows better performance. Nonetheless, the method in [6] is computationally much expensive as it requires spectrum peak searching, while the method in [7] needs to place the antenna in an elaborate design.

Recently, the emerging sparse reconstruction methods for DOA estimation, including \({\ell _p}\)-norm \(\left( {0 \le p \le 1} \right)\) methods [8,9,10,11,12], orthogonal matching pursuit (OMP) methods [13, 14] and the sparse Bayesian learning (SBL) methods [15,16,17,18], have aroused a lot of attention in DOA estimation. The essential idea of these algorithms is that the directions of incident source are substantially sparse in the spatial domain, which is intrinsically different from the subspace-based algorithms. Related methods have been shown to gain much enhanced performance over the subspace-based methods in the condition of low SNR and limited snapshots. In [19], a joint DOA, power and polarization estimation method using the cocentered orthogonal loop and dipole array is proposed by utilizing the signal reconstruction method. By exploiting the sparsity of the incident signals in the spatial domain, [20] proposed a novel method to estimated the DOA and polarization parameters by using SBL method. In [21], a novel off-grid hierarchical block-sparse Bayesian method for DOA and polarization parameters estimation was presented to improve the estimation accuracy [22]. Addressed a DOA and polarization estimation method based on the spatially separated polarization sensitive array under the SBL framework. However, these methods mentioned above focus on the estimation problem based on linear array or planar array, and do not consider the CPSA. As a result, the DOA and polarization estimation based on sparse reconstruction framework for CPSA needs further research.

This paper follows sparse reconstruction to address the joint DOA and polarization estimation based on the CPSA. By using the 2D joint sparsity signals of incident signals, a comprehensive array model is established first and a singular value decomposition (SVD) method is then used to reduce the dimension of array output matrix. And then, a variational sparse Bayesian learning (VSBL)-based method named CPSA-VSBL and OMP-based method named CPSA-OMP are proposed to realize DOA estimation. Finally, the polarization parameters are obtained by the minimum eigenvector method. The scenario when cylinder CPSA is taken as example, so as to show how the CPSA-VSBL and CPSA-OMP realize DOA and polarization estimation jointly. Numerical examples also be provided to show how the performance of the proposed methods in DOA and polarization estimation and resolution under low SNR and limited snapshots.

Notations: Bold-italic letters are used to represent vectors and matrices. Lower case letters denotes scalars. \({\mathcal {C}}\) denotes complex numbers. \({\left( \cdot \right) ^{ - 1}}\), \({\left( \cdot \right) ^{\mathrm{T}}}\) and \({\left( \cdot \right) ^{\mathrm{H}}}\) denote the inverse operation, transpose operation and conjugate transpose operation, respectively. \(\left\langle \cdot \right\rangle\) denotes the statistical expectation. \(\bullet\), \(\otimes\) and \(\odot\) denote Hadamard Product, Kronecker product and Khatri-Rao Product, respectively. For a vector \({\varvec{x}}\), \(\mathrm{{diag}}\left( {{\varvec{x}}} \right)\) is diagonal matrix with \({\varvec{x}}\) being its diagonal. \({\left\| \cdot \right\| _2}\) represents 2-norm.

2 2D sparse signal model

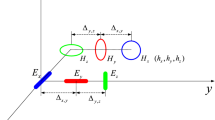
As shown in Fig. 1, suppose that there are K narrowband far-field true sources \(\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right) , k = 1,2, \cdots ,K\), impinging on an arbitrary CPSA with M electromagnetic vector sensor (EMVS), where \({\theta _k}\) is azimuth and \({\varphi _k}\) is elevation, \({\gamma _k} \in \left[ {0,{\pi / 2}} \right)\) and \({\eta _k} \in \left[ { - \pi ,\pi } \right)\) are the polarization auxiliary angle and polarization phase difference angle of the k-th signal, respectively. \({{\varvec{{{r}}}}_i} = {\left[ {{x_i},{y_i},{z_i}} \right] ^{\mathrm{T}}}, \mathrm{{ }}i\mathrm{{ = 1,2,}} \cdots \mathrm{{,}}M\) is position vector of i-th sensor. The propagation direction vector of the signal is \({\varvec{{{u}}}} = \left[ {\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta } \right] ^{\mathrm{T}}\). Each EMVS can output three electric-field vectors \({\varvec{E}} = \left[ {{{{\varvec{e}}}_x},{{{\varvec{e}}}_y},{{{\varvec{e}}}_z}} \right]\) and three magnetic-field vectors \({\varvec{H}} = \left[ {{{{\varvec{h}}}_x},{{{\varvec{h}}}_y},{{{\varvec{h}}}_z}} \right]\) [23]. For the k-th fully polarization wave, the polarization steering vector of each sensor can be written as

Fig. 1
figure 1

Arbitrary conformal polarization sensitive array

Full size image
$$\begin{aligned} \begin{aligned} {{\varvec{{{b}}}}}\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right)&= {\left[ {\begin{array}{*{20}{c}} {{{\varvec{{{E}}}}_k}}&{{{\varvec{{{H}}}}_k}}\end{array}} \right] ^{\mathrm{{T}}}}\\&= {\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}}{{{{\varvec{e}}}_{xk}}}&{\begin{array}{*{20}{c}}{{{{\varvec{e}}}_{yk}}}&{{{{\varvec{e}}}_{zk}}}\end{array}}\end{array}}&{{{{\varvec{h}}}_{xk}}}&{{{{\varvec{h}}}_{yk}}}\end{array}}&{{{{\varvec{h}}}_{zk}}}\end{array}} \right] ^{\mathrm{{T}}}}\\&=\left[ {\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\cos {\varphi _k}\cos {\theta _k}}\\ {\sin {\varphi _k}\cos {\theta _k}}\\ { - \sin {\theta _k}}\end{array}}\\ { - \sin {\varphi _k}}\\ {\cos {\varphi _k}}\\ 0\end{array}}&{}{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{ - \sin {\varphi _k}}\\ {\cos {\varphi _k}}\\ 0\end{array}}\\ { - \cos {\varphi _k}\cos {\theta _k}}\\ { - \sin {\varphi _k}\cos {\theta _k}}\\ {\sin {\theta _k}}\end{array}}\end{array}} \right] \left[ {\begin{array}{*{20}{c}}{\sin {\gamma _k}{e^{j{\eta _k}}}}\\ {\cos {\gamma _k}}\end{array}} \right] \\&={{\varvec{{{v}}}}}\left( {{\theta _k},{\varphi _k}} \right) {\varvec{\rho } }\left( {\gamma _k ,\eta _k } \right) \mathrm{{ }} \end{aligned}, \end{aligned}$$
(1)

where \({\varvec{b}}\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right) \in {{\mathcal {C}}^{6 \times 1}}\), \({{\varvec{{v}}}}\left( {{\theta _k},{\varphi _k}} \right)\) and \({\varvec{\rho } }\left( {\gamma _k ,\eta _k } \right) \mathrm{{ }}\) represent the source’s spatial information and polarization information, respectively.

\(O\left( {X,Y,Z} \right)\) represents the global coordinate system in Fig. 1, and accordingly, \({{O'}_i}\left( {X',Y',Z'} \right)\) represents the local coordinate system of i-th element [24]. Hence, \({\theta }\) is azimuth and \({\varphi }\) is elevation in the global coordinate system, and accordingly, \({\theta '}\) and \({\varphi '}\) are azimuth and elevation in the local coordinate system, respectively. Given the effect of the CPSA curvature, the element pattern and polarization characteristics of each sensor is not uniform any more. There exists a rotation matrix \({\varvec{R}}\) in [25], so that the pattern of i-th sensor can be transformed from local coordinate system \({{g}}_i\left( {\theta ',\varphi '} \right)\) to global coordinate system \({{g}}_i\left( {\theta ,\varphi } \right)\). Therefore, the array steering vector of the k-th signal can be written as

$$\begin{aligned} \begin{aligned} \bar{{\varvec{a}}} \left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right)&= {\varvec{g}}\left( {{\theta _k},{\varphi _k}} \right) \bullet {\varvec{a}}\left( {{\theta _k},{\varphi _k}} \right) \odot {\varvec{b}}\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right) \\&= {{\varvec{d}}}\left( {{\theta _k},{\varphi _k}} \right) \odot {\varvec{b}}\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right) , \end{aligned} \end{aligned}$$
(2)

where \({\varvec{a}}\left( {{\theta _k},{\varphi _k}} \right) \in {{\mathcal {C}}^{M \times 1}}\) denotes the spatial steering vector, \({{\varvec{g}}\left( {{\theta _k},{\varphi _k}} \right) \in {{\mathcal {C}}^{M \times 1}}}\) denotes the element pattern in the global coordinate system. \({{\varvec{d}}}\left( {{\theta _k},{\varphi _k}} \right) = {{\varvec{g}}}\left( {{\theta _k},{\varphi _k}} \right) \bullet {{\varvec{a}}}\left( {{\theta _k},{\varphi _k}} \right)\) and its expression is formulated as follows

$$\begin{aligned} {{\varvec{d}}} \left( {{\theta _k},{\varphi _k}} \right) = \left[ {{g_1}\left( {\theta ,\varphi } \right) {e^{ - j\frac{{2\pi }}{\lambda }{{\varvec{r}}_1} \bullet {{\varvec{u}}_k}}}, \cdots ,{g_M}\left( {\theta ,\varphi } \right) {e^{ - j\frac{{2\pi }}{\lambda }{{\varvec{r}}_M} \bullet {{\varvec{u}}_k}}}} \right] ^{\mathrm{{T}}}, \end{aligned}$$
(3)
$$\begin{aligned} {g_i}\left( {\theta ,\varphi } \right) =\left| {{f_i}} \right| \left| e \right| \cos \left( {{\theta _{ife}}} \right) = {{\varvec{f}}_i} \cdot {\varvec{e}} = {g_{i{\theta }}}{k_\theta } + {g_{i{\varphi }}}{k_\varphi }\mathrm{{ }}, i = 1,2,...,M, \end{aligned}$$
(4)
$$\begin{aligned} {{\varvec{r}}_i }= \left[ {{x_i},{y_i}},{z_i}\right] ^{\mathrm{{T}}}, i = 1,2, \cdots ,M , \end{aligned}$$
(5)
$$\begin{aligned} {{\varvec{u}}_k} = \left[ {\sin {\theta _k}\cos {\varphi _k},\sin {\theta _k}\sin {\varphi _k},\cos {\theta _k}} \right] ^{\mathrm{{T}}}, \end{aligned}$$
(6)

where \(\lambda\) is the carrier wavelength. As shown in Fig. 2 [26], \({f_i}\) is the direction diagram of the i-th sensor, \({u_\theta }\) and \({u_\varphi }\) are unit vectors, \({k_\theta }\) and \({k_\varphi }\) are the polarization parameters of the true sources. \({g_{i{\theta }}}\) and \({g_{i{\varphi }}}\) are the response of i-th sensor to the \({\theta '}\) and \({\varphi '}\) in the local coordinate system [27]. Thus, the received data model is expressed as

$$\begin{aligned} \bar{{\varvec{x}}} \left( t \right) = \sum \limits _{k = 1}^K {\bar{{\varvec{a}}} \left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right) {{\bar{s}}_k}\left( t \right) } + \bar{{\varvec{n}}} \left( t \right) , \end{aligned}$$
(7)

where \(\bar{{\varvec{x}}}\left( t \right) = \left[ {{\bar{x}_1}\left( t \right) , \cdots ,{{\bar{x}}_{6M}}\left( t \right) } \right] ^{\mathrm{{T}}} \in {{\mathcal {C}}^{6M \times 1}}\) and \(\bar{{\varvec{n}}}\left( t \right) = \left[ {{{\bar{n}}_1}\left( t \right) , \cdots ,{{\bar{n}}_{6M}}\left( t \right) } \right] ^{\mathrm{{T}}} \in {{\mathcal {C}}^{6M \times 1}}\) are the received data vector and complex Gaussian noise vector, respectively. Consider that all the K true sources are incident on the CPSA [28]. As a result, the array steering matrix is

$$\begin{aligned} \begin{aligned} {\bar{{\varvec{A}}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right)&= {{{\varvec{G}}}\left( {\theta ,\varphi } \right) \bullet {{\varvec{A}}}\left( {\theta ,\varphi } \right) \odot {{\varvec{B}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) } \\&= {{{\varvec{D}}}\left( {\theta ,\varphi } \right) \odot {{\varvec{B}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) }\\&= {{{\varvec{D}}}\left( {\theta ,\varphi } \right) {{\varvec{I}}} \odot {{\varvec{V}}}\left( {\theta ,\varphi } \right) {{\varvec{Q}}}\left( {\gamma ,\eta } \right) } \\&= \left( {{{\varvec{D}}}\left( {\theta ,\varphi } \right) \otimes {{\varvec{V}}}\left( {\theta ,\varphi } \right) } \right) \left( {{{\varvec{I}}} \otimes {{\varvec{Q}}}\left( {\gamma ,\eta } \right) } \right) \end{aligned}, \end{aligned}$$
(8)

where \({{\varvec{D}}}\left( {\theta ,\varphi } \right) = {{\varvec{G}}}\left( {\theta ,\varphi } \right) \bullet {{\varvec{A}}}\left( {\theta ,\varphi } \right)\) and \({{\varvec{B}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = {{\varvec{V}}}\left( {\theta ,\varphi } \right) {{\varvec{Q}}}\left( {\gamma ,\eta } \right)\). \({\varvec{I}}\) is the \(K \times K\) identity matrix. \({\bar{{\varvec{A}}}}\) is a \(6M \times K\) matrix denoting the response of the array. It is seen that \({\varvec{G}}\) denotes \(M \times K\) element pattern matrix of K signals, \({\varvec{A}}\) denotes the \(M \times K\) full-rank steering matrix, \({\varvec{B}}\) denotes the \(6 \times K\) polarization steering matrix, \({{\varvec{V}}}\left( {\theta ,\varphi } \right)\) denotes \(6 \times 2K\) spatial information matrix of \({\varvec{B}}\), \({{\varvec{Q}}}\left( {\gamma ,\eta } \right)\) denotes \(2K \times K\) polarization information matrix of \({\varvec{B}}\).

$$\begin{aligned} {{\varvec{G}}}\left( {\theta ,\varphi } \right) = \left[ {{\varvec{g}}\left( {{\theta _1},{\varphi _1}} \right) , \cdots ,{\varvec{g}}\left( {{\theta _K},{\varphi _K}} \right) } \right] , \end{aligned}$$
(9)
$$\begin{aligned} {{\varvec{A}}}\left( {\theta ,\varphi } \right) = \left[ {{\varvec{a}}\left( {{\theta _1},{\varphi _1}} \right) , \cdots ,{\varvec{a}}\left( {{\theta _K},{\varphi _K}} \right) } \right] , \end{aligned}$$
(10)
$$\begin{aligned} \begin{aligned} {{\varvec{B}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right)&= \left[ {{\varvec{b}}\left( {{\theta _1},{\varphi _1},{\gamma _1},{\eta _1}} \right) , \cdots ,{\varvec{b}}\left( {{\theta _K},{\varphi _K},{\gamma _K},{\eta _K}} \right) } \right] \\&=\left[ {{{\varvec{{v}}}}\left( {{\theta _1},{\varphi _1}} \right) {\varvec{\rho } } \left( {{\gamma _1},{\eta _1}} \right) , \cdots ,{{\varvec{{v}}}}\left( {{\theta _K},{\varphi _K}} \right) {\varvec{\rho } } \left( {{\gamma _K},{\eta _K}} \right) } \right] \end{aligned}, \end{aligned}$$
(11)
$$\begin{aligned} {{\varvec{D}}}\left( {\theta ,\varphi } \right) = \left[ {{{\varvec{d}}}\left( {{\theta _1},{\varphi _1}} \right) ,{{\varvec{d}}}\left( {{\theta _2},{\varphi _2}} \right) , \cdots ,{{\varvec{d}}}\left( {{\theta _K},{\varphi _K}} \right) } \right] \end{aligned}$$
(12)
$$\begin{aligned} {{\varvec{V}}}\left( {\theta ,\varphi } \right) = \left[ {{{\varvec{v}}}\left( {{\theta _1},{\varphi _1}} \right) , \cdots ,{{\varvec{v}}}\left( {{\theta _K},{\varphi _K}} \right) } \right] , \end{aligned}$$
(13)
$$\begin{aligned} {{\varvec{Q}}}\left( {\gamma ,\eta } \right) = \mathrm {diag}\left( {{\varvec{\rho } } \left( {{\gamma _1},{\eta _1}} \right) , \cdots ,{\varvec{\rho }} \left( {{\gamma _K},{\eta _K}} \right) } \right) . \end{aligned}$$
(14)
Fig. 2
figure 2

Response of sensor

Full size image

Hence, the received array data model is given by

$$\begin{aligned} \bar{{\varvec{X}}}\left( t \right) = {\bar{{\varvec{A}}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) \bar{{\varvec{S}}}\left( t \right) + \bar{{\varvec{N}}}\left( t \right) , \end{aligned}$$
(15)

For simplicity, (15) can be rewritten as

$$\begin{aligned} \bar{{\varvec{X}}} = {\bar{{\varvec{A}}}}\bar{{\varvec{S}}} + \bar{{\varvec{N}}}, \end{aligned}$$
(16)

where \(\bar{{\varvec{S}}} = {\left[ {{{\varvec{s}}_1},{{\varvec{s}}_2}, \cdots ,{{\varvec{s}}_K}} \right] ^{\mathrm{{T}}}}\), \(\bar{{\varvec{N}}} = {\left[ {{{\varvec{n}}_1},{{\varvec{n}}_2}, \cdots ,{{\varvec{n}}_{6M}}} \right] ^{\mathrm{{T}}}}\). \(\bar{{\varvec{S}}}\) and \(\bar{{\varvec{N}}}\) denote \(K \times T\) source and \(6M \times T\) additive white Gaussian noise, respectively.

In order to use sparse reconstruction method to DOA estimation, generally [29], we can uniformly sample the range of azimuth and elevation to formulate a DOA set \(\left\{ {\left. {\left( {\tilde{\varvec{\theta }} ,\tilde{\varvec{\varphi }} } \right) } \right\} } \right. = \left\{ {\left. {\left( {{{\tilde{\theta }}_1},{{\tilde{\varphi }}_1}} \right) , \cdots ,\left\{ {\left. {\left( {{{\tilde{\theta }}_{{J_{\tilde{\theta }}}}},{{\tilde{\varphi }}_{{J_{\tilde{\varphi }}}}}} \right) } \right\} } \right. } \right\} } \right.\) with \(J = {J_{\tilde{\theta }}}{J_{\tilde{\varphi }}} \gg K\). Assume that all the true sources lie on a fixed DOA set. For simplicity, the sparsity of the polarization information is not considered. The proposed methods are derived in the multiple measurement vectors. Therefore, the observation matrix \({{\varvec{X}}}\) with the snapshots is T can be presented as

$$\begin{aligned} {{\varvec{X}}} = \tilde{{\varvec{A}}}{{\varvec{S}}} + {{\varvec{N}}}, \end{aligned}$$
(17)

It is noted that \(\tilde{{\varvec{A}}}\) is called the overcomplete dictionary and the number of \(\tilde{{\varvec{A}}}\) columns is much larger than that of rows. Similar to (8), it can be found that \(\tilde{{\varvec{A}}}\) not only depends spatial parameters but also depends polarization parameters. \({\varvec{{S}}}\) is called sparse direction weights, each sparse weight has non-zero value only at the true source directions. Compared with nonsparse method, sparse reconstruction method can obtain the the source targets DOA with smaller reconstruction error. It expolits the observation matrix to reconstruct the signals and then the reconstructed signals are used to realize the DOA and polarization parameters estimation.

3 Methods

The sparse reconstruction methods [30, 31] make use of the sparsity of signal in the spatial domain to reconstruct true signals. In this section, we propose a sparsity-prompting CPSA-VSBL method to realize DOA estimation based on the MMV array output formulation given in (17). Meanwhile, the CPSA-OMP method is also proposed.

3.1 Dimensionality reduction of received data

From (17), it is easy to note that the large dimension of the received data will degrade the computational efficiency. So, SVD is conducted on \({{\varvec{X}}}\), we have

$$\begin{aligned} {{\varvec{X}}} = {\varvec{{U}}}\varvec{\varSigma } {{\varvec{{V}}}^{\mathrm{{H}}}}, \end{aligned}$$
(18)

where \({\varvec{{U}}}\), \(\varvec{\varSigma }\) and \({\varvec{{V}}}\) is denoted as the left singular matrix, eigenvalue matrix and right singular matrix, respectively. Let \({\varvec{{V}}} = \left[ {{{\varvec{{V}}}_1},{{\varvec{{V}}}_2}} \right]\), \({\varvec{{V}}}\) is divided into \({{\varvec{{V}}}_1}\) and \({{\varvec{{V}}}_2}\) matrix according to the first K and the rest \(T-K\) columns. In the presence of noise, we have \({\varvec{{X}}}{\varvec{{V}}}=\left[ {{{\varvec{{X}}}_{\text {sv}}},{\varvec{{X}}}{{\varvec{{V}}}_2}} \right]\) by the SVD, where \({{{\varvec{{X}}}_{\text {sv}}}}\) preserves most true sources information while the \({\varvec{{X}}}{{\varvec{{V}}}_2}\) is abandoned. Denote \({\varvec{{Y}}}={{{\varvec{{X}}}_{\text {sv}}}}\), \({{\varvec{{S}}}_{\text {sv}}} = {\varvec{{S}}}{{\varvec{{V}}}_1}\) and \({{\varvec{{N}}}_{\text {sv}}} = {\varvec{{N}}}{{\varvec{{V}}}_1}\), then we have

$$\begin{aligned} {\varvec{{Y}}} = \tilde{{\varvec{A}}}{{\varvec{S}}_{\text {sv}}}+ {{\varvec{N}}_{\text {sv}}}, \end{aligned}$$
(19)

where \({{\varvec{S}}_{\text {sv}}}\) and \({{\varvec{N}}_{\text {sv}}}\) are the new matrices of sparse direction weights and measurement noise, respectively. \({\varvec{{Y}}} \in {{\mathcal {C}}^{6M{K^2} \times K}}\) represents the observation data matrix after reducing the dimension of \({{\varvec{X}}}\), and \(K \le T\). Hence, by using \({\varvec{{Y}}}\) in the following signal reconstruction process, the computational complexity of the algorithm is reduced greatly.

3.2 The proposed CPSA-VSBL method

The posterior distributions of all unknown parameters can be calculated by using the Bayesian criterion [32], we have

$$\begin{aligned} p\left( {{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta \left| {\varvec{{Y}}} \right. } \right) = \frac{{p\left( {{\varvec{{Y}}},{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right) }}{{p\left( {\varvec{{Y}}} \right) }}. \end{aligned}$$
(20)

Assume that all the variables are mutually independent, the joint probability density function (PDF) \(p\left( {{\varvec{{Y}}},{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right)\) is expressed as

$$\begin{aligned} p\left( {{\varvec{{Y}}},{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right) = p\left( {{\varvec{{Y}}}\left| {{\varvec{{S}}}_{\text {sv}},{\sigma ^2}} \right. } \right) p\left( {{\varvec{{S}}}_{\text {sv}}\left| {\varvec{\alpha }} \right. } \right) p\left( {{\varvec{\alpha }} \left| {\tau ,\beta } \right. } \right) p\left( {\beta \left| \nu \right. } \right) , \end{aligned}$$
(21)

where \({\varvec{\alpha }}\) and \(\beta\) are hyperparameters, \(\tau \ge 0\) is shape parameter and \(\nu \ge 0\) denotes rate parameter. The directed graphical model [33] of the factorization of the joint PDF is depicted in Fig. 3. \({\varvec{{N}}}_{\text {sv}}\) obeys complex zero-mean stationary Gaussian noise with known variance \({\sigma ^2}\). Thus, we have

Fig. 3
figure 3

Block diagram of variational Bayesian principle

Full size image
$$\begin{aligned} p\left( {{\varvec{{N}}}_{\text {sv}}\left| {{\sigma ^2}} \right. } \right) = \prod \limits _{t = 1}^K {{{{\mathcal {C}}}}{{{\mathcal {N}}}}\left( {n_{\text {sv}}\left( t \right) \left| 0 \right. ,{\sigma ^2}I} \right) }. \end{aligned}$$
(22)

As a result, a Gaussian likelihood function model of \({\varvec{{Y}}}\) can be obtained by

$$\begin{aligned} p\left( {{\varvec{{Y}}}\left| {{\varvec{{S}}}_{\text {sv}},{\sigma ^2}} \right. } \right) = \prod \limits _{t = 1}^K {{{{\mathcal {C}}}}\mathcal{N}\left( {{\varvec{{Y}}}\left( t \right) \left| {\tilde{{\varvec{A}}}{\varvec{{S}}}_{\text {sv}}\left( t \right) ,{\sigma ^2}I} \right. } \right) }. \end{aligned}$$
(23)

The non-zero rows of \({\varvec{{S}}}_{\text {sv}}\) contain all the angular information of the incident signals. The CPSA-VSBL method is employed to update the hidden variables and hyperparameters to approximate the posterior probability [34]. We apply a three-layer hierarchical prior [35] to \({\varvec{{S}}}_{\text {sv}}\). A zero-mean complex Gaussian (Gauss) distribution imposed on \({\varvec{{S}}}_{\text {sv}}\) as the first layer of prior

$$\begin{aligned} p\left( {{\varvec{{S}}}_{\text {sv}}\left| \alpha \right. } \right) = \prod \limits _{t = 1}^K {{{{\mathcal {C}}}}{{{\mathcal {N}}}}\left( {{\varvec{{S}}}_{\text {sv}}\left( t \right) \left| {0,{ \varvec{\varLambda }^{ - 1}}} \right. } \right) = \prod \limits _{t = 1}^K {\prod \limits _{j = 1}^J {{{{\mathcal {C}}}}{{{\mathcal {N}}}}\left( {{s_{\text {sv}}}\left( t \right) _{j}\left| {0,{\alpha _j}} \right. } \right) } } }, \end{aligned}$$
(24)

where \({\varvec{\varLambda } ^{\mathrm{{ }} - 1}} = \mathrm{{diag}}\left( {{1 \big / {{\alpha _1}}},{1 \big / {{\alpha _2}}}, \cdots {{,1} \big / {{\alpha _j}, \cdots }},{1 \big /{{\alpha _J}}}} \right)\), \({\alpha _j} = {\sigma _j}^{-2}\) and \({\alpha _j}\) is the j-th noise precision. The exponential (Exp) distribution is applied to the hyperparameter \(\alpha\) as the second-layer prior

$$\begin{aligned} p\left( {{\varvec{\alpha }} \left| {\tau ,\beta } \right. } \right) = \prod \limits _{j = 1}^J {Exp} \left( {{\alpha _j}\left| {\tau , \beta } \right. } \right) . \end{aligned}$$
(25)

The hyperparameter \(\beta\) obeys the chi-square (Chi2) distribution as the third-layer prior

$$\begin{aligned} p\left( {\beta \left| \nu \right. } \right) = {\chi ^2}\left( {\beta \left| \nu \right. } \right) . \end{aligned}$$
(26)

However, \(p\left( {{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta \left| {\varvec{{Y}}} \right. } \right)\) is not easy to solve. CPSA-VSBL minimizes Kullback-Leibler (KL) divergence [36] between approximate PDF \(q\left( \varTheta \right)\) and its posterior \(p\left( {{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta \left| {\varvec{{Y}}} \right. } \right)\), where \(\varTheta = \left\{ {{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right\}\). The independent variables in \(q\left( \varTheta \right)\) can be rewritten into the product form of the distribution function which is described as \(q\left( \varTheta \right) = q\left( {{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right) = q\left( {\varvec{{S}}}_{\text {sv}} \right) q\left( {\varvec{\alpha }} \right) q\left( \beta \right)\). We can get the mean, variance of \({\varvec{{S}}}_{\text {sv}}\), and hyperparameters through the following steps.

The posterior distribution \(q\left( {\varvec{{S}}}_{\text {sv}} \right)\) is updated by \(q\left( {\varvec{{S}}}_{\text {sv}} \right) \propto {\left( {p\left( {{\varvec{{Y}}},{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right) } \right) _{q\left( {\varvec{\alpha }} \right) }}\), where \({\left( \cdot \right) _{q\left( {\varvec{\alpha }} \right) }}\) denotes the subset of \(\varTheta\) that removes \({\varvec{\alpha }}\). \(p\left( {{\varvec{{Y}}},{\varvec{{S}}}_{\text {sv}},{\varvec{\alpha }} ,\beta } \right)\) can be obtained by the joint distribution of \(p\left( {{\varvec{{Y}}}\left| {\varvec{{S}}}_{\text {sv}} \right. } \right)\) and \(p\left( {{\varvec{{S}}}_{\text {sv}}\left| {\varvec{\alpha }} \right. } \right)\). We can acquire the approximate posterior for \(q\left( {\varvec{{S}}}_{\text {sv}} \right)\) as

$$\begin{aligned} q\left( {\varvec{{S}}}_{\text {sv}} \right) = \prod \limits _{t = 1}^K {{{{\mathcal {C}}}}{{{\mathcal {N}}}}} \left( {{\varvec{{S}}}_{\text {sv}}\left( t \right) \left| {\mu \left( t\right) ,\varGamma } \right. } \right) . \end{aligned}$$
(27)

The parameters of the approximate posterior in (27) can be renewed according to

$$\begin{aligned} \mu \left( t \right) = {\sigma ^{ - 2}}{\varGamma ^{ - 1}}{{\tilde{{\varvec{{A}}}}^{\mathrm{{H}}}}}{\varvec{{Y}}}\left( t \right) , \end{aligned}$$
(28)
$$\begin{aligned} \varGamma = {\left( {{\sigma ^{-2}}{{{\tilde{{\varvec{{A}}}}^{\mathrm{{H}}}}}}\tilde{{\varvec{{A}}}} + \left\langle \varLambda \right\rangle } \right) ^{ - 1}}, \end{aligned}$$
(29)

The \(q\left( {\varvec{\alpha }} \right)\) is updated according to \(q\left( {\varvec{\alpha }} \right) \propto {\left( {p\left( {{\varvec{{S}}}_{\text {sv}}\left| {\varvec{\alpha }} \right. } \right) p\left( {{\varvec{\alpha }} \left| \tau \right. ,\beta } \right) } \right) _{q\left( {\varvec{{S}}}_{\text {sv}} \right) q\left( \beta \right) }}\) and can be approximated as the product of the PDF of the generalized inverse Gaussian distribution, and thus, we have

$$\begin{aligned} \left\langle {\alpha _j^n} \right\rangle = {\left( {\frac{{\left\langle {h_j^2} \right\rangle }}{{2\tau \left\langle \beta \right\rangle }}} \right) ^{\frac{n}{2}}}\frac{{{\kappa _{ \frac{n -1}{2}}}\left( {\sqrt{2\tau \left\langle \beta \right\rangle \left\langle {h_j^2} \right\rangle } } \right) }}{{{\kappa _{ - \frac{1}{2}}}\left( {\sqrt{2\tau \left\langle \beta \right\rangle \left\langle {h_j^2} \right\rangle } } \right) }}, \end{aligned}$$
(30)

where \(\left\langle {h_j^2} \right\rangle = \mu _j^2 + {\varGamma _j}\), \({\kappa _p}\left( \cdot \right)\) is referred to the third kind Bessel function with order p. When n = -1, the estimated \(\varGamma\) and \(\left\langle \varLambda \right\rangle\) in (29) are obtained.

The posterior distribution \(q\left( \beta \right)\) is updated by \(q\left( \beta \right) \propto {\left( {p\left( {\alpha \left| \tau \right. ,\beta } \right) p\left( {\beta \left| \nu \right. } \right) } \right) _{q\left( \alpha \right) }}\) and complies with Gamma distribution as

$$\begin{aligned} \beta \thicksim \mathrm{{Gamma}} \left( {J + \frac{\nu }{2},\tau \sum \limits _{j = 1}^J {\left\langle {{\alpha _j}} \right\rangle + \frac{1}{2}} } \right) . \end{aligned}$$
(31)

Thus, the mean value of \(\beta\) can be expressed as

$$\begin{aligned} \left\langle \beta \right\rangle = \frac{{J + \frac{v}{2}}}{{\tau \sum \limits _{j = 1}^J {\left\langle {{\alpha _j}} \right\rangle + \frac{1}{2}} }}. \end{aligned}$$
(32)
Table 1 The execution steps of CPSA-VSBL algorithm
Full size table

CPSA-VSBL firstly carries out the initialization of constant variables in the selected distribution function, and then iteratively update the hidden variables and hyperparameters in turn until the set convergence conditions are satisfied [37]. The CPSA-VSBL algorithm in this paper is summarized in Table 1.

3.3 The proposed CPSA-OMP method

In the CPSA-OMP method, \({{\varvec{S}}}\) can be reconstructed from the known matrix \({\varvec{Y}}\) and \(\tilde{{\varvec{A}}}\) based on the idea of dictionary atomic matching. In each iteration of CPSA-OMP, a column of \(\tilde{{\varvec{A}}}\) is selected by orthogonal projection method, which is most relevant to the \({\varvec{{Y}}}\) . Then we subtract off its contribution to \({\varvec{{Y}}}\) and iterate over the remaining residual \({\varvec{{w}}}_{re{s^i}}^i\). The algorithm will identify the index set of the correct column when the residual is zero. The minimization of \({\varvec{{w}}}_{re{s^i}}^i\) is selected by as follows

$$\begin{aligned} {\varvec{{w}}}_{re{s^i}}^i = \mathop {\arg \min }\limits _{{{\varvec{{Y}}}_{re{s^i}}}} \left\| {{\varvec{{Y}}} - \tilde{{\varvec{A}}}_{re{s^i}}^i{{\varvec{{Y}}}_{re{s^i}}}} \right\| _2^2, \end{aligned}$$
(33)

where \({\varvec{{w}}}_{re{s^i}}^i\) is the residual matrix in the i-th iteration, \(\tilde{{\varvec{{A}}}}_{re{s^i}}^i\) denotes the remaining part of \(\tilde{{\varvec{A}}}\) after the i-th iteration. The execution steps of CPSA-OMP algorithm are shown in Table 2.

Table 2 The execution steps of CPSA-OMP algorithm
Full size table

Some remarks of specific implementation of CPSA-VSBL and CPSA-OMP are shown as follows.

Remark 1

The number of target sources K is used as known condition. Estimation K as a significant study topic is outside the scope of this paper. Furthermore, the scenarios of coherent sources and colored noise are not considered.

Remark 2

Compared with the conventional two-layer prior, the CPSA-VSBL method benefits from the selected three-layer prior (Gauss-Exp-Chi2) with the property of a sharp peak at the origin and heavy tails. It has the effect of prompting the sparsity of its solutions.

Remark 3

In this paper, CPSA-VSBL and CPSA-OMP methods only discussed the CPSA-based structure. It is noted that the proposed methods can be generalized to arbitrary array geometries.

Remark 4

According to empirical, the hyperparameters \(\alpha\) and \(\beta\) are initialized to the \(\frac{1}{T}\sum \nolimits _{t = 1}^K {\tilde{{\varvec{A}}}{\varvec{{Y}}}\left( t \right) }\) and 0.1, respectively. \(\tau = 1.5\) and \(\nu = 1\) are set in the third level prior distribution. \(\varepsilon = {10^{ - 3}}\) and \({i_{\max }} = 2000\) represent the termination threshold and maximum iterative number, respectively.

3.4 Refined DOA estimation

The mean and variance of \(\bar{{\varvec{S}}}\) can be output in \(\left\{ {\left[ {{\mu _1},{\varGamma _1}} \right] ,} \right. \left[ {{\mu _2},{\varGamma _2}} \right] , \cdots ,\left. {\left[ {{\mu _J},{\varGamma _J}} \right] } \right\}\) after the iteratively update termination criterion \(\left\| {{{\left\langle {{\alpha _j}} \right\rangle }^{\left( i \right) }} - {{\left\langle {{\alpha _j}} \right\rangle }^{\left( {i - 1} \right) }}} \right\| /\left\| {{{\left\langle {{\alpha _j}} \right\rangle }^{\left( {i - 1} \right) }}} \right\| < \varepsilon\) or \(i > {i_{\max }}\) is reached. The powers from different directions are obtained by substituting the estimated \(\left[ {{ \varvec{\mu }},{ \varvec{\varGamma } }} \right]\) into the power function, where the power of the j-th impinging signal in the \(\varvec{\varOmega }\) is expressed as \({{\hat{P}}_j}\)

$$\begin{aligned} {{\hat{P}}_j} = \frac{1}{L}\left\langle {\left\| {{{\varvec{{S}}}_{s{v_j}}}} \right\| _2^2} \right\rangle \mathrm{{ = }}\frac{1}{L}\left( {\left\| {\left\langle {{{\varvec{{S}}}_{s{v_j}}}} \right\rangle } \right\| _2^2 + \left\langle {\left\| {{{\varvec{{S}}}_{s{v_j}}} - \left\langle {{{\varvec{{S}}}_{s{v_j}}}} \right\rangle } \right\| _2^2} \right\rangle } \right) \mathrm{{ = }}\frac{{\left\| {{\mu _j}} \right\| _2^2}}{L} + {\varGamma _j}. \end{aligned}$$
(34)

We use all the estimated signal powers to form a power spectrum. Similar to other spectral-searching-based methods, the DOA is estimated by finding the positions of the highest peaks of the spectrum. Suppose that the grid indices of the highest K power values are the position of the true sources. The estimated K DOA will be \(\left\{ {\left[ {{{\hat{\theta }}_1},{{\hat{\varphi }}_1}} \right] ,\left[ {{{\hat{\theta }}_2},{{\hat{\varphi }}_2}} \right] , \cdots ,\left[ {{{\hat{\theta }}_K},{{\hat{\varphi }}_K}} \right] } \right\}\)

3.5 The polarization parameters estimation

Consider that the true sources \(\bar{{\varvec{{S}}}} = \left[ {{{\varvec{s}}_1},{{\varvec{s}}_2}, \cdots ,{{\varvec{s}}_K}} \right] ^{\mathrm{{T}}}\) impinge on the surface of the CPSA as shown in Fig. 1. Then the steering vector of the k-th source is

(35)

where \({\varvec{{g}}}\left( {{\theta _k},{\varphi _k}} \right) =\left[ {{g_1}\left( {{\theta _k},{\varphi _k}} \right) ,{g_2}\left( {{\theta _k},{\varphi _k}} \right) , \cdots ,{g_M}\left( {{\theta _k},{\varphi _k}} \right) } \right]\), \({g_i}\left( {{\theta _k},{\varphi _k}} \right)\) is the response of unit signal by the i-th array element to the k-th signal, and \({\mathop {{{\varvec{a}}}}\limits ^{\frown }} \left( {{\theta _k},{\varphi _k}} \right) = {\left[ {{{\hbox {e}}^{ - j\frac{{2\pi }}{\lambda }{{\varvec{u}}_k} \bullet {{{\varvec{r}}}_1}}},{{\hbox {e}}^{ - j\frac{{2\pi }}{\lambda }{{\varvec{u}}_k} \bullet {{{\varvec{r}}}_2}}}, \ldots ,{{\hbox {e}}^{ - j\frac{{2\pi }}{\lambda }{{\varvec{u}}_k} \bullet {{{\varvec{r}}}_M}}}} \right] ^{\mathrm{T}}}\) is phase delay vector.

The array manifold matrix of the CPSA is shown as

$$\begin{aligned} \hat{{\varvec{{A}}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) = \left[ {\hat{{\varvec{{a}}}}\left( {\theta _1 ,\varphi _1 ,\gamma _1 ,\eta _1 } \right) ,\hat{{\varvec{{a}}}}\left( {\theta _2 ,\varphi _2 ,\gamma _2 ,\eta _2 } \right) , \cdots ,\hat{{\varvec{{a}}}}\left( {\theta _K ,\varphi _K ,\gamma _K ,\eta _K } \right) } \right] . \end{aligned}$$
(36)

The received data model of polarization parameters estimation could be written as

$$\begin{aligned} \hat{{\varvec{X}}} =\hat{{\varvec{A}}} \bar{{\varvec{{S}}}}. \end{aligned}$$
(37)

In order to catch the noise subspace \({{\varvec{{U}}}_\text {N}}\) of \(\hat{{\varvec{{X}}}}\), by taking the eigenvalue decomposition of the covariance matrix \({\varvec{{R}}} = \frac{1}{L}{\hat{{\varvec{{X}}}}}{{\hat{{\varvec{{X}}}}}^\mathrm{{H}}}\) and let the K eigenvectors corresponding to the K significant eigenvalues to form the signal subspace \({{\varvec{{U}}}_\text {S}}\). Hence, \({{\varvec{{U}}}_\text {N}}\) can be expressed as

$$\begin{aligned} {{\varvec{{U}}}_\text {N}} ={{\varvec{{I}}}_{\text {MT}}} - {{\varvec{{U}}}_\text {S}}{{\varvec{{U}}}_\text {S}}^{\mathrm{{H}}}, \end{aligned}$$
(38)

where \({{\varvec{{I}}}_{MT}}\) symbolizes \(MT \times MT\) identity matrix. The K estimated DOA in section 3.4 are substituted into the constructed conventional spatial spectrum function to obtain the K functions as follows

$$\begin{aligned} {\varvec{{W}}} = \frac{1}{{{\hat{{\varvec{{A}}}}^\mathrm{{H}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) {{\varvec{{U}}}_N}\hat{{\varvec{{A}}}}\left( {\theta ,\varphi ,\gamma ,\eta } \right) }}. \end{aligned}$$
(39)

The polarization parameters can be calculated by the eigenvector corresponding to the minimum eigenvalue of \({\varvec{{W}}}\) [38].

$$\begin{aligned} {\gamma _k} = \arctan \left( {\mathrm{{abs}}\left( {{\varvec{\rho }_k}\left( 2 \right) /{\varvec{\rho } _k}\left( 1 \right) } \right) } \right) , \end{aligned}$$
(40)
$$\begin{aligned} {\eta _k} = \mathrm {angle}\left( {{\varvec{\rho } _k}\left( 2 \right) /{\varvec{\rho } _k}\left( 1 \right) } \right) , \end{aligned}$$
(41)

where \({\varvec{\rho } _k}\left( i \right)\) denotes the i-th element in the eigenvector.

4 The computational cost analysis

It is obviously that the proposed methods based on the sparse model will be more time consuming than the subspace-type methods. The reason is the dimension of the output matrix \({{\varvec{X}}}\) in sparse signal model is too large to iteratively update the mean, variance and hyperparameters in (28), (29), (30) and (32) quickly. As a result, SVD is utilized to reduce the dimension of \({{\varvec{X}}}\) to improve computational efficiency before the sparse component learning and inner product.

As far as the computational complexity, CPSA-VSBL in this paper mainly derives from solving for the hidden variables and hyperparameters. Among the mean and variance of \({\varvec{{S}}}_{\text {sv}}\) is approximately \(2{J^3} - 2{J^2} + 6{J^2}M + 4J{M^2} + {M^3} - 3JM\) and \({J^3} + 2{J^2}M + 2JMK - JM\), respectively. Then the hyperparameters \(\left\langle {{\alpha _j}} \right\rangle\) and \(\left\langle {{\alpha _j}^{ - 1}} \right\rangle \mathrm{{ }} \left( j = 1,2, \cdots ,J \right)\) are about 4J and 10J. The most time consuming of the CPSA-OMP is the selection of atoms in the dictionary \(\tilde{{\varvec{A}}}\), and the computational complexity of each inner product is MJ. An appended computational load for the SVD of \({{\varvec{X}}}\) is \(6M{K}{T^2}\). The computational complexity of covariance matrix and eigenvalue decomposition in Tensor-MUSIC and MUSIC is \(\mathrm{{36}}{M^2}T\) and \(21\mathrm{{6}}{M^3}\), and the spectral searching of subspace methods is \({n^2}\left[ {6M\left( {6M - K} \right) } \right]\). In addition to, Tensor-MUSIC also needs higher order singular value decomposition. The computational complexity of the above methods is given in Table 3 when an arbitrary conformal array with M=25, K=2, J=16471, T=50 and n=5000, where n is the number of angle searches. The computational complexity is represented as \(O_t\).

Table 3 Comparison of computational load
Full size table

5 Results and discussion

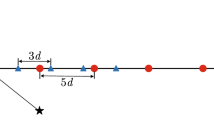
In this section, the simulation results of CPSA-VSBL and CPSA-OMP based on CPSA are analyzed, and compared with MUSIC and Tensor-MUSIC. As shown in Fig. 4, the array structure in the simulation is a cylindrical carrier and there are \({M_c} \times {M_z}\) sensors are uniformly distributed over the surface of the cylinder. The distance between the adjacent sensors along the Z-axis is \(\frac{\lambda }{2}\). For simplicity, we assume \({M_z} = 5\) and \({M_c} = 5\). The range of azimuth and elevation is sampled with \(1^{\circ }\) interval to form the direction set \(\left\{ {\left. {\left( {\tilde{\varvec{\theta }} ,\tilde{\varvec{\varphi }} } \right) } \right\} } \right.\). The RMSE of DOA estimation by independent Monte Carlo simulations is defined as

Fig. 4
figure 4

Uniform cylinder CPSA

Full size image
$$\begin{aligned} RMSE = \sqrt{\frac{1}{{QK}}\sum \limits _{q = 1}^Q {\sum \limits _{k = 1}^K {{{\left( {{{{\hat{u}}}_{kq}} - {u_k}} \right) }^2}}}}, \end{aligned}$$
(42)

where Q denotes the number of Monte Carlo simulations, \({u_k}\) is one of the parameters \(\left( {{\theta _k},{\varphi _k},{\gamma _k},{\eta _k}} \right)\), and \({{\hat{u}}_{kq}}\) is the estimation of \({u_k}\) in the q-th simulation.

5.1 The estimation accuracy versus SNR and the number of snapshots

In this simulations, the DOA estimation accuracy is evaluated by RMSE. The RMSE of the DOA estimation methods versus the SNR and number of snapshots are shown in Figs. 5 and 6, respectively. Consider two uncorrelated incident signals with DOA and polarization parameters \(\left( {\theta ,\varphi ,\gamma ,\eta } \right)\) are \(\left( { - {{14}^ \circ },{{35}^ \circ },{{25}^ \circ },{{10}^ \circ }} \right)\) and \(\left( { {{10}^ \circ },\mathrm{{5}}{\mathrm{{0}}^ \circ },{{50}^ \circ },{{45}^ \circ }} \right)\), respectively. The number of snapshots is fixed at 50. The RMSE versus SNR from \(-1\) to 25 dB for the four methods is presented in Fig. 5, and the RMSE versus snapshots number from to 10 to 150 while SNR=5 dB is presented in Fig. 6. In each experiment, we run 300 Monte Carlo simulations. From Figs. 5 and 6, it can be seen that, the RMSE performance of four methods are improved with the SNR and snapshots increasing. In Fig. 5, the proposed CPSA-VSBL has a more accurate DOA estimation than other methods at every SNR. The performance of the proposed CPSA-OMP is apparently superior to MUSIC and Tensor-MUSIC while the SNR is relatively high. In Fig. 6, the proposed CPSA-VSBL offers the best performance than that of CPSA-OMP, MUSIC and Tensor-MUSIC. CPSA-OMP provides an estimation with zero error when the number of snapshots is relatively large. We further examine the RMSE of polarization parameters estimation. For all the methods, it can be seen that the RMSE continuously decrease when SNR and the number of snapshots increase. It is observed that the RMSE \(\gamma\) and \(\eta\) of the proposed methods consistently outperform the Tensor-MUSIC and MUSIC methods in Fig. 7. From Fig. 8, the estimation performance of the proposed CPSA-VSBL is better than subspace methods at arbitrary number of snapshots. The CPSA-OMP performs better than the MUSIC and Tensor-MUSIC methods in the large number of snapshots.

Fig. 5
figure 5

The azimuth RMSE versus SNR

Full size image
Fig. 6
figure 6

The azimuth RMSE versus number of snapshots

Full size image
Fig. 7
figure 7

The RMSE of \(\gamma\) and \(\eta\) versus SNR

Full size image
Fig. 8
figure 8

The RMSE of \(\gamma\) and \(\eta\) versus number of snapshots

Full size image

5.2 The resolution performance versus SNR and number of snapshots

In this subsection, the resolution performance is evaluated by the probability of successful detection. For the MUSIC and Tensor-MUSIC methods, the “successful trial” is defined in this simulation as when both the \(\left| {\hat{\theta }- \theta } \right| < {2^ \circ }\) and \(\left| {\hat{\varphi }- \varphi } \right| < {2^ \circ }\). Set the two uncorrelated incident signals with DOA and polarization parameters \(\left( {\theta ,\varphi ,\gamma ,\eta } \right)\) are \(\left( { - {8^ \circ },{{45}^ \circ },{{10}^ \circ },{{30}^ \circ }} \right)\) and \(\left( {{2^ \circ },{{45}^ \circ },{{30}^ \circ },{{20}^ \circ }} \right)\), respectively. Set the number of snapshots is 50, the probability of successful detection of four methods varying SNR from \(-5\) to 20 dB in Fig. 9. Figure 10 shows the probability of successful detection for SNR=5 dB by varying the snapshots from 20 to 200 under the two uncorrelated incident signals with DOA and polarization parameters \(\left( {\theta ,\varphi ,\gamma ,\eta } \right)\) are \(\left( { - {4^ \circ },{{45}^ \circ },{{10}^ \circ },{{30}^ \circ }} \right)\) and \(\left( {{6^ \circ },{{45}^ \circ },{{30}^ \circ },{{20}^ \circ }} \right)\). It is seen from Figs. 9 and 10, both the probability of successful detection improve with the increasing of the SNR and the number of snapshots, whereas the proposed methods have higher resolution performance than the conventional MUSIC and Tensor-MUSIC methods, which gives us a strong evidence of the effectiveness of the proposed methods.

Fig. 9
figure 9

The probability of successful detection versus SNR

Full size image
Fig. 10
figure 10

The probability of successful detection versus number of snapshots

Full size image

6 Conclusions

In this paper, we have illustrated sparse reconstruction method-based DOA and polarization joint estimation for CPSA. By exploiting 2D spatial sparsity of incident signals, an array output model that is applicable to arbitrary CPSA is obtained. In order to improve the computational efficiency of the proposed methods, SVD is used to reduce the dimension of the array output matrix. The CPSA-VSBL and CPSA-OMP methods are proposed for DOA estimation. The minimum eigenvector method is used to obtain the polarization information of signals. As a result, both the estimation accuracy and the resolution of the proposed methods have been validated by a lot of simulations. The simulation results show that the proposed methods have low RMSE and optimal resolution than the state-of-the-art methods especially with low SNR and limited snapshots. In future work, we will focus on the multidimensional structural information in the array received data.