1 Introduction

Array signal processing plays an important role in many areas. However, the regular uniform linear array has many disadvantages, such like limited degree-of-freedom and redundant physical sensors, results in a confinement of its applications, e.g., direction-of-arrival (DOA) estimation and beamforming. Traditional spectrum estimations algorithms like multiple signal classification (MUSIC) algorithm have been widely applied in DoA estimations [1]. However, the number of sources that can be resolved with a uniform linear array is less than the number of sensors in the array while applying the MUSIC algorithm. Many researchers have been done regarding to the nonlinear sensor array, aiming at a lower mutual coupling and a higher degree-of-freedom.

The Minimum-redundancy linear array was first proposed in [2] in order to minimize the number of redundant spacings present in the array. Co-Prime array was introduced in [3] where a co-prime pair of M and N sensors achieves O(MN) freedoms which can be exploited in beamforming and in direction of arrival estimation. In [4], the authors proposed nested arrays, which can achieve \(O(N^{2})\) degree of freedom with N physical sensors. Nested array has then been widely studied. In [5], nested array is applied to increase the capacity of multi-cell cooperative cellular networks. In [6], the authors studied nested and co-prime-based underwater non-uniform sensor array networks (UWSANs) for underwater DOA estimation. In [7], the authors use 2D nested array deployment to accomplish channel estimation in massive multi-input multi-output (MIMO) scenario. DOA estimation is also studied over multiple dimensional nonlinear arrays, for example, in [8,9,10]. However, most of the array structures have certain disadvantages, i.e., Minimum Redundancy Array (MRA) has no closed-form expressions for its array geometry, Co-prime array has holes in its difference co-array, Nested array has higher mutual coupling than Co-prime array and MRA [4].

The concept of co-array is introduced in [11, 12] for incoherent and coherent imaging and aperture synthesis techniques. And the concept of sum co-array and difference co-array is then implemented in array geometries [13], as the difference co-array forms naturally in computation of the covariance matrix of the received signal at the sensor array.

DOA estimation for quasi-stationary signals was studied in [14] where a Khatri–Rao (KR) subspace-based MUSIC algorithm was implemented on uniform linear array. The proposed KR-MUSIC algorithm works on Khatri–Rao subspace instead of array manifold matrix and therefore, allows array with N sensors handles up to \(2N-2\) sources. This approach could also be implemented to nonlinear array since a well-designed sparse array could form a larger difference co-array compared to the uniform linear array. The authors of [15] proposed a nonlinear beamformer called convolutional beamforming algorithm (COBA) in their research to form B-mode images which is used in commercial medical ultrasound systems. This convolutional beamformer based on the convolution of the delayed RF signals prior to summation and sparse array structure shows a better resolution and contrast compares to the traditional delay and sum (DAS) beamformer. However, the authors research focused on sum co-array perspective, since the beam pattern of the convolutional beamformer depends on the sum co-array rather than the physical array and amplitude apodization is applied on the sum co-array for suppressing side lobes [16].

In this paper, we studied the sparse convolutional array structure in perspective of difference co-array and the approaches in DOA estimation. The sparse convolutional array is demonstrated in both one-dimension and two-dimension. The main purpose of implementing this array structure is to reduce the number of physical sensors. By adding a dense set of sensors on two sides of the sparse sensors, the proposed array shows improved resolution while reminds small number of physical sensors. The KR product-based MUSIC algorithm [14] is implemented for the proposed sensor array for DOA estimation. The spectrum was illustrated, and the root mean square error (RMSE) was simulated. We then extended this array to two-dimensional case.

The remainder of this chapter is organized as follows. In Sect. 2, we illustrate the Sparse Convolutional Array and the Extended Sparse Convolutional Array. The signal model based on difference co-array is discussed. In Sect. 3, we extend sparse convolutional array to two dimension. Numerical results and discussions are presented in Sect. 3. Finally, Sect. 4 concludes the paper.

2 Methods

2.1 Sparse convolutional array

2.1.1 Basic array construction

Assume N is a non-prime integer, \(N = N_{A}N_{B}\) where \(N_{A}, N_{B} \in N+\). A Sparse Convolutional Array \((N_{A},N_{B})\) can be present as the union of two sets of sensors:

$$\begin{aligned} U = U_A \cup U_B \end{aligned}$$
(1)

while the sensors of \(U_A\) and \(U_B\) are located at

$$\begin{aligned}&U_{A} = \{-(N_{A}-1), \ldots , 0, \ldots , N_{A}-1\}, \end{aligned}$$
(2)
$$\begin{aligned} U_{B} &=\{-(N_{B}-1)N_{A}, \ldots -(N_{B}-1),0,\\ &(N_{B}-1), \ldots , (N_{B}-1)N_{A}\}, \end{aligned}$$
(3)

To further illustrate the sparse convolutional array, we first introduce the concept of difference co-array:

Definition 1

(Difference Co-array) Assume \(\vec {\mathbf {v}}_N\) is a sensor array with N sensors, its difference co-array is defined as the array with its sensors’ location given by

$$\begin{aligned} {\vec {\mathbf {v}}_n-\vec {\mathbf {v}}_m}, \forall m,n = 1, 2, \ldots ,N. \end{aligned}$$
(4)

where \(\vec {v}_n\) denotes the location of nth sensor of the original array. The elements of the difference co-array are not necessarily physical sensor, but still can benefit the DOA estimation, as we will illustrate in later sections.

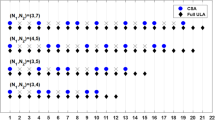
Figure 1 shows an example of the Sparse Convolutional Array of (3, 3) and the corresponding difference co-array.

Fig. 1
figure 1

Sparse convolutional array of (3, 3)

Full size image

2.1.2 Extended array construction

From Fig. 1, we can see that the regular sparse convolutional array has “hole” in its difference co-array. To perform a difference co-array that follows uniform linear array (ULA), we extend the sparse convolutional array as follow:

$$\begin{aligned} U = U_A \cup U_B \cup U_C \end{aligned}$$
(5)

while

$$\begin{aligned}&U_{A} = \{-(N_{A}-1), \ldots , 0, \ldots , N_{A}-1\}, \end{aligned}$$
(6)
$$\begin{aligned} U_{B} &=\{-(N_{B}-1)N_{A}, \ldots -(N_{B}-1),0,\\ &(N_{B}-1), \ldots , (N_{B}-1)N_{A}\}, \end{aligned}$$
(7)
$$\begin{aligned} U_{C} &=\{-(N-1),\ldots ,-(N-N_A),\\ &N-N_A,\ldots ,N-1\} \end{aligned}$$
(8)

Figure 2 shows an example of an extended sparse convolutional array of (3, 3) and the corresponding difference co-array. We can see from the figure that its difference co-array is a hole-free uniform linear array.

Fig. 2
figure 2

Extended sparse convolutional array of (3, 3)

Full size image

For a physical sensor array, the number of virtual sensors in its difference co-array directly decides the distinct values of the cross-correlation terms in its received signal’s covariance matrix [4]. Therefore, we illustrate the number of virtual sensors in the difference co-array as follow.

Lemma 2.1

The difference co-array of an extended sparse convolutional array \((N_{A},N_{B})\) is a uniform linear array of \(4N-3\) virtual sensors where \(N = N_{A}N_{B}\).

Proof

The leftmost virtual sensor is performed by the leftmost and rightmost sensors \(-(N-1)\) and \((N-1)\) in \(U_C\), which is \(-2(N-1)\). Similarly, we have the rightmost virtual sensor which is \(2(N-1)\). It is easy to obtain the elements between the leftmost and rightmost sensors are dense.

Therefore, the number of virtual sensors in the difference co-array can be calculated as

$$\begin{aligned} \begin{aligned} N_{vir}&= 2*[2(N-1)]+1\\&= 4N-3\\ \end{aligned} \end{aligned}$$
(9)

For example, in order to perform a uniform linear difference co-array of 33 virtual sensors, an extended sparse convolutional array needs 13 physical sensors. \(\square\)

2.1.3 Signal model

In array signal processing, while calculating the autocorrelation matrix of the received signal, the difference co-array could be formed naturally [17].

Consider a sparse convolutional array \(U(N_A,N_B)\) with \(N = N_AN_B\) sensors placed on a linear grid. The steering vector of this array is of size \(N \times 1\):

$$\begin{aligned} \mathbf {a}(\theta _{j}) = [e^{j(2 \pi / \lambda ) d_{1} \sin \theta _{j}},e^{j(2 \pi / \lambda ) d_{2} \sin \theta _{j}},\ldots ,e^{j(2 \pi / \lambda ) d_{N} \sin \theta _{j}}]^{T} \end{aligned}$$
(10)

where \(d_{i}\) is the location of the ith sensor.

Assume M narrow-band sources are impinging on this array, the array manifold matrix is of size \(N \times M\) and can be written as follow:

$$\begin{aligned} \begin{aligned} \mathbf {A}=[\mathbf {a}(\theta _{1}),\mathbf {a}(\theta _{2}),\ldots ,\mathbf {a}(\theta _{M})] \end{aligned} \end{aligned}$$
(11)

where \(\mathbf {a}(\theta _{j})\) is the steering vector corresponding to the direction \(\theta _{j}\) from the jth source.

The received signal \(\mathbf {x}[k]\) of the sensor array can then be formulated as

$$\begin{aligned} \mathbf {x}[k] = \mathbf {A}\mathbf {s}[k]+\mathbf {n}[k] \end{aligned}$$
(12)

where \(\mathbf {s}[k] = [s_{1}(k),s_{2}(k),\ldots ,s_{M}(k)]^{T}\) is the \(M \times 1\) source signal vector and \(\mathbf {n}[k]\) is the additive white Gaussian noise with power \(\sigma _{n}^{2}\).

Assume the sources are uncorrelated with each other, the autocorrelation matrix of \(\mathbf {s}[k]\) is diagonal. Therefore, we have

$$\begin{aligned} \begin{aligned} R_{\mathbf {x x}}&=E\left[ \mathbf {x} \mathbf {x}^{H}\right] \\&=\mathbf {A} R_{s s} \mathbf {A}^{H}+\sigma _{n}^{2} I \\&=\mathbf {A}\left[ \begin{array}{llllll} \sigma _{1}^{2} & & & \\ & \sigma _{2}^{2} \\ & & \ddots & \\ & & & \sigma _{M}^{2} \end{array}\right] \mathbf {A}^{H}+\sigma _{n}^{2} I \end{aligned} \end{aligned}$$
(13)

where \(\{\sigma _{j}^{2},j=1,2,\ldots ,M\}\) is the corresponding power of the jth source.

The autocorrelation matrix in (13) is then vectorized to perform the following vector

$$\begin{aligned} \begin{aligned} \vec {\mathbf {z}}&={\text {vec}}\left( R_{x x}\right) \\&={\text {vec}}\left[ \sum _{j=1}^{M} \sigma _{j}^{2}\left( a\left( \theta _{j}\right) a^{H}\left( \theta _{j}\right) \right) \right] +\sigma _{n}^{2} \overrightarrow{\mathbf {1}}_{n} \\&=\mathbf {A}_{diff} \mathbf {p}+\sigma _{n}^{2} \overrightarrow{\mathbf {1}}_{n} \end{aligned} \end{aligned}$$
(14)

\(\mathbf {A}_{diff} = \mathbf {A}^{*} \odot \mathbf {A}\) is a \((N*N) \times M\) matrix with \(\odot\) denotes the column-wise Khatri–Rao product [18], where the distinct columns of \(\mathbf {A}^{*} \odot \mathbf {A}\) equal the Kronecker product of the corresponding columns of \(\mathbf {A}^{*}\) and \(\mathbf {A}\), that is

$$\begin{aligned} \mathbf {a}^{*}(\theta _{j}) \odot \mathbf {a}(\theta _{j}) \end{aligned}$$
(15)

Hence, the element in the jth column of \(\mathbf {A}_{diff}\) is given by

$$\begin{aligned} \begin{aligned} e^{-j(2 \pi / \lambda ) d_{p} \sin \theta _{j}}*e^{j(2 \pi / \lambda ) d_{q} \sin \theta _{j}} = e^{j(2 \pi / \lambda ) (d_{q}-d_{p}) \sin \theta _{j}}, \\ 1 \le p,q \le N \end{aligned} \end{aligned}$$
(16)

(16) suggests that \(\mathbf {A}_{diff}\) could be treated as a manifold matrix of a new virtual array, with the sensors located at

$$\begin{aligned} \{\vec {\mathbf {v}}_q-\vec {\mathbf {v}}_p, \forall \vec {\mathbf {v}}_q,\vec {\mathbf {v}}_p \in U\} \end{aligned}$$
(17)

We can obtain from the definition of difference co-array that this new sensor array is exactly the difference co-array of the original sparse convolutional array [12].

Hence, by comparing (14) with (12), we can say that vector \(\mathbf {z}\) in (14) could be treated as the received signal at this new virtual array, where \(\mathbf {p}=[\sigma _{1}^{2},\sigma _{2}^{2},\ldots ,\sigma _{M}^{2}]^{T}\) is the corresponding \(M \times 1\) source signal vector. The equivalent \((N*N) \times 1\) noise vector becomes \(\sigma _{n}^{2} \overrightarrow{\mathbf {1}}_{n}\), where \(\vec {\mathbf {1}_{n}}=[e_{1}^{T},e_{2}^{T},\ldots ,e_{N}^{T}]^{T}\), with \(e_{i}\) being a \(N \times 1\) vector which has 1 in its ith entry and 0 elsewhere.

Therefore, we can accomplish the DOA estimation to the data in (14) and work with the new virtual array instead of the original physical array. A Khatri–Rao product-based MUSIC algorithm can be applied to do so, as discussed in [14].

2.2 2D sparse convolutional array

2.2.1 Array construction

Assume N is non-prime integer, \(N = N_{A}N_{B}\) where \(N_{A}, N_{B} \in N+\). A \(2-D\) Sparse Convolutional Array \((N_{A},N_{B})\) can be present as follow,

$$\begin{aligned} U = U_A \cup U_B, \end{aligned}$$
(18)

while

$$\begin{aligned}&U_{A} = \{(x,y), x,y \in \{-(N_{A}-1), \ldots , 0, \ldots , N_{A}-1\}\}, \end{aligned}$$
(19)
$$\begin{aligned} U_{B} = \{(x,y), x,y \in&\{-(N_{B}-1)N_{A}, \ldots -(N_{B}-1),\\ &0,(N_{B}-1), \ldots , (N_{B}-1)N_{A}\}\}, \end{aligned}$$
(20)

+

Similarly, we have 2D extended sparse convolutional array:

$$\begin{aligned} U = U_A \cup U_B \cup U_C, \end{aligned}$$
(21)

while

$$\begin{aligned}&U_{A} = \{(x,y), x,y \in \{-(N_{A}-1), \ldots , 0, \ldots , N_{A}-1\}\}, \end{aligned}$$
(22)
$$\begin{aligned} U_{B} = \{(x,y), x,y \in&\{-(N_{B}-1)N_{A}, \ldots -(N_{B}-1),\\ &0,(N_{B}-1), \ldots , (N_{B}-1)N_{A}\}\}, \end{aligned}$$
(23)
$$\begin{aligned} U_{C} = \{(x,y), x,y \in&\{-(N-1),\ldots ,-(N-N_A),\\ &N-N_A,\ldots ,N-1\}\} \end{aligned}$$
(24)

Figure 3 shows an example of a 2D Extended Sparse Convolutional Array of (2, 3), and Fig. 4 shows the corresponding difference co-array.

Fig. 3
figure 3

2D extended sparse conv array of (2, 3)

Full size image
Fig. 4
figure 4

Difference co-array of the (2, 3) 2D extended sparse conv array

Full size image

The number of virtual sensors in the difference co-array for the 2D extended sparse convolutional array is illustrated as follow:

Lemma 3.1

The difference co-array of a 2D Extended Sparse Convolutional Array contains a uniform rectangular array of \((4N-2N_A-1)^{2}\) virtual sensors.

Proof

It is obvious that the virtual sensors on the outline of the rectangular area are performed by the sensors on the outline of \(U_B\) and \(U_C\). Hence, the outline of the rectangular area is \(x=\pm (N-1)+(N_B-1)N_A\) and \(y=\pm (N-1)+(N_B-1)N_A\).

Therefore, the number of virtual sensors in the rectangular area can be calculated as

$$\begin{aligned} \begin{aligned} N_{vir}&= (2*[(N-1)+(N_B-1)N_A]+1)^{2}\\&=(2*[N-1+N_BN_A-N_A]+1)^{2}\\&=(2*[N-1+N-N_A]+1)^{2}\\&=(4N-2N_A-1)^{2} \end{aligned} \end{aligned}$$
(25)

Notice that we ignored some virtual sensors out of the rectangular area to simplify the calculations. \(\square\)

2.2.2 Signal model

Similar to the signal model in 1D case, we can construct the signal model for 2D Extended sparse convolutional array.

Consider a 2D extended sparse convolutional array \(U(N_A,N_B)\).

Assume there are M uncorrelated narrow-band sources where \((\theta _{j},\phi _{j})\) denotes the direction of the jth source and \(\sigma _{j}\) denotes the corresponding power. The signal received at the sensor array can be formulated as follow:

$$\begin{aligned} \begin{aligned} \mathbf {x}[k]&=\mathbf {A}\mathbf {s}[k]+\mathbf {n}[k] \\ \mathbf {A} &=\left[ \begin{array}{l} \mathbf {A}_{U_A} \\ \mathbf {A}_{U_B} \\ \mathbf {A}_{U_C} \end{array}\right] \end{aligned} \end{aligned}$$
(26)

where \(\mathbf {s}[k] = [s_{1}(k),s_{2}(k),\ldots ,s_{M}(k)]^{T}\) is the \(M \times 1\) source signal vector and \(\mathbf {n}[k]\) is the additive white Gaussian noise with power \(\sigma _{n}^{2}\). \(\mathbf {A}_{U_A}\),\(\mathbf {A}_{U_B}\),\(\mathbf {A}_{U_C}\) are the corresponding array manifold matrix for \(U_A\), \(U_B\) and \(U_C\), and the entries of \(\mathbf {A}\) are given by

$$\begin{aligned} \begin{aligned} \left[ \mathbf {A}\right] _{i, j}=e^{j (2 \pi / \lambda ) \sin \phi _{j} [\cos \theta _{j} \sin \theta _{j}] [x_{i} y_{i}]^{T}}\\ (x_i,y_i) \in U \end{aligned} \end{aligned}$$
(27)

where \({x_i,y_i}\) is the coordinate of the ith sensor.

Similarly, the sources are assumed to be uncorrelated with each other, the autocorrelation matrix of \(\mathbf {s}[k]\) is then diagonal, we have

$$\begin{aligned} \begin{aligned} R_{\mathbf {x x}}&=E\left[ \mathbf {x} \mathbf {x}^{H}\right] \\&=\mathbf {A} R_{s s} \mathbf {A}^{H}+\sigma _{n}^{2} I \\&=\mathbf {A}\left[ \begin{array}{llllll} \sigma _{1}^{2} & & & \\ & \sigma _{2}^{2} \\ & & \ddots & \\ & & & \sigma _{M}^{2} \end{array}\right] \mathbf {A}^{H}+\sigma _{n}^{2} I \end{aligned} \end{aligned}$$
(28)

Similar to the signal model of the 1D array, by vectorizing the autocorrelation matrix \(R_{xx}\), the “received” signal of the virtual sensor array can be formulated as:

$$\begin{aligned} \begin{aligned} \mathbf {z}&={\text {vec}}\left( R_{x x}\right) \\ &=\mathbf {A}_{diff} \mathbf {p}+\sigma _{n}^{2} \overline{\mathbf {1}}_{n} \end{aligned} \end{aligned}$$
(29)

where

$$\begin{aligned} \begin{aligned} \mathbf {A}_{diff}&=\mathbf {A}^{*} \odot \mathbf {A} \\ &=\left[ \begin{array}{l} \mathbf {A}_{U_A} \\ \mathbf {A}_{U_B} \\ \mathbf {A}_{U_C} \end{array}\right] ^{*} \odot \left[ \begin{array}{l} \mathbf {A}_{U_A} \\ \mathbf {A}_{U_B} \\ \mathbf {A}_{U_C} \end{array}\right] \end{aligned} \end{aligned}$$
(30)

is the array manifold matrix of the new virtual array, whose sensors coordinate is given by

$$\begin{aligned} \{(\mathbf {x}_p-\mathbf {x}_q,\mathbf {y}_p-\mathbf {y}_q), \forall (\mathbf {x}_p,\mathbf {y}_p),(\mathbf {x}_q,\mathbf {y}_q)\in U\} \end{aligned}$$
(31)

Similarly, vector \(\mathbf {z}\) in (29) could be treated as the received signal at this new virtual array. \(\mathbf {p}=[\sigma _{1}^{2},\sigma _{2}^{2},\ldots ,\sigma _{M}^{2}]^{T}\) is the corresponding \(M \times 1\) source signal vector and \(\sigma _{n}^{2} \overrightarrow{\mathbf {1}}_{n}\) is the corresponding noise vector.

Hence, by implementing MUSIC algorithm, the 2D DOA could be estimated.

3 Numerical results

3.1 Sparse convolutional array

According to the proposed signal model, we then performed Monte Carlo simulations on different sensor arrays. An extended Sparse Convolutional Array (3, 3) as shown in Fig. 2 and a Sparse Convolutional Array (3, 5) are constructed so that the total number of the physical sensors are identical. As a comparison, a nested array is performed, as illustrated in [4]. A uniform linear array is also constructed and simulated as a baseline. Both sensor arrays have 13 physical sensors in their grid. The sources are located at \([-45, -27, -9, 18, 36, 54] degrees\), while the \(SNR=0 dB\), and the number of snapshots is 500.

Figure 5 shows the MUSIC spectrum of the extended sparse convolutional array and sparse convolutional array versus the nested array and uniform linear array. We can obtain from the figure that both four sensor arrays are able to indicate the 6 sources. The uniform linear array has the highest normalized spectrum in dB, meanwhile the sparse convolutional array performs closely to the nested array, and both arrays have lower spectrum compared to the uniform linear array. The proposed extended sparse convolutional array shows the lowest spectrum compared to all the other three arrays.

Fig. 5
figure 5

MUSIC spectrum of the sparse convolutional array, nested array and uniform linear array, SNR = 0 dB, snapshots = 500

Full size image

In order to demonstrate the proposed array’s ability of detecting closely spaced sources, we then performed the simulation of two pairs of closely placed sources which locate at \([-42.3, -39.6, 27.9, 30.6]\) degrees. And the MUSIC spectrum of the four arrays is plotted in Fig. 6. The result shows that while ULA failed to resolve the two pairs of closely spaced sources, both Nested Array and the two proposed arrays can successfully distinguish the four sources. The performance of the proposed sparse convolutional array and nested array is very close. And the extended sparse convolutional array again shows its lower spectrum compared to the Nested Array.

Fig. 6
figure 6

MUSIC spectrum of the three arrays with closely spaced sources, SNR = 0 dB, snapshots = 500

Full size image

In the next simulations, we evaluated the performance over various SNR and number of snapshots in terms of RMSE. Since the Extended Sparse Convolutional Array shows a stably better performance than the Sparse Convolutional Array, only Extended Sparse Convolutional Array is considered in the following simulation. The extended sparse convolutional array, nested array and uniform linear array are constructed. Both arrays have 13 physical sensors in their grid, and 8 sources are generated with random locations.

Figure 7 shows the RMSE versus number of snapshots, while SNR = 0 dB. We can obtain from the figure that the RMSE drops for both arrays as the number of snapshots increases, since a larger number of snapshots gives a better approximation of the signal covariance matrix. While the uniform linear array has the highest RMSE in all snapshots range, the proposed extended sparse convolutional array shows its strictly lower RMSE compared to the nested array.

Fig. 7
figure 7

RMSE versus snapshots, SNR = 0 dB

Full size image

In Fig. 8, the RMSE is plotted versus SNR, while snapshots = 500. The simulation result shows that the RMSE drops for both arrays as the SNR increases, which is as expected. The RMSE of the proposed Extended Sparse Convolutional Array is slightly lower than the RMSE of the nested array, and both two arrays show much better performance than the uniform linear array.

Fig. 8
figure 8

RMSE versus SNR, snapshots = 500

Full size image

Therefore, we can conclude that the proposed Extended Sparse Convolutional Array has better performance compared to the nested array and the uniform linear array.

3.2 2D sparse convolutional array

We then demonstrated the 2D MUSIC spectrum of the 2D extended sparse convolutional array. With a (2, 3) configuration, the array has 45 physical sensors. 10 sources were generated with random azimuth and elevation angles, while the SNR = 10 dB, and number of snapshots is 1000. The 2D MUSIC spectrum of the 2D extended sparse convolutional array is plotted in Fig. 9.

Fig. 9
figure 9

2D MUSIC spectrum of the extended sparse conv array (2, 3), SNR = 10 dB, snapshots = 1000

Full size image

The next simulations consider the performance over various SNR for 2D Extended Sparse Convolutional Array. As a comparison, a 2D nested array is constructed, which has 9 sensors in its dense array and 34 sensors in the sparse array, raise a total of 43 physical sensors.

In Fig. 10, the RMSE is plotted versus SNR. As the SNR increases, the RMSE drops for both arrays decrease. And the RMSE of the proposed 2D extended sparse convolutional array is strictly lower than the 2D nested array, raise.

Fig. 10
figure 10

RMSE versus SNR for 2D DOA estimation, snapshots = 1000

Full size image

4 Conclusion and discussion

In this paper, we have illustrated the Sparse Convolutional Array from the difference co-array point of view. The proposed Sparse Convolutional Array is a union of three groups of physical sensors. We first illustrated the 1D sparse convolutional array and extended sparse convolutional array. By adding sensors on two sides instead of the center, the proposed array shows improved performance while reminds few physical sensors. The signal model has been illustrated, and the simulation results of DOA estimation are provided with MUSIC algorithm implemented. The results indicate that the proposed Sparse Convolutional Array can successfully detect the sources, even when the sources are placed at a close distance. The proposed sensor array shows better performance in terms of RMSE compared to Nested Array and Uniform Linear Array. We then introduced the structure of 2D extended sparse convolutional array and its signal mode. The 2D MUSIC spectrum was demonstrated, and the RMSE is simulated and compared.

As for the future work, mutual coupling is considered to be demonstrated since it reflects the electromagnetic interaction between the sensors in an array. Mutual coupling changes the current magnitude, phase, and distribution on each sensor elements from their free-space value [19].

Many researchers have been done regarding to the modeling of mutual coupling, for example [20,21,22]. In [21], the author shows that with a proper mutual coupling model, the performance could be improved. In the proposed Extended Sparse Convolutional Array, the physical sensors are more distributed. Hence, we are expecting a more obvious improvement compared to the uniform linear array or nested array.