Abstract
During the acquisition of a hyperspectral image (HSI), it is easily corrupted by many kinds of noises, which limits the subsequent applications. For decades, numerous HSI denoising methods have been proposed. However, these methods rarely consider the stripe noise as an independent component, thus cannot effectively remove the stripe noise. In this paper, we propose a mixed noise removal algorithm to destripe an HSI by taking advantage of the low-rank property of stripe noise. In the meantime, sparse representation and graph Laplacian regularization are utilized to remove Gaussian and sparse noise. Roughly speaking, the sparse representation helps achieve the approximation of the original image. A graph Laplacian regularization term can ensure the non-local spatial similarity of an HSI. Separate constraints on the sparse coefficient matrix and stripe noise components can help remove different types of noises. Experimental results on both simulated and real data demonstrate the effectiveness of the proposed method for HSI restoration.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.1 Introduction
Hyperspectral images (HSIs) data are acquired based on the radiance obtained by airborne or space-borne sensors, extracting information from objects or scenes on the earth surface. They contain rich spatial and spectral information, and have been widely used in numerous fields, e.g., terrain detection, environmental monitoring, biological diagnosis [1]. However, an HSI is always damaged by different noise because of photon effects, random errors in light counting, calibration errors and so on [2]. These degradations often damage the potential structure of an HSI and impede the subsequent tasks. Therefore, mixed noise removal in HSIs has become an essential and crucial step for further analysis and application.
In the past few decades, many different technologies have been developed for HSI denoising. The simplest and most intuitive idea is to denoise band-by-band. Representative examples in single-band image denoising include the maximum noise fraction (MNF) transformation [3], the non-local means (NLMs) filter [4], the collaborative filtering of groups of similar patches (BM3D) [5]. The HSI cube can be also denoised by multi-band image denoising methods, including blocks-matching and 4D filtering (BM4D) [6], video denoising using separable 4-D non-local spatio-temporal transforms (VBM4D) [7], and multi-spectral principal component analysis (MSPCA-BM3D) [8]. However, these methods only remove the spatial noise, and cannot take advantage of the correlation of all bands of HSI. Moreover, they introduce artifacts or distortions in restoration results. Hence, they are not able to provide satisfactory denoising results.
To achieve better denoising performance, spatial and spectral information needs to be considered comprehensively. Yuan et al. [9] proposed a spectral and spatial adaptive total variation (TV) denoising method, which takes into account the spectral difference and the spatial difference simultaneously. Fu et al. used the spectral correlation and non-local spatial similarity of each band to learn an adaptive dictionary for HSI denoising [10]. Chen et al. [11] take advantage of the different characteristics of an HSI in both the spatial and spectral domains, and establish a maximum a posteriori (MAP) framework for HSI denoising. In addition, subspace-based methods are widely used to describe spectral correlation, and have achieved good results, including fast hyperspectral denoising (FastHyDe) [12], global local factorization (GLF) [13], etc. Besides, the 2-D images at each band of an HSI have strong structural similarity, hence, a lot of methods utilizes the low-rank property along the adjacent spectral bands of the HSI. For instance, Zhang et al. [14] proposed a method based on low-rank matrix recovery (LRMR) for HSI restoration. Fan et al. built a 3-D low-rank tensor model to handle HSI denoising problem [15]. Zhang et al. [16] proposed a double low-rank matrix decomposition method for HSI denoising and destriping. To better restore the matrix, one can resort to [17,18,19], which can be used to recover the data and reveal its internal characteristics efficiently and effectively.
In addition, the deep learning methods represented by convolutional neural networks (CNNs) are also applied to HSI denoising problems, e.g., the HSI denoising method based on residual convolutional neural network (HSID-CNN) [20], the HSI single-denoising CNN (HSI-SDeCNN) [21], etc. Despite these deep learning-based methods achieve the state-of-the-art performance, they are not necessarily robust. Besides, these methods do not fully explore the inner relationship of an HSI, either spectrally or spatially. Hence, they cannot adapt to different data and noise types. When the type of noise in the test data becomes complex, the users should train the model from scratch, which is time-consuming.
In recent years, sparse representation has been favored for image denoising [22] and restoration [23]. Signals are usually approximated by a set of sparse atoms in a dictionary. This set of sparse atoms helps reduce the redundancy of the original high-dimensional, so that the information contained in the signal can be retrieved more easily. Sparse representation has been applied to 2-D image denoising [24]. However, it usually faces difficulties for HSI denoising because it does not consider the correlation between bands and spatial pixels of HSI. To make full use of the characteristics of HSI’s spectral correlation and spatial similarity, Ye et al. put forward a method for sparse representation using non-local spectral-spatial structure [25]. Zhao et al. raised a model that combines sparse representation with low-rank constraints to solve the HSI restoration problem [26].
The HSI denoising problem can also be regarded as an inverse imaging problem. Therefore, the use of appropriate image priors for regularization is very important. As a recently widely-used prior, graph Laplacian regularization has been empirically proven useful in denoising [27, 28], sharpening [29], HSI unmixing [30, 31], etc. Extended to the denoising problem of HSI, Lu et al. [32] proposed a new HSI destriping method by considering the local flow pattern structure of HSI and adopting the method of graph regularization and low rank.
Although the methods described above can achieve good results, few methods view stripe noise as a separate component, hence most mixed noise removal methods cannot successfully remove stripe noise. The stripe noise has significant structural and directional characteristics, and the stripes occur periodically, leading to the low-rank property. In this paper, we propose to add a low-rank constraint on the stripe noise to the HSI denoising method based on sparse representation and graph Laplacian regularization. The contributions of this paper lie in that:
-
1
We regard the stripe noise as an independent component, and use a nuclear norm to regularize the low-rank property of the stripe noise, thus resulting in satisfying de-striping and denoising performance;
-
2
We use an iterative update algorithm to solve our proposed non-convex model, which helps us minimize the least square error to find the local optimal solution;
-
3
We conduct numerous experiments on the simulated and real data to find out the most appropriate parameters, and the experimental results demonstrate that the proposed method outperforms many mainstream methods in both quantitative evaluation indexes and visual effects.
The remainder of this paper is organized as follows: Sect. 2 introduces graph regularized non-negative matrix factorization and multi-task graph-regularized sparse non-negative matrix factorization related work. Section 3 proposes the model of our method and derives the solution process. The results of different methods on simulated data and real data are in Sect. 4. Finally, conclusions are drawn in Sect. 5.
2 Related work
An HSI is a superposition of the same area images under different spectra. Hence, it has strong correlations between bands, which leads to information redundancy [33]. In this paper, we use matrix decomposition to reduce the redundancy [34]. Matrix decomposition helps us find the product of two or more low-dimensional data matrices to approximate the original high-dimensional data. Therefore, it can reduce the data dimension, thus decreasing the redundancy of HSI.
Because of its convenience and simplicity, the nonnegative matrix factorization (NMF) algorithm is proposed and widely applied in computer vision, document clustering, recommendation system and other fields [35]. Different from sparse dictionary learning, the NMF requires that the original matrix, the corresponding bases and the coefficient matrix are nonnegative. Hence, it is more useful for nonnegative data such as images, because the pixel intensity of an image is always nonnegative. However, it does not consider the geometric structure of the data. To address this issue, Cai et al. constructed an affinity graph to encode geometric information, and sought a matrix factorization that respects the structure of the graph [36]. The algorithm is called graph regularized nonnegative matrix factorization (GNMF). The objective function of GNMF is defined as:
where \(\mathbf {Z}=[{{z}_{1}},{{z}_{2}},\ldots ,{{z}_\mathcal {N}}]\in {{\mathbb {R}^{\mathcal {M}\times \mathcal {N}}}}\) is the given data matrix. Each column of \(\mathbf {Z}\) is a sample vector, and \(\mathcal {M}\) represents the dimension of the vector, \(\mathcal {N}\) indicates the number of samples of the data. \(\mathbf {U}\in {\{{\mathbb {R}_{+},0\}^{\mathcal {M}\times \mathcal {R}}}}\) means the basis of \(\mathbf {Z}\) in the representation of NMF, and \(\mathbf {V}=[{{v}_{1}},{{v}_{2}},\ldots ,{{v}_\mathcal {N}}]\in {\{{\mathbb {R}_{+},0\}^{\mathcal {R}\times \mathcal {N}}}}(\mathcal {R}\ll \mathcal {N})\) denotes the coefficient matrix. A \(\mathcal {N}\)-node graph \(\mathcal {G}\) is formed with \(\{{{v}_{1}},{{v}_{2}},\ldots ,{{v}_\mathcal {N}}\}\) the graph signals. \({{\textbf {W}}}\) is the corresponding adjacency matrix, and its element \({{\textbf {W}}}_{i,j}\) is the edge weight between nodes \({v_i}\) and \({v_j}\). \(\mu\) is the regularization parameter that controls the regularization term. In (1), the second term usually represents the association between nodes [37], which can be further modified as follows:
where \(T\text {r}(\cdot )\) stands for the trace of a matrix, \(\mathbf {D}\) is a diagonal matrix in which \({\mathbf {{D}}_{i,i}}=\sum \nolimits _{j=1}^{\mathcal {N}}{{\mathbf {{W}}_{i,j}}}\), and the graph Laplacian matrix is \(\mathbf {L}=(\mathbf {D}-\mathbf {W})\in {{\mathbb {R}}^{\mathcal {N}\times \mathcal {N}}}\), which is symmetric positive semidefinite [38]. Therefore, GNMF can be simplified to:
The GNMF algorithm can reveal the geometric relationship inside the high-dimensional data. Based on GNMF, Lei et al. developed this method to the denoising task of HSI, and proposed multi-task graph-regularized sparse nonnegative matrix factorization (MTGSNMF) [39]. In this methd, they added an \(\ell _1\) norm to regularize the sparse noise, and the restoration model is as follows:
3 Method
3.1 Problem formulation
As mentioned above, HSI is usually affected by different noises. In this article, we assume that the noises are independent, and we have:
where \(\mathbf {Y}\in {{\mathbb {R}}^{M\times N\times P}}\) is the observed HSI has M rows, N columns, and P bands, respectively. \({{\textbf {X}}}\) is the clean image, and the remaining variables represent the additive noise components. \({{\textbf {N}}}\) represents the Gaussian noise, \({{\textbf {B}}}\) denotes the sparse noise, and \({{\textbf {S}}}\) indicates the stripe noise. Given the observed noise data \({{\textbf {Y}}}\), we try to restore \({{\textbf {X}}}\) from \({{\textbf {Y}}}\).
3.2 Proposed model
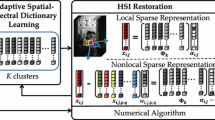
The sparse representation method can achieve the approximation of the recovered clean HSI. Additionally, the introduction of graph Laplacian regularization can describe the non-local similarity of the entire HSI. Besides, the stripe noise has low-rank property, hence, we combine the constraint on the stripe noise with the MTGSNMF. The proposed HSI reconstruction model is as follows:
where \(\mathbf {Y'}\) and \(\mathbf {S'}\) are auxiliary variables that represent \(\mathbf {Y}\) and \(\mathbf {S}\). To make better use of the redundant information of HSI and the relevant characteristics between bands, we are inspired by NLMs [4] and divide the observed \(\mathbf {Y}\) into a set of K overlapping full-band blocks \(\{\mathbf{Y}_1, \mathbf{Y}_2,\ldots ,\mathbf{Y}_K\}\). In addition, to simplify the representation of each graph node and facilitate subsequent calculations, each \(\mathbf{Y}_k \in \mathbb {R}^{m\times m\times P}\) is then vectorized to \(\mathbf {Y}_k' \in \mathbb {R}^{m^2P\times 1}\), where m is the width and height of the block, P is the number of bands, \(\mathbf {Y'}=[{\mathbf {Y}_1'},{\mathbf {Y}_2'},\ldots ,{\mathbf {Y}_K'}]\). \(\mathbf {S'}\) is obtained in the same way as \(\mathbf {Y'}\), and \(\mathbf {Y',S'}\in {{\mathbb {R}}^{m^2P\times K}}\). \(\mathbf {S}_b \in \mathbb {R}^{M\times N}\) is the 2-D stripe noise image at \(b_{th}\) band, and \(\mathbf {S} = [\mathbf {S}_1, \mathbf {S}_2,\ldots ,\mathbf {S}_b,\ldots ,\mathbf {S}_P]\).
As the low-rank constraint is non-convex, solving the problem (6) is challenging. Therefore, we replace the low-rank constraint by the nuclear norm \({\left\| \cdot \right\| _{\mathbf {*}}}\) [40, 41], where \(\left\| C \right\| _* =tr\sqrt{C^{T}C}=tr\sqrt{(U \Sigma V^{T})^TU \Sigma V^{T}}=tr( \Sigma )\), where \(\Sigma\) stands for the singular values of C. Thus, the reconstruction model is reformulated as:
where \(\left\| \mathbf {Y'}-\mathbf {UV}-\mathbf {S'} \right\| _{\mathbf {F}}^{\mathbf {2}}\) is the data fidelity item, which can help remove Gaussian noise through the \(\left\| \cdot \right\| _{\mathbf {F}}^{\mathbf {2}}\) norm constraint. \({\left\| {{\textbf {V}}} \right\| _{\mathbf {1}}}\) is sparsity constraint item, which can ensure the sparseness of the coefficient matrix, and can also constrain the sparse noise. \(\sum \limits _{b = 1}^P {{{\left\| {{{{\textbf {S}}}_b}} \right\| }_{\mathbf {*}}}}\) is the constraint on stripe noise.
Furthermore, \(Tr({{\textbf {VL}}}{{{\textbf {V}}}^T})\) is a graph Laplacian regularizer which helps preserve the spatial relation. As mentioned above, the graph is formed by K nodes, and each node is equipped with a signal \(\mathbf{Y}_k'\). We implement the k-means clustering algorithm for the graph nodes, so that all nodes are divided into c classes [39]. The weight of the edge of any two nodes in the same category is assigned as 1, and the connection weight of any two nodes not in the same category is assigned as 0. So the edge weight is defined as:
The corresponding graph Laplacian matrix \(\mathbf {L}\) is obtained by \(\mathbf {L}=\mathbf {D}-\mathbf {W}\).
Moreover, \(\lambda\), \(\mu\), \(\beta\) are the regularization parameters. \(\lambda\) controls the sparseness, and \(\mu\) dominates the strength of graph regularization, and \(\beta\) regulates the stripe low-rank regularizer. Finally, We need to optimize three variables in the objective function, which are \({{\textbf {U}}}\), \({{\textbf {V}}}\) and \({{\textbf {S}}}\). Next, we use the alternate minimization strategy to solve the problem. The optimization process is as follows.
3.3 Optimization procedure
The objective function in (7) is non-convex, so it is difficult to find a global minimum. The product \({{\textbf {UV}}}\) of two random variables \({{\textbf {U}}}\) and \({{\textbf {V}}}\) between 0 and 1 is a rough approximation of the original observation matrix \(\mathbf {Y'}\in {{\mathbb {R}}^{m^2P\times K}}\). Therefore, to solve \({{\textbf {U}}}\) and \({{\textbf {V}}}\), we use an iterative update algorithm that minimize the least square error to find the local optimal solution [42]. In addition, for solving the stripe component \({{\textbf {S}}}\), we convert the 2-D data matrix recovered from \({{\textbf {U}}{} {\textbf {V}}}\) into a 3-D matrix. Then, we use the low-rank constraint band by band for the recovered HSI, and use the soft threshold operation for the singular value [43]. For the convenience of description, let
To find the minimum value of \(\mathcal {L}\), firstly, we should obtain the partial derivatives of \(\mathcal {L}\) w.r.t. \({{\textbf {U}}}\) and \({{\textbf {V}}}\) respectively:
where the Laplacian matrix \({{\textbf {L}}}\) satisfies \({{\textbf {L}}} = {{\textbf {D}}} - {{\textbf {W}}}\), so \(\frac{{\partial \mathcal{L}}}{{\partial {{\textbf {V}}}}}\) can be transformed into:
Utilizing KKT conditions \({{\textbf {U}}} \odot \frac{{\partial \mathcal{L}}}{{\partial {{\textbf {U}}}}} = 0\) and \({{\textbf {V}}} \odot \frac{{\partial \mathcal{L}}}{{\partial {{\textbf {V}}}}} = 0\), where \(\odot\) represents the multiplication of the corresponding elements of the matrix, we can get the following equation w.r.t. \({{\textbf {U}}}\) and \({{\textbf {V}}}\):
The above equation will result in the following update rules of \({{\textbf {U}}}\) and \({{\textbf {V}}}\), the proof of this rule can refer to theorem 1 in GNMF [36].
Upon obtaining \({{\textbf {U}}}\) and \({{\textbf {V}}}\) according to (13), we convert \(\mathbf {UV}\) to a 3-D matrix \(\mathbf {E}\), which is the approximation of the denoised image. The stripe component \({{\textbf {S}}}\) is solved band by band. We use the augmented Lagrange multiplier (ALM) method [44] as follows:
It is a low-rank matrix approximation (LRMA) problem and solve it through the soft threshold operation of SVD [43]. Thus, we have the following update rules:
where \(\rho\) is the penalty factor, \({Y_b^S}\) is the Lagrange multiplier. \({{\sum }_{rii}}\) is the diagonal element of the singular value matrix \({\sum _r} = \mathrm{diag}({\sigma _i}(1< i < r))\), \(\mathrm{shrink}\_{{L}_{*}(\cdot )}\) is the soft threshold operation, r is the upper limit of the low-rank matrix.
Finally, the Lagrange multiplier can be updated in parallel:
The proposed algorithm for HSI denoising, termed SRGLR, is summarized in Algorithm 1.

4 Experiments
4.1 Experimental setup
For the simulated experiments, the Pavia City Center dataset and the Washington DC Mall dataset are used for clean HSI. The Pavia City Center dataset is collected by the reflection optical system imaging spectrometer (ROSIS-03), and we choose a \(200\times 200\times 80\) sub-image. Washington DC Mall dataset is obtained from a hyperspectral digital image (HYDICE) sensor in a shopping mall in Washington, and the size is selected \(256\times 256\times 80\).
For real data experiments, we use the Indian Pines dataset and the Gaofen (GF-5) Shanghai dataset. The Indian Pines dataset data is captured by the Airborne Visual Infrared Imaging Spectrometer (AVIRIS) and has \(145\times 145\) pixels and 220 channels, The GF-5 Shanghai dataset is acquired by the advanced Hyperspectral Imager (AHSI) in GF-5 satellite. A subimage with the size of \(300\times 300\times 155\) is selected. The two real datasets are severely degraded by various noises at some bands.
To evaluate the performance, we use the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM). The PSNR measures the quality of the restored image based on the mean square error, and the SSIM computes the similarity between the target image and the reference image. The higher PSNR and SSIM, the better the denoised image. Besides, to further objectively evaluate the recovery results, we introduce the spectral angle mapper (SAM). The SAM calculates the spectral similarity based on the angle difference between the restored HSI and the noise-free HSI spectral vector. The smaller the SAM, the more similar the recovery image is to the original image. To reflect the overall recovery quality among all bands, we use the mean PSNR (MPSNR), mean SSIM (MSSIM), and mean SAM (MSAM).
To testify the effectivness of our method in both simulated and real data condition, we conduct a serious of comparative experiments with six classical or state-of-the-art model-based denoising methods and a deep learning method : BM4D [6], low-rank matrix recovery (LRMR) [14], the noise-adjusted iterative low-rank matrix approximation (NAILRMA) [45], spatial-spectral total variation regularized local low-rank matrix recovery (LLRGTV) [46], multi-task graph-regularized sparse non-negative matrix factorization (MTGSNMF) [39], stripe spectral low-rank and spatial-spectral TV regularization (SSTVSSLR) [44], and HSI-SDeCNN [21]. Since the pre-trained HSI-DeCNN model provided by the authors only considers the Gaussian noise. To be fair, we retrained the network by adding the salt and pepper noise and stripe noise to the training and validation data. After 56.7 hours of training, the best training model is obtained.Footnote 1
Before denoising, to converge to the local optimal solution more efficiently, we normalized the HSI data to [0,1] by dividing the maximum value of the HSI data cube. Besides, we randomly select \(30\%\) of the band to simulate stripe noise. Empirically, we set the penalty parameter as \(\lambda =10\), \(\mu =10\), \(\beta =5\), and the initial block size is \(4\times 4\), and the step size in both the horizontal and vertical directions is 2. Finally, the threshold of stopping criterion and the max number of iterations are set to be \(\varepsilon ={{10}^{-6}}\) and \({{I}_{\max }=300}\), respectively. To simulate different noisy cases, we consider using the following different levels of noise types:
Case 1 We add Gaussian noise with standard variance \(\sigma\) = 0.05 and salt and pepper noise with the percentage of o = 0.01. Besides, the intensity of the stripe noise is v = 0.075. For the percentage of stripe noise, we use an increasing value r = 0.3 (Case 1.1), r = 0.5 (Case 1.2), and r = 0.7 (Case 1.3), respectively.
Case 2 Gaussian noise and salt and pepper noise are the same as Case 1. The stripe noise with the percentage of r = 0.3 and the intensity range from v = 0.05 (Case 2.1) to v = 0.1 (Case 2.2).
4.2 Simulated experimental results
Figures 1 and 2 shows the denoising results of different methods under Case 1.3 for the fourth band of the Pavia City Center image and Case 2.2 for the second band of Washington DC Mall image, respectively. In the two figures, the first row represents the restored image, and the second row indicates the locally enlarged detail region. Figures 1a, b and 2a, b separately displays the original noiseless image and the noisy image. Figures 1c–i and 2c–i are restored images by using different denoising methods. Figures 1j and 2j are the results of our proposed method. Through visual analysis and comparison, we can see that BM4D cannot remove stripe noise and salt and pepper noise, and this is because the BM4D ignores the correlation amongst the bands. NAIRLMA only considers Gaussian noise, so the output effects are not ideal. The LRMR, LLRGTV, MTGSNMF and HSI-SDeCNN can remove Gaussian noise and salt and pepper noise, but they fails in removing stripe noise. Though SSTVSSLR removes mixed noise very well, in some areas, such as the enlarged image of Fig. 1, it either enhances or decays the bright points at the top of the image, while our method can present better results in detail preservation and mixed noise removal.
The Pavia City Center image (4th band) [top] and zoom-in image [bottom] before and after denoising in Case 1.3 with \(\sigma\) = 0.05 and o = 0.01, r = 0.7, v = 0.075. a Original image; b Noisy image; the denoising results obtained by c BM4D; d LRMR; e NAILRMA; f LLRGTV; g MTGSNMF; h SSTVSSLR; i HSI-SDeCNN; j SRGLR (proposed)
The Washington DC Mall image (2nd band) [top] and zoom-in image [bottom] before and after denoising in Case 2.2 with \(\sigma\) = 0.05 and o = 0.01, r = 0.3, v = 0.1. a Original image; b Noisy image; the denoising results obtained by c BM4D; d LRMR; e NAILRMA; f LLRGTV; g MTGSNMF; h SSTVSSLR; i HSI-SDeCNN; j SRGLR (proposed)
Vertical mean profiles of band 4 in the Pavia City Center image a Original image; b Noisy image; before and after denoising via the different methods: c BM4D; d LRMR; e NAILRMA; f LLRGTV; g MTGSNMF; h SSTVSSLR; i HSI-SDeCNN; j SRGLR (proposed). The green, red, and blue curves represent the mean DN of the clean, noisy and restored images, respectively
Vertical mean profiles of band 2 in the Washington DC Mall image a Original image; b Noisy image; before and after denoising via the different methods: c BM4D; d LRMR; e NAILRMA; f LLRGTV; g MTGSNMF; h SSTVSSLR; i HSI-SDeCNN; j SRGLR (proposed). The green, red, and blue curves represent the mean DN of the clean, noisy and restored images, respectively
Figures 3 and 4 display the vertical average profile that corresponds to Figs. 1 and 2. The horizontal axis represents the number of columns, and the vertical axis indicates the mean gray-level or digital number (DN) of each column. The green, red, and blue curves represent the mean DN of the clean, noisy and restored images, respectively. Note that the more similarity between the blue and green curves, the better the denoising effect. Figures 3b–i and 4b–i show the mean DN of the denoised images using different methods and their comparisons with the ground-truth. Obviously, the results obtained by BM4D, LRMR, NAILRMA, LLRGTV, and MTGSNMF are similar to the original noisy image (red curve). This is because the 4th band of the Pavia dataset has strong stripe noise, while stripes significantly impact the mean DN. None of the above six methods can remove stripe noise, so the restored mean DN curve is almost equivalent to the noisy curve. Compared with the above model-based methods, HSI-SDeCNN can provide a slightly better visual performance. However, it fails to preserve the details and to remove some stripe noise. SSTVSSLR and our method perform well on both types of data, which demonstrates that the low-rank constraint on the stripe is an essential term to remove the stripe noise. In addition, the curve obtained by our method is closer to the original clean HSI curve, which further illustrates the advantages of our method.
Figure 5 shows the PSNR and SSIM of each band of the Pavia City Center in Case 1.3 and the Washington DC Mall dataset in Case 2.2. As can be seen from the figure, our method can generate the highest PSNR and SSIM in some bands. In addition, our method can bring comparatively stable denoising results for each band. In other words, we can see that the curves of some methods have serious sawtooth phenomena, which seriously limits the overall assessment index, while our approach can result in a better overall effect by giving relatively smooth and steady curves.
Table 1 shows the MPSNR, MSSIM and MSAM of different methods for the Pavia City Center dataset and Washington DC Mall dataset in both noisy cases, i.e., Case 1 and Case 2. The optimal indexes are shown in bold. From the table, we can see our method achieves the highest MPSNR, the largest MSSIM, and the lowest MSAM in most cases. Moreover, in terms of the indexes, our method behaves more excellent than other methods when increasing the percentage and intensity of stripe noise. The above experiments demonstrate the effectiveness of the proposed method in simulated cases.
4.3 Real noisy data experimental results
Figure 6 depicts the result on the Indian Pines dataset. Figure 6a displays the original noisy image at band 219, and Fig. 6b–i show the denoising results gained by different methods. We can see from Fig. 6b that BM4D cannot remove mixed noise. As shown in Fig. 6c, d, LRMR and NAIRLMA can deduct a certain amount of noise, but there still remains significant noise. In Fig. 6e, LLRGTV produces artifacts in a local area. In Fig. 6f, MTGSNMF brings too smooth a result and filters the details of the image. In Fig. 6h, HSI-DeCNN has obvious stripes in local areas and generates chessboard artifacts. Through visual comparison, SSTVSSLR and our proposed method have better visual effects.
Figure 7a is the image of the GF-5 Shanghai dataset at band 155. As shown in Fig. 7a, the image is seriously corrupted by Gaussian noise, impulse noise, dense stripe noise and dead lines. Comparing the detailed views from denoising images of different methods, BM4D and LRMR still contain heavy stripe noise, deadlines and some sparse noise. NAIRLMA, LLRGTV, MTGSNMF and HSI-DeCNN behave better but can not fully remove the stripe noise and dead lines. SSTVSSLR performs better than the above methods, but in the lower left and upper right corner, there is still some noise left. In the end, our proposed method delivers the best visual effect.
In addition, we provide the vertical average profile of the 155th band in the GF-5 Shanghai dataset before and after denoising. We can see from Fig. 8a that the original data is severely affected by various types of noises, and the mean DN curve fluctuates rapidly. Figure 8b–i show the mean DN curves after denoising by different methods. From the results, BM4D and LRMR barely generate any changes compared with the original noisy curve. The left methods can suppress the noise more or less, but SSTVSSLR, HSI-DeCNN and our method can bring a better result with the smoother curve. Compared with other methods, our method can get the best effect both in the global and in the local details. This result further proves the superiority of the proposed method.
Vertical mean profiles of band 155 in the GF-5 Shanghai image before and after denoising via the different methods: a Original image; b BM4D; c LRMR; d NAILRMA; e LLRGTV; f MTGSNMF; g SSTVSSLR; h HSI-SDeCNN; i SRGLR (proposed). The red and blue curves represent the mean DN of the original and restored images, respectively
Change in the MPSNR values of Proposed method for the Pavia City Center image (top) and the Washington DC Mall image (bottom) by varying parameters \(\lambda\), \(\mu\) and \(\beta\). The data were corrupted by the noise simulated in Case 1 and Case 2 with \(\sigma\) = 0.05 and o = 0.01: a, f r = 0.3, v = 0.075; b, g r = 0.5, v = 0.075; c, h r = 0.7, v = 0.075; d, i r = 0.3, v = 0.05; e, j r = 0.3, v = 0.1;
4.4 Discussion
The adjustment of the parameters is essential for the denoising task. In this paper, there are three parameters that need adjusting, i.e., \(\lambda\), \(\mu\), \(\beta\). \(\lambda\) controls the regularization of the salt and pepper noise. \(\mu\) is a graph Laplacian regularization parameter. \(\beta\) is the parameter for stripe noise. Figure 9 shows the changes of the MPSNR value on the Pavia City Center data and the Washington DC Mall data under Case 1 and Case 2 by using different parameters along the three coordinate axes.
As mentioned in Sect.3.3, it is not easy to find the global optimal solution of the cost function (7) because it is not a convex optimization problem. This is the reason that we can barely see a convergence point in Fig. 9 but several local maximums. Therefore, we choose the optimal local solution as our solution goal. According to a trade-off between the experimental results under different noise conditions and data, the optimal parameters are finally set to be: \(\lambda = 10\), \(\mu = 10\), \(\beta = 5\). As the above experimental results demonstrate, the selected parameters are robust to various noise conditions and distinct data.
5 Conclusions
Concentrating on the high-dimensional and particular geometric structure of the HSIs, in this paper, we propose a sparse representation and graph Laplacian regularization (SRGLR) method to solve the destriping and denoising problem. By analyzing the properties of the mixed noise, we combine a graph Laplacian regularization, sparse representation, and low-rank term to construct our denoising model. The sparse representation ensures the approximation of the restored image, and the graph Laplacian regularization term enhances the non-local similarity of HSI. In addition, the low-rank constraint helps remove the stripe noise, and the sparse regularizer eliminates the sparse noise. To solve the proposed model, an iterative algorithm of local minimum is used to recover the final restored image. Finally, simulation experiments and real experimental results show that our method has certain advantages in removing mixed noise. In future, we will consider the removal of more complex mixed noise such as deadlines, dead-zones, poisson noise, etc.
Availability of data and materials
The data that support the findings of this study are available on request from the corresponding author F.Y.
Notes
The training process is performed in MATLAB (R2018b) on the computing platform with an Intel Core I7-8700 CPU and a 16GB RAM.
Abbreviations
- HSI:
-
Hyperspectral image
- MNF:
-
Maximum noise fraction
- NL-means:
-
Non-local means
- BM3D:
-
Collaborative filtering of groups of similar patches
- BM4D:
-
Blocks-matching and 4D filtering
- VBM-4D:
-
Video denoising using separable 4-D non-local spatiotemporal transforms
- TV:
-
Total variation
- MAP:
-
Maximum a posteriori
- FastHyDe:
-
Fast hyperspectral denoising
- GLF:
-
Global local factorization
- LRMR:
-
Low-rank matrix recovery
- CNNs:
-
Convolutional neural networks
- HSI-SDeCNN:
-
HSI single-denoising CNN
- NMF:
-
Nonnegative matrix factorization
- GNMF:
-
Graph regularized nonnegative matrix factorization
- MTGSNMF:
-
Multi-task graph-regularized sparse nonnegative matrix factorization
- NAILRMA:
-
Noise-adjusted iterative low-rank matrix approximation
- LLRGTV:
-
Spatial-spectral total variation regularized local low-rank matrix recovery
- SSTVSSLR:
-
Stripe spectral low-rank and spatial-spectral TV regularization
- SRGLR:
-
Sparse representation and graph Laplacian regularization
- ALM:
-
Augmented Lagrange multiplier
- LRMA:
-
Low-rank matrix approximation
- PSNR:
-
Peak signalto-noise ratio
- SSIM:
-
Structural similarity
- SAM:
-
Spectral angle mapper
References
J.M. Bioucas-Dias, A. Plaza, G. Camps-Valls, P. Scheunders, N. Nasrabadi, J. Chanussot, Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 1(2), 6–36 (2013)
D. Hong, W. He, N. Yokoya, J. Yao, L. Gao, L. Zhang, J. Chanussot, X. Zhu, Interpretable hyperspectral artificial intelligence: When nonconvex modeling meets hyperspectral remote sensing. IEEE Geosci. Remote Sens. Mag. 9(2), 52–87 (2021)
A.A. Green, M. Berman, P. Switzer, M.D. Craig, A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 26(1), 65–74 (1988)
A. Buades, B. Coll, J.M. Morel, A non-local algorithm for image denoising, in IEEE Computer Society Conference On Computer Vision and Pattern Recognition, 2005. CVPR 2005 (2005)
K. Dabov, A. Foi, V. Katkovnik, K. Egiazarian, Image denoising by sparse 3-d transform-domain collaborative filtering. IEEE Trans. Image Process. 16(8), 2080–2095 (2007)
M. Maggioni, V. Katkovnik, K. Egiazarian, A. Foi, Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 22(1), 119–133 (2013)
M. Maggioni, G. Boracchi, A. Foi, K. Egiazarian, Video denoising, deblocking, and enhancement through separable 4-d nonlocal spatiotemporal transforms. IEEE Trans. Image Process. 21(9), 3952 (2012)
A. Danielyan, A. Foi, V. Katkovnik, K. Egiazarian, Denoising of multispectral images via nonlocal groupwise spectrum-pca (2014)
Q. Yuan, L. Zhang, H. Shen, Hyperspectral image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 50(10), 3660–3677 (2012)
F. Ying, A. Lam, I. Sato, Y. Sato, Adaptive spatial-spectral dictionary learning for hyperspectral image denoising, in 2015 IEEE International Conference on Computer Vision (ICCV), pp. 343–351 (2015)
S.L. Chen, X.Y. Hu, S.L. Peng, Hyperspectral imagery denoising using a spatial-spectral domain mixing prior. J. Comput. Sci. Technol. 27(4), 851–861 (2012)
L. Zhuang, J.M. Bioucas-Dias, Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 11(99), 730–742 (2018)
L. Zhuang, J.M. Bioucas-Dias, Hyperspectral image denoising based on global and non-local low-rank factorizations, in 2017 IEEE International Conference on Image Processing (ICIP), pp. 1900–1904 (2018)
H. Zhang, W. He, L. Zhang, H. Shen, Q. Yuan, Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 52(8), 4729–4743 (2014)
H. Fan, Y. Chen, Y. Guo, H. Zhang, G. Kuang, Hyperspectral image restoration using low-rank tensor recovery. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 10(10), 4589–4604 (2017)
H. Zhang, J. Cai, W. He, H. Shen, L. Zhang, Double low-rank matrix decomposition for hyperspectral image denoising and destriping. IEEE Trans. Geosci. Remote Sens. 60(99), 1–19 (2021)
J. Fan, L. Ding, Y. Chen, M. Udell, Factor group-sparse regularization for efficient low-rank matrix recovery. Adv. Neural Inf. Process. Syst. 32 (2019)
J. Fan, M. Udell, Online high rank matrix completion, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 8690–8698 (2019)
J. Fan, Multi-mode deep matrix and tensor factorization, in International Conference on Learning Representations (2021)
Q. Yuan, Q. Zhang, J. Li, H. Shen, L. Zhang, Hyperspectral image denoising employing a spatial-spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 57(2), 1205–1218 (2019)
A. Maffei, J.M. Haut, M.E. Paoletti, J. Plaza, L. Bruzzone, A. Plaza, A single model cnn for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 58(4), 2516–2529 (2020)
M. Elad, M. Aharon, Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 15(12), 3736–3745 (2006)
J. Mairal, M. Elad, G. Sapiro, Sparse representation for color image restoration. IEEE Trans. Image Process. 17(1), 53–69 (2007)
M. Elad, M. Figueiredo, Y. Ma, On the role of sparse and redundant representations in image processing. Proc. IEEE 98(6), 972–982 (2010)
M. Ye, Y. Qian, J. Zhou, Multitask sparse nonnegative matrix factorization for joint spectral-spatial hyperspectral imagery denoising. IEEE Trans. Geosci. Remote Sens. 53(5), 2621–2639 (2015)
Y.-Q. Zhao, J. Yang, Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 53(1), 296–308 (2014)
X. Liu, D. Zhai, D. Zhao, G. Zhai, W. Gao, Progressive image denoising through hybrid graph laplacian regularization: a unified framework. IEEE Trans. Image Process. 23(4), 1491–1503 (2014)
J. Pang, G. Cheung, Graph laplacian regularization for image denoising: analysis in the continuous domain. IEEE Trans. Image Process. 26(4), 1770–1785 (2017)
A. Kheradmand, P. Milanfar, A general framework for regularized, similarity-based image restoration. IEEE Trans. Image Process. 23(12), 5136–5151 (2014)
R. Ammanouil, A. Ferrari, C. Richard, A graph laplacian regularization for hyperspectral data unmixing, in 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1637–1641 (2015). IEEE
T. Ince, Superpixel-based graph laplacian regularization for sparse hyperspectral unmixing. IEEE Geosci. Remote Sens. Lett. 1–5 (2020)
X. Lu, Y. Wang, Yuan: graph-regularized low-rank representation for destriping of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 51(7), 4009–4018 (2013)
J.M. Bioucas-Dias, A. Plaza, N. Dobigeon, M. Parente, Q. Du, P. Gader, J. Chanussot, Hyperspectral unmixing overview: geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 5(2), 354–379 (2012)
Y.-X. Wang, Y.-J. Zhang, Nonnegative matrix factorization: a comprehensive review. IEEE Trans. Knowl. Data Eng. 25(6), 1336–1353 (2012)
P. Paatero, U. Tapper, Positive matrix factorization: a non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 5(2) (1994)
D. Cai, X. He, J. Han, T.S. Huang, Graph regularized non-negative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 33(8), 1548–1560 (2011)
M. Belkin, P. Niyogi, Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural. Inf. Process. Syst. 14(6), 585–591 (2001)
A. Ortega, P. Frossard, J. Kovacevic, J. Moura, P. Vandergheynst, Graph signal processing: overview, challenges, and applications. Proc. IEEE 106(5), 808–828 (2018)
L. Lei, B. Huang, M. Ye, H. Chen, Y. Qian, A graph-regularized non-local hyperspectral image denoising method, in Geometry and Vision, pp. 327–340 (2021)
M. Fazel, Matrix rank minimization with applications. PhD thesis, PhD thesis, Stanford University (2002)
Y.-M. Huang, H.-Y. Yan, Y.-W. Wen, X. Yang, Rank minimization with applications to image noise removal. Inf. Sci. 429, 147–163 (2018)
D.D. Lee, H.S. Seung, Algorithms for non-negative matrix factorization. Adv. Neural. Inf. Process. Syst. 7, 535–541 (2001)
J.F. Cai, E. Candès, Z. Shen, A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20(4), 1956–1982 (2010)
F. Yang, X. Chen, L. Chai, Hyperspectral image destriping and denoising using stripe and spectral low-rank matrix recovery and global spatial-spectral total variation. Remote Sens. 13(4), 827 (2021)
W. He, H. Zhang, L. Zhang, H. Shen, Hyperspectral image denoising via noise-adjusted iterative low-rank matrix approximation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 8(6), 1–12 (2015)
W. He, H. Zhang, H. Shen, L. Zhang, Hyperspectral image denoising using local low-rank matrix recovery and global spatial spectral total variation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 11(99), 1–17 (2018)
Acknowledgements
Not applicable.
Funding
This research was funded by National Natural Science Foundation of China (62101392).
Author information
Authors and Affiliations
Contributions
Z.Z conceived of the presented idea and wrote the manuscript. F.Y developed the scheme and checked the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Z., Yang, F. Hyperspectral image denoising and destriping based on sparse representation, graph Laplacian regularization and stripe low-rank property. EURASIP J. Adv. Signal Process. 2022, 96 (2022). https://doi.org/10.1186/s13634-022-00901-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13634-022-00901-3