1 Introduction

Compared with 5G, 6G has the advantages of wider wireless coverage, faster transmission speed, and more intelligence, which has attracted substantial attention from academic community [1,2,3]. Non-orthogonal multiple access (NOMA) has been recognized as a promising technique for 6G communication networks, due to its benefits of enhancing spectrum efficiency and accommodating massive connectivity [4,5,6]. NOMA mainly includes two categories: code-domain NOMA and power-domain NOMA. Code domain NOMA allows controllable interference at the destinations on the same time-frequency resources by leveraging different but partially overlapping codes [7]. Differently, power-domain NOMA separates the user messages by leveraging different received power levels. In this paper, we focus on power-domain NOMA, in which multiple user signals are superposed linearly by well-designed weights at the transmitter to share the same time/frequency/code resource. In order to distinguish multiple desired signals, successive interference cancellation (SIC) is employed at the receiver [8]. More specifically, the SIC performed in NOMA systems enables the users with better channel conditions to decode not only their own information but also the messages of the users with small channel gains.

Recently, significant research efforts have been shifted toward the combination of NOMA with cooperative communication due to its superiority in improving system performance. Ding et al. [9] proposed a novel cooperative NOMA transmission scheme, in which users with strong channels act as relays to forward other users’ messages by following NOMA principle in the cooperation stage. It was shown that the strength of the signal received by weak users is improved substantially. Compared to pure NOMA method, cooperative NOMA has the capability of yielding a lower outage probability [9]. To further exploit spectral efficiency and space diversity, relay selection scheme in cooperative NOMA systems has been widely investigated, such as [10, 11]. In a decode-and-forward (DF) cooperative NOMA systems, the authors devised a two-stage relay selection algorithm and derived closed-form expressions of outage probability in [10]. It was shown that the two-stage relay selection scheme is capable of achieving the maximal diversity order and the minimal outage probability. Yu et al. [11] derived the expressions of system throughput for cooperative NOMA network with relay selection. It was verified that system throughput of cooperative NOMA with relay selection outperforms those of the conventional orthogonal multiple access (OMA) and the non-cooperative NOMA. Furthermore, the authors in [12] studied energy efficiency and outage probability of cooperative NOMA in both full-duplex and half-duplex relay assisted heterogeneous networks. In addition, the authors proposed a two-stage relay selection strategy for NOMA networks based on user-specific quality of services (QoSs) in [13], where the closed-form expressions of outage probabilities were derived with the DF and amplify-and-forward (AF) relaying protocols, respectively.

Moreover, in [14], an antenna selection (AS) problem was considered for multiple-input multiple-output (MIMO) NOMA systems, in which two efficient AS algorithms were developed, i.e., NOMA with fixed power allocation (F-NOMA) and NOMA with cognitive radio-inspired power allocation (CR-NOMA). Furthermore, the asymptotic closed-form expressions of average sum-rate were derived. The authors investigated a multi-antenna two-way relay assisted NOMA system in [15], in which two cooperative strategies, namely multiple-access broadcast NOMA and time division broadcast NOMA, were proposed. For each of the two cooperative strategies, a joint antenna-and-relay selection scheme was devised to enhance the transmission reliability. Besides, the closed-form expressions of both outage probability and diversity order were derived to evaluate the system performance. However, if eavesdropping nodes are within the coverage of the relays, there may have a chance to wiretap legitimate users’ messages. Thus, physical layer security (PLS) is an important issue in cooperative NOMA systems [16, 17], but it was not considered in the above literature.

Currently, the relay selection schemes for improving PLS in cooperative NOMA system have been investigated in some prior works, e.g., [18,19,20]. In [18], a relay selection method was proposed to minimize the secrecy outage probability for cooperative NOMA system with multiple DF relays, in which the transmission rate of the source should be adjusted according to the channel gains in two hops. Moreover, considering two users with different QoS requirements, three relay selection schemes with fixed power allocation and dynamic power allocation were studied in [19] aiming at enhancing secrecy outage probability. Furthermore, the authors in [20] proposed a two-stage relay selection scheme and derived the outage probability in DF cooperative NOMA system. However, the impact of multiple relays and multiple antennas was not analyzed for cooperative NOMA networks.

In this paper, we intend to study the PLS of a cooperative NOMA system with multiple relays and multiple antennas. To the best of our knowledge, the secrecy performance of cooperative NOMA systems with joint relay and antenna selection has not been reported by the existing works. Motivated by these observations, we will focus on deriving the secrecy outage probabilities (SOP) of cooperative NOMA networks with AF relays (DF relays will be investigated in future) and the optimal antenna selection strategy in the presence of a multi-antenna eavesdropper, in which both selection combining (SC) and maximum ratio combining (MRC) are taken into account. The contributions of this work can be summarized as follows:

First, an analytical framework of a multi-AF relay multi-antenna NOMA system with joint relay and antenna selection is developed. Besides, the impacts of various eavesdropping scenarios are modelled and investigated thoroughly. Specifically, in the considered model, four transmission scenarios are included, i.e., SC adopted at the eavesdropper with/without the channel state information (CSI) of the eavesdropper links, MRC employed at the eavesdropper with/without the CSI of the eavesdropper links.

Second, in order to improve secrecy performance in a cost-effective way, a two-stage joint relay and antenna selection scheme is proposed. The benefit of the proposed scheme is that diversity gains stemming from both relay selection and antenna selection can be achieved. Based on the statistics of the channel gains, the SOPs are derived in closed-forms for the proposed relay–antenna selection scheme in four different circumstances. To gain more useful insights on the derived results, the secrecy diversity orders of the proposed scheme are derived.

The rest of this paper is organized as follows. In Section II, the secure cooperative NOMA system model and relay–antenna selection scheme are presented. The closed-form of SOP for AF-based cooperative NOMA in four eavesdropping scenarios are derived in Section III. In Section IV, the asymptotic SOPs for AF-based cooperative NOMA in four eavesdropping scenarios are derived. Moreover, in Section V, we derive the secrecy diversity order for different eavesdropping environments. Numerical results are presented in Section VI to reveal valuable insights on the secrecy performance of the proposed schemes. Finally, this paper is concluded in Section VII.

The aim of this paper is to analyze the secrecy performance of NOMA based on multi-relay and multi-antenna assistance, specifically, analyzing the secrecy outage probability and secrecy diversity order of this system. For multi-relay and multi-antenna systems, we propose an optimal single relay and single antenna selection scheme, which minimizes the secrecy outage probability. The main link adopts SC mode to save radio frequency (RF) chains. The eavesdropping link adopts SC or MRC in order to compare the two receiving merging methods. Brief introduction to the design idea: When the CSI of the eavesdropping link is known; Firstly, a relay is specified and an antenna set is selected from the antennas equipped with the relay. The antennas in the antenna set meet the requirements of transmitting signals with this antenna, so that the cell-edge user can safely decode his own signal. Secondly, in the antenna set mentioned above, the antenna that enables the cell-center user to obtain the maximum secure decoding rate (decoding rate minus eavesdropping rate) is selected as the best antenna for this relay. Thirdly, in all the remaining relays, adopt similar steps to find the best antenna corresponding to the relay. Finally, the maximum rate obtained by the cell-center user from all relays and all antennas is found. Accordingly, the corresponding relay and antenna is the best single relay and single antenna in the system. When the CSI of the eavesdropping link is not known; The process of optimal relay antenna is similar to the above, with some differences: First, specify a relay and select an antenna set from the antennas equipped with the relay. Among them, the antennas in the antenna set meet the requirements of transmitting signals with this antenna, so that the cell-edge user can decode his own signal. Secondly, in the antenna set mentioned above, the antenna that enables the cell-center user to obtain the maximum decoding rate is selected as the best antenna for this relay; Thirdly, in all the remaining relays, adopt similar steps to find the best antenna corresponding to the relay; Finally, the maximum rate obtained by the cell-center user from all relays and antennas is found. At this time, the corresponding relay and antenna is the best single relay and single antenna in the system.

Fig. 1
figure 1

System model. A illustration of system architecture of cooperative NOMA system with a single source and multiple AF relays

Full size image

2 System model and relay–antenna selection

2.1 System model

2.1.1 Network description

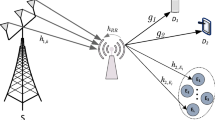
Consider a downlink secure cooperative NOMA system including a single source S, N AF relaysFootnote 1\(\{R_1,\ldots ,R_N\}\), two legitimate users, i.e., the cell-edge user \(U_1\) and the cell-center user \(U_2\), and an eavesdropper E, as shown in Fig. 1. The relays operate in half-duplex mode. It is assumed that there is no direct link between the source and the legitimate users due to long propagation distance and severe obstacle blocking. We also assume that the eavesdropper is located in the vicinity of the users but far from the source. In such case, the eavesdropper can only overhear the messages coming from the relays. The source is equipped with a single antennaFootnote 2. The numbers of antennas equipped at each relay, the user \(U_i\) and the eavesdropper are M, \(L_i\) and K, respectively. Let \(h_{S R_{n,m} }\) and \(h_{R_{n,m} U_i}\) denote the channel from the source to the m-th antenna of the n-th relay (\(S \rightarrow R_{n,m}\)) and from the m-th antenna of the n-th relay to the user \(U_i\) (\(R_{n,m} \rightarrow U_i\)), respectively. It is assumed that both \(h_{S R_{n,m} }\) and \(h_{R_{n,m} U_i}\) are available at the legitimate nodes [21]. Besides, let \(h_{R_{n,m}E_{k} }\) denote the channel coefficient between the m-th antenna of the n-th relay and the k-th antenna of the eavesdropper, i.e., \(R_{n,m} \rightarrow E_k\). We assume that all the CSI is perfectFootnote 3. All the channels in the system follow the block Rayleigh fading, in which the channel coefficients remain unchanged within one block, but vary independently from one block to another, i.e., \(h_{S R_{n,m}} \sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Omega _{S R_{n,m}} )\), \(h_{R_{n,m}U_i }\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Omega _{R_{n,m}U_i} )\), and \(h_{R_{n,m}E_{k} }\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\Omega _{R_{n,m}E_k} )\).

In the considered model, the data transmission is divided into two phases. In the first phase, the source S broadcasts the superposed signal, \(\sqrt{P_S}x\), to the relays, where \(P_S\) denotes the transmit power of the source S, the transmit data \(x=\sqrt{\alpha } s_1 + \sqrt{(1-\alpha )} s_2\), \(s_1\) and \(s_2\) are the signals for \(U_1\) and \(U_2\) with unit power, respectively. The power allocation coefficient of \(s_1\) is \(\alpha\) with \(0.5< \alpha < 1\), and the rest transmit power is allocated to the signal \(s_2\) [9]. It is known that the power allocation coefficients affect the relay-source selection scheme in cooperative NOMA system. In order to facilitate the development of the relay-source selection scheme, the power allocation coefficients at the source are chosen to maximize the secrecy capacity of an arbitrary source-relay-users link. Therefore, the received signal at the m-th antenna of the relay \(R_{{n}}\) is given by

$$\begin{aligned} y_{R_{{n,m}}} = h_{S R_{n,m}} \sqrt{P_S} x + n_{R_{n,m}}, \end{aligned}$$
(1)

where \(n_{R_{n,m}}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\sigma _{R_{n,m}}^{2})\) represents the additive white Gaussian noise (AWGN) at \(R_{n,m}\) with zero mean and variance \(\sigma _{R_{n,m}}^{2}\).

In the second phase, the selected relay transmits the received signal to the users \(U_1\) and \(U_2\) following the NOMA principle. More details about the transmission in the second phase will be presented in the remaining of this section. Hereafter, the AF protocol is considered at the relays.

2.1.2 Secrecy capacity

In order to reduce the cost of circuit caused by expensive RF chains, the antenna selection technique is used at the relays and the users. In the considered model, only one antenna is selected for reception or transmission at each relay. It is worth mentioning that the selected receiving antenna and transmission antenna may be different because the channel conditions in two hops are independent. Suppose the relay \(R_n\) employing the m-th antenna amplifies and forwards its received signals to the two legitimate users in the second phase. In order to satisfy the power budget at the selected relay in the AF mode, the power amplification factor is expressed as \(G_{n,m}=\sqrt{\frac{P_{R_{n}}}{| h_{SR_{n,m}} |^2 P_S+\sigma _{R_{n,m}}^2}}\), where \(P_{R_{n}}\) is the transmit power of the relay \(R_n\). As a result, the received signals at \(U_i\), \(i\in (1,2)\), and the eavesdropper E are respectively given by

$$\begin{aligned} y_{U_i}^{n,m}= & {} h_{R_{n,m}U_i} G_{n,m} y_{R_{n,m}} + n_{U_i}, \end{aligned}$$
(2)
$$\begin{aligned} y_{E}^{n,m}= & {} h_{R_{n,m}E} G_{n,m} y_{R_{n,m}} + n_{E}, \end{aligned}$$
(3)

where \(n_{U_i}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\sigma _{U_i}^{2})\) and \(n_{E}\sim {{\mathcal {C}}}{{\mathcal {N}}}(0,\sigma _{E}^{2})\) are the AWGNs at the user \(U_i\) and the eavesdropper E, respectively. For mathematical tractability, we assume that \(P_S=P_{R_n}=P\), \(\sigma _{R_n}^{2}=\sigma _{U_i}^{2}=\sigma _{E}^{2}=\sigma _{0}^{2}\) in the following. According to the decoding order in the NOMA system, the cell-edge user’s signal \(s_1\) is first decoded at both the user \(U_i\) and the eavesdropper E. When decoding signal \(s_1\), the signal \(s_2\) is treated as the interference. Then, the received signal-to-interference-plus-noise ratio (SINR) of \(s_1\) at \(U_i\) and E can be respectively expressed as

$$\begin{aligned} \gamma _{U_i \leftarrow s_1}^{n,m}= & {} \frac{\alpha \rho ^{2} X_{n,m} Y_{U_i,n,m}}{ (1-\alpha )\rho ^{2} X_{n,m} Y_{U_i,n,m}+ \rho X_{n,m}+\rho Y_{U_i,n,m} +1}, \end{aligned}$$
(4)
$$\begin{aligned} \gamma _{E \leftarrow s_1}^{n,m}= & {} \frac{ \alpha \rho ^{2} X_{n,m} Z_{n,m}}{ (1-\alpha )\rho ^{2} X_{n,m} Z_{n,m}+ \rho Z_{n,m}+\rho X_{n,m}+ 1}, \end{aligned}$$
(5)

where \(X_{n,m}=|h_{SR_{n,m}}|^{2}\), \(Y_{U_i,n,m}=|h_{R_{n,m} U_i}|^{2}\), \(Z_{n,m}=|h_{R_{n,m} E}|^{2}\), and \(\rho =\frac{P}{\sigma ^2 }\) denotes the transmit signal-to-noise ratio (SNR).

After the signal \(s_1\) is decoded, it is subtracted from the received signal at the user \(U_2\) and the eavesdropper E with the aid of SIC. In such case, the user \(U_2\) and the eavesdropper E detect \(s_2\) without the inter-user interference. Then, the SINR of \(s_2\) at \(U_2\) and E can be, respectively, given by

$$\begin{aligned} \gamma _{U_2 \leftarrow s_2}^{n,m}= & {} \frac{(1-\alpha )\rho ^{2}X_{n,m} Y_{U_2,{n,m}}}{ \rho Y_{U_2,{n,m}}+\rho X_{n,m} + 1}, \end{aligned}$$
(6)
$$\begin{aligned} \gamma _{E \leftarrow s_2}^{n,m}= & {} \frac{(1-\alpha )\rho ^{2} X_{n,m} Z_{n,m}}{ \rho Z_{n,m}+\rho X_{n,m} + 1}. \end{aligned}$$
(7)

Based on the SINR derived above, the capacity of the user \(U_i\) to decode its own signal \(s_i\) is expressed as

$$\begin{aligned} C_{U_i}^{n,m} = \frac{1}{2} \log _2 \left( {1+\gamma _{U_{i} \leftarrow s_i}^{n,m}}\right) . \end{aligned}$$
(8)

Similarly, the capacity of the cell-center user \(U_2\) to detect \(s_1\) is given by

$$\begin{aligned} C_{U_2 \leftarrow s_1}^{n,m} = \frac{1}{2} \log _2 \left( {{1+\gamma _{U_{2} \leftarrow s_1}^{n,m}}}\right) . \end{aligned}$$
(9)

Besides, the channel capacity of the \(R_n \rightarrow E\) link can be expressed as

$$\begin{aligned} C_{E \leftarrow s_i}^{n,m} = \frac{1}{2} \log _2 \left( {{1+\gamma _{E \leftarrow s_i}^{n,m}}}\right) . \end{aligned}$$
(10)

Accordingly, the secrecy capacities obtained at \(U_i\) are respectively given by

$$\begin{aligned} C_{sec, U_i }^{n,m}= & {} {\left[ { {C_{U_i}^{n,m}-C_{E \leftarrow s_i}^{n,m}}}\right] ^{+}}, \end{aligned}$$
(11)
$$\begin{aligned} C_{sec, U_2\leftarrow s_1 }^{n,m}= & {} {\left[ { {C_{U_2\leftarrow s_1}^{n,m}-C_{E \leftarrow s_1}^{n,m}}}\right] ^{+}}, \end{aligned}$$
(12)

where \([x]^+=\max \left\{ {x,0}\right\}\).

2.2 Relay–antenna selection schemes

In order to improve system performance in a cost-effective way, the optimal single-relay and single-antenna is selected to assist the data transmission in both the reception and the transmissionFootnote 4. The proposed joint relay and antenna selection schemes are respectively presented when the CSI of the eavesdropper is available and unavailable.

2.2.1 Relay–antenna selection scheme with the CSI of the eavesdropper

The optimal relay–antenna selection (ORAS) algorithm is implemented by three steps:

Firstly, for a given relay \(R_n\), the candidate transmit antenna subset \(\Phi _{n,m}^{w/}\) (w/ means with the CSI of the eavesdropper) is selected, in which the antenna can transmit \(s_1\) to both users successfully, i.e., the secrecy capacity of \(s_1\) is larger than the rate requirement at both users. Thus, \(\Phi _{n,m}^{w/}\) can be expressed as

$$\begin{aligned} \Phi _{n,m}^{w/} = \left\{ m: {C_{sec, U_1 }^{n,m}\ge {R_{1}^{s}}},{C_{sec, U_2 \leftarrow s_1}^{n,m}\ge {R_{1}^{s}}}, m\in [1,2,\ldots ,M] \right\} , \end{aligned}$$
(13)

where \(R_{1}^{s}\) denotes the required secrecy rate of \(s_1\).

Secondly, from the candidate transmit antenna subset \(\Phi _{n,m}^{w/}\), the best transmit antenna is selected to achieve the maximum secrecy rate of \(s_2\) at the cell-center user \(U_2\). Then, in the subset \(\Phi _{n,m}^{w/}\), the index of the best transmit antenna is given by

$$\begin{aligned} m_{n,*}^{w/}=\mathop {\mathrm {argmax}}_{m\in \Phi _{n,m}^{w/}}\left\{ {C_{sec,U_2}^{n,m}}\right\} , \end{aligned}$$
(14)

where \(R_{2}^{s}\) denotes the required secrecy rate for \(s_2\).

Finally, the optimal relay is selected to achieve the maximum secrecy rate of \(U_2\) among all the relays. Thus, the index of the optimal relay is obtained by

$$\begin{aligned} n_{*}^{w/}=\mathop {\mathrm {argmax}}_{n\in [1,N]}\left\{ {C_{sec,U_2}^{ n,m_{n,*}^{w/} }}\right\} . \end{aligned}$$
(15)

Accordingly, the index of the optimal transmit antenna for the optimal relay \(R_{n_{*}^{w/}}\) can be obtained by \(m_{n,*}^{w/}\) shown in (14).

2.2.2 Relay–antenna selection scheme without the CSI of the eavesdropper

In this scenario, the achieved SOP is less than that of the case with the CSI. Thus, the optimal relay–antenna selection scheme hereafter. Since the CSI of the eavesdropper is unavailable, the wiretap capacity is not considered in this scheme. The detailed algorithm is described as follows:

Firstly, for a given relay \(R_n\), the candidate transmit antenna subset \(\Phi _{n,m}^{w/o}\) (w/o means without the CSI of the eavesdropper) is selected, in which the antenna can transmit the signal \(s_1\) to the both users successfully without considering the CSI of the eavesdropper, i.e., the capacity of \(s_1\) is larger than the rate requirement at both users. Thus, \(\Phi _{n,m}^{w/o}\) is expressed as

$$\begin{aligned} \Phi _{n,m}^{w/o} = \left\{ m: {C_{U_1 }^{n,m}\ge {R_{1}^{th}}},{C_{U_2 \leftarrow s_1}^{n,m}\ge {R_{1}^{th}}}, m\in [1,2,\ldots ,M] \right\} , \end{aligned}$$
(16)

where \(R_{1}^{th}\) denotes the rate requirement of signal \(s_1\).

Secondly, from the candidate transmit antenna subset \(\Phi _{n,m}^{w/o}\), the best transmit antenna is selected to achieve the maximum required rate of \(s_2\) at the cell-center user \(U_2\). Then, the index of the best transmit antenna is given by

$$\begin{aligned} m_{n,*}^{w/o}=\mathop {\mathrm {argmax}}_{m\in \Phi _{n,m}^{w/o}}\left\{ {C_{U_2}^{n,m}}\right\} , \end{aligned}$$
(17)

where \(R_{2}^{th}\) denotes the rate requirement of signal \(s_2\).

Finally, the optimal relay is selected to achieve the maximum rate of \(U_2\) among all the relays. Thus, the index of the optimal relay is obtained by

$$\begin{aligned} n_{*}^{w/o}=\mathop {\mathrm {argmax}}_{n\in [1,N]}\left\{ {C_{U_2}^{ n,m_{n,*}^{w/o} }}\right\} . \end{aligned}$$
(18)

Accordingly, the index of the optimal transmit antenna for the optimal relay \(R_{n^{*}}\) can be obtained by \(m_{n,*}^{w/o}\) given in (17).

3 Secrecy outage performance analysis

In this section, the SOPs of \(U_i\) to detect \(s_i\) are respectively derived for the proposed relay–antenna selection schemes. For each relay, each user, and the eavesdropper, two practical signal processing techniques, i.e., SC and MRC, are considered. As such, the proposed relay–antenna selection schemes should be designed in four casesFootnote 5: (1) SC-SC w/ CSI: SC at the legitimate nodes (relays and users), and SC at the eavesdropper with the CSI of the eavesdropping channel; (2) SC-MRC w/ CSI: SC at the legitimate nodes, and MRC at the eavesdropper with the CSI of the eavesdropping channel; (3) SC-SC w/o CSI: SC at the legitimate nodes, and SC at the eavesdropper without the CSI of the eavesdropping channel; (4) SC-MRC w/o CSI: SC at the legitimate nodes, and MRC at the eavesdropper without the CSI of the eavesdropping channel.

3.1 The SOP derivation for ORAS w/ CSI

3.1.1 SC at the eavesdropper

In the case of SC at the eavesdropper, each antenna wiretaps the transmission date independently. Hence, the individual secrecy performance is limited by the antenna with the best channel condition. In such case, the probability density function (PDF) of the equivalent eavesdropping channel gain is given by [22]

$$\begin{aligned} f_{Z}(z)=\sum _{k=1}^{K}{\left( {\begin{array}{c}K\\ k\end{array}}\right) }(-1)^{k+1}\frac{k}{\Omega _Z}e^{-\frac{kz}{\Omega _Z}}, \end{aligned}$$
(19)

where Z stands for eavesdropping channel gain, \(\Omega _{Z}\) represents the reciprocal of the expected gain of the eavesdropping channel.

As a result, the SOP of \(U_1\) can be expressed as

$$\begin{aligned} P_{U_{1},w/}^{SC-SC}={\prod \limits _{n{\mathrm {=1}}}^{N}} \underbrace{\Pr \left\{ {{\left| {\Phi _{U_{1},w/}}\right| =0}} \right\} }_{\Psi _{1,w/}^{{SC-SC}}}, \end{aligned}$$
(20)

and the SOP of \(U_2\) can be expressed as

$$\begin{aligned} P_{U_{2},w/}^{SC-SC}&=\prod _{n=1}^{N} \bigg [ {\underbrace{\Pr \left( {{\left| {\Phi _{U_2,w/}}\right| =0}}\right) }_{\Psi _{2,w/}^{SC-SC}}}+\sum _{m=1}^{M} {\underbrace{\Pr \left( {{\left| {\Phi _{U_2,w/}}\right| =m}}\right) }_{\Psi _{3,w/}^{SC-SC}}} \nonumber \\&\quad \times {\underbrace{\Pr \left( {{\left. { {C_{_{sec,{U_{2}}}} < {R_{2}^{s}}} }\right| \left| {\Phi _{U_2,w/}}\right| = m} }\right) }_{\Psi _{4,w/}^{SC-SC}}}\bigg ], \end{aligned}$$
(21)

To further derive the expression of the SOPs in (20) and (21), Lemma 1 is developed in the following.

Lemma 1

By using the statistics of channel gains, the analytical expressions of \(\Psi _{1,w/}^{SC-SC}\), \(\Psi _{2,w/}^{SC-SC}\), \(\Psi _{3,w/}^{SC-SC}\) and \(\Psi _{4,w/}^{SC-SC}\) can be derived as

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi _{i,w/}^{SC-SC} = \prod _{m=1}^{M} \left( 1-\Delta _{i,w/}^{SC-SC} \right) ,i\in (1,2), {~{}} \\ \Psi _{3,w/}^{SC-SC} = {\left( {\begin{array}{c}M\\ m\end{array}}\right) } (\Delta _{2,w/}^{SC-SC})^{m}(1-\Delta _{2,w/}^{SC-SC})^{M-m}, {~{}} \\ \Psi _{4,w/}^{SC-SC} = ( 1-\Delta _{3,w/}^{SC-SC}/\Delta _{2,w/}^{SC-SC})^{m} , \end{array}\right. } \end{aligned}$$
(22)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _{1,w/}^{SC-SC} = Q_1 Q_2 J_{1} \exp {(- W_1)}, {~{}} \\ \Delta _{2,w/}^{SC-SC} = Q_1 Q_3 J_{1} \exp {(- W_2)}, {~{}} \\ \Delta _{3,w/}^{SC-SC} = Q_1 Q_3 G_{1} O_1 \mu _1^{-1} , \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} Q_1 = \sum _{k=1}^{K}{\left( {\begin{array}{c}K\\ k\end{array}}\right) }(-1)^{k+1}, {~{}} \\ Q_2 = \sum _{l_1=1}^{L_1}{\left( {\begin{array}{c}L_1\\ l_1\end{array}}\right) }(-1)^{l_1+1}, {~{}} \\ Q_3 = \sum _{l_2=1}^{L_2}{\left( {\begin{array}{c}L_2\\ l_2\end{array}}\right) }(-1)^{l_2+1}, {~{}} \\ \mu _1 = { \frac{B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}}+ \frac{k}{\Omega _{R_{n,m}E}} , {~{}} \\ G_1 = \frac{k}{\Omega _{R_{n,m}E}}\exp \left( -\frac{ A_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}\right) , {~{}} \\ W_1 = \frac{k E (t +1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t), {~{}} \\ W_2 = \frac{k E (t +1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_2}}{{\Omega _{R_{n,m}U_{2}}}}}\right) F(t), {~{}} \\ J_1 =\sum _{l_{0}=1}^{N_0} \frac{k\pi E\sqrt{1-t^2}}{2 N_o \Omega _{R_{n,m}E}} , O_1 = 1-\exp \left( - \mu _1 E \right) , \end{array}\right. } \end{aligned}$$

\(t=\cos \left( \frac{2l_0-1}{2N_0}\pi \right)\), \(A_0=2^{2R_{1}^{s}}-1\), \(B_0=\rho \left( A_0+\alpha \right)\), \(C_0=\rho \left( \alpha +\alpha A_0 -A_0 \right)\), \(D_0=\rho ^{2} A_0 \left( 1-\alpha \right)\), \(E= \frac{C_0}{D_0}\), \(A_1=\frac{2^{2R_{2}^{s}}-1}{\rho \left( 1-\alpha \right) }\), \(B_1=2^{2R_{2}^{s}}\), \(F\left( t\right) =\frac{ 2A_0+B_0E\left( t+1\right) }{2C_0-D_0E\left( t+1\right) }\), and \(N_0\) denotes the number of terms for the quadrature approximation.

Proof

The proof of Lemma 1 is shown in Appendix 1.

By substituting (22) into (20) and (21), we can get the closed-form expressions of the SOPs for \(P_{U_{1},w/}^{SC-SC}\) and \(P_{U_{2},w/}^{SC-SC}\). Thus, in the presence of SC at the eavesdropper, the total SOP can be expressed as

$$\begin{aligned} P_{out,w/}^{SC-SC}= \frac{\left( P_{U_{1},w/}^{SC-SC}+P_{U_{2},w/}^{SC-SC} \right) }{2}. \end{aligned}$$
(23)

Accordingly, the SOP for NOMA system with SC at the eavesdropper in ORAS scheme w/ CSI can be approximated as

$$\begin{aligned} P_{out,w/}^{SC-SC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1-\Delta _{1,w/}^{SC-SC} \right) +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1-\Delta _{3,w/}^{SC-SC} \right) . \end{aligned}$$
(24)

3.1.2 MRC at the eavesdropper

In the case of MRC at the eavesdropper, the antenna cooperates with each other to wiretap the transmission date. Hence, the PDF of the equivalent eavesdropping channel gain is given by [22]

$$\begin{aligned} f_{Z}(z)=\frac{Z^{K-1}}{{\Omega _Z}^{K} (K-1)!}e^{-\frac{z}{\Omega _Z}}. \end{aligned}$$
(25)

In this scheme, the SOPs of \(U_1\) and \(U_2\) can be gotten by changing the superscript “SC-SC” in (20) and (21) to “SC-MRC”. However, the derivation of each term is different. Similar to Lemma 1, Lemma 2 is given as follows.

Lemma 2

The analytical expressions of \(\Psi _{1,w/}^{SC-MRC}\), \(\Psi _{2,w/}^{SC-MRC}\), \(\Psi _{3,w/}^{SC-MRC}\) and \(\Psi _{4,w/}^{SC-MRC}\) can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi _{i,w/}^{SC-MRC} = \prod _{m=1}^{M} \left( 1-\Delta _{i,w/}^{SC-MRC} \right) ,i\in (1,2), {~{}} \\ \Psi _{3,w/}^{SC-MRC} = {\left( {\begin{array}{c}M\\ m\end{array}}\right) } (\Delta _{2,w/}^{SC-MRC})^{m}(1-\Delta _{2,w/}^{SC-MRC})^{M-m}, {~{}} \\ \Psi _{4,w/}^{SC-MRC} = ( 1-\Delta _{3,w/}^{SC-MRC}/\Delta _{2,w/}^{SC-MRC})^{m} , \end{array}\right. } \end{aligned}$$
(26)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _{1,w/}^{SC-MRC} = Q_2 J_{2} \exp {(-W_3 )}, {~{}} \\ \Delta _{2,w/}^{SC-MRC} = Q_3 J_{2} \exp {(-W_4 )}, {~{}} \\ \Delta _{3,w/}^{SC-MRC} =Q_3 G_{2} O_2, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} G_2 = \frac{\exp \left( -\frac{ A_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}\right) }{(\Omega _{R_{n,m}E})^K (K-1)!}, {~{}} \\ \mu _2 = { \frac{B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}}+ \frac{1}{\Omega _{R_{n,m}E}} , {~{}} \\ O_2 = (\mu _2)^{-K} ( \Gamma (K)-\Gamma (K,\mu _2 E)),{~{}}\\ W_{3} = \frac{ E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t), {~{}} \\ W_{4} = \frac{ E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_2}}{{\Omega _{R_{n,m}U_{2}}}}}\right) F(t), {~{}} \\ J_2 =\sum _{l_{0}=1}^{N_0} \frac{\pi E \sqrt{1-t^2}}{2 N_o (\Omega _{R_{n,m}E})^K (K-1)!} \bigg [\frac{{E}{(t+1)}}{2}\bigg ]^{K-1}, \end{array}\right. } \end{aligned}$$

where \(\Gamma (x)\) is the Gamma function, and \(\Gamma (x,y)\) is the upper incomplete Gamma function [23].

Similar to that of the “SC-SC” case in the ORAS scheme w/ CSI, the total SOP of the “SC-MRC” case can be computed by (23). The detailed proof is omitted here to avoid redundancy.

By substituting (26) into (20) and (21), the closed-form expression of the SOP with MRC at the eavesdropper can be obtained accordingly. Thus, for the ORAS scheme w/ CSI, the SOP with MRC at the eavesdropper can be approximated as

$$\begin{aligned} P_{out,w/}^{SC-MRC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1-\Delta _{1,w/}^{SC-MRC} \right) +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1-\Delta _{3,w/}^{SC-MRC} \right) . \end{aligned}$$
(27)

3.2 The SOP derivation for ORAS w/o CSI

3.2.1 SC at the eavesdropper

In this scenario, the SOPs of the users \(U_1\) and \(U_2\) can be expressed as (28) and (29), respectively,

$$\begin{aligned} P_{U_{1},w/o}^{SC-SC}&= {\underbrace{\Pr \left( {{\left| {\Phi _{U_1,sub.}}\right| =(0,0)}}\right) }_{\Psi _{1,w/o}^{SC-SC}}}+\sum _{n=1}^{N} {\underbrace{\Pr \left( {{\left| {\Phi _{U_1,w/o}}\right| =(n,m)}}\right) }_{\Psi _{2,w/o}^{SC-SC}}} \nonumber \\&\quad\times {\underbrace{\Pr \left( {{\left. { {C_{_{sec,{U_{1}\leftarrow s_1}}} < {R_{1}^{s}}} }\right| \left| {\Phi _{U_1,w/o}}\right| = (n,m)} }\right) }_{\Psi _{3,w/o}^{SC-SC}}}, \end{aligned}$$
(28)

and

$$\begin{aligned} P_{U_{2},w/o}^{SC-SC}&= {\underbrace{\Pr \left( {{\left| {\Phi _{U_2,w/o}}\right| =(0,0)}}\right) }_{\Psi _{4,w/o}^{SC-SC}}}+\sum _{n_{+}=1}^{N} {\underbrace{\Pr \left( {{\left| {\Phi _{U_2,w/o}}\right| =(n_{+},m_{+})}}\right) }_{\Psi _{5,w/o}^{SC-SC}}}\nonumber \\&\quad\times {\underbrace{\Pr \left( {{\left. { {C_{_{sec,{U_{2} }}} < {R_{2}^{s}}} }\right| \left| {\Phi _{U_2,w/o}}\right| = (n_{+},m_{+})} }\right) }_{\Psi _{6,w/o}^{SC-SC}}}, \end{aligned}$$
(29)

To further derive the expressions of the above SOPs, Lemma 3 is developed in the following.

Lemma 3

The analytical expressions of \(\Psi _{1,w/o}^{SC-SC}\), \(\Psi _{2,w/o}^{SC-SC}\), \(\Psi _{3,w/o}^{SC-SC}\), \(\Psi _{4,w/o}^{SC-SC}\),\(\Psi _{5,w/o}^{SC-SC}\) and \(\Psi _{6,w/o}^{SC-SC}\) can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi _{1,w/o}^{SC-SC} = \prod _{m=1}^{M} \prod _{n=1}^{N} \left( 1-\Delta _{1,w/o}^{SC-SC} \right) , {~{}} \\ \Psi _{2,w/o}^{SC-SC} =\beta _1 \left( \Delta _{1,w/o}^{SC-SC} \right) ^{\zeta _1}\left( 1-\Delta _{1,w/o}^{SC-SC} \right) ^{MN-\zeta _1}, {~{}} \\ \Psi _{3,w/o}^{SC-SC} = 1-\Delta _{2,w/o}^{SC-SC} /\left( \Delta _{1,w/o}^{SC-SC} \right) ^{\zeta _1}, {~{}} \\ \Psi _{4,w/o}^{SC-SC} = \prod _{m=1}^{M} \prod _{n=1}^{N} \left( 1-\Delta _{3,w/o}^{SC-SC} \right) , {~{}} \\ \Psi _{5,w/o}^{SC-SC} =\beta _2 \left( \Delta _{3,w/o}^{SC-SC} \right) ^{\zeta _2}\left( 1-\Delta _{3,w/o}^{SC-SC} \right) ^{MN-\zeta _2}, {~{}} \\ \Psi _{6,w/o}^{SC-SC} = 1-\Delta _{4,w/o}^{SC-SC} /\left( \Delta _{3,w/o}^{SC-SC} \right) ^{\zeta _2}, \end{array}\right. } \end{aligned}$$
(30)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _{1,w/o}^{SC-SC} =Q_2 \exp \left( -\frac{ C_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{1}C_{1}}{\Omega _{R_{n,m}U_{1}}}\right) , {~{}} \\ \zeta _{1}=m_1+\ldots +m_n, \zeta _{2}=m_{+}^{1}+\ldots +m_{+}^{n_+}, {~{}} \\ \beta _{1}={\left( {\begin{array}{c}N\\ n\end{array}}\right) }\sum _{m_{1}=1}^{M}\ldots \sum _{m_{n}=1}^{M}{\left( {\begin{array}{c}M\\ m_1\end{array}}\right) }\ldots {\left( {\begin{array}{c}M\\ m_n\end{array}}\right) }, {~{}} \\ \Delta _{2,w/o}^{SC-SC} = Q_1Q_4 G_3 J_1 \exp (-W_5) ,{~{}} \\ \Delta _{3,w/o}^{SC-SC} =Q_{3} \exp \left( -\frac{ D_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{2}D_{1}}{\Omega _{R_{n,m}U_{2}}}\right) ,{~{}} \\ \beta _{2}={\left( {\begin{array}{c}N\\ n_+\end{array}}\right) }\sum _{m_{+}^{1}=1}^{M}\ldots \sum _{m_{+}^{n_+}=1}^{M}{\left( {\begin{array}{c}M\\ m_{+}^1\end{array}}\right) }\ldots {\left( {\begin{array}{c}M\\ m_{+}^{n_+}\end{array}}\right) }, {~{}} \\ \Delta _{4,w/o}^{SC-SC} = Q_1 Q_5 G_4 \mu _3^{-1} k/\Omega _{R_{n,m}E}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} Q_{4} = \sum _{j=0}^{\zeta _1} {\left( {\begin{array}{c}\zeta _1\\ j\end{array}}\right) }(-1)^{j} (Q_2)^{j}, {~{}} \\ Q_{5} = \sum _{j=0}^{\zeta _2} {\left( {\begin{array}{c}\zeta _2\\ j\end{array}}\right) }(-1)^{j} (Q_3)^{j}, {~{}} \\ \mu _3 =(\frac{jB_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{j l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}+ \frac{k}{\Omega _{R_{n,m}E}}), {~{}} \\ G_3 = \exp \left( -\frac{ C_{1}(\zeta _1-j)}{\Omega _{SR_{n,m}}}-\frac{ l_1 C_{1}(\zeta _1-j)}{\Omega _{R_{n,m}U_{1}}}\right) , {~{}} \\ C_1 = \frac{2^{2R_{1}^{th}}-1}{\rho \left( 1-(1-\alpha ) 2^{2R_{1}^{th}}\right) }, D_1 = \frac{2^{2R_{2}^{th}}-1}{(1-\alpha ) \rho },{~{}} \\ W_{5} = \frac{k E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{j}}{{\Omega _{SR_{n,m}}}}+ \frac{{j l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t), {~{}} \\ G_4 =\exp \left( -\frac{ D_{1}(\zeta _2-ii)+jA_1}{\Omega _{SR_{n,m}}}-\frac{l_{2}D_{1}(\zeta _2-j)+j l_2 A_1}{\Omega _{R_{n,m}U_{2}}}\right) . \end{array}\right. } \end{aligned}$$

Proof

The proof of Lemma 3 is shown in Appendix 2.

By substituting (30) into (28) and (29), the closed-form expression of the SOP can be obtained by

$$\begin{aligned} P_{out,w/o}^{SC-SC} =\frac{1}{2} \bigg (1- Q_1 Q_6 G_5 J_1\exp (-W_6)\bigg )+\frac{1}{2} \left( 1- Q_1 Q_7 G_6 \mu _4^{-1} k/\Omega _{R_{n,m}E}\right) , \end{aligned}$$
(31)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} Q_{6} = \sum _{i_{o}=0}^{MN} {\left( {\begin{array}{c}MN\\ i_o\end{array}}\right) }(-1)^{i_o} (Q_2)^{i_o}, {~{}} \\ Q_{7} = \sum _{i_{oo}=0}^{MN} {\left( {\begin{array}{c}MN\\ i_{oo}\end{array}}\right) }(-1)^{i_{oo}} (Q_3)^{i_{oo}}, {~{}} \\ \mu _4 =(\frac{i_{oo}B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{i_{oo} l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}+ \frac{k}{\Omega _{R_{n,m}E}}), {~{}} \\ G_5 = \exp \left( -\frac{ C_{1}(MN-i_{o})}{\Omega _{SR_{n,m}}}-\frac{ l_1 C_{1}(MN-i_{o})}{\Omega _{R_{n,m}U_{1}}}\right) , {~{}} \\ W_{6} = \frac{k E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{i_{o}}}{{\Omega _{SR_{n,m}}}}+ \frac{{i_{o} l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t), {~{}} \\ G_6 =\exp \left( -\frac{ D_{1}(MN-i_{oo})+i_{oo}A_1}{\Omega _{SR_{n,m}}}-\frac{l_{2}D_{1}(MN-i_{oo})+i_{oo} l_2 A_1}{\Omega _{R_{n,m}U_{2}}}\right) . \end{array}\right. } \end{aligned}$$

3.2.2 MRC at the eavesdropper

In this case, the SOPs of \(U_1\), \(U_2\) have the similar forms with (28) and (29). Following Lemma 3, Lemma 4 is given as follows.

Lemma 4

The analytical expressions of \(\Psi _{1,w/o}^{SC-MRC}\), \(\Psi _{2,w/o}^{SC-MRC}\), \(\Psi _{3,w/o}^{SC-MRC}\), \(\Psi _{4,w/o}^{SC-MRC}\),\(\Psi _{5,w/o}^{SC-MRC}\) and \(\Psi _{6,w/o}^{SC-MRC}\) can be expressed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \Psi _{1,w/o}^{SC-MRC} = \Psi _{1,w/o}^{SC-SC}, {~{}} \\ \Psi _{2,w/o}^{SC-MRC} =\Psi _{2,w/o}^{SC-SC}, {~{}} \\ \Psi _{3,w/o}^{SC-MRC} = 1-\Delta _{2,w/o}^{SC-MRC} /\left( \Delta _{1,w/o}^{SC-SC} \right) ^{\zeta _1}, {~{}} \\ \Psi _{4,w/o}^{SC-MRC} = \Psi _{4,w/o}^{SC-SC}, {~{}} \\ \Psi _{5,w/o}^{SC-MRC} =\Psi _{5,w/o}^{SC-SC}, {~{}} \\ \Psi _{6,w/o}^{SC-MRC} = 1-\Delta _{4,w/o}^{SC-MRC} /\left( \Delta _{3,w/o}^{SC-SC} \right) ^{\zeta _2}, \end{array}\right. } \end{aligned}$$
(32)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _{2,w/o}^{SC-MRC} = Q_4 G_3 J_2 \exp (-W_7),{~{}} \\ \Delta _{4,w/o}^{SC-MRC} = Q_5 G_7 (\mu _5)^{-K} \Gamma (K), \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _5 = { \frac{j B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{j l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}}+ \frac{1}{\Omega _{R_{n,m}E}} , {~{}} \\ G_7 = \frac{\exp \left( -\frac{ (\zeta _2-j) A_{1}}{\Omega _{SR_{n,m}}}-\frac{(\zeta _2-j) l_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}\right) }{(\Omega _{R_{n,m}E})^K (K-1)!} , {~{}} \\ W_7 = \frac{ E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{j}}{{\Omega _{SR_{n,m}}}}+ \frac{{j l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t). \end{array}\right. } \end{aligned}$$

The derivation is similar to that for the “SC-SC” case in the ORAS scheme w/o CSI. The detailed proof is omitted here to avoid redundancy.

By substituting (32) into (28) and (29), the closed-form of the SOP can be expressed as

$$\begin{aligned} P_{out,w/o}^{SC-MRC} =\frac{1}{2} \bigg (1- Q_6 G_5 J_2\exp (-W_8)\bigg )+\frac{1}{2} \left( 1- Q_7 G_{6} O_3\right) , \end{aligned}$$
(33)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _6 =(\frac{i_{oo}B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{i_{oo} l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}+ \frac{1}{\Omega _{R_{n,m}E}}), {~{}} \\ W_{8} = \frac{ E (t+1)}{2\Omega _{R_{n,m}E}}+\left( { \frac{{i_{o}}}{{\Omega _{SR_{n,m}}}}+ \frac{{i_{o} l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t), {~{}} \\ O_3 =(\mu _6)^{-K} \Gamma (K)\bigg {/}\bigg ((\Omega _{R_{n,m}E})^K (K-1)!\bigg ). \end{array}\right. } \end{aligned}$$

4 Asymptotic secrecy outage performance analysis for ORAS

The closed-form expressions of the SOPs have been derived for four cases in the last section. However, the expressions are quite complicated. In order to get more useful insights on the derived results, we derive a closed-form expression for the asymptotic SOP in the high transmit power region, where \(P_{S}=P_{R}\rightarrow \infty\). The asymptotic SOPs are presented in the following four subsections.

4.1 SC at the eavesdropper for ORAS w/ CSI

When \(P_S=P_R=\rightarrow \infty\), one can easily obtain \(\gamma _{U_{i}\leftarrow s_1}\approx \frac{\alpha }{1-\alpha }\). Recalling (24), the asymptotic SOP of the “SC-SC” case in the ORAS scheme w/ CSI is derived as

$$\begin{aligned} P_{out,w/,\infty }^{SC-SC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1-Q_1 Q_2 G_{8} \mu _7^{-1} \right) +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1-Q_1 Q_3 G_{1} \mu _1^{-1} \right) , \end{aligned}$$
(34)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} A_2=\frac{A_o}{C_o},B_2=\frac{B_o}{C_o}, {~{}} \\ \mu _7 = { \frac{B_{2}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{1}B_{2}}{{\Omega _{R_{n,m}U_{1}}}}}+ \frac{k}{\Omega _{R_{n,m},E}} , {~{}} \\ G_8 = \frac{k}{\Omega _{R_{n,m}E}}\exp \left( -\frac{ A_{2}}{\Omega _{SR_{n,m}}}-\frac{l_{1}A_{2}}{\Omega _{R_{n,m}U_{1}}}\right) . \end{array}\right. } \end{aligned}$$

Remark 1

A factor of \(\frac{1}{2}\) is used to determine the rate requirement and the eavesdroppers’ channel capacity for the RAS-NOMA schemes. Although, the capacity of the \(S-R_i-U_1\) links in the RAS-NOMA scheme is limited by the ratio of the power allocation coefficients (i.e.,\(\alpha /(1-\alpha )\) ), the eavesdroppers’ channel capacity is not interference-limited. Therefore, when the transmit power at the source is in the low and medium regimes, the capacity of the \(S-R_i-U_1\) links in the RAS-NOMA schemes is larger than that in the RAS-OMA schemes. This indicates that the RAS-NOMA schemes outperform the RAS-OMA schemes when the transmit power is in the low and medium regimes. In addition, when the transmit power is in the high regime, by optimizing the power allocation coefficient, the capacity of the \(S-R_i-U_1\) links in the RAS-NOMA schemes is also larger than that in the RAS-OMA schemes.

4.2 MRC at the eavesdropper for ORAS w/ CSI

Referring to the asymptotic expression of the “SC-SC” case in the ORAS scheme w/ CSI, the asymptotic SOP of (27) is expressed as

$$\begin{aligned}&P_{out,w/,\infty }^{SC-MRC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1- Q_2 G_{9} \mu _8^{-K} \Gamma (K) \right) \nonumber \\&\quad\quad\quad\quad +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1- Q_3 G_{2} \mu _2^{-K} \Gamma (K) \right) , \end{aligned}$$
(35)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} G_9 = \frac{\exp \left( -\frac{ A_{2}}{\Omega _{SR_{n,m}}}-\frac{l_{1}A_{2}}{\Omega _{R_{n,m}U_{1}}}\right) }{(\Omega _{R_{n,m}E})^K (K-1)!} , {~{}} \\ \mu _8 = { \frac{B_{2}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{1}B_{2}}{{\Omega _{R_{n,m}U_{1}}}}}+ \frac{1}{\Omega _{R_{n,m}E}}. \end{array}\right. } \end{aligned}$$

The derivation is similar to that of the “SC-MRC” case in the ORAS scheme w/ CSI. The detailed proof is omitted here to avoid redundancy.

Remark 2

Focusing on the \(S-R_i-U_2\) links in the second phase, our proposed schemes always achieve a larger capacity than the RAS-OMA schemes. This is due to the fact that the capacity of the \(S-R_i-U_2\) links for the RAS-NOMA schemes is not interference-limited. Due to the use of SIC, a half loss in the capacity of the \(S-R_i-U_2\) links exists for the RAS-OMA schemes. This indicates that the advantage of the RAS-NOMA schemes over the RAS-OMA schemes increases as \(R_{2}^{th}\) increases.

Remark 3

From (34) and (35), it is known that the asymptotic SOPs of the “SC-SC” and the “SC-MRC” cases in the ORAS scheme w/ CSI are constant values. Moreover, the asymptotic SOP of the former case is less than that of the latter.

4.3 SC at the eavesdropper for ORAS w/o CSI

Recalling (31), the asymptotic SOP of the “SC-SC” case in the ORAS scheme w/o CSI is expressed as

$$\begin{aligned} P_{out,w/o,\infty }^{SC-SC} =\frac{1}{2} \left( 1- Q_1 Q_4 G_{10} \mu _9^{-1} \right) +\frac{1}{2} \left( 1-Q_1 Q_5 G_{11} \mu _3^{-1} \right) , \end{aligned}$$
(36)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \mu _9 = { \frac{B_{2}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{1}B_{2}}{{\Omega _{R_{n,m}U_{1}}}}}+ \frac{k}{\Omega _{R_{n,m}E}}, {~{}} \\ G_{10} =\frac{k}{\Omega _{R_{n,m}E} } \exp \left( -\frac{ jA_{2}}{\Omega _{SR_{n,m}}}-\frac{jl_{1}A_{2}}{\Omega _{R_{n,m}U_{1}}}\right) , {~{}} \\ G_{11} =\frac{k}{\Omega _{R_{n,m}E} } \exp \left( -\frac{j A_{1}}{\Omega _{SR_{n,m}}}-\frac{jl_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}\right) . \end{array}\right. } \end{aligned}$$

The derivation is similar to the proof of Lemma 3. The detailed proof is omitted here to avoid redundancy.

4.4 MRC at the eavesdropper for ORAS w/o CSI

Referring to (33), we can obtain the asymptotic SOP of the “SC-MRC” case in the ORAS scheme w/o CSI, which can be expressed as

$$\begin{aligned} P_{out,w/o,\infty }^{SC-MRC} =\frac{1}{2} \left( 1- Q_4 G_{12} \mu _{10}^{-K} \Gamma (K) \right) +\frac{1}{2} \left( 1- Q_5 G_{13} \mu _4^{-K} \Gamma (K) \right) , \end{aligned}$$
(37)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} G_{12} =\frac{\exp \left( -\frac{ jA_{2}}{\Omega _{SR_{n,m}}}-\frac{jl_{1}A_{2}}{\Omega _{R_{n,m}U_{1}}}\right) }{(\Omega _{R_{n,m}E})^K (K-1)!} , {~{}} \\ G_{13} =\frac{\exp \left( -\frac{ jA_{1}}{\Omega _{SR_{n,m}}}-\frac{jl_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}\right) }{(\Omega _{R_{n,m}E})^K (K-1)!},{~{}} \\ \mu _{10} = { \frac{jB_{2}}{{\Omega _{SR_{n,m}}}}+ \frac{jl_{1}B_{2}}{{\Omega _{R_{n,m}U_{1}}}}}+ \frac{1}{\Omega _{R_{n,m}E}}. \end{array}\right. } \end{aligned}$$

The derivation is similar to that for the “SC-MRC” case in the ORAS scheme w/o CSI. The detailed proof is omitted here to avoid redundancy.

Remark 4

Referring to Remark 1 and Remark 2, we can get the asymptotic secrecy outage probability of the RAS-NOMA schemes is prior to that of the RAS-OMA schemes. Moreover, from (36) and (37), it can be obtained that the asymptotic SOPs of the “SC-SC” and the “SC-MRC” cases in the ORAS scheme w/o CSI are constant values. Besides, the constant value of the former is less than that of the latter. In addition, the asymptotic SOP of the “SC-SC” case in the ORAS scheme w/ CSI is less than that of the “SC-MRC” case in the ORAS scheme w/o CSI.

Remark 5

The complexity of equation (34) is O(MN), since equation (34) is M times N. In the same way, the complexity of equations (35), (36) and (37) can be obtained as O(MN). The detailed proof is omitted here to avoid redundancy.

5 Secrecy diversity order in ORAS

Although the SOP expressions shown in (24) ,(27), (31), and (33) can be used to evaluate the secrecy performance of the proposed relay–antenna selection schemes, they fail to provide intuitive insights. To gain more deep insights, we further analyze the secrecy diversity order of the proposed schemes. As indicated by [24,25,26], the secrecy diversity order is achieved when both the transmit power and main-to-eavesdropper ratio (MER) are sufficiently high, i.e., \(P_S=P_R \rightarrow \infty\) and \(MER=\frac{\Omega _{main}}{\Omega _{RE}}\rightarrow \infty\), where \(\Omega _{main}\) is related to the average channel gain of the main links, \(\Omega _{RE}\) is related to the average channel gain of the eavesdropping link. Specifically, we rewrite \(\Omega _{RU_{1}}=MER \cdot \Omega _{RE}\) , \(\Omega _{SR}=\lambda _{1} MER \cdot \Omega _{RE}\) and \(\Omega _{RU_{2}}=\lambda _{2} MER \cdot \Omega _{RE}\), where \(\lambda _{1}\) and \(\lambda _{2}\) are positive constants. Hence, the secrecy diversity order is defined as

$$\begin{aligned} d_{u}=-\mathop {\mathrm{lim}}_{{MER}\rightarrow \infty } \frac{log{P_{out}^{\infty }}}{log_{MER}} , \end{aligned}$$
(38)

where \({{u}\in (U_{1},U_{2}) }\) and \(P_{out}^{\infty }\) denotes the asymptotic SOP.

5.1 SC at the eavesdropper for ORAS w/ CSI

Recalling (34), we rewrite the asymptotic SOP in this case as

$$\begin{aligned} P_{out,w/,\infty }^{SC-SC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1-Q_1 Q_2 T_1\right) +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1-Q_1 Q_3 T_2\right) , \end{aligned}$$
(39)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} T_1=\exp \bigg (\frac{-\eta _1}{MER}\bigg )\frac{MER}{MER+\nu _1},{~{}} \\ T_2=\exp \bigg (\frac{-\eta _2}{MER}\bigg )\frac{MER}{MER+\nu _2}, {~{}} \\ \nu _{1}=\frac{B_2}{k\lambda _{1}}+\frac{l_{1}B_2}{k}, \nu _{2}=\frac{B_1}{k\lambda _{1}}+\frac{l_{2}B_1}{k\lambda _{2}},{~{}} \\ \eta _{1}=\frac{A_2}{\lambda _{1}\Omega _{RE}}+\frac{l_{1}A_2}{\Omega _{RE}}, \eta _{2}=\frac{A_1}{\lambda _{1}\Omega _{RE}}+\frac{l_{2}A_1}{\lambda _{2}\Omega _{RE}}. \end{array}\right. } \end{aligned}$$

By substituting (39) into (38) and using \(e^{-x}=1-x\) for small x, when \(MER\rightarrow \infty\), we obtain the secrecy diversity order of the ORAS scheme w/ CSI, which is given by

$$\begin{aligned} d_{w/}^{SC-SC}= MN\min (L_1,L_2). \end{aligned}$$
(40)

The derivation is similar to the asymptotic analysis of the “SC-SC” in the ORAS scheme w/ CSI. The detailed proof is omitted here to avoid redundancy.

5.2 MRC at the eavesdropper for ORAS w/ CSI

Recalling (35), the asymptotic SOP, \(P_{out,w/,\infty }^{SC-MRC}\), is reexpressed as

$$\begin{aligned} P_{out,w/,\infty }^{SC-MRC} =\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M} \left( 1- Q_2 T_3\right) +\frac{1}{2} \prod _{n=1}^{N}\prod _{m=1}^{M}\left( 1- Q_3 T_4 \right) , \end{aligned}$$
(41)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} T_3=\exp \bigg (\frac{-\eta _1}{MER}\bigg )\frac{MER}{MER+\nu _3}, {~{}} \\ T_4=\exp \bigg (\frac{-\eta _2}{MER}\bigg )\frac{MER}{MER+\nu _4}, {~{}} \\ \nu _{3}=\frac{B_2}{\lambda _{1}}+l_{1}B_2, \nu _{2}=\frac{B_1}{\lambda _{1}}+l_{2}B_1. \end{array}\right. } \end{aligned}$$

By substituting (41) into (38), the secrecy diversity order for “SC-MRC” in the ORAS scheme w/ CSI can be written as

$$\begin{aligned} d_{w/}^{SC-MRC}= MN\min (L_1,L_2). \end{aligned}$$
(42)

The derivation is similar to the asymptotic analysis in the ORAS scheme w/ CSI. The detailed proof is omitted here to avoid redundancy.

5.3 SC at the eavesdropper for ORAS w/o CSI

Recalling (36), the aspmptotic SOP, \(P_{out,w/o,\infty }^{SC-SC}\), can be rewrriten as

$$\begin{aligned} P_{out,w/o,\infty }^{SC-SC} =&\frac{1}{2} \left( 1- Q_1 Q_{14} \exp \bigg (\frac{-\eta _3}{MER}\bigg )\frac{MER}{MER+\nu _5}\right) \nonumber \\&+\frac{1}{2} \left( 1- Q_1 Q_{15}\exp \bigg (\frac{-\eta _4}{MER}\bigg )\frac{MER}{MER+\nu _6}\right) , \end{aligned}$$
(43)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} Q_{14}=Q_4/Q_{2}^{j}, Q_{15}=Q_5/Q_{3}^{j},{~{}} \\ \nu _{5}=\frac{jB_2}{k\lambda _{1}}+\frac{jl_{1}B_2}{k}, \nu _{6}=\frac{jB_1}{k\lambda _{1}}+\frac{jl_{2}B_1}{k\lambda _{2}}, {~{}} \\ \eta _{3}=\frac{jA_2}{\lambda _{1}\Omega _{RE}}+\frac{jl_{1}A_2}{\Omega _{RE}}, \eta _{4}=\frac{jA_1}{\lambda _{1}\Omega _{RE}}+\frac{jl_{2}A_1}{\lambda _{2}\Omega _{RE}}. \end{array}\right. } \end{aligned}$$

By substituting (43) into (38), the secrecy diversity order for this scenario can be obtained as

$$\begin{aligned} d_{w/o}^{SC-SC}= MN\min (L_1,L_2). \end{aligned}$$
(44)

The derivation is similar to the asymptotic analysis of the “SC-SC” case in the ORAS scheme w/o CSI. The detailed proof is omitted here to avoid redundancy.

5.4 MRC at the eavesdropper for ORAS w/o CSI

Similar to SC at the eavesdropper for SRAS, by using (37), we rewrite the asymptotic SOP for this scenario as

$$\begin{aligned} P_{out,w/o,\infty }^{SC-MRC} =&\frac{1}{2} \left( 1- Q_6 \exp \bigg (\frac{-\eta _3}{MER}\bigg )\frac{MER}{MER+\nu _7}\right) \nonumber \\&+\frac{1}{2} \left( 1- Q_7 \exp \bigg (\frac{-\eta _4}{MER}\bigg )\frac{MER}{MER+\nu _8}\right) , \end{aligned}$$
(45)

where \(\nu _{7}=\frac{jB_2}{\lambda _{1}}+jl_{1}B_2, \nu _{8}=\frac{jB_1}{\lambda _{1}}+jl_{2}B_1\).

By substituting (45) into (38), one can easily obtain the secrecy diversity order for this scheme as

$$\begin{aligned} d_{w/o}^{SC-MRC}= MN\min (L_1,L_2). \end{aligned}$$
(46)

The derivation is similar to the asymptotic analysis for “SC-MRC” in the ORAS scheme w/o CSI. The detailed proof is omitted here to avoid redundancy.

Remark 6

From (40), (42), (44), and (46), we can get that the secrecy diversity order of “SC-SC/MRC” for the proposed ORAS schemes is equal to \(MN\min (L_1,L_2)\). It indicates that the secrecy diversity order can be improved by increasing the number of the relays or the antennas per legitimate node (relays, a pair of NOMA users).

6 Results and discussion

In this section, simulation results are presented to validate the theoretical expressions. The simulation parameters used in this section are presented in Table 1. All the noise powers are set to \(\sigma _{0}^{2}\), and the transmit power of the source is equal to that of each relay. The simulation results are averaged over \(10^6\) channel realizations. In the ORAS scheme w/ CSI, the power allocation coefficient \(\alpha\) is computed by minimizing (24) for SC at the eavesdropper and by minimizing (27) for MRC at the eavesdropper with \(M = 1\) and \(N = 1\); in the ORAS scheme w/o CSI, the power allocation coefficients \(\alpha\) is obtained by minimizing (31) for SC at the eavesdropper and by minimizing (33) for MRC at the eavesdropper with \(M = 1\) and \(N = 1\).

Table 1 Simulation Parameters
Full size table
Fig. 2
figure 2

The theoretical results and simulation results of SOP versus transmit power. The SOP of the four cases for NOMA VS OMA

Full size image

Figure 2 demonstrates the SOP of relay–antenna selection schemes for cooperative NOMA and conventional OMA systems with SC and MRC at the eavesdropper, respectively. In this figure, it is observed that the analytical results of the SOPs agree with the simulations. It is also shown that the cooperative NOMA system achieves a lower SOP than the OMA system. This is due to the fact that the achievable capacity of cooperative NOMA is larger than that of OMA system. As expected, the secrecy performance of the “SC-SC” case is better than that of the “SC-MRC” case, as discussed in Remark 1 and Remark 2. It is because the wiretapping signals can be enhanced by the joint detection for the MRC scheme at the eavesdropper.

Fig. 3
figure 3

The theoretical results and simulation results of SOP versus transmit power. The SOP of the four cases for NOMA VS [20]

Full size image

Figure 3 demonstrates the SOP of relay–antenna selection schemes for cooperative NOMA and [20] with SC and MRC at the eavesdropper, respectively. It is also shown that the cooperative NOMA system achieves a lower SOP than [20]. This is due to the fact that the achievable capacity of cooperative NOMA is larger than that of [20]. The power allocation coefficient is optimized to increase the safety rate and obtain a beneficial secrecy outage probability.

Fig. 4
figure 4

The theoretical results and simulation results of SOP versus transmit power. (a) The channel estimation error is 0.1; (b) The channel estimation is zero, i.e., perfect CSI. The SOP of the proposed schemes VS [28]

Full size image

Besides, the average SOP of the statistical CSI method in the work [28] and proposed methods are also plotted. Figure 4 depicts the average SOP of cooperative NOMA networks versus under the scenario of imperfect and perfect CSI, where \(M=L_1=L_2=K=1\). As seen from the figures, the proposed scheme outperforms the statistical CSI (imperfect CSI) method when the channel estimated error is not small. Clearly, when the channel estimated error is large of the proposed scheme, the achievable secrecy capacity is reduced. Moreover, it is also observed that the two schemes have nearly the same average SOP when the channel estimation error is close to zero.

Fig. 5
figure 5

SOP versus the rate requirement of each user. (a) The rate requirement of cell-edge user; (b) The rate requirement of cell-center user. When the transmission power is constant, the influence of different information transmission rates is on the SOP

Full size image

Figure 5 illustrates the SOP of cooperative NOMA system versus different secrecy rate requirements. From this figure, it can be observed that the SOP of the proposed relay–antenna selection scheme becomes degraded as the secrecy rate increases for both the ORAS scheme w/o and the w/o CSI in cooperative NOMA system. That is because the successful transmission occurs at the case with more stringent channel condition when the requirement of secrecy rate increases. Moreover, the variance of the security rate requirement of the cell-edge user has a greater impact on the SOP than that of the cell-center user. This is due to the fact that a lower security rate requirement of the cell-edge user leads to a higher successful probability of decoding \(s_1\) for the proposed relay–antenna selection schemes.

Fig. 6
figure 6

SOP for the different number of relays. When the transmission power is constant, the influence of different number of relays is on the SOP

Full size image

Figure 6 illustrates the SOP of cooperative NOMA network versus the number of relays. It can be seen in this figure that the SOPs of both the SC and the MRC scenarios at the eavesdropper decrease with the number of relays because the secrecy capacity of cooperative NOMA system is enhanced by transmit diversity gain. Moreover, the ORAS scheme w/ CSI achieves a better secrecy performance than the ORAS scheme w/o CSI. The reason is that the ORAS scheme w/ CSI takes advantage of the CSI of the eavesdropper link over the ORAS scheme w/o CSI. In addition, when the number of relays is large, the decline rate of the SOP becomes slow for the ORAS scheme w/o CSI.

Fig. 7
figure 7

The effects of the eavesdropper on SOP. (a) The different number of antenna on eavesdropper; (b) The different eavesdropping distance. When the transmission power is constant, the impact of the number of antennas and eavsdropping distances is on the SOP

Full size image

Figure 7(a) examines the SOP of cooperative NOMA system versus the number of antennas at the eavesdropper. The SOP increases with the increasing number of antennas for both ORAS scheme w/ and w/o CSI in cooperative NOMA systems. It is because the capacity of the wiretap link is increased, and thus the secrecy outage probability is increased as a consequence. Moreover, when the number of antennas at the eavesdropper is one, both the SC and the MRC methods at the eavesdropper have the same secrecy outage performance. Figure 7(b) demonstrates the SOP of cooperative NOMA network versus different eavesdropping distances. It is shown that the SOPs of both w/ and w/o CSI schemes are decreased when the distance between the relays and the eavesdropper increases. It is obvious that the capacity of the wiretap link is decreased when the propagation distance is increased. It is observed that the closer is the distance between the eavesdropper and the legitimate user, the greater is the system security outage probability. The reason is that as the distance from the legitimate user to the eavesdropper decreases, the capacities achieved by the legitimate user and the eavesdropper are nearly the same.

Fig. 8
figure 8

SOP versus secrecy diversity order. When the transmission power is constant, the impact of the MER is on the SOP

Full size image

Figure 8 shows the secrecy outage probability of the proposed scheme versus MER. As seen from this figure, both the ORAS scheme w/ CSI and w/o CSI scheme have a better secrecy performance than the random relay–antenna selection (RRAS) scheme. Interestingly, the secrecy diversity order of the ORAS scheme w/ CSI remains the same as that of the ORAS scheme w/o CSI, when MER is in the medium to high regime, which is consistent with our discussion in Remark 4. Moreover, the secrecy diversity order of the RRAS scheme is one, that is to say, the performance of the RRAS is equivalent to that of single-relay single-antenna scheme.

7 Conclusion

In this paper, we proposed two relay–antenna selection schemes to enhance PLS in cooperative NOMA systems, in which a single source transmitted data to two legitimate users with the aid of multiple relays in the presence of an eavesdropper, where the relays, the users and the eavesdropper were equipped with multiple antennas. The SOP was derived in closed-form for four cooperative NOMA scenarios. A close agreement was observed between the analytical results and simulation results, and the proposed NOMA scheme outperformed the conventional OMA scheme in terms of SOP. In addition, the proposed ORAS schemes had a better secrecy performance than the RRAS scheme. Infuture, we will investigate the secrecy performance of a more complicated scenario with multiple relays and multiple eavesdroppers, in which each of them is equipped with multiple antennas.

8 Appendix

8.1 Appendix

Based on (20), the SOP of the cell-edge user for a given relay can be written by

$$\begin{aligned} \Psi _{1,w/}^{SC-SC}=&\Pr \left( \mathop {\mathrm{argmax}}_{{m}\in (1,2,\cdots ,M) } {C_{sec,U_1}^{n,m}}<R_{1}^{s}\right) \nonumber \\ =&\Pr \left\{ \frac{1+ {\gamma _{U_1 \leftarrow s_1}^{n,m_{n,*}^{w/}}} }{1+{\gamma _{E \leftarrow s_1}^{n,m_{n,*}^{w/}}}}<2^{2R_{1}^{s}} \right\} . \end{aligned}$$
(47)

According to \(\frac{ab}{a+b+1}\approx \min \left( a,b \right)\), \(\gamma _{U_1 \leftarrow s_1}^{m_{n,*}^{w/}}\) and \(\gamma _{E \leftarrow s_1}^{m_{n,*}^{w/}}\) can be further expressed as

$$\begin{aligned} {\gamma _{U_1 \leftarrow s_1}^{n,m_{n,*}^{w/}}} \approx \frac{\alpha \rho \min \left( X ,Y_{1}^{*} \right) }{ (1-\alpha )\rho \min \left( X ,Y_{1}^{*} \right) +1 } =\frac{\alpha \omega _1 }{(1-\alpha )\omega _1+1}, \end{aligned}$$
(48)
$$\begin{aligned} {\gamma _{U_1 \leftarrow s_1}^{n,m_{n,*}^{w/}}} \approx \frac{\alpha \rho \min \left( X ,Y_{1}^{*} \right) }{ (1-\alpha )\rho \min \left( X ,Y_{1}^{*} \right) +1 } =\frac{\alpha \omega _1 }{(1-\alpha )\omega _1+1}, \end{aligned}$$
(49)

where \(Y_{1}^{*}= \left| h_{R_{n,m^{*}}U_1} \right| ^{2}\), \(Z^{*}= \left| h_{R_{n,m^{*}}E} \right| ^{2}\). Furthermore, \(\omega _1=\rho \min \left( X, Y_{1}^{*} \right)\), \(\omega _2=\rho \min \left( X, Z^{*} \right)\). Then, \(\Psi _{1,w/}^{SC-SC}\) in (20) can be written as

$$\begin{aligned} \Psi _{1,w/}^{SC-SC}=&\Pr \bigg [ \frac{(\omega _1+1)(\alpha \omega _2+1)}{(\omega _2+1)(\alpha \omega _1+1)}<2^{2R_{1}^{s}} \bigg ] \nonumber \\ \overset{(a)}{=}&\prod \limits _{m{\mathrm {=1}}}^{M} \bigg [ \min (X,Y_1)<\frac{A_0+B_0Z}{C_0-D_0Z}\bigg ]\nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M} \bigg [ 1- \int _{0}^{E}f_{Z}(z)\int _{\frac{A_0+B_0Z}{C_0-D_0Z}}^{+\infty }f_{X}(x)\nonumber \\&\times \int _{\frac{A_0+B_0Z}{C_0-D_0Z}}^{+\infty }f_{Y_1}(y_1)d{y_1}d{x}d{z}\bigg ]\nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M} \bigg [ 1-\Delta _{1,w/}^{SC-SC} \bigg ], \end{aligned}$$
(50)

where equation (a) holds by following \(X \ge Z\) [20, 27].

It is challenging to derive the exact closed-form of the integral in (50). By using the Gaussian-Chebyshev quadrature [23], the approximate expression of (50) can be given by \(\Delta _{1,w/}^{SC-SC}\), which can be written as

$$\begin{aligned} \Delta _{1,w/}^{SC-SC}=&\sum _{k=1}^{K}\sum _{l_1=1}^{L_1}{\left( {\begin{array}{c}K\\ k\end{array}}\right) }{\left( {\begin{array}{c}L_1\\ l_1\end{array}}\right) }(-1)^{k+l_1}\sum _{l_{0}=1}^{N_0}\frac{k\pi E\sqrt{1-t^2}}{2 N_o \Omega _{R_{n,m}E}} \nonumber \\&\times \exp {\bigg [ -\frac{k E (t +1)}{2\Omega _{R_{n,m}E}}-\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t) \bigg ]}. \end{aligned}$$
(51)

Then, we can derive the SOP for the cell-center user. The expression of \(\Psi _{2,w/}^{SC-SC}\) can be expressed as

$$\begin{aligned} \Psi _{2,w/}^{SC-SC}=&\Pr \bigg [ \frac{(\omega _3+1)(\alpha \omega _2+1)}{(\omega _2+1)(\alpha \omega _3+1)}<2^{2R_{1}^{s}} \bigg ]\nonumber \\ \overset{(a)}{=}&\prod \limits _{m{\mathrm {=1}}}^{M} \bigg [ \min (X,Y_2)<\frac{A_0+B_0Z}{C_0-D_0Z}\bigg ]\nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M} \bigg [ 1-\Delta _{2,w/}^{SC-SC} \bigg ], \end{aligned}$$
(52)

where \(Y_{2}^{*}= \left| h_{R_{n,m^{*}}U_2} \right| ^{2}\), \(\omega _3=\rho \min \left( X, Y_{2}^{*} \right)\), the approximate expression of (53) can be given by \(\Delta _{2,w/}^{SC-SC}\), which can be expressed as

$$\begin{aligned} \Delta _{2,w/}^{SC-SC}=&\sum _{k=1}^{K}\sum _{l_2=1}^{L_2}{\left( {\begin{array}{c}K\\ k\end{array}}\right) }{\left( {\begin{array}{c}L_2\\ l_2\end{array}}\right) }(-1)^{k+l_2}\sum _{l_{0}=1}^{N_0}\frac{k\pi E\sqrt{1-t^2}}{2 N_o \Omega _{R_{n,m}E}} \nonumber \\&\times \exp {\bigg [ -\frac{k E(t +1)}{2\Omega _{R_{n,m}E}}-\left( { \frac{{1}}{{\Omega _{SR_{n,m}}}}+ \frac{{l_2}}{{\Omega _{R_{n,m}U_{2}}}}}\right) F(t) \bigg ]}. \end{aligned}$$
(53)

Next, the expression of \(\Psi _{3,w/}^{SC-SC}\) can be calculated as

$$\begin{aligned} \Psi _{3,w/}^{SC-SC}= \Pr \left( {{{\left| {\Phi _{U_{2},w/}}\right| =m}}}\right) =\left( {\begin{array}{c}M\\ m\end{array}}\right) (\Delta _{2,w/}^{SC-SC})^{m}(1-\Delta _{2,w/}^{SC-SC})^{M-m}. \end{aligned}$$
(54)

Besides, \(\Psi _{4,w/}^{SC-SC}\) can be calculated as

$$\begin{aligned} \Psi _{4,w/}^{SC-SC} =&\Pr \left( {{\left. { {C_{_{sec,{U_{2}}}}^{n,m} < {R_{2}^{s}}} }\right| \left| {\Phi _{U_2,w/}}\right| = m} }\right) \nonumber \\ =&( 1-\Delta _{3,w/}^{SC-SC}/\Delta _{2,w/}^{SC-SC})^{m} , \end{aligned}$$
(55)

where \(\Delta _{3,w/}^{SC-SC}\) can be expressed as

$$\begin{aligned} \Delta _{3,w/}^{SC-SC}=&\sum _{k=1}^{K}\sum _{l_2=1}^{L_2}{\left( {\begin{array}{c}K\\ k\end{array}}\right) }{\left( {\begin{array}{c}L_2\\ l_2\end{array}}\right) }(-1)^{k+l_2}\nonumber \\&\times \frac{k\exp {\bigg [ -\frac{ A_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{2}A_{1}}{\Omega _{R_{n,m}U_{2}}}-(\frac{B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}+ \frac{k}{\Omega _{R_{n,m}E}})E \bigg ]}}{\Omega _{R_{n,m}E}(\frac{B_{1}}{{\Omega _{SR_{n,m}}}}+ \frac{l_{2}B_{1}}{{\Omega _{R_{n,m}U_{2}}}}+ \frac{k}{\Omega _{R_{n,m}E}})} . \end{aligned}$$
(56)

By substituting (56), (53) , (51) into (55), (54), (50) and then into (20), (21), (23), the expression in (24) can be obtained. Here, the proof is completed.

8.2 Appendix

On one hand, based on (28), the SOP of the cell-edge user for a given relay can be expressed as

$$\begin{aligned} \Psi _{1,w/o}^{SC-SC}=&\Pr \left( {{{\left| {\Phi _{U_1,w/o}}\right| =(0,0)}}}\right) \nonumber \\ =&\left\{ { { \mathop {\mathrm{argmax}}_{\begin{array}{c} {m}\in (1,2,\cdots ,M) \\ {n}\in (1,2,\cdots ,N) \end{array}} {\min }(X_{m,n},Y_{m,n}^1)< C_1 } }\right\} \nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M}\prod \limits _{n{\mathrm {=1}}}^{N} \bigg [ {\min }(X,Y^1)< C_1\bigg ] \nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M}\prod \limits _{n{\mathrm {=1}}}^{N} \bigg [ 1-\Delta _{1,w/o}^{SC-SC} \bigg ], \end{aligned}$$
(57)

where \(C_1=\frac{2^{2R_{1}^{th}}-1}{\rho (1-(1-\alpha ) 2^{2R_{1}^{th}})}\). \(\Delta _{1,w/o}^{SC-SC}\) can be expressed as

$$\begin{aligned} \Delta _{1,w/o}^{SC-SC} =\sum _{l_1=1}^{L_1}{\left( {\begin{array}{c}L_1\\ l_1\end{array}}\right) }(-1)^{l_1+1} \exp \left( -\frac{ C_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{1}C_{1}}{\Omega _{R_{n,m}U_{1}}}\right) . \end{aligned}$$
(58)

On the other hand, \(\Psi _{2,w/o}\) can also be derived as

$$\begin{aligned} \Psi _{2,w/o}^{SC-SC}=&\Pr \left( {{{\left| {\Phi _{U_1,w/o}}\right| =(m,n)}}}\right) \nonumber \\ =&{\left( {\begin{array}{c}N\\ n\end{array}}\right) } \sum _{m^1=1}^{M}\ldots \sum _{m^n=1}^{M}{\left( {\begin{array}{c}M\\ m^1\end{array}}\right) }\ldots {\left( {\begin{array}{c}M\\ m^n\end{array}}\right) } \nonumber \\&\times \left( \Delta _{1,w/o}^{SC-SC}\right) ^{\zeta _1}\left( 1-\Delta _{1,w/o}^{SC-SC}\right) ^{MN-\zeta _1}, \end{aligned}$$
(59)

where \(\zeta _1=m^1+\ldots +m^n\), and \(\beta _1\) can be achieved. Then, \(\Psi _{3,w/o}^{SC-SC}\) can be given by

$$\begin{aligned} \Psi _{3,w/o}^{SC-SC}=&{ {\Pr \left( {{\left. { {C_{_{sec,{U_{1}}\leftarrow s_1}}^{n,m}< {R_{1}^{s}}} }\right| \left| {\Phi _{U_1,w/o}}\right| = (m,n)} }\right) }}\nonumber \\ =&\frac{ {\Pr \left( {{\left. { {C_{_{sec,{U_{1}}\leftarrow s_1}}^{n,m} < {R_{1}^{s}}} }, \right| \left| {\Phi _{U_1,w/o}}\right| = (m,n)} }\right) } }{ {\Pr \left( {{\left| {\Phi _{U_1,w/o}}\right| = (m,n)} }\right) }} \nonumber \\ =&\frac{\Delta _{2,w/o}^{SC-SC}}{(\Delta _{1,w/o}^{SC-SC})^{\zeta _1}}, \end{aligned}$$
(60)

where the expression for \(\Delta _{2,w/o}^{SC-SC}\) in (60) can be written as

$$\begin{aligned} \Delta _{2,w/o}^{SC-SC} = \int _{0}^{+\infty } \bigg [ \min (X,Y_1)>C_1,\min (X,Y_1)<\frac{A_0+B_0Z}{C_0-D_0Z} \bigg ]^{\zeta _1} f_{Z}(z)d{z}. \end{aligned}$$
(61)

After a complicated mathematical derivation, \(\Delta _{2,w/o}^{SC-SC}\) can be given by

$$\begin{aligned} \Delta _{2,w/o}^{SC-SC} =&\sum _{j=1}^{\zeta _1}\sum _{k=1}^{K} {\left( {\begin{array}{c}\zeta _1\\ j\end{array}}\right) }{\left( {\begin{array}{c}K\\ k\end{array}}\right) }(-1)^{j+k+1}\left( \sum _{l_1=1}^{L_1} {\left( {\begin{array}{c}L_1\\ l_1\end{array}}\right) }(-1)^{l_1+1}\right) ^{j} \nonumber \\&\sum _{l_{0}=1}^{N_0}\frac{k\pi E\sqrt{1-t^2}}{2 N_o \Omega _{R_{n,m}E}} \exp \left( -\frac{ C_{1}(\zeta _1-j)}{\Omega _{SR_{n,m}}}-\frac{l_{1}C_{1}(\zeta _1-j)}{\Omega _{R_{n,m}U_{1}}}\right) \nonumber \\&\exp {\bigg [ -\frac{k E (t +1)}{2\Omega _{R_{n,m}E}}-\left( { \frac{{j}}{{\Omega _{SR_{n,m}}}}+ \frac{{j l_1}}{{\Omega _{R_{n,m}U_{1}}}}}\right) F(t) \bigg ]}. \end{aligned}$$
(62)

Furthermore, we derive the SOP for the cell-center user. The derivations of \(\Psi _{4,w/o}^{SC-SC}\), \(\Psi _{5,w/o}^{SC-SC}\) and \(\Psi _{6,w/o}^{SC-SC}\) are similar to those of \(\Psi _{1,w/o}^{SC-SC}\),\(\Psi _{2,w/o}^{SC-SC}\),and \(\Psi _{3,w/o}^{SC-SC}\) are similar to those of the \(\Psi _{4,w/o}^{SC-SC}\) can be calculated as

$$\begin{aligned} \Psi _{4,w/o}^{SC-SC}=&\Pr \left( {{{\left| {\Phi _{U_2,w/o}}\right| =(0,0)}}}\right) \nonumber \\ =&\left\{ { { \mathop {\mathrm{argmax}}_{\begin{array}{c} {m}\in (1,2,\cdots ,M) \\ {n}\in (1,2,\cdots ,N) \end{array}} {\min }(X_{m,n},Y_{m,n}^2)< C_1 } }\right\} \nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M}\prod \limits _{n{\mathrm {=1}}}^{N} \bigg [ {\min }(X,Y^2)< C_1\bigg ] \nonumber \\ =&\prod \limits _{m{\mathrm {=1}}}^{M}\prod \limits _{n{\mathrm {=1}}}^{N} \bigg [ 1-\Delta _{3,w/o}^{SC-SC} \bigg ], \end{aligned}$$
(63)

where \(D_1=\frac{2^{2R_{2}^{th}}-1}{\rho (1-\alpha )}\).

From (63), \(\Delta _{3,w/o}^{SC-SC}\) can be expressed as

$$\begin{aligned} \Delta _{3,w/o}^{SC-SC} =\sum _{l_2=1}^{L_2}{\left( {\begin{array}{c}L_2\\ l_2\end{array}}\right) }(-1)^{l_2+1} \exp \left( -\frac{ D_{1}}{\Omega _{SR_{n,m}}}-\frac{l_{2}D_{1}}{\Omega _{R_{n}U_{2}}}\right) . \end{aligned}$$
(64)

Besides, \(\Psi _{5,w/o}\) can also be computed by

$$\begin{aligned} \Psi _{5,w/o}^{SC-SC}=&\Pr \left( {{{\left| {\Phi _{U_2,w/o}}\right| =(m_+,n_+)}}}\right) \nonumber \\ =&{\left( {\begin{array}{c}N\\ n_+\end{array}}\right) } \sum _{m_+^1=1}^{M}\ldots \sum _{m_+^n=1}^{M}{\left( {\begin{array}{c}M\\ m_+^1\end{array}}\right) }\ldots {\left( {\begin{array}{c}M\\ m_+^n\end{array}}\right) } \nonumber \\&\times \left( \Delta _{3,w/o}^{SC-SC}\right) ^{\zeta _2}\left( 1-\Delta _{3,w/o}^{SC-SC}\right) ^{MN-\zeta _2}, \end{aligned}$$
(65)

where \(\zeta _2=m_+^1+\ldots +m_+^n\), and \(\beta _2\) can be achieved. Then, \(\Psi _{6,w/o}^{SC-SC}\) can be given by

$$\begin{aligned} \Psi _{6,w/o}^{SC-SC}= { {\Pr \left( {{\left. { {C_{_{sec,{U_{2}}}}^{n,m} < {R_{2}^{s}}} }\right| \left| {\Phi _{U_2,sub.}}\right| = (m,n)} }\right) }} =\frac{\Delta _{4,w/o}^{SC-SC}}{(\Delta _{3,w/o}^{SC-SC})^{\zeta _2}}. \end{aligned}$$
(66)

The expression for \(\Delta _{4,w/o}^{SC-SC}\) in (66) can be written as

$$\begin{aligned} \Delta _{4,w/o}^{SC-SC} = \int _{0}^{+\infty } \bigg [ \min (X,Y_2)>D_1,\min (X,Y_2)<A_1+B_1Z \bigg ]^{\zeta _2} f_{Z}(z)d{z}. \end{aligned}$$
(67)

After a complicated mathematical derivation, \(\Delta _{4,w/o}^{SC-SC}\) can be given by

$$\begin{aligned} \Delta _{4,w/o}^{SC-SC} =&\sum _{j=1}^{\zeta _2}\sum _{k=1}^{K} {\left( {\begin{array}{c}\zeta _2\\ j\end{array}}\right) }{\left( {\begin{array}{c}K\\ k\end{array}}\right) }(-1)^{j+k+1}\left( \sum _{l_2=1}^{L_2} {\left( {\begin{array}{c}L_2\\ l_2\end{array}}\right) }(-1)^{l_2+1}\right) ^{j} \nonumber \\&\frac{k\exp \left( -\frac{ D_{1}(\zeta _2-j)+jA_1}{\Omega _{SR_{n,m}}}-\frac{l_{2}D_{1}(\zeta _2-j)+j l_2 A_1}{\Omega _{R_{n,m}U_{2}}}\right) }{\Omega _{R_{n,m}E}\bigg ( -\frac{kE }{\Omega _{R_{n,m}E}}-{ \frac{{j}B_1E}{{\Omega _{SR_{n,m}}}}- \frac{{j l_2B_1E}}{{\Omega _{R_{n,m}U_{2}}}}} \bigg )}. \end{aligned}$$
(68)

By substituting (58), (62), (64), (68) into (57), (59), (60), (63), (65), (66) and then into (28), (29), (31) can be obtained. Here, the proof is completed.