1 Introduction

In wireless sensor networks where a large number of battery-powered sensor nodes are spatially distributed, the nodes transmit their measurements with limited communication bandwidth to achieve certain application objectives such as target localization and monitoring of physical field intensities (e.g., temperature, sound, humidity and pollution). Since each node can observe an unknown parameter or a field intensity at a particular location, determination of sensor locations makes a critical impact on performance criteria (e.g., target localization [1] and field reconstruction [2]). Especially when a subset of linear sensing measurements collected by the sensor networks is selected to accomplish a certain objective, the optimal sensing locations can be obtained by solving linear inverse problems [3,4,5,6,7]. Notably, the sensor selection problem is basically combinatorial in nature and optimization of sensing locations is computationally expensive. To tackle this problem, heuristic approaches based on cross-entropy optimization [4] and convex relaxation [3] were presented but they show no guaranteed performance and still suffer from a prohibitive computational cost especially for large sensor networks.

However, since greedy methods are computationally feasible and shown to achieve a near-optimality by maximizing the metric which is a monotonically increasing and submodular set function [8], much effort has been made to practically solve the sensor selection problem in recent years by developing greedy algorithms with near-optimal performance [5,6,7, 9]. Instead of directly minimizing the reconstruction mean squared error (MSE) for the parameters to be estimated, a submodular cost function called the frame potential was devised to guarantee near-optimality with regards to the MSE and a greedy removal algorithm was proposed to select optimal sensor locations [5]. In addition, the log-determinant of the inverse error covariance matrix proved to be a monotone submodular function was employed as a cost function to present a near-optimal greedy method [6]. A computationally efficient greedy algorithm for sensor placement was presented to determine the least number of sensor nodes and their sensing locations with the maximum projection onto the minimum eigenspace of the dual observation matrix [7]. Recently, when high-dimensional multisensor data over multiple domains are generated, greedy sampling techniques were developed to obtain a near-optimal subset of measurements based on the submodular optimization methods [9].

The sensor selection can also be conducted by using the solutions to the graph sampling problem which is one of the essential tasks in the field of the graph signal processing (GSP). In graph sampling, the optimal subset of nodes in the graph is searched to recover the original signals from the signal samples on the nodes in the sampling set. As in the sensor selection, finding an optimal sampling set is computationally prohibitive and hence, greedy methods have been adopted in many practical applications to ensure good performance at a low computational cost [10, 11]: to evaluate the MSE for graph sampling techniques, universal performance bounds were developed and despite the fact that the MSE is generally not a supermodular function, greedy algorithms that minimize the MSE were shown to achieve a near-optimality with introduction of the concept of the approximate supermodularity [10]. Recently, a greedy sampling method based on the QR factorization was proposed to accomplish a good reconstruction performance with a competitive complexity and to attain its near-optimality based on the approximate supermodularity [11].

In this paper, we present a greedy sensor selection algorithm that chooses one sensor node at a time so as to minimize the MSE for the parameters to be estimated from the noisy linear sensor measurements on the nodes selected. We extend the previous work in [11] to solve the sensor selection problem in which the parameters are assumed to be normal distributed. Whereas the greedy sampling technique in [11] was derived to minimize only the reconstruction error caused by the noise term which is approximately equal to the MSE at high signal-to-noise ratio (SNR), we take into account the statistics of the parameters in computing the MSE. We then seek to iteratively select the sensor nodes so as to minimize the MSE which is reduced to a simple metric by using the QR decomposition. As in the graph sampling where sampling sets can be constructed by selecting a subset of rows from the eigenvector matrix of variation operators (e.g., graph Laplacian) [12, 13], we aim to greedily choose one node at each iteration by selecting one row of the known observation matrix since the MSE can be expressed by a function of rows of the observation matrix, given the statistics of the parameter and the measurement noise. We employ the derivation process in [11] to propose a simple selection criterion by which the next node is efficiently selected so as to minimize the MSE computed at that iteration. We discuss that the proposed algorithm can achieves a near optimality with respect to the MSE by the approximate supermodularity. We make a complexity analysis of the proposed algorithm to offer a reasonable complexity as compared with the different greedy methods. We finally perform extensive experiments to demonstrate that the proposed selection method produces a competitive performance in terms of the estimation accuracy and the computational cost when compared with various selection methods.

This paper is organized as follows. The sensor selection problem is formulated in Sect. 2 in which the MSE is expressed in terms of the observation matrix and the statistics of the parameters and the measurement noise. In Sect. 3, the QR factorization is employed to express the MSE which is further manipulated by useful matrix formulae to derive a simple selection criterion. The complexity analysis of the proposed algorithm is provided in Sect. 4.1. Extensive experiments are conducted in Sect. 4.2 and conclusions in Sect. 5.

2 Problem formulation

In wireless sensor networks where N nodes are spatially deployed in a sensor field, we consider the problem of estimating the parameter vector \({\theta }\in {\mathbb {R}}^p\) from n \((< N)\) measurements collected by the n selected nodes in the set S. The noise-corrupted measurement vector \({\mathbf {y}}=[y_1 \cdots y_N]^\top\) is assumed to be given by a linear observation model:

$$\begin{aligned} {\mathbf {y}}={\mathbf {H}}{\theta }+{\mathbf {w}} \end{aligned}$$
(1)

where \({\mathbf {H}}\) is an \(N\times p\) known full column-rank observation matrix consisting of N row vectors \({\mathbf {h}}_i^\top =[h_{i1} \cdots h_{ip}],\quad i\in V=\{1,\ldots ,N\}\) and the parameter \({\theta }\) and the additive noise \({\mathbf {w}}\) are assumed to be independent of each other and drawn from the Gaussian distribution \({\mathcal {N}}({\mathbf {0}},\varvec{\Sigma }_{\theta })\) and \({\mathcal {N}}({\mathbf {0}},\sigma ^2{\mathbf {I}})\), respectively. Then, the parameter \({\theta }\) is assumed to be estimated by using the optimal Bayesian linear estimator given by [14]:

$$\begin{aligned} \hat{{\theta }}=\left( \varvec{\Sigma }_{\theta }^{-1}+\frac{1}{\sigma ^2}\sum _{i\in S}{\mathbf {h}}_i{\mathbf {h}}_i^\top \right) ^{-1}\frac{1}{\sigma ^2}\sum _{i\in S}{\mathbf {h}}_iy_i \end{aligned}$$
(2)

where (2) corresponds to the maximum a posteriori (MAP) estimator or minimum mean squared error (MMSE) estimator. The estimation error covariance matrix \(\varvec{\Sigma }(S)\) is derived as follows [6, 10]:

$$\begin{aligned} \varvec{\Sigma }(S)&= {\mathbb {E}}[({\theta }-\hat{{\theta }})({\theta }-\hat{{\theta }})^\top ]\nonumber \\& = \left( \varvec{\Sigma }_{\theta }^{-1}+\frac{1}{\sigma ^2}\sum _{i\in S}{\mathbf {h}}_i{\mathbf {h}}_i^\top \right) ^{-1}\nonumber \\&= \left( \varvec{\Sigma }_{\theta }^{-1}+\frac{1}{\sigma ^2}{\mathbf {H}}_S^\top {\mathbf {H}}_S\right) ^{-1} \end{aligned}$$
(3)

where \({\mathbf {H}}_S\) is the matrix with rows of the observation matrix \({\mathbf {H}}\) indexed by S.

In this work, we assume that the parameter \({\theta }\) is a random vector with known prior distribution. Instead, we can also consider the problem of estimating the parameter which is deterministic but unknown. For this case, the parameter is estimated by the maximum likelihood (ML) estimator. The ML estimator and the estimation error covariance matrix can be obtained as follows [14]:

$$\begin{aligned} \hat{{\theta }}&= \left( \frac{1}{\sigma ^2}\sum _{i\in S}{\mathbf {h}}_i{\mathbf {h}}_i^\top \right) ^{-1}\frac{1}{\sigma ^2}\sum _{i\in S}{\mathbf {h}}_iy_i \end{aligned}$$
(4)
$$\begin{aligned} \varvec{\Sigma }(S)&= \left( \frac{1}{\sigma ^2}{\mathbf {H}}_S^\top {\mathbf {H}}_S\right) ^{-1} \end{aligned}$$
(5)

Note that the ML estimation becomes equal to the Bayesian estimation in the limit of \(\varvec{\Sigma }_{\theta }=\sigma _{\theta }^2{\mathbf {I}}_p, \sigma _{\theta }^2\rightarrow \infty\).

Now, we formulate the problem of finding the best set \(S^*\) of sensors that minimizes the MSE in (3):

$$\begin{aligned} S^*=\arg \min _{S, |S|=n} \text {MSE}(S)=\arg \min _{S, |S|=n} tr\left[ \varvec{\Sigma }(S)\right] \end{aligned}$$
(6)

It should be noticed from (3) and (6) that given the statistics of the parameter and the noise, the MSE is determined by the matrix \({\mathbf {H}}_S\). In other words, the optimal locations of sensor nodes can be found by selecting the most informative rows of the observation matrix \({\mathbf {H}}\). Obviously, in a noise-free situation (\({\mathbf {w}}={\mathbf {0}}\) in (1)), the parameter vector can be perfectly recovered by simply picking up any of p independent rows of \({\mathbf {H}}\). In this work, we aim to find the optimal set of p sensor nodes that minimizes the MSE in noisy cases.

To solve the problem in (6), we consider a greedy approach in which one sensor node at each iteration is selected so as to minimize the intermediate MSE: that is, at the ith iteration, the intermediate MSE is given by \(\text {MSE}(S_i)=tr\left[ \varvec{\Sigma }(S_i)\right]\), where \(S_i\) consists of i sensors selected until the ith iteration. We continue to choose the next node at the (\(i+1\))th iteration from the set of the remaining sensors denoted by \(S_i^C\equiv (V-S_i)\) until \(|S_i|\) reaches p:

$$\begin{aligned} j^*&= \arg \min _{S_{i+1}=S_i+\{j\},j\in S_i^C} tr\left[ \varvec{\Sigma }(S_{i+1})\right] \nonumber \\&= \arg \min _{S_{i+1}=S_i+\{j\},j\in S_i^C} tr\left[ \left( \varvec{\Sigma }_{\theta }^{-1}+\frac{1}{\sigma ^2}{\mathbf {H}}_{S_{i+1}}^\top {\mathbf {H}}_{S_{i+1}}\right) ^{-1}\right] \end{aligned}$$
(7)
$$\begin{aligned} S_{i+1}&= S_i+\{j^*\} \end{aligned}$$
(8)

where \({\mathbf {H}}_{S_{i+1}}\) consists of \((i+1)\) row vectors selected from \({\mathbf {H}}\) and is expressed by

$$\begin{aligned} {\mathbf {H}}_{S_{i+1}}^\top = \begin{bmatrix} {\mathbf {h}}^{(1)}&\cdots&{\mathbf {h}}^{(i+1)} \end{bmatrix} \end{aligned}$$
(9)

where \(({\mathbf {h}}^{(i)})^\top\) denotes the row vector selected at the ith iteration. The selection procedure described by (7) and (8) is conducted repeatedly until \(|S|=p\) sensor nodes are selected.

In the following section, we prove a theorem that provides a simple selection criterion by which the next sensor node minimizing the metric in (7) is iteratively selected. We first manipulate the matrix \({\mathbf {H}}_{S_{i+1}}^\top\) based on the QR factorization which is obtained in this work by using the Householder transformation due to its low complexity and robust sensitivity to rounding error as compared to the Gram-Schmidt orthogonalization [15].

3 Method: greedy sensor selection algorithm

Using the QR factorization, we have \({\mathbf {H}}_{S_{i+1}}^\top ={\mathbf {Q}}\bar{{\mathbf {R}}}^{(i+1)}\) where \({\mathbf {Q}}\) is the \(p\times p\) matrix and \(\bar{{\mathbf {R}}}^{(i+1)}\) the \(p\times (i+1)\) matrix. Assuming \(\varvec{\Sigma }_{\theta }=\sigma _{\theta }^2{\mathbf {I}}_p\) where \({\mathbf {I}}_p\) is the \(p\times p\) identity matrix, we then manipulate the cost function in (7) to derive a simpler form. Specifically,

$$\begin{aligned} \text {MSE}(S_{i+1})&= tr\left[ \left( \varvec{\Sigma }_{\theta }^{-1}+\frac{1}{\sigma ^2}{\mathbf {H}}_{S_{i+1}}^\top {\mathbf {H}}_{S_{i+1}}\right) ^{-1}\right] \nonumber \\&= tr\left[ \left( \frac{1}{\sigma _{\theta }^2}{\mathbf {I}}_p+\frac{1}{\sigma ^2}{\mathbf {Q}}\bar{{\mathbf {R}}}^{(i+1)}(\bar{{\mathbf {R}}}^{(i+1)})^\top {\mathbf {Q}}^\top \right) ^{-1}\right] \nonumber \\&= tr\left[ \left( \frac{1}{\sigma _{\theta }^2}{\mathbf {I}}_p+\frac{1}{\sigma ^2}\bar{{\mathbf {R}}}^{(i+1)}(\bar{{\mathbf {R}}}^{(i+1)})^\top \right) ^{-1}\right] \end{aligned}$$
(10)

where (10) follows from the notion that \({\mathbf {Q}}^\top ={\mathbf {Q}}^{-1}\) and the cyclic property of the trace operation. Noting that \(\bar{{\mathbf {R}}}^{(i+1)}\) can be written by

$$\begin{aligned} \bar{{\mathbf {R}}}^{(i+1)}= \begin{bmatrix} {\mathbf {R}}^{i+1}\\ {\mathbf {0}}_{(p-i-1)\times (i+1)} \end{bmatrix}, \end{aligned}$$
(11)

where \({\mathbf {0}}_{a\times b}\) indicates the \(a\times b\) zero matrix, we have

$$\begin{aligned}&\left( \frac{1}{\sigma ^2}\bar{{\mathbf {R}}}^{(i+1)}(\bar{{\mathbf {R}}}^{(i+1)})^\top +\frac{1}{\sigma _{\theta }^2}{\mathbf {I}}_p\right) ^{-1}\\ &\quad = \sigma ^2\left[\begin{array}{cc} \left( {\mathbf {R}}^{(i+1)}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1} & {\mathbf {0}}_{(p-i-1)\times (i+1)}^\top \\ {\mathbf {0}}_{(p-i-1)\times (i+1)} &{} \frac{\sigma _{\theta }^2}{\sigma ^2}{\mathbf {I}}_{p-i-1} \end{array}\right] \end{aligned}$$
(12)

Thus, we simplify the MSE as follows:

$$\begin{aligned} \text {MSE}(S_{i+1})\propto & {} tr\left[ \left( {\mathbf {R}}^{(i+1)}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1}\right] + tr\left( \frac{\sigma _{\theta }^2}{\sigma ^2}{\mathbf {I}}_{p-i-1}\right) \end{aligned}$$
(13)
$$\begin{aligned}\propto & {} tr\left[ \left( {\mathbf {R}}^{(i+1)}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1}\right] \end{aligned}$$
(14)

where (14) follows since the second term in (13) is irrelevant in finding the \((i+1)\)th sensor node at \((i+1)\)th iteration.

We present a theorem in which a simple criterion is provided to select the minimizing row (equivalently, the corresponding sensor node) from \({\mathbf {H}}\) at each iteration. We employ the derivation process in [11] to prove the theorem.

Theorem

Let the (\(i+1\))th column vector \({\mathbf {r}}_{i+1}\) of \({\mathbf {R}}^{i+1}\) be given by \({\mathbf {r}}_{i+1}^\top =[{\mathbf {b}}^\top \quad d]\) where the (\(i\times 1\)) column vector \({\mathbf {b}}\) and the (\(i+1\))th entry d are computed from the QR factorization. Then, the sensor node at the \((i+1)\)th iteration that minimizes the MSE formulated in (14) is selected from the remaining \((N-i)\) nodes as follows:

$$\begin{aligned} {\mathbf {h}}^{(i+1)*}=\arg \min _{{\mathbf {h}}^{(i+1)}} \frac{1+k-\sigma ^2/\sigma _{\theta }^2\parallel \left( {\mathbf {R}}^i ({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i}\right) ^{-1} {\mathbf {b}}\parallel ^2}{d^2+(1+k)\sigma ^2/\sigma _{\theta }^2} \end{aligned}$$
(15)

where \(({\mathbf {h}}^{(i+1)})^\top\) is one of the rows of \({\mathbf {H}}_{S_i^C}\) selected at the \((i+1)\)th iteration and \(k={\mathbf {b}}^\top \left( {\mathbf {R}}^i({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i}\right) ^{-1}{\mathbf {b}}\).

Proof

We further manipulate the cost function in (14) to produce

$$\begin{aligned}&\left( {\mathbf {R}}^{i+1}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1}\\&\quad =\left( \begin{bmatrix} {\mathbf {R}}^i({\mathbf {R}}^i)^\top &{} {\mathbf {0}}_{i\times 1} \\ {\mathbf {0}}_{i\times 1}^\top &{} 0 \end{bmatrix}+{\mathbf {r}}_{i+1}{\mathbf {r}}_{i+1}^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1}\\&\quad =\left( \begin{bmatrix} {\mathbf {R}}^i({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i} &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\frac{\sigma ^2}{\sigma _{\theta }^2} \end{bmatrix}+ \begin{bmatrix} {\mathbf {b}}\\ 0 \end{bmatrix} \begin{bmatrix} {\mathbf {b}}^\top&0 \end{bmatrix}\right) ^{-1} \end{aligned}$$

For simplified notations, we denote \({\mathbf {R}}^i({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i}\) and \(\frac{\sigma ^2}{\sigma _{\theta }^2}\) by \({\mathbf {P}}^i\) and \(\alpha ^2\), respectively. Then, we have

$$\begin{aligned}&\left( {\mathbf {R}}^{i+1}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2} {\mathbf {I}}_{i+1}\right) ^{-1}\nonumber \\&\quad =\left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1}\nonumber \\&\qquad -\frac{ \left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1} \left[\begin{array}{c} {\mathbf {b}}\\ 0 \end{array}\right] \left[\begin{array}{cc} {\mathbf {b}}^\top&0 \end{array}\right] \left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1}}{1+ \left[\begin{array}{cc} {\mathbf {b}}^\top&0 \end{array}\right] \left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1} \left[\begin{array}{c} {\mathbf {b}}\\ 0 \end{array}\right]} \end{aligned}$$
(16)

where (16) follows from the Sherman–Morrison–Woodbury formula [16]. The first term in (16) is computed by using the block matrix inversion [16]:

$$\begin{aligned} \begin{bmatrix} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{bmatrix}^{-1}= \begin{bmatrix} \left( {\mathbf {P}}^i\right) ^{-1}+\frac{d^2\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}}{d^2(1-k)+\alpha ^2} &{} -\frac{d\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}}{d^2(1-k)+\alpha ^2}\\ -\frac{d{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}}{d^2(1-k)+\alpha ^2} &{} \frac{1}{d^2(1-k)+\alpha ^2} \end{bmatrix} \end{aligned}$$
(17)

where k is used to denote \({\mathbf {b}}^\top \left( {\mathbf {R}}^i({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i}\right) ^{-1}{\mathbf {b}}\) for a simpler notation. Furthermore, the denominator and the nominator of the second term in (16) are computed as follows:

$$\begin{aligned}&1+ \left[\begin{array}{cc} {\mathbf {b}}^\top&0 \end{array}\right] \left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1} \left[\begin{array}{c}{\mathbf {b}}\\ 0 \end{array}\right]=\frac{d^2+(1+k)\alpha ^2}{d^2(1-k)+\alpha ^2}. \end{aligned}$$
(18)
$$\begin{aligned}&\left[\begin{array}{cc} {\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1} \left[\begin{array}{c} {\mathbf {b}}\\ 0 \end{array}\right]\left[\begin{array}{cc} {\mathbf {b}}^\top&0 \end{array}\right] \left[\begin{array}{cc}{\mathbf {P}}^i &{} {\mathbf {b}}d\\ {\mathbf {b}}^\top d &{} d^2+\alpha ^2 \end{array}\right]^{-1}\nonumber \\&\quad = \left[\begin{array}{cc}\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}\frac{(d^2+\alpha ^2)^2}{(d^2(1-k)+\alpha ^2)^2} &{} -\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}\frac{dk(d^2+\alpha ^2)}{(d^2(1-k)+\alpha ^2)^2}\\ -{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}\frac{dk(d^2+\alpha ^2)}{(d^2(1-k)+\alpha ^2)^2} &{} \frac{d^2k^2}{(d^2(1-k)+\alpha ^2)^2} \end{array}\right] \end{aligned}$$
(19)

From (17)–(19), we finally have

$$\begin{aligned} \left( {\mathbf {R}}^{i+1}({\mathbf {R}}^{i+1})^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i+1}\right) ^{-1}= \begin{bmatrix} \left( {\mathbf {P}}^i\right) ^{-1}-\frac{\alpha ^2}{d^2+(1+k)\alpha ^2}\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1} &{} -\frac{d\left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}}{d^2+(1+k)\alpha ^2}\\ -\frac{d{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}}{d^2+(1+k)\alpha ^2} &{} \frac{1+k}{d^2+(1+k)\alpha ^2} \end{bmatrix} \end{aligned}$$
(20)

Thus, the MSE is computed as follows:

$$\begin{aligned} \text {MSE}(S_{i+1})&= tr\left[ \left( {\mathbf {P}}^i\right) ^{-1}\right] -\frac{\alpha ^2}{d^2+(1+k)\alpha ^2}tr\left[ \left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}{\mathbf {b}}^\top \left( {\mathbf {P}}^i\right) ^{-1}\right] +\frac{1+k}{d^2+(1+k)\alpha ^2} \end{aligned}$$
(21)
$$\begin{aligned}\propto & {} \frac{1+k-\sigma ^2/\sigma _{\theta }^2\parallel \left( {\mathbf {P}}^i\right) ^{-1}{\mathbf {b}}\parallel ^2}{d^2+(1+k)\sigma ^2/\sigma _{\theta }^2} \end{aligned}$$
(22)

Note that the first term in (21) is given at the ith iteration and irrelavant in finding the next sensor node at the \((i+1)\)th iteration that minimizes the MSE. \(\square\)

Initially, we can compute \(({\mathbf {p}}^1)^{-1}\) for each \({\mathbf {h}}^{(1)}\) as follows:

$$\begin{aligned} ({\mathbf {p}}^1)^{-1}&= \left( {\mathbf {R}}^1({\mathbf {R}}^1)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}\right) ^{-1}\nonumber \\&= \frac{1}{\parallel {\mathbf {h}}^{(1)}\parallel ^2+\frac{\sigma ^2}{\sigma _{\theta }^2}} \end{aligned}$$
(23)

Thus, the first sensor node is selected by finding the row vector \({\mathbf {h}}^{(1)*}\) that minimizes the MSE given by (23). Starting with \(({\mathbf {p}}^1)^{-1}\) with \({\mathbf {h}}^{(1)*}\), the algorithm continues by evaluating (22) at the next iteration until the p sensor nodes are selected. In what follows, the proposed sensor selection algorithm is briefly explained.

figure a

4 Results and discussion

4.1 Optimality and complexity of proposed algorithm

The concept of the approximate supermodularity ensures near-optimality of greedy methods that seek to minimize the MSE given in (14) [10]. Specifically, it is shown that the \(\text {MSE}(S)\) is monotone-decreasing and \(\gamma\)-supermodular and greedy searches minimizing the MSE by repeatedly conducting (7) and (8) can provide a bound on suboptimality of the greedy solution to the problem in (6) as follows:

$$\begin{aligned} \frac{\text {MSE}(S_i)-\text {MSE}(S^*)}{\text {MSE}(\emptyset )-\text {MSE}(S^*)}\le e^{-\frac{\gamma i}{p}} \end{aligned}$$
(24)

where \(\text {MSE}(S_i)\) and \(\text {MSE}(S^*)\) indicate the MSE at the ith iteration of the greedy search and the MSE achieved by the optimal solution \(S^*\) to (6), respectively and \(\gamma \ge \frac{1+2\sigma _{\theta }^2/\sigma ^2}{(1+\sigma _{\theta }^2/\sigma ^2)^4}\) (for the detailed information on the definition of the \(\gamma\)-supermodular set function and the bound in (24), see Theorem 2 and 3 in [10]). The performance bound in (24) explains good empirical results of greedy methods that have been encountered in many practical applications. Hence, it can be said that our greedy solution iteratively minimizing the MSE achieves a near-optimal performance.

The proposed algorithm consists of two main parts: first, given \(\left( {\mathbf {P}}^i\right) ^{-1}=\left( {\mathbf {R}}^i({\mathbf {R}}^i)^\top +\frac{\sigma ^2}{\sigma _{\theta }^2}{\mathbf {I}}_{i}\right) ^{-1}\) at the \((i+1)\)th iteration, the minimizing row is determined by computing the selection criterion in (15) for each \({\mathbf {h}}^{(i+1)}\) selected out of \(N-i\) remaining rows in \({\mathbf {H}}_{S_i^C}\). Thus, the operation count of the first work at the \((i+1)\)th iteration is given by \(C_{tr}\approx (N-i)(2pi+2i^2)\) flops. Second, after \({\mathbf {h}}^{(i+1)*}\) is obtained, the inverse matrix \(\left( {\mathbf {P}}^{i+1}\right) ^{-1}\) is computed from (20) for the next iteration, requiring the operation count \(C_{inv}\approx 3i^2+i\) flops. In addition, the the Householder matrix for the QR decomposition is performed for each \({\mathbf {h}}^{(i+1)*}\), producing the operation count \(C_H\approx 2pi^2-4p^2i+2p^3\). Noting that this process is repeated \(|S|-1\) times, the total operation count of the proposed algorithm is given by \(C_{\mathrm{total}}=O(Np|S|^2)\) which is the complexity of the same order as that of [11] except for the extra computation \(O(N|S|^2)\) needed for our algorithm which is ignorable in computing the total operation count \(C_{\mathrm{total}}\).

For the performance comparison, we first consider the efficient sampling method (ESM) [13], which has been developed for sampling of graph signals. ESM selects the next row (or the next sensor node) by applying a column-wise Gaussian elimination on \({\mathbf {H}}\), yielding a low weight selection process. We next compare the proposed algorithm with a greedy sensor selection (GSS) [6], which is shown to achieve a near-optimal performance in a sense that the log-determinant of the inverse error covariance matrix \(\varvec{\Sigma }(S)^{-1}\) is maximized. We also compare with the QR factorization-based selection method (QRM) [11] which employs the QR factorization to derive a simple selection criterion. QRM seeks to minimize \(tr\left[ \left( {\mathbf {H}}_S^\top {\mathbf {H}}_S\right) ^{+}\right] =\parallel {\mathbf {H}}_{S}^+\parallel _F^2\) which corresponds to the MSE at the high SNR (\(\sigma _{\theta }\gg \sigma\)). The complexity and the metrics of the above mentioned algorithms are provided in Table 1. Obviously, the proposed algorithm offers a competitive complexity as compared with GSS and QRM for \(|S|\le p\) while ESM runs faster than the others at the expense of poor performance caused by its suboptimal approach. We finally investigate the estimation performance of the various methods for the case of \(|S|=p\) in the experiments in Sect. 4.2

Table 1 Comparison with various greedy selection methods
Full size table

4.2 Experimental results

In this section, we investigate the performance of the proposed sensor selection algorithm in comparison with various selection methods for two different types of observation matrices \({\mathbf {H}}\) given below:

  • Random matrices with Gaussian iid entries, \(h_{ij} \sim {\mathcal {N}}(0,1)\)

  • Random matrices with Bernoulli iid entries, \(h_{ij}\) which take binary values (0 or 1) with the probability 0.5.

We generate 500 different realizations of random matrices for each type of \({\mathbf {H}}\in {\mathbb {R}}^{N\times p}\) with \(N=100\). For each realization of \({\mathbf {H}}\), we apply one of the various sensor selection methods such as ESM, GSS, QRM and the proposed algorithm to construct the selection set S with the cardinality \(|S|=p\). We then collect the selected measurements \(y_i, i\in S\) from which the parameter vector \({\theta }\) is estimated by using the optimal linear estimator given in (2). Note that the measurements are noise-corrupted by the measurement noise \({\mathbf {w}}\), the variance of which is changed by varying the SNR (dB)= \(10\log _{10}\sigma _{{\theta }}^2/\sigma ^2\). We evaluate the performance of the different selection methods by computing the MSE given by \({\mathbb {E}}\parallel {\theta }-\hat{{\theta }}\parallel ^2\) which is averaged over 500 different realizations of \({\mathbf {H}}\).

4.2.1 Performance evaluation with respect to parameter dimension

Fig. 1
figure 1

Estimation performance with respect to various parameter dimensions for Gaussian random matrix \({\mathbf {H}}\): the proposed algorithm is compared with different selection methods by varying the dimension of the parameter, \(|S|=p\)

Full size image
Fig. 2
figure 2

Estimation performance with respect to various parameter dimensions for Bernoulli random matrix \({\mathbf {H}}\): the proposed algorithm is compared with different selection methods by varying the dimension of the parameter, \(|S|=p\)

Full size image

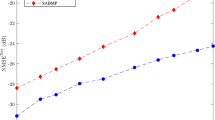
In this experiment, we construct the sets S with \(|S|=p\) by using the four selection methods for two types of \({\mathbf {H}}\) with \(p=20, 25, \dots , 40\). We test them from the noisy measurements generated at SNR=2dB by evaluating the MSEs achieved by the methods which are plotted in Figs. 1 and 2. Notably, the MSE becomes worse with increased dimension of the parameter vector because the set S consisting of more informative nodes is less likely to be selected with increased cardinality, given a fixed number of the nodes in the sensor networks. As expected, the proposed algorithm outperforms the other methods in terms of the MSE for most cases since ESM and GSS focus on optimizing the indirect metrics such as the worst case of the MSE (equivalently, the spectral matrix norm \(\parallel {\mathbf {H}}_{S}^+\parallel ^2_2\)) and the log-determinant of the inverse error covariance matrix, respectively. It is also noticed that QRM shows good performance in a noisy situation while it is designed to minimize the MSE at the high SNR. The complexity of the selection methods is experimentally evaluated in terms of the execution time in second. Figure 3 demonstrates the execution times of the methods for the Gaussian random matrix \({\mathbf {H}}\) with respect to the parameter dimension \(p=|S|=20,\ldots ,40\). On the average, GSS and QRM run 1.51 and 1.22 times faster than the proposed method for the case of \(|S|=p\), respectively.

Fig. 3
figure 3

Execution time in second with respect to various parameter dimensions for Gaussian random matrix \({\mathbf {H}}\): the proposed algorithm is compared with different selection methods by varying the dimension of the parameter, \(|S|=p\)

Full size image

4.2.2 Performance investigation with respect to noise level

Fig. 4
figure 4

Performance investigation with respect to SNR for Gaussian random matrix \({\mathbf {H}}\): the various sensor selection algorithms with \(|S|=p=30\) are evaluated by varying the SNR

Full size image
Fig. 5
figure 5

Performance investigation with respect to SNR for Bernoulli random matrix \({\mathbf {H}}\): the various sensor selection algorithms with \(|S|=p=30\) are evaluated by varying the SNR

Full size image

We investigate the sensitivity of the different selection methods to the noise level \(\sigma\) which takes different values by varying the SNR from 0 dB to 10 dB. In Figs. 4 and 5 , we compare the MSEs achieved by the methods given \(|S|=p=30\) to demonstrate the superiority of the proposed algorithm to the other ones in the presence of the measurement noise. It is noted that ESM and QRM work only on the observation matrix \({\mathbf {H}}\) without taking into account the statistics about the parameter and noise. Nonetheless, QRM shows a good estimation performance at the moderate and high SNR.

5 Conclusions

We studied an optimization problem in which a given number of sensor nodes are selected so as to minimize the estimation error computed by using the measurements on the selected nodes. We presented a greedy sensor selection method which iteratively selects one node minimizing the estimation error at each step. We employed the QR factorization and useful matrix formulae to derive a simple criterion by which the next minimizing node is selected without computation of large matrix inversion. We discussed that a near-optimality of the proposed method can be ensured from the approximate supermodularity and also analyzed the complexity of the proposed algorithm in comparison with the previous novel methods. We finally examined the estimation performance of different selection methods through extensive experiments in various situations, demonstrating that the proposed algorithm offers an competitive estimation performance with a reasonable complexity as compared with the novel methods.