1 Introduction

Multiple-input multiple-output (MIMO) technology was introduced into the radar field by Lincoln Laboratory in the USA in 2003 [1], and the concept of MIMO radar was proposed. Compared with traditional radars, MIMO radar has greater advantages in azimuth resolution, array freedom, multi-target parameter estimation, and anti-jamming capabilities and has been studied and paid attention by many scholars. Direction of arrival [2,3,4,5,6] (DOA) estimation, as an important research content in array signal processing, has been widely used in sonar, radar, medical, and wireless communication fields [7,8,9]. In recent years, the DOA estimation problem of MIMO radar has been widely concerned and has become a research hotspot.

MIMO radar generally uses a uniform linear array as the transmitter and receiver array and combines it with the classic high-resolution DOA estimation method to estimate the direction of arrival [10,11,12,13,14,15,16]. Classical high-resolution DOA estimation methods such as the multiple signal classification (MUSIC) method [17, 18] or estimating signal parameter via the rotational invariance techniques (ESPRIT) method [19, 20]. However, because uniform linear array is used as the transmitter and receiver array, the spacing of its array elements is generally half a wavelength, and the array aperture is greatly restricted, which affects the performance of MIMO radar angle resolution and multi-target parameter estimation. Therefore, sparse arrays [21,22,23,24,25] such as nested arrays, coprime arrays [26, 27], and minimum redundant arrays, are proposed. Compared with uniform array, Sparse array can use the special arrangement of the array to obtain a larger number of virtual array elements with the same actual number of array elements and has higher angular resolution and parameter resolution. Vaidyanathan et al. [28] proposed the structural model of coprime array, two uniform subarrays form coprime array. The number of the subarray elements is M and N, and the distance between the array elements is Nd and Md (d is half the wavelength), and M, N are mutually prime numbers. Zhou et al. [29] proposed a coprime array DOA estimation method based on the joint MUSIC algorithm. This method decomposes the coprime array into two uniform subarrays and performs MUSIC estimation separately and then combines the estimation results of the two subarrays to obtain the final DOA estimation, thereby eliminating the phase ambiguity problem. But this method decomposes the coprime array into two subarrays lose part of the received data, thereby reducing the DOA estimation performance. Pal et al. [30] proposed a DOA estimation method based on a coprime array. This method expands the coprime array to obtain a virtual array and introduces spatial smoothing technology to solve the problem that the virtual array is not linear uniform array. But this method will lose the discontinuous information of the array elements, thereby affecting the degree of freedom of DOA estimation. Li et al. [31, 32], respectively, proposed the ESPRIT algorithm and the unitary ESPRIT algorithm for the MIMO radar coprime array to jointly estimate the direction of departure (DOD) and the direction of arrival (DOA). This method divides the coprime array into two uniform sparse subarrays as transmitter and receiver arrays. The coprime array formed by them increases the aperture of the array, thereby improving the performance of DOA estimation. However, the degree of freedom of the above method is limited by the number of elements of the subarray, and additional calculations are required to eliminate the ambiguity problem. Zhou et al. [33] proposed the DOA estimation method based on the expanded coprime array MIMO radar MUSIC algorithm. This method uses the expanded coprime array as the transmitter and receiver arrays of the MIMO radar to increase the array aperture and uses the MUSIC algorithm to estimate the DOA, which effectively improves the DOA estimates performance. But this method involves the eigenvalue decomposition of a high-dimensional matrix, which requires a lot of computation.

The above literature does not involve DOA estimation methods for non-circular signals. However, there are a large number of non-circular signals in the actual environment [34,35,36], such as minimum shift keying (MSK) signals, binary phase shift keying (BPSK) signals, and amplitude modulation (AM) signals. The unique non-circular characteristics of non-circular signals can further expand the virtual array, increase the array aperture, effectively double the dimension of the receiver array, and improve the performance of target parameter estimation and the resolution of multiple sources. Therefore, based on the array model of literature [33], this article proposes a non-circular signal dimensionality reduction DOA estimation method based on the expanded coprime array MIMO radar (NRC-MIMO MUSIC). This method uses the expanded coprime array MIMO radar model to obtain a larger virtual array when the actual number of array elements is the same. This method firstly uses the characteristics of non-circular signals to reconstruct the receiver array in the MUSIC algorithm. Then the reconstructed two-dimensional DOA estimation problem is transformed into an optimization problem, and the optimization problem is reconstructed using constraints, and then the Lagrange multiplier method is used to construct the cost function, and the one-dimensional spectral peak search function is obtained. Aiming at the problem of poor accuracy of the method in the environment of low signal-to-noise ratio (SNR) and small number of snapshots, the power series of noise eigenvalues is used to modify the noise subspace to further improve the accuracy of the algorithm. The method proposed in this article uses a coprime array as the transceiver array of the MIMO radar, which greatly increases the array aperture of the virtual array, eliminates the phase ambiguity problem caused by the array element spacing larger than half the wavelength, and significantly improves the DOA estimation performance. Finally, simulation experiments verify the effectiveness of the algorithm. Compared with the classic MUSIC algorithm and the traditional coprime array MUSIC algorithm, the method in this article has better performance in DOA estimation accuracy, successful resolution, and low signal-to-noise ratio (SNR) environments.

Notations: Lower-case (upper-case) bold characters are used to represent vectors (matrices). The superscripts (·)T, (·)*, (·)H denote the transpose, conjugate, and conjugate transpose of operation, respectively. E{·} is exploited to represent the expectation of \(\otimes\) refers Kronecker product, \(\circ\) refers the Khatri–Rao product. diag{·} denotes the diagonal matrix whose diagonal elements are the elements ·.

2 Preliminaries

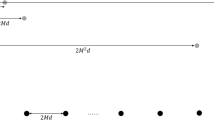
The geometric structure of the expanded coprime array MIMO radar is shown in Fig. 1. Both the transmitter array and the receiver array are composed of two uniform sparse subarrays, the two subarrays are expanded side by side, and the last element of subarray 1 is used as the first element of subarray 2. The sparse uniform subarray 1 and subarray 2 together form the expanded coprime array. Subarray 1 contains M array elements, and the distance between each adjacent array element is Nd (where N is the number of array elements and d is half the wavelength). The other subarray 2 contains N array elements, and the distance between each adjacent array element is Md (where M is the number of array elements and d is half the wavelength). The two numbers M and N are mutually prime, and the distance between adjacent elements of subarray 1 and subarray 2 is greater than half of the wavelength. The formed coprime array contains M + N − 1 elements, as shown in Fig. 1. The coprime array takes the first element as the reference point, and the position of the element can be expressed as:

$$L_{{\text{s}}} = \left\{ {Mnd|0 \le n \le N - 1} \right\}U\left\{ {Nmd|0 \le m \le M - 1} \right\}$$
(1)

where d = λ/2, λ is the wavelength.

Fig. 1
figure 1

Coprime MIMO radar array geometry

Full size image

Assume that there are K narrowband far-field uncorrelated signals that are incident on the coprime array at angles [θ1, θ2, …, θk], and then the direction vectors of the Kth target of the transmitter array and the receiver array are:

$${\varvec{a}}_{{\text{t}}} \left( {\theta_{k} } \right) = \left[ {{\kern 1pt} {\varvec{a}}_{{{\text{t}}1}}^{{\text{T}}} \left( {\theta_{k} } \right),{\varvec{a}}_{{{\text{t}}2}}^{{\text{T}}} \left( {\theta_{k} } \right){\kern 1pt} } \right]^{{\text{T}}}$$
(2)
$${\varvec{a}}_{{\text{r}}} \left( {\theta_{k} } \right) = \left[ {{\varvec{a}}_{{{\text{r}}1}}^{{\text{T}}} \left( {\theta_{k} } \right),{\varvec{a}}_{{{\text{r}}2}}^{{\text{T}}} \left( {\theta_{k} } \right)} \right]^{{\text{T}}}$$
(3)

where at1(θk), at2(θk) are the direction vectors of the transmitter array subarray 1 and subarray 2, respectively. ar1(θk), ar2(θk) are the direction vectors of the receiver array subarray 1 and subarray 2, respectively. The expressions of the direction vectors of the transmitter subarray and the receiver subarray are, respectively:

$${\varvec{a}}_{{{\text{t}}1}} \left( {\theta_{k} } \right) = {\varvec{a}}_{{{\text{r}}1}} \left( {\theta_{k} } \right) = \left[ {1,e^{{ - j\frac{{2\pi Nd\sin \left( {\theta_{k} } \right)}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\pi \left( {M - 1} \right)Nd\sin \left( {\theta_{k} } \right)}}{\lambda }}} } \right]^{{\text{T}}}$$
(4)
$${\varvec{a}}_{{{\text{t}}2}} \left( {\theta_{k} } \right) = {\varvec{a}}_{{{\text{r}}2}} \left( {\theta_{k} } \right) = \left[ {1,e^{{ - j\frac{{2\pi Md\sin \left( {\theta_{k} } \right)}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\pi \left( {N - 1} \right)Md\sin \left( {\theta_{k} } \right)}}{\lambda }}} } \right]^{{\text{T}}}$$
(5)

Therefore, the array flow matrix of the transmitter array and the receiver array are At and Ar, respectively. It can be expressed as:

$${\varvec{A}}_{{\text{t}}} \left( \theta \right) = \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{\text{t}}} \left( {\theta_{1} } \right),{\varvec{a}}_{{\text{t}}} \left( {\theta_{2} } \right), \ldots ,{\varvec{a}}_{{\text{t}}} \left( {\theta_{K} } \right)} \\ \end{array} } \right]$$
(6)
$${\varvec{A}}_{{\text{r}}} \left( \theta \right) = \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{\text{r}}} \left( {\theta_{1} } \right),{\varvec{a}}_{{\text{r}}} \left( {\theta_{2} } \right), \ldots ,{\varvec{a}}_{{\text{r}}} \left( {\theta_{K} } \right)} \\ \end{array} } \right]$$
(7)

From the formula (6) and (7), the flow pattern A of the entire virtual array can be obtained as:

$$\begin{aligned} {\varvec{A}} & = {\varvec{A}}_{{\text{r}}} \circ {\varvec{A}}_{{\text{t}}} = \left[ {\begin{array}{*{20}c} {{\varvec{a}}\left( {\theta_{1} } \right),{\varvec{a}}\left( {\theta_{2} } \right), \ldots ,{\varvec{a}}\left( {\theta_{K} } \right)} \\ \end{array} } \right] \\ & = \left[ {{\varvec{a}}_{{\text{r}}} \left( {\theta_{1} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\theta_{1} } \right),{\varvec{a}}_{{\text{r}}} \left( {\theta_{2} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\theta_{2} } \right), \ldots ,{\varvec{a}}_{{\text{r}}} \left( {\theta_{K} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\theta_{K} } \right)} \right] \\ \end{aligned}$$
(8)

where \({\varvec{A}}_{{\text{r}}} \circ {\varvec{A}}_{{\text{t}}}\) is the Khatri–Rao operator, \({\varvec{a}}\left( {\theta_{k} } \right){ = }{\varvec{a}}_{{\text{r}}} \left( {\theta_{K} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\theta_{K} } \right)\), \(\otimes\) represents the Kronecker product. The received signal of the coprime array can be expressed as [15]:

$${\varvec{x}}(t) = {\varvec{As}}(t) + {\varvec{n}}(t)$$
(9)

where s(t) is the source signal vector (non-circular signal vector in this article), n(t) is the noise vector, and A is the array flow matrix.

For the non-circular signal s(t), according to its definition, the non-circular signal is relative to the circular signal. If the signal has the characteristics of rotation invariance, the signal s(t) is called the circular signal. That is, when E{s(t)} = 0, \(E\{{\varvec{s}}(t){\varvec{s}}^{{\text{H}}} (t)\} \ne {\mathbf{0}}\) and \(E\{{\varvec{s}}(t){\varvec{s}}^{{\text{T}}} (t)\} = {\mathbf{0}}\) are established at the same time, s(t) is the circular signal. Conversely, if the signal does not have the characteristics of rotation invariance, then the signal s(t) is called a non-circular signal. That is, when E{s(t)} = 0, \(E\{{\varvec{s}}(t){\varvec{s}}^{{\text{H}}} (t)\} \ne {\mathbf{0}}\) and \(E\{{\varvec{s}}(t){\varvec{s}}^{{\text{T}}} (t)\} = {\mathbf{0}}\) are established at the same time, s(t) is the non-circular signal. The non-circular signal s(t) can be expressed as [34, 35]:

$${\varvec{s}}(t) = \user2{\psi s}_{0} (t)$$
(10)

where \({\varvec{\psi}} = {\text{diag}}\{e_{1}^{{ - j\phi_{1} }} ,e^{{ - j\phi_{2} }} , \ldots ,e^{{ - j\phi_{K} }} \}\), ϕK is the Kth non-circular phase of the non-circular signal, \({\varvec{s}}_{0} (t) \in {\mathbb{R}}^{K \times 1}\).

3 Methods

3.1 Expanded coprime array MIMO radar non-circular signal dimensionality reduction DOA estimation method

From the formula (9) and (10), the received signal of the coprime array can be expressed as:

$${\varvec{x}}(t) = \user2{A\psi s}_{0} (t) + {\varvec{n}}(t)$$
(11)

Using the non-circular characteristic of the signal s(t), the array flow matrix can be reconstructed, and the received signal can be reconstructed as:

$$\begin{aligned} {\varvec{y}}(t) & = \left[ {\begin{array}{*{20}l} {{\varvec{x}}(t)} \hfill \\ {{\varvec{x}}^{*} (t)} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\user2{A\psi }} \\ {{\varvec{A}}^{*} {\varvec{\psi}}^{*} } \\ \end{array} } \right]{\varvec{s}}_{0} (t) + \left[ {\begin{array}{*{20}c} {{\varvec{n}}(t)} \\ {{\varvec{n}}^{*} (t)} \\ \end{array} } \right] \\ & = {\varvec{Bs}}_{0} (t) + {\varvec{n}}_{0} (t) \\ \end{aligned}$$
(12)

where \({\varvec{n}}_{0} (t) = \left[ {\begin{array}{*{20}c} {{\varvec{n}}(t)} \\ {{\varvec{n}}^{ * } (t)} \\ \end{array} } \right]\), \({\varvec{B}} = \left[ {\begin{array}{*{20}c} {{\varvec{A\varPsi}}} \\ {{\varvec{A}}^{ * }{\varvec{\varPsi}}^{ * } } \\ \end{array} } \right]{ = }\left[ {{\varvec{b}}\left( {\theta_{1} ,\phi_{1} } \right),{\varvec{b}}\left( {\theta_{2} ,\phi_{2} } \right), \ldots ,{\varvec{b}}\left( {\theta_{K} ,\phi_{K} } \right)} \right]^{{\text{T}}}\), where

$${\varvec{b}}\left( {\theta_{K} ,\phi_{K} } \right){ = }\left[ {\begin{array}{*{20}l} {{\varvec{a}}\left( {\theta_{k} } \right)e^{{ - j\phi_{k} }} } \hfill \\ {{\varvec{a}}^{*} \left( {\theta_{k} } \right)e^{{j\phi_{k} }} } \hfill \\ \end{array} } \right]$$
(13)

Then the covariance matrix \({\varvec{R}} = E[{\varvec{y}}(t){\varvec{y}}^{{\text{H}}} (t)]\) of the received signal can be obtained from L snapshots. That is

$$\hat{\user2{R}} = \frac{1}{L}\sum\limits_{l = 1}^{L} {{\varvec{y}}\left( {t_{l} } \right){\varvec{y}}^{{\text{H}}} \left( {t_{l} } \right)}$$
(14)

Perform eigen decomposition on the covariance matrix A, we can get

$$\hat{\user2{R}}{ = }{\varvec{E}}_{{\text{s}}} {\varvec{D}}_{{\text{s}}} {\varvec{E}}_{{\text{s}}}^{{\text{H}}} + {\varvec{E}}_{{\text{n}}} {\varvec{D}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}}$$
(15)

where Ds is K × K diagonal matrix, whose diagonal elements are composed of K larger eigenvalues of the covariance matrix. Es is the signal subspace, which is the space formed by the eigenvectors corresponding to the K larger eigenvalues of the covariance matrix. Dn is composed of 2(M + N − 1)2 − K smaller eigenvalues with smaller diagonal elements. En is the noise subspace, which is the space formed by the eigenvectors corresponding to the 2(M + N − 1)2 − K smaller eigenvalues of the covariance matrix \(\hat{\user2{R}}\). According to the orthogonality between the noise subspace and the direction vector, the following spatial spectrum function is constructed as [17]:

$$P(\theta ,\phi ) = \frac{1}{{{\varvec{b}}^{{\text{H}}} (\theta ,\phi ){\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{b}}(\theta ,\phi )}}$$
(16)

After reconstructing the receiving matrix from non-circular signals, the spatial spectrum function is a two-dimensional spectral peak search, which is highly complex, and the following dimensionality reduction processing is performed. Firstly, reconstruct the formula (16), then:

$${\varvec{b}}(\theta ,\phi ) = \left[ {\begin{array}{*{20}l} {{\varvec{a}}\left( \theta \right)e^{ - j\phi } } \hfill \\ {{\varvec{a}}^{*} \left( \theta \right)e^{j\phi } } \hfill \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {{\varvec{a}}(\theta )} & {{\mathbf{0}}_{{M_{1} \times 1}} } \\ {{\mathbf{0}}_{{M_{1} \times 1}} } & {{\varvec{a}}^{ * } (\theta )} \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} {e^{ - j\phi } } \\ {e^{j\phi } } \\ \end{array} } \right] = {\varvec{P}}(\theta ){\varvec{e}}_{0} (\phi )$$
(17)

where

$${\varvec{a}}\left( \theta \right){ = }{\varvec{a}}_{{\text{r}}} \left( \theta \right) \otimes {\varvec{a}}_{{\text{t}}} \left( \theta \right)$$
(18)
$${\varvec{P}}(\theta ) = \left[ {\begin{array}{*{20}c} {{\varvec{a}}(\theta )} & {{\mathbf{0}}_{{M_{1} \times 1}} } \\ {{\mathbf{0}}_{{M_{1} \times 1}} } & {{\varvec{a}}^{ * } (\theta )} \\ \end{array} } \right]$$
(19)
$${\varvec{e}}_{0} (\phi ){ = }\left[ {\begin{array}{*{20}c} {e^{ - j\phi } } \\ {e^{j\phi } } \\ \end{array} } \right]$$
(20)

Define function V(θ,ϕ):

$$V(\theta ,\phi ) = \frac{1}{P(\theta ,\phi )}{ = }{\varvec{b}}^{{\text{H}}} (\theta ,\phi ){\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{b}}(\theta ,\phi )$$
(21)

substituting formula (17) into the formula (21), we can get:

$$\begin{aligned} V(\theta ,\phi ) & = {\varvec{e}}_{0} (\phi )^{{\text{H}}} {\varvec{P}}(\theta )^{{\text{H}}} {\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{P}}(\theta )e_{0} (\phi ) \\ & = {\text{e}}^{ - j\phi } {\varvec{e}}_{0} (\phi )^{{\text{H}}} {\varvec{P}}(\theta )^{{\text{H}}} {\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{P}}(\theta ){\varvec{e}}_{0} (\phi ){\text{e}}^{j\phi } \\ \end{aligned}$$
(22)

where let \({\varvec{q}}(\phi ) = {\varvec{e}}_{0} (\phi ){\text{e}}^{j\phi }\), \({\varvec{Q}}(\theta ){\mathbf{ = }}{\varvec{P}}(\theta )^{{\text{H}}} {\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{H} {\varvec{P}}(\theta )\). Then V(θ,ϕ) can be expressed as:

$$V(\theta ,\phi ) = {\varvec{q}}(\phi )^{{\text{H}}} {\varvec{Q}}(\theta ){\varvec{q}}(\phi )$$
(23)

where the formula (22) is about the problem of quadratic optimization, to find its optimal solution (θ,ϕ). Firstly, increase the constraint of eHq(ϕ) = 1 to eliminate the solution of q(ϕ) = 0, so as to obtain the optimal solution (θ,ϕ) of V(θ,ϕ). Use constraints to reconstruct the secondary optimization problem and seek the optimal solution, that is:

$$\min {\varvec{q}}(\phi )^{{\text{H}}} {\varvec{Q}}(\theta ){\varvec{q}}(\phi )\quad {\text{s.t.}}\quad {\varvec{e}}^{{\text{H}}} {\varvec{q}}(\phi ) = 1$$
(24)

The method of solving the optimal solution using the Lagrange multiplier method, construct the cost function L(θ,ϕ), that is:

$$L(\theta ,\phi ) = {\varvec{q}}(\phi )^{{\text{H}}} {\varvec{Q}}(\theta ){\varvec{q}}(\phi ) - \lambda \left( {{\varvec{e}}^{{\text{H}}} {\varvec{q}}(\phi ) - 1} \right)$$
(25)

where λ is constant. The partial derivative of formula (25) can be obtained as follows:

$$\frac{\partial L(\theta ,\phi )}{{\partial {\varvec{q}}(\phi )}} = 2{\varvec{Q}}(\theta ){\varvec{q}}(\phi ) + \lambda {\varvec{e}}$$
(26)

where let the formula (26) be equal to 0, then we can get:

$${\varvec{q}}(\phi ){ = } - \frac{\lambda }{2}{\varvec{eQ}}^{ - 1} (\theta )$$
(27)

Because of the constraint of eHq(ϕ) = 1, combined with formula (27), we can get:

$${\varvec{q}}(\phi ) = \frac{{{\varvec{Q}}^{ - 1} (\theta ){\varvec{e}}}}{{{\varvec{e}}^{{\text{H}}} {\varvec{Q}}^{ - 1} (\theta ){\varvec{e}}}}$$
(28)

Combining formulas (24) and (28) we can obtain:

$$\hat{\theta } = {\text{argmin}}\frac{1}{{{\varvec{e}}^{{\text{H}}} {\varvec{Q}}^{ - 1} (\theta ){\varvec{e}}}} = {\text{argmax}}\,{\varvec{e}}^{{\text{H}}} {\varvec{Q}}^{ - 1} (\theta ){\varvec{e}}$$
(29)

Because \({\varvec{Q}}(\theta ){\mathbf{ = }}{\varvec{P}}(\theta )^{{\text{H}}} {\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{P}}(\theta )\), then the one-dimensional spectral peak search function can be obtained:

$$f(\theta ) = {\varvec{e}}^{{\text{H}}} {\varvec{Q}}^{ - 1} (\theta ){\varvec{e}} = {\varvec{e}}^{{\text{H}}} \left( {{\varvec{P}}(\theta )^{{\text{H}}} {\varvec{E}}_{{\text{n}}} {\varvec{E}}_{{\text{n}}}^{{\text{H}}} {\varvec{P}}(\theta )} \right)^{ - 1} {\varvec{e}}$$
(30)

In the process of searching for the above-mentioned spectral peaks, the number of snapshots is limited due to the actual situation, which affects the accuracy of the noise subspace En, and reduces the DOA estimation performance of the algorithm. For this reason, use the power series of the noise feature to modify the corresponding noise subspace En, and the power series of the noise feature:

$${\varvec{C}}_{n} = \left[ {\lambda_{K + 1}^{n} e_{K + 1} ,\lambda_{K + 2}^{n} e_{K + 2} , \ldots ,\lambda_{{(M + N - 1)^{2} }}^{n} e_{{(M + N - 1)^{2} }} } \right]$$
(31)

where using formula (31), the above Q(θ) can be re-expressed as:

$${\varvec{Q}}(\theta ) = \mathop \sum \limits_{i = K + 1}^{{(M + N - 1)^{2} }} \lambda_{i}^{2n} \left( {\left| {{\varvec{P}}(\theta )^{{\text{H}}} {\varvec{e}}_{i} } \right|^{2} } \right)$$
(32)

where substituting formula (32) into the formula (30), the corrected one-dimensional peak search function can be obtained:

$$f(\theta ) = {\varvec{e}}^{{\text{H}}} {\varvec{Q}}^{ - 1} (\theta ){\varvec{e}} = {\varvec{e}}^{{\text{H}}} \left( {\mathop \sum \limits_{i = K + 1}^{{(M + N - 1)^{2} }} \lambda_{i}^{2n} \left( {\left| {{\varvec{P}}(\theta )^{{\text{H}}} {\varvec{e}}_{i} } \right|^{2} } \right)} \right)^{ - 1} {\varvec{e}}$$
(33)

In summary, the implementation steps of the non-circular signal dimensionality reduction DOA estimation method based on the expanded coprime array MIMO radar proposed in this article are shown in Table 1.

Table 1 The method steps of this article
Full size table

3.2 No phase ambiguity proof

Since the element spacing of the sparse array is greater than half a wavelength, there is a problem of angular ambiguity. But the method in this article adopts the expanded coprime array, which can effectively suppress the phase ambiguity problem. The proof is as follows:

Suppose there is phase ambiguity, that is, there is an ambiguity angle θm, which satisfies:

$${\varvec{a}}(\hat{\theta }_{k} ) = {\varvec{a}}(\theta_{m} )$$
(34)

where \(\hat{\theta }_{k}\) is the estimated value of the direction of arrival, and θm is the value of the ambiguity angle. From formula (34), we can get:

$${\varvec{a}}_{{\text{r}}} \left( {\hat{\theta }_{k} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\hat{\theta }_{k} } \right){ = }{\varvec{a}}_{{\text{r}}} \left( {\theta_{m} } \right) \otimes {\varvec{a}}_{{\text{t}}} \left( {\theta_{m} } \right)$$
(35)

Substituting formulas (2) and (3) into formula (35), we can get:

$$\left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{{\text{r}}1}} \left( {\hat{\theta }_{k} } \right)} \\ {{\varvec{a}}_{{{\text{r}}2}} \left( {\hat{\theta }_{k} } \right)} \\ \end{array} } \right] \otimes \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{{\text{t}}1}} \left( {\hat{\theta }_{k} } \right)} \\ {{\varvec{a}}_{{{\text{t}}2}} \left( {\hat{\theta }_{k} } \right)} \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{{\text{r}}1}} \left( {\theta_{m} } \right)} \\ {{\varvec{a}}_{{{\text{r}}2}} \left( {\theta_{m} } \right)} \\ \end{array} } \right] \otimes \left[ {\begin{array}{*{20}c} {{\varvec{a}}_{{{\text{t}}1}} \left( {\theta_{m} } \right)} \\ {{\varvec{a}}_{{{\text{t}}2}} \left( {\theta_{m} } \right)} \\ \end{array} } \right]$$
(36)

Expand the formula (36), we can get:

$$\frac{{2\pi d_{l} \sin \hat{\theta }_{k} }}{\lambda } - \frac{{2\pi d_{l} \sin \theta_{m} }}{\lambda } = 2k\pi$$
(37)

where dl is the element spacing. From the formula (37), we can get:

$$\left\{ {\begin{array}{*{20}l} {\sin \hat{\theta }_{k} - \sin \theta_{m} = 2k_{1} {/}M} \hfill \\ {\sin \hat{\theta }_{k} - \sin \theta_{m} = 2k_{2} {/}N} \hfill \\ \end{array} } \right.$$
(38)

where \(k_{1} \in ( - N,N)\), \(k_{2} \in ( - M,M)\). In the coprime array, M and N are integers that are mutually prime numbers. According to theorem 1 of the literature [29], it can be known that there is no M and N in formula (36), that is, there is no blur angle θm that holds true in Eq. (34). That is, it proves that there is no phase ambiguity problem.

3.3 Complexity analysis

It can be seen from the above that the complexity of the NRC-MIMO MUSIC algorithm proposed in this article mainly focuses on the calculation of covariance, the eigenvalue decomposition of the covariance matrix, and the peak search calculation of the DOA angle. Let q = M + N − 1, then the calculation of the algorithm in this article is complicated. The degree is O[4q4(L − K) + 16q6 + 8n2(q4 + q2)], and the complexity of the two-dimensional MUSIC algorithm is O[4q4(L − K) + 16q6 + n2(4q4 + 2q2)], n is the number of peak searches. For clarity, we list the computational complexity of these methods in Table 2 with L = 500, M = 3, N = 4, K = 2, and n = 5000. In order to be more intuitive, we compare the computational complexity of the two methods under different snapshots, as shown in Fig. 2. Therefore, we can see that the method proposed in this article is less complex.

Table 2 Computational complexity of different methods
Full size table
Fig. 2
figure 2

The computational complexities of different methods versus snapshots

Full size image

4 Results and discussion

In order to verify the effectiveness of the algorithm in this article, the NRC-MIMO MUSIC algorithm in this article is compared with the classic MUSIC algorithm and the traditional coprime array MUSIC algorithm. Define the root mean square error (RMSE) formula as follows:

$${\text{RMSE}} = \frac{1}{k}\mathop \sum \limits_{1}^{k} \sqrt {\frac{1}{100}\mathop \sum \limits_{J = 1}^{100} \left( {\hat{\theta }_{k,J} - \theta_{k} } \right)^{2} }$$
(39)

where J represents the number of Monte Carlo experiments, \(\hat{\theta }_{k,J}\) represents the estimated DOA value of θk in the Jth experiment, and θk is the true value of the angle.

The proposed algorithm is simulated on MATLAB R2018b software to verify its performance. Set the transmitting array element and the receiving array element to M = 3 and N = 4, respectively. The number of sources is 2, the target angle is 10° and 20°, the number of snapshots is 100, and the number of Monte Carlo experiments is 100. Figure 3 shows the estimation results of the proposed algorithm for all targets when the SNR = 10 dB. It can be seen that the algorithm in this article can accurately estimate the angle of multiple independent targets at the same time.

Fig. 3
figure 3

Algorithm estimation performance under SNR = 10 dB

Full size image

Figure 4 shows the DOA of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm under the condition of 100 snapshots under different SNB estimated performance. It can be seen from Fig. 4 that with the gradual improvement in the signal-to-noise ratio of the three algorithms, the root mean square error RMSE is all getting smaller, and the DOA estimation performance is improved. In addition, it can be seen from the above figure that the algorithm proposed in this article is better than the other two algorithms, and the DOA estimation performance is better. It can also be seen that the relatively prime array can significantly improve the DOA estimation performance compared to the uniform linear array.

Fig. 4
figure 4

Estimation performance changes under different SNR

Full size image

Figure 5 shows the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm under 100 effective computer simulation experiments, the target detection success rate varies with the SNR. Target detection success rate, that is, the ratio of the number of successful DOA estimates to the number of trials. When \(\left| {\hat{\theta }_{K} - \theta_{K} } \right| < 1\) (where \(\hat{\theta }_{k}\) is the estimated value of DOA and θk is the actual value), it is deemed to be a successful estimate of DOA. It can be seen from Fig. 5 that the success rate of the three algorithms increases as the SNR increases. When the SNR is equal to 10 dB, the success rates of the three algorithms all reach 100%. But when the SNR is less than 10 dB, the success rate of this algorithm is better than the other two algorithms. In the case of low SNR, it still maintains a high success rate. This shows that the algorithm in this article is still applicable under the condition of low SNR. The algorithm in this paper uses MIMO radar, which greatly expands the array aperture and improves the degree of freedom of the array. The introduction of non-circular signals further expands the receiving array and improves the measurement accuracy of the algorithm. Finally, the noise subspace is further modified to further improve the DOA estimation accuracy. Therefore, the success rate of this algorithm is higher than the other two algorithms.

Fig. 5
figure 5

The target detection success rate varies with SNR

Full size image

Table 3 shows the specific values of the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO non-circular signal dimensionality reduction MUSIC algorithm under different SNR. It can be seen from Table 3 that as the SNR increases, the estimation performance of the three algorithms gradually improves. However, the algorithm proposed in this article is better than the other two algorithms under different SNR, and the estimation accuracy is higher. When the SNR is 15 dB, the estimation performance of the algorithm proposed in this article can be equivalent to that of the classic MUSIC when the SNR is 25 dB. When the SNR = 10 dB, the RMSE of the algorithm in this article is reduced by about 64% compared to the classic MUSIC algorithm, and about 39% compared with the traditional coprime array MUSIC algorithm. The RMSE of the traditional coprime array MUSIC algorithm is reduced by about 41% Compared with the classic MUSIC algorithm. Therefore, it can be seen that compared to the other two algorithms, the estimation accuracy of the algorithm in this article is higher, and the coprime array can significantly improve the DOA estimation accuracy of the algorithm compared with the uniform linear array.

Table 3 RMSE value under different SNR
Full size table

Figure 6 shows the variation of the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm under different snapshots. It can be seen from Fig. 6 that as the number of snapshots increases, the RMSE of the three algorithms gradually decreases, and the estimation performance gradually improves. Among them, the classic MUSIC algorithm has the worst angle estimation performance, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm has the best angle estimation performance and is more stable. The algorithm in this article still has good estimation performance when the number of snapshots is low.

Fig. 6
figure 6

Estimated performance changes under different snapshots

Full size image

Figure 7 shows the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm under 100 effective computer simulation experiments, the target detection success rate varies with the snapshots. It can be seen from Fig. 7 that the success rate of the three algorithms increases as the number of snapshots increases. When the number of snapshots is equal to 300, the target detection success rate of the algorithm proposed in this article is almost 100%, and when the number of snapshots is large enough, the target detection success rate of all algorithms can reach 100%. In the case of the same number of snapshots, the algorithm proposed in this article has a higher target detection success rate than the other two algorithms. In the case of a lower number of snapshots, the target detection success rate of the algorithm proposed in this article is significantly higher than that of the classic MUSIC algorithm and traditional coprime array MUSIC algorithm.

Fig. 7
figure 7

The success rate of target detection varies with the number of snapshots

Full size image

Table 4 shows the specific values of the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO non-circular signal dimensionality reduction MUSIC algorithm under different snapshots. It can be seen from Table 4 that, when the number of snapshots is low, the angle estimation accuracy of the classic MUSIC algorithm is the lowest, and the angle estimation accuracy of the algorithm proposed in this article is the highest. As the number of snapshots increases, the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO non-circular signal dimensionality reduction MUSIC algorithm gradually decreases, and the accuracy of the algorithm is gradually improved. Among them, the angle estimation accuracy of the algorithm proposed in this article is the highest, and the angle estimation accuracy of the classic MUSIC algorithm is the lowest. In the case of 100 snapshots, the RMSE of the proposed algorithm is about 62% lower than that of the classic MUSIC algorithm, and the RMSE of the traditional coprime array MUSIC algorithm is about 41% lower than that of the classic MUSIC algorithm. Therefore, in practical applications, the number of snapshots should be selected as high as possible when practically permitted, so as to improve the DOA estimation performance.

Table 4 RMSE values under different snapshots
Full size table

Figure 8 shows the variation of the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO radar non-circular signal dimensionality reduction MUSIC algorithm under different numbers of array elements. Set the number of transmitting array elements to 4, and the number of receiving array elements to 3, 5, 7, 9, and 11. The number of sources is 2, the target angle is 10° and 20°, the number of snapshots is 100, and the number of Monte Carlo experiments is 100. The experiment parameters are simulated by MATLAB, and RMSE of the three algorithms decreases with the increase of the number of elements, and the accuracy of angle estimation is improved. Among them, the classic MUSIC algorithm has the lowest angle estimation accuracy, and the algorithm proposed in this article has the highest accuracy. In the case of a small number of transmitted array elements, the algorithm proposed in this article has higher estimation accuracy than the other two algorithms.

Fig. 8
figure 8

Relationship between the estimation accuracy and the number of array elements

Full size image

Table 5 shows the specific values of the RMSE of the classic MUSIC algorithm, the traditional coprime array MUSIC algorithm, and the expanded coprime array MIMO non-circular signal dimensionality reduction MUSIC algorithm under different numbers of array elements. It can be seen from Table 5 that when the number of array elements is small, the angle estimation accuracy of the classic MUSIC algorithm is the lowest, and the angle estimation accuracy of the expanded coprime array MIMO non-circular signal dimensionality reduction MUSIC algorithm is the highest. When the number of array elements is 3, the RMSE of the proposed algorithm is about 62% lower than that of the classic MUSIC, and the RMSE of the traditional coprime array MUSIC algorithm is about 54% lower than that of the classic MUSIC algorithm. As the number of array elements increases, the accuracy of each algorithm is gradually improved. The angle estimation accuracy of the algorithm proposed in this article is the highest, and the angle estimation accuracy of the classic MUSIC algorithm is the lowest.

Table 5 RMSE values under different numbers of array elements
Full size table

Under the expanded coprime array MIMO radar signal model, set the number of snapshots to 100, the number of sources to 2, the target angle to 10° and 20°, the number of receiving array elements N remains unchanged, and the number of transmitting array elements M to 3, 5, 7. Carry out 100 Monte Carlo experiments, get the RMSE graph of angle measurement accuracy with SNR under different numbers of transmitting array elements. It can be seen from Fig. 9 that in the case of different transmitting array elements, the RMSE of the algorithm proposed in this paper decreases as SNR increases, and the angle measurement estimation accuracy becomes better. The larger the SNR, the smaller the influence of noise on the algorithm, and the higher the accuracy of DOA estimation. When the number of transmitter array elements is 3, the root mean square error is large and the measurement accuracy is low. However, when the number of transmitter array elements is 7, the RMSE becomes smaller and the angle measurement estimation accuracy is improved. It can be seen that under the same circumstances, the more the number of launching array elements, the smaller the root mean square error, and the better the accuracy of the measurement angle.

Fig. 9
figure 9

Performance comparison of NRC-MIMO MUSIC algorithm with different numbers of transmitting array elements

Full size image

Table 6 shows the specific values of the root mean square error (RMSE) of the algorithm proposed in this paper with the change of the SNR under different numbers of transmitting array elements. It can be seen from Table 6 that, in the case of the same SNR, the angle estimation accuracy of the transmitting array element number 3 is the lowest, and the angle estimation accuracy of the transmitting array element number 7 is the highest. As the SNR increases, the RMSE becomes smaller and the algorithm accuracy improves. When the SNR is 5 dB, the RMSE of the transmitting array element M = 5 is about 45% lower than the RMSE of M = 3. The RMSE of the transmitting array element M = 7 is about 60% lower than the RMSE of M = 3. Therefore, the number of array elements has a great influence on the DOA estimation accuracy. The more the number of array elements, the higher the DOA estimation accuracy. However, the actual number of array elements is affected by the hardware. The more array elements, the larger the hardware volume. Therefore, the number of array elements is not infinite and needs to be selected according to the actual situation.

Table 6 RMSE values under different transmitting array elements M and SNR
Full size table

5 Conclusion

This paper proposes a non-circular signal DOA estimation method based on coprime array MIMO radar, which solves the problems of low degree of freedom, small array aperture, and phase ambiguity of traditional coprime array DOA estimation methods. In this paper, the array model combines a coprime array with MIMO radar, which greatly improves the array aperture, increases the degree of freedom, and improves the accuracy of DOA estimation. Then, the non-circular signal is introduced, and the receiving matrix is effectively expanded by using the non-circular characteristic, and the parameter estimation performance and the estimation accuracy of multiple sources are improved. Then use the idea of dimensionality reduction to reduce the dimensionality of the two-dimensional MUSIC algorithm to reduce the complexity of the algorithm. The power series of noise eigenvalues is used to correct the noise subspace, which further improves the accuracy of the algorithm. In addition, coprime array is used as the receiving array, which eliminates the phase ambiguity problem caused by the distance between the array elements larger than half the wavelength. Finally, the effectiveness of the algorithm is verified by simulation experiments. Compared with the classic MUSIC algorithm and the traditional MUSIC algorithm, the algorithm in this paper can better improve the DOA estimation accuracy and successful resolution. And it still maintains superior performance under low SNR. In the future, the propagator method will be integrated into the method research of this paper to further reduce the complexity of the algorithm, so as to improve the real-time performance of the algorithm in practical applications. The research method will be applied to vehicle radar. And continue to study the processing of multi-source signals and circular signals.