1 Introduction

As a fundamental topic in image and video processing, denoising has been widely studied in [1,2,3,4,5,6]. In recent years, image denoising methods mainly exploit three paradigms, i.e., global methods, filtering methods and patch-based methods. Originated from the literature [7], patch-based approaches [8,9,10,11,12] have shown great success to various image processing tasks, in which the essence of these methods is to exploit the recurrence of similar patches extracted from the noise image and the nonlocal self-similarity of natural images.

The most important thing of these patch-based methods is how to accurately measure the similarity between different patches of a natural image. Nearest neighbor search (NNS) that based on Euclidean distance (ED), that is the square error of corresponding two patches, is one of widely used patches searching method, and the so-called BM3D algorithm [13] is one of its classical application. NNS method performs similar patches searching in a local window of image, thus is a local searching method. However, patches with significant structures, for example round edges or corners in an image, do not have a repeating pattern within a local window, which indicates that only using NNS to find similar patches is not an optimal method.

In order to better capture the structural similarity patches in natural images, various similar patches searching methods have been established in the literature. In [14], a so-called Needle patch representation method is proposed to improve on the reliability of patch-matching when the image quality deteriorates, and the patch representation Needle consists of small multi-scale versions of the patch and its immediate surrounding region. With the development of recent innovations in training deep convolutional neural network, a deep learning local image patches matching methods that based on Triplet and Siamese networks using a combination of triplet loss and global loss has been proposed in [15]. In [16], a 2-channel based neural network is established to learn a general image patches similarity function directly from raw image pixels.

Patch priors that give high likelihoods for patches will yield better patches restoration performance [17]. Recently, using learned specific probabilistic distribution of patches from noise-free image dataset to globally search and recover similar patches from a degraded image has become a hot research issue in image processing. In principle, the probabilistic distribution of patches can be modeled using arbitrary distributions, but most commonly, Gaussian mixture model (GMM) is often used to model patches priors [17], even though the literature [18] argues that a generalized Gaussian mixture model is a better fit for image patches prior modeling. In fact, patches priors are learned over small image patches by GMM will make computational tasks such as learning, inference and likelihood estimation much easier than working with whole images. GMM also has been shown to be a powerful tool for patches classification and for similar patches matching. In addition, the learned means, covariance matrices and mixing weights over all patches can greatly improve the accuracy for searching similar patches.

The expected patch log likelihood (EPLL) algorithm [17] based on GMM employs a global prior to search patch such that every selected patch is more like the given local prior. In [19], by integrating the external patch prior and internal self-similarity into one framework, the learned GMM (external patch prior) is used to guide the clustering of patches from the input degraded images, and then a patches matrix low-rank approximation process (internal self-similarity) is used to estimate the latent subspace for image recovery. In [20], a patch searching method that clusters similar patch candidates into patch groups using GMM-based clustering is proposed, and the selected patch groups that contain the reference patch are used to image denoising.

However, the simple GMM clustering method generally puts some nonsimilar patches, especially geometric nonsimilar patches, into a group which indicates this kind of similarity measure between patches is not accuracy. In other words, we need a more refined clustering method to determine which patches are similar or nonsimilar, which will motivate us to refine the GMM patches clustering method. To this end, in this paper, we exploit two additional operations to refine the GMM patches cluster: firstly, we employ a simple K-means methods to refine the patches classification by using the mean intensity of each patch; secondly, for each reference patch in a certain group, we gradually expand the search radius until the number of similar patches contained in this circle satisfy our needs. The aim to do this is because the more similar images patches are grouped together (in the patches matrix sense [19] or the patches tensor used in this paper), the better the patches denoising effect will be. To better exploit the spatial geometric structural information of similar patches, we apply the 3D patches tensor \({\mathcal{X}}\), as shown in Fig. 1, to organize the similar patches instead of vectorizing each patches to form a similar patches matrix as in [19], then low-rank tensor approximation method based on HOSVD is used to perform image denoising. An iterative adaptive weighted core tensor thresholding algorithm is proposed to achieve low-rank tensor approximation. The reason using this algorithm are twofold, firstly, the tensor nuclear norm [21] (in fact is the \(\ell _{1}\) norm penalization) will result in significantly biased estimation to the values in core tensor, thus cannot achieve a reliable image recovery. Secondly, although the nonconvex penalty, such as \(\ell _{p}\) with \((0\le p <1)\), can also provide unbiased solution, it is computationally cumbersome. As a surrogate to nonconvex penalty [22], the weighted \(\ell _{1}\) norm not only can ameliorate the bias to the larger values in core tensor, but also is low computational complexity.

Fig. 1
figure 1

A third-order tensor \({\mathcal{X}}\in R^{I\times J\times K}\)

Full size image

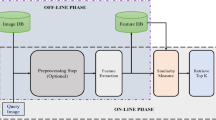
The initial motivation of this work come from two observations: firstly, tensor organization of image patches can preserve more structural information of image than matrix form of vectorized image patches exploited in the literature; secondly, the more accurate the distance/similarity measure between image patches is, the better the image denoising effect achieved by low-rank image patches tensor approximation method will be. These observations inspire us to propose an image similar patches clustering method, denoted as GKGLM, i.e., “GMM” + “k-means” + “inter-class geometry location similarity patches searching.” The advantages of these variants of GMM are the hybrids globally patches searching (i.e., GMM) and the locally patches searching (i.e., the k-means and inter-class geometry location similarity patches searching). Furthermore, consider the high computational complexity of training process of GMM using expectation maximization (EM) method, we propose a novel GPU based GMM training method using the back propagation and gradient descent method. Meanwhile, an iterative weighted image patches tensor approximation is proposed to perform image denoising, which the key advantage of this iterative method is the unbiased estimation to larger entry values in core tensor that are the main feature of images. See Fig. 2 for the flowchart of this paper.

Fig. 2
figure 2

Flowchart of clustering and denoising

Full size image

The main contributions of this paper arise from the following analysis:

  1. 1.

    A global similar patches searching method is proposed based on GMM patches clustering method, the k-means method and a local searching method within patches group are also being integrated into this framework to improve the accuracy of this patches clustering method, which will preserve more geometric structural similar information of patches.

  2. 2.

    A GPU based parallel training method is proposed to accelerate the GMM modeling training solved by EM algorithm.

  3. 3.

    In order to preserve more spatial geometric structural image information and fine details information image during denoising, an iterative adaptive weighted patches tensor approximation method is proposed.

The rest of the paper is organized as follows. In Sect. 2, we provide a brief introduction of the GMM and discuss how to search similar patches of the reference patch, including the algorithm of training GMM by the expectation maximization (EM) algorithm. In Sect. 3, we introduce the definition of three-order tensor, the properties of the corresponding core tensor and HOSVD algorithm. The iterative weighted image patches tensor approximation algorithm for image denoising is discussed in Sect. 4. We present numerical experiments and results in Sect. 5.The conclusion is presented in Sect. 6.

2 Similar patches matching by deep cluster based GMM training

2.1 GMM patches prior modeling

As being beforementioned, the probabilistic distribution of patches can be modeled using arbitrary distributions; but most commonly, GMM is used to learn patches priors. We take advantage of GMM as a probabilistic model to learn patch priors from noise-free patches set; then, noisy image patches clustering guided by the learned Gaussian mixture priors. GMM makes global searching for similar patches of a reference patch in the whole noise image.

The probability of a random patch from clean images sets will be defined as follows:

$$\begin{aligned} p(x_{i}|\varTheta )=\sum _{k=1}^{K}w_{k}p(x_{i}|\theta _{k}) \end{aligned}$$
(1)

where \(\varTheta =(w_{1}, \dots , w_{K}, \theta _{1}, \ldots , \theta _{K} )\) is a set of parameters; \(w_{k}\) denotes the weight that probability function \(p(x_{i}|\theta _{k})\) (\(k=1,\ldots K\)) contributes to \(p(x_{i}|\varTheta )\) and \(\sum _{k=1}^{K}w_{k}=1\); \(\theta _k=(\mu _{k},\varSigma _{k})\) are mean value and covariance matrix, respectively, in density function \(p(x_{i}|\theta _{k})\). One of the most important feature of the patches is that it is close to a low-dimensional manifold for many natural images. Therefore, to more accurately measure the distance between different patches, we replace the frequently used Euclidean distance (ED) with Mahalanobis distance (MD) to measure the patches difference used in patches cluster problem, i.e., \(p(x_{i}|\theta _{k})=c\cdot \exp (-\frac{1}{2}(x_{i}-\mu _{k})^{T}\varSigma _{k}^{-1}(x_{i}-\mu _{k}))\), where c is a constant. As shown the patches correct matching rates results in Table 1 from [19], even though the correct matching rates of ED is better than that of MD in image homogenous region, the MD overwhelmingly surpass that of ED in the structural and textural region, which indicates that using Mahalanobis distance to measure the difference between image patches is more reasonable than using Euclidean distance.

Table 1 Patches correct matching rates (ED vs. MD) [19]
Full size table

2.2 Parameters estimation using EM algorithm based on GPU

To accelerate image denoising algorithm, we exploit a pre-trained GMM for the first step to cluster the similar patches. That is the parameters in GMMs modeling in (1) will be learned from training image patches set using the expectation maximization (EM) algorithm. However, most traditional implementation of EM algorithm is high computational complexity, thus cost a large amount of time in training processing. On the other hand, because the most time-consuming process in training is the calculation of distance between different patches, thus, it is easy to consider to apply parallel computing to accelerate GMM training with GPU.

It is well known that an EM based GMM training methods include these two steps, i.e., expectation step and maximization step, respectively. Expectation step in EM algorithm is a kind of evaluation and cluster processing, that is the model parameters learned in the maximization step will be checked by evaluating the difference between the last and the current clustering results. And the maximization step is the parameters estimation processing, which is used to fit the new cluster results by using maximum likelihood estimation (MLE) method.

In the following, we establish a deep cluster based GMM training to accelerate the EM training algorithm. Particularly, in the parameters estimation step (maximization step), we first establish a binary cross-entropy (BCE) loss function based on the difference between the last clustering results \(Y^{k}\) and the current clustering results \({\hat{Y}}\) in the testing step (i.e., the Expectation step), then, the back-propagation algorithm and the stochastic gradient descent (SGD) method based on GPU are used to estimate the parameters of GMM modeling. See more details in Algorithm (1). We train the GMM prior model from a set of 2 million overlapping patches that randomly sampled from [23] with their DC removed. Allowing for overlapping when sampling patches is important because otherwise there would appear blocking artifact. See Fig. 3 for the GMM model learned flowchart.

figure a
Fig. 3
figure 3

Flowchart of training GMM

Full size image

2.3 Similar patches searching by deep cluster based GMM training

Based on the previously trained GMM patches model, given a reference patch, we propose a “GMM” + “k-means” + “inter-class geometry location similarity patches searching” method to refine the patches similarity matching.

Given a noisy image Y, we firstly split it into a set of overlapping patches, then we denote \(P_{i}Y\) by the i-th patch of Y. The likelihood of the i-th patch belongs to the kth (\(k=1,\ldots ,K\)) cluster under parameter \(\varTheta\) is defined:

$$\begin{aligned} p(k|P_{i}Y)=\frac{w_{k}p(P_{i}Y|\theta _{k})}{\sum _{j=1}^{K}w_{j}p(P_{i}Y|\theta _{j})}. \end{aligned}$$
(6)

It is should be noticed that here \(\varTheta =(w_{1}, \ldots , w_{K}, \theta _{1}^{'}, \dots , \theta _{K}^{'} )\) with \(\theta _i=(\mu _{i},\varSigma _{i}{'})\) are estimated by \(\varSigma _{k}{'}=\varSigma _{k}+\sigma ^{2}I\), where \(\varSigma _{k}\) is a covariance matrix of the learned GMMs, \(\sigma\) is the noise standard deviation and I is an identity matrix. Maximizing the likelihood (6) to determine Gaussian component that makes the likelihood maximum, then we denote it to be the \({\hat{k}}\)th Gaussian component and assign the ith noisy patch into the \({\hat{k}}\) cluster. This is the GMM based noisy patches globally cluster, and all patches of the noisy image Y are split into different several clusters. As we have been emphasized in Sect. 2.1, there exists a deficiency of GMM based clustering method, i.e., in image homogenous region, the Euclidean distance based clustering method is better than the GMM based patches clustering method. Motivated by this observation, to improve the accuracy of patches matching, we employ a simple K-means method to each GMM based cluster to refine patches classification. After that, if there exists a class with the number of patches in it is less than 10, we will merge the patches in this class to the other classes most likely.

Next, we explain how to choose number of similar patches of a reference patch in each class to form a patches tensor. We firstly determine which class each reference patch is in, then we select similar patches for each reference from this class by calculating the location distance from reference patch to each patch in this class, i.e., the distance from the upper-left pixel of reference patch and the patches in this class. Secondly, the first T least distance corresponding to the patches is selected to form a similar patches tensor. We call this process to be the inter-class geometry location similarity patches searching method.

Thus, our similarity patches searching method can utilize the global information and the local location information of image. For convenience, we denote this clustering method as GKGLM, i.e., “GMM” + “k-means” + “inter-class geometry location similarity patches searching.” At last, we summarize the GKGLM algorithm in Algorithm 2.

figure b

3 Low-rank image patches tensor approximation

3.1 Rank of patches tensor and HOSVD

Third-order patches tensors have column, row and tube fibers; Figs. 4 and 5 show the horizontal, lateral and frontal slides of a third-order. Low-rank matrix approximation methods are to measure the low-rank structure of the observed matrix X by minimizing its rank. Similarly, the latent tensor data can be approximated from low-rank version of observed tensor measurements. But, the low-rank decomposition to a multidimensional tensor usually is ticklish, and generally, there exist at least three different rank definitions of multidimensional tensor relative to different low-rank tensor decompositions, and it is hard to find a tight convex relaxation to the nonconvex rank function of multidimensional tensor. Two often used rank definitions of tensor are the CANDECOMP/PARAFAC (CP) rank and Tucker rank.

Fig. 4
figure 4

Fibers of a third-order tensor

Full size image
Fig. 5
figure 5

Slices of a third-order tensor

Full size image

Definition 1

The CP rank of a tensor \({\mathcal{X}}\in R^{I_{1}\times \cdots \times I_{N}}\) is defined as the minimum number of rank-1 decomposition,

$$\begin{aligned} {\text{rank}}_{CP}({\mathcal{X}})=\min \left\{ r|{\mathcal{X}}=\sum _{i=1}^{r}c_{i}{\mathcal{V}}_{i}\right\} \end{aligned}$$
(7)

where \({\mathcal{V}}_{i}=a_{1}^{(i)}\otimes \cdots \otimes a_{k}^{(i)}\), symbol \(\otimes\) denotes vector outerproduct, \(a_{j}^{(i)}\in R^{n_{j}}\) is a vector and \(c_{i}\) is the decomposition coefficient [24].

Definition 2

Tucker rank of a tensor \({\mathcal{X}}\in R^{I_{1}\times \cdots \times I_{N}}\) is denoted by \({\text{rank}}_{T}({\mathcal{X}})\) and is a N-dimensional vector expressed as follows:

$$\begin{aligned} {\text{rank}}_{T}({\mathcal{X}})=\big ({\text{rank}}(X_{(1)}), \ldots , {\text{rank}}\big (X_{(N)}\big )\big ) \end{aligned}$$
(8)

where \({\text{rank}}(X_{(i)})\) denotes the matrix rank of ith-mode matricization(see the following section) \(X_{i}\) to tensor \({\mathcal{X}}\) for \(i=1,2, \ldots , N\).

Based on these two definitions of tensor rank, tensor has a similar nuclear norm like the matrix nuclear norm, i.e., tensor nuclear norm (TNN), which is one extension of matrix nuclear norm [21].

$$\begin{aligned} ||{\mathcal{X}}||_{*}=\mathop {\min }\limits _{\mathcal{X}}\sum _{i=1}^{N}||X_{(i)}||_{*} \end{aligned}$$
(9)

The tensor trace norm (TTN) is similar to TNN, it is developed in [25]

$$\begin{aligned} ||{\mathcal{X}}||_{*}=\sum _{i=1}^{N}\alpha _{i}||X_{(i)}||_{*} \end{aligned}$$
(10)

where \(\alpha _{i}>0\) and \(\sum _{i=1}^{N}\alpha _{i}=1\).

TNN and TTN, in essence, merely is a convex combination of trace norms of the nth-mode unfolding \(X_{(i)}\). A novel tensor nuclear norm \(||{\mathcal{X}}||_{\mathrm{TNN}}\) is proposed in the literature [26] and is defined as the sum of the singular values of all frontal slices. This tensor nuclear norm has also been proved to be a norm and be the tightest convex relaxation to \(\ell _{1}\) norm of tensor multilinear rank.

A HOSVD to a tensor \({\mathcal{X}}\in R^{I_{1}\times \cdots \times I_{N}}\) can be expressed as a core tensor \({\mathcal{S}}\in R^{r_{1}\times \cdots \times r_{N}}\) and matrices multiplication shown as follows,

$$\begin{aligned} {\mathcal{X}}={\mathcal{S}}\times _{1}U^{(1)}\times _{2}U^{(2)}\times _{3}\cdots \times _{N}U^{(N)} \end{aligned}$$
(11)

where \(U^{(i)}\in R^{I_{i}\times r_{i}}\) \((1\le i \le R)\) is the left singular orthogonal matrix calculated by performing SVD on matrix \(X_{i}\). Figure 6 shows a HOSVD to a third-order tensor. The inverse HOSVD is defined by:

$$\begin{aligned} {\mathcal{S}}={\mathcal{X}}\times _{1}{U^{(1)}}^{T}\times _{2}{U^{(2)}}^{T}\times _{3}\cdots \times _{N}{U^{(N)}}^{T} \end{aligned}$$
(12)

where \((\cdot )^{T}\) denotes the matrix transpose operation.

Fig. 6
figure 6

HOSVD to third-order tensor

Full size image

In some tensor decompositions, we need to unfold or flatten the tensor into matrix, a.k.s. matricization. There are N mode matricization to a Nth-order tensor. The nth-mode matricization of a tensor \(\varvec{{\mathcal{X}}} \in {\mathbb{R}}^{I_{1} \times I_{2} \times \cdots \times I_{N}}\) is denoted by \(X_{(n)}\in {\mathbb{R}}^{I_{n}\times (I_{1}I_{2}\ldots I_{n-1} I_{n+1} \ldots I_{N})}\) \((n=1,2,\ldots ,N)\) is a matrix. We also denote functions \({\text{unfold}}_{n}(\cdot )\) and \({\text{fold}}_{n}(\cdot )\) to be the nth-mode unfolding and folding operation, that is, \(X_{(n)}={\text{unfold}}_{n}({\varvec{{\mathcal{X}}}})\) and \({\varvec{{\mathcal{X}}}}={\text{fold}}_{n}(X_{(n)})\).

There are many different arrangement ways of the nth-mode matricization, but in practice, permutation of elements doesn’t affect the result of calculation [27]. See Fig. 7 for a third-order tensor matricization. The nth-mode product is denoted by \({\varvec{{\mathcal{X}}}} \times _{n} U\) where \({\varvec{{\mathcal{X}}}} \in {\mathbb{R}}^{I_{1} \times I_{2} \times \cdots \times I_{N}}\) is a tensor and \(U \in {\mathbb{R}}^{J \times I_{n}}\) is a matrix. We can obtain a tensor \({\mathcal{Y}}={\varvec{{\mathcal{X}}}} \times _{n} U\) of size \(I_{1} \times I_{2} \times \cdots \times I_{n-1} \times J \times I_{n+1} \times \cdots \times I_{N}\). The nth-mode product can be expressed by matrix multiplication using \({\text{fold}}_{n}(\cdot )\) as follows

$$\begin{aligned} {\varvec{{\mathcal{Y}}}}={\text{fold}}_{n}(U \times X_{(n)}) \Leftrightarrow Y_{(n)}=U \times X_{(n)} \end{aligned}$$
(13)

At last, the Frobenius norm of tensor \({\mathcal{X}}\) is denoted by \(\Vert {\mathcal{X}}\Vert _{F}=(\sum _{i_{1,\ldots ,i_{N}}} |x_{i_{1,\ldots ,i_{N}}}|^{2})^{1/2}\); 2-norm of vector v is denoted by \(\Vert v\Vert _{2}\).

Fig. 7
figure 7

Matricization of tensor \({\mathcal{X}}^{3\times 4 \times 2}\)

Full size image

3.2 Low-rank patches tensor approximation

In this section, we establish a low-rank patches tensor approximation method that begin by an example. Consider a tensor \({\mathcal{X}} \in {\mathbb{R}}^{3 \times 2 \times 3}\) and the corresponding core tensor \(\varvec{{\mathcal{S}}}\) with three horizontal slices, shown in Fig. 8. Three associated singular values matrices \(\varSigma _{(i)},(i=1,2,3)\) obtained by SVD to the corresponding nth-mode matricization of tensor \(\varvec{{\mathcal{X}}}\), i.e., \(X_{(i)},(i=1,2,3)\), are listed as follows

$$\begin{aligned} \varSigma _{(1)}= & {} \begin{bmatrix} 7.5284 &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 5.9433 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}\\ \varSigma _{(2)}= & {} \begin{bmatrix} 9.3063 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 2.3221 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}\\ \varSigma _{(3)}= & {} \begin{bmatrix} 7.2051 &{}\quad 0 &{}\quad 0&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 5.9551 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 2.1502&{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}. \end{aligned}$$

Three nth-mode matricization of core tensor \(\varvec{{\mathcal{S}}}\) shown as follows,

$$\begin{aligned} S_{(1)}= & {} \begin{bmatrix} -\,7.1846 &{}\quad 0.0615 &{}\quad -\,0.1703 &{}\quad 0.7654 &{}\quad 0.0035 &{}\quad 2.1071\\ 0.2235 &{}\quad -\,0.4906 &{}\quad -\,5.9024 &{}\quad -\,0.0991 &{}\quad 0.2675 &{}\quad 0.3350\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}\\ S_{(2)}= & {} \begin{bmatrix} -\,7.1846 &{}\quad -\,0.1703 &{}\quad 0.0035 &{}\quad 0.2235 &{}\quad -\,5.9024 &{}\quad 0.2675 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0.0615 &{}\quad 0.7654 &{}\quad 2.1071 &{}\quad -\,0.4906 &{}\quad -\,0.0991 &{}\quad 0.3350 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}\\ S_{(3)}= & {} \begin{bmatrix} -\,7.1846 &{}\quad 0.0615 &{}\quad 0.2235 &{}\quad -\,0.4906 &{}\quad 0 &{}\quad 0\\ -\,0.1703 &{}\quad 0.7654 &{}\quad -\,5.9024 &{}\quad -\,0.0991 &{}\quad 0 &{}\quad 0\\ 0.0035 &{}\quad 2.1071 &{}\quad 0.2675 &{}\quad 0.3350 &{}\quad 0 &{}\quad 0\\ \end{bmatrix}. \end{aligned}$$

From this example, we can find that the quadratic sum of the ith row of \(S_{(n)}\) equals to the square of the ith singular values of the corresponding \(\varSigma _{(n)}\), which proves one property, that is, \(\Vert {\mathcal{S}}\Vert _{F}^{2}\) = \(\Vert {\mathcal{X}}\Vert _{F}^{2}\). For instance, \(7.2051^{2}=51.9134\) exactly equals \((-7.1846)^{2} + 0.0615^{2} + 0.2235^{2} + (-0.4906)^{2}\). Not only that, but all the \(\Vert \varSigma _{(i)}\Vert _{F}^{2}\), \((i=1,2,3)\) are identical, and equal to \(\Vert {\mathcal{S}}\Vert _{F}^{2}=\Vert {\mathcal{X}}\Vert _{F}^{2}\), i.e., 92. That is, we have illustrated the following properties:

$$\begin{aligned} ||S_{(n)}^{l}||_{2}=\sigma _{(n)}^{l}, (l=1, \dots , I_{n}) \end{aligned}$$
(14)

and

$$\begin{aligned} ||{\mathcal{S}}||_{F}^{2}=\sum _{l=1}^{I_{n}}(\sigma _{(n)}^{l})^{2}=||{\mathcal{X}}||_{F}^{2} \end{aligned}$$
(15)

where \(S_{(n)}^{l}\) is the lth row vector of the nth-mode matricization of core tensor S, \(\sigma _{(n)}^{l}\) denotes the lth singular value of the nth-mode matricization of tensor \({\mathcal{X}}\).

Fig. 8
figure 8

Visualization of tensor and its corresponding core tensor

Full size image

Based on these observations, we propose a novel low-rank patches tensor approximation method, i.e., by directly penalizing the adaptive weighted singular values of core tensor obtained by HOSVD to patches tensor.

4 Image denoising algorithm based on low-rank patches tensor approximation

4.1 Image denoising based on iterative low-rank patches tensors approximation algorithm

First, we introduce the objection function for image denoising in this paper.

$$\begin{aligned} \mathop {arg\min }\limits _X \frac{1}{2}||Y-X||^{2}_{F}+{\mathcal{W}}\Vert \digamma (X)\Vert _{*} \end{aligned}$$
(16)

where Y and X denote noise image and the latent clean image, respectively, \({\mathcal{W}}\) denotes adaptive weights, and \(||\digamma (X)||_{*}\) denotes the proposed low-rank patches tensor nuclear norm (15). \(\digamma (X)\) denotes tensor formulation and HOSVD to image X.

Low rank is a common assumption to natural image in image processing, so we usually use \(\ell _{1}\) or nuclear norm to approximate rank function. \(\ell _{1}\) or nuclear norm regularization can lead to sparse solution, and their convexity is another important reason why they have become so popular in signal processing field. However, both of them will result in significantly biased estimates since the convexity, thus, cannot achieve a reliable solution. In comparison, as a nonconvex penalty, such as the \(\ell _{q}\) (\(0\le q<1\)), smoothly clipped absolute deviation (SCAD) or minimax concave (MC) penalty is superior to \(\ell _{1}\) or nuclear norm regularization because it can ameliorate the bias problem. The advantages of nonconvex penalty regularization have been verified in many applications, and in fact, a nonconvex penalty can yield significantly better performance than a convex penalty regularization. On the other hand, nonconvex regularization based sparse and low-rank recovery are of becoming considerable interest in recent years, also partly attributes to the recent progress in nonconvex and nonsmooth optimization algorithm theory. Motivated by these observations, we exploit iterative adaptive weights to the regularization term. We claim that such an iterative adaptive weighted scheme is equivalent to a kind of nonconvex penalty to the core tensors, where the singular values are assigned different penalty weights.

Proximity operator plays a central role in tackling nonconvex and nonsmooth inverse problem, and it is a highly efficient first-order algorithms which can scale well for high-dimensional problems. For a proper and lower semi-continuous penalty function \(P_{\lambda }(\cdot )\), where \(\lambda >0\) is a threshold parameter, consider the following scalar proximal projection:

$$\begin{aligned} {\text{proxp}}_{\lambda }( t)=\mathop {{\mathrm{arg}}\min }\limits _x \left\{ P_{\lambda }(x)+\frac{1}{2}(x- t)^{2}\right\} \end{aligned}$$
(17)

As \(P_{\lambda }(\cdot )\) is separable, the proximity operator of a vector \({\mathbf {t}}=[t_{1},\ldots ,t_{n}]\in R^{n}\), denoted by \({\text{proxo}}_{\lambda }({\mathbf {t}})\) can be computed in an element-wise manner as:

$$\begin{aligned} {\text{proxo}}_{\lambda }({\mathbf {t}})=[{\text{proxp}}_{\lambda }(t_{1}),\ldots ,{\text{proxp}}_{\lambda }(t_{n})]^{\mathrm{T}} \end{aligned}$$
(18)

For commonly used proximity operators, refer to Table 2.

Table 2 Regularization penalties and the corresponding proximity operator (\(\lambda >0\))
Full size table

For a patch tensor \({\mathcal{M}}\), we denote a generalized penalty for low-rank promotion to its core tensor by \({\hat{P}}_{\lambda }(\cdot )\), which is defined as :

$$\begin{aligned} {\hat{P}}_{\lambda }({\mathcal{M}})=\sum _{i}P_{\lambda }(\lambda _{i}) \end{aligned}$$
(19)

where \(\lambda _i\) is the entry values in core tensor of tensor \({\mathcal{M}}\).

Exploiting the adaptive weights \(\ell _{1}\)-norm we can better preserve essential characteristic of image, and the nonconvex objective function can be solved easily by using the soft-thresholding operator. For each GKGLM patches tensor \({\mathcal{X}}^{k}\), \(k=1 \ldots K\), K is the number of reference patches, we have the following minimization

$$\begin{aligned} \mathop {\min }\limits _X {\mathcal{W}}^{k}||{\mathcal{X}}^{k}||_{*}=\sum _{j}W_{j}^{k}\big |\lambda _{j}^{k}\big | \end{aligned}$$
(20)

where \(W_{j}^{k}\) is the adaptive weight, and \(\lambda _{j}^{k}\) is the value in core tensor \({\mathcal{S}}^{k}\) of tensor \({\mathcal{X}}^{k}\).

It is worth note that the adaptive weighted \(\ell _{1}\)-norm penalized optimization problem is nonconvex due to its varying weights \(W_{j}^{k}\). But, if the weight \(W_{j}^{k}\) is nonincreasing assigned to the increasing core tensor absolute values \(|\lambda _{j}^{k}|\), the penalized optimization problem is a convex function, the conclusion has been proved in the literature. In this paper, we are not to tackle the noise image directly, but to perform denoising for each tensor of being constituted by similar patches of reference patches. So, the objective function can be written as the following subproblems.

$$\begin{aligned} \mathop {{\mathrm{arg}}\min }\limits _{{\mathcal{X}}_{x}^{s}}\frac{1}{2}||{\mathcal{X}}_{y}^{s}-{\mathcal{X}}_{x}^{s}||^{2}_{F}+\sum _{j}W_{j}^{s}|\lambda _{j}^{s}|,\quad s=1,\ldots , S \end{aligned}$$
(21)

where \({\mathcal{X}}_{y}^{s}\) represents the kth reference patch tensor of noisy image Y, \({\mathcal{X}}_{x}^{s}\) is latent clear patches tensor corresponding to \({\mathcal{X}}_{y}^{s}\), \(\lambda _{j}^{s}\) is the value of core tensor of noisy patches tensor \({\mathcal{X}}_{y}^{s}\), and \(W_{j}^{s}\) is the adaptive weight and assigned to \(|\lambda _{j}^{s}|\). It is obvious that the optimization problem can be solved easily by using the soft-thresholding operator. After achieving \({\mathcal{X}}_{x}^{s}\) for each given noisy tensor \({\mathcal{X}}_{y}^{s}\), we will put the new patches back into the image to constitute a new one, and an aggregation procedure is need. Until now, we finish the nth image denoising and obtain the clean image \({\hat{X}}_{n}\).

4.2 Adaptive weight setting to \(W_{j}^{s}\)

Adding residual \((Y-{\hat{X}}_{n})\) of nth iteration back to the \((n+1)\)th step denoised image \(Y_{n+1}\) is the essence of the iterative algorithm. For a better denoising performance, we formulate the \(Y_{n+1}\) as follows:

$$\begin{aligned} Y_{n+1}={\hat{X}}_{n}^{s}+\eta (Y-{\hat{X}}_{n}^{s}) \end{aligned}$$
(22)

where n is the outer iteration number, k is the inner iteration number, and \(\eta\) is the relaxation parameter. Since, we want to add the residual back to the denoised image, the variance of noise remaining can be estimated by

$$\begin{aligned} \sigma _{n}=\gamma \sqrt{\sigma ^{2}-\frac{1}{k\times l}||Y-Y_{n-1}||_{F}^{2}} \end{aligned}$$
(23)

where \(\sigma\) is noise variance of Y, \(\gamma\) is a scaling factor used to control the re-estimation of noise variance, \(k\times l\) is the number of all pixels in Y.

A advantages of adaptive-thresholding is to preserve large coefficients while filters small coefficients, so the features in image can be survived through thresholding. Then, we set the weight corresponding to each \(\lambda _j\) to be:

$$\begin{aligned} W_{j}^{s}=\frac{2\sqrt{2}\sqrt{N}\sigma ^{2}_{n}}{|\lambda _{j}|+\varepsilon } \end{aligned}$$
(24)

where N is the number of image patches of each tensor \({\mathcal{S}}_{y}^{s}\), \(\sigma _{n}\) can be computed by 23, \(\varepsilon >0\) is a sufficient small positive parameter for avoiding dividing by zero. We apply \(W_{j}^{s}\) as adaptive weight to solve the optimization problem 21 by the soft-thresholding proximal operator shown in Table 2, thus solution \(\tau _{j}^{s}\) to the jth element of \({\mathcal{S}}^{s}_{x}\) can be expressed by as follows

$$\begin{aligned} \tau _{j}^{k}={\text{sign}}(\lambda _{j})\max \{|\lambda _{j}|-W_{j}^{s},0\}. \end{aligned}$$
(25)

4.3 Aggregation

When we put these patches back into the image, different patches tensor will be assigned different weights. Therefore, we use the weighted averaging to give more weight to patches tensors with less noise and less weight to those with much noise. Specifically, we use the following equation to define weight.

$$\begin{aligned} w=\left\{ \begin{aligned} \frac{p^{2}\times N}{p^{2}\times N+I},&\quad {\text{if}}\; I\ge 1\\ 0,&\quad {\text{otherwise}} \end{aligned} \right. \end{aligned}$$
(26)

where N is the number of patches in current tensor, p is the patch size and I is the number of thresholded elements in core tensor of this patches tensor. The result image can be calculated by the following formulation

$$\begin{aligned} {\hat{X}}_{(x,y)}=\frac{\sum _{i\in N_{x,y}}\sum _{j\in J(j)_{x,y}}w_{i,j}\varOmega _{i,j}}{\sum _{i\in N_{x,y}}\sum _{j\in J(j)_{x,y}}w_{i,j}} \end{aligned}$$
(27)

where \(N_{x,y}\) are all GKGLM patches tensor overlapping in position (x, y), \(J(i)_{x,y}\) are all patches in ith tensor that overlap in position (x, y) and \(\varOmega _{i,j}\) is a pixel in the ith tensor, the jth tensor in position (x, y). The proposed algorithm is summarized in Algorithm 3, we denote the algorithm as GKGLM-Tensor.

figure c

5 Experiments

In this section, we conduct image denoising experiments on several widely used natural images, for example, House, Peppers, Barbara, Monarch and C.man. And we compare the proposed GMMH algorithm with several state-of-the-art denoising methods, including NNM [28], BM3D [13], EPLL [17], LSSC [12], NCSR [29], SAIST [30], WNNM [31], \({\text{BM3D}}_{bst}\) that is the BM3D based on boosted patch searching method [20] denoising algorithms, SLR [23] and LR-GSC [32]. As a common experimental setting in the literature, we add white Gaussian noise with zero mean and standard deviation \(\sigma\) to the noise-free images and to test the performance of competing denoising methods. The MATLAB source code of our proposed algorithm can be downloaded at https://github.com/KazukiAmakawa/HOSVD_denoise_patch.

5.1 Implementation details

Our presented image denoising method contains two stages: the searching image similar patches stage and the denoising stage. In the denoising stage, there exist four parameters need to be set: \(\gamma\), \(\beta\), the patch size p, the number M of patches in a tensor \({\mathcal{X}}\). These parameters pick different values when the standard variation \(\sigma\) of noise is different (shown in Table 3). Intuitively, if you want to exploit more global image information of image, number M of patches in a tensor should be set as big as possible.

Table 3 Parameter setting
Full size table

5.2 Results and discussion

We evaluate the competing methods from peak signal to noise ratio (PSNR), structural similarity index measurement (SSIM), normalized cross-correlation coefficient (NCC) and visual quality viewpoints.

5.2.1 PSNR

In Table 4, we present the average PSNR results on three noise levels \(\sigma =10, 30, 50\) for image House, Peppers, Barbara, Monarch and C.man. Higher PSNR results on each noise level are highlighted in bold. From the results shown in Table 4, it can be seen that our proposed algorithm achieves much better PSNR results than NNM. Secondly, our proposed algorithm has higher PSNR values than BM3D, LSSC, EPLL and NCSR, \({\text{BM3D}}_{bst}\), SLR and is only slightly inferior to WNNM and LR-GSC for low noise level. With the noise level increasing, the performance of our proposed algorithm will be improved significantly, which can be verified for \(\sigma =50\) noise level.

Table 4 Average PNSR scores by different methods
Full size table

5.2.2 SSIM & NCC

In Table 5, we report the average SSIM and NCC results on three noise levels \(\sigma =20, 40, 60\) for image House, Peppers, Barbara, Monarch and C.man. We only compare our methods to BM3D, \({\text{BM3D}}_{bst}\), EPLL, WNNM, SLR and LR-GSC, which outperforms the other algorithms. It can be seen from the SSIM viewpoint that our proposed method is comparable to these methods, and particularly, our method is superior to other method for \(\sigma =50\) noise level. The NCCNCC (normalized cross-correlation) shows the similarity of the denoised image with original clear image. The range of NCC \([-1,1]\), and the closer the 1 is, the more similar the two image are, the closer the \(-1\) indicates that the more dissimilar the two images. The NCC results in Table 5 show that there exists positive correlation between SSIM and NCC, which indicates that the higher SSIM value is, the bigger NCC value is.

Table 5 Average SSIM scores by different methods
Full size table

5.2.3 Visual quality

Considering that human subjects are the ultimate judge of the image quality, the visual quality of denoised image is essential to evaluate a denoising algorithm. Figures 9 and 10 show the denoised images of Pepper and Monarch by the competing method. We obtain that WNNM has strong ability to image denoising by Table 4, so we just compare the visual effect of WNNM with our proposed algorithm. It can be seen that the proposed algorithm in this paper is likely to generate artifacts than WNNM, but our algorithm preserves edge more better.

Fig. 9
figure 9

Denoised images of Pepper by WNNM and our algorithm (the standard deviation of noise is \(\sigma =50\))

Full size image
Fig. 10
figure 10

Denoised images of Monarch by WNNM and our algorithm (the standard deviation of noise is \(\sigma =50\))

Full size image

In summary, comparing to state-of-the-art denoising algorithm, our proposed method has performed a comparable job in image denoising, especially in high noise level.

6 Conclusion

In this paper, a new denoising approach based on image internal self-similarity prior, external patch priors and the low-rank patches tensor property of natural image is established. We search similar patches to each reference patch to form a tensor \({\mathcal{X}}^{(k)}\), and we decompose the tensor \({\mathcal{X}}^{(k)}\) by HOSVD, then we use soft-threshold to tackle core tensor \({\mathcal{S}}^{(k)}\). In order to improve the performance of denoising, we have trained GMM by EM based on deep cluster. To enhance the accuracy for searching similar patches, a globally searching similar patches methods within the whole image is established and a geometric searching method is used to further improve the accuracy for finding similar patches.