1 Introduction

The anterior cruciate ligament (ACL) contributes mainly to the knee joint stability which can stabilize translation and rotation of the tibia relative to the femur [1, 2]. ACL injury is one of the most common musculoskeletal pathology causing pain and reduced performance of daily living activities, which is also linked to altered joint kinematics, kinetics and load partitioning in gait because of the loss of stability [3,4,5]. Currently, diagnosis of ACL injury mainly relies on clinical exam [6], arthroscopy [7] or imaging like X-rays [8] and magnetic resonance imaging (MRI) [9]. However there exist some limitations in these tools. For example, it is subjective through clinical exam due to the experience of the physicians. It is invasive for the arthroscopy [7] while it is highly required for the imaging in terms of cost, radiation, and equipment requirements [10]. In addition, the obtained images do not provide any functional or dynamical information concerning the association between ACL and daily activities [10]. Because of the radiation, subjects are not recommended to be exposed to X-rays or MRI frequently when undergoing medical examinations, which makes it difficult to monitor the progression of ACL injury over time.

Therefore, developing an alternative diagnosis method, such as gait analysis, which can offer quick, dynamic, non-invasive, objective and low cost measurement is required in the clinical applications. It has been reported in the literature that ACL-deficient (ACLD) patients may demonstrate abnormalities in their gait patterns several years after the injury [11,12,13,14,15,16,17]. It has been revealed that patients with ACL deficiency tend to adopt an asymmetrical gait pattern which includes reduced knee flexion and internal knee extensor moment, thereby reproduce the abnormality of the injured leg also in the contralateral intact leg [18, 19]. Some studies have deduced that degenerative changes might result from altered gait or functional mechanics of the ACL deficiency [20, 21]. All these findings indicate that gait analysis might act as an alternative or assistant tool for the diagnosis of ACL deficiency in addition to the traditional techniques. How to extract variable and effective information from gait for the diagnosis of ACL injury still remains an open question.

In the ACL literature, clinical and biomechanical studies typically rely on discrete measures to characterize movement disorders [22]. However, singular measures are limited in their ability to capture all the variability and complexity of human gait. Hence, statistical parametric mapping [23] and nonlinear dynamics [24, 25] have been used as alternative methods to provide additional insights. Hebert-Losier et al. [26] proposed a functional analysis of variance (ANOVA) method based on the interval testing procedure to examine knee-kinematic curves. It helped detect precise time intervals where statistical differences occurred between ACLD and ACL-intact (ACLI) groups. Many nonlinear parameters linked to the variability of knee motion have been extracted to quantify and classify gait patterns between ACLD and ACLI knees. Among these parameters, the Lyapunov exponent can assess the knee joint stability [27], the fractal dimension and entropy can measure the complexity or the degree of disorder of the knee motion [28], the sample entropy (SampEn) [29] and detrended fluctuation analysis (DFA) can quantify the regularity of the knee joint signals [30, 31]. Stergiou et al. [32] and Moraiti et al. [33] proposed the nonlinear measures including Lyapunov exponent to compute the local stability in ACLD knee when compared to the contralateral intact knee. However extraction of these parameters relies on long-length time series of gait signals (i.e., hundreds to thousands of gait cycles included). This may not be easy to achieve in clinical practice since it is usually required to measure three-dimensional (3D) gait kinematics and kinetics of patients with ACL deficiency in a short period.

In addition, the lower extremities act as links of a chain [34, 35]. The position of each link in space will influence the adjoining links. Forces applied at one link can propagate up and down the entire chain [34]. For example, if one link is injured which results in a limitation of motion between two links, then in order to achieve fully normal motion, the collection of healthy connections in the chain must necessarily increase their motion to make up for the loss in one connection [34]. There exist conditions of the ankle and hip that will compel the knee to be subjected to pathological forces through the kinetic chain. Movement patterns in the hip and ankle joints of the injured limb have been found to be altered after ACL injury [35,36,37]. It is also necessary to focus on the kinematic and kinetic variation of knee, hip and ankle joints between ACLD and ACLI groups. Related gait parameters are recommended to be extracted for analysis.

Another potential diagnosis tool is with the dynamical and nonlinear features and machine learning algorithms [38,39,40,41]. Christian et al. [38] proposed a machine learning method with SVM tool for the discrimination of kinematic gait patterns in patients with a ruptured ACL. Features were extracted from motional 3D marker trajectories of knees with principal component analysis (PCA) and recursive feature elimination method. Seven patients were involved and \(100\%\) classification accuracy was achieved. Nonetheless, the experiments were based on a small database and the effectiveness is doubtable. Berruto et al. [39] employed tibial accelerometers to measure the variation of knee pivot-shift in patients with unilateral ACL injuries. Magnitudes of accelerations were used as features for the classification of ACLD and ACLI knees and the achieved accuracy was roughly \(90\%\). Kopf et al. [40] carried out a study with similar method to Berruto et al. [39], in which inertial sensor modules fastened to the tibia and femur were used to grade 20 patients with unilateral ACL deficiency. Acceleration difference between ACLD and ACLI knees were used for classification and the reported accuracy was 95\(\%\) (19 of 20). Almosnino et al. [41] used strength curve features to measure the difference between injured and uninjured knees with PCA method. Forty-three patients with unilateral ACL deficiency were involved and the reported specificity, sensitivity and accuracy were 60.5\(\%\), 60.5\(\%\) and 62.20\(\%\), respectively. Nonlinear analysis has been widely applied to assess the human locomotion during normal and pathological gait. Considering the characteristics of non-stationary and recurrent nature of gait signals [42], it is not suitable to perform the Fourier analysis on long-length biological signals. Therefore, in the present study, we adopted a nonlinear data analysis technique, namely Recurrence Quantification Analysis (RQA) [43], to analyse the gait signals [44]. This is due to its advantages of analyzing linear and nonlinear time signals [45]. RQA is prone to quantifying the dynamics of gait data whose working principle is explore the recurrent nature of gait signal in the reconstructed phase space [46]. Phase space reconstruction (PSR) of the gait signals facilitates the understanding of gait dynamics with more observables [47,48,49]. PSR further employs Recurrence Plots (RP) to visualize the recurrence of gait signal in phase space and depict the structures including single dots, horizontal lines, diagonal lines and vertical lines. Quantifying these structures called as RQA, yields several parameters based on different aspects of quantification [46]. In comparison to RQA, entropy is used to measure the uncertainty of nonlinear dynamical system and equals the rate of information production. Calculation of entropy is usually based upon long data sets. Fuzzy entropy is a method suited to measure the complexity of short length time series. The key aspects are the use of fuzzy membership function to quantify the similarity between a pair of vectors and fuzzy probability to determine the disorder or uncertainty [50]. The nonlinear Teager-Kaiser energy operator is able to localize instantaneous amplitude changes of signals. Its usefulness has been approved in some biomedical signal processing field [51,52,53]. It generates a time series that can represent the instantaneous energy of the original gait system dynamics, which can be used as a characteristic feature for the classification of pathological and normal gait patterns.

The main purpose of the current study is to evaluate the effectiveness of different dynamical features for the discrimination between ACLD and contralateral ACLI knees based on different classification models. Thereby we can assess the capabilities of optimal features representing gait characteristics. In addition, we can develop an automatic and non-invasive pattern recognition system to detect the presence of ACL injury. Since the lower extremities act as a kinetic chain during dynamic tasks, control of the hip and ankle joint will interact with knee motion. Related gait kinematic and kinetic parameters from the three joints are extracted. A general feature extraction framework is proposed and various dynamical features, such as recurrence rate, determinism and entropy from the recurrence quantification analysis (RQA), fuzzy entropy (FuzzyEn), Teager-Kaiser energy (TKE) feature and statistical analysis, are included. Different classification models, including support vector machine (SVM), K-nearest neighbor (KNN), naive Bayes (NB) classifier, decision tree and ensemble learning based Adaboost (ELA) classifier, derived for discriminant analysis of multiple dynamical gait features are evaluated and combined with optimal feature set on the classification accuracy for a comparative study.

2 Methods

2.1 Design

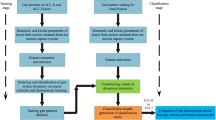
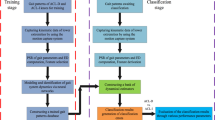
In this section, we propose a pattern recognition method to differentiate gait patterns between ACLD knees and contralateral intact knees using dynamical features obtained from kinematic and kinetic gait signals. Figure 1 illustrates the block diagram of the proposed method for the binary classification problem. The method includes the feature extraction and classification stages and follows the following steps. In the first step, nonlinear and statistical features (including Mean, Standard Deviation, Skewness and Kurtosis) are extracted by using different methods, including RQA, fuzzy entropy, Teager-Kaiser energy and statistical analysis. In the second step, feature vectors are fed into different classification models to discriminate between ACLD and ACLI gait patterns. Finally, different performance parameters are used to evaluate the classification results.

Fig. 1
figure 1

Block diagram of the proposed method for the discrimination of ACLD and ACLI knees using different features and classification models

Full size image

2.2 Dataset description

We conducted a cross-sectional, observational study of individuals with chronic, unilateral ACLD knees. The contralateral unaffected knee was considered as intact. Potential participants were identified from an orthopaedic clinic database. Those who met the inclusion criteria (e.g. diagnosed with full tear of their ACL by magnetic resonance imaging) were either contacted by telephone or email. The subjects were excluded if they had accompanying damage to the posterior cruciate or collateral ligaments, had injuries on the contralateral limb, or had difficulty or pain in performing activities of daily living including walking. Forty-three participants were recruited from November 2015 to July 2016. Subjects’ characteristics are summarized in Table 1. The study was approved by the ethical review board (2014/547), The University of Sydney, Australia. A written informed consent was obtained from each participant before data collection began.

Table 1 Descriptive characteristics of the participated patients with unilateral ACL injury
Full size table

2.3 Measurement

All measurements and assessments were conducted in a single session at a laboratory with one assessor. Before undergoing the gait analysis procedure, the participants completed a questionnaire that collected demographic information (age, dominant leg and time since injury) and three other patients reported outcome measures (visual analogue scale, Tegner activity scale and knee injury and osteoarthritis outcome score). Participated patients had their height and weight measured.

A 16-camera 3D motion capture system (Motion Analysis Corporation, Santa Rosa, USA) and force plates (model 9281, Kistler, Winterter, Switzerland) were used to collect the data. The camera sampling rate was 200 Hz and it was synchronized with the kinetic data sampled at 1000 Hz. Thirty (18-mm-diameter) passive markers were attached bilaterally on the head of the second metatarsal, navicular tuberosity, calcaneal tuberosity, medial and lateral malleolus, lateral tibia distally, lateral midtibia, tibia tuberosity, medial and lateral femoral epicondyle, anterior mid-thigh, greater trochanter and anterior superior iliac spine and one single marker on the spinous process of Sacrum level 2, thoracic spine level 10 and cervical spine level 7 and manubrium using double-sided tape. Each segment was defined using three markers (six degrees of freedom) and idealized as a rigid body with a local coordinate system defined to coincide with a set of anatomical axes. The 3D positions of markers were used to calculate the location of the joint centres. A static trial was collected as a reference to determine body mass and positions of joint centres of rotation. Segment angles relative to the laboratory and relative joint angles were calculated using joint coordinate systems. Three-dimensional moments were calculated using inverse dynamics via Kintrak™ version 7.0 (The University of Calgary, Canada) and were normalized to the individual’s body weight to compensate for anatomical differences between the participants.

Fig. 2
figure 2

Experimental setup

Full size image

Subjects walked barefoot along a 10-m walkway at their self-selected habitual (normal) and fast (walking at a speed fast enough to catch a bus without breaking into a jog) speeds. Figure 2 demonstrates the setting used in this study. We investigated whether walking speed will influence classification accuracy of the proposed classification models and evaluate the robustness of the extracted features and classification models to the walking speed. Fast speed trials occurred after normal speed trials and subjects rested for 2–3 min between the trials and 5–10 min between each walking condition. The average values from repeated trials at both velocities were calculated for comparisons between ACLD and ACLI knee. Kinematics and kinetics of knee, hip and ankle joints have been obtained from the motion capture system and used for the following feature extraction and selection.

2.4 Feature extraction

In order to obtain more efficient features, this paper considers parameters of recurrence quantification analysis (RQA), Fuzzy entropy and Teager-Kaiser energy along with statistical features of knee, hip and ankle joint gait data.

2.4.1 Recurrence quantification analysis (RQA)

RQA is utilized to help understand the nature of gait signals and quantify gait with disorders without relaxing the real-time constraints [46]. In the present study, RQA parameters are extracted from the recurrence plots (RP) of the knee, hip and ankle kinematic and kinetic data, which are various measures of the complexity of the gait signals. RP describes the recurrent property of a dynamical system, i.e. visualizing the time dependent behavior of a gait signal \(x_i\) in a phase space [54], and is defined as follows.

$$\begin{aligned} R_{i,j}(\epsilon )=\Theta (\epsilon -\Vert x_i-x_j \Vert ), i,j=1,2,...,N \end{aligned}$$
(1)

where \(\epsilon\) is a predefined cutoff distance, N is the total number of considered states, \(\Vert \cdot \Vert\) is the Euclidean norm, \(\Theta\) is the Heaviside function. The binary values of \(R_{i,j}\) can be easily visualized using the colours black 1 and white 0, which indicates the time evolution of a signal trajectory. In practical applications, RP alone is not a good choice since it is difficult to witness the small-scale patterns by visual inspection. Hence several measures of complexity which can quantify the small-scale structures in the RP, namely RQA, have been proposed. The present study only adopted three measure variables: recurrence rate (RR), determinism (DET) and entropy (ENTR). For more details please refer to [43].

RR measures the density of recurrent points in a recurrence plot and is given by

$$\begin{aligned} RR(\epsilon )=\frac{1}{N}\sum \limits _{i,j=0}^{N}R_{i,j}(\epsilon ) \end{aligned}$$
(2)

DET measures the ratio of recurrence points forming diagonal lines which represent epochs of similar time evolution of the system state. Longer diagonal lines are usually discovered in periodic signals while shorter diagonal lines appear in chaotic signals. Hence long diagonal lines can be more often visualized in subjects with pathological gait than in normal subjects. DET is calculated as follows.

$$\begin{aligned} \mathrm{{DET}}=\frac{\sum \limits _{\ell =\ell _{min}}^{N}\ell p(\ell )}{N^2\times RR} \end{aligned}$$
(3)

where \(\ell _{min}\) is the length of the minimal diagonal line, \(p(\ell )\) is the histogram of these diagonal lines.

ENTR measures the complexity of the recurrence structure, which is given by

$$\begin{aligned} \mathrm{{ENTR}}=-\sum \limits _{\ell =\ell _{min}}^{N}p(\ell )\mathrm {ln}p(\ell ) \end{aligned}$$
(4)

The more complex the recurrence structure is, the larger the value of ENTR is. For ACLD knees, their pathological gait appears more recurrence while the complexity is less.

2.4.2 Fuzzy entropy

Fuzzy entropy is used to measure the variability or irregularity of nonlinear time series based on the concept of approximate entropy and sample entropy. Compared to the other two kinds of entropy, it is suitable for short-length time series and is described as follows [55, 56].

Given a time series \(\{x_1,x_2,...,x_N\}\) with N samples, one can construct the following vector sequence

$$\begin{aligned} X_i^m=\{x_1,x_2,...,x_{i+m-1}\}-\bar{x}_i, i=1,2,...,N-m+1, \end{aligned}$$
(5)

where \(X_i^m\) represents m consecutive x values commencing with the ith point, m is the embedding dimension, \(\bar{x}_i\) is the average of vector \(X_i^m\) and is given by

$$\begin{aligned} \bar{x}_i=\frac{1}{m}\sum \limits _{j=0}^{m-1}x_{i+j} \end{aligned}$$
(6)

Define the distance \(d_{ij}^m\) between \(X_i^m\) and its neighbor \(X_j^m\) as the maximum absolute difference of corresponding scalar components:

$$\begin{aligned} d_{ij}^m=d[X_i^m,X_j^m]= & {} \max \limits _{k\in (0,m-1)} \vert X_i^m(k)- X_j^m(k)\vert \nonumber \\= & {} \max \limits _{k\in (0,m-1)} \vert [x_{i+k}-\bar{x}_i]+[x_{j+k}-\bar{x}_j]\vert \nonumber \\&(i,j=1,...,N-m+1,j\ne i) \end{aligned}$$
(7)

where \(X_i^m(k)\) and \(X_j^m(k)\) are the k element of \(X_i^m\) and \(X_j^m\), respectively.

Given n and r, calculate the degree of fuzzy similarity \(S_{ij}^m\) between \(X_i^m\) and \(X_j^m\) by using the exponential function

$$\begin{aligned} S_{ij}^m=\exp (-(d_{ij}^m)^n/r) \end{aligned}$$
(8)

For each vector \(X_i^m\), average all the degrees of fuzzy similarity to its neighboring vectors \(X_j^m\) and lead to the average degree of fuzzy similarity

$$\begin{aligned} S_r^m(i)=\frac{1}{N-m}\sum \limits _{j=1,j\ne i}^{N-m+1}S_{ij}^m \end{aligned}$$
(9)

The fuzzy probability \(p_r^m\) (defined in Buckley [57]) that two vector sequences match for all m-dimensional points within tolerance r is calculated by

$$\begin{aligned} p_r^m=\frac{1}{N-m+1}\sum \limits _{i=1}^{N-m+1}S_r^m(i) \end{aligned}$$
(10)

Similarly, for the vector sequence \(X_i^{m+1}\), we can also define the fuzzy similarity \(S_{ij}^{m+1}\) between \(X_i^{m+1}\) and \(X_j^{m+1}\), and the average degrees of fuzzy similarity \(S_r^{m+1}(i)\). The fuzzy probability \(p_r^{m+1}\) is defined as

$$\begin{aligned} p_r^{m+1}=\frac{1}{N-m}\sum \limits _{i=1}^{N-m}\left( \frac{1}{N-m-1}\sum \limits _{j=1,j\ne i}^{N-m}S_{ij}^{m+1}\right) \end{aligned}$$
(11)

Fuzzy entropy FuzzyEn(m, r) of sequence \(\{x_1,x_2,...,x_N\}\) is defined as the negative natural logarithm of the conditional fuzzy probability

$$\begin{aligned} \mathrm{{FuzzyEn}}(m,r)=\lim \limits _{N\rightarrow \infty }\left( -\ln \left( \frac{p_r^{m+1}}{p_r^m}\right) \right) \end{aligned}$$
(12)

For a finite-length time series \(x_i\) (\(1 \le i \le N\)), the Fuzzy entropy can be changed to

$$\begin{aligned} \mathrm{{FuzzyEn}}(m,r,N)=-\ln \left( \frac{p_r^{m+1}}{p_r^m}\right) \end{aligned}$$
(13)

2.4.3 Teager-Kaiser energy (TKE) feature

The nonlinear Teager–Kaiser energy operator (TKEO) provides an unconventional perspective on the instantaneous energy of a signal [58]. It relates energy to square of the signal amplitude and the square of its frequency. The TKEO is defined for discrete-time signal x(n) as follows [59]

$$\begin{aligned} \phi [x(n)]=x^2(n)-x(n-1)x(n+1) \end{aligned}$$
(14)

One of the advantages of TKEO is its nearly instantaneous since only three samples are required for the energy computation at each time instant. In addition, high time revolution combined with a simple operator provides the ability to capture the energy fluctuations of the original gait system dynamics as well as efficiently conduct in implementation [60]. TEKO generates a time series which can represent the instantaneous energy of the original gait system dynamics. To measure the variant energy sequence, the average value of nonlinear energy in the time domain is calculated as [61]

$$\begin{aligned} \mathrm{{TKE}} =\frac{1}{N}\sum \limits _{n=0}^{N-1}\phi [x(n)] \end{aligned}$$
(15)

where N is the number of samples in the time series of gait signals, TKE is used as a feature of the original time series.

2.5 Feature selection

In order to improve the classification accuracy, this work considers four statistical features (Mean, Standard Deviation (Std), Skewness, and Kurtosis) of gait signals in addition to the parameters of RQA, Fuzzy entropy and TKE. All the 243 features calculated from the kinematic and kinetic data of the ankle, knee and hip joints are demonstrated in Table 2.

Table 2 Description of feature extraction
Full size table

In addition, Mann-Whitney test is utilized to retain the statistically significant features between ACLD and ACLI legs. Features with p value less than 0.05 are considered to be statistically significant and used for classification. It is seen from Tables 2 and 3 that there exist significant differences in 38 features, which are highlighted with red color and ‘*’ marker.

In order to obtain more efficient features, Hill climbing feature selection method [62] is utilized to find the optimal feature subset from the 38 statistically significant features, which can relieve the computational burden of performing the complete search for different feature combinations. It performs step-by-step search by considering one feature after the other. The set of features that gives better accuracy is considered to be the optimal feature set. In the present study, the optimal feature set contains the follwoing features: F1, F2, F10, F19, F24, F29, F30, F61, F67, F96, F149, F176, F191, F207, F217, F227, which is also summarized in Table 2.

Table 3 Comparison of features extracted from different gait time series
Full size table

2.6 Classification models

To carry out a comparative study, five popular machine learning methods, i.e., the support vector machine (SVM), K-nearest neighbor (KNN), naive Bayes (NB) classifier, decision tree, and ensemble learning based Adaboost (ELA) classifier were evaluated because they are usually utilized to solve the classification problem in nonlinear feature space and are suitable for a small size dataset, which is the case in the present study. For detailed introductions of these models, please refer to references [63,64,65,66,67,68].

2.6.1 Support vector machine (SVM)

SVM is a prevalent machine learning and pattern classification technique which transforms data points into a high-dimensional feature space and identifies an optimum hyperplane separating the classes present in the data [63]. In the present study we adopted the popular radial basis function (RBF) kernel.

2.6.2 K-nearest neighbor (KNN)

KNN is an effective nonparametric classifier which performs the classification by searching for the test data’s k nearest training samples in the feature space [64]. It utilizes Euclidean or Manhattan distance as a distance metric for the similarity measurement.

2.6.3 Naive Bayes (NB) classifier

NB classifier is a probabilistic method relying on the assumption that every pair of features involved are independent of each other whose weights are of equal importance [65]. The main advantages of NB are the conditional independence assumption, which leads to a quick classification and the probabilistic hypotheses (results obtained as probabilities of belonging of each class).

2.6.4 Decision tree (DT)

In DT, features are used as input to construct a tree structure in which several rules are extracted to recognize the class of the test data [66].

2.6.5 Ensemble learning based Adaboost (ELA) classifier

Ensemble learning techniques combine the outputs of several base classification techniques to form an integrated output and enhance classification accuracy. Compared to other machine learning methods that try to learn one hypothesis from the training data, ensemble learning relies on constructing a set of hypotheses and combines them for use [67]. For the popular Boosting ensemble method, we adopted the addative boosting (Adaboost) algorithm [68] in this study.

3 Experimental results

We evaluate the classification performance of ACLD knees against ACLI knees using dynamical features on different classification models. Several experiments are carried out to verify the effectiveness of the proposed method. Each participant walked five trials under normal and fast walking speeds, respectively. Ten and fourteen trials under normal and fast speeds, respectively, were abandoned because of the malfunction of the motion capture system during the experimental procedure. Hence training size for the ACL-D and ACL-I knees under normal speed is \(43\times 5-10=205\). The total training size is \(205+205=410\). Training size for the ACL-D and ACL-I knees under fast speed is \(43\times 5-14=201\). The total training size is \(201+201=402\). The number of gait patterns/trials for the training and classification of ACLI and ACLD knees in different walking conditions is shown in Table 4, which is used to testify the robustness of our proposed method to the variation of walking speed.

Table 4 Experiments for gait patterns classification between ACLI and ACL-D knees under different walking conditions
Full size table

Experiments are conducted to assess the effectiveness of the proposed features on different classifiers. For the purpose of evaluation, six performance parameters are utilized, including the Sensitivity (SEN), the Specificity (SPF), the Accuracy (ACC), the Positive Predictive Value (PPV), the Negative Predictive Value (NPV) and the Matthews Correlation Coefficient (MCC). These measurements are defined as follows [69]:

$$\begin{aligned} \mathrm{SEN}= & {} \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}\times 100(\%) \end{aligned}$$
(16)
$$\begin{aligned} \mathrm{SPF}= & {} \frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}}\times 100(\%) \end{aligned}$$
(17)
$$\begin{aligned} \mathrm{ACC}= & {} \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FN}+\mathrm{FP}}\times 100(\%) \end{aligned}$$
(18)
$$\begin{aligned} \mathrm{PPV}= & {} \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}\times 100(\%) \end{aligned}$$
(19)
$$\begin{aligned} \mathrm{NPV}= & {} \frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FN}}\times 100(\%) \end{aligned}$$
(20)
$$\begin{aligned} \mathrm{MCC}= & {} \frac{\mathrm{TP}\times \mathrm{TN}-\mathrm{FN}\times \mathrm{FP}}{\sqrt{(\mathrm{TP}+\mathrm{FN})(\mathrm{TP}+\mathrm{FP})(\mathrm{TN}+\mathrm{FN})(\mathrm{TN}+\mathrm{FP})}} \end{aligned}$$
(21)

where TP is the number of true positives, FN is the number of false negatives, TN is the number of true negatives and FP is the number of false positives. The sensitivity and specificity correspond to the probabilities that PD patients and healthy controls, respectively, are correctly classified. To be accurate, a classifier must have a high classification accuracy, a high sensitivity, as well as a high specificity [70]. For a larger value of MCC, the classifier performance will be better [69, 71].

Binary classification problems classified using five classificaton models: SVM, KNN, NB, Decision Tree and ELA. Two-fold, ten-fold and leave-one-out cross-validation techniques are used and performance outcome such as SEN, SPF, ACC, PPV, NPV and MCC, is calculated to obtain reliable and stable evaluation on the performance of the proposed method. Instead of using all the 243 features (as listed in Table 3) for classification, the 38 statistically significant features that demonstrate the significant difference between ACLD and ACLI knees are employed. In addition, in order to improve the performance of the five classifiers by reducing the computation burden, the optimal feature set containing 16 features (shown in Table 2) was derived using features selection method [62]. The classification performance outcome for the five classifier models under normal and fast walking speeds is illustrated in Tables 5, 6, 7, 8, 9 and 10. Among the five classifier models, the SVM classifier achieves the best classification performance in all the 2-fold, 10-fold and leave-one-out cross-validation styles. It also possesses the best robustness to the variation of walking speed. On the contrary, the NB classifier did not work well under both walking speeds and its classification performance is inferior to the other four classifiers.

Table 5 Performance indexes for the optimal subset and for each classification algorithm using 2-fold style under normal walking speed
Full size table
Table 6 Performance indexes for the optimal subset and for each classification algorithm using 10-fold style under normal walking speed
Full size table
Table 7 Performance indexes for the optimal subset and for each classification algorithm using leave-one-out style under normal walking speed
Full size table
Table 8 Performance indexes for the optimal subset and for each classification algorithm using 2-fold style under fast walking speed
Full size table
Table 9 Performance indexes for the optimal subset and for each classification algorithm using 10-fold style under fast walking speed
Full size table
Table 10 Performance indexes for the optimal subset and for each classification algorithm using leave-one-out style under fast walking speed
Full size table

4 Discussion

Experimental results of this study illustrate that it is with high efficiency and accuracy to detect the gait disparity between chronic ACLD and contralateral ACLI knees and to differentiate between them by means of the established pattern recognition system. The impact of feature extraction and selection on five different classification models has also been demonstrated.

The present study not only revealed that ACLD leg demonstrates altered gait patterns in comparison to contralateral ACLI leg, but also provided effective and objective feature extraction and classification methods to discriminate between the two groups. Comparison of the classification performance to other state-of-the-art methods between ACLD and ACLI knees is demonstrated in Fig. 3. Overall, our classification approach achieves greatest accuracy considering the size of the databases. Different from the methods in the above-mentioned literature, our method extracted several linear and nonlinear dynamical features to represent the disparity of gait patterns between ACLD and ACLI legs for the discrimination task.

Currently, to the authors’ knowledge, RQA, fuzzy entropy and Teager-Kaiser energy have never been considered for the classification of gait patterns between ACLD and ACLI knees in previous literature. The gait signals were recorded for short durations of about 3 min, which was usually required in clinical practice. The present study demonstrated improved accuracy because RQA, fuzzy entropy and Teager-Kaiser energy work well irrespective of data length. The other possible reason could be that RQA could depict the hidden relationship of gait signal (for example: periodic or chaotic nature) without assuming the signal to be stationary, linear and noiseless and thus extract the set of features.

Fig. 3
figure 3

Comparing the results of accuracy (in leave-one-out style) in classifying gait patterns between ACLD and ACLI knees using different methods under normal walking speed

Full size image

The proposed pattern recognition system may serve not only as a measure of kinematic variability and discrimination between two groups of ACLD and ACLI knees, but also as a non-invasive, objective and assistant technical means to other diagnostic approaches such as X-rays, MRI, arthroscopy, etc.

5 Conclusion

This study investigated the performance of different gait features on five classification models for discriminating between ACLD and contralateral ACLI knees. The results of this study indicate that the pattern classification of lower extremity kinematic and kinetic data can offer an objective and non-invasive method to assess the gait disparity between ACLD and ACLI knees. These results demonstrate the potential of the proposed technique for detecting pathological gait patterns caused by ACL deficiency by analysing and measuring the gait difference using RQA, fuzzy entropy, Teager-Kaiser energy and statistical features on different classification models. Utilizing RQA on gait signals assist in understanding the nature of gait signals and quantify gait with disorders. It does not rely on assumptions like non-linearity and non-stationarity, and is suited for short length gait time series. Fuzzy entropy measures the variability of gait signals with short length. The main objectives of this study include understanding the dynamics of human gait, quantitatively analyzing the gait pattern of ACLD and ACLI knees and improving the accuracy of binary classification problems through different machine learning classifiers.

In terms of the limitations in the present study, there are two concerns: (1) the method was evaluated on a small size of database. In addition, the discriminative model constructed in this study enabled only limited clinical usefulness in discerning between the ACLD and contralateral healthy knees. Improvement in discrimination capabilities may perhaps be achieved by consideration of additional control groups. Future work will include a clinical validation of the proposed technique with a larger number of patients with ACL deficiency and age-matched healthy controls. (2) there are limited types of gait signals extracted from the participants, including knee joint angles and translations in 6DOF. Various gait signals like knee joint angular velocity and acceleration, knee kinetic parameters (force, moment, etc) may also considered in future work to comprehensively reflect the characteristic of pathological and normal gait patterns between ACLD and ACLI knees.