Realified L1-PCA for direction-of-arrival estimation: theory and algorithms

Abstract

Subspace-based direction-of-arrival (DoA) estimation commonly relies on the Principal-Component Analysis (PCA) of the sensor-array recorded snapshots. Therefore, it naturally inherits the sensitivity of PCA against outliers that may exist among the collected snapshots (e.g., due to unexpected directional jamming). In this work, we present DoA-estimation based on outlier-resistant L1-norm principal component analysis (L1-PCA) of the realified snapshots and a complete algorithmic/theoretical framework for L1-PCA of complex data through realification. Our numerical studies illustrate that the proposed DoA estimation method exhibits (i) similar performance to the conventional L2-PCA-based method, when the processed snapshots are nominal/clean, and (ii) significantly superior performance when the snapshots are faulty/corrupted.

1 Introduction

Direction-of-arrival (DoA) estimation is a fundamental problem in signal processing theory with important applications in localization, navigation, and wireless communications [1–6]. Existing DoA-estimation methods can be broadly categorized as (i) likelihood maximization methods [7–13], (ii) spectral estimation methods, as in the early works of [14, 15], and (iii) subspace-based methods [16–19]. Subspace-based methods have enjoyed great popularity in applications, mostly due to their favorable trade-off between angle estimation quality and computational simplicity in implementation.

In their most common form, subspace-based DoA estimation methods rely on the L2-norm principal components (L2-PCs) of the recorded snapshots, which can be simply obtained by means of singular-value decomposition (SVD) of the sensor-array data matrix, or by eigenvalue decomposition (EVD) of the received-signal autocorrelation matrix [20]. Importantly, under nominal system operation (i.e., no faulty measurements or unexpected jamming/interfering sources), in additive white Gaussian noise (AWGN) environment, such methods are known to offer unbiased, asymptotically consistent DoA estimates [21–23] and exhibit high target-angle resolution (“super-resolution” methods).

However, in many real-world applications, the collected snapshot record may be unexpectedly corrupted by faulty measurements, impulsive additive noise [24–26], and/or intermittent directional interference. Such interference may appear either as an endogenous characteristic of the underlying communication system, as for example in frequency-hopped spread-spectrum systems [27], or as an exogenous factor (e.g., jamming). In cases of such snapshot corruption, L2-PC-based methods are well known to suffer from significant performance degradation [28–30]. The reason is that, as squared error-fitting minimizers, L2-PCs respond strongly to corrupted snapshots that appear in the processed data matrix as points that lie far from the nominal signal subspace [29]. Accordingly, DoA estimators that rely upon the L2-PCs are inevitably misled.

At the same time, research in signal processing and data analysis has shown that absolute error-fitting minimizers place much less emphasis on individual data points that diverge from the nominal signal subspace than square-fitting-error minimizers. Based on this observation, in the past few years, there have been extended documented research efforts toward defining and calculating L1-norm principal components (L1-PCs) of data under various forms of L1-norm optimality, including absolute-error minimization and projection maximization [31–46]. Recently, Markopoulos et al. [47, 48] calculated optimally the maximum-projection L1-PCs of real-valued data, for which up to that point only suboptimal approximations were known [36–38]. Experimental studies in [47–53] demonstrated the sturdy resistance of optimal L1-norm principal-component analysis (L1-PCA) against outliers, in various signal processing applications. Recently, [43, 45] introduced a heuristic algorithm for L1-PCA that was shown to attain state-of-the-art performance/cost trade-off. Another popular approach for outlier-resistant PCA is “Robust PCA” (RPCA), as introduced in [29] and further developed in [54, 55].

In this work, we consider system operation in the presence of unexpected, intermittent directional interference and propose a new method for DoA-estimation that relies on the L1-PCA of the recorded complex snapshots. Importantly, this work introduces a complete paradigm on how L1-PCA, defined and solved over the real field [47, 48], can be used for processing complex data, through a simple “realification" step. An alternative approach for L1-PCA of complex-valued data was presented in [46], where the authors reformulated complex L1-PCA into unimodular nuclear-norm maximization (UNM) and estimated its solution through a sequence of converging iterations. It is noteworthy that for the UNM introduced in [46], no general exact solver exists to date.

Our numerical studies show that the proposed L1-PCA-based DoA-estimation method attains performance similar to the conventional L2-PCA-based one (i.e., MUSIC [16]) in the absence of jamming sources, while it offers significantly superior performance in the case of unexpected, sporadic contamination of the snapshot record.

Preliminary results were presented in [56]. The present paper is significantly expanded to include (i) an Appendix section with all necessary technical proofs, (ii) important new theoretical findings (Proposition 3 on page 7), (iii) new algorithmic solutions (Section 3.5), and (iv) extensive numerical studies (Section 4).

The rest of the paper is organized as follows. In Section 2, we present the system model and offer a preliminary discussion on subspace-based DoA estimation. In Section 3, we describe in detail the proposed L1-PCA-based DoA-estimation method and present three algorithms for L1-PCA of the snapshot record. Section 4 presents our numerical studies on the performance of the proposed DoA estimation method. Finally, Section 5 holds some concluding remarks.

1.1 Notation

We denote by $\mathbb {R}$ and $\mathbb {C}$ the set of real and complex numbers, respectively, and by j the imaginary unit (i.e., j²=−1). ℜ{(·)},I{(·)},(·)^∗,(·)^⊤, and (·)^H denote the real part, imaginary part, complex conjugate, transpose, and conjugate transpose (Hermitian) of the argument, respectively. Bold lowercase letters represent vectors and bold uppercase letters represent matrices. diag(·) is the diagonal matrix formed by the entries of the vector argument. For any $\mathbf {A} \in \mathbb {C}^{m \times n}, [\mathbf {A}]_{i,q}$ denotes its (i,q)th entry, [A]_:,q its qth column, and [A]_i,: its ith row; $\left \| \mathbf {A} \right \|_{p} \stackrel {\triangle }{=} \left (\sum \nolimits _{i=1}^{m} \sum \nolimits _{q=1}^{n} | [\mathbf {A}]_{i,q} |^{p}\right)^{\frac {1}{p}}$ is the pth entry-wise norm of A,∥A∥_∗ is the nuclear norm of A (sum of singular values), span(A) represents the vector subspace spanned by the columns of A,rank(A) is the dimension of span(A), and null(A^⊤) is the kernel of span(A) (i.e., the nullspace of A^⊤). For any square matrix $\mathbf {A} \in \mathbb {C}^{m \times m}, \text {det} (\mathbf {A})$ denotes its determinant, equal to the product of its eigenvalues. ⊗ and ⊙ are the Kronecker and entry-wise (Hadamard) product operators [57], respectively. 0_m×n,1_m×n, and I_m are the m×n all-zero, m×n all-one, and size-m identity matrices, respectively. Also, $\mathbf {E}_{m} \stackrel {\triangle }{=} \left [ \begin {array}{cc} 0 & -1 \\ 1 & 0 \end {array} \right ] \otimes \mathbf {I}_{m}$, for $m \in \mathbb {N}_{\geq 1}$, and e_i,m is the ith column of I_m. Finally, E{·} is the statistical-expectation operator.

2 System model and preliminaries

We consider a uniform linear antenna array (ULA) of D elements. The length-D response vector to a far-field signal that impinges on the array with angle of arrival $\theta \in (-\frac {\pi }{2}, \frac {\pi }{2}]$ with respect to (w.r.t.) the broadside is defined as

$$\begin{array}{*{20}l} \mathbf{s} (\theta) \stackrel{\triangle}{=} \left[1,~ e^{- j \frac{2 \pi f_{c} d \sin (\theta)}{c}},~ \ldots,~ e^{-j \frac{(D-1) 2 \pi f_{c} d \sin (\theta)}{c}}\right]^{\top} \end{array} $$

(1)

where f_c is the carrier frequency, c is the signal propagation speed, and d is the fixed inter-element spacing of the array. We consider that the uniform inter-element spacing d is no greater than half the carrier wavelength, adhering to the Nyquist spatial sampling theorem; i.e., $d \leq \frac {c}{2 f_{c}}$. Accordingly, for any two distinct angles of arrival $\theta, \theta ' \in (-\frac {\pi }{2}, \frac {\pi }{2}]$, the corresponding array response vectors s(θ) and s(θ^′) are linearly independent.

The ULA collects N narrowband snapshots from K sources of interest (targets) arriving from distinct DoAs $\theta _{1}, \theta _{2}, \ldots, \theta _{K} \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ], K < D \leq N$. We assume that the system may also experience intermittent directional interference from L independent sources (jammers), at angles $\theta _{1}^{\prime }, \theta _{2}^{\prime }, \ldots, \theta _{L}^{\prime } \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]$. A schematic illustration of the targets and jammers is given in Fig. 1. We assume that $\theta _{i} \neq \theta _{q}^{\prime }$, for any i∈{1,2,…,K} and q∈{1,2,…,L}. For any l∈{1,2,…,L}, the l-th jammer may be active during any of the N snapshots with some fixed and unknown to the receiver probability p_l. Accordingly, the n-th down-converted received data vector is of the form

$$ {}\begin{aligned} \mathbf{y}_{n} &= \sum\limits_{k=1}^{K} x_{n,k} \mathbf{s} (\theta_{k}) + \sum\limits_{l=1}^{L} \gamma_{n,l} x_{n,l}^{\prime} \mathbf{s} \left(\theta_{l}^{\prime}\right)+ \mathbf{n}_{n} \in \mathbb{C}^{D \times 1},\\ n&=1,2, \ldots, N, \end{aligned} $$

(2)

Fig. 1

Schematic representation of the K target sources and the L directional jammers

where, x_n,k and $x_{n,l}^{\prime } \in \mathbb {C}$ denote the statistically independent signal values of target k and jammer l, respectively, comprising power-scaled information symbols and flat-fading channel coefficients, and γ_n,l is the activity indicator for jammer l, modeled as a {0,1}-Bernoulli random variable with activation probability p_l. $\mathbf {n}_{n} \in \mathbb {C}^{D \times 1}$ accounts for additive white Gaussian noise (AWGN) with mean equal to zero and per-element variance σ²; i.e., $\mathbf {n}_{n} \sim \mathcal {CN} \left (\mathbf {0}_{D}, \sigma ^{2} \mathbf {I}_{D}\right)$. Henceforth, we refer to the case of target-only presence in the collected snapshots (i.e., γ_n,l=0 for every n=1,2,…,N and every l=1,2,…,L) as normal system operation.

Defining $\mathbf {x}_{n}\! \stackrel {\triangle }{=} [x_{n,1}, x_{n,2}, \ldots, x_{n,K}]^{\top }, \mathbf {x}_{n}^{\prime } \stackrel {\triangle }{=} [x_{n,1}^{\prime }, x_{n,2}^{\prime }, \ldots, x_{n,L}^{\prime }]^{\top }, {\mathbf {\Gamma }}_{n} \stackrel {\triangle }{=} \mathbf {diag}\left ([\gamma _{n,1}, \gamma _{n,2}, \ldots, \gamma _{n,L}]^{\top }\right)$, and $\mathbf {S}_{\Phi } \stackrel {\triangle }{=} \left [ \mathbf {s} (\phi _{1}), \mathbf {s} (\phi _{2}), \ldots, \mathbf {s}(\phi _{m}) \right ] \in \mathbb {C}^{D \times m}$ for any size-m set of angles $\Phi \stackrel {\triangle }{=} \{{\phi }_{1}, {\phi }_{2}, \dots, {\phi }_{m} \} \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]^{m}$,¹ (2) can be rewritten as

$$ {}\mathbf{y}_{n} = \mathbf{S}_{\Theta} \mathbf{x}_{n} + \mathbf{S}_{\Theta^{\prime}} {\mathbf{\Gamma}}_{n} \mathbf{x}_{n}^{\prime} + \mathbf{n}_{n} \in \mathbb{C}^{D \times 1}, \,\,n=1,2, \ldots, N, $$

(3)

for $\Theta \stackrel {\triangle }{=} \left \{{\theta }_{1}, {\theta }_{2}, \dots, {\theta }_{K} \right \}$ and $\Theta ^{\prime } \stackrel {\triangle }{=} \left \{{\theta }_{1}^{\prime }, {\theta }_{2}^{\prime }, \dots, {\theta }_{L}^{\prime }\right \}$. The goal of a DoA estimator is to identify correctly all angles in the DoA set Θ. Importantly, by the Vandermonde structure of S_Θ, it holds that

$$\begin{array}{*{20}l} {\kern35pt}\mathbf{s} (\phi) \subseteq \text{span}(\mathbf{S}_{\Theta}) \Leftrightarrow \phi \in \Theta, \end{array} $$

(4)

for any $\phi \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]$ [16]. That is, given $\mathcal {S} \stackrel {\triangle }{=} \text {span}(\mathbf {S}_{\Theta })$, the receiver can decide accurately for any candidate angle $\phi \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]$ whether it is a DoA in Θ, or not.

2.1 DoA estimation under normal system operation.

Considering for a moment p_l=0 for every l∈{1,2,…,L}, (2) becomes

$$\begin{array}{*{20}l} \mathbf{y}_{n} = \mathbf{S}_{\Theta} \mathbf{x}_{n} + \mathbf{n}_{n} \in \mathbb{C}^{D \times 1}, ~~n=1,2, \ldots, N \end{array} $$

(5)

with autocorrelation matrix $\mathbf {R} \stackrel {\triangle }{=} E \left \{\mathbf {y}_{n} \mathbf {y}_{n}^{\mathrm {H}} \right \} = \mathbf {S}_{\Theta } E \left \{\mathbf {x}_{n} \mathbf {x}_{n}^{\mathrm {H}}\right \} \mathbf {S}_{\Theta }^{\mathrm {H}} + \sigma ^{2} \mathbf {I}_{D}$. Certainly, $\mathcal {S} = \text {span}(\mathbf {S}_{\Theta })$ coincides with the K-dimensional principal subspace of R, spanned by its K highest-eigenvalue eigenvectors [5]. Therefore, being aware of R, the receiver could obtain $\mathcal {S}$ through standard EVD and then conduct accurate DoA estimation by means of (4). However, in practice, the nominal received-signal autocorrelation matrix R is unknown to the receiver and sample-average estimated as $\hat {\mathbf {R}} = \frac {1}{N} \sum \nolimits _{n=1}^{N} \mathbf {y}_{n} \mathbf {y}_{n}^{\mathrm {H}}$ [5, 16]. Accordingly, $\mathcal {S}$ is estimated by the span of the K highest-eigenvalue eigenvectors of $\hat {\mathbf {R}}$, which coincide with the K highest-singular-value left singular-vectors of Y=△[y₁,y₂,…,y_N]. The eigenvectors of $\hat {\mathbf {R}}$, or left singular-vectors of Y, are also commonly referred to as the L2-PCs of Y, since they constitute a solution to the L2-PCA problem

$$\begin{array}{*{20}l} {\kern30pt}\mathbf{Q}_{L2} = \underset{{\mathbf{Q} \in \mathbb{C}^{D \times K},~\mathbf{Q}^{\mathrm{H}}\mathbf{Q} = \mathbf{I}_{K}}}{\text{argmax}}~ \left\| \mathbf{Q}^{\mathrm{H}} \mathbf{Y} \right\|_{2}^{2}. \end{array} $$

(6)

In accordance to (4), the DoA set Θ is estimated by the arguments that yield the K local maxima (peaks) of the familiar MUSIC [16] spectrum

$$\begin{array}{*{20}l} {}P (\phi) = \left\| \left(\mathbf{I}_{D} - \mathbf{Q}_{L2} \mathbf{Q}_{L2}^{\mathrm{H}} \right) \mathbf{s} (\phi) \right\|_{2}^{-2},~~\phi \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right], \end{array} $$

(7)

which clarifies why MUSIC is, in fact, an L2-PCA-based DoA estimation method. Certainly, as N increases asymptotically, $\hat {\mathbf {R}}$ tends to R,Q_L2 tends to span S_Θ, and P(ϕ) goes to infinity for every ϕ∈Θ and finding its peaks becomes a criterion equivalent to (4). Therefore, for sufficient N, L2-PCA-based MUSIC is well-known to attain high performance in normal system operation.

2.2 Complications in the presence of unexpected jamming

In this work, we focus on the case where p_l>0 for all l, so that some snapshots in Y are corrupted by unexpected, unknown, directional interference, as modeled in (2). In this case, the K eigenvectors of $\mathbf {R} = E \left \{\mathbf {y}_{n} \mathbf {y}_{n}^{\mathrm {H}}\right \}$ do not span $\mathcal {S}$ any more. Thus, the K eigenvectors of $\hat {\mathbf {R}}$ or singular-vectors of Y would be of no use, even for very high sample-support N. In fact, interference-corrupted snapshots in Y may constitute outliers with respect to $\mathcal {S}$. Accordingly, due to the well documented high responsiveness of L2-PCA in (6) to outlying data, Q_L2 may diverge significantly from $\mathcal {S}$ [29, 48], rendering DoA estimation by means of (7) highly inaccurate. Below, we introduce a novel method that exploits the outlier-resistance of L1-PCA [36, 47, 48] to offer improved DoA estimates.

3 Proposed DoA estimation method

3.1 Operation on realified snapshots

In order to employ L1-PCA algorithms that are defined for the processing of real-valued data, the proposed DoA estimation method operates on real-valued representations of the recorded complex snapshots in (2), similar to a number of previous works in the field [58–60]. In particular, we define the real-valued representation of any complex-valued matrix $\mathbf {A} \in \mathbb {C}^{m \times n}$, by concatenating its real and imaginary parts, as

$$\begin{array}{*{20}l} {\kern30pt}\overline{\mathbf{A}} & \stackrel{\triangle}{=} \left[ \begin{array}{lr} \Re\{\mathbf{A}\}, & -\Im\{\mathbf{A}\} \\ \Im\{\mathbf{A}\}, & \Re\{\mathbf{A}\} \end{array} \right] \in \mathbb{R}^{2m \times 2n}. \end{array} $$

(8)

In Lie algebras and representation theory, this transition from C^m×n to $\mathbb {R}^{2m \times 2n}$ is commonly referred to as complex-number realification [61, 62] and is a method that allows for any complex system of equations to be converted into (and solved through) a corresponding real system [63]. Lemmas 1, 2, and 3 presented in the Appendix provide three important properties of realification. By (8) and Lemma 1, the nth complex snapshot y_n in (3) can be realified as

$$\begin{array}{*{20}l} {\kern20pt}\overline{\mathbf{y}}_{n} = \overline{\mathbf{S}}_{\Theta} \overline{\mathbf{x}}_{n} + \overline{\mathbf{S}}_{\Theta^{\prime}} \overline{\mathbf{\Gamma}}_{n} \overline{\mathbf{x}^{\prime}}_{n} + \overline{\mathbf{n}}_{n} \in \mathbb{R}^{2D \times 2}. \end{array} $$

(9)

In accordance with Lemma 2, the rank of $\overline {\mathbf {S}}_{\Theta }$ is 2K and, hence, $\mathcal {S}_{R} \stackrel {\triangle }{=} \text {span} \left (\overline {\mathbf {S}}_{\Theta }\right)$ is a 2K-dimensional subspace wherein the K realified signal components of interest with angles of arrival in Θ lie. The following Proposition, deriving straightforwardly from (4) by means of Lemma 1 and Lemma 2, highlights the utility of $\mathcal {S}_{R}$ for estimating the target DoAs.

Proposition 1

For any $\phi \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]$, it holds that

$$\begin{array}{*{20}l} {\kern35pt}\text{span}\left(\overline{\mathbf{s}} (\phi) \right) \subseteq \mathcal{S}_{R} ~ \Leftrightarrow~ \phi \in \Theta. \end{array} $$

(10)

Set equality may hold only if K=1. ■

By Proposition 1, given an orthonormal basis $\mathbf {Q}_{R} \in \mathbb {R}^{2D \times 2K}$ that spans $\mathcal {S}_{R}$, the receiver can decide accurately whether some $\phi \in \left (-\frac {\pi }{2}, \frac {\pi }{2} \right ]$ is a target DoA, or not, by means of the criterion

$$\begin{array}{*{20}l} \left(\mathbf{I}_{2D} - \mathbf{Q}_{R}\mathbf{Q}_{R}^{\top} \right) \overline{\mathbf{s}}(\phi) = \mathbf{0}_{2D \times 2} ~ \Leftrightarrow ~ ~\phi \in \Theta. \end{array} $$

(11)

Similar to the complex-data case presented above, in normal system operation, $\mathcal {S}_{R}$ coincides with the span of the K dominant eigenvectors of $\mathbf {R}_{R} \stackrel {\triangle }{=} \mathrm {E} \left \{\overline {\mathbf {y}}_{n} \overline {\mathbf {y}}_{n}^{\top } \right \}$. When the receiver, instead of R_R, possesses only the realified snapshot record $\overline {\mathbf {Y}}, \mathcal {S}_{R}$ can be estimated as the span of

$$\begin{array}{*{20}l} \mathbf{Q}_{R,L2} = \underset{{\mathbf{Q} \in \mathbb{R}^{2D \times 2K},~\mathbf{Q}^{\top}\mathbf{Q} = \mathbf{I}_{2K}}}{\text{argmax}}~ \left\| \mathbf{Q}^{\top} \overline{\mathbf{Y}} \right\|_{2}^{2}. \end{array} $$

(12)

Then, in accordance with (11), the target DoAs can be estimated as the arguments that yield the K highest peaks of the spectrum

$$ \begin{aligned} P_{R}(\phi; ~ {\mathbf{Q}}_{R,L2}) & \stackrel{\triangle}{=} 2\left\| \left(\mathbf{I}_{2D} - {\mathbf{Q}}_{R,L2} {\mathbf{Q}}_{R,L2}^{\top} \right) \overline{\mathbf{s}} (\phi) \right\|_{2}^{-2},\\ &~~\phi \in (-\frac{\pi}{2}, \frac{\pi}{2} ]. \end{aligned} $$

(13)

Similar to (6), the solution to (12) can be obtained by singular-value decomposition (SVD) of $\overline {\mathbf {Y}}$. Interestingly, the L2-PCA-based DoA estimator of (13) is equivalent to the complex-field MUSIC estimator presented in Section 2. In fact, as we prove in the Appendix,

$$\begin{array}{*{20}l} {\kern20pt}P_{R}(\phi; {\mathbf{Q}}_{R,L2}) = P(\phi) ~~\forall \phi \in \left[-\frac{\pi}{2},\frac{\pi}{2} \right). \end{array} $$

(14)

Hence, exhibiting performance identical to that of MUSIC, (12) can offer highly accurate estimates of the target DoAs under normal system operation. However, when Y contains corrupted snapshots, the L2-PCA-calculated span(Q_R,L2) is a poor approximation to $\mathcal {S}_{R}$ and DoA estimation by means of P_R(ϕ;Q_R,L2) tends to be highly inaccurate. In the following subsection, we present an alternative, L1-PCA-based method for obtaining an outlier-resistant estimate of Θ.

3.2 DoA estimation by realified L1-PCA

Over the past few years, L1-PCA has been shown to be far more resistant than L2-PCA against outliers in the data matrix [31–40, 47, 48]. In this work, we propose the use of a DoA-estimation spectrum analogous to that in (13) that is formed by the L1-PCs of $\overline {\mathbf {Y}}$. Specifically, the proposed method has two steps. First, we obtain the L1-PCs of $\overline {\mathbf {Y}}$, solving the L1-PCA problem

$$\begin{array}{*{20}l} \mathbf{Q}_{R,L1} = \underset{\mathbf{Q} \in \mathbb{R}^{2D \times 2K},~ \mathbf{Q}^{\top} \mathbf{Q} = \mathbf{I}_{2K}}{\text{argmax}} \sum\limits_{n=1}^{N} \left\| \mathbf{Q}^{\top} \overline{\mathbf{y}}_{n} \right\|_{1}. \end{array} $$

(15)

That is, (15) searches for the subspace that maximizes data presence, quantified as the aggregate L1-norm of the projected points.

Then, similarly to MUSIC, we estimate the target angles in Θ by the K highest peaks of the L1-PCA-based spectrum

$$ \begin{aligned} P_{R}(\phi; \mathbf{Q}_{R,L1}) & = 2\left\| \left(\mathbf{I}_{2D} - \mathbf{Q}_{R,L1} \mathbf{Q}_{R,L1}^{\top}\right) \overline{\mathbf{s}} (\phi) \right\|_{2}^{-2},\\ &~~\phi \in (-\frac{\pi}{2}, \frac{\pi}{2} ]. \end{aligned} $$

(16)

In accordance to standard practice, to find the K highest peaks of (16), we examine every angle in $\left \{\phi =-\frac {\pi }{2}+k \Delta \phi :~ k\in \left \{1, 2, \ldots, \left \lfloor \frac {\pi }{\Delta \phi } \right \rfloor ~ \right \}\right \}$, for some small scanning step Δϕ>0. Next, we place our focus on solving the L1-PCA in (15).

3.3 Principles of realified L1-PCA

Although L1-PCA is not a new problem in the literature (see, e.g., [36–38]), its exact optimal solution was unknown until the recent work in [48], where the authors proved that (15) is formally NP-hard and offered the first two exact algorithms for solving it. Proposition 2 below, originally presented in [48] for real-valued data matrices of general structure (i.e., not having necessarily the realified structure of $\overline {\mathbf {Y}}$) translates L1-PCA in (15) to a nuclear-norm maximization problem over the binary field.

Proposition 2

If B_opt is a solution to

$$\begin{array}{*{20}l} {\kern55pt}\underset{\mathbf{B} \in \{\pm 1\}^{2N \times 2K}}{\text{maximize}}~\| \overline{\mathbf{Y}} \mathbf{B}\|_{*}^{2} \end{array} $$

(17)

and $\overline {\mathbf {Y}} \mathbf {B}_{\text {opt}}$ admits SVD $\overline {\mathbf {Y}} \mathbf {B}_{\text {opt}} \overset {\text {}}{=} \mathbf {U} \mathbf {\Sigma }_{2K \times 2K} \mathbf {V}^{\top }$, then

$$\begin{array}{*{20}l} {\kern63pt}{\mathbf{Q}}_{R,L1} = \mathbf{U} \mathbf{V}^{\top} \end{array} $$

(18)

is a solution to ( 15 ). Moreover, $\left \| {\mathbf {Q}}_{R,L1}^{\top } \overline {\mathbf {Y}}\right \|_{1} = \left \| \overline {\mathbf {Y}} \mathbf {B}_{\text {opt}}\right \|_{*}$. ■

Since Q_R,L1 can be obtained by B_opt via standard SVD, L1-PCA is in practice equivalent to a combinatorial optimization problem over the 4N,K binary variables in B. The authors in [48] presented two algorithms for exact solution of (17), defined upon real-valued data matrices of general structure.

In this work, for the first time, we simplify the solutions of [48] in view of the special, realified structure of $\overline {\mathbf {Y}}$. Specifically, in the following Proposition 3, we show that for K=1 we can exploit the special structure of $\overline {\mathbf {Y}}$ and reduce (17) to a binary quadratic-form maximization problem over half the number of binary variables (i.e., 2N instead of 4N). A proof for Proposition 3 is provided in the Appendix.

Proposition 3

If b_opt is a solution to

$$\begin{array}{*{20}l} {\kern63pt}\underset{\mathbf{b} \in \{\pm 1\}^{2N \times 1}}{\text{maximize}}~\| \overline{\mathbf{Y}} \mathbf{b}\|_{2}^{2}, \end{array} $$

(19)

then [b_opt, E_Nb_opt] is a solution to

$$\begin{array}{*{20}l} {\kern63pt}\underset{\mathbf{B} \in \{\pm 1\}^{2N \times 2}}{\text{maximize}}~\| \overline{\mathbf{Y}} \mathbf{B}\|_{*}^{2}. \end{array} $$

(20)

with $\| \overline {\mathbf {Y}}~[\mathbf {b}_{\text {opt}}, \mathbf {E}_{N} \mathbf {b}_{\text {opt}}]\|_{*}^{2} = 4~ \|\overline {\mathbf {Y}} \mathbf {b}_{\text {opt}} \|_{2}^{2}. \label {nucnorm5}$ ■

In view of Propositions 2 and 3, Q_R,L1 derives easily from the solution of

$$\begin{array}{*{20}l} {\kern63pt}\underset{\mathbf{B} \in \{\pm 1 \}^{2N \times m}}{\text{maximize}}~\| \overline{\mathbf{Y}} \mathbf{B} \|_{*}, \end{array} $$

(21)

for m=1, if K=1, or m=2K, if K>1.

Since (21) is a combinatorial problem, the conceptually simplest approach for solving it is an exhaustive search (possibly in parallel fashion) over all elements of its feasibility set {±1}^2N×m. By means of this method, one should conduct 2^2Nm nuclear norm evaluations (e.g., by means of SVD of $\overline {\mathbf {Y}} \mathbf {B}$) to identify the optimum argument in the feasibility set; thus, the asymptotic complexity of this method is $\mathcal {O}\left (2^{2Nm}\right)$. Exploiting the well-known nuclear-norm properties of column-permutation and column-negation invariance, we can expedite practically the exhaustive procedure by searching for a solution to (21) in the set of all binary matrices that are column-wise built by the elements of a size-m multiset² of {b∈{±1}^2N: [b]₁=1}. By this modification, the exact number of binary matrices examined (thus, the number of nuclear-norm evaluations) decreases from 2^2Nm to ${{2^{2N-1}+2K-1}\choose {m}}$. Of course, exhaustive-search approaches, being of exponential complexity in N, become impractical as the number of snapshots increases. For completeness, in Fig. 2, we provide a pseudocode for the exhaustive-search algorithm presented above.

Fig. 2

Algorithm for optimal computation of the 2K L1-PCs of rank- 2D data matrix $\overline {\mathbf {Y}}_{2D \times 2N}$ with exponential (w.r.t. N) asymptotic complexity ${\mathcal {O}}\left (2^{2Nm}\right)$ (m=1, for K=1; m=2K, for K>1)

For the case of engineering interest where N>D and D is a constant, the authors in [48] presented a polynomial-cost algorithm that solves (21) with complexity $\mathcal {O}(N^{2Dm})$. In the following subsection, we exploit further the structure of $\overline {\mathbf {Y}}$ and reduce significantly the computational cost of this algorithm.

3.4 Polynomial-cost realified L1-PCA

The authors in [48] showed that, according to Proposition 2, a solution to (21) can be found among the binary matrices that draw columns from

$$\begin{array}{*{20}l} \mathcal{B} \stackrel{\triangle}{=} \left\{\text{sgn} \left(\overline{\mathbf{Y}}^{\top} \mathbf{a}\right):~\mathbf{a} \in \Omega_{2D}\right\} \subseteq \{\pm 1 \}^{2N \times 1} \end{array} $$

(22)

where $\Omega _{2D} \stackrel {\triangle }{=} \left \{\mathbf {a} \in \mathbb {R}^{2D \times 1}:~ \|\mathbf {a} \|_{2}=1, [\!\mathbf {a}]_{2D} >0\right \}$ –with the positivity constraint in the last entry of a deriving from the invariance of the nuclear norm to column negations of its matrix argument. That is, a solution to (21) belongs to the mth Cartesian power of $\mathcal {B}, \mathcal {B}^{m} \subseteq \{\pm 1 \}^{2N \times m}$.

In addition, [48] pointed out that, since the nuclear-norm maximization is also invariant to column permutations of the argument, we can maintain problem equivalence while further narrowing down our search to the elements of a set $\tilde {\mathcal {B}}$, subset of $\mathcal {B}^{m}$, that contains the ${{|\mathcal {B}| +m-1}\choose {m}}$ binary matrices that are built by the elements of all size-m multisets of $\mathcal {B}$. That is, we can obtain a solution to (21) by solving instead

$$\begin{array}{*{20}l} {\kern60pt}\underset{\mathbf{B} \in \tilde{\mathcal{B}}} {\text{maximize}} \left\| \overline{\mathbf{Y}} \mathbf{B}\right\|_{*}^{2}. \end{array} $$

(23)

Importantly, $|\tilde {\mathcal {B}}| = {{|\mathcal {B}| +m-1}\choose {m}} < |\mathcal {B}|^{m} = |\mathcal {B}^{m}|$. The exact multiset-extraction procedure for obtaining $\tilde {\mathcal {B}}$ from $\mathcal {B}$ follows.

Calculation of$\tilde {\boldsymbol{\boldsymbol{\mathcal {B}}}}$ from$\boldsymbol{\boldsymbol{\mathcal {B}}}$[48]. For every $i \in \left \{1,2,\ldots, \binom {|\mathcal {B}| + m-1 }{m} \right \}$, we define a distinct indicator function $f_{i} : \mathcal {B} \mapsto \{0, 1, \ldots, m\}$ that assigns to every $\mathbf {b} \in \mathcal {B}$ a natural number f_i(b)≤m, such that $\sum \nolimits _{\mathbf {b}\in \mathcal {B}} f_{i}(\mathbf {b})=m$. Then, for every $i \in \left \{1,2,\ldots, {{|\mathcal {B}| +m-1}\choose {m}}\right \}$, we define a unique binary matrix B_i∈{±1}^2N×m such that every $\mathbf {b} \in \mathcal {B}$ appears exactly f_i(b) times among the columns of B_i. Finally, we define the sought-after set as $\tilde {\mathcal {B}} \stackrel {\triangle }{=} \left \{\mathbf {B}_{1}, \mathbf {B}_{2}, \ldots, \mathbf {B}_{{{|\mathcal {B}| +m-1}\choose {m}}}\right \}$.

Evidently, the cost to solve (23), and thus (21), amounts to the cost of constructing the feasibility set $\tilde {\mathcal {B}}$ added to the cost of conducting nuclear-norm evaluations (through SVD) over all its elements. Therefore, the cost to solve (23) depends on the construction cost and cardinality of $\tilde {\mathcal {B}}$. As seen above, $|\tilde {\mathcal {B}}| = {{|\mathcal {B}| + m-1}\choose {m}}$ and $\tilde {\mathcal {B}}$ can be constructed online, by multiset selection on $\mathcal {B}$, with negligible computational cost. Therefore, for determining the cardinality and construction cost of $\tilde {\mathcal {B}}$, we have to find the cardinality and construction cost of $\mathcal {B}$.

Next, we present a novel method to construct ${\mathcal {B}}$, different than the one in [48], that exploits the realified structure of $\overline {\mathbf {Y}}$ to achieve lower computational cost.

Construction of $\boldsymbol{\boldsymbol{\mathcal {B}}}$ , in view of the structure of $\overline {\mathbf {Y}}$ .

Considering that any group of m≤2D columns of $\overline {\mathbf {Y}}$ spans a m-dimensional subspace, for each index set $\mathcal {X} \subseteq \{1, 2, \ldots, 2N \}$ –elements in ascending order (e.a.o.)– of cardinality $|\mathcal {X}| = 2D-1$, we denote by $\mathbf {z}(\mathcal {X})$ the unique left-singular vector of $\left [\overline {\mathbf {Y}}\right ]_{:,\mathcal {X}}$ that corresponds to zero singular value. Calculation of $\mathbf {z}(\mathcal {X})$ can be achieved either by means of SVD or by simple Gram-Schmidt Orthonormalization (GMO) of $\left [\overline {\mathbf {Y}}\right ]_{:,\mathcal {X}}$ –both SVD and GMO are of constant cost with respect to N. Accordingly, we define

$$\begin{array}{*{20}l} {\kern25pt}\mathbf{c}(\mathcal{X}) \stackrel{\triangle}{=} \text{sgn}([\mathbf{z}(\mathcal{X})]_{2D})\mathbf{z}(\mathcal{X}) \in \Omega_{2D}. \end{array} $$

(24)

Being a scaled version of $\mathbf {z}(\mathcal {X}), \mathbf {c}(\mathcal {X})$ also belongs to $\text {null}\left (\left [\overline {\mathbf {Y}}\right ]_{:,\mathcal {X}}^{\top }\right)$, satisfying $\left [\overline {\mathbf {Y}}\right ]_{:,\mathcal {X}}^{\top } \mathbf {c}(\mathcal {X}) = \mathbf {0}_{2D-1} \label {c}.$ Next, we define the set of binary vectors

$$\begin{array}{*{20}l} {}\mathcal{B}(\mathcal{X})\! \stackrel{\triangle}{=} \!\left\{\!\mathbf{b} \in \{\pm 1 \}^{2N \times 1}\!:~ [\!\mathbf{b}]_{\mathcal{X}^{c}}=\text{sgn}\left(\![\!\overline{\mathbf{Y}}]_{:, \mathcal{X}^{c}}^{\top}\mathbf{c} (\mathcal{X})\! \right) \!\right\} \end{array} $$

(25)

of cardinality $|\mathcal {B}(\mathcal {X})| = 2^{2D-1}$, where $\mathcal {X}^{c} \stackrel {\triangle }{=} \{1, 2, \ldots, 2N \} \setminus \mathcal {X}$ (e.a.o.) is the complement of $\mathcal {X}$. In [48], the authors showed that

$$\begin{array}{*{20}l} {\kern48pt}\mathcal{B} = \underset{\underset{|\mathcal{X}| = 2D-1}{\mathcal{X} \subseteq \{1, 2, \ldots, 2N \}}}{\bigcup} \mathcal{B} (\mathcal{X}). \end{array} $$

(26)

Since $\mathcal {X}$ can take ${{2N}\choose {2D-1}}$ different values, $\mathcal {B}$ can be built by (26) through ${{2N}\choose {2D-1}}$ nullspace calculations in the form of (24), with cost ${{2N}\choose {2D-1}}D^{3} \in \mathcal {O}\left (N^{2D}\right)$. Accordingly, $\mathcal {B}$ consists of

$$\begin{array}{*{20}l} {\kern25pt}|\mathcal{B}| \leq 2^{2D-1} {{2N}\choose{2D-1}} \in \mathcal{O}\left(N^{2D-1}\right) \end{array} $$

(27)

elements. In fact, in view of [64], the exact cardinality of $\mathcal {B}$ is

$$\begin{array}{*{20}l} {\kern25pt}|\mathcal{B}| = \sum\limits_{d=0}^{2D-1}{{2N-1}\choose{d}} \in \mathcal{O}\left(N^{2D-1}\right). \end{array} $$

(28)

Next, we show for the first time how we can reduce the cost of calculating $\mathcal {B}$, exploiting the realified structure of $\overline {\mathbf {Y}}$.

Consider $\mathcal {X}_{1} \subseteq \{1, 2, \ldots, N \}$ (e.a.o.), $\mathcal {X}_{2} \subseteq \{N+1, N+2, \ldots, 2N \}$ (e.a.o.), and their union $\mathcal {X}_{A} = \{\mathcal {X}_{1}, \mathcal {X}_{2} \}$ (e.a.o.), such that $|\mathcal {X}_{1}| < D$ and $|\mathcal {X}_{A}|=|\mathcal {X}_{1}| + |\mathcal {X}_{2}| = 2D-1$. Define also the set of indices $\mathcal {X}_{B} = \{\mathcal {X}_{1} + N, \mathcal {X}_{2} - N\}$ (e.a.o.) with $|\mathcal {X}_{B}| = 2D-1$. By the structure of $\overline {\mathbf {Y}}$, it is straightforward that

$$\begin{array}{*{20}l} {\kern23pt}\mathbf{c}(\mathcal{X}_{B}) = \mathbf{E}_{D} \mathbf{c}(\mathcal{X}_{A}) \text{sgn}([\mathbf{c}(\mathcal{X}_{A})]_{D}). \end{array} $$

(29)

In turn, by the definition in (25) and (29), it holds that

$$\begin{array}{*{20}l} {\kern22pt}\mathcal{B}(\mathcal{X}_{B}) = \text{sgn}([\mathbf{c}(\mathcal{X}_{A})]_{D}) \mathbf{E}_{N} \mathcal{B}(\mathcal{X}_{A}). \end{array} $$

(30)

The proof of (29) and (30) is offered in the Appendix. Notice now that, for every $\mathcal {X} \subset \{1, 2, \ldots, 2N \}$ with $|\mathcal {X}| = 2D-1$, there exist $\mathcal {X}_{1} \subset \{1, 2, \ldots, N\}$ and $\mathcal {X}_{2} \subset \{N+1, N+2, \ldots, 2N\}$, satisfying $|\mathcal {X}_{1}| < D$ and $|\mathcal {X}_{1}| + |\mathcal {X}_{2}|=2D-1$, such that

$$\begin{array}{*{20}l} \text{either}\ \mathcal{X} = \{\mathcal{X}_{1}, \mathcal{X}_{2} \}, ~~\text{or}~~ \mathcal{X} = \{\mathcal{X}_{1} +N, \mathcal{X}_{2} -N\}. \end{array} $$

(31)

Thus, by (26) and (31), $\mathcal {B}$ can constructed as

$$ {\begin{aligned} \mathcal{B} &= \bigcup_{d=0}^{D-1} \hspace{0.1cm} \underset{\underset{\mathcal{X}_{2} \subset \{\{1, 2, \ldots, N \}+N\}, \; |\mathcal{X}_{2}|=2D-1-d}{\mathcal{X}_{1} \subset \{1, 2, \ldots, N \}, \; |\mathcal{X}_{1}|=d}}{\bigcup} \left\{\mathcal{B} (\{\mathcal{X}_{1}, \mathcal{X}_{2}\}), \mathcal{B} (\{\mathcal{X}_{1} +N, \mathcal{X}_{2} -N \})\right\}. \end{aligned}} $$

(32)

In view of (30), $\mathcal {B} (\{\mathcal {X}_{1} +N, \mathcal {X}_{2} -N\})$ can be directly constructed from $\mathcal {B} (\{\mathcal {X}_{1}, \mathcal {X}_{2} \})$ with negligible computational overhead. In addition, for $|\mathcal {X}_{1}| < D$ and $|\mathcal {X}_{1}|+|\mathcal {X}_{2}| =2D-1$, by the Chu-Vandermonde binomial-coefficient property [65], $\{\mathcal {X}_{1}, \mathcal {X}_{2} \}$ can take

$$\begin{array}{*{20}l} \sum\limits_{d=0}^{D-1} {{N}\choose{d}} {{N}\choose{2D-1-d}} = \frac{1}{2} {{2N}\choose{2D-1}} \end{array} $$

(33)

values. Therefore, exploiting the structure of $\overline {\mathbf {Y}}$, the proposed algorithm constructs $\mathcal {B}$ by (32), avoiding half the nullspace calculations needed in the generic method of [48], presented in (26).

In view of (28), the feasibility set of (23), $\tilde {\mathcal {B}}$, consists of exactly

$$ \begin{aligned} |\tilde{\mathcal{B}}|& = {{|\mathcal{B}| +m-1}\choose{m}} = {{\sum\nolimits_{d=0}^{2D-1}\binom{2N-1}{d} +m-1}\choose{m}}\\ &\in \mathcal{O}\left(N^{2Dm - m}\right) \end{aligned} $$

(34)

elements. Thus, $\mathcal {O}(N^{2Dm - m})$ nuclear-norm evaluations suffice to obtain a solution to (17). The asymptotic complexity for solving (15) by the presented algorithm is then $\mathcal {O}\left (N^{2Dm-m}\right)$. The described polynomial-time algorithm is presented in detail in Fig. 3, including element-by-element construction of $\mathcal {B}$.

Fig. 3

Algorithm for optimal computation of the 2K L1-PCs of the rank- 2D data matrix $\overline {\mathbf {Y}}_{2D \times 2N}$ with polynomial (w.r.t. N) asymptotic complexity ${\mathcal {O}}\left (N^{4DK - m+1}\right)$ (m=1 for K=1; m=2K, for K>1)

3.5 Iterative realified L1-PCA

For large problem instances (large N,D), the above presented optimal L1-PCA calculators could be computationally impractical. Therefore, at this point we present and employ the bit-flipping-based iterative L1-PCA calculator, originally introduced in [43] for processing general real-valued data matrices. Given $\overline {\mathbf {Y}} \in \mathbb {R}^{2D \times 2N}$, and some m<2 min(D,N), the algorithm presented below attempts to solve (21), by conducting a converging sequence of optimal single-bit flips.

Specifically, the algorithm is initializes at a 2N×m binary matrix B⁽¹⁾ and conducts optimal single-bit flipping iterations. Specifically, at the tth iteration step (t>1), the algorithm generates the new matrix B^(t) so that (i) B^(t) differs from B^(t−1) in exactly one entry (bit flipping) and (ii) $\| \overline {\mathbf {Y}} \mathbf {B}^{(t)} \|_{*} > \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} \|_{*}$. Mathematically, we notice that if we flip at the tth iteration the (n,k)th bit of B^(t−1) setting B^(t)=B^(t−1)−2[B^(t−1)]_n,ke_n,2Ne_k,m^⊤, it holds that

$$\begin{array}{*{20}l} \overline{\mathbf{Y}} \mathbf{B}^{(t)} = \overline{\mathbf{Y}} \mathbf{B}^{(t-1)} - 2 \left[\mathbf{B}^{(t-1)}\right]_{n,k} [\!\overline{\mathbf{Y}}]_{:,n} {\mathbf{e}_{k,m}}^{\top}. \end{array} $$

(35)

Therefore, at step t, the presented algorithm searches for a solution (n,k) to

$$\begin{array}{*{20}l} \underset{\underset{(l-1)2N+j \in \mathcal{L}^{(t)}}{(j,l) \in \{1, 2, \ldots, 2N \} \times \{1, 2, \ldots, m \}}}{\text{maximize}} \left\| \overline{\mathbf{Y}} \mathbf{B}^{(t-1)} - 2 \left[\mathbf{B}^{(t-1)}\right]_{j,l} [\!\overline{\mathbf{Y}}]_{:,j} {{\mathbf{e}_{l}^{m}}}^{\top} \right\|_{*}. \end{array} $$

(36)

The constraint set $\mathcal {L}^{(t)} \subseteq \{1,2, \ldots, 2Nm \}$, employed to restrain the greediness of the presented iterations, contains the indices³ of bits that have not been flipped before and, thus, is initialized as $\mathcal {L}^{(1)} = \{1,2, \ldots, 2Nm \}$. Having obtained the solution to (36), (n,k), the algorithm proceeds as follows. If $\left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} - 2 \left [\mathbf {B}^{(t-1)}\right ]_{n,k} [\!\overline {\mathbf {Y}}]_{:,n} \mathbf {e}_{k,m}^{\top } \right \|_{*} > \left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} \right \|_{*}$, the algorithm generates $\mathbf {B}^{(t)} = \mathbf {B}^{(t-1)} - 2 \left [\mathbf {B}^{(t-1)}\right ]_{n,k} \mathbf {e}_{n,2N}\mathbf {e}_{k,m}^{\top }$ and updates $\mathcal {L}^{(t+1)}$ to $\mathcal {L}^{(t)} \setminus \{ (k-1)2N+n\}$. If, otherwise, $\left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} - 2 \left [\mathbf {B}^{(t-1)}\right ]_{n,k}[\!\overline {\mathbf {Y}}]_{:,n} \mathbf {e}_{k,m}^{\top } \right \|_{*} \leq \left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} \right \|_{*}$, the algorithm obtains a new solution (n,k) to (36) after resetting $\mathcal {L}^{(t)}$ to {1,2,…,2Nm}. If this new (n,k) is such that $\left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} - 2 \left [\mathbf {B}^{(t-1)}\right ]_{n,k} [\!\overline {\mathbf {Y}}]_{:,n} \mathbf {e}_{k,m}^{\top } \right \|_{*} > \left \| \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} \right \|_{*}$, then the algorithm sets $\mathbf {B}^{(t)} = \mathbf {B}^{(t-1)} - 2 [\mathbf {B}^{(t-1)}]_{n,k} \mathbf {e}_{n,2N}\mathbf {e}_{k,m}^{\top }$ and updates $\mathcal {L}^{(t+1)} = \mathcal {L}^{(t)} \setminus \{(k-1)2N+n\}$. Otherwise, the iterations terminate and the algorithm returns B^(t) as a heuristic solution to (21). Notice that since at each iteration, the optimization metric increases. At the same time, the metric is certainly upper-bounded by $\| \overline {\mathbf {Y}} \mathbf {B}_{opt}\|_{*}$. Therefore, the iterations are guaranteed to terminate in a finite number of steps, for any initialization B⁽¹⁾. Our studies have shown that, in fact, the iterations terminate for t<2Nm, with very high frequency of occurrence.

For solving (36), one has to calculate $\left \|{\vphantom {\mathbf {e}_{l,m}^{\top }}} \overline {\mathbf {Y}} \mathbf {B}^{(t-1)} -2 \left [\mathbf {B}^{(t-1)}\right ]_{j,l} [\!\overline {\mathbf {Y}}]_{:,j} \mathbf {e}_{l,m}^{\top } \right \|_{*}$, for all (j,l)∈{1,2,…,2N}×{1,2,…,m} such that $(l-1)2N+j \in \mathcal {L}$. At worst case, $\mathcal {L} = \{1, 2, \ldots, 2Nm \}$ and this demands 2Nm independent singular-value/nuclear-norm calculations. Therefore, the total cost for solving (36) is $\mathcal {O}\left (N^{2}m^{3}\right)$. If we limit the number of iterations to 2Nm, for the sake of practicality, then the total cost for obtaining a heuristic solution to (21) is $\mathcal {O} \left (N^{3} m^{4}\right)$ –significantly lower than the cost of the polynomial-time optimal algorithm presented above, $\mathcal {O}\left (N^{2Dm-m}\right)$. When the iterations terminate, the algorithm returns the bit-flipping-derived L1-PC matrix ${\mathbf {Q}}_{R,BF} \stackrel {\triangle }{=} \mathbf {U} \mathbf {V}^{\top }$, where $\mathbf {U} \mathbf {\Sigma }_{2K \times 2K} \mathbf {V}^{\top } \overset {\text {svd}}{=} \overline {\mathbf {Y}} \mathbf {B}_{\text {opt}}$. Formal performance guarantees for the presented bit-flipping procedure were offered in [43], for general real-valued matrices and K=1.

A pseudocode of the presented algorithm for the calculation of the 2K L1-PCs $\overline {\mathbf {Y}}_{2D \times 2N}$ is presented in Fig. 4.

Fig. 4

Algorithm for estimation of the 2K L1-PCs of rank- 2D data matrix $\overline {\mathbf {Y}}_{2D \times 2N}$ with cubic (w.r.t. N) asymptotic complexity $\mathcal {O} \left (N^{3} m^{4}\right)$ (m=1 for K=1; m=2K, for K>1)

4 Numerical results and discussion

We present numerical studies to evaluate the DoA estimation performance of realified L1-PCA, compared to other PCA calculation counterparts. Our focus lies on cases where a nominal source (the DoA of which we are looking for) operates in the intermittent presence of a jammer located at a different angle. Ideally, we would like the DoA estimator to be able to identify successfully the DoA of the source of interest, despite the unexpected directional interference.

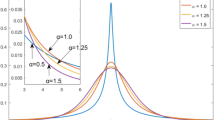
To offer a first insight into the performance of the proposed method, in Fig. 5 we present a realization of the DoA-estimation spectra P_R(ϕ;Q_R,L1) and P_R(ϕ;Q_R,L2), as defined in (14) and (16), respectively. In this study, we calculate the exact L1-PCs of $\overline {\mathbf {Y}}$, using the polynomial-cost optimal algorithm of Fig. 3. The receiver antenna-array is equipped with D=3 elements and collects N = 8 snapshots. All snapshots contain a signal from the single source of interest (K=1) impinging on the array with DoA − 20^∘. One out of the eight snapshots is corrupted by two jamming sources with DoAs 31^∘ and 54^∘. The signal-to-noise ratio (SNR) is set to 2 dB for the target source and to 5 dB for each of the jammers. We observe that standard MUSIC (L2-PCA) is clearly misled by the two jammer-corrupted measurement. Interestingly, the proposed L1-PCA-based method manages to identify the target location successfully.

Fig. 5

DoA-estimation spectra P_R(ϕ;Q_R,L2) (MUSIC) and P_R(ϕ;Q_R,L2) (proposed); one target and two jamming signals with angles of arrival marked by $\blacktriangle$ and ∙,∙, respectively

Next, we generalize our study to include probabilistic presence of an jammer. Specifically, we keep D=3 and N=8 and consider K=1 target at θ=− 41^∘ with SNR 2 dB, and L=1 jammer at θ^′=24^∘ with activation probability p taking values in {0,.1,.2,.3,.4,.5}.

In Fig. 6, we plot the root-mean-square-error (RMSE)⁴, calculated over 5000 independent realizations, vs. jammer SNR, for three DoA estimators: (a) the standard L2-PCA-based one (MUSIC), (b) the proposed L1-PCA DoA estimator with the L1-PCs calculated optimally by means of the polynomial-cost algorithm of Fig. 3, and (c) the proposed L1-PCA estimator with the L1-PCs found by means of the algorithm of Fig. 4. For all three methods, we plot the performance attained for each value of p∈{0,.1,.2,.3,.4,.5}. Our first observation is that the two L1-PCA-based estimators exhibit almost identical performance for every value of p and jammer SNR. Then, we notice that, in normal system operation (p=0) the RMSEs of the L2-PCA-based and L1-PCA-based estimators are extremely close to each other and low, with slight (almost negligible) superiority of the L2-PCA-based method. Quite interestingly, for any non-zero jammer activation probability p and over the entire range of jammer SNR values, the RMSE attained by the proposed L1-PCA-based methods is lower than that attained by the L2-PCA-based one. For instance, for jammer SNR 12 dB and p=.1, the proposed methods offer 8^∘ smaller RMSE than MUSIC. Of course, at high jammer SNR values and p =.5 the RMSE of both methods approaches 65^∘, which is the angular distance of the target and the jammer; i.e. both methods tend to peak the significantly (18 dB) stronger jammer present in half the snapshots.

Fig. 6

Root-mean-squared-error (RMSE) vs. jammer SNR, for: L2-PCA (MUSIC), optimal L1-PCA, calculated by means of Algorithm 2 in Fig. 3, and L1-PCA by means of Algorithm 3 in Fig. 4. For each estimator, we present the RMSE curves for p=0,.1,.2,.3,.4,.5. N=8,D=3,θ=− 41^∘,θ^′=24^∘, source SNR 2 dB

In Fig. 7, we change the metric and study the more general Subspace Representation Ratio (SRR), attained by L2-PCA and L1-PCA. For any orthonormal basis $\mathbf {Q} \in \mathbb {R}^{2D \times 2K}$, SRR is defined as

$$\begin{array}{*{20}l} {\kern22pt}\text{SRR} (\mathbf{Q}) \stackrel{\triangle}{=} \frac{\left\| \mathbf{Q}^{\top} \overline{\mathbf{s}} ({\theta})\right\|_{2}^{2}}{\left\| \mathbf{Q}^{\top} \overline{\mathbf{s}}({\theta^{\prime}})\right\|_{2}^{2}+\left\| \mathbf{Q}^{\top} \overline{\mathbf{s}}({\theta})\right\|_{2}^{2}}. \end{array} $$

(37)

Fig. 7

Average SRR vs. jammer SNR, for: L2-PCA (MUSIC), optimal L1-PCA, calculated by means of Algorithm 2 in Fig. 3, and L1-PCA by means of Algorithm 3 in Fig. 4. For each estimator, we present the RMSE curves for p=0,.1,.2,.3,.4,.5. N=8,D=3,θ=− 41^∘,θ^′=24^∘, source SNR 2 dB

In Fig. 7, we plot SRR(Q_R,L2) (L2-PCA), SRR(Q_R,L1) (optimal L1-PCA), and SRR(Q_R,BF) averaged over 5000 realizations, for multiple values of p, versus the jammer SNR. We observe that, again, the performance of the optimal and heuristic L1-PCA calculators almost coincides for every value of p and jammer SNR. Also, we notice that under normal system operation (p=0) the spans of Q_R,L2,Q_R,L1, and Q_R,BF are equally good approximations to $\mathcal {S}_{R}$ and their respective SRR curves lie close (as close as the target SNR and the number of snapshots allow) to the benchmark of SRR(U), where U is an orthonormal basis for the exact $\mathcal {S}_{R}$. On the other hand, when half the snapshots are jammer corrupted (p=.5) both methods capture more of the interference. Similar to Fig. 6, for any jammer activation probability and over the entire range of jammer SNR values, the SRR attained by L1-PCA (both algorithms) is superior to that attained by conventional L2-PCA.

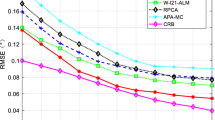
Next, we set D=4,N=10,θ=− 20^∘ and θ^′=50^∘. The source SNR is set to 5 dB. In Fig. 8, we plot the RMSE vs. jamming SNR performance attained by L2-PCA, RPCA⁵ (algorithm of [29]), and L1-PCA (proposed –computed by efficient Algorithm 3), all computed on the realified snapshots. We observe that for p = 0 (i.e., no jamming corruption) all methods perform well; in particular, L2-PCA and L1-PCA demonstrate almost identical performance of about 3^∘ RMSE. For jammer operation probability p>0, we observe that the proposed L1-PCA method outperforms clearly all counterparts, exhibiting from 5^∘ (for jammer SNR 6 dB) to 20^∘ (for jammer SNR 11 dB) lower RMSE.

Fig. 8

RMSE vs. jammer SNR, for: L2-PCA (MUSIC), RPCA [29], and L1-PCA by means of Algorithm 3 in Fig. (4). For each estimator, we present the RMSE curves for p=0,.2. N=10,D=4,θ=− 20^∘,θ^′=50^∘, source SNR 5 dB

In Fig. 9. we plot the RMSE attained by the three counterparts, this time fixing jamming SNR to 10 dB and varying the snapshot corruption probability p∈{0,.1,.2,.3,.4,.5,.6}. Once again, we observe that, for p=0 (no jamming activity), all methods perform well. For p>0, L1-PCA outperforms both counterparts across the board.

Fig. 9

RMSE vs. jammer operation probability p, for: L2-PCA (MUSIC), RPCA [29], and L1-PCA by means of Algorithm 3 in Fig. 4. N=10,D=4,θ=−20^∘,θ^′=50^∘, source SNR 5dB, jammer SNR 10 dB

Finally, in the study of Fig. 9, we measure the computation time expended by the three PCA methods, for p=0 and p=0.5. We observe that standard PCA, implemented by SVD, is the fastest method, with average computation time about 4·10⁻⁵ s, for both values of p. The computation time of RPCA is 1.5·10⁻² s for p = 0 and 1.9·10⁻² s for p=0.5. L1-PCA (Algorithm 3) computation takes, on average, 4.3·10⁻² s for both values of p, comparable to RPCA.⁶

5 Conclusions

We considered the problem of DoA estimation in the possible presence of unexpected, intermittent directional interference and presented a new method that relies on the L1-PCA of the recorded snapshots. Accordingly, we presented three algorithms (two optimal ones and one iterative/heuristic) for realified L1-PCA; i.e., L1-PCA of realified complex data matrices. Our numerical studies showed that the proposed method attains performance similar to conventional L2-PCA-based DoA estimation (MUSIC) in normal system operation (absence of jammers), while it attains significantly superior performance in the case of unexpected, sporadic corruption of the snapshots.

6 Appendix

6.1 Useful properties of realification

Lemma 1 below follows straightforwardly from the definition in (8).

Lemma 1

For any $\mathbf {A}, \mathbf {B} \in \mathbb {C}^{m \times n}$, it holds that $\overline {(\mathbf {A} + \mathbf {B})} = \overline {\mathbf {A}} + \overline {\mathbf {B}}$. For any $\mathbf {A} \in \mathbb {C}^{m \times n}$ and $\mathbf {B} \in \mathbb {C}^{n \times q}$, it holds that $\overline {(\mathbf {A} \mathbf {B})} = \overline {\mathbf {A}}\; \overline {\mathbf {B}}$ and $\overline {\left (\mathbf {A}^{\mathrm {H}} \right)} = \overline {\mathbf {A}}^{\top }$. ■

Lemma 2 below was discussed in [70] and [20], in the form of problem 8.6.4. Here, we also provide a proof, for the sake of completeness.

Lemma 2

For any $\mathbf {A} \in \mathbb {C}^{m \times n}, \text {rank}(\overline {\mathbf {A}}) =2~ \text {rank}(\mathbf {A})$. In particular, each singular value of A will appear twice among the singular values of $\overline {\mathbf {A}}$. ■

Proof

Consider a complex matrix $\mathbf {A} \in \mathbb {C}^{m \times n}$ of rank k≤ min{m,n} and its singular value decomposition $\mathbf {A} \overset {\text {SVD}}{=} \mathbf {U}_{m \times m} \mathbf {\Sigma }_{m \times n} \mathbf {V}_{n \times n}^{\mathrm {H}}$, where

$$\begin{array}{*{20}l} {\kern25pt}\boldsymbol \Sigma = \left[\begin{array}{cc} \mathbf{diag}(\boldsymbol \sigma) & \mathbf{0}_{k \times (n-k)} \\ \mathbf{0}_{(m-k) \times k} & \mathbf{0}_{(m-k) \times (n-k)} \end{array}\right] \end{array} $$

(38)

and $\boldsymbol \sigma \stackrel {\triangle }{=} [\sigma _{1}, \sigma _{2}, \ldots, \sigma _{k}]^{\top } \in \mathbb {R}_{+}^{k}$ is the length k vector containing (in descending order) the positive singular values of A. By Lemma 1,

$$\begin{array}{*{20}l} {\kern65pt}\overline{\mathbf{A}} = \overline{\mathbf{U}} \; \overline{\boldsymbol \Sigma} \; \overline{\mathbf{V}}^{\top} \end{array} $$

(39)

with $\overline {\mathbf {U}}^{\top } \overline {\mathbf {U}} = \overline {\mathbf {U}} \; \overline {\mathbf {U}}^{\top } = \mathbf {I}_{2m}$ and $\overline {\mathbf {V}}^{\top } \overline {\mathbf {V}} = \overline {\mathbf {V}} \; \overline {\mathbf {V}}^{\top } = \mathbf {I}_{2n}$. Define now, for every $a,b \in \mathbb {N}_{\geq 1}$, the ab×ab permutation matrix

$$\begin{array}{*{20}l} \mathbf{Z}_{a,b} \stackrel{\triangle}{=} \left[\mathbf{I}_{a} \otimes {\mathbf{e}_{1}^{b}},\; \mathbf{I}_{a} \otimes {\mathbf{e}_{2}^{b}},\; \ldots, \; \mathbf{I}_{a} \otimes {\mathbf{e}_{b}^{b}} \right]^{\top} \end{array} $$

(40)

where ${\mathbf {e}_{i}^{b}} \stackrel {\triangle }{=} [\mathbf {I}_{b}]_{:,i}$, for every i∈{1,2,…,b}. Then,

$$\begin{array}{*{20}l} \mathbf{Z}_{a,b}^{\top} \mathbf{Z}_{a,b} & = \sum\limits_{i=1}^{b} \left(\mathbf{I}_{a} \otimes \left({\mathbf{e}_{i}^{b}}\right)^{\top} \right)^{\top} \left(\mathbf{I}_{a} \otimes \left({\mathbf{e}_{i}^{b}}\right)^{\top} \right) \\ & = \mathbf{I}_{a} \otimes \left(\sum\limits_{i=1}^{b} {\mathbf{e}_{i}^{b}} \left({\mathbf{e}_{i}^{b}}\right)^{\top} \right) = \mathbf{I}_{a} \otimes \mathbf{I}_{b} = \mathbf{I}_{ab}. \end{array} $$

(41)

By (39),

$$\begin{array}{*{20}l} \overline{\mathbf{A}} & = \overline{\mathbf{U}} \mathbf{Z}_{2,m}^{\top} \mathbf{Z}_{2,m} \overline{\boldsymbol \Sigma} \mathbf{Z}_{2,n}^{\top} \mathbf{Z}_{2,n} \overline{\mathbf{V}}^{\top} \\ & = \left(\overline{\mathbf{U}} \mathbf{Z}_{2,m}^{\top}\right) \left(\mathbf{Z}_{2,m} (\mathbf{I}_{2} \otimes \boldsymbol \Sigma) \mathbf{Z}_{2,n}^{\top}\right) \left(\overline{\mathbf{V}} \mathbf{Z}_{2,n}^{\top}\right)^{\top} \\ & = \check{\mathbf{U}} \check{\boldsymbol \Sigma} \check{\mathbf{V}}^{\top} \end{array} $$

(42)

where $\check {\mathbf {U}} \stackrel {\triangle }{=} \overline {\mathbf {U}} \mathbf {Z}_{2,m}^{\top }, \check {\mathbf {V}} \stackrel {\triangle }{=} \overline {\mathbf {V}} \mathbf {Z}_{2,n}^{\top }$, and $\check {\boldsymbol \Sigma } \stackrel {\triangle }{=} \mathbf {Z}_{2,m} (\mathbf {I}_{2} \otimes \boldsymbol \Sigma) \mathbf {Z}_{2,n}^{\top }$. It is easy to show that $\check {\mathbf {U}}^{\top } \check {\mathbf {U}} = \check {\mathbf {U}} \check {\mathbf {U}}^{\top } = \mathbf {I}_{2m}, \check {\mathbf {V}}^{\top } \check {\mathbf {V}} = \check {\mathbf {V}} \check {\mathbf {V}}^{\top } = \mathbf {I}_{2n}$, and $\check {\boldsymbol \Sigma } = \boldsymbol \Sigma \otimes \mathbf {I}_{2}$. Therefore, (42) constitutes the standard (sorted singular values) SVD of $\overline {\mathbf {A}}$ and $\text {rank}(\overline {\mathbf {A}}) = 2k$. □

Lemma 3 below follows from Lemmas 1 and 2.

Lemma 3

For any $\mathbf {A} \in \mathbb {C}^{m \times n}, \| \mathbf {A}\|_{2}^{2} = \frac {1}{2}\| \overline {\mathbf {A}} \|_{2}^{2}$. ■

6.2 Proof of (14)

We commence our proof with the following auxiliary Lemma 4.

Lemma 4

For any matrix $\mathbf {A} \in \mathbb {C}^{m \times n}$, if $\mathbf {Q}_{real} \in \mathbb {R}^{2m \times 2l}, l < m \leq n$ is a solution to

$$\begin{array}{*{20}l} {\kern43pt}\underset{\mathbf{Q}\in\mathbb{R}^{2m \times 2l}, ~\mathbf{Q}^{\top}\mathbf{Q} = \mathbf{I}_{2l}}{\text{maximize}}~\| \overline{\mathbf{A}}^{\top} \mathbf{Q}\|_{2}. \end{array} $$

(43)

and $\mathbf {Q}_{comp.} \in \mathbb {C}^{m \times l}$ is a solution to

$$\begin{array}{*{20}l} {\kern43pt}\underset{\mathbf{Q}\in\mathbb{C}^{m \times l}, ~\mathbf{Q}^{\mathrm{H}}\mathbf{Q} = \mathbf{I}_{l} }{\text{maximize}}~\| {\mathbf{A}}^{\mathrm{H}} \mathbf{Q}\|_{2}, \end{array} $$

(44)

then $\mathbf {Q}_{{\text {real}}} \mathbf {Q}_{{\text {real}}}^{\top } = \overline {\left (\mathbf {Q}_{{\mathrm {comp.}}} \mathbf {Q}_{{\mathrm {comp.}}}^{\mathrm {H}}\right)} = \overline {\mathbf {Q}}_{{\mathrm {comp.}}}\vspace *{-2pt} \overline {\mathbf {Q}}_{{\mathrm {comp.}}}^{\top }$. ■

Proof

Orthonormal basis $[\check {\mathbf {U}}]_{:,1:2l}$, defined in the proof of Lemma 2 above, contains the 2l highest-singular-value left-singular vectors of $\overline {\mathbf {A}}$, and, thus, solves (43) [20]. Since the objective value in (43) is invariant to column permutations of the argument Q, any column permutation of $[\check {\mathbf {U}}]_{:,1:2l}$ is still a solution to (43). Next, we define the permutation matrix W_m,l=△[I_l, 0_l×(m−l)]^⊤ and notice that $[\check {\mathbf {U}}]_{:,1:2l} = \overline {\mathbf {U}} [\mathbf {I}_{2} \otimes {\mathbf {e}_{1}^{m}}, \mathbf {I}_{2} \otimes {\mathbf {e}_{2}^{m}}, \ldots, \mathbf {I}_{2} \otimes {\mathbf {e}_{l}^{m}}]$ is a column permutation of $\overline {\mathbf {U}} (\mathbf {I}_{2} \otimes \mathbf {W}_{m,l}) =\overline {\mathbf {U}} \; \overline {\mathbf {W}_{m,l}}$, which, by Lemma 1, equals $\overline {\left (\mathbf {U} \mathbf {W}_{m,l} \right)} = \overline {[\mathbf {U}]_{:,1:l}}$. Thus, $\overline {[\mathbf {U}]_{:,1:l}}$ solves (43) too. At the same time, by (39), [U]_:,1:l contains the l highest-singular-value left-singular vectors of A and solves (44) [20]. By the above, we conclude that a realification per (8) of any solution to (44) constitutes a solution to (43) and, thus, $\mathbf {Q}_{{\text {real}}} \mathbf {Q}_{{\text {real}}}^{\top } = \overline {\left (\mathbf {Q}_{{\mathrm {comp.}}} \mathbf {Q}_{{\mathrm {comp.}}}^{\mathrm {H}}\right)} = \overline {\mathbf {Q}}_{{\mathrm {comp.}}} \overline {\mathbf {Q}}_{{\mathrm {comp.}}}^{\top }$. □

By Lemmas 1, 3, and 4, (14) holds true.

6.3 Proof of (29)

We commence our proof by defining $d = |\mathcal {X}_{1}|$ and the sets ${\mathcal {X}_{A}^{c}} \stackrel {\triangle }{=} \{1, 2, \ldots, 2N \}\setminus \mathcal {X}_{A}$ (e.a.o.) and ${\mathcal {X}_{B}^{c}} \stackrel {\triangle }{=} \{1, 2, \ldots, 2N \}\setminus \mathcal {X}_{B}$ (e.a.o.) Then, we notice that

$$\begin{array}{*{20}l} {\kern43pt}[\mathbf{I}_{2N}]_{:,\mathcal{X}_{B}} = \mathbf{E}_{N} [\mathbf{I}_{2N}]_{:,\mathcal{X}_{A}} \mathbf{P}, \end{array} $$

(45)

where $\mathbf {P} \stackrel {\triangle }{=} \left [ -[\mathbf {I}_{2D-1}]_{:,d+1:2D-1}, ~[\mathbf {I}_{2D-1}]_{:,1:d} \right ]$. Similarly,

$$\begin{array}{*{20}l} {\kern43pt}[\mathbf{I}_{2N}]_{:,{\mathcal{X}_{B}^{c}}} = \mathbf{E}_{N} [\mathbf{I}_{2N}]_{:,{\mathcal{X}_{A}^{c}}} \mathbf{P}_{c}, \end{array} $$

(46)

where $\mathbf {P}_{c} \stackrel {\triangle }{=} \left [ -[\mathbf {I}_{2N- 2D+1}]_{:,N-d+1:2N-2D+1}, ~[\mathbf {I}_{2N- 2D + 1}]_{:,1:N-d} \right ]$. Then,

$$\begin{array}{*{20}l} {\kern13pt}[\!\overline{\mathbf{Y}}]_{:,\mathcal{X}_{B}}& = \overline{\mathbf{Y}} [\mathbf{I}_{2N}]_{:,\mathcal{X}_{B}} = \overline{\mathbf{Y}} \mathbf{E}_{N} [\mathbf{I}_{2N}]_{:,\mathcal{X}_{A}} \mathbf{P} \\ &= \mathbf{E}_{D} \overline{\mathbf{Y}} [\mathbf{I}_{2N}]_{:,\mathcal{X}_{A}} \mathbf{P} = \mathbf{E}_{D} [\!\overline{\mathbf{Y}}]_{:,\mathcal{X}_{A}} \mathbf{P}. \end{array} $$

(47)

Consider now $\mathbf {z} = \text {sgn}{([\mathbf {c}(\mathcal {X}_{A})]_{D})} \mathbf {E}_{D} \mathbf {c}(\mathcal {X}_{A})$. It holds that [z]_2D>0 and

$$\begin{array}{*{20}l} [\!\overline{\mathbf{Y}}]_{:,\mathcal{X}_{B}}^{T} \mathbf{z} &= \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}^{\top} [\!\overline{\mathbf{Y}}]_{:,\mathcal{X}_{A}}^{\top} \mathbf{E}_{D}^{\top} \mathbf{E}_{D} \mathbf{c}(\mathcal{X}_{A}) \\ &=\text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}^{\top} [\!\overline{\mathbf{Y}}]_{:,\mathcal{X}_{A}}^{\top} \mathbf{c}(\mathcal{X}_{A}) = \mathbf{0}_{2D}. \end{array} $$

(48)

Therefore, $\mathbf {z} = \mathbf {c}(\mathcal {B}) = \in \text {null} \left ([\!\overline {\mathbf {Y}}]_{:,\mathcal {X}_{B}}^{\top }\right) \cap \Omega _{2D}$ and, hence, (29) holds true.

6.4 Proof of Prop. 3

We begin by rewriting the maximization argument of (20) as

$$\begin{array}{*{20}l} \| \overline{\mathbf{Y}} \mathbf{B}\|_{*}^{2} &= \| \overline{\mathbf{Y}} \mathbf{B} \|_{2}^{2} + 2\sqrt{\text{det}\left(\mathbf{B}^{\top} \overline{\mathbf{Y}}^{\top} \overline{\mathbf{Y}} \mathbf{B}\right)} \\ &= \|\overline{\mathbf{Y}} \mathbf{b}_{1} \|_{2}^{2} + \|\overline{\mathbf{Y}} \mathbf{b}_{2} \|_{2}^{2} \\&\quad+ 2 \sqrt{ \|\overline{\mathbf{Y}} \mathbf{b}_{1} \|_{2}^{2}\|\overline{\mathbf{Y}} \mathbf{b}_{2} \|_{2}^{2} - \left(\mathbf{b}_{1}^{\top} \overline{\mathbf{Y}}^{\top} \overline{\mathbf{Y}} \mathbf{b}_{2}\right)^{2}}, \end{array} $$

(49)

where b₁ and b₂ are the first and second columns of B, respectively. Evidently, the maximum value attained at (17) is upper bounded as

$$\begin{array}{*{20}l} \underset{\mathbf{B} \in \{\pm 1\}^{2N \times 2}}{\text{max}}~\| \overline{\mathbf{Y}} \mathbf{B}\|_{*}^{2} & \leq \underset{\mathbf{b}_{1} \in \{\pm 1\}^{2N}, \mathbf{b}_{2} \in \{\pm 1\}^{2N}}{\text{max}}~ \|\overline{\mathbf{Y}} \mathbf{b}_{1} \|_{2}^{2}\\ & + \|\overline{\mathbf{Y}} \mathbf{b}_{1} \|_{2}^{2} + 2 {\|\overline{\mathbf{Y}} \mathbf{b}_{1} \|_{2} \|\overline{\mathbf{Y}} \mathbf{b}_{2} \|_{2} } \\ & = 4~\underset{\mathbf{b} \in \{\pm 1\}^{2N}}{\text{max}}~ \|\overline{\mathbf{Y}} \mathbf{b} \|_{2}^{2}. \end{array} $$

(50)

Considering now a solution b_opt to ${\text {maximize}}_{\mathbf {b} \in \{\pm 1\}^{2N \times 1}}~ \|\overline {\mathbf {Y}} \mathbf {b} \|_{2}^{2},$ and defining $\mathbf {b}_{\text {opt}}^{\prime } = \mathbf {E}_{N} \mathbf {b}_{\text {opt}}$, we notice that $\|\overline {\mathbf {Y}} \mathbf {b}_{\text {opt}}^{\prime } \|_{2}^{2} = \|\overline {\mathbf {Y}} \mathbf {E}_{N} \mathbf {b}_{\text {opt}} \|_{2}^{2} = \|\mathbf {E}_{D} \overline {\mathbf {Y}} \mathbf {b}_{\text {opt}} \|_{2}^{2} = \| \overline {\mathbf {Y}} \mathbf {b}_{\text {opt}} \|_{2}^{2}$ and $\mathbf {b}_{\text {opt}}^{\top } \overline {\mathbf {Y}}^{\top } \overline {\mathbf {Y}} \mathbf {b}_{\text {opt}}^{\prime } = \mathbf {b}_{\text {opt}}^{\top } \overline {\mathbf {Y}}^{\top } \overline {\mathbf {Y}} \mathbf {E}_{N} \mathbf {b}_{\text {opt}} = \mathbf {b}_{\text {opt}}^{\top } \overline {\mathbf {Y}}^{\top } \mathbf {E}_{D} \overline {\mathbf {Y}} \mathbf {b}_{\text {opt}} = 0.$ Therefore, $\| \overline {\mathbf {Y}}~\left [\mathbf {b}_{\text {opt}}, \mathbf {b}_{\text {opt}}^{\prime }\right ]\|_{*}^{2} = 4~ \|\overline {\mathbf {Y}} \mathbf {b}_{\text {opt}} \|_{2}^{2}$ and, in view of (50), [b_opt, E_Nb_opt] is a solution to (20).

6.5 Proof of (30)

By (29) and (46), it holds that

$$\begin{array}{*{20}l} [\!\overline{\mathbf{Y}}]_{:,{\mathcal{X}_{B}^{c}}}^{\top} \mathbf{c}(\mathcal{X}_{B}) &= \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} [\!\overline{\mathbf{Y}}]_{:,{\mathcal{X}_{A}^{c}}}^{\top} \mathbf{E}_{D}^{\top} \mathbf{E}_{D} \mathbf{c}(\mathcal{X}_{A}) \\ & = \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} [\!\overline{\mathbf{Y}}]_{:,{\mathcal{X}_{A}^{c}}}^{\top} \mathbf{c}(\mathcal{X}_{A}). \end{array} $$

(51)

Consider now some $\mathbf {b} \in \mathcal {B}(\mathcal {X}_{A})$ and define $\mathbf {b}^{\prime } \stackrel {\triangle }{=} \text {sgn}{([\mathbf {c}(\mathcal {X}_{A})]_{D})} \mathbf {E}_{N} \mathbf {b}$. By (46), (51), and the definition in (25), it holds that

$$ \begin{aligned} [\mathbf{b}^{\prime}]_{{\mathcal{X}_{B}^{c}}} &= [ \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{E}_{N} \mathbf{b}]_{{\mathcal{X}_{B}^{c}}} = \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} [\mathbf{I}_{2N}]_{:,{\mathcal{X}_{B}^{c}}}^{\top} \mathbf{E}_{N} \mathbf{b} \\ &=\text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} (\mathbf{E}_{N} [\mathbf{I}_{2N}]_{:,X_{A}} \mathbf{P}_{c})^{\top} \mathbf{E}_{N} \mathbf{b} \\ & = \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} [\mathbf{I}_{2N}]_{:,X_{A}}^{\top} \mathbf{b} = \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} [\mathbf{b}]_{:,X_{A}} \\ &= \text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} \text{sgn}([\!\overline{\mathbf{Y}}]_{:,X_{A}}^{\top} \mathbf{c}(\mathcal{A})) \\ &= \text{sgn}(\text{sgn}{([\mathbf{c}(\mathcal{X}_{A})]_{D})} \mathbf{P}_{c}^{\top} [\!\overline{\mathbf{Y}}]_{:,X_{A}}^{\top} \mathbf{c}(\mathcal{A})) \\ &= \text{sgn}([\!\overline{\mathbf{Y}}]_{:,{\mathcal{X}_{B}^{c}}}^{\top} \mathbf{c}(\mathcal{X}_{B})). \end{aligned} $$

(52)

Hence, b^′ belongs to $\mathcal {B}(\mathcal {X}_{B})$ and (30) holds true.