1 Introduction

In a recent paper [1], a low-complexity transformation was introduced, which is claimed to be a good approximation to the discrete cosine transform (DCT). We wish to evaluate this claim.

The introduced transformation is given by the following matrix:

$$\begin{array}{*{20}l} \mathbf{T} = \left[ \begin{array}{cccccccc} 1 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & -1 & -1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & -1 & -1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 \end{array} \right]. \end{array} $$

We aim at analyzing the above matrix and showing that it does not consist of a meaningful approximation for the 8-point DCT. In the following, we adopted the same methodology described in [2–11] which the authors also claim to employ.

2 Criticisms

2.1 Inverse transformation

The authors of [1] claim that inverse transformation T −1 is given by

$$\begin{array}{*{20}l} \frac{1}{2} \cdot \left[ \begin{array}{cccccccc} 1 & \phantom{-}0 & 0 & \phantom{-}0 & 1 & 0 & 0 & 0 \\ -1 & 1 & 0 & 0 & -1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & -1 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & -1 & 1 & 0 & 0 & 1 & -1 \\ 0 & 0 & 1 & 0 & 0 & 0 & -1 & 0 \\ -1 & 1 & 0 & 0 & 1 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \end{array} \right]. \end{array} $$

However, simple computation reveal that this is not accurate, being the actual inverse given by:

$$\begin{array}{*{20}l} \mathbf{T}^{-1} = \frac{1}{2} \cdot \left[ \begin{array}{cccccccc} 1 & \phantom{-}0 & 0 & \phantom{-}0 & 0 & 0 & 0 & 1 \\ -1 & 1 & 0 & 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & -1 & 1 & 1 & -1 & 0 & 0 \\ 0 & 0 & -1 & 1 & -1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0 \\ -1 & 1 & 0 & 0 & 0 & 0 & -1 & 1 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & -1 \end{array} \right]. \end{array} $$

2.2 Lack of DC component

The first point to be noticed is that the matrix T lacks a row of constant entries. Therefore, it is not capable of computing the mean value or the DC component of a signal under analysis. In terms of image compression, the DC value is the single most important coefficient concentrating most of the image energy. To illustrate this fact, Fig. 1 shows the reconstructed standard Lena image by means of (i) the DC component of the standard DCT, (ii) all DCT coefficients, except the DC component, (iii) the first row of matrix T [1], and (iv) all T coefficients, except the first row, respectively. In [12], Britanak meticulously cataloged dozens of DCT approximations; all of them computed the DC component. The lack of the DC component computation suggests that compressed images resulting from the application of T are expected to be severely degraded in terms of perceived image quality. The associated PSNR values in Fig. 1 also show the poor quality of the reconstructed images using T. Considering M×N pixel images, the PSNR measure is calculated by:

$$\begin{array}{*{20}l} {\text{PSNR}} = 10 \cdot \log_{10}{\left(\frac{{\text{MAX}}^{2}}{{\text{MSE}}}\right)}, \end{array} $$
Fig. 1
figure 1

Reconstructed Lena image based a only on the DC component of the DCT, b on all DCT transform coefficient except the DC component, c only on the first row of the T [1], and d on all T coefficients, except the first row

Full size image

where \(\text {MSE} = \frac {1}{M\cdot N} {\sum \nolimits }_{i=1}^{M}{\sum \nolimits }_{j=1}^{N} (a_{i,j} - b_{i,j})^{2}\), a i,j and b i,j are the (i,j)-th element of the original and reconstructed images, respectively; and MAX is the maximum pixel valye. For 8-bit greyscale images, MAX = 255.

2.3 Fast algorithm

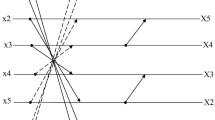
In the ‘Fig. 1’ of [1], the authors display a signal flow graph (SFG) which does not correspond to the computation implied by their proposed matrix. Their proposed SFG consists of two addition butterfly sections and one final permutation, which correspond to the following matrices, respectively:

$$\begin{array}{*{20}l} \mathbf{A}_{1} = \left[ \begin{array}{cccccccc} 1 & \phantom{-}0 & \phantom{-}0 & \phantom{-}0 & 0 & 0 & 0 & -1 \\ 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 0 & 1 & 0 & 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right], \end{array} $$
$$\begin{array}{*{20}l} \mathbf{A_{2}} = \left[ \begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \end{array} \right], \mathbf{P}=\left[\begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right]. \end{array} $$

However, this fast algorithm induces to the following matrix:

$$\begin{array}{*{20}l} {}\mathbf{P} \cdot \mathbf{A}_{2} \cdot \mathbf{A}_{1} = \left[ \begin{array}{cccccccc} 1 & \phantom{-}1 & \phantom{-}0 & \phantom{-}0 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & -1 & -1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & -1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & -1 & -1 \\ \end{array} \right] = \mathbf{T}_{\text{SFG}}, \end{array} $$

which is different from T. Therefore, the SFG is incorrect and does not correspond to the proposed matrix. We assume that the intended method is T SFG, which is the matrix implied by the fast algorithm. Indeed, this transformation is shown again in the schematics of the hardware realization of their work. Nevertheless, hereafter, we analyze both matrices: T and T SFG. Similar to T, the matrix T SFG does not evaluate the DC value, being subject to the criticism detailed in the previous subsection.

2.4 Lack of energy concentration

Contrary to the expected behavior for a data compression transformation, the matrix T does not exhibit good decorrelation and energy concentration properties. Energy concentration can be quantified by submitting data to a considered transformation and then computing the energy distribution along transform-domain coefficients. Thus, we considered a Monte Carlo simulation with 10,000 8-point input vectors modeled after the first-order Markov process with correlation coefficient of 0.95 [12]. For comparison, we considered the following transformations: the DCT [12], the SDCT [2] the BAS-2013 [9], and the BC-2012 [3]. Obtained mean values are displayed in Fig. 2. In clear contrast with the other methods, transformations T and T SFG perform very poorly.

Fig. 2
figure 2

Energy distribution of transform coefficients

Full size image

Moreover, the lack of energy concentration in the first transform coefficients indicates that the standard zigzag pattern employed in the quantization step is not adequate for this transformation. Nevertheless, the authors claim to employ the zigzag pattern with success. We could not verify this claim.

To further assess the claim of good coding capabilities, we considered the unified coding gain and the transform efficiency as measures to quantify the coding performance [12] of T in comparison with bona fide transforms, such as: DCT, SDCT [2], BAS-2008 [4], BAS-2009 [6], BAS-2010 [8], BAS-2011 [9], CB-2011 [13], and CB-2012 [3]. In addition, we also considered the transformation in [14] and transformation in [15]. Results are shown in Table 1. We emphasize in bold the unfavorable measurements associated to the transformations proposed by the authors. Such transformations are not expected to be suitable for image compression, since both coding measures resulted in very low values.

Table 1 Transform coding assessment
Full size table

2.5 Irreproducibility of results

The results shown by Dhandapani and Ramachandran could not be repeated. The authors state that they employ simultaneously a quantization step, which corresponds to variable bitrate encoding, and a fixed number of retained transform-domain coefficients, which suggests constant bitrate. This seems contradictory. However, to examine the transformation suggested by the authors, we adopted a constant bitrate encoding based on the retention of r transform-domain coefficients, as suggested originally by Haweel and others [2–11].

Although the authors do not explicitly inform the number of retained coefficients (r) in their computations. Only for high values of r we could obtain similar values. We calculated the PSNR values considering r=60. Notice that for such a high value of r data is practically not compressed. This is because only 4 coefficients are discarded, implying a compression rate of only 6.25%. Table 2 shows the results. Additionally, at low compression, most orthogonal transforms tend to behave similarly. However, even under this scenario, the transformation proposed by the authors performed poorly—roughly 10 dB lower PSNR measurements. Indeed, the pivotal character of a good transform is its behavior in a wide range of compression rates, specially at high compression. For instance, considering the more realistic case of r=10, as suggested in [2], we obtain the PSNR values shown in Table 3. Notice that the transformation proposed by the authors exhibits extremely high errors, which are emphasized in bold. We also report that the results linked to the transformations described in [14] and [15] display also acutely poor results as shown in Table 3.

Table 2 PSNR of reconstructed images (r=6w0)
Full size table
Table 3 PSNR of reconstructed images (r=10)
Full size table

In ‘Fig. 3’ of their work, the authors show reconstructed compressed images according to the following transformations: T SFG, CB-2012, and BAS-2011. All images showed high PSNR values with T SFG offering PSNR values greater than 41 dB. We could no reproduce these results. The authors does not detail the employed parameters, in particular the value of r. However, for r=45, we could obtain comparable PSNR measurements in terms of the traditional DCT approximations. Considering T or T SFG the image degradation is very high, as shown in Fig. 3. For r=15, a more realistic value, we obtain the images shown in Fig. 4. Images associated to T or T SFG are severely degraded—roughly 25–30 dB lower than the typical values offered by traditional approximations. These results are evidence that the transformation proposed by the authors is not suitable for image compression.

Fig. 3
figure 3

Reconstructed images for r=45. a T (PSNR=23.743), b T SFG (PSNR=24.244), c CB-2012 (PSNR=36.977), d BAS-2011 (PSNR=39.835), e T (PSNR=23.350), f T SFG (PSNR=22.926), g CB-2012 (PSNR=34.782), h BAS-2011 (PSNR=37.152), i T (PSNR=23.512), j T SFG (PSNR=23.653), k CB-2012 (PSNR=29.913), l BAS-2011 (PSNR=31.298), m T (PSNR=22.282), n T SFG (PSNR=22.184), o CB-2012 (PSNR=36.785) and p BAS-2011 (PSNR=40.433)

Full size image
Fig. 4
figure 4

Reconstructed images for r=15. a T (PSNR=8.572), b T SFG (PSNR=8.578), c CB-2012 (PSNR=27.500), d BAS-2011 (PSNR=31.271), e T (PSNR=8.231), f T SFG (PSNR=8.239), g CB-2012 (PSNR=25.777), h BAS-2011 (PSNR=28.602), i T (PSNR=9.274), j T SFG (PSNR=9.281), k CB-2012 (PSNR=24.116), l BAS-2011 (PSNR=25.275), m T (PSNR=5.711), n T SFG (PSNR=5.715), o CB-2012 (PSNR=26.201) and p BAS-2011 (PSNR=29.152)

Full size image

Authors also show in ‘Fig. 4’ of their paper a curve relating PSNR measurements of compressed images to the parameter r. We could not reproduce their results. Figure 5 shows the curves that we obtained considering the same images as the authors. Our results are compatible to the computations independently found in [2, 4–11]. The curves associated to T and T SFG indicate a significantly lower performance. For r<25—a more realistic scenario—the PSNR loss compared to the traditional transformations is roughly 20 dB. Such evidence points towards the ineffectiveness of T and T SFG for image compression.

Fig. 5
figure 5

PSNR measurements in terms of the number of retained coefficients r for selected standard images. a Lena, b Cameraman, c Barbara and d Mandrill

Full size image

3 Conclusion

The transformation proposed in [1] performs poorly when compared to archived DCT approximations. The results in [1] could not be reproduced and some corrections are supplied for the benefit of community.